Numerical simulation study of the effect of coal dust on gas explosion overpressure

Abstract

A numerical simulation study was conducted using Ansys Fluent 2023 R1 simulation software to investigate the influence of coal dust on the overpressure of gas explosion. The results demonstrated that the reliability of the selected mathematical model was validated through comparisons across three data sources: (1) experimental data from a gas and coal dust explosion propagation test system, (2) experimental results from full-scale mine roadway tests reported in the literature, and (3) the current numerical simulation outcomes. Based on elemental and industrial analyses, the stoichiometric concentration for various coal dust explosions was determined, and a formula was established to calculate the actual mass concentration of coal dust participating in the explosion process. A conversion relationship between the equivalent ratio and the mass concentration of coal dust was developed for different coal types. The equivalent ratio is defined as the ratio of the stoichiometric air–fuel ratio to the actual air–fuel ratio, used to quantify whether reactants are in excess or deficiency. When the equivalence ratio Φ equals 1, the methane volume concentration is 9.5%. If the methane volume concentration is below this stoichiometric level, the addition of a small amount of coal dust enhances the explosion intensity. Conversely, when the methane concentration is equal to or exceeds the stoichiometric value, coal dust exerts an inhibitory effect on the gas explosion. When varying concentrations of fat coal dust were introduced into explosions with 7.5% methane, the maximum explosion pressure occurred at a coal dust concentration of 200 g/m³. At Φ = 1, the stoichiometric mass concentration of fat coal dust was calculated as 107.2 g/m³; however, the actual amount of coal dust involved in the reaction did not reach this theoretical value, indicating that the equivalent ratio-based concentration exceeded the stoichiometric concentration. When 7.5% methane reacted with oxygen, the residual oxygen could only support combustion corresponding to a stoichiometric coal dust concentration of approximately 29.7 g/m³, meaning that only about 29.7 g/m³ of the 200 g/m³ fat coal dust participated in the explosion. Under conditions of 7.5% gas concentration and 200 g/m³ coal dust concentration, smaller coal dust particle sizes resulted in higher explosion pressures. Furthermore, under identical experimental conditions, as the degree of coal metamorphism decreased—from lean coal to coking coal, fat coal, gas coal, and finally lignite—the peak overpressure of the gas–coal dust coupled explosion increased sequentially, indicating a negative correlation between explosion overpressure and the degree of coal metamorphism.

Introduction

Despite the substantial efforts and resources invested globally to enhance coal mine production safety, coal mine accidents continue to occur with regrettable frequency in recent years. Among these accidents, gas and coal dust explosions are particularly prominent, which is one of the main types of thermodynamic disasters in coal mines, and the high temperature, high pressure and toxic and harmful gases generated at the moment of the explosion pose a serious threat to the safety of the lives of the people underground as well as the safety of the mine equipment¹. The coupled explosion phenomenon of gas and coal dust, compared with a single methane explosion or coal dust explosion, its accident-causing factors are more intricate and complex. In view of this, in-depth investigation of the influence of coal dust on the characteristics of gas explosion is of great practical significance.

In recent years, many scholars at home and abroad have carried out a large number of studies on the characteristics of gas-coal-dust coupled explosion. Cashdollar² using 20 L ball explosive device, the dust explosion of pulverized coal under various particle size distribution conditions is systematically analyzed, and the important influence of particle size distribution on explosion characteristics is revealed. Jensen³ conducted a series of explosion tests on the mixture of methane and coal dust, and the study showed that the presence of methane, the increase of volatiles of coal dust, the refining of coal dust particles and the enhancement of ignition energy would jointly reduce the lower explosive limit of the mixture. Eckhoff⁴ explored in depth how particle size dispersion, dust cloud polymerization degree, dust cloud concentration and turbulence affect the intensity of the explosion. Sun et al.^5,6 conducted a detailed analysis of particle dispersion during dust explosion to reveal its specific impact on dust explosion characteristics. Wang et al.⁷ analyzed the influence of coal dust particle size on gas and coal dust explosion, and found that in mixed coal dust, when the particle size becomes smaller, the maximum explosion pressure and flame propagation speed both show an increasing trend. Zhang⁸ mainly discussed how factors such as methane concentration and coal dust particle size affect the maximum explosion pressure and its rise rate caused by the mixed explosion of methane and coal dust. Pu et al.⁹ experimental results reveal the important effects of dust turbulence intensity, dust particle size and concentration, ignition energy and mode on the dust flame acceleration process. The changes of these parameters directly determine the speed and intensity of flame propagation. Pei et al.¹⁰ conducted an experimental study on the accelerating characteristics of the composite flame and pressure changes during the initial stage of gas and coal dust explosions in a 20 L sphere. Liu et al.¹¹ a 20-liter spherical explosive device was used to conduct an in-depth analysis of the explosion characteristics of coal dust with different metamorphic degrees. The experimental results showed that under the condition of optimal coal dust concentration, the maximum explosion pressure of coal dust was negatively correlated with its metamorphic degree. Lin et al.^{12,13,14,15,16,17} conducted an in-depth study on the composition characteristics of post-explosion solids under the coexistence of coal dust and gas and coal dust by means of explosive ball device and horizontal pipe explosion test device. Their study revealed an obvious trend: In the solid residue after coal dust explosion, the content of combustible components such as volatile and fixed carbon decreased significantly, while the content of ash increased significantly, which was affected by many factors such as coal dust concentration, coal dust particle size and ignition energy. Mishra et al.¹⁸ studied the effect of particle size on the minimum ignition temperature and explosion process of coal dust clouds. Li et al.¹⁹ conducted an experimental study on the effect of particle size and particle size dispersion on the explosion characteristics of pulverised coal dust using a 20 L explosive container. Wang²⁰ used 20 L spherical explosive device for coal dust explosion experiments, the experimental results show that the explosive power of coal dust with the increase in the dispersion of coal dust particle size decreases. Liu et al.^21,22,23,24 research shows that the degree of coal metamorphism affects the minimum ignition temperature, the lower the degree of metamorphism, the easier the coal dust is to ignite, the greater the risk, the more intense the flame diffusion and propagation, and the farther the propagation distance. Li et al.²⁵ used a small-scale glass tube coal dust explosion test device to analyse the influencing factors of the flame propagation characteristics of coal dust with different degrees of deterioration during the explosion process, and the results of the study showed that the combustible volatile gases released from low-deteriorated coal in the combustion process not only prolonged the flame duration, i.e., the flame period, but also significantly increased the length of the flame. Ajrash et al.^{26,27,28,29,30,31,32,33} investigated the relationship between coal quality indexes of coal dust and the minimum ignition temperature and flame length of coal dust, and found that the correlation analysis revealed that the coal quality indexes were highly correlated with the minimum ignition temperature and flame length, and that volatile matter had the greatest influence on the minimum ignition temperature and flame length of coal dust. length. Based on the chemical element composition of coal, Andrews et al.^34,35,36,37 regarded coal as an equivalent molecule composed of carbon, hydrogen, oxygen, nitrogen, sulfur, etc., and assumed that coal dust could completely react with air to generate CO₂, NO₂, H₂O and SO₂, and derived the equivalent ratio of coal dust explosion.

In summary, previous studies have extensively investigated gas and coal dust explosions, identifying and analyzing the key characteristic parameters that influence explosion behavior. However, few studies have derived the equivalent chemical molecular formula of coal dust based on both industrial and elemental analyses, nor have they quantitatively examined how gas concentration, coal dust concentration, and other factors affect explosion pressure through the stoichiometric and equivalence ratio concentrations. To address these gaps, this study employs a large-scale tunnel model with dimensions of 4 m in width, 3 m in height, and 100 m in length to simulate the impact of coal dust on gas explosion characteristics. The equivalent chemical molecular formula of coal dust is determined using industrial and elemental analysis data, and both the stoichiometric and equivalence ratio concentrations are calculated to enable a quantitative analysis of how variations in gas and coal dust concentrations influence explosion pressure. The findings of this research aim to provide a solid theoretical foundation and technical support for the prevention and control of gas and coal dust explosion disasters.

Experimental and numerical simulation studies on gas and coal dust explosions

Experimental research on gas and coal dust explosions

Experimental system

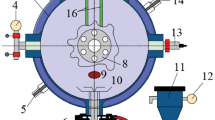
The relevant experiments were conducted using a self-developed 5 L pipeline explosion test apparatus, as illustrated in Fig. 1. The experimental system comprises a transparent quartz glass pipeline fixed with steel plates, a powder spraying system, an ignition system, an image acquisition system, and a control system. The explosion pipeline is constructed from acrylic material, allowing for visual observation during the experiment. It features a square cross-section with a side length of 100 mm and a height of 500 mm, capable of withstanding explosion pressures up to 2 MPa. At the bottom of the quartz glass pipeline, a powder spraying device and an ignition electrode are installed. The powder spraying device utilizes high-pressure gas to uniformly disperse the powder into the pipeline, forming a well-distributed dust cloud. To prevent dust leakage during the experiment, the top of the pipeline is sealed with a PVC film that has relatively low pressure resistance. The ignition electrode is a high-energy igniter manufactured by Xi’an Shuntai Thermal Engineering and Electrical Equipment Co., Ltd., delivering an output voltage of 6 kV and generating an electric spark with an energy of approximately 30 J. A CYG1406G type pressure sensor was used, with a measurement range of -0.1 MPa to 0.1 MPa and an accuracy class of 0.25. Prior to the formal experiments, preliminary tests were conducted to optimize the powder spraying pressure, spraying duration, and ignition delay time, ensuring uniform dust cloud distribution at the moment of ignition. Consequently, the optimal parameters were determined as follows: a powder spraying pressure of 0.2 MPa, a spraying duration of 500 ms, and an ignition delay of 100 ms after the completion of powder spraying. Considering the inherent randomness in dust distribution within the pipeline, each test group was repeated at least three times, and the most consistent results were selected for analysis to minimize experimental errors caused by dust dispersion variability.

Fig. 1

5 L pipeline explosion test device.

Experimental materials

The coal dust used in the experiment was sourced from the No. 10 Mine of Pingdingshan. It is a type of coking coal characterized by relatively high volatile matter content and consistent explosive properties, making it suitable for the study. The chemical composition of the coal dust is presented in Table 1. Methane with a purity of 99.9% was used as the gaseous fuel in the experiment. Prior to testing, the coal powder was dried in a vacuum drying oven at 60 °C for 12 h to eliminate the influence of environmental humidity.

Table 1 Analysis of coal dust components.

Experimental results

The pressure sensor is positioned at the geometric center of the cross-section, 250 mm above the bottom of the 5 L pipeline explosion test device, and continuously records pressure variations at this measurement point. Figure 2 presents the overpressure variation curves at this location under two experimental conditions—5.5% methane and 7.5% methane—both combined with a coal dust concentration of 100 g/m³, plotted as functions of time during the explosion process.

Fig. 2

Overpressure curve with time under different concentration conditions.

As shown in the figure, the explosion shock wave generated by the ignition and combustion of methane and coal dust results in zero overpressure at the measurement point before the wave reaches it. Upon arrival of the shock wave, the overpressure at this location increases rapidly. After reaching its peak value, the overpressure drops sharply, then rises again to a second peak before declining once more. This oscillatory behavior continues until the overpressure gradually approaches zero. When the explosion occurs, the shock wave propagates toward the monitoring point, causing the overpressure there to begin rising. The intense chemical reaction between methane and oxygen continuously supplies energy to sustain the propagation of the shock wave, leading to a continuous increase in overpressure. When the overpressure reaches its maximum at the monitoring point, it exceeds that of the surrounding area, forming a pressure gradient. This gradient causes the air at the measurement point to transition from a compressed state to an expanding one, resulting in a subsequent pressure drop. As the pressure continues to decrease and becomes lower than that of the surrounding region, the air at the measurement point is compressed again, leading to another rise in overpressure. This cycle of compression and expansion repeats, causing the observed oscillations in overpressure. With each cycle, energy is dissipated, gradually reducing the amplitude of oscillation until the overpressure stabilizes near the ambient pressure.

Mathematical model

Continuous phase flow field models

The flow field generated by the methane-coal dust explosion is inherently turbulent, and the turbulence characteristics are analyzed using large eddy simulation (LES) in the numerical simulation. In LES, the Navier-Stokes (N-S) equations are filtered through the Favre filtering approach. The core concept of this method involves applying three-dimensional spatial filtering to pressure and density terms, while employing density-weighted averaging for all other variables. The density-weighted average of a variable is expressed as:

$$\:\tilde{\varnothing\:}=\frac{\overline{\rho\:\varnothing\:}}{\overline{\rho\:}}$$

(1)

.

where “~” denotes density-weighted averaging; “-” denotes three-dimensional spatial filtration with filter size$\:\:\varDelta\:={(\varDelta\:\text{x}\varDelta\:\text{y}\varDelta\:\text{z})}^{\frac{1}{3}}$。

After processing the N-S equations in the above filtering manner, the large eddy simulation control equations are obtained as follows:

• (1) Mass conservation Equation 

  $$\:\frac{\partial\:\overline{\rho\:}}{\partial\:t}+\frac{\partial\:}{\partial\:{x}_{i}}\left(\overline{\rho\:}{\tilde{u}}_{i}\right)={\tilde{S}}_{m}$$

  (2)

  where $\:\rho\:$ is the fluid density, kg/m³; t is the time, s;$\:\:{x}_{i}$ is the spatial coordinate in the i-direction;$\:\:{u}_{i}$is the velocity in the direction of the i-coordinate, m/s; and $\:{S}_{m}$ is the mass of the continuous phase added from the particle phase, kg/m³ s.

• (2) Conservation of momentum Equation 

  $$\:\frac{\partial\:}{\partial\:t}\left(\overline{\rho\:}{\tilde{u}}_{i}\right)+\frac{\partial\:}{\partial\:{x}_{j}}\left(\overline{\rho\:}{\tilde{u}}_{j}{\tilde{u}}_{i}\right)\frac{\partial\:}{\partial\:{x}_{j}}\left[\overline{\rho\:}\left(\overline{{u}_{i}{u}_{j}}-{\tilde{u}}_{i}{\tilde{u}}_{j}\right)\right]=-\frac{\partial\:\overline{\rho\:}}{\partial\:{x}_{i}}+\frac{\partial\:{\tilde{\tau\:}}_{ij}}{\partial\:{x}_{j}}+\overline{\rho\:}{\tilde{f}}_{i}$$

  (3)

  where $\:{u}_{j}$is the velocity in the j-coordinate direction, m/s; $\:p$ is the pressure, p.a.;$\:\:{\tau\:}_{ij}$ is the viscous force tensor, W/m.K; and $\:{f}_{i}$ is the volume force in the i-direction, N.

• (3) The conservation of energy equation

  $$\:\frac{\partial\:}{\partial\:t}\left(\overline{\rho\:}\tilde{E}\right)+\frac{\partial\:}{\partial\:{x}_{i}}\left(\overline{\rho\:}\tilde{E}{\tilde{u}}_{i}\right)\frac{\partial\:}{\partial\:{x}_{i}}\left[\overline{\rho\:}\left(\overline{{u}_{i}E}-\tilde{u}\tilde{E}\right)\right]=-\frac{\partial\:}{\partial\:{x}_{i}}\left(\overline{p}{\tilde{u}}_{i}\right)+\frac{\partial\:}{\partial\:{x}_{i}}\left(K\frac{\partial\:\tilde{T}}{\partial\:{x}_{i}}\right)+\frac{\partial\:}{\partial\:{x}_{i}}\left({\tilde{u}}_{j}{\tilde{\tau\:}}_{ij}\right)+\overline{\rho\:}{\tilde{f}}_{i}{\tilde{u}}_{i}+{\tilde{S}}_{h}$$

  (4)

  Where $\:E$ is the energy per unit mass of fluid, J/kg;$\:\:K$ is the thermal conductivity; $\:T$ is the temperature, k; and $\:{S}_{h}$ is the chemical reaction source term, W kg/m³ mol.

• (4) Component mass conservation Equation 

  $$\:\frac{\partial\:}{\partial\:t}\left(\overline{\rho\:}{\tilde{m}}_{l}\right)+\frac{\partial\:}{\partial\:{x}_{i}}\left(\overline{\rho\:}{\tilde{u}}_{i}{\tilde{m}}_{l}\right)+\frac{\partial\:}{\partial\:{x}_{i}}\left[\overline{\rho\:}\left(\overline{{u}_{i}{m}_{l}}-\tilde{u}{\tilde{m}}_{l}\right)\right]=\frac{\partial\:}{\partial\:{x}_{i}}\left({D}_{l}\frac{\partial\:{\tilde{m}}_{l}}{\partial\:{x}_{i}}\right)+{\tilde{R}}_{i}+{\tilde{S}}_{i}$$

  (5)

  Where$\:\:{m}_{l}$ is the mass fraction of each component; $\:{D}_{l}$is the diffusion coefficient; $\:{R}_{i}$is the net rate of chemical reaction to produce component i, kg/m³ s; and $\:{S}_{i}$is the rate created by other sources, kg/m³ s.

Mathematical modelling of methane combustion explosions

A vortex dissipation model was used to simulate methane combustion as follows:

$$\:{R}_{i,r}=\text{min}({{R}_{i,r}}^{\left(R\right)},{{R}_{i,r}}^{\left(P\right)})$$

(6)

$$\:{{R}_{i,r}}^{\left(R\right)}=\left({v}_{i,r}^{{\prime \prime\:}}-{v}_{i,r}^{{\prime\:}}\right){M}_{w,i}A\rho\:\frac{\epsilon\:}{k}{min}_{R}\left[\frac{{Y}_{R}}{{v}_{R,r}^{{\prime\:}}{M}_{w,R}}\right]$$

(7)

$$\:{{R}_{i,r}}^{\left(P\right)}=\left({v}_{i,r}^{{\prime \prime\:}}-{v}_{i,r}^{{\prime\:}}\right){M}_{w,i}AB\rho\:\frac{\epsilon\:}{k}\left[\frac{\sum\:_{P}{Y}_{P}}{\sum\:_{j}^{N}{v}_{j,r}^{{\prime \prime\:}}{M}_{w,j}}\right]$$

(8)

.

where$\:{\:v}_{i,r}^{{\prime\:}}$ and $\:{v}_{i,r}^{{\prime \prime\:}}$ denote the chemical correction coefficients for the reaction and production of component i in the rth reaction; $\:{M}_{w,i}$ denotes the molecular weight of substance i; $\:{Y}_{R}$ denotes the mass fraction of the reactant; $\:{Y}_{P}$denotes the mass fraction of the product; A and B are empirical constants taken as 4.0 and 0.5, respectively; and N denotes the number of the chemical components in the system.

When a large eddy simulation turbulence model is used, the turbulent mixing rate ε/k will be replaced by a sub-grid scale mixing rate, which is calculated as follows:

$$\:{{\tau\:}^{-1}}_{sgs}=\sqrt{2{S}_{ij}{S}_{ij}}$$

(9)

.

where $\:{{\tau\:}^{-1}}_{sgs}$denotes the subgrid scale mixing rate; $\:{S}_{ij}$ denotes the strain rate tensor.

Mathematical modelling of particle phase simulation

The discrete phase model (DPM) used for the particle phase predicts the trajectory of the discrete phase particles by integrating the force balance on the particles, which is represented by a Lagrangian reference system.

The force balance equations for the coal dust particles are:

$$\:\frac{\text{d}{u}_{p}}{\text{d}\text{t}}={F}_{D}\left(u-{u}_{p}\right)+\frac{{g}_{x}\left({\rho\:}_{p}-\rho\:\right)}{{\rho\:}_{p}}+{F}_{x}$$

(10)

.

Where $\:u$ is the fluid phase velocity, m/s; $\:{u}_{p}$ is the particle settling velocity, m/s; $\:\rho\:$ is the fluid density, kg/m³; $\:\:{\rho\:}_{p}$is the particle density, kg/m³; $\:g$ is the gravitational acceleration, m/s²; $\:{F}_{D}$is the drag force acting on the particle, N; $\:{F}_{x}$ is the other forces acting on the particle, N.

The combustion of coal dust is modelled as:

$$\:\begin{array}{c}{v}_{coal,A}=-{S}_{coal}\overline{A}\text{exp}\left(-\frac{E}{RT}\right){d}_{coal}^{\frac{3}{2}}{Y}_{coal}{Y}_{{o}_{2}}^{\frac{1}{2}}\end{array}$$

(11)

$$\:\begin{array}{c}{v}_{coal,T}={C}_{EBU}\frac{k}{\epsilon\:}\text{min}\left({Y}_{coal},{Y}_{{o}_{2}},{Y}_{{co}_{2}}\right)\end{array}$$

(12)

$$\:\begin{array}{c}{v}_{coal}=min\left|{v}_{coal,A},{v}_{coal,T}\right| \end{array}$$

(13)

Where $\:{S}_{coal}$ is the specific surface area of coal particles, m²;$\:\:\overline{A}$is the pre-exponential factor, ($\:{{m}^{3}\text{k}\text{g}）}^{\frac{1}{2}}\text{s}$;E is the activation energy, J/mol. R is the universal gas constant, 8.314 J/mol$\:\text{k}$; d_coal is the diameter of coal particles, m;$\:\:{Y}_{coal}$is the mass fraction of coal dust; $\:{C}_{EBU}$ is the correction factor; $\:{Y}_{{o}_{2}}$is the mass fraction of $\:{o}_{2}$; and $\:{Y}_{{co}_{2}}$ is the mass fraction of $\:{co}_{2}$.

Coal dust volatilisation was analysed using a two-step competitive reaction rate model with the volatilisation analysis rate equation shown below:

$$\:\frac{{m}_{v\left(t\right)}}{{m}_{p,0}-{m}_{\alpha\:}}={\int\:}_{0}^{t}{(\alpha\:}_{1}{R}_{1}+{\alpha\:}_{2}{R}_{2})\text{exp}\left[-{\int\:}_{0}^{t}{(R}_{1}+{R}_{2}){d}_{t}\right]{d}_{t}$$

(14)

.

where $\:{R}_{1}$ and $\:{R}_{2}$control the competitive rate of volatilisation in different temperature ranges; $\:{m}_{v\left(t\right)}$ is the volatilisation time; $\:{m}_{p,0}$ is the initial particle mass at the time of injection; $\:{m}_{\alpha\:}$ is the ash content of the pulverised coal particles; $\:{\alpha\:}_{1}$ is the rate of volatilisation at low temperatures, with a default of 0.3; and $\:{\alpha\:}_{2}$ is the rate of volatilisation at high temperatures, with a default of 1.

Coke surface combustion reaction rate expression:

$$\:\begin{array}{c}\frac{d{m}_{p}}{dt}=-{A}_{P}{P}_{OX}\frac{{D}_{0}R}{{D}_{0}+R} \end{array}$$

(15)

Where $\:{A}_{P}$is the surface area of the particles,$\:\:{\uppi\:}{dp}^{2}$; $\:{P}_{OX}$ is the partial pressure of the oxidant in the gas surrounding the combustion particles; R is the kinetic rate, which includes the effect of the chemical reaction on the diffusion on the inner surface and pores of the coke particles; and $\:{D}_{0}$ is the diffusion rate coefficient.

Verification of numerical simulation method of small-scale gas and coal dust explosion propagation

Physical modelling

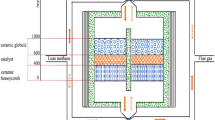
To validate the accuracy of the numerical calculation method employed in the constructed mathematical model, a full-scale physical model (1:1 ratio) was developed based on the actual dimensions of the experimental platform. The coal dust concentration was set to 100 g/m³, while methane concentrations were configured at 5.5% and 7.5%, respectively. The filling length was maintained at 500 mm. As illustrated in Fig. 3.

Fig. 3

5 L pipeline explosion experimental device model diagram.

Initial and boundary conditions

Initial conditions

① The initial pressure p₀ in the calculation area is set to p₀ = 0 with respect to atmospheric pressure;

② Calculate the initial temperature in the region T₀ = 300k;

③ Calculate the initial velocity of the gas in the region as V0 = 0;

④ Calculate the region filled with air.

Boundary conditions

① The opening is set as the pressure outlet, and the pressure outlet is set to 0 relative to atmospheric pressure;

② The lower end of the explosion chamber is a fully sealed boundary. Both this sealed end and the remaining pipe wall surfaces are defined as non-slip, rigid, and adiabatic boundaries, indicating that heat exchange and energy loss between the fluid flow and the walls are neglected in the simulation. The wall temperature is fixed at 300 K.

Comparison between numerical calculation results and experimental results

To validate the accuracy of the numerical calculation method used in the developed mathematical model, a verification process was carried out. The three-dimensional geometric model, as illustrated in Fig. 3, was constructed based on experimental data from a previous 5 L pipeline gas-dust explosion propagation study. The model was discretized into an appropriate mesh for numerical simulation. A monitoring point was placed at the geometric center of the cross-section located 250 mm from the closed end, and ignition was initiated using a localized high-temperature zone (patch method). Figure 4 displays the time-dependent variation of explosion shock wave overpressure at the monitoring point. In this figure, the solid line represents the results from the numerical simulation, while the dashed line corresponds to the outcomes of the laboratory experiments.

Fig. 4

Comparison curve between experimental value and numerical simulation value of 5 L pipeline explosion.

The overpressure curve obtained through numerical simulation exhibits a shape that is consistent with the experimentally measured curve, and the overall trend of shock wave overpressure rise and decay aligns well between the two methods. Regarding the peak overpressure values, the numerical simulation yields higher results than those observed in the experiments under both test conditions. The relative errors under these two conditions are 7.04% and 6.66%, respectively. Nevertheless, the simulated maximum overpressure remains generally consistent with the experimental data, which confirms the reliability of the combustion model based on the large eddy simulation (LES) turbulence model combined with the eddy dissipation model (EDM).

Validation of numerical simulation method for mine scale gas and coal dust explosion propagation.

Physical modelling

In order to verify the correctness of the numerical calculation method of the constructed mathematical model, it is necessary to verify the mathematical model of this paper. According to the experimental results of the gas coal dust explosion propagation experiment carried out by previous scholars³⁸ as an experimental sample, according to which the three-dimensional geometric model shown in Fig. 5 is constructed and meshed, the pipeline model is 160 m long, with a section cross-sectional area of 7.2 m²and numerical simulation is carried out for the solution. In 20 m, 30 m, 40 m, 60 m, 80 m, 100 m, 120 m, 140 m, 160 m from the closed end of the set 9 monitoring points (monitoring points are located in the pipeline wall), and the use of patch high temperature zone way to achieve ignition.

Fig. 5

Mine scale model diagram.

Initial and boundary conditions

Same as 1.3.2.

Comparison between numerical calculation results and experimental results

Through the simulation can be obtained by the explosion shock wave propagation process from the closed end of 20 m, 30 m, 40 m, 60 m, 80 m, 100 m, 120 m, 140 m, 160 m at the overpressure value, and with the experimental overpressure value for comparison, as shown in Fig. 6.

Fig. 6

Comparison chart of experimental data and numerical simulation data.

As shown in Fig. 6, the maximum relative error between the simulated and experimental values is 14.81%, while the minimum relative error is 5.26%. The peak overpressure values obtained through numerical simulation are generally consistent with the experimental results, which confirms the reliability of the combustion models based on the large eddy simulation (LES) and eddy dissipation model (EDM). However, the pressure values from the simulation are generally higher than those observed in the experiments. This discrepancy primarily arises from the idealized initial and boundary conditions used in the numerical simulation, where the roadway is assumed to be smooth and adiabatic. In contrast, the actual experimental roadway closely resembles real mine roadway walls, which are rough and non-adiabatic. Therefore, neglecting wall thermal effects and surface roughness leads to differences between simulated and experimental results. Nevertheless, the relative discrepancies remain within an acceptable range, indicating that the numerical simulation achieves a reasonable level of accuracy for quantitative analysis of the explosion process.

The effect of coal dust on the explosive overpressure of a gas explosion

Gas and coal dust explosion stoichiometric ratios

Industrial and elemental analysis of coal samples

Five coal samples were selected for this study, including lignite, gas coal, fat coal, coking coal, and poor coal, which collectively represent all major categories of coal. The industrial and elemental compositions of these selected coal samples are summarized in Table 2.

Table 2 Industrial and elemental analyses of different coal samples.

Gas and coal dust explosion stoichiometric ratio

In combustion and explosion processes, the equivalence ratio, often referred to as the “fuel coefficient,” is defined as the ratio of the stoichiometric air-fuel ratio to the actual air-fuel ratio, and is denoted by the symbol Φ. Theoretical combustion occurs when the fuel in a mixture is completely reacted with the available oxygen in the air, leaving no residual oxygen or unburned fuel. In other words, the value of Φ reflects the relative proportions of fuel and oxidizer (oxygen) in a combustible mixture.

$$\:\begin{array}{c}\varPhi\:=\frac{{\left(A/F\right)}_{stoic}}{\left(A/F\right)}=\frac{\left(F/A\right)}{{\left(F/A\right)}_{stoic}} \end{array}$$

(16)

where A is the amount of air, F is the amount of combustible material, and stoic indicates the stoichiometric ratio condition. For gas reactions, the above equation uses either volume or molar ratios.

$\:{\Phi\:}>1$, known as rich combustion or residual fuel combustion;

$\:{\Phi\:}<1$, referred to as lean combustion or residual oxygen combustion;

$\:{\Phi\:}=1$, the stoichiometric ratio when the combustible reacts exactly and completely with the oxygen in the air.

For the hydrocarbon chemical $\:\text{C}{\text{H}}_{y}$, the chemical reaction equation with oxygen is:

$$\:\begin{array}{c}C{\text{H}}_{y}+\left(1+\frac{y}{4}\right){O}_{2}\to\:C{O}_{2}+\frac{y}{2}{H}_{2}O \end{array}$$

(17)

The mass ratio of oxygen in air is 23.14 per cent, which leads to the mass ratio of hydrocarbon air to fuel:

$$\:\begin{array}{c}{\left(A/F\right)}_{mass}=\frac{32\left(1+\frac{y}{4}\right)/23.14\%}{12+y}=\frac{138.29\left(1+\frac{y}{4}\right)}{12+y} \end{array}$$

(18)

The chemical reaction equation of methane with oxygen is:

$$\:\begin{array}{c}C{\text{H}}_{4}+2{O}_{2}\to\:C{O}_{2}+2{H}_{2}O \end{array}$$

(19)

According to Eq. (18) and Eq. (19), the mass ratio of methane air to fuel is derived:$\:\:{\left(A/F\right)}_{mass}=17.28$

In the standard state (0 °C, at standard atmospheric pressure), the density of air is 1.29 kg/m³, and the general experimental conditions are carried out at room temperature, when the temperature is 20 °C, the density of air is 1.205 kg/m³. When methane is completely combusted, the stoichiometric and equivalence ratios (Φ) for the complete combustion of methane can be derived directly and can be converted to the corresponding volume concentration c(g/m³).

$$\:\begin{array}{c}{c}_{stoic}=\frac{\rho\:}{{\left(A/F\right)}_{stoic、mass}} \end{array}$$

(20)

Where$\:\:\rho\:$ is the density of air at room temperature, g/m³.

According to Eq. (20), the stoichiometric concentration of methane is $\:{c}_{stoic}$ = 0.0697 kg/m³ when methane is completely combusted. From this, it can be calculated that when methane reacts with the premixed gas of oxygen to reach the state of complete reaction, when converted to mass fraction, the mass fraction of methane is 0.055, and at this time methane corresponds to a volume fraction of 9.5 per cent. That is, when the volume concentration of methane is 9.5%, the stoichiometric ratio is reached, and methane reacts with oxygen in the air completely, which is the most violent reaction at this time, and the reaction in the oxygen-rich and oxygen-poor state is not as violent as in the stoichiometric ratio state.

The combustion of pulverized coal particles under specific conditions involves several distinct stages: First, moisture within the coal evaporates and is released. Upon further heating, the coal undergoes pyrolysis, producing volatile matter and leaving behind coke residue. The volatile matter ignites and burns initially, followed by the ignition and combustion of the coke. Subsequently, additional volatile matter continues to be released, while the coke undergoes progressive combustion until it is fully consumed. To simulate these different stages in pulverized coal combustion and explosion processes, ANSYS FLUENT employs appropriate sub-models for each phase. The gas-phase combustion reaction can be described by the following equation:

$$\:\begin{array}{c}{C}_{x}{H}_{p}{O}_{q}{N}_{n}{S}_{m}+\left(x+n+m-\frac{q}{2}\right){O}_{2}\to\:xC{O}_{2}+\frac{y}{2}{H}_{2}O+nN{O}_{2}+mS{O}_{2} \end{array}$$

(21)

In the formula, x, p, q and n are stoichiometric numbers, which are set according to the type of coal.

The reaction equation of coke combustion is as follows:

$$\:\begin{array}{c}C+0.5{O}_{2}\to\:CO \end{array}$$

(22)

$$\:\begin{array}{c}C+C{O}_{2}\to\:2CO \end{array}$$

(23)

$$\:\begin{array}{c}C+{H}_{2}O\to\:{H}_{2}+CO \end{array}$$

(24)

The pre-exponential factors and activation energies of Equations (21) to (24) are shown in Table 3:

Table 3 Kinetic parameters of reaction.

When coal dust undergoes combustion and explosion, both gas-phase combustion and coke combustion are involved. Due to differences in the degree of coal metamorphism, the ash and moisture contents vary among different coal types. Consequently, dust clouds with the same mass concentration may exhibit different explosion intensities, making direct comparisons under identical mass concentrations inappropriate. Therefore, the concept of equivalence ratio—commonly used in gaseous combustion—can also be applied to solid dust explosions by expressing the air-to-fuel ratio in terms of mass. Based on the elemental composition of coal, it is treated as an equivalent molecule composed of carbon, hydrogen, oxygen, nitrogen, sulfur, and other elements. It is further assumed that coal dust can fully react with air to produce CO₂, NO₂, H₂O, and SO₂. The equivalence ratio for coal dust explosions is then derived based on this assumption. Although this is a simplification—as real coal dust explosions are typically incomplete and only a portion of the dust participates in the reaction—the calculated equivalence ratio provides a useful reference for quantitative analysis and further research.

For coal and certain biomass fuels, which contain carbon, hydrogen, oxygen, nitrogen, sulfur, and other elements, the chemical composition of the combustible material can be simplified as CH_yO_zN_jS_k. In this formula, y represents the ratio of hydrogen atoms to carbon atoms, z denotes the ratio of oxygen atoms to carbon atoms, j indicates the ratio of nitrogen atoms to carbon atoms, and k signifies the ratio of sulfur atoms to carbon atoms. Assuming that coal undergoes complete and stoichiometric combustion with oxygen in the air, the corresponding chemical reaction equation between coal and oxygen can be expressed as:

$$\:\begin{array}{c}C{H}_{y}{O}_{z}{N}_{j}{S}_{k}+\left(1+\frac{y}{4}+j+k-\frac{z}{2}\right){O}_{2}\to\:C{O}_{2}+\frac{y}{2}{H}_{2}O+jN{O}_{2}+kS{O}_{2} \end{array}$$

(25)

It can be concluded that the mass ratio of air to fuel at this point is:

$$\:\begin{array}{c}{\left(A/F\right)}_{mass}=\frac{32\left(1+\frac{y}{4}+j+k-\frac{z}{2}\right)/23.14\%}{12+y+16z+14j+32k}=138.29\frac{1+\frac{y}{4}+j+k-\frac{z}{2}}{12+y+16z+14j+32k} \end{array}$$

(26)

At this point the equivalence ratio (mass) Φ of this combustible is:

$$\:\begin{array}{c}\varPhi\:=\frac{{\left(A/F\right)}_{stoic、mass}}{\left(A/F\right)}=\frac{\left(F/A\right)}{{\left(F/A\right)}_{stoic、mass}} \end{array}$$

(27)

Ideally, when coal dust is completely combusted, if the mass ratio of the elements involved in combustion in the coal dust is known, the stoichiometric ratio and the equivalence ratio (Φ) for the complete combustion of that coal dust can be directly obtained from Eq. (20) and can be converted to the corresponding mass concentration c(g/m³). For any mass concentration c of coal dust, its conversion to the equivalence ratio Φ is:

$$\:\begin{array}{c}c=\varPhi\:\frac{\rho\:}{{\left(A/F\right)}_{stoic, mass}}=\varPhi\:{c}_{stoic} \end{array}$$

(28)

Ash in coal is a non-combustible component. Prior to the experimental tests, the coal dust was vacuum-dried and stored in a desiccator to prevent moisture absorption. Therefore, when determining the actual coal dust concentration, the effects of both moisture and ash content in the samples must be accounted for. Hence, the actual mass concentration of coal dust can be calculated as:

$$\:\begin{array}{c}{c}_{r}=c\times\:\frac{100-{M}_{ad}}{100-{M}_{ad}-{A}_{ad}}=\varPhi\:\frac{\rho\:}{{\left(A/F\right)}_{stoic、mass}}\times\:\frac{100-{M}_{ad}}{100-{M}_{ad}-{A}_{ad}} \end{array}$$

(29)

where $\:{c}_{r}$ is the actual required coal dust mass concentration (g/m³), and $\:{M}_{ad}$ and$\:{A}_{ad}$ are the moisture content and ash content of the coal dust in the industrial analysis, respectively.

Based on the elemental analysis data of each coal sample presented in Table 2, the elemental composition was expressed as the mass percentage of each element. Using the molar mass of each element, the mass percentages were converted into corresponding atomic ratios. From these atomic ratios, the equivalence ratio and the associated stoichiometric concentration for each coal sample were calculated, as summarized in Table 4.

Table 4 Theoretical stoichiometric concentration of different coal samples.

As shown in Table 4, the stoichiometric mass ratios of air to fuel for the five coal samples selected in this paper when they reacted exactly with oxygen, i.e., when the equivalence ratio Φ = 1, ranged from 9.2486 to 11.4724, which corresponded to stoichiometric mass concentrations of 130.3 g/m³ at the maximum and 105 g/m³ at the minimum. The equivalence ratios of the five selected coal samples for the different concentrations were obtained according to Eq. (28). as shown in Table 5.

Table 5 Dust cloud concentration vs. equivalence ratio for different coal samples.

As shown in Table 5, when the concentration of the five types of coal dust is kept constant, the equivalence ratio for each coal sample varies. Therefore, to ensure a consistent basis for comparing explosion characteristics across different coal samples, it is more appropriate to use the stoichiometric ratio concentration as a standardized reference.

Effect of gas concentration on gas coal dust explosive pressure

The Ansys Fluent 2023 R1 simulation software was utilized to develop a straight roadway model measuring 4 m in width, 3 m in height, and 100 m in length. Within this model, a 20-meter section was filled with methane gas and coal dust particles, each at varying concentrations. The physical model is illustrated schematically in Fig. 7. The left end of the model is defined as a closed boundary, while the right end is set as a pressure outlet. The boundary conditions and solver settings are consistent with those described in Sect. 1.3.2. Along the tunnel axis, monitoring points were placed at 10 m intervals to record overpressure data during the numerical simulation. The entire physical model was discretized using a cubic mesh with an edge length of 0.2 m.

Fig. 7

Schematic of the model.

In this numerical simulation, five different gas concentrations were set at 5.5%, 7.5%, 9.5%, 11.5%, and 13.5%, respectively. Fat coal was selected as the simulation object, with the coal dust concentration fixed at 100 g/m³ and a particle size of 200 mesh (75 μm). Numerical simulations were then conducted under these specified conditions. The simulation results were compiled and plotted to show the variation of peak overpressure with distance for both single-phase gas explosions and gas-coal dust explosion shock waves, as illustrated in Figs. 8 and 9, respectively.

Fig. 8

Different concentrations of methane explosion overpressure peak along the course of the change of the graph.

As shown in Fig. 8, the gas-filled area is 20 m in length, and each monitoring point is located within this region. The explosion shock wave overpressure first increases and then decreases along the propagation path. This trend occurs because, upon ignition, the gas undergoes a violent chemical reaction, during which the flame burns and continuously propagates forward. The pressure wave is replenished by energy from compression waves generated in the channel, which catch up and superimpose on the primary wave. Only when multiple compression waves meet and superimpose at a specific location does the overpressure reach its maximum value at that point, which corresponds to the peak overpressure along the entire roadway. Within the general air zone, the peak overpressure at each monitoring point gradually decays along the propagation path. Once the methane–air reaction is complete, the shock wave continues to propagate using only the initial energy it gained from the combustion process. During propagation, the air ahead of the shock wave is compressed, leading to energy dissipation. As a result, the shock wave’s energy decreases, causing the peak pressure to decline with increasing distance from the ignition source. When the methane volume concentration is 9.5%, the explosion generates the highest overpressure. As the analysis above indicates, this is because a methane concentration of 9.5% corresponds to the stoichiometric ratio, where methane and oxygen in the air react completely. At this concentration, the combustion reaction is most intense, resulting in greater explosion overpressure compared to other methane concentrations.

Fig. 9

Explosive pressure propagation characteristics of coal dust with different concentrations of methane and different concentrations of methane plus 100 g/m³.

Figure 9 presents the variation of peak overpressure along the propagation path for shock waves generated by explosions involving different gas concentrations, as well as gas mixed with 100 g/m³ of coal dust. It can be observed that both single-phase gas explosions and gas–coal dust explosions exhibit a relatively consistent trend: the explosion shock wave overpressure first increases and then decreases along the propagation path. Furthermore, when the gas concentration is 5.5% or 7.5%, the addition of a small amount of coal dust enhances the gas explosion to some extent, resulting in a slight increase in the peak overpressure of the shock wave. In contrast, when the gas concentration is 9.5%, 11.5%, or 13.5%, the presence of coal dust exerts a certain inhibitory effect on the explosion, leading to a reduction in the peak overpressure value compared to the pure gas explosion.

During a methane–coal dust explosion, the resulting overpressure is greater than that of a single-phase gas explosion. This occurs because the roadway represents a confined space with limited oxygen availability. Based on the previous analysis of methane stoichiometry, the stoichiometric volume concentration of methane for complete combustion is 9.5%. Therefore, when the methane concentration is 5.5% or 7.5%, which are below this threshold, some oxygen remains in the roadway after the methane has fully reacted with oxygen, placing the environment in an oxygen-rich state. When coal dust is added to the gas mixture, it effectively increases the amount of fuel available. The coal dust reacts with the residual oxygen, releasing additional heat and raising the internal temperature of the roadway, thereby increasing the explosion overpressure. Hence, when the methane concentration is below the stoichiometric ratio, the presence of coal dust promotes the coupled explosion effect. The greater the amount of residual oxygen, the more pronounced the enhancement of the explosion pressure due to coal dust. When the methane concentration reaches the stoichiometric ratio (9.5%), the oxygen in the air is fully consumed by the reaction with methane, leaving no excess oxygen for further reactions. If the methane concentration exceeds the stoichiometric value, the roadway becomes fuel-rich. In such cases, adding coal dust increases the total fuel load, leading to incomplete combustion. This incomplete reaction results in increased heat absorption and reduced heat release, ultimately decreasing the overall explosion pressure. In summary, coal dust and methane enter into a competitive relationship for oxygen during the explosion process. If the environment is oxygen-rich, the addition of coal dust enhances the explosion power. Conversely, if the environment is oxygen-poor, the addition of coal dust accelerates oxygen consumption and increases the rate of heat dissipation, thereby reducing the explosive energy.

Effect of coal dust concentration on gas explosion pressure

In this numerical simulation, six different coal dust concentrations were set: 0, 100 g/m³, 200 g/m³, 300 g/m³, 400 g/m³, and 500 g/m³. The gas concentration was fixed at 7.5%, with fat coal selected as the simulation object and a coal dust particle size of 200 mesh (75 μm). Numerical simulations were conducted under these specified conditions. The resulting data were organized and used to plot the peak overpressure of the methane–coal dust coupled explosion at varying coal dust concentrations (methane concentration: 7.5%), as shown in Fig. 10.

Fig. 10

7.5 per cent methane coupled with different concentrations of coal dust Explosion pressure propagation characteristics.

For explosions involving 7.5% methane and coal dust concentrations of 0, 100 g/m³, 200 g/m³, 300 g/m³, 400 g/m³, and 500 g/m³, the peak overpressure at different monitoring points is shown in Fig. 10. The gas-filled area is 20 m in length, with individual monitoring points located within the methane–coal dust mixture zone. The explosion shock wave overpressure first increases and then decreases along the propagation path. When the coal dust concentration increases from 0 to 200 g/m³, the maximum peak overpressure at the monitoring point rises from 1227 kPa to 1389 kPa. However, when the coal dust concentration further increases from 200 g/m³ to 300 g/m³, the maximum peak overpressure decreases from 1389 kPa to 1254 kPa. It can be observed that the maximum pressure in the roadway initially increases and subsequently decreases with increasing coal dust concentration. The peak overpressure reaches its highest value of 1389 kPa during the explosion of 7.5% methane and 200 g/m³ coal dust. This indicates that, under these conditions, the maximum explosive effect occurs at a coal dust concentration of 200 g/m³, which corresponds to the optimal equivalent concentration for the methane–coal dust coupled explosion.

From Eq. (19), it can be seen that methane and oxygen premixed gas reaction to reach the state of complete reaction, methane volume concentration of 9.5 per cent reached the stoichiometric ratio, methane and oxygen in the air just completely reacted, at this time the reaction is the most violent. When the volume concentration of methane is 7.5 per cent, it can consume the volume concentration of 15 per cent of oxygen, and at this time the volume concentration of 6 per cent of oxygen is still remaining in the air. According to the formula (25), the chemical equation of the reaction between coal and oxygen, it can be calculated that 1 mol of fat coal needs to consume about 1.14 mol of oxygen to react completely with oxygen. Through elemental analysis, it is known that the chemical formula of fat coal is CH_0.621O_0.069N_0.017S_0.002, then the relative molecular mass of fat coal is 14 g/mol. under the standard state (0℃, standard atmospheric pressure), the air density is 1.29 kg/m³, the volume of the gas coal dust filling area is 240 m³then the mass of the air in the gas coal dust filling area is 309.6 kg, and 7.5% methane reaction with the remaining mass of oxygen is 18.576 kg, that is, the remaining 580.5 mol of oxygen. From the above, it is known that it takes about 1.14 mol of oxygen for 1 mol of fat coal to react with oxygen completely, then the remaining 580.5 mol of oxygen can also react with 509.2 mol of fat coal. 509.2 mol of fat coal converted to mass, that is, 7.129 kg of fat coal, corresponding to the mass concentration of 29.7 g/m³. From the above simulation can be seen, 7.5% methane and coal dust coupled with the explosion of coal dust, coal dust, the maximum explosion equivalent concentration of 200 g/m³ This is because unlike the gas deflagration, coal dust explosions, as well as other explosions involving particles of organic matter, often can not achieve a complete combustion reaction. When 7.5% volume concentration of methane and oxygen reaction, the remaining oxygen can be consumed by the stoichiometric ratio of coal dust concentration of 29.7 g/m³, i.e., 200 g/m3 of fertiliser coal dust actually involved in the reaction of the amount of coal dust is 29.7 g/m³.

Furthermore, as previously discussed, the stoichiometric mass concentration of fat coal is 107.2 g/m³ when it reacts completely with oxygen in air, i.e., when the equivalence ratio Φ = 1. Gas deflagration is typically considered a homogeneous reaction due to its extremely short reaction time, allowing for rapid and nearly complete combustion. In contrast, a coal dust explosion is a heterogeneous reaction, and its complex mechanism involves multiple stages, including pyrolysis of organic matter, release of volatile components, and combustion of residual coke. During the initial stage of a coal dust explosion, coal dust particles first release internal moisture under thermal influence. Subsequently, these particles undergo pyrolysis, releasing volatile matter that mixes with oxygen in the air and participates in homogeneous combustion reactions. Meanwhile, the fixed carbon in the coal dust also undergoes heterogeneous combustion. Due to the time required for momentum, heat, and mass transfer between coal dust particles and oxygen molecules, the overall reaction process of a coal dust explosion tends to be relatively prolonged. Therefore, unlike gas deflagrations, coal dust explosions—and other explosions involving organic particles—often do not achieve complete combustion. Even when coal dust is present at the stoichiometric concentration (Φ = 1), the actual amount involved in the reaction may fall short of the theoretical value. This explains why, under a methane volume concentration of 7.5%, the addition of 200 g/m³ of coal dust results in the maximum explosion pressure.

Effect of coal dust particle size on gas explosion pressure

In this numerical simulation, fat coal was selected as the simulation object, with particle sizes set at 150 mesh (106 μm), 200 mesh (75 μm), and 300 mesh (48 μm). The gas concentration was fixed at 7.5%, and the coal dust concentration was set to 200 g/m³. Numerical simulations were conducted under these specified conditions. The resulting data were organized and used to plot the variation in peak overpressure of the gas–coal dust coupled explosion under different coal dust particle sizes (gas concentration: 7.5%; coal dust concentration: 200 g/m³), as shown in Fig. 11.

Fig. 11

Explosive pressure propagation characteristics of 7.5% methane and coal dust of different particle sizes 200 g/m³.

As shown in Fig. 11, the shock wave overpressure of the gas–coal dust coupled explosion (gas concentration: 7.5%, coal dust concentration: 200 g/m³) under different coal dust particle size conditions follows a relatively consistent trend. That is, the explosion shock wave overpressure first increases and then decreases along the propagation path. Among the three tested particle sizes, the 300 mesh (48 μm) coal dust produced the highest peak overpressure during the gas–coal dust coupled explosion. The 200 mesh (75 μm) coal dust resulted in intermediate overpressure values, while the 150 mesh (106 μm) coal dust generated the lowest peak overpressure. This indicates that coal dust particle size significantly influences the explosion intensity of the gas–coal dust coupling system. Specifically, smaller coal dust particles lead to more intense explosions. This phenomenon can be attributed to several factors. First, as the particle size decreases, the specific surface area of the same mass of coal dust increases exponentially, which enhances chemical reactivity and accelerates the reaction rate. Smaller particles also allow for faster interaction with oxygen. Second, when the coal dust concentration remains constant, a reduction in particle radius leads to an increase in the total number of particles. This increases the contact area between coal dust and oxygen, promoting more complete combustion. Additionally, smaller particles exhibit stronger activation performance, resulting in greater heat release, higher temperatures, and consequently, higher explosion pressure.

Influence of coal dust of different degrees of deterioration on gas explosion pressure

The five types of coal dust samples used in the numerical simulation include lignite, gas coal, fat coal, coking coal, and lean coal. The industrial and elemental compositions of these coal dust samples are presented in Table 2. The gas concentration was set at 7.5%, the coal dust concentration at 200 g/m³, and the coal dust particle size at 200 mesh (75 μm). Numerical simulations were conducted under these specified conditions. The resulting data were analyzed and used to plot the variation in peak overpressure of the gas–coal dust coupled explosion (gas concentration: 7.5%, coal dust concentration: 200 g/m³) across different coal types with varying degrees of metamorphism, as shown in Fig. 12.

Fig. 12

Explosive pressure propagation characteristics of 7.5 per cent methane and 200 g/m³ coal dust of different coal qualities.

As can be seen from Fig. 12, 7.5% methane and different coal quality 200 g/m³ coal dust coupled with the explosion shock wave overpressure show a more consistent pattern, that is, the explosion shock wave overpressure along the course of the first increase and then decrease. As can be seen from Fig. 12, in the selected five different degrees of metamorphosis of coal dust, the lowest degree of metamorphosis, that is, the highest volatile content of lignite explosion overpressure peak is the largest. And with the decrease of the degree of metamorphism, the peak explosion overpressure of poor coal, coking coal, fat coal, gas coal and lignite under the condition of the same gas concentration (7.5%) increased in turn. The origin of this phenomenon lies in the fact that the respective explosive properties of gas and coal dust are closely linked to their chemical composition. At a constant gas concentration, the explosion of gas releases a fixed amount of heat, while coal dust releases a fixed amount of volatiles during the heating process. Similarly, when the concentration of coal dust is consistent, the amount of oxygen required for it to participate in an explosion is fixed. However, the overpressure generated by the explosion is mainly influenced by the amount of combustible gases released from the coal dust at high temperatures, which in turn is directly related to the amount of volatiles contained in the coal type. In short, the higher the volatile content of the coal, the more significant the explosion overpressure caused by its combination with the gas. This indicates that the volatile content of coal dust is one of the key factors determining the explosive power of a gas-coal dust mixture. After the industrial analysis of coal dust, it can be seen that the volatile matter content of coal type increases according to poor coal, coking coal, fat coal, gas coal, lignite, so the maximum pressure of explosion is poor coal, coking coal, fat coal, gas coal, lignite in descending order, and the degree of deterioration is negatively correlated.

Conclusion

• (1) Through a comparative analysis of simulation and experimental results, the maximum error between experimental data and numerical simulation results for the gas and coal dust explosion propagation experiment system is 7.04%, while the minimum error is 6.66%. In addition, for the numerical simulation of explosion propagation in a large-scale mine roadway with a cross-sectional area of 7.2 m² and a length of 160 m reported in the literature, the maximum and minimum errors are 14.81% and 5.26%, respectively. These results confirm the reliability of using the large eddy simulation (LES) model combined with the eddy dissipation model in simulating gas–coal dust coupled explosions.

• (2) The explosion equivalence ratio concentration of coal dust provides a more accurate representation of the characteristics of combustible dust clouds compared to mass concentration. Based on elemental and industrial analyses, the stoichiometric ratio concentrations for various types of coal dust explosions were determined. To obtain the actual coal dust concentration involved in the explosion, the effects of moisture and ash content in the coal dust samples were accounted for and subtracted. A formula was established to calculate the mass concentration of coal dust that actively participates in the explosion process. Furthermore, a conversion relationship between the explosion equivalence ratio and the mass concentration was developed for different coal types.

• (3) When the equivalence ratio Φ = 1, the methane volume concentration is 9.5%. When the methane volume concentration is below the stoichiometric concentration, the addition of a small amount of coal dust promotes the methane explosion to some extent, resulting in an increase in the peak value of the explosion shock wave overpressure. Conversely, when the methane volume concentration is greater than or equal to the stoichiometric concentration, the addition of coal dust exerts a certain inhibitory effect on the gas explosion, leading to a reduction in the peak overpressure value.

• (4) When different concentrations of fat coal dust were added to 7.5% methane to participate in the explosion, the maximum explosion pressure was achieved at a coal dust concentration of 200 g/m³. At the equivalence ratio Φ = 1, the corresponding stoichiometric mass concentration of fat coal dust is 107.2 g/m³. However, under these conditions, the actual amount of coal dust involved in the reaction does not reach the stoichiometric concentration. In other words, the equivalent ratio-based concentration of coal dust is higher than its stoichiometric concentration. When 7.5% volume concentration of methane reacts with oxygen, the remaining oxygen can only support the complete combustion of approximately 29.7 g/m³ of fat coal dust. This means that, among the 200 g/m³ of fat coal dust present, only about 29.7 g/m³ actually participates in the explosion reaction.

• (5) The particle size of coal dust has a significant influence on the explosion intensity of gas–coal dust coupled explosions. When the gas concentration is 7.5% and the coal dust concentration is 200 g/m³, a smaller coal dust particle size results in a higher explosion pressure value.

• (6) Among the five types of coal dusts with different degrees of metamorphism selected, the peak explosion overpressure of lignite with the lowest degree of metamorphism, i.e., the highest volatile content, was the largest. When the gas concentration of 7.5%, coal dust concentration of 200 g/m³, with the decrease of the degree of metamorphism, poor coal, coking coal, fat coal, gas coal and lignite explosion overpressure peak value increases in turn.