Modeling COVID-19 transmission: effects of age structure and vaccination

Abstract

A mathematical model for COVID-19 dynamics is developed, incorporating age structure, disease progression, and vaccination. Addressing gaps in existing literature, the model integrates heterogeneous intercohort mixing for realistic disease transmission, with a primary focus on Pakistan and global applicability. Well-posedness is established via the abstract Cauchy problem framework. Threshold parameters and stability analysis identify conditions for disease persistence or eradication. An age-free sub-model gives additional insights. Numerical simulations using the finite differences method confirm analytical results. The study shows the crucial role of age structure and vaccination in controlling COVID-19. It provides a strong mathematical foundation for effective public health strategies.

Introduction

Corona virus disease is a highly contagious respiratory infectious disease that emerged from Wuhan China in Dececember 2019 and very rapidly spread throughout the globe¹. Corona viruses are a family of viruses that can make humans sick, as well as animals like cats and bats. COVID-19 is transmitted when those droplets or surfaces that carry the virus come into contact with other people, either via direct touch with an infected person or proximity to one. In Pakistan, the virus infiltrated the country within the first week of February 2020 and since then, the disease infected a total of 1,580,631 individuals with 30,656 reported deaths. Various biological components can interact with one another and reduce consequences^{2,45,46,47,51}. These interactions can be described by a mathematical model. Health and other related factors at the population level are clinically tested in infectious disease, which primarily focuses on infectious diseases. It was suggested in the 1800s, when the mechanisms underlying the spread of infectious diseases were still unclear, that the majority of infectious diseases spread by coming into contact with infected people². These pioneering discoveries made it possible to model infectious diseases mathematically. The interplay among these groups can provide a framework for understanding the dynamics of epidemics, which rely on important factors like transmission and recovery rates². In addition to other variables and parameters, one of the most crucial and inherent factors used to structure a population is age. Age has a major impact on a number of internal and external characteristics, such as behavior, social interactions, reproductive abilities, and survival skills, all of which change over time³. For this reason, age structure has long been important in ecology, cell growth, and demography in addition to epidemiology. Age and immuno compromised comfortabilities are risk factors for extensive illness. Vaccines have demonstrated some effectiveness in halting the spread of the disease and will also be effective in reducing mortality and serious illness. Mathematical models are also useful for public health policy makers because they can illustrate how different interventions impact the spread of illness.

Reputable scientists have therefore created and carefully analyzed a number of mathematical models that describe the dynamics and regulation of COVID-19^{4,5,6,7,8,9,10,48}. In order to comprehend the coronavirus illness, Chen et al.⁴ developed a network model that included both human and animal populations. Mondal et al.  developed a compartmental model⁵, forecasted the pandemic’s trajectory and devised an effective control strategy. Khajanchi et al.⁶ used the extended SEIR model to provide a short-term prediction of COVID-19. In order to explain the COVID-19 outbreak⁷, the authors proposed and expanded the traditional SEIR compartment model, which was improved by contact tracing and hospitalization tactics. While everyone is initially considered susceptible, certain risk factors, like age and underlying health conditions, increase vulnerability to diseases⁸. Most severe cases and deaths have been observed among the elderly, a trend supported by the WHO. The WHO also advocates for age-stratified epidemiological studies, as disease dynamics vary with age^9,10. Therefore, incorporating age-specific factors into COVID-19 modeling is essential, as both the disease’s dynamics and its impact differ across age groups.

Hoppensteadt’s work on age-structured modelling¹⁸ emphasises the need of age-dependent vaccination in epidemic models. Infection rates have been shown to decrease when active youth are vaccinated. Since COVID-19 has no known cure, researchers are looking into several ways to stop its spread.Age affects global health and plays a significant role in the outcomes and spread of the pandemic. Different populations react differently to vaccinations, despite the fact that they are still required. By focusing on Pakistan’s unique social and medical context and providing insights into the dynamics of COVID-19 through a model that blends state-of-the-art techniques with heterogeneous intercohort mixing, this study addresses these variations. This study aims to enhance global public health strategies for managing COVID-19 and associated diseases by integrating age-structured and age-independent sub-models, validated through numerical simulations. A significant contribution of this research is the development of a continuous age-structured model that incorporates heterogeneous intercohort mixing, offering a more realistic and thorough understanding of COVID-19 dynamics. By employing the abstract Cauchy problem, this research presents a solid mathematical framework that guarantees the existence, uniqueness, and boundedness of solutions. This model distinguishes itself from earlier models, which were based on discrete age structures or overly simplistic assumptions, by effectively incorporating age-dependent compartments for various disease stages and vaccination, thus capturing critical age-related factors in disease transmission and control strategies. Nonetheless, the model’s assumptions, such as population homogeneity and constant rates, may not accurately reflect the complexities of real-world situations. Furthermore, large-scale simulations still require significant computational resources, even with optimizations for efficiency, especially when expanding to additional age groups or integrating complex interactions. Adapting the model for other diseases or populations with different transmission characteristics may require further adjustments, as it was specifically designed for the dynamics of HIV/AIDS. The organization of this paper is as follows: This paper is structured to start with Section 1 where model formulation is presented in Section 2. The analysis of the model’s solution existence and uniqueness appears in Section 3. Section 4 evaluates the stability of steady states found at both disease-free and endemic equilibrium points. Section 5 presents an analysis of a specific case of our model which uses age-free parameters. The paper demonstrates numerical solutions in Section 6 which confirm our theoretical results.

This study makes several key contributions. Our newly introduced age-structured model enables different cohorts to interact heterogeneously which improves the accuracy of modeling population interactions. We prove the well-posedness of the model by applying the abstract Cauchy problem framework to maintain mathematical precision. We calculate threshold parameters and perform an extensive stability analysis to find which conditions allow diseases to either persist or be eradicated. The final step involves numerical simulations to verify our theoretical findings which clearly show how disease management effectiveness depends heavily on age-specific factors and vaccination practices.

Model formulation

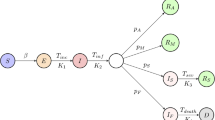
We have developed a six-compartment model to represent the entire population, which is structured as follows:

• The population susceptible to COVID-19 is denoted by $S(t, \theta )$.

• Unquarantined people who may have COVID-19 infection are denoted by $U(t, \theta )$, where $U(t) = \int_0^{\theta_+} U(t, \theta ) \, d\theta$ represents the total population of unquarantined infected people at any time t.

• Similarly, at any time t and age $\theta$, with a maximum attainable age $\theta _{+}$, $C(t, \theta )$, $Q(t, \theta )$, $V(t, \theta )$, and $R(t, \theta )$ represent the confirmed-infected persons, quarantined-infected individuals, vaccinated individuals, and recovered individuals, respectively. Their total populations can be written as:

  $$\begin{aligned} C(t) = \int _{0}^{\theta _{+}} C(t, \theta ) d\theta , ~~ Q(t) = \int _{0}^{\theta _{+}} Q(t, \theta ) d\theta , ~~ R(t) = \int _{0}^{\theta _{+}} R(t, \theta ) d\theta , ~~ V(t) = \int _{0}^{\theta _{+}} V(t, \theta ) d\theta . \end{aligned}$$

• We assume that the variable intake into the susceptible population is represented by $MP(t, \theta )$, with M being a constant.

• The size of the entire population at any given time t and age $\theta$ is denoted by:

  $$\begin{aligned} P(t, \theta ) = S(t, \theta ) + U(t, \theta ) + Q(t, \theta ) + C(t, \theta ) + R(t, \theta ) + V(t, \theta ). \end{aligned}$$

Our model is different from other studies in several key aspects:

• We employ a heterogeneous mixing assumption, where individuals in different age cohorts interact differently, reflecting the age-structured nature of COVID-19 transmission.

• Unlike simpler models that treat the population as a single homogeneous group, our model introduces multiple compartments based on the infection and recovery stages, quarantined and vaccinated groups, and age structure.

• The use of age-dependent compartments for susceptible, infected, quarantined, and vaccinated individuals allows for a more detailed and realistic analysis of disease dynamics across different age groups.

By comparing our assumptions with those of Ferguson, Moore, Giordano, and other relevant studies, we aim to highlight the novel contributions of our work, including the age-structured approach and its potential to offer more accurate predictions and insights for both local and global COVID-19 control strategies.

Fig. 1

Flow diagram of the model (1).

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {S(t,\theta )}}{\partial {t}}+\frac{\partial {S(t,\theta )}}{\partial {\theta }}= & MP(t,\theta )-({\hat{\lambda }}(t,\theta )+\epsilon (\theta )+\delta (\theta ))S(t,\theta )+\beta _{2}(\theta )V(t,\theta ),\\ \frac{\partial {U(t,\theta )}}{\partial {t}}+\frac{\partial {U(t,\theta )}}{\partial {\theta }}= & {\hat{\lambda }}(t,\theta )S(t,\theta )-(\gamma (\theta )+\delta (\theta ))U(t,\theta ),\\ \frac{\partial {Q(t,\theta )}}{\partial {t}}+\frac{\partial {Q(t,\theta )}}{\partial {\theta }}= & \gamma (\theta )U(t,\theta )-(\beta _{1}(\theta )+\vartheta (\theta )+\delta (\theta ))Q(t,\theta ),\\ \frac{\partial {C(t,\theta )}}{\partial {t}}+\frac{\partial {C(t,\theta )}}{\partial {\theta }}= & \beta _{1}(\theta )Q(t,\theta )-(\delta (\theta )+v(\theta ))C(t,\theta ),\\ \frac{\partial {R(t,\theta )}}{\partial {t}}+\frac{\partial {R(t,\theta )}}{\partial {\theta }}= & v(\theta )C(t,\theta )+\vartheta (\theta )Q(t,\theta )-\delta (\theta )R(t,\theta ) ,\\ \frac{\partial {V(t,\theta )}}{\partial {t}}+\frac{\partial {V(t,\theta )}}{\partial {\theta }}= & \epsilon (\theta )S(t,\theta )-(\delta (\theta )+\beta _{2}(\theta ))V(t,\theta ). \end{array}\right. } \end{aligned}$$

(1)

Along with boundary and initial conditions

$$\begin{aligned} S(t,0)=&\int _{0}^{\theta _{+}}{b(\theta )P(t,\theta )d\theta },U(t,0)=Q(t,0)=C(t,0)=R(t,0)=V(t,0)=0, \end{aligned}$$

(2a)

$$\begin{aligned} (S,U,&Q,C,R,V)(0,\theta )=(S_0,U_0,Q_0,C_0,R_0,V_0). \end{aligned}$$

(2b)

The age distribution functions of every class are denoted as $S_{0}(\theta )>0,U_{0}(\theta )\ge 0 ,Q_{0}(\theta )\ge 0$Let us assume that $K(\theta )$ is the kernal of separable type. While term ${\hat{\lambda }}(t,\theta )$ reflects the force of infection in inter-cohort mixing form, as described by

$$\begin{aligned} {\hat{\lambda }}(t,\theta )= K(\theta )\int _{0}^{\theta _{+}}\beta (\theta ) \frac{[U(t,\theta )+ C(t,\theta )]}{P(t,\theta )} d\theta . \end{aligned}$$

Therefore, we can write the force of infection as a separable kernel as ${\hat{\lambda }}(t,\theta )=K(\theta )\lambda (t)$, with

$$\begin{aligned} \lambda (t)= \int _{0}^{\theta _{+}}\beta (\theta ) \frac{[U(t,\theta )+ C(t,\theta )]}{P(t,\theta )} d\theta . \end{aligned}$$

(3)

The description of other parameters are shown in Table 1.

Table 1 Parameters utilized in the model (1): biological interpretation.

All of the model parameters are regarded as being bounded in the age interval $[0,\theta _+]$ and non-negative continuous. By combining each of the model equations (1) along with the boundary and initial conditions (2) we get

$$\begin{aligned} \frac{\partial {P(t,\theta )}}{\partial {t}}+\frac{\partial {P(t,\theta )}}{\partial {\theta }}=&[M-\delta (\theta )]P(t,\theta ),\nonumber \\ P(t,0)=&\int _{0}^{\theta _{+}}b(\theta )P(t,\theta )d\theta ,~~P(0,\theta )=P_{0}(\theta ). \end{aligned}$$

(4)

The steady state solution of the system (4) is given by

$$\begin{aligned} {\hat{P}}(\theta ) ={\hat{P}}(0)e^{\int _{0}^{\theta } [M-\delta (\tau _{1})]d\tau _{1}}, \end{aligned}$$

from which we get an important result

$$\begin{aligned} \int _{0}^{\infty }b(\theta )e^{\int _{0}^{\theta } [M-\delta (\tau _{1})]d\tau _{1}}d\theta =1. \end{aligned}$$

(5)

Now, let eliminate $\delta (\theta )$ from the model. For this purpose, the following use the foolowing:

$$\begin{aligned} s(t,\theta )=\frac{S(t,\theta )}{P_{\infty }(\theta )},~u(t,\theta )=\frac{U(t,\theta )}{P_{\infty }(\theta )},~q(t,\theta )=\frac{Q(t,\theta )}{P_{\infty }(\theta )},~ c(t,\theta )=\frac{C(t,\theta )}{P_{\infty }(\theta )},~r(t,\theta )=\frac{R(t,\theta )}{P_{\infty }(\theta )},~v(t,\theta )=\frac{V(t,\theta )}{P_{\infty }(\theta )}, \end{aligned}$$

(6)

where $P_{\infty }(\theta )$ stand for the total steady state population. By using the changes of variables (6) in the proposed model (1), we obtained the following system of equations along with initial and boundary conditions (see¹⁷):

$$\begin{aligned} \frac{\partial {s(t,\theta )}}{\partial {t}}+\frac{\partial {s(t,\theta )}}{\partial {\theta }}=&M-[M+\lambda (t)\beta _{3}(\theta )+\epsilon (\theta )]s(t,\theta )+\beta _{2}(\theta )v(t,\theta ), \end{aligned}$$

(7a)

$$\begin{aligned} \frac{\partial {u(t,\theta )}}{\partial {t}}+\frac{\partial {u(t,\theta )}}{\partial {\theta }}=&-[M+\gamma (\theta )] u(t,\theta )+\lambda (t)\beta _{3}(\theta )s(t,\theta ),\end{aligned}$$

(7b)

$$\begin{aligned} \frac{\partial {q(t,\theta )}}{\partial {t}}+\frac{\partial {q(t,\theta )}}{\partial {\theta }}=&-[M+\beta _{1}(\theta )+\vartheta (\theta )]q(t,\theta )+\gamma (\theta )u(t,\theta ),\end{aligned}$$

(7c)

$$\begin{aligned} \frac{\partial {c(t,\theta )}}{\partial {t}}+\frac{\partial {c(t,\theta )}}{\partial {\theta }}=&\beta _{1}(\theta )q(t,\theta )-[M+v(\theta )]c(t,\theta ),\end{aligned}$$

(7d)

$$\begin{aligned} \frac{\partial {r(t,\theta )}}{\partial {t}}+\frac{\partial {r(t,\theta )}}{\partial {\theta }}=&v(\theta )c(t,\theta )+\vartheta (\theta )q(t,\theta )-Br(t,\theta ) ,\end{aligned}$$

(7e)

$$\begin{aligned} \frac{\partial {v(t,\theta )}}{\partial {t}}+\frac{\partial {v(t,\theta )}}{\partial {\theta }}=&\epsilon (\theta )s(t,\theta )-[M+\beta _{2}(\theta )]v(t,\theta ),\end{aligned}$$

(7f)

$$\begin{aligned} s(t,0)=1,u(t,0)=&q(t,0)=c(t,0)=r(t,0)=v(t,0)=0,\end{aligned}$$

(7g)

$$\begin{aligned} s(0,\theta )=s_{0}(\theta ),u(0,\theta )=&u_{0}(\theta ),q(0,\theta )=q_{0}(\theta ), c(0,\theta )=c_{0}(\theta ),\nonumber \\ r(0,\theta )=&r_{0}(\theta ),v(0,\theta )=v_{0}(\theta ),\end{aligned}$$

(7h)

$$\begin{aligned} s(t,\theta )+u(t,\theta )+q(t,\theta )+&c(t,\theta )+r(t,\theta )+v(t,\theta )=1, \end{aligned}$$

(7i)

and

$$\begin{aligned} \lambda (t,\theta )=\int _{0}^{\theta _{+}}\beta (\theta )[u(t,\theta )+c(t,\theta )]d\theta . \end{aligned}$$

(8)

Generally, in the stability analysis, we will consider model (7) instead of its equivalent model (1) unless otherwise stated.

Uniqueness and existence of solution

We will follow the methods of^38,39,40 and will examine the uniqueness and existence of solution to the initial boundary value problem (7) or equivalently (1) along with the initial and boundary conditions. Since, the equation governing the dynamics of recovered population does not appear explicitly in the other five equations of the model (7), therefore, we will eliminate equation (21e) from the system (7) by using (7i). Further, by using the notation $\tilde{\tilde{s}}(t,\theta )=s(t,\theta )-1$ in system (7), we have

$$\begin{aligned} \frac{\partial {\tilde{\tilde{s}}(t,\theta )}}{\partial {t}}+\frac{\partial {\tilde{\tilde{s}}(t,\theta )}}{\partial {a}}=&M-[M+\lambda (t)\beta _{3}(\theta )+\epsilon (\theta )](\tilde{\tilde{s}}(t,\theta )+1)+\beta _{2}(\theta )v(t,\theta ),\end{aligned}$$

(9a)

$$\begin{aligned} \frac{\partial {u(t,\theta )}}{\partial {t}}+\frac{\partial {u(t,\theta )}}{\partial {a}}=&-[M+\gamma (\theta )] u(t,\theta )+\lambda (t)\beta _{3}(\theta )(\tilde{\tilde{s}}(t,\theta )+1),\end{aligned}$$

(9b)

$$\begin{aligned} \frac{\partial {q(t,\theta )}}{\partial {t}}+\frac{\partial {q(t,\theta )}}{\partial {a}}=&-[M+\beta _{1}(\theta )+\vartheta (\theta )]q(t,\theta )+\gamma (\theta )u(t,\theta ),\end{aligned}$$

(9c)

$$\begin{aligned} \frac{\partial {c(t,\theta )}}{\partial {t}}+\frac{\partial {c(t,\theta )}}{\partial {a}}=&\beta _{1}(\theta )q(t,\theta )-[M+v(\theta )]c(t,\theta ),\end{aligned}$$

(9d)

$$\begin{aligned} \frac{\partial {r(t,\theta )}}{\partial {t}}+\frac{\partial {r(t,\theta )}}{\partial {a}}=&v(\theta )c(t,\theta )+\vartheta (\theta )q(t,\theta )-Br(t,\theta ) ,\end{aligned}$$

(9e)

$$\begin{aligned} \frac{\partial {v(t,\theta )}}{\partial {t}}+\frac{\partial {v(t,\theta )}}{\partial {a}}=&\epsilon (\theta )(\tilde{\tilde{s}}(t,\theta )+1)-[M+\beta _{2}(\theta )]v(t,\theta ),\end{aligned}$$

(9f)

$$\begin{aligned} \tilde{\tilde{s}}(t,0)=0,u(t,0)=&q(t,0)=c(t,0)=r(t,0)=v(t,0)=0,\end{aligned}$$

(9g)

$$\begin{aligned} \tilde{\tilde{s}}(0,\theta )=s_{0}(\theta )-1,&u(0,\theta )=u_{0}(\theta ),q(0,\theta )=q_{0}(\theta ),\nonumber \\ c(0,\theta )=c_{0}(\theta ),r(0,\theta )&=r_{0}(\theta ),v(0,\theta )=v_{0}(\theta ). \end{aligned}$$

(9h)

Now, the folllowing³⁸, we can write (9) as Cauchy abstract problem in the Banach space

$$\begin{aligned} {\mathcal {X}} = {\mathcal {U}}^{1}(0,\theta _{+})\times {\mathcal {U}}^{1}(0,\theta _{+})\times {\mathcal {U}}^{1}(0,\theta _{+})\times {\mathcal {U}}^{1}(0,\theta _{+})\times {\mathcal {U}}^{1}(0,\theta _{+}), \end{aligned}$$

(10)

with norm defined by $\psi =\sum ^{5}_{i=1}||{\psi _{i}}||_{1}$ where $\psi (\theta )=(\psi _{1}(\theta ),\psi _{2}(\theta ),\psi _{3}(\theta ),\psi _{4}(\theta ))^{T}\in {\mathcal {X}},$ and $||{\psi _{i}}||_{1}$ is the norm of $\psi _{i}$ in ${\mathcal {U}}^{1}(0,\theta _{+})$. The Cauchy abstract problem in ${\mathcal {X}}$ becomes

$$\begin{aligned} \frac{dz(t)}{dt}=\mathcal {{\mathcal {U}}}z(t)+{\mathcal {N}}z(t),~~~z(0)=z_{0}\in {\mathcal {X}}, \end{aligned}$$

(11)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} z(t)=& (\tilde{\tilde{s}}(t,0),u(t,0),q(t,0),c(t,0),v(t,0))^{T},\\ z_{0}=& (s_{0}(\theta )-1,u_{0}(\theta ),q_{0}(\theta ),c_{0}(\theta ),v_{0}(\theta ))^{T}. \end{array}\right. } \end{aligned}$$

Here, ${\mathcal {L}}$ is the linear operator from ${\mathcal {X}}$ to ${\mathcal {X}}$ defined by the assuming the derivative with respect to age and negative terms of the system

$$\begin{aligned} ({\mathcal {L}}\psi )(\theta )=\begin{pmatrix}\begin{array}{ll} -\frac{d\psi _{1}(\theta )}{d\theta } & -M\psi _{1} \\ -\frac{d\psi _{2}(\theta )}{d\theta } & -(\gamma (\theta )+M)\psi _{2} \\ -\frac{d\psi _{3}(\theta )}{d\theta } & -(M+\beta _{1}(\theta )+\vartheta (\theta ))\psi _{3} \\ -\frac{d\psi _{4}(\theta )}{d\theta } & -(M+v(\theta ))\psi _{4} \\ -\frac{d\psi _{5}(\theta )}{d\theta } & -(M+\beta _{2}(\theta ))\psi _{5} \end{array} \end{pmatrix}, \end{aligned}$$

with $\{\psi \in {\mathcal {X}} : \psi _i \text { is absolutely continuous on } [0,\theta _{+}], \psi (0)=0\}$. Similarly, ${\mathcal {N}}$ is the nonlinear operator from ${\mathcal {X}}$ to ${\mathcal {X}}$ defined by (considering the remaining terms of the system)

$$\begin{aligned} ({\mathcal {N}}\psi )(\theta )=\begin{pmatrix}\begin{array}{l} M-T(\psi _{1}(\theta ),\psi _{4}(\theta ))(\theta )+\epsilon (\psi _{1}+1)(\theta ) +\beta _{2} \psi (\theta ) \\ T(\psi _{2}(\theta ),\psi _{4}(\theta ))(\theta ) (\psi _{1}+1) \\ \gamma (\theta )\psi _{2} \\ \beta _{1}(\theta )\psi _{3} \\ \epsilon (\theta )(\psi _{1}+1) \end{array} \end{pmatrix}, \end{aligned}$$

and the operator $T:{\mathcal {U}}^{1}(0,\theta _{+})\times {\mathcal {U}}^{1}(0,\theta _{+})\times {\mathcal {U}}^{\infty }(0,\theta _{+})$ is a bounded and linear, given by

$$\begin{aligned} T(\psi _{1}(\theta ),\psi _{4}(\theta ))(\theta )=\beta _{3}(\theta )\int _{0}^{\theta _{+}} \beta (\theta )[\psi _{2}(\theta )+\psi _{4}(\theta )]d\theta . \end{aligned}$$

(12)

From the definition of linear and non-linear operator ${\mathcal {L}}$ and ${\mathcal {N}}$ by using³⁹ we can say that ${\mathcal {L}}$ is a generator of $C_{0}$-semigroup $\psi$ and ${\mathcal {N}}$ is Frechet differentiable on ${\mathcal {X}}$. Therefore, using⁴⁰ we have come to the following conclusion.

Theorem 1

There is a unique continuous mild solution $t\rightarrow z(t,z_{0})$ and a maximal interval of occurrence $[0,\theta _{1})$ for each $z_{0}\in {\mathcal {X}}$.

$$\begin{aligned} z(t,z_{0})=\psi (t)z_{0}+\int _{0}^{t}\psi (t-s){\mathcal {N}}(z(s,z_{0})ds, \forall t\in [0,\theta ), \end{aligned}$$

(13)

with $\theta _{1}=\infty$ or $\lim _{t\rightarrow a_{1}^{-}}||z(t,z_{0})||=\infty$.

2. The mild solution $z(t,z_0)$ is continuously differentiable it satisfying (12) on the interval $[0,\theta _{+})$ if $z_{0}\in D({\mathcal {L}})$. Similarly, for $t\in [0,\theta _{1})$, $z(t,z_{0})\in D({\mathcal {L}})$.

Let us define two sets

$$\begin{aligned} D=\{(\tilde{\tilde{s}},u,q,c,v)\in {\mathcal {X}}: \tilde{\tilde{s}}\ge -1, u\ge 0,q\ge 0, c\ge 0, v\ge 0\}, \end{aligned}$$

(14)

and

$$\begin{aligned} D_{0}=\{(\tilde{\tilde{s}},u,q,c,v)\in {\mathcal {X}}:0\ge \tilde{\tilde{s}}\ge -1, 1\ge u\ge 0, 1\ge q\ge 0, 1\ge c\ge 0, 1 \ge v\ge 0\}. \end{aligned}$$

(15)

We need to prove the following Lemma in order to show that a unique global classical solution exist for the abstract Cauchy problem (12).

Lemma 1

The mild solution $z(t,z_0)$ with $z_{0}\in D$ of the abstract cauchy problem (12), enters in finite time to $D_0$ which is positively-invariant set.

Proof

By using the techniques of^38,39, first we need to write the solution of system (7) along the characteristic line $t-\theta = constant$. Solution of equation (7a) along the characteristic curve can be written as

$$\begin{aligned} s(t,\theta )={\left\{ \begin{array}{ll} & s_{0} e^{-\int _{0}^{t}(\beta +\beta _{3}(\theta -t+\tau _{2})\lambda (xi)+\epsilon (\theta -t+\tau _{2})d\tau _{2}}+\beta \int _{0}^{t}e^{-\int _{\tau _{1}}^{t}(\beta +\beta _{3}(\theta -t+\tau _{2})\lambda (xi))d\tau _{2}}\\ & +\int _{0}^{t}\beta _{2}(\theta -t+\tau _{1})v(\tau _{1},\theta -t+\tau _{1})\times e^{-\int _{\tau _{1}}^{t}(\beta +\beta _{3}(\theta -t+\tau _{2})\lambda (\tau _{2}))+\epsilon (\theta -t+\tau _{2})d\tau _{2}}d\tau _{1}, \theta>t,\\ & e^{-\int _{0}^{\theta }(\beta +\lambda (t-\theta +\tau _{2})\beta _{3}(\tau _{2})+\epsilon (\tau _{2}))d\tau _{2}}+ M\int _{0}^{\theta } e^{-\int _{0}^{\theta }(\beta +\lambda (t-\theta +\tau _{2})\beta _{3}(\tau _{2})+\epsilon (\tau _{2}))d\tau _{2}}\\ & +\int _{0}^{\theta }\beta _{2}(t-\theta +\tau _{1})v(\tau _{1},\theta -t+\tau _{1})\times e^{-\int _{\tau _{1}}^{t}(\beta +\beta _{3}(t-\theta +\tau _{2})\lambda (\tau _{2}))+\epsilon (t-\theta +\tau _{2})d\tau _{2}}d\tau _{1}, \theta \le t. \end{array}\right. } \end{aligned}$$

Clearly $s(t,\theta )\ge 0$ and thus $\tilde{\tilde{s}}(t,\theta ) \ge -1$.

Similarly, by integrating (21c) and (21d) along characteristic curve:

$$\begin{aligned} q(t,\theta )={\left\{ \begin{array}{ll} & q_{0} e^{-\int _{0}^{t}(M+\beta _{1}(\theta -t+\tau _{2})+\vartheta (\theta -t+\tau _{2})d\tau _{2}}+\int _{0}^{t}\gamma (\theta -t+\tau _{1})u(\tau _{1},\theta -t+\tau _{1})\\ & \times e^{-\int _{\tau _{1}}^{t}(M+\beta _{1}(\theta -t+\tau _{2})+\vartheta (\theta -t+\tau _{2}))d\tau _{2}}d\tau _{1}, \theta>t,\\ & \int _{0}^{\theta } e^{-\int _{0}^{\tau _{1}}(M+\beta _{1}(\tau _{2}))d\tau _{2}}\gamma (\tau _{1})u(t-\theta +\tau _{1},\tau _{1})d\tau _{1}, \theta \le t, \end{array}\right. } \end{aligned}$$

where $q_{0}=q_{0}(\theta -t)$ and

$$\begin{aligned} c(t,\theta )={\left\{ \begin{array}{ll} & c_{0}(\theta -t) e^{-\int _{0}^{t}(M+v(\theta -t+\tau _{2})d\tau _{2}}+\int _{0}^{t}e^{-\int _{\tau _{1}}^{t}(M+v(\theta -t+\tau _{2}))d\tau _{2}} M(\theta -t+\tau _{1})q(\tau _{1},\theta -t+\tau _{1}))d\tau _{1}, \theta>t,\\ & \int _{0}^{\theta } e^{-\int _{\tau _{1}}^{\theta }(M+\beta _1(\tau _{2}))d\tau _{2}}\beta (\tau _{1})q(t-\theta +\tau _{1},\tau _{1})d\tau _{1}, \theta \le t. \end{array}\right. } \end{aligned}$$

We can notice that $c(t,\theta )$ depend on $q(t,\theta )$ which required $u(t,\theta )$. Thus, we can write equation (9) as

$$\begin{aligned} \lambda (t) = (Gu)(t,\theta ), \end{aligned}$$

where G is positive transformation from $u(t,\theta )$ to $\lambda (t)$ for the given initial data. Using this fact in mind, we can write equation (21b) as

$$\begin{aligned} \frac{du}{dt}=\mathscr {F}u(t,\theta )+(Gu(t,\theta ))\beta _{3}(\theta )s(t,\theta ), ~~~~~~~~~u(0)=u_{0}, \end{aligned}$$

(16)

where $\mathscr {F}$ is an operator of the form

$$\begin{aligned} \mathscr {F}=-\frac{d}{d\theta } -(M+\gamma (\theta )), \text { with } D(\mathscr {F})=D({\mathcal {L}}). \end{aligned}$$

By solving (16), we have

$$\begin{aligned} u(t)=e^{-t(\frac{d}{d\theta } +M+\gamma (\theta ))} u(0)+\int _{0}^{t}e^{-(t-\tau _{1})(\frac{d}{d\theta } +M+\gamma (\theta ))}(Gu(\tau _{1}))ksd\tau _{1},\end{aligned}$$

(17)

where the positive $c_{0}$-semigroup $e^{-t(\frac{d}{d\theta } +M+\gamma (\theta ))}$ is generated by the operator $\mathscr {F}$ clearly (16) shows that u is positive and thus q and c are also positive. Thus, $z(t,z_{0})\in D \forall t\ge 0$ and $z_{0}\in D_{0}$.

The above lemma shows that the norm of the local solution (when it is defined) of the problem (12) is finite and thus we can state the following results regarding uniqueness of positive global solution of the model (7). $\square$

Theorem 2

The abstract Cauchy problem (12) has a unique global classical solution on X with respect to the initial data $z_{0}\in D({\mathcal {L}})\cap D$.

Steady states existence and stability

Here, we will explore the stability and occurrence of possible steady states of the system (7). In the beginning we will show that the system necessarily has locally and globally asymptotically stable disease-free steady state when $R_{0}>1$. Additionally, we will demonstrate that the disease will continue to affect the population anytime when $R_{0}>1$ which is locally asymptotically stable under the same condition.

Stability and existence of disease-free steady state

In order to find the model disease-free steady state, we must convert system (7) into time absent problem and will assume that there is no patient of COVID-19 in the population (the disease is absent), then it is easy to show that model (7) has the disease-free equillibrium. In equillibrium solution $(s^{0}(\theta ), u^{0}(\theta ),q^{0}(\theta ),c^{0}(\theta )$, $r^{0}(\theta ),v^{0}(\theta ),)$ of the model (7) is actually the solution of the following system of ODEs.

$$\begin{aligned} \frac{ds^{0}}{d\theta }=&M-[M+\Lambda \beta _{3}(\theta )+\epsilon (\theta )]s^{0}(\theta )+\beta _{2}(\theta )v^{0}(\theta ), \end{aligned}$$

(18a)

$$\begin{aligned} \frac{du^{0}}{d\theta }=&-[M+\gamma (\theta )] u^{0}(\theta )+\Lambda \beta _{3}(\theta )s^{0}(\theta ),\end{aligned}$$

(18b)

$$\begin{aligned} \frac{dq^{0}}{d\theta }=&-[M+\beta _{1}(\theta )+\vartheta (a]s^{0}(\theta )+\gamma (\theta )u^{0}(\theta ),\end{aligned}$$

(18c)

$$\begin{aligned} \frac{dc^{0}}{d\theta }=&\beta _{1}(\theta )q^{0}(\theta )-[M+v(\theta )]c^{0}(\theta ),\end{aligned}$$

(18d)

$$\begin{aligned} \frac{dr^{0}}{d\theta }=&v(\theta )c^{0}(\theta )+\vartheta (\theta )q^{0}(\theta )-Br^{0}(\theta ) ,\end{aligned}$$

(18e)

$$\begin{aligned} \frac{dv^{0}}{d\theta }=&\epsilon (\theta )s^{0}(\theta )-[M+\beta _{2}(\theta )]v^{0}(\theta ),\end{aligned}$$

(18f)

$$\begin{aligned} s^{0}(0)=&1,u^{0}(0)=q^{0}(0)=c^{0}(0)=r^{0}(0)=v^{0}(0)=0, \end{aligned}$$

(18g)

and

$$\begin{aligned} \Lambda = \int _{0}^{\theta _{+}}\beta (\theta )[u^{0}(\theta )+c^{0}(\theta )]d\theta . \end{aligned}$$

(19)

This is simple to show that the model (7) has the disease-free steady state

$$\begin{aligned} E^{0}=(s^{0}(\theta ), u^{0}(\theta ),q^{0}(\theta ),c^{0}(\theta ),r^{0}(\theta ),v^{0}(\theta ),)=(1,0,0,0,0,0). \end{aligned}$$

(20)

In order to show that (20) is locally stable, we will follow the method of⁴⁰ to linearize the system (7) around the disease-free steady state. Let $\overline{s}(t,\theta ),\overline{u}(t,\theta ),\overline{q}(t,\theta ),$ $\overline{c}(t,\theta ),\overline{r}(t,\theta ),\overline{v}(t,\theta )$ by the perturbation of $s^{0}(\theta ),u^{0}(\theta ),q^{0}(\theta ),$

$c^{0}(\theta ),r^{0}(\theta ),v^{0}(\theta )$ respectively by using the perturbation we can write

$$\begin{aligned} S(t,\theta ) =&\overline{s}(t,\theta )+s^{0}(\theta ),U(t,\theta ) =\overline{u}(t,\theta )+u^{0}(\theta ), Q(t,\theta ) =\overline{q}(t,\theta )+q^{0}(\theta ),\\C(t,\theta ) =&\overline{c}(t,\theta )+c^{0}(\theta ), R(t,\theta ) =\overline{r}(t,\theta )+r^{0}(\theta ),V(t,\theta ) =\overline{v}(t,\theta )+v^{0}(\theta ), \end{aligned}$$

by putting these perturbations in our system (7) we can say that the perturbed parameters $\overline{s}, \overline{u},\overline{q},\overline{c},\overline{r},\overline{v},$ will hold the system.

$$\begin{aligned} \frac{\partial {\overline{s}(t,\theta )}}{\partial {t}}+\frac{\partial {\overline{s}(t,\theta )}}{\partial {\theta }}=&-[M+\epsilon (\theta )]\overline{s}(t,\theta )-\Lambda (t)\beta _{3}(\theta )+\beta _{2}(\theta )\overline{v}(t,\theta ),\end{aligned}$$

(21a)

$$\begin{aligned} \frac{\partial {\overline{u}(t,\theta )}}{\partial {t}}+\frac{\partial {\overline{u}(t,\theta )}}{\partial {\theta }}=&-[M+\gamma (\theta )] \overline{u}(t,\theta )+\Lambda (t)\beta _{3}(\theta ),\end{aligned}$$

(21b)

$$\begin{aligned} \frac{\partial {\overline{q}(t,\theta )}}{\partial {t}}+\frac{\partial {\overline{q}(t,\theta )}}{\partial {\theta }}=&-[M+\beta _{1}(\theta )+\vartheta (\theta )]\overline{q}(t,\theta )+\gamma (\theta )\overline{u}(t,\theta ),\end{aligned}$$

(21c)

$$\begin{aligned} \frac{\partial {\overline{c}(t,\theta )}}{\partial {t}}+\frac{\partial {\overline{c}(t,\theta )}}{\partial {\theta }}=&\beta _{1}(\theta )\overline{q}(t,\theta )-[M+v(\theta )]\overline{c}(t,\theta ),\end{aligned}$$

(21d)

$$\begin{aligned} \frac{\partial {\overline{r}(t,\theta )}}{\partial {t}}+\frac{\partial {\overline{r}(t,\theta )}}{\partial {\theta }}=&v(\theta )\overline{c}(t,\theta )+\vartheta (\theta )\overline{q}(t,\theta )-M\overline{r}(t,\theta ) ,\end{aligned}$$

(21e)

$$\begin{aligned} \frac{\partial {\overline{v}(t,\theta )}}{\partial {t}}+\frac{\partial {\overline{v}(t,\theta )}}{\partial {\theta }}=&\epsilon (\theta )\overline{s}(t,\theta )-[M+\beta _{2}(\theta )]\overline{v}(t,\theta ),\end{aligned}$$

(21f)

$$\begin{aligned} \overline{s}(t,0)=\overline{u}(t,0)=\overline{q}(t,0)=\overline{c}(t,0)&=\overline{r}(t,0)=\overline{v}(t,0)=0,\end{aligned}$$

(21g)

$$\begin{aligned} \overline{s}(0,\theta )=s_{0}(\theta )-s^{0}(\theta ),u(0,\theta )=&u_{0}(\theta )-u^{0}(\theta ),q(0,\theta )=q_{0}(\theta )-q^{0}(\theta ),\nonumber \\ c(0,\theta )=c_{0}(\theta )-c^{0}(\theta ),r(0,\theta )=&r_{0}(\theta )-r^{0}(\theta ),v(0,\theta )=v_{0}(\theta )-v^{0}(\theta ), \end{aligned}$$

(21h)

and

$$\begin{aligned} \Lambda = \int _{0}^{\theta _{+}}\beta (\theta )[\overline{u}(t,\theta )+\overline{c}(t,\theta )]d\theta . \end{aligned}$$

(22)

Let the linear system has a separable solution (exponential in time) of the type

$$\begin{aligned} \overline{s}(t,\theta )=e^{\lambda t}\overline{s}(\theta ),~ \overline{u}(t,\theta )=e^{\lambda t}\overline{u}(\theta ),~ \overline{q}(t,\theta )=e^{\lambda t}\overline{q}(\theta ),~\overline{c}(t,\theta )=e^{\lambda t}\overline{c}(\theta ),~ \overline{r}(t,\theta )=e^{\lambda t}\overline{r}(\theta ),~ \overline{v}(t,\theta )=e^{\lambda t}\overline{v}(\theta ), \end{aligned}$$

(23)

whose parameter $\lambda$ will be determined later. Thus $\Lambda (t)=e^{\lambda t}$ with

$$\begin{aligned} {\overline{\Lambda }}=\int _{0}^{\theta _{+}}\beta (\theta )[\overline{u}(t,\theta )+\overline{c}(t,\theta )]d\theta , \end{aligned}$$

by putting the exponential solutions in the system (23), along with the derivatives in the perturb system, we get

$$\begin{aligned} \frac{d\overline{s}(\theta )}{d\theta }=&-[\lambda +M+\epsilon (\theta )]\overline{s}(\theta )-{\overline{\Lambda }}\beta _{3}(\theta )+\beta _{2}(\theta )\overline{v}(\theta ),\end{aligned}$$

(24a)

$$\begin{aligned} \frac{d\overline{u}(\theta )}{d\theta }=&-[\lambda +M+\gamma (\theta )] \overline{u}(\theta )+{\overline{\Lambda }}\beta _{3}(\theta ),\end{aligned}$$

(24b)

$$\begin{aligned} \frac{d\overline{q}(\theta )}{d\theta }=&-[\lambda +M+\beta _{1}(\theta )+\vartheta (\theta )]\overline{q}(\theta )+\gamma (\theta )\overline{u}(\theta ),\end{aligned}$$

(24c)

$$\begin{aligned} \frac{d\overline{c}(\theta )}{d\theta }=&\beta _{1}(\theta )\overline{q}(\theta )-[\lambda +M+v(\theta )]\overline{c}(\theta ),\end{aligned}$$

(24d)

$$\begin{aligned} \frac{d\overline{r}(\theta )}{d\theta }=&-[\lambda +\beta ]\overline{r}(\theta )+v(\theta )\overline{c}(\theta )+\vartheta (\theta )\overline{q}(\theta ),\end{aligned}$$

(24e)

$$\begin{aligned} \frac{d\overline{v}(\theta )}{d\theta }=&\epsilon (\theta )\overline{s}(\theta )-[\lambda +M+\beta _{2}(\theta )]\overline{v}(\theta ),\end{aligned}$$

(24f)

$$\begin{aligned} {\overline{\Lambda }}=&\int _{0}^{\theta _{+}}\beta (\theta )[\overline{u}(t,\theta )+\overline{c}(t,\theta )]d\theta ,\end{aligned}$$

(24g)

$$\begin{aligned} \overline{s}(0)=&\overline{u}(0)=\overline{q}(0)=\overline{c}(0)=\overline{r}(0)=\overline{v}(0)=0. \end{aligned}$$

(24h)

Solving eqs. 24b and 24d, we get

$$\begin{aligned} \overline{u}(\theta )=&{\overline{\Lambda }}\int _{0}^{\theta }\beta _{3}(\tau _{1})e^{-(\lambda +M)(\theta -\tau _{1})}e^{-\int _{\tau _{1}}^{\theta }\gamma (\xi )d\theta }d\tau _{1},\end{aligned}$$

(25)

$$\begin{aligned} \overline{q}(\theta )=&\int _{0}^{\theta }\gamma (\tau _{1})\big ({\overline{\Lambda }}\int _{0}^{\tau _{1}}\beta _{3}(\tau _{2})e^{-(\lambda +M)(\theta -\tau _{2})}e^{-\int _{\tau _{1}}^{\theta }\gamma (\xi )d\xi }d\tau _{2}\big )\times e^{-(\lambda +M)(\theta -\tau _{1})} e^{-\int _{\tau _{1}}^{\theta }[\beta _{1}(\xi )+\vartheta (\xi )]d\xi }d\tau _{1}, \end{aligned}$$

(26)

$$\begin{aligned} \overline{c}(\theta )=&\int _{0}^{\theta } \beta _{1}(\tau _{1})\Big \{\int _ { 0 } ^ { \tau _{1} } \gamma ( \omega ) \Big ({\overline{\Lambda }} \int _0^\omega \beta _{3}(\tau _{2}) e^{-(\lambda +M)(\tau _{1}-\tau _{2})} e^{-\int _{\tau _{2}}^{\omega } \gamma (\xi ) d \xi d \tau _{2}}\Big ) e^{-(\lambda +M)(\tau _{1}-\omega )} \nonumber \\&\times e^{-\int _{\omega }^{\tau _{1}}[B_{1}(\xi )+\tau _{1}(\xi )] d \xi } d \omega \Big \} e^{-(\lambda +M)(\theta -\tau _{1})} e^{-\int _{\tau _{1}}^{\theta } v(\xi ) d \xi } d \tau _{1}. \end{aligned}$$

(27)

Now put the values of $\overline{u}(\theta )$ and $\overline{c}(\theta )$ in (24g), we get

$$\begin{aligned} {\overline{\Lambda }}= & \int _{0}^{\theta _{+}} \beta (\theta )\Big [{\overline{\Lambda }} \int _{0}^{\theta } \beta _{3}(\tau _{1}) e^{-(\lambda +M)(\theta -\tau _{1})} e^{-\int _{\tau _{1}}^{\theta } \gamma (\tau _{1}) d \xi } d \tau _{1} +\int _{0}^{\theta } \beta _{1}(\tau _{1})\Big \{ \int _0^{\tau _{1}} \gamma (\omega )\Big ({\overline{\Lambda }} \int _{0}^{\omega } \beta _{3}(\tau _{2})\\ & e^{-(\lambda +\beta )(\tau _{1}-\tau _{2})} e^{-\int _{\tau _{2}}^{\omega } \gamma (\xi ) d \xi } d \tau _{2}\Big ) e^{-(\lambda +M)(\tau _{1}-\omega )} e^{-\int _{\omega }^{\tau _{1}} [\beta _{1}(\xi ) +\vartheta (\xi )]d \xi } d\omega \Big \}e^{-(\lambda +M)(\theta -\tau _{1})}e^{-\int _{\tau _{1}}^{a}v(\xi )d\xi }\Big ]d\theta , \end{aligned}$$

and thus we obtained the characteristic equation of the form

$$\begin{aligned} 1= & \int _{0}^{\theta _{+}} \beta (\theta )\Big [ \int _{0}^{\theta } \beta _{3}(\tau _{1}) e^{-(\lambda +M)(\theta -\tau _{1})} e^{-\int _{\tau _{1}}^{\theta } \gamma (\tau _{1}) d \xi } d \tau _{1} +\int _{0}^{\theta } \beta _{1}(\tau _{1})\Big \{ \int _0^{\tau _{1}} \gamma (\omega )\Big ( \int _{0}^{\omega } \beta _{3}(\tau _{2}) \nonumber \\ & e^{-(\lambda +\beta )(\tau _{1}-\tau _{2})} e^{-\int _{\tau _{2}}^{\omega } \gamma (\xi ) d \xi } d \tau _{2}\Big ) e^{-(\lambda +M)(\tau _{1}-\omega )} e^{-\int _{\omega }^{\tau _{1}} [\beta _{1}(\xi ) +\vartheta (\xi )]d \xi } d\omega \Big \}e^{-(\lambda +M)(\theta -\tau _{1})}e^{-\int _{\tau _{1}}^{\theta }v(\xi )d\xi }\Big ]d\theta . \end{aligned}$$

(28)

For calculation of $R_0$ we follow⁴⁰. Thus, the basic reproduction number $R_0$ is actually ${\mathcal {H}}(O)$ or explicitly.

$$\begin{aligned} R_{0}= & \int _{0}^{\theta _{+}} \beta (\theta )\Big [ \int _{0}^{\theta } \beta _{3}(\tau _{1}) e^{-M(\theta -\tau _{1})} e^{-\int _{\tau _{1}}^{\theta } \gamma (\tau _{1}) d \xi } d \tau _{1} +\int _{0}^{\theta } \beta _{1}(\tau _{1})\Big \{ \int _0^{\tau _{1}} \gamma (\omega )\Big ( \int _{0}^{\omega } \beta _{3}(\tau _{2}) \nonumber \\ & e^{-\beta (\tau _{1}-\tau _{2})} e^{-\int _{\tau _{2}}^{\omega } \gamma (\xi ) d \xi } d \tau _{2}\Big ) e^{-M(\tau _{1}-\omega )} e^{-\int _{\omega }^{\tau _{1}} [\beta _{1}(\xi ) +\vartheta (\xi )]d \xi } d\omega \Big \} e^{-M(\theta -\tau _{1})}e^{-\int _{\tau _{1}}^{\theta }v(\xi )d\xi }\Big ]d\theta . \end{aligned}$$

(29)

The characteristic equation (28) demonstrates that ${\mathcal {H}}$ is a positive decreasing function of $\lambda$, with limits of 0 and $\infty$ as $\lambda$ approaches $\infty$ and $-\infty$. Thus (28) is satisfied by $\lambda <0$ under the condition $R_{0} <1$ and in this case disease-free steady state is locally asymptotically stable otherwise unstable. Therefore, we present the following theorem regarding the local stability of disease-free steady state of the model.

Theorem 3

When $R_{0}<1,$ the disease-free steady state of the model (7) is locally asymptotically stable and otherwise, it is unstable.

This theorem shows that if the initial data of each compartment of $P(t, \theta )$ is in the neighborhood (with sufficiently small radius) of $E^0$ then the COVID-19 could be eliminated from the population. If this is not the case then for COVID-19 elimination, the following theorem has to be stated and proved.

Theorem 4

If $R_0 < 1$, then the disease-free steady state of the model (7) is globally asymptotically stable.

Proof

For global stability of the disease-free steady state, we must prove that $s(t, \theta )=1,\quad u(t, \theta )=0,\quad q(t, \theta )=0,$ $v(t, \theta)=0$ as t tends to $\infty$. First of all characteristics method to be used to solve (21b) as

$$\begin{aligned} u(\theta , t)=\left\{ \begin{array}{l} u_0(\theta -t) e^{-\int _0^t(M+\gamma (\theta -t+\omega )) d \omega }+\int _0^t e^{-\int _{\tau _{1}}^{t}(M+\gamma (\theta -t+\omega )) d \omega } \\ \times \beta _{3}(\theta -t+\tau _{1}) \lambda (\tau _{1}) s(\tau _{1}, \theta -t+\tau _{1}) d \tau _{1}, ~ \theta>t, \\ \int _0^{\theta } e^{-\int _{\tau _{1}}^{\theta }(M+\gamma (\omega )) d \omega } \beta _{3}(\tau _{1}) \lambda (t-\theta +\tau _{1}) s(t-\theta +\tau _{1}, \tau _{1}) d \tau _{1}, ~ \theta \le t. \end{array}\right. \end{aligned}$$

By using equations (10) and (16) (solutions of equations (21b), (21c) and (2) obtained by using the method of characteristic) and considering part of solution for the case $t \ge \theta$ and putting the required values in (9), we get

$$\begin{aligned} \lambda (t)= & \int _0^{\theta _{+}} \beta (\theta )[u(t, \theta )+c(t, \theta )] d \theta, \nonumber \\= & \int _0^t \beta (\theta )[u(t, \theta )+c(t, \theta )] d \theta +\int _t^{\theta _{+}} \beta (\theta )[u(t, \theta )+c(t, \theta )] d \theta . \end{aligned}$$

(30)

Since $P(t, \theta ) \le 1$ so that $u(t, \theta )+c(t, \theta ) \le 1$ and $s(t, \theta ) \le 1$, thus

$$\begin{aligned} \lambda (t)\le & \int _0^t \beta (\theta )\left[ \int _0^{\theta } e^{-\int _{\tau _{1}}^{\theta }(M+\gamma (\omega )) d \omega } \beta _{3}(\tau _{1}) \lambda (t-\theta +\tau _{1}) d \tau _{1}\right. \nonumber \\ & \left. +\int _0^{\theta } e^{-\int _{\tau _{1}}^{\theta }(M+v(\omega )) d \omega } \beta _1(\tau _{1})\left\{ \int _0^{\tau _{1}} e^{-\int _{\tau _{2}}^{\tau _{1}}\left( M+\beta _1(\omega )+\vartheta (\omega )\right) d \omega }\right. \right. \nonumber \\ & \left. \left( \int _0^{\tau _{2}} e^{-\int _{\tau _{1}}^{\tau _{2}}(M+\gamma (\omega )) d \omega } \beta _{3}(\tau _{1}) \lambda (t-\theta +\tau _{1}) d \tau _{1}\right) \gamma (\tau _{2}) d \tau _{2}\} d \tau _{1}\right] d \theta +\int _t^{\theta _{+}} \beta (\theta ) d \theta . \end{aligned}$$

(31)

By applying Fatou’s Lemma⁴¹, keeping in mind relation (30) and taking the $\lim \limits _{t \rightarrow \infty }sup$ we get

$$\begin{aligned} \lim _{t \rightarrow \infty } \lambda (t) \le R_0 \lim _{t \rightarrow \infty } \sup \lambda (t). \end{aligned}$$

If we assume that $R_0<1$, then we must accept that

$$\begin{aligned} \lim _{t \rightarrow \infty } \lambda (t)=0, \end{aligned}$$

in order to hold (31). By using this value of $\lambda (t)$ in equation (10) (in the part of solution $t>\theta$ as we interested in long-term behavior of the problem), we have $\lim \limits _{t \rightarrow \infty } u(t, \theta )=0$ which guarantees that $\lim \limits _{t \rightarrow \infty } q(t, \theta )=0$ and $\lim \limits _{t \rightarrow \infty } c(t, \theta )=0$ by using solutions of equations (21c) and (21d). Similarly, by considering equation (21e) and applying the techniques of⁴², we can show that $\lim \limits _{t \rightarrow \infty } r(t, \theta )=0$. Finally, by using relation (21g) we obtained the required objective of the theorem that $(s(t, \theta ), u(t, \theta ), q(t, \theta ), c(t, \theta ), r(t, \theta )) \rightarrow$ (1, 0, 0, 0, 0) as $t \rightarrow \infty$. $\square$

Endemic steady state existence and stability

To find the endemic steady state of model (7), we need to solve the model for the time-steady case.

Theorem 5

If $R_0>1$, then there exist an endemic equilibrium of system (7).

Proof

To check

$$\begin{aligned} \frac{d s^{\star }(\theta )}{d \theta }=&M-[M+\beta _{3}(\theta ) \lambda ^{\star }+\epsilon (\theta )] s^{\star }(\theta )+\beta _{2}(\theta )v^{\star }(\theta ), \end{aligned}$$

(32a)

$$\begin{aligned} \frac{d u^{\star }(\theta )}{d \theta }=&-[M+\gamma (\theta )] u^{\star }(\theta )+\beta _{3}(\theta ) \lambda ^{\star } s^{\star }(\theta ), \end{aligned}$$

(32b)

$$\begin{aligned} \frac{d q^{\star }(\theta )}{d \theta }=&-[M+\beta _{1}(\theta )+\vartheta (\theta )] q^{\star }(\theta )+\gamma (\theta ) u^{\star }(\theta ), \end{aligned}$$

(32c)

$$\begin{aligned} \frac{d c^{\star }(\theta )}{d \theta }=&\beta _1(\theta ) q^{\star }(\theta )-[M+v(\theta )] c^{\star }(\theta ), \end{aligned}$$

(32d)

$$\begin{aligned} \frac{d r^{\star }(\theta )}{d \theta }=&v(\theta ) c^{\star }(\theta )+\vartheta (\theta ) q^{\star }(\theta )-M r^{\star }(\theta ), \end{aligned}$$

(32e)

$$\begin{aligned} \frac{d v^{\star }(\theta )}{d \theta } =&\epsilon (\theta )s^{\star }(\theta )-[M+\beta _{2}(\theta )]v^{\star }(\theta ),\end{aligned}$$

(32f)

$$\begin{aligned} \lambda ^{\star }=&\int _{0}^{\theta } \beta (\theta )\left[ u^{\star }(\theta )+c^{\star }(\theta )\right] d \theta , \end{aligned}$$

(32g)

$$\begin{aligned} s^{\star }(\theta )+&u^{\star }(\theta )+q^{\star }(\theta )+c^{\star }(\theta )+r^{\star }(\theta )=1,\end{aligned}$$

(32h)

$$\begin{aligned} s^{\star }(0)=&1,\quad u^{\star }(0)=q^{\star }(0)=c^{\star }(0)=r^{\star }(0)=0, \end{aligned}$$

(32i)

to show that a solution $E^{\star }=(s^{\star }(\theta ), u^{\star }(\theta ),q^{\star }(\theta ),c^{\star }(\theta ),r^{\star }(\theta ),v^{\star }(\theta ),)$, does really exist for the time absent problem (32), we will follow⁴⁰. Solution of equation eqs. 32a and 32d is of the form

$$\begin{aligned} s^{\star }(\theta )=&e^{-\int _0^{\theta } {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }+\int _{0}^{\theta }\left( M+ \beta _{2}(\tau _{1})v(\tau _{1})e^{- \int _{\tau _{1}}^{\theta } {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }\right) d\tau _{1}, \end{aligned}$$

(33)

$$\begin{aligned} u^{\star }(\theta )=&\lambda ^{\star }\int _0^{\theta } \beta _{3}(\tau _{1}) \left( e^{- \int _{0}^{\tau _{1}} {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }+\int _{0}^{\tau _{1}}\left( M+ \beta _{2}(\tau _{1})v(\tau _{1})\right) d\tau _{1}\right. \nonumber \\&\left. \times e^{- \int _{\tau _{1}}^{\theta } {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }\right) e^{- \int _{\tau _{1}}^{\theta } (M+\gamma (\xi ))d\xi }d\tau _{1}, \end{aligned}$$

(34)

$$\begin{aligned} q^{\star }(\theta )=&\int _0^{\theta } e^{- \int _{0}^{\tau _{1}} [M+\beta _{1} (\xi )+\vartheta (\xi )]d\xi }\gamma (\tau _{1})\left\{ \lambda ^{\star }\int _{0}^{\tau _{1}} e^{- \int _{\omega }^{\tau _{1}} {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }\right. \nonumber \\&+\left. \int _{0}^{\omega }\left( M +\beta _{2}(\tau _{2})v(\tau _{2})\right) d\tau _{2} e^{- \int _{\tau _{2}}^{\omega } {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }\right\} \beta _{3}(\omega )d\omega d\tau _{1}, \end{aligned}$$

(35)

$$\begin{aligned} c^{\star }(\theta )=&\int _{0}^{\theta } e^{- \int _{\tau _{1}}^{a}(M+v(\xi ))d\xi } \bigg [\int _{0}^{\tau _{1}} e^{- \int _{\textrm{x}}^{\tau _{1}} [M+\beta _{1} (\xi )+\vartheta (\xi )]d\xi }\bigg \{\lambda ^{\star }\int _{0}^{\textrm{x}} e^{- \int _{\omega }^{\textrm{x}} (M+\gamma (\xi ))d\xi }\bigg ( e^{- \int _{0}^{\omega } {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }+ \nonumber \\&\int _{0}^{\omega } \left( M +\beta _{2}(\tau _{2})v(\tau _{2})\right) d\tau _{2} e^{- \int _{\tau _{2}}^{\omega } {[}M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )]d\xi }\bigg ) \beta _{3}(\omega )d\omega \bigg \} \gamma (\textrm{x})v(\tau _{2})d\textrm{x} \bigg ] \beta _{1}(\tau _{1})d\tau _{1}, \end{aligned}$$

(36)

Next, we will use relation (34) and (36) in (32g) as

$$\begin{aligned} \lambda ^{\star } =&\int _{0}^{\theta _{+}} \beta (\theta ) \bigg [ \lambda ^{\star } \int _{0}^{\theta } \beta _{3}(\tau _{1})\bigg ( e^{- \int _{0}^{\tau _{1}} [M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon {(\xi )}] d \xi }+\int _{0}^{\tau _{1}}\left( M + \beta _{2}(\tau _{2}) v(\tau _{2}) \right) d \tau _{2} e^{- \int _{{\tau }_{2}}^{\tau _{1}}[M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon {(\xi )} d \xi } \bigg )\nonumber \\&e^{- \int _{\theta }^{\tau _{1}} (M+\gamma {(\xi )}) d \xi } d \tau _{1} +\int _{0}^{\theta } e^{- \int _{\tau _{1}}^{\theta } (M+v(\xi )) d \xi } \beta _{1} (\tau _{1}) \bigg \{\int _{0}^{\tau _{1}} e^{- \int _{\textrm{x}}^{\tau _{1}}[M+\beta _1 (\xi )+\vartheta {(\xi )}].(\xi )} \bigg (\lambda ^ { \star } \int _{ 0 }^{ \textrm{x} } e^{- \int _{ \omega }^{ \textrm{x}} ( M + \gamma ( \xi ) ) d \xi } \nonumber \\&\bigg (e^{- \int _0^{\omega }[M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon {(\xi )}] d \xi } \int _{0}^{\omega } \left( M +\beta _{2}(\tau _{2}) v(\tau _{2})\right) d \tau _{2} e^{- \int _{{\tau }_{2}}^{\omega }[M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon {(\xi )} d \xi } \bigg ) \beta _{3}(\omega )\gamma (\textrm{x})d\textrm{x}\bigg \}d\tau _{1}\bigg ]d\theta . \end{aligned}$$

(37)

Dividing both sides of equation (37) by $\lambda (\theta )^{\star }$ (because $\lambda ^{\star }\ne 0$ as by assuming its value zero, we will go bake to the case of no infection), we obtain

$$\begin{aligned} 1 =&\int _{0}^{\theta _+} \beta (\theta ) \bigg [ \int _0^{\theta } \beta _{3}(\tau _{1})\bigg ( e^{- \int _{0}^{\tau _{1}} [M+ \beta _{3}(\xi )+\epsilon {(\xi )}] d \xi }+\int _{0}^{\tau _{1}}\left( M + \beta _{2}(\tau _{2}) v(\tau _{2}) \right) d \tau _{2} e^{- \int _{\tau _{2}}^{\tau _{1}}[M+ \beta _{3}(\xi )+\epsilon (\xi ) d \xi } \bigg )\nonumber \\&e^{- \int _{\theta }^{\tau _{1}} (M+\gamma (\xi )) d \xi } d \tau _{1} +\int _{0}^{\theta } e^{- \int _{\tau _{1}}^{\theta } (M+v(\xi )) d \xi } \beta _{1} (\tau _{1}) \bigg \{\int _{0}^{\tau _{1}} e^{- \int _{\textrm{x}}^{\tau _{1}}[M+\beta _{1} (\xi )+\vartheta {(\xi )}].(\xi )} \bigg ( \int _{ 0 }^{ \textrm{x} } e^{- \int _{ \omega }^{ \textrm{x}} ( M + \gamma ( \xi ) ) d \xi } \nonumber \\&\bigg (e^{- \int _0^\omega [M+ \beta _{3}(\xi )+\epsilon (\xi )] d \xi } \int _{0}^\omega \left( M +\beta _{2}(\tau _{2}) v(\tau _{2})\right) d \tau _{2} e^{- \int _{\tau _{2}}^{\omega }[M+ \beta _{3}(\xi )+\epsilon {(\xi )} d \xi } \bigg ) \beta _{3}(\omega )\gamma (\textrm{x})d\textrm{x}\bigg \}d\tau _{1}\bigg ]d\theta . \end{aligned}$$

(38)

Let

$$\begin{aligned} G(\lambda ^{\star })=&\int _{0}^{\theta _{+}} \beta (\theta ) \bigg [ \lambda ^{\star } \int _{0}^{\theta } \beta _{3}(\tau _{1})\bigg ( e^{- \int _{0}^{\tau _{1}} [M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon (\xi )] d \xi }+\int _{0}^{\tau _{1}}\left( M + \beta _{2}(\tau _{2})v(\tau _{2}) \right) d \tau _{2} e^{- \int _{\tau _{2}}^{\tau _{1}}[M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon (\xi ) d \xi } \bigg )\nonumber \\&e^{- \int _{\theta }^{\tau _{1}} (M+\gamma (\xi )) d \xi } d \tau _{1} + \int _{0}^{\theta } e^{- \int _{\tau _{1}}^{\theta } (M+v(\xi )) d \xi } \beta _{1} (\tau _{1}) \bigg \{\int _{0}^{\tau _{1}} e^{- \int _{\textrm{x}}^{\tau _{1}}[M+\beta _{1} (\xi )+\vartheta (\xi )].(\xi )} \bigg (\lambda ^ { \star } \int _{ 0 }^{ \textrm{x} } e^{- \int _{ \omega }^{ \textrm{x}} ( M + \gamma ( \xi ) ) d \xi } \nonumber \\&\bigg (e^{- \int _0^\omega [M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon (\xi )] d \xi } \int _0^\omega \left( M +\beta _{2}(\tau _{2}) v(\tau _{2})\right) d \tau _{2} e^{- \int _{\tau _{2}}^{\omega }[M+\lambda ^{\star } \beta _{3}(\xi )+\epsilon (\xi ) d \xi } \bigg ) \beta _{3}(\omega )\gamma (\textrm{x})d\textrm{x}\bigg \}d\tau _{1}\bigg ]d\theta . \end{aligned}$$

(39)

From equation (39), we can see that the function $G(\lambda ^{\star })$ in a monotonic decreasing function of the argument and $G(0)=R_0$. Also

$$\begin{aligned} \lambda ^{\star }G(\lambda ^{\star })=\int _{0}^{\theta _+} M(\theta )[u^{\star }(\theta )+c^{\star }(\theta )]d\theta <\int _{0}^{\theta _+}\beta (\theta )d\theta , \end{aligned}$$

as $u^{\star }(\theta )+c^{\star }(\theta )<1$. Thus

$$\begin{aligned} G(\lambda ^{\star })<\frac{1}{\lambda ^{\star }}\int _{0}^{\theta _{+}}\beta (\theta )d\theta , \end{aligned}$$

(40)

Since $\lambda ^{\star }$ is positive under assumptions for parameters of the model. From inequality (40), we can observe that $\int _{0}^{\theta _+}b(\theta )d\theta$ tend to zero as $\lambda ^{\star }\rightarrow \infty$. Therefore, $G(\lambda ^{\star })=1$ (equation (39)) has a unique solution in the interval $(0,\infty )$ and now we can state the following theorem. $\square$

Theorem 6

The proposed model (7) has a unique endemic steady state $E^{\star }$ whenever $R_0>1$.

Stability of the unique endemic steady state can be explored, by following the methods presented in³⁸. Let us assume that $\tilde{s}(t,\theta ),\tilde{u}(t,\theta ),\tilde{c}(t,\theta ),\tilde{q}(t,\theta ),\tilde{r}(t,\theta )$ and $\tilde{v}(t,\theta ),$ be the perturbation in the state variables around $E^{\star }.$ Next, we will consider the exponential solutions of the perturb system as

$$\begin{aligned} \tilde{s}(t,\theta )=e^{\lambda t}\tilde{s}(\theta ), \tilde{u}(t,\theta )=e^{\lambda t}\tilde{u}(\theta ),\tilde{q}(t,\theta )=e^{\lambda t}\tilde{q}(\theta ), \tilde{c}(t,\theta )=e^{\lambda t}\tilde{c}(\theta ), \tilde{r}(t,\theta )=e^{\lambda t}\tilde{r}(\theta ), \tilde{v}(t,\theta )=e^{\lambda t}\tilde{v}(\theta ), \end{aligned}$$

(41)

which satisfies

$$\begin{aligned} \frac{d\tilde{s}(\theta )}{d\theta }=&-[M+\lambda ^{\star }\beta _{3}(\theta )+\epsilon (\theta )+\phi ]\tilde{s}(\theta )-\tilde{\lambda }\beta _{3}(\theta )\tilde{s}(\theta )+\beta _{2}(\theta )\tilde{v}(\theta ),\end{aligned}$$

(42a)

$$\begin{aligned} \frac{d\tilde{u}(\theta )}{d\theta }=&-[M+\gamma (\theta )+\phi ] \tilde{u}(\theta )+\beta _{3}(\theta )[\tilde{\Lambda }s^{\star }(\theta )+\Lambda ^{\star }\tilde{s}(\theta )],\end{aligned}$$

(42b)

$$\begin{aligned} \frac{d\tilde{q}(\theta )}{d\theta }=&-[\phi +M+\beta _{1}(\theta )+\vartheta (\theta )]\tilde{q}(\theta )+\gamma (\theta )\tilde{u}(\theta ),\end{aligned}$$

(42c)

$$\begin{aligned} \frac{d\tilde{c}(\theta )}{d\theta }=&\beta _{1}(\theta )\tilde{q}(\theta )-[\phi +M+v(\theta )]\tilde{c}(\theta ),\end{aligned}$$

(42d)

$$\begin{aligned} \frac{d\tilde{r}(\theta )}{d\theta }=&-[\phi +M]\tilde{r}(\theta )+v(\theta )\tilde{c}(\theta )+\vartheta (\theta )\tilde{q}(\theta ),\end{aligned}$$

(42e)

$$\begin{aligned} \frac{d\tilde{v}(\theta )}{d\theta }=&\epsilon (\theta )\tilde{s}(\theta )-[\phi +M+\beta _{2}(\theta )]\tilde{v}(\theta ),\end{aligned}$$

(42f)

$$\begin{aligned} \tilde{\Lambda }=&\int _{0}^{\theta _{+}}\beta (\theta )[\tilde{u}(\theta )+\tilde{c}(\theta )]d\theta ,\end{aligned}$$

(42g)

$$\begin{aligned} \tilde{s}(0)=&\tilde{u}(0)=\tilde{q}(0)=\tilde{c}(0)=\tilde{r}(0)=\tilde{v}(0)=0. \end{aligned}$$

(42h)

Setting the fractions and incorporating the new variables

$$\begin{aligned} {\bar{s}}(\theta )=\frac{\tilde{s}(\theta )}{\tilde{\lambda }},~{\bar{u}}(\theta )=\frac{\tilde{u}(\theta )}{\tilde{\lambda }},~{\bar{q}}(\theta )=\frac{\tilde{q}(\theta )}{\tilde{\lambda }},~{\bar{c}}(\theta )=\frac{\tilde{c}(\theta )}{\tilde{\lambda }},~{\bar{r}}(\theta )=\frac{\tilde{v}(\theta )}{\tilde{\lambda }},~{\bar{v}}(\theta )=\frac{\tilde{v}(\theta )}{\tilde{\lambda }}. \end{aligned}$$

By using these new variables, system (42) becomes

$$\begin{aligned} \frac{d{\bar{s}}(\theta )}{d\theta }=&-[M+\lambda ^{\star }\beta _{3}(\theta )+\epsilon (\theta )+\phi ]{\bar{s}}(\theta )-\beta _{3}(\theta ){\bar{s}}(\theta )+\beta _{2}(\theta ){\bar{v}}(\theta ),\end{aligned}$$

(43a)

$$\begin{aligned} \frac{d{\bar{u}}(\theta )}{d\theta }=&-[M+\gamma (\theta )+\phi ] {\bar{u}}(\theta )+\beta _{3}(\theta )[s^{\star }(v)+\Lambda ^{\star }{\bar{s}}(\theta )],\end{aligned}$$

(43b)

$$\begin{aligned} \frac{d{\bar{q}}(\theta )}{d\theta }=&-[\phi +M+\beta _{1}(\theta )+\vartheta (\theta )]{\bar{q}}(\theta )+\gamma (\theta ){\bar{u}}(\theta ),\end{aligned}$$

(43c)

$$\begin{aligned} \frac{d{\bar{c}}(\theta )}{d\theta }=&\beta _{1}(\theta ){\bar{q}}(\theta )-[\phi +M+v(\theta )]{\bar{c}}(\theta ),\end{aligned}$$

(43d)

$$\begin{aligned} \frac{d{\bar{r}}(\theta )}{d\theta }=&-[\phi +M]{\bar{r}}(\theta )+v(\theta ){\bar{c}}(\theta )+\vartheta (\theta ){\bar{q}}(\theta ),\end{aligned}$$

(43e)

$$\begin{aligned} \frac{d{\bar{v}}(\theta )}{d\theta }=&\epsilon (\theta ){\bar{s}}(\theta )-[\phi +M+\beta _{2}(\theta )]{\bar{v}}(\theta ),\end{aligned}$$

(43f)

$$\begin{aligned} 1=&\int _{0}^{\theta _{+}}\beta (\theta )[{\bar{u}}(\theta )+{\bar{c}}(\theta )]d\theta ,\end{aligned}$$

(43g)

$$\begin{aligned} {\bar{s}}(0)=&{\bar{u}}(0)={\bar{q}}(0)={\bar{c}}(0)={\bar{r}}(0)={\bar{v}}(0)=0. \end{aligned}$$

(43h)

Solving system (43) for ${\bar{s}}(\theta )$, ${\bar{s}}(u)$, ${\bar{q}}(\theta )$ and ${\bar{s}}(c)$

$$\begin{aligned} {\bar{s}}=&-\int _{0}^{\theta }[\beta _{3}(\tau _{1})s^{\star }(\tau _{1})-\beta _{2}(\tau _{1}){\bar{v}}(\tau _{1})]e^{-\int _{\tau _{1}}^{\theta }[M+\lambda ^{\star }\beta _{3}(\xi )+\epsilon (\xi )+\phi ]d\xi }d\tau _{1},\end{aligned}$$

(44a)

$$\begin{aligned} {\bar{u}}=&\int _{0}^{\theta }\beta _{3}(\tau _{1})[s^{\star }(\tau _{1})+\lambda ^{\star }{\bar{s}}(\tau _{1})]e^{-\int _{\tau _{1}}^{\theta }[M+\epsilon (\xi )+\phi ]d\xi }d\tau _{1},\end{aligned}$$

(44b)

$$\begin{aligned} {\bar{q}}=&\int _{0}^{\theta }\gamma (\tau _{1})\biggl \{\int _{0}^{\tau _{1}}\beta _{3}(\omega )\bigl (s^{\star }(\omega )+\lambda ^{\star }{\bar{s}}(\omega )\bigr )e^{-\int _{\omega }^{\tau _{1}}[M+\epsilon (\xi )+\phi ]d\xi }d\omega \biggr \}\nonumber \\&e^{-\int _{\tau _{1}}^{\theta }[M+\beta _1 (\xi )+\vartheta (\xi )+\phi ]d\xi }d\tau _{1},\end{aligned}$$

(44c)

$$\begin{aligned} {\bar{c}}=&\int _{0}^{\theta }\biggl [\int _{0}^{\tau _{1}}\biggl \{\int _{0}^{\tau _{1}}\beta _{3}(\tau _{2})\bigl (s^{\star }(\tau _{2})+\lambda ^{\star }{\bar{s}}(\tau _{2})\bigr )e^{-\int _{\tau _{2}}^{\omega }[M+\epsilon (\xi )+\phi ]d\xi }d\tau _{2}\biggr \}\nonumber \\&e^{-\int _{\tau _{1}}^{\theta }[M+\beta _1 (\xi )+\vartheta (\xi )+\phi ]d\xi }\gamma (\omega )d\omega \biggr ]e^{-\int _{\tau _{1}}^{\theta }[M+v(\xi )+\phi ]d\xi }\beta _{1}(\tau _{1})d\tau _{1}, \end{aligned}$$

(44d)

For the sake of simplicity, let us denote the RHS of equation (43g) by ${\mathcal {Q}}(\varphi )$, thus

$$\begin{aligned} {\mathcal {Q}}(\varphi )=\int _{0}^{\theta _{+}}\beta (\theta )[{\bar{u}}(\theta )+{\bar{c}}(\theta )]d\theta =1. \end{aligned}$$

(45)

By plugging the values of ${\bar{u}}(\theta )$ and ${\bar{c}}(\theta )$ from equation (44b) and (44d) into ${\mathcal {Q}}(\varphi )$ and rearranging the terms, we get

$$\begin{aligned} {\mathcal {Q}}(\varphi )=&\int _{0}^{\theta _+}\beta (\theta )\biggl [ \int _{0}^{\theta }\beta _{3}(\tau _{1})[s^{\star }(\tau _{1})+\lambda ^{\star }{\bar{s}}(\tau _{1})]e^{-\int _{\tau _{1}}^{\theta }[M+\epsilon (\xi )+\phi ]d\xi }d\tau _{1}\biggr ]d\theta +\int _{0}^{\theta _+}\beta (\theta )\nonumber \\&\biggl [\int _{0}^{\theta }\int _{0}^{\tau _{1}}\biggl \{\int _{0}^{\tau _{1}}\biggl (\beta _{3}(\tau _{2})\Bigl (s^{\star }(\tau _{2})+\lambda ^{\star }{\bar{s}}(\tau _{2})\Bigr )e^{-\int _{\tau _{2}}^{\omega }[M+\epsilon (\xi )+\phi ]d\xi }d\tau _{2}\biggr )\nonumber \\&e^{-\int _{\tau _{1}}^{\theta }[M+\beta _1 (\xi )+\vartheta (\xi )+\phi ]d\xi }\gamma (\omega )d\omega \biggr \}e^{-\int _{\tau _{1}}^{\theta }[M+v(\xi )+\phi ]d\xi }\beta _{1}(\tau _{1})d\tau _{1}\biggr ]d\theta . \end{aligned}$$

(46)

Splitting the integral, letting $\varphi =0$ and upon simplification, we get

$$\begin{aligned} {\mathcal {Q}}(0)=&\int _{0}^{\theta _+}\beta (\theta )\biggl [ \int _{0}^{\theta }\beta _{3}(\tau _{1})[s^{\star }(\tau _{1})+\lambda ^{\star }{\bar{s}}(\tau _{1})]e^{-\int _{\tau _{1}}^{\theta }[M+\epsilon (\xi )+\phi ]d\xi }d\tau _{1}\biggr ]d\theta +\int _{0}^{\theta _+}\beta (\theta )\nonumber \\&\biggl [\int _{0}^{\theta }\int _{0}^{\tau _{1}}\biggl \{\int _{0}^{\tau _{1}}\biggl (\beta _{3}(\tau _{2})\Bigl (s^{\star }(\tau _{2})+\lambda ^{\star }{\bar{s}}(\tau _{2})\Bigr )e^{-\int _{\tau _{2}}^{\omega }[M+\epsilon (\xi )+\phi ]d\xi }d\tau _{2}\biggr )\nonumber \\&e^{-\int _{\tau _{1}}^{a}[M+\beta _1 (\xi )+\vartheta (\xi )+\phi ]d\xi }\gamma (\omega )d\omega \biggr \}e^{-\int _{\tau _{1}}^{\theta }[M+v(\xi )+\phi ]d\xi }\beta _{1}(\tau _{1})d\tau _{1}\biggr ]d\theta . \end{aligned}$$

(47)

Using $s^{\star }(\tau _{1})$ and ${\bar{s}}(\tau _{1})$ from equations (33) and (44a), we can say that the first integral on the RHS is exactly equal to 1 by (38), while the second is negative. Thus ${\mathcal {Q}}(0)<1.$ Moreover, equations in (44) show that ${\bar{s}},~~{\bar{u}},~~{\bar{q}}$, and ${\bar{c}}$ approaches zero when $\epsilon \rightarrow \infty$, resulting in $\lim _{\epsilon \rightarrow \infty } {\mathcal {Q}}(\epsilon )=0$. Thus, the equation (45) has a unique negative real solution, however, every complex solution has real parts that are smaller than the single true answer. Thus, for the stability of the endemic steady state the following results will be utilized.

Theorem 7

System (7) has endemic steady state $E^{\star }$ which is locally asymptotically stable if $R_0>1$.

Based on these discussions, if $R_0<1$, the suggested model provides a disease-free state that is locally and globally asymptotically stable. While the model has a unique endemic steady state which is shown to be locally asymptotically stable under the same condition whenever $R_0$ is exceeding than one. To demonstrate the global stability of the endemic steady state, we will look at a specific instance of the model in the following section.

Model with constant parameter values

In previous work, we evaluated the model (system (1) or equivalently (7)) and considered that all of the parameters are dependent on age. In this part, we will explore a special example of model (1), by employing the age independent parameter as established in³⁹. Assuming constant rates, model (1) will becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {S(t,\theta )}}{\partial {t}}+\frac{\partial {S(t,\theta )}}{\partial {\theta }}= & MP(t,\theta )-(\lambda (t)+\delta +\epsilon )+\beta _{2} V(t,\theta ),\\ \frac{\partial {U(t,\theta )}}{\partial {t}}+\frac{\partial {U(t,\theta )}}{\partial {\theta }}= & \lambda (t)S(t,\theta )-(\gamma +\delta )U(t,\theta ),\\ \frac{\partial {Q(t,\theta )}}{\partial {t}}+\frac{\partial {Q(t,\theta )}}{\partial {\theta }}= & \gamma U(t,\theta )-(\beta _{1}+\vartheta +\delta )Q(t,\theta ),\\ \frac{\partial {C(t,\theta )}}{\partial {t}}+\frac{\partial {C(t,\theta )}}{\partial {\theta }}= & \beta _{1}Q(t,\theta )-(\delta +v)C(t,\theta ),\\ \frac{\partial {R(t,\theta )}}{\partial {t}}+\frac{\partial {R(t,\theta )}}{\partial {\theta }}= & vC(t,\theta )+\vartheta Q(t,\theta )-\delta R(t,\theta ) ,\\ \frac{\partial {V(t,\theta )}}{\partial {t}}+\frac{\partial {V(t,\theta )}}{\partial {\theta }}= & \epsilon S(t,\theta )-(\delta +\beta _{2})V(t,\theta ), \end{array}\right. } \end{aligned}$$

(48)

with the conditions

$$\begin{aligned} S(t,0)=\int _{0}^{\theta _{+}}{bP(t,\theta )d\theta },U(t,0)=&Q(t,0)=C(t,0)=R(t,0)=V(t,0)=0, \end{aligned}$$

(49a)

$$\begin{aligned} (S,U,Q,C,R,V)(0,\theta )=(S_0(\theta )&,U_0(\theta ),Q_0(\theta ),C_0(\theta ),R_0(\theta ),V_0(\theta )), \end{aligned}$$

(49b)

and

$$\begin{aligned} \lambda (t)=\beta ^{\prime } \int _0^{\theta +} \frac{[U(t, \theta )+C(t, \theta )]}{P(t, \theta )} d \theta , \end{aligned}$$

(50)

where $\beta ^{\prime }=k \beta$. Let us take

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{S}(t)=\int _{0}^{\theta _{+}} S(t, \theta ) d \theta , \tilde{U}(t)=\int _{0}^{\theta _{+}} U(t, \theta ) d \theta , \tilde{Q}(t)=\int _{0}^{\theta _{+}} Q(t, \theta ) d \theta , \\ \tilde{C}(t)=\int _{0}^{\theta _{+}} C(t, \theta ) d \theta , \tilde{R}(t)=\int _{0}^{\theta _{+}} R(t, \theta ) d \theta , \tilde{V}(t)=\int _{0}^{\theta _{+}} V(t, \theta ) d \theta . \end{array}\right. \end{aligned}$$

Consider the model assumptions outlined in⁴¹. :

$H_1$ $\tilde{S}+\tilde{U}+\tilde{Q}+\tilde{C}+\tilde{R}+\tilde{V}=P_0$ (where $P_0$ is the initial population), which assumes finite $\tilde{S}, \tilde{U}, \tilde{Q}, \tilde{C}$, $\tilde{R}$ and $\tilde{V}$, $\forall$ t.

$\textrm{H}_2$ The relation

$$\begin{aligned} \frac{d X(t)}{d t}=\int _0^{\theta } \frac{\partial X}{\partial t} d\theta , \end{aligned}$$

(51)

is true for all values of $X=\tilde{S},$ $\tilde{U}$, $\tilde{Q},$ $\tilde{C}$, $\tilde{R}$ and $\tilde{V}$.

$H_3$ The starting distribution of ages functions are capable of differentiation, continuous, and positive. They approach zero as $\theta \rightarrow \theta _{+}$.

$H_4$ The condition $\lim _{\theta \rightarrow 0} X(0, \theta )=\lim _{t \rightarrow 0} X(t, 0)$ and the right derivative of $X(0, \theta )$ is zero at $\theta =0$ for each $X=S, U, Q, C,R$ and V.

On integrating system (48) with respect to $\theta$ and observing the assumptions $H_1-H_4$ which yields the following ODE model.

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d \tilde{S}(t)}{d t}=(M+b) P_0-(\tilde{\lambda }(t)+\delta ) \tilde{S}(t)+\beta _{2} \tilde{V}(t), \\ \frac{d \tilde{U}(t)}{d t}=\tilde{\lambda }(t) \tilde{S}(t)-(\gamma +\delta ) \tilde{U}(t), \\ \frac{d \tilde{Q}(t)}{d t}=\gamma \tilde{U}(t)-\left( \beta _1+\vartheta +\delta \right) \tilde{Q}(t), \\ \frac{d \tilde{C}(t)}{d t}=\beta _1 \tilde{Q}(t)-(\delta +v) \tilde{C}(t), \\ \frac{d \tilde{R}(t)}{d t}=v \tilde{C}(t)+\vartheta \tilde{Q}(t)-\delta \tilde{R}(t),\\ \frac{d \tilde{V}(t)}{d t}=\epsilon \tilde{S}(t)-(\beta _{2}+\delta ) \tilde{V}(t), \end{array}\right. } \end{aligned}$$

(52)

where

$$\begin{aligned} \tilde{\lambda }(t)=\frac{\beta ^{\prime }}{P_{0}}[\tilde{U}(t)+\tilde{C}(t)], \end{aligned}$$

(53)

and $\tilde{S}(0)=\tilde{S}_{0}>0$, $\tilde{U}(0)=\tilde{U}_0 \ge 0$, $\tilde{Q}(0)=\tilde{Q}_0 \ge 0$, $\tilde{C}(0)=\tilde{C}_0 \ge 0$, $\tilde{R}(0)= \tilde{R}_0 \ge 0$ and $\tilde{V}(0)=\tilde{V}_{0} \ge 0$. The attainable area for the suggested ODE model (52) is

$$\begin{aligned} \Delta =\left\{ (\tilde{S}, \tilde{U}, \tilde{Q}, \tilde{C}, \tilde{R}), \tilde{V} \in R_{+}^5: \tilde{S}+\tilde{U}+\tilde{Q}+\tilde{C}+\tilde{R}+\tilde{V} \le P_{0}\right\} . \end{aligned}$$

(54)

The system has the disease free equilibrium as given by

$$\begin{aligned} E_{0 c}=\left( \frac{(b+M) P_0}{\delta }, 0,0,0,0,0\right) . \end{aligned}$$

(55)

We will use the standard method to calculate the fundamental reproduction number $R_0^c$ for the ODE model. For this, choose the infected classes $\varepsilon =(U, Q, C)^T$, then by using

$$\begin{aligned} {\bar{F}}=\left( \begin{array}{c} \frac{\beta ^{\prime }}{P_0}[\tilde{U}+\tilde{C}] \tilde{S} \\ 0 \\ 0 \end{array}\right) , {\bar{W}}=\left( \begin{array}{c} (\gamma +\delta ) \tilde{U}(t) \\ -\gamma \tilde{U}+\left( \beta _1+\vartheta +\delta \right) \tilde{Q} \\ -\beta _1 \tilde{Q}(t)+(\delta +v) \tilde{C}(t) \end{array}\right) {. } \end{aligned}$$

(56)

The system (52) center three equations will be expressed as

$$\begin{aligned} \frac{d \varepsilon }{d t}={\bar{F}}-{\bar{W}}. \end{aligned}$$

(57)

The linear and non-linear terms are represented by the matrices ${\bar{W}}$ and F. By Utilizing the Jacobean of matrices (54) at disease free equilibrium point. $E_{0 c}=\left( S^0, 0,0,0,0,0\right)$ where $S^0=\frac{(b+M) P_0}{\delta }$, we get

$$\begin{aligned} F=\left( \begin{array}{ccc} \frac{\beta _0^{\prime }}{F_0} S^0 & 0 & \frac{\beta ^{\prime }}{p} S^0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right) , W=\left( \begin{array}{ccc} \gamma +\delta & 0 & 0 \\ -\gamma & \beta _1+\vartheta +\delta & 0 \\ 0 & \beta _1 & \delta +\nu \end{array}\right) . \end{aligned}$$

(58)

The threshold number $R_0^c$ of ${\bar{K}}=F W^{-1}$ denotes its spectral radius $\rho(\lambda)$, which is the dominating eigenvalue. Thus, we get

$$\begin{aligned} R_{0}^c=\frac{\beta ^{\prime }}{P_{0}} S^0 \frac{\left( \gamma \beta _1+\left( \beta _1+\vartheta +\delta \right) (\delta +\nu )\right) }{(\gamma +\delta )\left( \beta _1+\vartheta +\delta \right) (\delta +\nu )} . \end{aligned}$$

(59)

It is better to see that the model (52) is a sub-case of the system (1).Thus, the disease-free equilibrium $E_{0 c}$ of the ODE model (52) will be locally and globally asymptotically stable under the same circumstances of $R_0^c$ less and higher than one, respectively. The existence of endemic steady has been presented earlier; nevertheless, for the case of ODE models, consult the references^2,43. Utilizing these references, the endemic equilibrium point of the model (52) is given by

$$\begin{aligned} E_{1 c}=\left( S^{\star *}, U^{\star *}, Q^{\star *}, C^{\star *}, R^{\star *}\right). \end{aligned}$$

(60)

The previously defined force of infection $\lambda$ should be stated as an endemic steady state, as shown below

$$\begin{aligned} \lambda ^{\star \star }=\frac{\beta ^{\prime }}{P^{0}}\left[ U^{\star \star }+C^{\star \star }\right] , \end{aligned}$$

(61)

thus

$$\begin{aligned} \lambda ^{\star \star }=\frac{\delta (\delta +\beta _{2})S^0+\beta _{2} \epsilon S^{\star \star }}{(\delta +\beta _{2})S^{0}+\delta +\epsilon )}. \end{aligned}$$

(62)

The component of $E_{1 c}$ will takes the form by inserting the unique value of $\lambda ^{\star \star }$ (62). Thus we get

$$\begin{aligned}&S^{\star \star }=\frac{S^0}{R_0^c}, \end{aligned}$$

(63a)

$$\begin{aligned}&U^{\star \star }=\frac{\gamma S^0 \left[ R_0^c (\delta (\beta _{2}+\delta )+\beta _{2}\epsilon )-(\delta +\epsilon )(\delta +\beta _{2})\right] }{R_0^c (\delta +\beta _{2})(\gamma +\delta )}, \end{aligned}$$

(63b)

$$\begin{aligned}&Q^{\star \star }=\frac{\gamma S^0 \left( ( \delta (\beta _{2}+\delta )R_0^c+\beta _{2}\epsilon )-(\delta +\epsilon )(\delta +\beta _{2})\right) }{R_0^c (\delta +\beta _{2})(\gamma +\delta )(\beta _1+\vartheta +\delta )}, \end{aligned}$$

(63c)

$$\begin{aligned}&C^{\star \star }=\frac{\beta _1 \gamma S^0 \left( ( \delta (\beta _{2}+\delta )R_0^c+\beta _{2}\epsilon )-(\delta +\epsilon )(\delta +\beta _{2})\right) }{R_0^c (\delta +\beta _{2})(\nu +\delta )(\gamma +\delta )(\beta _1+\vartheta +\delta )}, \end{aligned}$$

(63d)

$$\begin{aligned}&R^{\star \star }=\frac{\gamma S^0 \left( ( \delta (\beta _{2}+\delta ) R_0^c+\beta _{2} \epsilon )-(\delta +\epsilon )(\delta +\beta _{2})\right) }{ R_0^c \left( \delta (\delta +\beta _{2})(\nu +\delta )(\gamma +\delta )(\beta _1+\vartheta +\delta )\right) },\end{aligned}$$

(63e)

$$\begin{aligned}&V^{\star \star }=\frac{\epsilon s^{0}}{(\delta +\beta _{2})R_0^c}, \end{aligned}$$

(63f)

on the basis of relations (63) we can state the following theorem.

Theorem 8

Model (52) has the unique EE point $E_{1 c}$ defined by (60), whenever $R_0^c>1$.

Let us proceed further and define another region.

$$\begin{aligned} \Delta _1=\left\{ \tilde{S}, \tilde{U}, \tilde{Q}, \tilde{C}, \tilde{R}, \tilde{V} \in \Delta \,|\, \tilde{S}=P_0, \tilde{U}=\tilde{Q}=\tilde{C}=\tilde{R}=\tilde{V}=0\right\} . \end{aligned}$$

(64)

For endemic equilibrium $E_{1 c}$ to be globally stable, we will state and prove following theorem.

Theorem 9

The unique EE point of the model (52) is globally asymptotically stable in $\Delta _{1}$ whenever $R_{0}^{c}>1$.

Proof

Since $R0^c>1$, therefore, Theorem 8 ensures us the existence of the unique endemic equilibrium E1c of the model (52). To get our desire goal, we will define the non-linear Lyapunov function of the form

$$\begin{aligned} H=&\tilde{S}-S^{\star \star }-S^{\star \star } \ln \frac{\tilde{S}}{S^{\star \star }}+\frac{\beta ^{\prime } S^{\star \star }\left( U^{\star \star }+C^{\star \star }\right) }{P_0(\gamma +\delta ) U^{\star \star }}\left[ \tilde{U}-U^{\star \star }-U^{\star \star } \ln \frac{\tilde{U}}{U^{\star \star }}\right] \\&+\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }}\left[ \tilde{Q}-Q^{\star \star }-Q^{\star \star } \ln \frac{\tilde{Q}}{Q^{\star \star }}\right] +\frac{\beta ^{\prime } S^{\star \star }}{P_0(\delta +v)}\left[ \tilde{C}-C^{\star \star }-C^{\star \star } \ln \frac{\tilde{C}}{C^{\star \star }}\right] , \end{aligned}$$

with the derivative

$$\begin{aligned} \frac{d H}{d t}=&\frac{d \tilde{S}}{d t}-\frac{S^{\star \star }}{\tilde{S}} \frac{d \tilde{S}}{d t}+\frac{\beta ^{\prime } S^{\star \star }\left( U^{\star \star }+C^{\star \star }\right) }{P_0(\gamma +\delta ) U^{\star \star }}\left[ \frac{d \tilde{U}}{d t}-\frac{U^{\star \star }}{\tilde{U}} \frac{d \tilde{U}}{d t}\right] +\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }} \\&\times \left[ \frac{d {\bar{Q}}}{d t}-\frac{Q^{\star \star }}{{\bar{Q}}} \frac{d \tilde{Q}}{d t}\right] +\frac{\beta ^{\prime } S^{\star \star }}{P_0(v+\delta )}\left[ \frac{d \tilde{C}}{d t}-\frac{C^{\star \star }}{\tilde{C}} \frac{d \tilde{C}}{d t}\right] \\ =&(b+M) P_0-\frac{\beta ^{\prime }}{P_0} \tilde{U} \tilde{S}-\frac{\beta ^{\prime }}{P_0} \tilde{C} \tilde{S}-\delta \tilde{S}-\epsilon \tilde{S}+\beta _{2}\tilde{V}-\frac{S^{\star \star }}{\tilde{S}}\left[ (b+M) P_0 - \frac{\beta ^{\prime }}{P_0} \tilde{U} \tilde{S}-\frac{\beta ^{\prime }}{P_0} \tilde{C} \tilde{S} -\delta \tilde{S}-\epsilon \tilde{S}\right. \\&\left. +\beta _{2}\tilde{V}\right] +\frac{\beta ^{\prime } S^{\star \star }\left( U^{\star \star }+C^{\star \star }\right) }{P_0(\gamma +\delta ) U^{\star \star }}\left[ \frac{\beta ^{\prime }}{P_0}(\tilde{U}+\tilde{C}) \tilde{S}(t)-(\gamma +\delta ) \tilde{U}(t)-\frac{U^{\star \star }}{\tilde{U}}\left( \frac{\beta ^{\prime }}{P_0}(\tilde{U}+\tilde{C}) \tilde{S}(t)-(\gamma +\delta ) \tilde{U}(t)\right) \right] \\&+\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }}\left[ \tilde{U}-\left( \beta _1+\vartheta +\delta \right) \tilde{Q}-\frac{Q^{\star \star }}{{\bar{Q}}}\left( \gamma {\bar{U}}-\left( \beta _1+\vartheta +\delta \right) {\bar{Q}}\right) \right] +\frac{\beta ^{\prime } S^{\star \star }}{P_0(\nu +\delta )}\left[ \beta _1 {\bar{Q}}-(\delta +v) {\bar{C}}\right. \\&\left. -\frac{C^{\star \star }}{{\bar{C}}}\left( \beta _1 {\bar{Q}}-(\delta +v) \tilde{C}\right) \right] . \end{aligned}$$

By applying the first steady-state equation $(b+M) P_0 -\frac{\beta ^{\prime }}{P_0}\left( U^{\star \star }+C^{\star \star }\right) S^{\star \star }-\delta S^{\star \star }-\epsilon S^{\star \star }+\beta _{2} V^{\star \star }=0,$ and simplifying, we obtain

$$\begin{aligned} \frac{dH}{dt}=&\left( \delta +\epsilon \right) S^{\star \star }\left( 2-\frac{S^{\star \star }}{\tilde{S}}-\frac{\tilde{S}}{S^{\star \star }}\right) -\frac{\beta _{2}\left( S^{\star \star }-\tilde{S}\right) \left( \tilde{v}-V^{\star \star }\right) }{\tilde{S}} +\frac{\beta ^{\prime }}{P_{0}}\left( U^{\star \star }+C^{\star \star }\right) S^{\star \star }\\&-\frac{\beta ^{\prime }}{P_{0}}\left( U^{\star \star }+C^{\star \star }\right) \frac{{S^{\star \star }}^{2}}{\tilde{S}} -\frac{\beta ^{\prime }}{P_{0}}\left( \tilde{U}+\tilde{C}\right) \tilde{S}+\frac{\beta ^{\prime }}{P_0}\left( \tilde{U}+\tilde{C}\right) S^{\star \star }+\frac{{\beta ^{\prime }}^{2}\tilde{S}}{P_{0}^{2}(\gamma +\delta )}\left( \tilde{U}+\tilde{C}\right) S^{\star \star }\\&-\frac{\beta ^{\prime }}{P_{0}}\tilde{U}S^{\star \star }-\frac{\beta ^2 S^{\star \star }}{P_{0}^2(\gamma +\delta )} U^{\star \star } \tilde{S}-\frac{\beta ^{\prime 2} S^{\star \star }}{P_0^2(\gamma +\delta )} \frac{U^{\star \star }}{\tilde{U}} \tilde{C} \tilde{S}+\frac{\beta ^{\prime }}{P_0} S^{\star \star } U^{\star \star }-\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 U^{\star \star }} \tilde{U} \\&+\frac{\beta ^2 S^{\star \star } C^{\star \star }}{P_0^2(\gamma +\delta ) U^{\star \star }}(\tilde{U}+\widetilde{C}) \tilde{S}-\frac{\beta ^2 S^{\star \star } C^{\star \star }}{P_0^2(\gamma +\delta )} \tilde{S}-\frac{\beta ^{\prime 2} S^{\star \star } C^{\star \star }}{P_0^2(\gamma +\delta )} \frac{\widetilde{C} \tilde{U}}{\tilde{U}}+\frac{\beta ^{\prime }}{P_0} S^{\star \star } C^{\star \star } +\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }} \gamma {\bar{U}}\\&-\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }}\left( \beta _1+\vartheta +\delta \right) {\bar{Q}}-\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }} \gamma Q^{\star \star } \frac{\widetilde{U}}{{\bar{Q}}} +\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0 \gamma U^{\star \star }}\left( \beta _{1}+\vartheta +\delta \right) Q^{\star \star }+\frac{\beta ^{\prime } S^{\star \star }}{P_{0}(\nu +\delta )} \beta _{1} \tilde{Q}\\&-\frac{\beta ^{\prime }}{P_{0}} S^{\star \star } {\bar{C}} -\frac{\beta ^{\prime } \beta _{1} S^{\star \star } C^{\star \star }}{P_{0}(\nu +\delta )} \frac{\tilde{Q}}{\check{C}}+\frac{\beta ^{\prime }}{P_0} S^{\star \star } C^{\star \star }. \end{aligned}$$

Similarly, by utilizing the following relations $\frac{\beta ^{\prime }}{P_0}\left( U^{\star \star }+C^{\star \star }\right) S^{\star \star }-(\delta +\gamma ) U^{\star \star }= 0, \gamma U^{\star \star }-\left( \beta _1+\vartheta +\delta \right) Q^{\star \star }=0$ and $\beta _1 Q^{\star \star }-(\delta +v) C^{\star \star }=0$, we obtain $\epsilon S^{\star \star }-(\delta +\beta _{2})V^{\star \star }=0.$

$$\begin{aligned} \frac{d H}{d t}=&(\delta +\epsilon ) S^{\star \star }\left( 2-\frac{S^{\star \star }}{\tilde{S}}-\frac{{\bar{S}}}{S^{\star \star }}\right) -\frac{\beta _{2}\left( S^{\star \star }-\tilde{S}\right) \left( \tilde{v}-V^{\star \star }\right) }{\tilde{S}}+\frac{\beta ^{\prime } S^{\star \star } U^{\star \star }}{P_0}\left( 2-\frac{S^{\star \star }}{\tilde{S}}-\frac{\tilde{S}}{S^{\star \star }}\right) \nonumber \\&+\frac{\beta ^{\prime } S^{\star \star } C^{\star \star }}{P_0}\left( 4-\frac{S^{\star \star }}{\tilde{S}}-\frac{Q^{\star \star } {\bar{U}}}{{\bar{Q}} U^{\star \star }}-\frac{U^{\star \star \tilde{C} \tilde{S}}}{{\bar{U}} C^{\star \star } S^{\star \star }}-\frac{C^{\star \star } \tilde{Q}}{\tilde{C} Q^{\star \star }}\right) . \end{aligned}$$

(65)

Since we know that the geometric mean is always less than or equal to arithmetic mean, so can conclude that

$$\begin{aligned} \left( 2-\frac{S^{\star \star }}{{\bar{S}}}-\frac{\tilde{S}}{S^{\star \star }}\right)&\le 0, \end{aligned}$$

(66a)

$$\begin{aligned} \left( 4-\frac{S^{\star \star }}{\tilde{S}}-\frac{Q^{\star \star } \tilde{U}}{\tilde{Q} U^{\star \star }}-\frac{U^{\star \star } {\bar{C}} {\bar{S}}}{\tilde{U} C^{\star \star } S^{\star \star }}-\frac{C^{\star \star } \tilde{Q}}{{\bar{C}} Q^{\star \star }}\right)&\le 0 . \end{aligned}$$

(66b)

Thus, by using (66) in (65) we have $\frac{d H}{d t} \le 0$ whenever $R_{0}^{c}>1$ and hence the unique endemic equilibrium point is globally asymptotically stable, by using the LaSalles Invariance Principle, that is, $(\tilde{S}, \tilde{U}, \tilde{Q}, \tilde{C}, \tilde{R},\tilde{V}) \rightarrow \left( S^{\star \star }, U^{\star \star }, C^{\star \star }, Q^{\star *}, R^{\star *},V^{\star \star }\right)$ as t tends to $\infty$. $\square$

Numerical concepts

In the present section, we will explain the numerical method used for simulation purpose. Since, the original model (1) and its equivalent system (7) and the adjoint system are containing PDEs, therefore, utilizing the finite difference method of characteristics is preferable for numerically solving the systems. We have also explored a sub-case of the proposed model that consists of ODEs and we plan to use the standard Runge-Kutta 4th order (RK4) method for numerical solution. In the case of a system with PDEs, the domain will be

$$\begin{aligned} Y=\left\{ (t, \theta ): 0 \le t \le T_{f}, 0 \le \theta \le J\right\} , \end{aligned}$$

where $T_f$ represents the final time, and J denotes the maximum age that a population unit can reach. In the present case, $J=90$ years and $T_{f}=100$ weeks are considered. The $\theta _{i}=i \Delta \theta$ and $t_{n}=n \Delta t$ show age and time. Further, we considered $K=\left[ \frac{J}{\Delta \theta }\right]$ and ${\mathcal {U}}=\left[ \frac{T_{f}}{\Delta t}\right]$. Applying an implicit partial linearization method, the requirements and the descritized version of equation (7a) will take the following form

$$\begin{aligned} \left\{ \begin{array}{l} \frac{s_{i+1}^{n+1}-s_{i}^{n}}{\Delta t}=M-\left( M+\lambda ^{n} k_{i+1}+\epsilon _{i+1}\right) s_{i+1}^{n+1}+\eta _{i+1}v_{i+1}^{n+1}, i=0, \cdots , K-1, n=0, \cdots , {\mathcal {U}}-1 ,\\ s_{0}^{n+1}=\sum _{j=1}^{K} b_{j}\left[ s_{j}^{n+1}+u_{j}^{n+1}+q_{j}^{n+1}+c_{j}^{n+1}+r_{j}^{n+1}\right] \Delta t, \quad n=0, \cdots , {\mathcal {U}}-1 ,\\ s_{i}^{0}=s_{0}\left( a_{i}\right) . \end{array}\right. \end{aligned}$$

(67)

Equation (67) is linear in $s_{i+1}^{n+1}$ and can be readily solved. The development technique for the other PDEs system utilized in the simulation follows the same methodology.

Simulation of the model dynamical aspects

All of the parameters utilized in model (7) must have their values specified in order to do simulations for studying the meaningful behavior of the model. The estimation and fitting of parameters need to be done with more caution, especially when determining the age-dependent parameters. The mortality rate is mathematically fitted using data from the source³⁵

$$\begin{aligned} \delta (\theta )=202.9002-\frac{202.8968438}{\left( 1+7.481194593 \times 10^{-24} {\theta }^{9.252623}\right) ^{171.1121}}. \end{aligned}$$

(68)

The parameter $\beta (\theta )$ was approximated from the fitted figure 2b and thus

$$\begin{aligned} \beta (\theta )=0.001140673 e^{-\frac{(\theta -59.07313)^{2}}{2 \times (26.07842)^{2}}}. \end{aligned}$$

(69)

Since there is a lack of information on $\beta _{1}(\theta )$, $\beta _{1}(\theta )=\beta (\theta )$ is assumed. Thus, we may express the birth function $b(\theta )$ as follows by following¹⁷.

$$\begin{aligned} b(\theta )=\left\{ \begin{array}{cc} \frac{1}{5} \sin ^{2}\left( \frac{(\theta -15) \pi }{27.9}\right) , & \text{ for } 15 \le \theta \le 45, \\ 0, & \text{ otherwise. } \end{array}\right. \end{aligned}$$

(70)

Clearly, $\int _{0}^{\theta _{+}} b(\theta ) d \theta =3.5029$ indicates that a woman will, on average give birth to 3 or 4 children during her lifetime. In the same way, we calculated the age-dependent recovery rate using the data of³⁴, we have

$$\begin{aligned} v(\theta )=0.20 e^{-\left( \frac{a-28.7}{12.71}\right) ^{2}}+0.1372 e^{-\left( \frac{\theta -55.3}{19.01}\right) ^{2}}. \end{aligned}$$

(71)

Fitting of the parameters $\delta (\theta ), \beta (\theta )$ and $v(\theta )$ with real data were explained in Figure 2, where for the rest of the parameters see Table 2.

Figure 2 shows the fitting of parameters with the real data. The mortality trends ($\delta (\theta )$) is fitted with the real data in Figure 2a and this informs policies around shielding older populations, who are more vulnerable to severe outcomes. To estimate the infection dynamics ($\beta (\theta )$), we used the available data and estimated a suitable function for the underlying parameter in Figure 2b. Understanding transmission rates across age groups helps in prioritizing interventions for those most at risk of spreading or contracting the disease (e.g., school closures for younger populations or work-from-home policies for adults). For approximating the recovery rate ($v(\theta )$), we used recovery data and age-specific recovery rate is estimated in Figure 2a that guide the allocation of health care resources, such as ICU beds and rehabilitation services.

Fig. 2

Fitting of the parameters $\delta (\theta ), \beta (\theta )$ and $v(\theta )$ with real data.

Table 2 Parameters values used in simulating model (7).

We plotted the density of susceptible population both in age and time directions for the case of $R_{0}<1$. As expected, in the absence of infection or in the case when $R_{0}<1$, the population of susceptible will tend to build irrespective of their ages and eventually reach to 1. These figures depict that middle will reach to the steady state very quickly compare to people in old ages. As we move along the age-direction, the time of stabilization will tend to increase and the susceptible population with age greater or equals 40 will take almost 40 weeks to reach to its steady state of $s^{0}=1$.

Figure 3 demonstrates the dynamics of the individual compartments both in age and time directions. Figure 3a depicts the density of the susceptible compartment $s(t,\theta )$ in the age and time directions and one can easily notice the as the time progresses, the corresponding population approaches toward the respective component of the disease free equilibrium, that is, approaching to 1. The population of the unquarantined infected individuals $u(t, \theta )$ is plotted in Figure 3b. This density function also confirms the conclusion of the theorem concerning global stability of the disease-free equilibrium. Likewise, we plotted the rest of the state variables and the figures validating our theoretical findings.

The subplot 4a shows that the susceptible population density $s(t, \theta )$ at fixed ages $\theta = 15, 35, 55, 75$ shows an increase toward the steady state ($s_0 = 1$) over time. Younger ages stabilize more quickly due to stronger immunity and lower initial exposure. The subplot 4b represents that along the time axis $t = 15, 30, 45, 60$, $s(t, \theta )$ reveals a slower stabilization for older age groups, reflecting their vulnerability to slower recovery or higher risks of infection. The subplot 4c illustrates that the vaccinated infected $v(t, \theta )$, the dynamics illustrate a rapid decline in younger individuals but a slower decay in older populations, aligning with delayed intervention impacts in older groups.

Over all, plots in Figure 4 and 5 showcases the behavior of all population compartments (susceptible, unquarantined, quarantined, vaccinated, and recovered) when the basic reproduction number $R_0$ is less than 1. The subplots illustrate the following dynamics:

• A steady increase over time as individuals avoid infection, stabilizing faster in younger populations due to better immunity and lower exposure.

• A rapid decline as $R_0$ suggests insufficient spread to maintain infection.

• A slow decrease in older populations compared to younger ones, reflecting delayed intervention efficacy.

• Shows consistent growth as vaccination reduces the susceptible compartment, limiting new infections.

• Gradual stabilization as the epidemic fades.

Fig. 3

The dynamic behavior of the compartments in both age and time directions.

The following figures as well as a few of the above, demonstrates the importance of ensuring widespread and equitable vaccine distribution to maintain a growing vaccinated compartment, encouraging timely testing and quarantine protocols to prevent overwhelmed healthcare systems during infection peaks, and developing immunity-based strategies, such as booster vaccination campaigns, to sustain immunity in the population.

Control of epidemic spread occurs when $R_0 < 1$, indicating successful public health measures such as vaccination and quarantine, which lead to the epidemic’s decline. Targeted vaccination programs are crucial, as the slow recovery of older populations highlights the need to prioritize these groups in vaccination efforts. Effective vaccination campaigns can drive $R_0$ below 1, ultimately achieving control or elimination of the disease. Additionally, resource allocation is optimized by reducing the burden on healthcare systems, as fewer individuals require quarantine or treatment. This underscores the importance of early interventions to limit the spread of infection, particularly in high-risk groups.

Fig. 4

The plot shows the behavior of susceptible and vaccinated population by considering fixed ages and time, when $R_{0}<1$.

Fig. 5

The plot shows the behavior of susceptible individuals, unquarantined individuals, quarantine-infected individuals, vaccinated individuals and recovered population by considering fixed ages and time, when $R_{0}<1$.

Simulation based on constant parameter values

Assuming constant values for the parameters, we will attempt to simulate model (52) as a special instance of model (1) in this Section 6.2.

Parameters are estimated using³⁶; $\delta =\frac{1}{67.7 \times 365}$ and $M=8966$. The confirmed cases are used to fit the other parameters. After solving the model with the RK4 approach, we estimated the parameter values utilizing the lsqcurvefit tools. In Table 3, the estimated and fitted parameters are shown.

Table 3 Values of the parameters used to simulate model (52).

We plotted the corresponding compartments in Figure 6 using the parameter values from Table 3. During the course of the epidemic, the population may partially stabilize itself; nevertheless, it may take a very long period for the disease to stabilize after numerous waves. It might take centuries for the disease to reach endemic stability if current trends continue. The disease might be eliminated from the population if we reduce $R_{0}^{c}$ below unity, but this will also take a long time to achieve the disease-free equilibria.

Fig. 6

Solution curves of the model (52), with constant parameters.

Conclusion

This study presented a new mathematical model for COVID-19 dynamics, incorporating vaccination and age-structured interactions. The model was analyzed to assess the impact of vaccination on disease control. The positivity and boundedness of solutions were established, and the basic reproduction number was derived using the force of infection. Stability analysis confirmed the model’s local and global stability at both disease-free and endemic equilibria, with global stability demonstrated through limit theory. Numerical simulations, performed using the finite difference method of characteristics and the fourth-order Runge-Kutta Method, validated the analytical results. This work provides valuable insights into the role of vaccination and age structure in controlling COVID-19, offering a robust framework for public health strategies.

Future work

The proposed model can be extended to a stochastic age-structured framework to account for randomness and uncertainties in COVID-19 transmission and demographic variations, allowing for a more realistic representation of disease dynamics across age groups. A hospitalized class stratified by age groups can be incorporated into the model to analyze age-specific hospitalization rates and health care resource allocation for COVID-19. This extension would help optimize intervention strategies and better understand age-dependent recovery and mortality trends. The proposed model can be studied for a fractional-order framework to capture memory effects and hereditary properties in disease dynamics. Additionally, a time-delayed model can be analyzed to incorporate delays in infection progression, treatment initiation, and recovery processes.