Introduction

The failure location and failure pattern of the slope have a substantial impact on the runout distance and the land collapse affected area. Currently, there are many computational methods for dynamic simulation of slope failure/landslides triggered by earthquakes or rainfall, such as the Discrete Element Method (DEM)1,2, Discontinuous Deformation Analysis (DDA)3,4,5, Smoothed Particle Hydrodynamics (SPH)6,7,8 and Material Point Method (MPM)9,10,11,12,13 and so on. However, the modeling and calculation process of these methods requires a lot of computing time. If a mountainous region experiences a major earthquake (magnitude 6 or above) or a heavy rainfall event that affects a very large area in the future, the number of slope failures/landslides may be dozens or even hundreds. Earthquakes and heavy rainfall events are often sudden and drastic, which usually cause huge damage and casualties within a few hours or tens of minutes14. To ensure that warning information can be quickly released to the designated area, the early warning system (EWS) of geological disasters has to make concessions on accuracy to greatly improve the efficiency of disaster warning. In the EWS, the early warning information should include the occurrence time, the occurrence location, the scope of influence, and the extinction time of the disaster. However, in many current early warning systems, the time and location of geological disasters have received considerable attention. The size of the landslide failure mass and its potential impact area have not been given enough attention.

Over the last few decades, numerous early warning systems for geological hazards have been implemented across many developing and/or developed regions or countries. For example, in 1977, the first regional geographical Landslip Warning System (LEW) was implemented in Hong Kong, China15, which made Hong Kong one of the first regions in the world to implement an early warning system16. In 1985, the United States Geological Survey (USGS) and the United States National Weather Service (USNWS) jointly established a real-time landslide prediction system17. In addition, more than 20 other early warning systems have been collected in the works of Guzzetti et al. (2020)18.

In road embankments or natural slopes, it is considered that four patterns of slope failure are commonly observed in the field, which was also observed in the indoor tests conducted by Wang et al. (2021)19 and in the slope stability assessment using the limit-equilibrium method (LEM) simulated by GEO-SLOPE/W20. The classification of the four slope failure patterns refers to the definition of hillslope failure modes of brittle rock materials by Huber et al. (2024)21 as displayed in Fig. 1, e.g., Pattern I: Sliding. Failure begins in the lower slope portion and advances upward along a rupture zone, eventually extending to the slope’s crest. The slip surface traverses both the upper and lower sections of the slope. Pattern II: Buckling. The material swells outward toward the surface in the lower slope portion, followed by a rotational motion and significant fragmentation. Pattern III: Toppling. The soil fails at the slope’s shoulder position. A substantial section of the slope inclines and rotates toward the slope’s toe, after which the soil material eventually breaks apart. Pattern IV: Crumbling. Soil collapses on the slope surface, and no distinct overall failure was observed. A shallow layer of surface particles separates and falls down the slope face. The nomenclature of the four landslide patterns references the terminology used by Huber et al. (2024)21 for classifying slope failure patterns. However, since their study primarily focused on the influence of anisotropy angle on slope stability, which differs from the scope of our research, regarding the classification methodology proposed by Zhu and Cao (2023)22 for four landslide types, this study has systematically redefined and reclassified the corresponding potential slip surface locations for each failure pattern.

Fig. 1
figure 1

Flowchart for identification of Landslide Pattern in the SWI-based EWS.

Full size image

However, the current early warning systems (EWSs) focus on predicting the time and location of a slope failure/landslide, but can rarely predict the failure pattern of a slope failure/landslide. If the landslide pattern can be identified with coarse precision in the EWSs, it will be easier to evaluate the impact scale of the disaster or determine which landslide pattern is more likely to occur, even though the exact potential slip depth cannot be given. Rainfall intensity, duration, and distribution are the critical rainfall characteristics that influence the two types of landslide, i.e., shallow and deep-seated landslides in mountainous regions. In mountainous areas, Phakdimek et al. (2025)23 highlighted that understanding the sizes and types of rainfall-induced landslides and identifying areas at high risk are critical challenges for disaster management. Besides, based on an official database of a total of 413 landslides occurring in Ehime Prefecture and SWI, Mori and Ono (2019)24 analyzed characteristics of slope failures and landslide flows and various rainfall characteristics. They found that landslide density tended to rapidly increase as rainfall increased beyond the threshold. By identifying the rainfall characteristics that triggered 10 shallow and deep-seated landslides in Japan using the three-layer tank model and SWI, Sato and Shuin (2024)25 found that rainfall characteristics and magnitude affect landslide volume via the subsurface depth at which pore pressure occurs and the amount of groundwater. Similarly, based on the Tank model, Kuo et al. (2021)26 illustrated that the occurrences of landslides can be estimated by their correlations with the phenomenological SWI of a given catchment. Therefore, this paper attempts to use parametric analysis to realize the identification and classification of slope failure/landslide patterns in the SWI-based EWS. In this way, the SWI-based EWS can not only predict the time and location of a landslide, but also give a judgment of the landslide pattern, so as to provide a decision-making basis for more accurate evaluation of landslide volume, influence range, and coping approaches. Therefore, this study enriches the prediction range of the SWI-based EWS in the non-structural landslide defense strategy and provides a simpler and more effective technical means for the hazard assessment of the landslide.

Soil water index (SWI)-based early warning system (EWS)

Sugawara et al. (1974)27 proposed a three-layered Tank model to simulate surface water storage, soil moisture variation, and outflow within the watershed as shown in Fig. 2(a). In the Tank model, the average water depth, the soil moisture variation, and the fluctuations in groundwater levels are expressed as the water height within each layer. The water height, infiltration rate, and outflow rate of each layer multiplied by the watershed area are the total water storage, total infiltration, and total runoff. The sum of the three water heights in the Tank model is referred to as the “Soil Water Index (SWI)”, which reflects the variation of water storage in the watershed caused by a rainfall event. Geological disasters such as floods, debris flows, and slope failure/landslides are mainly caused by rainwater falling on the ground or penetrating the soil. Therefore, the SWI-based EWS employs two rainfall indicators, rainfall intensity and SWI, for warning sediment-related disasters triggered by heavy rainfall, as shown in Fig. 2(b). In the Japanese early warning system, the SWI serves as a conceptual indicator of groundwater levels. Although parameter adjustments for different regions result in similar SWI time-series trends28, the Japanese government employs fixed parameters nationwide despite varying geological conditions. To address this, local early warning criteria incorporate differences in geological features and material properties28. Kuramoto et al. (2001)29 proposed to set a non-linear Critical Line (hereinafter, CL) by using the RBFN (Radial Basis Function Network) method. In 2005, the Japanese government launched the EWS30 by setting CL in each 5.0 km square grid covering all of Japan, i.e., when the Snake Line (hereafter, SL) exceeds CL, geological disasters may take place as shown in Fig. 2 (b). In 2020, the grid size for setting CL was updated to 1.0 km square. In the same year, Zhu et al. (2020)31 incorporated the snowmelt water with the consideration of the changes in snow density into the calculation of SWI, which successfully developed the SWI-based EWS for forecasting slope failures induced by rainfall and/or snowmelt during the snowmelt season.

Fig. 2
figure 2

Conceptual framework of the SWI-based EWS (a) Tank model32; (b) forecasting of geological disasters based on CL and SL31.

Full size image

In the Tank model, the outflow rates and infiltration rates are determined as,

$$\:{\text{q}}_{{{\text{11}}}} {\text{ = }}\left\{ {\begin{array}{*{20}c} {{\text{a}}_{{{\text{11}}}} \times \left( {{\text{H}}_{{\text{1}}} \left( {\text{t}} \right){\text{ - L}}_{{{\text{11}}}} } \right),\;{\text{if}}\;\;{\text{H}}_{{\text{1}}}> {\text{L}}_{{{\text{11}}}} } \\ {\:{\text{0}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:,\:{\text{if}}\;\;{\text{H}}_{{\text{1}}} {\text{ }} \le {\text{ L}}_{{{\text{11}}}} } \\ \end{array} } \right.$$
(1)
$$\:{\text{q}}_{{{\text{12}}}} {\text{ = }}\left\{ {\begin{array}{*{20}c} {{\text{a}}_{{{\text{12}}}} \times \left( {{\text{H}}_{{\text{1}}} {\text{(t) - L}}_{{{\text{12}}}} } \right),\;{\text{if}}\;\;{\text{H}}_{{\text{1}}}> {\text{L}}_{{{\text{12}}}} } \\ {\:{\text{0}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:,\:{\text{if}}\;\;{\text{H}}_{{\text{1}}} {\text{ }} \le {\text{ L}}_{{{\text{12}}}} } \\ \end{array} } \right.$$
(2)
$$\:{\text{q}}_{{\text{2}}} {\text{ = }}\left\{ {\begin{array}{*{20}c} {{\text{a}}_{{\text{2}}} \times \left( {{\text{H}}_{{\text{2}}} {\text{(t) - L}}_{{\text{2}}} } \right),\;{\text{if}}\;\;{\text{H}}_{{\text{2}}}> {\text{L}}_{{\text{2}}} } \\ {\:{\text{0}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:,\:{\text{if}}\;\;{\text{H}}_{{\text{2}}} {\text{ }} \le {\text{ L}}_{{\text{2}}} } \\ \end{array} } \right.$$
(3)
$$\:{\text{q}}_{{\text{3}}} {\text{ = }}\left\{ {\begin{array}{*{20}c} {{\text{a}}_{{\text{3}}} \times \left( {{\text{H}}_{{\text{3}}} {\text{(t) - L}}_{{\text{3}}} } \right),\;{\text{if}}\;\;{\text{H}}_{{\text{3}}}> {\text{L}}_{{\text{3}}} } \\ {\:{\text{0}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:,\:{\text{if}}\;\;{\text{H}}_{{\text{3}}} {\text{ }} \le {\text{L}}_{{\text{3}}} } \\ \end{array} } \right.$$
(4)
$$\:{\text{I}}_{{\text{1}}} \;{\text{ = }}\;\beta _{{\text{1}}} \times {\text{H}}_{{\text{1}}} {\text{(t)}},\:{\text{I}}_{{\text{2}}} \;{\text{ = }}\;\beta _{{\text{2}}} \times {\text{H}}_{{\text{2}}} {\text{(t)}},\:{\text{I}}_{{\text{3}}} \;{\text{ = }}\;\beta _{{\text{3}}} \times {\text{H}}_{{\text{3}}} {\text{(t)}}$$
(5)

where H1, H2, and H3 indicates water height in each layer (mm); L11, L12, L2, and L3 indicates the height of the outlet; α11, α12, α2, and α3 indicates outflow coefficients (1/s); I1, I2, and I3 indicates infiltration (mm/s); β1, β2, and β3 indicates infiltration coefficients (1/s).

The calculation of water height in each layer and SWI is expressed as,

$$\:{\text{H}}_{{\text{1}}} \left( {{\text{t + }}\Delta {\text{t}}} \right)\;{\text{ = }}\;{\text{H}}_{{\text{1}}} \left( {\text{t}} \right){\text{ - q}}_{{{\text{11}}}} {\text{ - q}}_{{{\text{12}}}} {\text{ - I}}_{{\text{1}}} {\text{ + R}}$$
(6)
$$\:{\text{H}}_{{\text{2}}} \left( {{\text{t + }}\Delta {\text{t}}} \right)\;{\text{ = }}\;{\text{H}}_{{\text{2}}} \left( {\text{t}} \right){\text{ - q}}_{{\text{2}}} {\text{ - I}}_{{\text{2}}} {\text{ + I}}_{{\text{1}}}$$
(7)
$$\:{\text{H}}_{{\text{3}}} \left( {{\text{t + }}\Delta {\text{t}}} \right)\;{\text{ = }}\;{\text{H}}_{{\text{3}}} \left( {\text{t}} \right){\text{ - q}}_{{\text{3}}} {\text{ - I}}_{{\text{3}}} {\text{ + I}}_{{\text{2}}}$$
(8)
$$\:\text{SWI}\left(\text{t}\right)\;\text{=}\;{\text{H}}_{\text{1}}\left(\text{t}\right)\text{+}{\text{H}}_{\text{2}}\left(\text{t}\right)\text{+}{\text{H}}_{\text{3}}\left(\text{t}\right)$$
(9)

where R is the rainfall intensity (mm/hr.), t is time; ∆t is the time step.

Numerical modeling, boundary conditions, and soil properties

The slope stability analysis of a two-dimensional (2D) homogeneous slope model (Fig. 3) is performed by using GEO-SLOPE/W. In the numerical simulation, the slope model made up of two kinds of materials, i.e., volcanic soil and Toyoura sand, features different effective cohesion and internal friction angles. Volcanic soil is widespread throughout Japan, covering approximately 40% of the surface area in Hokkaido33. Toyoura sand is a representative type of clean sand commonly found in Japan34, which is a uniform fine sand with sub-angular grains35 and is extensively used in Japan as the standard sand for geotechnical engineering studies36. The hydraulic characteristic curves of the volcanic soil and Toyoura sand are plotted in Fig. 4. Table 1 lists the 22 kinds of designed rainfall conditions. The soil properties measured by Sato et al. (2017)37 and Lin (2020)38 are listed in Table 2.

Fig. 3
figure 3

Homogeneous slope numerical model with boundary conditions.

Full size image
Fig. 4
figure 4

Soil hydraulic characteristic curves39: (a) grain size curve; (b) soil water characteristic curve (SWCC); (c) hydraulic conductivity curve.

Full size image
Table 1 Different designed rainfall conditions.
Full size table

Variation of slope failure pattern in SWI-based EWS

After the test analysis, the calculation results show that the SWI-based EWS can indeed identify and classify the landslide pattern as plotted in Fig. 5(a). It can be observed that the Pattern I slope failures (Blue points) gather at the bottom of the critical line (CL). The rainfall intensity in this area is very low (nearly 10 mm/h), but the SWI is very high (ranges from 140 mm to 180 mm), indicating that the sliding pattern of slope instability (deep-seated landslides) is caused by long-term low-intensity (LL) type rainfall. It is consistent with the isolated heavy rainfall only has a temporary impact on the groundwater level (GWL) rise in shallow layers and a negligible effect on the GWL rise in deeper layers, found by Prokešová et al. (2013)40 through long-term observation of hydrogeological monitoring and repeated geoelectrical imaging from March 2007 to April 2011 in a large deep-seated landslide near Ľubietová (Western Carpathians).

Table 2 Soil properties of volcanic soil and Toyoura sand.
Full size table

As the rainfall intensity increases, the SWI gradually decreases when landslides occur. The slope failure pattern gradually changes from Pattern I (sliding) to Pattern II (Buckling), to Pattern III (Toppling), and finally to Pattern IV (Crumbling) during short-term high-intensity (SH) type rainfall, as shown in Fig. 5(b). This means that there is a strong correlation between landslide patterns and rainfall intensity, as well as the soil rainfall index (SWI). The potential pattern of landslides can be determined by meteorological prediction and the SWI, which is calculated based on the predicted rainfall intensity. That is, when SL exceeds CL and the point on SL is located in an early warning zone in EWS, the occurrence of the landslide pattern in this early warning zone will be easier to observe. Correspondingly, the strengthening and implementation of structural measures, as well as the formulation of refuge plans and evacuation strategies for downstream residential areas of disasters, have a more credible basis. When a large number of potential landslides occur, although it is less accurate than on-site monitoring, EWS can greatly improve the efficiency of disaster early warning.

Fig. 5
figure 5

Variation of slope failure patterns in SWI-based EWS (a) four slope failure patterns in the SWI-based EWS; (b) transition paths of failure patterns under different rainfall types.

Full size image

Identification and classification of slope failure patterns with volcanic soil

The effects of soil shear strength parameters of volcanic soil on the slope instabilities and slope failure patterns are investigated in the SWI-based EWS as plotted in Figs. 6 and 7. From Fig. 6, it can be recognized that SWI-based EWS successfully predicted all slope failures under the different soil shear strength parameters. However, from Fig. 6(a), it can be observed that the cohesion significantly affects SWI when slope failure occurs under heavy rainfall, while the internal friction angle has a remarkable impact on SWI when slope failure occurs under weak rainfall. The main reason could be that the cohesion controls the FOS of the shallow layer, whereas the internal friction angle controls the FOS of the deep layer, which is consistent with the findings of Yue and Kang (2021)41, that the contribution from cohesion decreases sharply and inversely, while the contribution from the internal friction angle rises gradually and linearly as the slip depth increases.

In reality, the Critical Line (CL) is set in a 1 m×1 m grid cell based on rainfall and disaster history statistics. However, not all grid cells possess recorded rainfall and landslide history data. Consequently, the CL for grid cells lacking such observational records must typically be determined based on adjacent grid cells where CL values have been established. The soil strength parameters within individual grid cells can be determined through laboratory testing. Soils exhibiting higher cohesion or internal friction angle possess greater shear strength, which necessitates assigning a higher Critical Line (CL) value. However, the current methodology primarily involves adjusting the CL through translation or scaling while maintaining its original shape. Consequently, it means that in the SWI-based EWS, when adjusting CL for different soil slopes in different regions, the CL cannot be simply scaled or translated. The adjustment of CL considering the difference in cohesion is mainly focused on heavy rainfall, while the adjustment of CL based on the difference in internal friction angle should be focused on LL-type rainfall.

Fig. 6
figure 6

Effect of soil shear strength parameters of volcanic soil on slope instability in SWI-based EWS (a) different c’; (b) different ϕ’.

Full size image

After identifying and classifying slope failure patterns in the SWI-based EWS of geological disasters, as displayed in Fig. 7, it can be observed that near CL, the slope failure pattern interval division is clear. The distribution range of the Toppling landslide (Pattern III) is most concentrated on the shoulder of the CL curve. Under heavy rainfall, short-term heavy rainfall (SH type) is more likely to trigger Crumbling (Pattern IV) landslides, which will mainly cause a lot of shallow erosion on the surface of the slope, which can be confirmed by the erosion survey results of by Baartman et al. (2012)42 by investigating the erosion of five rainfall event from 1997 to 2009 period in Prado catchment in SE Spain. They found that the contribution of a single rainfall event could constitute 42% of total erosion and high EVI (i.e., event index, EVI = Ppeak×Ptot/T. Ppeak is peak rainfall intensity (mm/h); Ptot is total rainfall (mm); T is total duration (min.). A high EVI signifies a strong rainstorm with SH type, while a low EVI represents a weak rainfall event with LL type. Low-frequency events play a crucial role in contributing to total soil erosion. With the increase in rainfall duration, the landslide gradually develops from surface erosion to failure at the slope’s toe (Pattern II), and finally, the failure surface extends upward and evolves into overall failure (Pattern I). However, under LL-type rainfall, since the rainfall intensity is very low, most of the rainwater directly infiltrates into the soil without generating surface runoff, so the main landslides induced are Pattern I and Pattern II slope failure/landslides.

The identification and classification of landslide patterns in SWI-based EWS means that different structural measures need to be adjusted. Although the potential slip depth of Toppling landslides (Pattern III) and Crumbling landslides (Pattern IV) is very shallow, it may be widely distributed. With the high rainfall intensity, it is easy to form a debris flow. Therefore, during heavy rainfall periods such as the typhoon season, the application of debris flow protection measures, such as drainage channels or dredging channels, in advance should receive more attention than the prevention of giant landslides. In this case, it is more valuable to accurately determine the influence range of debris flow than to determine the location and time of shallow landslides. In contrast, structural measures to prevent Sliding landslides (Pattern I) and Buckling landslides (Pattern II) should be strengthened during LL-type rainfall-intensive periods, such as the persistent snowmelt season in spring or the rainy season in autumn. At this time, although the number of giant landslides is not large, their huge amount of collapse may induce catastrophic damage to downstream residential areas. In this case, it will be more important to accurately determine the location and time of the giant landslide.

Fig. 7
figure 7

Four slope failure patterns of volcanic soil in SWI-based EWS (a) different c’; (b) different ϕ’.

Full size image

Identification and classification of slope failure patterns with Toyoura sand

The effects of soil shear strength parameters of Toyoura sand on the slope instabilities and landslide patterns are also investigated in the SWI-based EWS, as shown in Figs. 8 and 9. It can be observed that SWI-based EWS successfully predicted all slope failures under the different rainfall conditions for Toyoura sand. However, unlike the volcanic soil slope, the slope instability composed of Toyoura sand did not respond significantly to changes in shear strength parameters. Figure 9 suggests that the main landslide patterns are Toppling landslides (Pattern III) and Crumbling landslides (Pattern IV). The slope failures/landslides of the Sliding landslide (Pattern I) and Buckling landslide (Pattern II) are not triggered by the rise of groundwater level caused by LL-type rainfall but are transformed from Pattern III and Pattern IV when the rainfall duration increases. This is because the steep-shaped grain-size curve of Toyoura sand causes poor water storage capacity. The LL type of light rain is drained away in the coarse pores of the sand and cannot cause a significant increase in the groundwater level. On the contrary, slope surface erosion (Pattern IV) induced by heavy rainfall or the failure of slope topsoil (Pattern III) has become the main failure pattern.

Fig. 8
figure 8

Effect of soil shear strength parameters of Toyoura sand on slope instability in SWI-based EWS (a) different c’; (b) different ϕ’.

Full size image

In addition, more than 83% of landslides are within a narrow area within an early warning system with rainfall intensity between 20 mm/h and 40 mm/h and SWI between 200 mm and 250 mm. This means that the rainfall conditions inducing non-cohesive soil landslides are relatively special. Most of the failure of non-cohesive soil occurs in the transition stage of LL- and SH-type rainfall, i.e., when the rainfall intensity changes greatly in a short period. Therefore, in the early warning of slope failures composed of non-cohesive soil such as sand, gravel, and weathered gravel in the SWI-based EWS, the contribution of rainfall conditions to slope stability is significantly greater than that of the shear strength characteristics of non-cohesive soil. At this time, accurately predicting the future rainfall development near the non-cohesive soil slope has become a key issue to improve landslide prediction. When comparing Fig. 9 with Fig. 7, it can be observed that the CL of Toyoura sand is larger than that of volcanic soil. This does not mean that non-cohesive soil is safer than cohesive soil. The reason for this is that we have given Toyoura sand a cohesion of 1.5 kPa to 3.0 kPa to observe the process of slope from stability to instability under the same rainfall conditions. If the cohesion of Toyoura sand is set to zero, then under the same groundwater level, slope failure will occur even before rainfall occurs.

Fig. 9
figure 9

Four slope failure patterns of Toyoura sand in the SWI-based EWS (a) different c’; (b) different ϕ’.

Full size image

Effect of soil water index on the potential slip depth of four slope failure patterns

After collecting all the potential slip depths of slope composed of two kinds of soils, it is found that there is no obvious relationship between the potential slip depth and the SWI, except for slopes composed of volcanic soils when the cohesion changes (Fig. 10b). In Fig. 10(b), the slope failure patterns and the potential slip depths show a step-like distribution when SWI increases. However, when the internal friction angle changes, the potential slip depths composed of volcanic soil are concentrated in the range of SWI from 100 mm to 175 mm (Fig. 10a). Similarly, when the shear strength parameters are varied, the slip surface depths of the slope composed of Tayoura sand are concentrated in the range of SWI from 200 mm to 275 mm (Fig. 10c and d). While, if SWI is replaced by the water storage height (H2) in the second tank layer, all of the slope failure patterns and the potential slip depths of the slope show the similar step-like distribution with the rise of the water storage height (H2) in the second tank layer as shown in Fig. 11. It means that the correlation between the slope failure pattern and the potential slip depth and SWI is very poor, but there is a strong correlation between the slope failure pattern and the potential slip depth and water storage height (H2) in the second tank layer. In the other wards, when slope failure occurs, a higher water storage height (H2) in the second tank layer corresponds to a larger slope failure scale. Finally, it can be summarized that the soil water index (SWI) could be utilized to forecast the time and location of the landslide, and the water storage height (H2) in the second tank layer might be used to evaluate the scale of slope failure, although the evaluation accuracy is not as accurate as the computational slip surface obtained by numerical simulations.

Fig. 10
figure 10

Potential slip depths of four slope failure patterns vs. SWI (a) volcanic soil with different ϕ’; (b) volcanic soil with different c’; (c) Toyoura sand with different ϕ’; (d) Toyoura sand with different c’.

Full size image
Fig. 11
figure 11

Potential slip depths of four patterns vs. the water storage height (H2) in the second tank layer (a) volcanic soil with different ϕ’; (b) volcanic soil with different c’; (c) Toyoura sand with different ϕ’; (d) Toyoura sand with different c’.

Full size image

Validation of the identification and classification method of landslide pattern in the SWI-based EWS along highway E5 in hokkaido, Japan

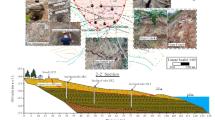
In mid-August 2010, Typhoon No.4, namely, DIANMU, struck Japan. Typhoon No.4 was born at 2010/08/08 21:00 and died at 2010/08/13 03:00. On August 12rd, 2010, Typhoon No.4 landed in Hokkaido, Japan, causing heavy rain and dozens of landslides along highway E5 in Hokkaido, Japan as displayed in Fig. 12. Table 3 listed the occurrence time, location and scale of collapsing soil mass of landslides along highway E5 in Hokkaido, Japan during Typhoon No.4. From the point of view of the occurrence time of the landslide, the occurrence of the landslide is successive, not at the same time. This is because the movement of Typhoon No.4 leads to the spatial and temporal variation of the rainstorm center. Judging from the volume of the landslide, most of the landslides are shallow landslides with a depth of 0.2 m. However, the landslides have a wide range of damage, with a length of 2.0 m to 10.0 m and a width of 2.0 m to 20.0 m. To describe the 10 major landslides recorded more clearly, the landslides are numbered L1 to L10. The photography of the landslide scene along highway E5 in Hokkaido, Japan, during Typhoon No.4 is shown in Fig. 13.

Fig. 12
figure 12

Occurrence of landslides along highway E5 in Hokkaido, Japan during Typhoon No.4.

Full size image
Table 3 Occurrence time, location, and scale of collapsing soil mass of landslides along highway E5 in hokkaido, japan.
Full size table
Fig. 13
figure 13

Photography of the landslide scene along highway E5 in Hokkaido, Japan during Typhoon No.4.

Full size image

According to the five years of rainfall distribution recorded data along highway E5 in Hokkaido, Japan from 2008 to 2012, the short-duration heavy rainfall caused by Typhoon No.4 was more serious than other years as shown in Fig. 14. At Sakayagawa Bridge weather station (near L 1), the recorded cumulative rainfall reached 215.5 mm with the maximum intensity of 57.0 mm/h. At Date-shi weather station, the recorded cumulative rainfall reached 126.5 mm, with the maximum intensity of 33.5 mm/h. At Motowanishikawa weather station (near L 4), the recorded cumulative rainfall reached 179.5 mm with the maximum intensity of 63.5 mm/h. Short-duration intense rainfall leads to the rapid accumulation of rainwater on the ground surface, subsequently forming runoff. This runoff erodes the topsoil, making it more susceptible to the initiation of shallow landslides. This is the reason why 70% of the landslides in Table 3 have depths ranging between 0.2 m and 0.5 m.

Fig. 14
figure 14

Recorded rainfall along highway E5 in Hokkaido, Japan (from 2008 to 2012).

Full size image

Although the majority of landslides induced by typhoons are shallow landslides, there are still instances where deep-seated landslides are triggered, e.g., L6 and L10. Soil water indexes of L10, L5, L6, and L4 are calculated, and the slip surfaces of the four landslides are plotted in Fig. 15(a) to Fig. 15(g). From Fig. 15, it can be seen that in the vicinity of L10 and L5, despite the occurrence of heavy rainfall in the initial stages, no landslides were triggered. As they are situated on the periphery of the typhoon, the intensity of the rainfall is insufficient to trigger the occurrence of shallow landslides. With the persistence of rainfall, the SWI (Soil Water Index) gradually increased, indicating that the rise in moisture content within the deeper soil layers or the elevation of the groundwater table is the primary factor responsible for initiating deep-seated landslides. While in the L6 and L4 regions, the initial rainfall intensity surpassed 30 mm/h, approaching 40 mm/h, which precipitated the occurrence of shallow landslides.

Fig. 15
figure 15

Identification and classification of landslide pattern in the SWI-based EWS along highway E5 in Hokkaido, Japan.

Full size image

Discussions

Currently, research on landslide patterns predominantly focuses on mechanical mechanism analysis, remote sensing monitoring, empirical research, field implementation, and advanced modeling etc. For example, based on the test results of three model experiments with different slope structures, Li et al. (2024)43 found that structure features influence the failure mode of the slope, and preferential seepage along vertical joints promotes the increase in landslide volume. Zhao et al. (2024)44 conducted a centrifugal model test and found that with the enrichment of the soil water content, retrogressive sliding, deep subsidence, and surface sinkhole failures occurred successively up to areas with relatively high pore water pressure. Yang et al. (2025)45 conducted a shaking table model test, and experimental results show that there exist three failure modes of deposit slope, i.e., local slip failure, transitional local-overall slip failure, and overall slip failure. In terms of remote sensing monitoring, techniques such as InSAR (Interferometric Synthetic Aperture Radar), multispectral imaging, and LiDAR (Light Detection and Ranging) have been widely applied to identify the landslide patterns, e.g., Alam et al. (2024)46 highlighted that with the advent of the Internet of Things (IoT), artificial intelligence, and high-speed internet, the potential to use such technologies for remotely monitoring soil hydrological parameters and slope movement is becoming increasingly important. Du et al. (2025)47 employed multidimensional InSAR observations to analyze the displacement characteristics and sliding geometry of the Li-Kan Road landslide located on the right bank of the Lijia Gorge Reservoir in China. However, due to challenges such as rigorous experimental requirements, complexities in point cloud modeling, and time-intensive data processing, these research findings are unable to rapidly predict and evaluate landslide patterns within short timeframes, particularly when integrated with Early Warning Systems (EWS).

Therefore, this study attempts to propose an identification and classification method of landslide patterns in the SWI-based EWS. It is useful for both a broad-scale evaluation of slope failure magnitude and the improvement strategies of structural measures for four distinct slope failure patterns, considering varying soil parameters, in actual design and maintenance projects. The definitions of the four landslide modes are derived from phenomena observed in laboratory experiments, as illustrated in Fig. 1. The classification of landslide modes is conducted within an Early Warning System (EWS) based on the physical hydrological model, i.e., the TANK model, regarding extensive parametric numerical analysis results shown in Fig. 5(a). The validity of this classification has been verified through observed deformation mechanisms in real-world landslide cases, as shown in Fig. 15, which ensures the high reliability of the proposed identification and classification method of landslide patterns in the SWI-based EWS. However, this study focuses solely on examining the effects of shear strength parameters of volcanic soil and Toyoura sand on identifying and classifying landslide patterns within the SWI-based EWS. The influence of hydraulic characteristics of other soils or freeze-thaw actions on the judgment of landslide patterns in seasonal cold regions deserves further research.

Moreover, the characteristics exhibited by partial results indicate that there is a poor correlation between slope failure patterns and the potential slip depth and SWI. Conversely, there is a strong correlation between landslide patterns and the potential slip depth and water storage height (H2) in the second tank layer. The primary reason could be that the water heights in the three-layer tanks of the Tank model represent moisture fluctuations at different soil layer positions. The water height in the topmost tank corresponds to the average surface water depth of the watershed, the water height in the middle tank reflects moisture variations within the vadose zone, and the water height in the bottom tank represents fluctuations in the groundwater table. Among these components, surface water (the water height in the topmost tank) primarily controls flooding and surface erosion, while groundwater table fluctuations (the water height in the bottom tank) represent a slow hydrological process. The water level in the middle tank (H2)-reflecting moisture variations in the vadose zone, i.e., changes in matric suction-plays a dominant role in slope stability. Consequently, the landslide patterns and the potential slip depth exhibit a strong correlation with the water height in the second tank but only a weak correlation with the SWI. Therefore, whether the current SWI-based early warning system should be replaced with an H2-based early warning system to improve its effectiveness remains a subject requiring further and broader discussion, supported by empirical evidence from actual landslide events.

In addition, the numerical simulations and field investigations in this study are specifically focused on soil slopes, thereby achieving landslide pattern recognition in the SWI-based EWS for either embankment slopes or roadside cut slopes. In contrast, rock slopes involve more complex geological factors, such as the subsurface flow, dip direction, dip angle, and intensity of joint development. Consequently, the judgment of landslide patterns for rock slopes within the SWI-based EWS still requires further investigation.

Conclusions

  1. 1.

    The SWI-based EWS can indeed identify and classify the landslide pattern. The failure pattern of slope instability (deep-seated landslides) is caused by long-term low-intensity (LL) type rainfall, and as the rainfall intensity increases, the SWI gradually decreases when slope failure occurs. The slope failure pattern gradually changes from Pattern I (sliding) to Pattern II (Buckling), to Pattern III (Toppling), and finally to Pattern IV (Crumbling) during short-term high-intensity (SH) type rainfall.

  2. 2.

    The cohesion has a significant impact on SWI when slope failure occurs under heavy rainfall, while the internal friction angle has a remarkable effect on SWI when slope failure occurs under LL-type rainfall. Therefore, in the SWI-based EWS, when adjusting CL for different soil slopes in different regions, the CL cannot be simply scaled or translated. The adjustment of CL considering the difference in cohesion is mainly focused on heavy rainfall, while the adjustment of CL based on the difference in internal friction angle should be focused on LL-type rainfall.

  3. 3.

    The correlation between the slope failure pattern and the potential slip depth and SWI is very poor, but there is a strong correlation between the landslide pattern and the potential slip depth and water storage height (H2) in the second tank layer. In the other wards, when slope failure occurs, a higher water storage height (H2) in the second tank layer corresponds to a larger slope failure scale. Finally, it can be summarized that the soil water index (SWI) can be utilized to forecast the time and location of landslides, and the water storage height (H2) in the second tank layer might be used to evaluate the scale of slope failure.