Abstract
Urban air pollution poses a major threat to public health and environmental sustainability. This study proposes a structured machine learning (ML)-based framework to examine how temporal and spatial resolution choices affect the accuracy of urban air pollution modeling. The research is conducted in two distinct phases. In the temporal phase, the impact of incorporating pollutant autocorrelation into ML models (Multilayer Perceptron (MLP) and Random Forest (RF)) is analyzed by comparing results with and without temporal lag features derived through autoregressive (AR) modeling. In the spatial phase, emission inventory data are aggregated at three spatial resolutions (500 m, 750 m, and 1000 m) to evaluate their effect on model performance in predicting PM and NOx concentrations. Results from the temporal modeling phase indicate that including lag features significantly improves PM predictions: RMSE for PM₁₀ is reduced by 25.9% (from 92.56 µg/m3 to 68.59 µg/m3), and for PM2.5 by 38.9% (from 61.10 µg/m3 to 37.30 µg/m3). Conversely, for NOx, RMSE increases by 53.2% (from 7.90 µg/m3 to 12.10 µg/m3), indicating pollutant-specific temporal behavior. In spatial modeling, a coarser resolution (1000 m) yields better performance for PM (RMSE = 13.51 kg/year), while a finer resolution (500 m) is more effective for NOx (RMSE = 307.50 kg/year). Among the evaluated algorithms, MLP consistently achieves the highest predictive accuracy across both temporal and spatial scenarios. These findings underscore the importance of selecting appropriate temporal and spatial resolutions tailored to each pollutant type. The proposed framework offers a flexible, resolution-aware modeling strategy that can support more effective urban air quality management policies.
Similar content being viewed by others
Introduction and background
Air pollution is currently recognized as one of the most critical challenges facing human society due to its adverse effects on public health. Several factors contribute to rising air pollution levels, including urban sprawl, population growth, industrial expansion, and increased fossil fuel consumption. Furthermore, inefficiencies in public transportation systems, poor fuel quality, and traffic congestion contribute significantly to pollutant emissions1,2,3,4,5,6,70,77.
Numerous studies have examined various aspects of air pollution modeling, such as temporal forecasting and the impact of spatial resolution on urban air pollution models. For instance, Stroh et al.7 studied the optimal spatial resolution in terms of temporal resolution and discovered that accuracy enhanced as spatial resolution increased when comparing simulated concentrations between high-resolution reference grids (fine grids) and coarser grids. Shad et al.8 applied Kriging to estimate PM10 concentrations under a variety of conditions, demonstrating its utility for spatial forecasting. Nishikawa & Kannari9 assessed emission maps of Osaka Prefecture at 1 km and 3 km resolutions, reporting enhanced modeling performance for NH₃ emissions at lower resolutions and NOx emissions at higher resolutions. There were no significant differences in model performance for SO2 between the two resolutions. Tan et al.10 employed the WRF/CMAQ system to examine the impact of spatial resolution on air quality modeling, with a particular emphasis on industrial areas. Their findings suggested that emissions inventories with spatial resolutions ranging from 1 to 3 km provided more accurate representations of pollutant distributions. Additionally, they compared the combined effects of spatial and temporal resolution in industrial, urban, and rural environments, emphasizing the importance of fine-scale data for simulation accuracy. Han et al.11 examined the spatial distributions of PM2.5 and PM10 in Xi’an, China. They generated two regression-based prediction models and performed spatial mapping with 1 km2 grid cells. Their findings revealed that pollutant distribution patterns were closely related to the layout of industrial land and the location of polluting enterprises.
Song et al.12 employed Machine Learning (ML) to analyze daily variations in PM2.5 and NO2 concentrations across Shanghai. They specifically used the Random Forest (RF) algorithm and compared its predictive performance to that of a traditional land use regression model. Spatial estimates for unsampled areas were generated using a 1 km grid. Their findings showed that the RF model had higher predictive accuracy than the land use regression approach. Saez and Barceló13 designed a hierarchical Bayesian spatiotemporal model to generate spatial forecasts of air pollution levels with low computational cost. Their model was built on stochastic partial differential equations and implemented with the integrated nested Laplace approximation (INLA) framework. This approach enabled them to estimate the spatial distribution of four key air pollutants associated with significant health risks in Catalonia, Spain. Ketu14 developed a hybrid ML model (Recursive Feature Elimination with Random Forest Regression (RFERF)) for spatial prediction of Air Quality Index (AQI) and NOx concentrations using sensor data from multiple urban monitoring sites in India. The model outperformed seven benchmark methods, highlighting the importance of spatial feature selection in improving prediction accuracy. Dawar et al.16 employed various ML models to predict AQI based on two years of environmental data. Key pollutants such as NO2, CO, SO3, PM2.5, PM10, and O3 were used as input features. Among the models tested, the Lasso regressor achieved the highest accuracy (R2 = 0.99). The study indicated the potential of ML in predicting air quality and provided actionable insights for managing air pollution in mountainous urban areas like Dehradun. Singh and Suthar17 investigated PM2.5 prediction in Jaipur, India, using a range of ML and deep learning methods, including MLR, Support Vector Regression (SVR), RF, K-Nearest Neighbors (KNN), and Convolutional Neural Network (CNN). Their results showed that CNN achieved the highest prediction accuracy (R2 = 0.98), highlighting the potential of these approaches for accurate urban air quality modeling. Kaviani Rad et al.18 compared deep learning and traditional ML methods to predict air pollutant concentrations in Tehran between 2013 and 2023. Using models like Fully Connected Neural Networks (FCNN) and CNN alongside meteorological data, they found that deep learning significantly outperformed ML in terms of accuracy and efficiency. FCNN achieved the highest performance (R2 = 0.93 for PM2.5), while temperature and humidity were key influencing factors.
Given the negative effects of air pollution on human health and the environment, accurate modeling is critical for urban planning and implementing effective mitigation strategies. While numerous studies have explored air pollution modeling using various spatial resolutions and ML techniques, there remains a significant research gap regarding the separate evaluation of spatial and temporal resolution effects on model performance under controlled, scenario-based conditions. Most existing works either focus on one resolution type in isolation without systematic comparison, or combine both spatial and temporal dimensions without clarifying their individual impacts. Additionally, the potential role of pollutant autocorrelation in improving temporal modeling accuracy remains underexplored, and limited efforts have been made to assess how spatial grid size alone influences predictive accuracy using consistent temporal settings. Moreover, comprehensive comparisons across ML models in these resolution-specific contexts are still lacking, particularly in real-world urban environments.
To address these gaps, the present study investigates the individual effects of temporal and spatial resolutions on the predictive accuracy of air pollution models using structured, scenario-based modeling. In the first phase, the study focuses on temporal modeling by keeping the spatial resolution constant and examining how different modeling scenarios—with and without incorporating pollutant autocorrelation, affect the prediction accuracy of PM10, PM2.5, and NOx concentrations. In the second phase, spatial modeling is conducted by fixing the temporal resolution and analyzing how changes in spatial grid size (500 m, 750 m, and 1000 m) influence the accuracy of spatial predictions. Throughout both phases, the performance of several ML algorithms, including Multilayer Perceptron (MLP), RF, Decision Tree (DT), and SVR, is compared to determine the most effective approaches under each resolution condition. This study thus offers resolution-specific insights and contributes to more robust and interpretable air quality modeling strategies for environmental policy and planning. Moreover, a significant part of this study focuses on integrating emission inventory data—such as industrial, vehicular, and power plant sources—into both spatial modeling and pollutant dispersion estimation. By explicitly analyzing how spatial resolution and source-based emission distributions interact, the study offers new insights into the spatial structure of urban air pollution and its linkage to real-world emission data.
An important consideration in these spatial resolution analyses is that varying resolutions inherently come with different data volumes, making direct comparison challenging and potentially leading to misleading conclusions if not carefully accounted for. Our study embraces this real-world complexity by examining how predictive accuracy evolves alongside changing spatial resolution and associated data volume.
Although MLP and RF have been widely used in air pollution modeling, the methodological novelty of this study lies in embedding autoregressive (AR) temporal dependencies—identified through AIC and BIC selection criteria—into these ML models. Unlike many previous studies that treat pollutant time series as independent observations, this research explicitly incorporates optimal lag structures into the input space, enabling the models to learn from pollutant autocorrelation. This hybrid approach has received limited attention in prior literature, particularly in urban contexts such as Ahvaz, where short-term temporal memory is crucial for understanding emission dynamics. Additionally, by applying this framework under controlled resolution-based scenarios, the study provides a new perspective on how time-series structure and spatial granularity interact to influence model accuracy. Moreover, while spatial statistical models such as Geographically Weighted Regression (GWR) and Eigenvector Spatial Filtering (ESF) have proven useful for analyzing spatial patterns in pollutant concentrations, they rely on assumptions of local linearity and stationarity that may not adequately represent the complex, nonlinear, and multi-source nature of air pollution in cities like Ahvaz. Therefore, this study emphasizes flexible ML frameworks that can integrate heterogeneous data sources and better capture spatial and temporal interactions.
Materials and methods
Study area
Ahvaz is a major urban center located in the southwestern region of Iran, within the Khuzestan province. Geographically, the city is located in the Khuzestan plains at approximately 48°40′ east longitude and 31°20′ north latitude. Ahvaz is located at an elevation of 18 m above sea level. According to the 2017 census, Ahvaz had a population of around 1,169,000 individuals19,20. Due to its important geographical location and closeness to key industrial, economic, and agricultural areas, the city is critical to the development of Iran’s southern region21. Ahvaz has become one of Iran’s most polluted cities due to a number of problems including rapid urban expansion, population growth, industrial and power plant emissions, increased motor vehicle usage, the operation of oil and gas facilities, and insufficient environmental management20. Figure 1 provides a visual representation of the study area’s location.
The study area/the authors created the maps using ArcGIS 10.8.1 software (https://support.esri.com).
Data preprocessing
The effectiveness of a supervised ML method can be influenced by various factors, both positively and negatively. Among these, the quality and accuracy of the input data play a pivotal role. Datasets that include irrelevant, redundant, or noisy features can substantially hinder the training procedure, making it more complicated and prone to errors. Therefore, data preprocessing such as cleaning, filtering, and feature selection is an essential and often time-consuming phase that demands substantial effort from both the researcher and the computational resources22,23. Despite being computationally demanding, this step is crucial to improving the effectiveness of ML models.
Outliers and missing data
After identifying outliers and missing values, it is essential to replace them with appropriate substitutes to maintain data integrity.For this purpose, the KNN algorithm is applied. KNN is a non-parametric, instance-based learning method and one of the most widely used algorithms in ML24. KNN is based on the idea that similar data points tend to be near each other. It classifies a new data point by identifying its k nearest neighbors and assigning the label that is most common among them, using a majority voting approach. The optimal value of k can be determined using the following formula.
In this formula, n is the number of samples, and K indicates the number of neighbors in the algorithm25.
KNN was used to impute missing values in air pollution time series data because it preserves the local structure of the data, leading to more accurate results than simple methods like mean imputation. By averaging the values of the nearest neighbors, KNN captures complex patterns and relationships. It is flexible, works with both numerical and categorical data, and does not require strong assumptions about data distribution, enhancing the robustness and reliability of subsequent analysis26,27.
Autocorrelation test
The similarity between observations is examined as a function of the time lag between them. Actually, there is a temporal relationship between observations and as a result AR models as static models can be utilized to capture trends in the time series data.
The AR model analyzes the correlation between a given data point and its preceding values. In this study, it is assumed that pollutant concentrations at time tare influenced by their past values. The AR model estimates this relationship using a weighted sum of previous observations, as expressed in the following Eq28..
where yt represents the concentration of pollutants at time t, vt is the amount of noise, αi are the weights associated with the time series in the past, and yt−i is the concentration of pollutants at time t-1. The AR models can be defined in various orders, with each representing the degree of dependence on previous time steps. For example, an AR model of order 3 implies that the current pollutant concentration depends on the values from the three preceding time points, whereas an AR(7) model indicates a dependency on the previous seven observations.
The optimal order of an AR model, denoted as AR(n), is typically selected using information criteria, which balance model accuracy and complexity. There are several forms of information criterion.
-
Akaike information criterion (AIC): is a widely used information criterion for determining the appropriate order of an AR model. It balances model fit and complexity by penalizing the number of estimated parameters, helping to prevent overfitting. AIC is calculated using the following formula:
where L is the likelihood of the model and k is the number of estimated parameters.
-
Bayesian information criterion (BIC): The BIC is a model selection criterion that balances goodness of fit with model complexity. In the context of an AR model, it is calculated using the following formula28,29:
where L is the likelihood function of the model, T is the sample size, and k is the number.
of parameters in the model.
ML methods
In this research four ML methods are used as follow:
-
MLP is one of the most common neural network methods and as the name indicates, each network comprises numerous layers, each of which contains input, weight, bias, and output30. MLP can handle nonlinear problems and is widely used for air pollution modeling and prediction. An MLP consists of an input layer, one or more hidden layers, and an output layer31,32,33. A hidden neuron (aj) has the following mathematical structure:
where f illustrates the activation functions that applies to the inputs. The activation function, in a sense, translates the amount of input multiplication in weight to a given interval. Activation functions include sigmoid, linear, radial functions, and so on. Finally, Zj is reported in Eq. 9.
where wij is the weight of input ui at neuron j and bj is neuron j’s bias34,35.
MLP operates by initially assigning random weights and biases, then processing input values and comparing the output to actual values. It calculates the mean squared error, and if the error is below a target threshold, training stops; otherwise, weights and biases are adjusted to reduce the error15,36,37,38,70. The structure of the proposed MLP models varies based on the number of input features, with a single output neuron. Different numbers of hidden layer neurons were tested using a trial-and-error approach to find the optimal configuration. A sigmoid activation function is typically used in the hidden layer, while a linear function is applied in the output layer35.
-
SVR is one of the most well-known ML algorithms for classification and regression. SVR may be used to solve nonlinear regression models, a more advanced form of support vector machine for regression issues. This approach has an advantage in high dimensions since it is not affected by the dimensions of the inputs. SVR has a function that sends input data to a higher-dimensional space. SVR has the following mathematical structure2,39,40:
where f(x) is the predicted value, \(\omega\) is the weight, and b is the threshold. As previously stated, SVR is widely utilized to solve nonlinear issues41.
-
DT is a useful tool for displaying complex data structures and rules in a hierarchical format, dividing data into recursive divisions. This approach visualizes decision outcomes using branching. Initially, the DT examines the training dataset by picking variables based on training procedures and objectives. The program evaluates the dataset for each node and uses the Gini index to calculate the best division criterion for minimizing node impurity. This process is carried out iteratively, with the goal of lowering impurities to zero where possible. A simplification process is then applied to the tree to evaluate its performance on the test set, revealing insights into the model’s prediction accuracy42,43.
-
RF is a community-based technique that uses DT to solve classification and regression problems. This method chooses random parameters from a collection of input parameters and uses these values to build a massive number of decision trees. The classification output of the technique is computed based on the findings of these decision trees. In this method, the RF algorithm yields effective results because independent or unrelated factors are assessed using multiple decision trees44,45,46,47,74.
Performance evaluation
In order to analyze the outcomes of proposed approach and compare the results of utilizing different ML methods, the following statistical metrics were used:
-
RMSE demonstrates the actual extent of the error caused by the model, and it is a conventional way of determining the model’s quality. The RMSE number will be close to zero if the predicted values are close to the actual values, and it will be high if the predicted values are considerably different from the actual values46,48,49,50,51. The RMSE formula is as follows:
where Pi is the predicted value, Oi is the observed value and N is the number of observations.
-
MAE in statistics is the measurement of the difference between two observations that describe the same phenomena. Its value is often similar to but somewhat lower than the RMSE3,38,40,52. Its equation is as follows:
-
R2 is an analytical criterion that calculates the variance ratio of a dependent variable. R2 reveals how much the variation of one variable explains the variance of the second variable, whereas R represents the connection between an independent and dependent variable46,53.
-
Leave one out cross validation (LOOCV) is a cross-validation method in which the number of layers equals the number of training samples. The learning algorithm is trained from the entire data sample in this manner. In reality, a data point is withdrawn from the training process and treated as a test in the network during each training. Its value is computed using the network, and its accuracy is determined. This procedure is repeated for all the data, and the overall accuracy is averaged. LOOCV is particularly useful when the dataset is small, as it allows for efficient use of limited data by maximizing the training set size at each iteration. In this study, due to the relatively small number of available samples, LOOCV was chosen as the cross-validation method54,55.
Implementation, result and discussion
Details of the main steps of our proposed methodology to model urban air pollution using ML methods and assessing the importance of the spatial and temporal resolutions in modeling are shown in Fig. 2.
Phase one: assessing the effect of temporal resolution in modeling accuracy
Data source
-
Ground Measurement: Daily data for average PM10, PM2.5, NOx from 2017/03/21 to 2018/03/20 were downloaded from Tehran Air Quality Control Company. The missing and outlier values were examined, removed, and calculated in the preprocessing stage. These pollutants were selected as key indicators of urban air quality due to their well-documented health impacts and prevalence in vehicular and industrial emissions. The data consisted of numeric values in micrograms per cubic meter (µg/m3), recorded as daily averages. Using daily temporal resolution allows the model to detect short-term fluctuations and capture daily exposure levels relevant for public health assessments. The missing and outlier values were examined, removed, and calculated in the preprocessing stage.
-
Meteorological Parameters: The meteorological data of the Naderi monitoring station were obtained as a time series in the mentioned period by the I.R of Iran Meteorological Organization. These parameters included temperature (°C), humidity (%), wind speed (m/s), wind direction (degrees), pressure (hPa), and rainfall (mm). All variables were collected as daily numeric values, aligned temporally with the pollution data to ensure accurate input representation for modeling. The selection of these parameters is based on their influence on pollutant dispersion and accumulation processes, which are critical for accurate prediction. Regarding the wind direction parameter, according to Eqs. 14 and 15, the data undergoes a transformation from non-linear to linear56.
In these two equations, SinWD and CosWD are the linearized results of the wind direction parameter (WD), while v is the wind direction temporal parameter.
Identifying empty records and outlier values and replacing them using the KNN algorithm
Missing and outlier data points were identified using pollutant-specific AQI thresholds, with values above 500 considered outliers57. Missing and outlier values were imputed using the K-Nearest Neighbors (KNN) method. The neighborhood size (k) was optimized by testing values between 1 and 19, with the Root Mean Square Error (RMSE) of a Random Forest model trained on the imputed data used to evaluate performance. The RMSE results for different k values are summarized in Table 1. Optimal k values were determined as 11 for PM10, 9 for PM2.5, and 5 for NOx.
Autocorrelation of pollutants concentration
This procedure reveals that the concentration level of each pollutant is influenced by values from several days earlier. An AR model is used to accomplish this. This model can be used to examine a time series in which a value is influenced by several preceding time points. To identify this relationship, statistical metrics such as BIC and AIC are used. Various degrees of AR are then calculated, and the degree with the lowest BIC and AIC values is chosen as the optimal degree and value. In Table 2, the AIC and BIC values for various pollutants in degrees 1 to 13 of the AR model are presented. To better understand the temporal dependencies of each pollutant, autocorrelation function (ACF) plots were generated (see Fig. 3). These plots reveal how strongly current values of pollutant concentrations are correlated with their past values over a range of lags (in days).
For PM10, the research determined that the best degree of the AR model is AR(3). This result is based on the lowest AIC value of 4191.28 and the lowest BIC value of 4207.85 for the third-degree AR model. This shows that using pollutant concentrations from the previous three days yields the most accurate temporal modeling for PM10. The large decline in AIC and BIC values at AR(3) emphasizes the significance of using short-term historical data to adequately capture temporal relationships. The ACF plot for PM10 illustrates how the concentration levels of this pollutant are influenced by previous days’ values. The plot shows a significant autocorrelation at lag 1, 2, and 3, after which the autocorrelation rapidly decreases and falls within the confidence interval, indicating that values beyond the third lag have minimal influence on current concentrations. This pattern supports the selection of AR(3) as the optimal model, as it captures the short-term temporal dependencies effectively. The ACF plot thus confirms that incorporating data from the previous three days provides the most meaningful predictive power for PM10 levels.
For PM2.5, the best degree of the AR model is AR(6), as evidenced by the lowest AIC value of 3716.82 and the lowest BIC value of 3728.52. This study implies that PM2.5 concentrations are best predicted using data from the previous six days. When compared to PM10, PM2.5 has a longer temporal dependency, which may indicate the pollutant’s behavior and interaction with numerous environmental and meteorological elements throughout time. Incorporating a six-day historical background improves the model’s understanding and prediction of PM2.5 level fluctuations. The ACF plot of PM2.5 reveals significant autocorrelations up to lag 6, after which the values drop within the confidence bounds. This confirms that the temporal influence of prior values extends over a longer duration for PM2.5 compared to PM10. The sustained autocorrelation pattern up to six lags supports the selection of AR(6) as the most suitable model. Thus, the ACF visualization validates that incorporating data from the past six days improves the model’s ability to capture the pollutant’s delayed response to environmental and anthropogenic factors.
In the case of NOx, the study revealed AR(4) as the best degree, with the lowest AIC value of 2559.41 and the lowest BIC value of 2570.87. This suggests that using the previous four days of data to anticipate NOx amounts is the most accurate method. The use of AR(4) emphasizes the importance of accounting for short- to medium-term historical data in order to accurately reflect the temporal dynamics of NOx pollution. The model’s capacity to employ a four-day historical window aids comprehension of temporal patterns and swings in NOx levels, which are frequently impacted by factors such as traffic patterns and industrial activity. This information from the table is used in the modeling stages, where the data is prepared based on the correlation they have with their previous days. This finding is further supported by the ACF plot of NOx, which shows significant autocorrelation up to lag 4. Beyond this point, the autocorrelation values fall within the confidence bounds, confirming the appropriateness of using a four-day historical window in modeling. The plot visually reinforces the statistical selection of AR(4) as the optimal temporal dependency structure for NOx concentrations.
Temporal modeling and prediction
In this study, we employed daily averages of meteorological parameters and historical pollution data to predict PM10, PM2.5, and NOx at the temporal level, taking into account two unique scenarios. For this phase, only MLP and RF models were applied, as they are well-suited for handling lagged features derived from autoregressive modeling. In contrast, models such as SVM and DT were not used in the temporal modeling phase due to their lower adaptability to autoregressive time-series structures. Specifically, SVM often requires extensive hyperparameter tuning to effectively handle lagged inputs, while DT tends to overfit when faced with temporally dependent features. Thus, selecting MLP and RF helped ensure both computational efficiency and alignment with the core objective of assessing temporal autocorrelation effects71,72,73. In the first scenario, we assumed no autocorrelation, which meant that past pollutant values have no impact on current predictions, with a daily temporal resolution. In the second scenario, we accounted for autocorrelation by predicting present concentrations using prior values of pollutants and meteorological conditions, while also acknowledging the influence of historical data. This resulted in temporal resolutions of 3 days for PM10, 6 days for PM2.5, and 4 days for NOx, respectively, to capture the best temporal dependencies for each pollutant.
Scenario I: Temporal modeling and prediction of pollutants concentration without considering autocorrelation of air pollutants.
At this stage, modeling and prediction of pollutants are investigated without taking autocorrelation into account. Using daily averages of meteorological data over a year, we employed a MLP and the RF algorithm to predict pollutant concentrations. The dataset, spanning one year of daily averaged meteorological and pollutant data (365 days), was split into training and testing sets. Specifically, 75% of the data (approximately 274 days) were used to train the models, while the remaining 25% (approximately 91 days) were reserved as the test set for evaluating model performance. This temporal split was performed sequentially to avoid any data leakage from future to past observations. The models are designed to predict daily pollutant concentrations based solely on the meteorological parameters available for each specific day. Therefore, as long as meteorological input data are available, the model can provide predictions for any future day without being limited to a predefined forecasting horizon. The proposed MLP for each pollutant consists of eight input neurons and one output neuron. Finally, statistical parameters such as RMSE, MAE, and R2 are calculated to evaluate the model. Following data preparation, the aforementioned models are formed, and the modeling process is carried out. For PM10 prediction (without autocorrelation), the MLP model consisted of two hidden layers with 12 neurons each and ReLU activation functions. The input dimension was 7, and the model was trained for 200 epochs using the Adam optimizer with mean squared error (MSE) as the loss function. For PM2.5, the MLP had two hidden layers with 12 and 15 neurons respectively, trained for 300 epochs. NOx, the MLP had three hidden layers with 25 neurons each and 8 input features, trained for 150 epochs. The Random Forest models had 668 trees for PM10; 60 trees for PM2.5; and 64 trees for NOx. All RF models used default settings for maximum tree depth and bootstrap sampling.
The number of neurons, layers, and epochs were selected based on trial-and-error and grid search to minimize the validation error. The input dimensions correspond to selected meteorological and pollution variables. Epoch values varied depending on convergence behavior of the models.
Table 3 displays the modeling results for the PM10, PM2.5, and NOx pollutant using the MLP and RF methods. In Fig. 4 the regression relationship between actual values and modeled values is illustrated for various pollutants using different methods.
According to the Table 3; Fig. 3, the MLP and RF models have varying levels of efficacy for predicting PM10, PM2.5, and NOx. The relatively low predictive accuracy for PM10 and PM2.5 may be attributed to the high temporal variability of air pollutant concentrations, their complex non-linear relationships with meteorological variables, and possibly the limited temporal length of the dataset, which may not have captured all seasonal patterns adequately. For PM10, the RF model outperformed the MLP model, with an RMSE of 86.134 µg/m3 vs. 92.564 µg/m3 and an MAE of 52.770 µg/m3 vs. 54.165 µg/m3. This shows that RF was better at capturing complicated patterns in PM10 data. For PM2.5, the MLP model achieved a MAE of 25.807 µg/m3 and an RMSE of 61.096 µg/m3, whereas the RF model obtained an MAE of 21.342 µg/m3 and an RMSE of 53.284 µg/m3, showing that RF proved better for PM2.5 predictions. In contrast, the MLP model performed better for NOx, with an MAE of 5.770 µg/m3 and an RMSE of 7.905 µg/m3, than the RF model, which had an MAE of 5.877 µg/m3 and an RMSE of 8.482 µg/m3. This indicates that the MLP model outperformed the RF model in forecasting NOx concentrations, probably due to its ability to capture nonlinear interactions more efficiently in this situation. Also, the scatter plots in Fig. 4 for PM10 and PM2.5 demonstrate that the RF model makes predictions that are closer to the true values, as indicated by the tighter clustering of points along the line of perfect agreement. For NOx, the scatter plot shows that the MLP model has a modest advantage over the RF model, with predictions that are more closely related to the observed values. These visual representations provide further support for the quantitative findings in Table 3, demonstrating the relative strengths and shortcomings of each model in forecasting different contaminants.
Scenario II: Temporal modeling and prediction of pollutants concentration considering autocorrelation among pollutants.
In this stage, the data is generated based on the outcomes of the AR model, and modeling is performed using the MLP and RF methods. The proposed MLP for PM10 pollutant consists of eleven input neurons, for PM2.5 pollutant consists of fourteen input neurons, for NOx pollutant consists of twelve input neurons, and one output neurons. Statistical metrics such as RMSE, MAE, and R2 are calculated to evaluate the models’ performance.
In Scenario II, the same one-year dataset of daily averaged meteorological and pollutant data (365 days) was used. A temporal train-test split was applied sequentially, with 75% of the data (approximately 274 days) allocated for training and 25% (approximately 91 days) for testing. The lag values used (3 days for PM10, 6 days for PM2.5, and 4 days for NOx) were determined based on the results of the AR model to optimally capture temporal dependencies. It is important to clarify that the lagged inputs correspond exclusively to the target pollutant concentrations, and not to the meteorological variables. For each prediction, the model uses the pollutant concentrations from previous days (as determined by the selected lag) along with the meteorological parameters of the day being predicted. Therefore, as long as these input features are available, the model is capable of generating predictions for any subsequent day, without being limited to a fixed forecast horizon.
In this scenario, temporal autocorrelation was incorporated by adding lagged features of both target pollutants and meteorological variables. This increased the number of input features accordingly (from 7 to 9 or 11). For PM10, the MLP model consisted of two hidden layers with 16 neurons each and 9 input features. The model was trained for 2000 epochs. For PM2.5, a network with 14 and 16 neurons in two layers was used, with 11 input features. The NOx MLP model had two hidden layers with 18 and 19 neurons respectively and 10 inputs. For the Random Forest models, the number of trees was set to 55 for PM10, 59 for PM2.5, and 64 for NOx. Hyperparameters were selected based on grid search and validation performance. The lag selection was guided by AR model, and the inclusion of such lagged inputs significantly improved the model’s ability to capture temporal patterns in pollutant concentrations.
Table 4 illustrates the findings for PM10, PM2.5, and NOx, demonstrating the efficacy of each modeling technique when autocorrelation is taken into account. In Fig. 4 the regression relationship between actual values and modeled values is illustrated for various pollutants using different methods.
The results of Table 4 demonstrate that using autocorrelation improves predicted accuracy for PM10 and PM2.5 but not for NOx. For PM10, the MLP model produced an RMSE of 68.590 µg/m3 and an MAE of 35.569 µg/m3, indicating a considerable improvement over the scenario without autocorrelation. The RF model also improved for PM10, but the MLP model fared better overall. Similarly, for PM2.5, the MLP model outperformed the RF model with an RMSE of 37.299 µg/m3 and MAE of 18.479 µg/m3. These findings show the necessity of taking temporal dependencies into consideration for enhancing the accuracy of particulate matter air pollution estimates. In contrast, adding autocorrelation to the NOx model did not improve performance. The MLP model had an RMSE of 12.104 µg/m3 and an MAE of 7.747 µg/m3, but the RF model had a higher RMSE of 13.346 µg/m3 and MAE of 8.016 µg/m3. These data indicate that predicting patterns for NOx are less impacted by previous values than for PM10 and PM2.5, implying that other variables may play a more major role in determining NOx levels.
The scatter plots in Fig. 5 for PM10 and PM2.5 reveal that the MLP model’s predictions are highly matched with actual values, as seen by the tight clustering of dots around the line of perfect agreement. This visual evidence backs up the quantitative improvements observed in the RMSE and MAE values. For NOx, the scatter plots show a less obvious improvement, with a more dispersed distribution of dots around the line of perfect agreement, indicating that autocorrelation has a limited influence on NOx predictions. The relatively low predictive accuracy for NOx in this scenario may be due to its higher sensitivity to sudden changes in traffic volume, short-term industrial activities, or emission sources that are not captured by lagged meteorological or pollutant variables. This suggests that additional explanatory factors may be necessary to improve the model’s performance for NOx. The increase in error for NOx in Scenario II can be attributed to the fact that NOx emissions are often influenced more heavily by abrupt fluctuations caused by short-term traffic patterns or sudden meteorological changes, which are not effectively captured by temporal autocorrelation. Unlike particulate matter, NOx concentrations exhibit more abrupt variations, limiting the usefulness of historical data for accurate prediction.
Phase two: assessing the effect of different spatial resolution in accuracy of models
Data source
-
Emission Inventory: The annual emission inventory of the city of Ahvaz was obtained from 2017/03/21 to 2018/03/20, which included industries, oil facilities, power plants, and mobile resources (The Iranian Department of Environment). PM and NOx pollutants were considered to evaluate the effects of spatial resolutions on their prediction, and CO pollutant is also required for initial modeling. These data represent quantitative annual emissions (kg/year) distributed as point or polygon features in GIS format. Various spatial aggregation levels (500 m, 750 m, 1000 m) were generated to assess resolution impact. The emission inventory was selected for its detailed sector-specific data, which serves as a critical input for pollution source modeling and spatial analysis. Figure 6 illustrates distribution of the contaminant sources in the Ahvaz.
-
MODIS AOD (Aerosol Optical Depth): The Terra and Aqua MODIS C6 daily 1-km MCD19A2 products generated by the MAIAC algorithm were used in the present research. These satellite data are raster-based, unitless optical thickness values representing atmospheric aerosol content. The 1-km spatial resolution was retained to align with the high-resolution modeling requirements, and the mean AOD data for the study period were computed using Google Earth Engine (GEE). In this study, the MODIS MCD19A2 product, which includes data from both Terra (AM) and Aqua (PM) satellites, was used. To generate daily AOD values, all available granules within each day over the study region were filtered and their pixel-wise median was computed using the Google Earth Engine platform. This compositing approach reduces the impact of cloud contamination and missing data, providing a robust daily aerosol optical depth estimate. AOD was selected due to its strong correlation with ground-level particulate matter concentrations, offering an indirect but spatially comprehensive pollution indicator.
-
Meteorological Parameters: The meteorological data were obtained on an annual average in the mentioned time period by the I.R of Iran Meteorological Organization, including temperature, humidity, wind speed, wind direction, pressure, and rainfall. These parameters were interpolated using the inverse distance weighting (IDW) method to produce continuous raster maps. The maps were generated at varying spatial resolutions (500 m, 750 m, 1000 m) to match the model scenarios. All values are numeric and represent long-term average conditions, which are essential for evaluating spatial dispersion behavior of pollutants. The inclusion of meteorological rasters at multiple resolutions allows the model to capture the influence of spatial scale in physical dispersion dynamics.
-
Auxiliary Data: Auxiliary data, including the digital elevation model (DEM), was utilized to determine the elevation of each point in order to improve the accuracy of the models. The DEM used in this study had a spatial resolution of 30 m and was resampled as needed to match modeling resolutions. Elevation data play a role in influencing air movement and pollutant accumulation patterns, especially in areas with complex terrain, and thus serve as an important spatial input feature.
Distribution of the Industries, oil facilities and power plants in the territory of Ahvaz/the authors created the maps using ArcGIS 10.8.1 software (https://support.esri.com).
Spatial modeling and prediction
The PM and NOx pollutants were determined for modeling and prediction in this section. According to Ahvaz city’s emission inventory, the majority of PM emissions (66%) are generated by stationary sources, primarily industries, with power plants accounting for 31%. Similarly, power plants account for 63% of stationary NOx emissions, with industries contributing 33% (The Iranian Department of Environment). As a result, only industrial facilities, power plants, and oil units were considered for modeling among stationary sources in this study, along with mobile sources. Furthermore, because of the impact of sources outside the city on air pollution within the city, these sources were investigated as well.
Dispersion Modeling.
As previously stated, the main objective is to investigate the significance of spatial resolution in the dispersion of PM and NOx pollutants within cities, taking into account factories, oil facilities, power plants, and mobile sources. It is critical to understand that each pollution source has a particular radius of contamination after dispersion, necessitating the calculation of pollution quantities prior to modeling pollutant concentrations from all sources.
For this purpose, an MLP model with five parameters, including temperature, wind speed, wind direction, CO pollutant concentration, and AOD, is utilized for each pollution source. This model seeks to calculate the amount of pollution spread within a given radius. Temperature, wind speed, and wind direction are all variables to consider since they have a significant impact on the spread of contaminants throughout the city. Additionally, incorporating CO pollutant data is intended to improve modeling accuracy due to its significant association with PM and NOx pollutants. To justify the inclusion of CO as an input feature, Pearson correlation analysis was conducted. The results showed a moderate to strong positive correlation between CO and both PM (r = 0.56) and NOx (r = 0.63), indicating that CO levels can serve as a useful proxy for modeling these pollutants.
-
Industries and oil facilities.
Given the similarity in pollutant concentrations and the comparable radius for contaminant dispersion, a unified model is used for industries and oil facilities. For PM modeling, the architecture consisted of three hidden layers with 12 neurons each, all using ReLU activation functions. Due to the relatively small dataset size, LOOCV was applied to ensure robust performance evaluation. The model was trained for 200 epochs using the Adam optimizer and MSE as the loss function.
For NOx prediction in the same domain, a shallower MLP was employed, consisting of two hidden layers with 17 and 15 neurons, respectively. This model was trained for 200 epochs using the full training data, optimized via Adam with MSE as the loss.
The depth of the PM model was selected based on its improved convergence behavior during cross-validation. All models used 6 input features representing relevant meteorological and operational parameters. Standardization was performed prior to training to facilitate convergence and reduce gradient instability.
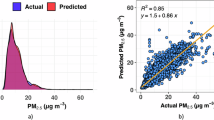
Table 5 presents the initial modeling results for PM and NOx pollutants from industries and oil facilities. In Fig. 7 the observed and predicted concentrations of PM and NOx are compared based on the initial modeling.
The findings of Table 5 demonstrate that the MLP model accurately forecasted pollutant concentrations in both PM and NOx emissions from industrial and oil facilities. The MLP model for PM showed an R2 of 0.86. These values show a good level of precision in capturing the dispersion patterns of PM from various sources. The MLP model accurately models NOx dispersion, with an R2 of 0.81.
The scatter plots (Fig. 7) for PM demonstrate a tight clustering of points around the line of perfect agreement, which supports the statistical measures’ excellent prediction accuracy. This graphic depiction demonstrates that the MLP model accurately captures the dispersion dynamics of PM emissions from industrial and oil sites. The scatter plots for NOx provide a high agreement between observed and anticipated values, but with slightly greater fluctuation than PM. Despite this, the points remain tightly packed around the line of perfect agreement, demonstrating the model’s overall accuracy in forecasting NOx dispersion. The slight spread in the NOx scatter figure indicates that, while the MLP model is robust, there may be additional factors driving NOx dispersion that require more exploration.
-
Mobility sources (Vehicles).
For modeling pollutant dispersion from mobile sources (Cars, Taxies, Buses, Motorcycles), separate MLP architectures were designed for PM and NOx. The PM model consisted of three hidden layers with 10, 50, and 50 neurons, respectively, each using ReLU activation. The model was trained for 200 epochs using the Adam optimizer with MSE loss. For NOx prediction, a deeper architecture was used, consisting of four hidden layers with 17, 20, 40, and 50 neurons, also using ReLU activation. This model was trained for 200 epochs as well, with the same optimizer and loss function.
Both models used 6 input features, representing a combination of traffic-related and meteorological variables. The architecture depth and neuron counts were determined through empirical tuning to optimize validation performance. All input data were standardized before training.
The results are reported in Table 6; Fig. 8 illustrates the comparison of observed and predicted concentrations of PM and NOx.
The findings present that the MLP model accurately predicted pollutant concentrations for both PM and NOx emissions from mobile sources. The MLP model accurately captured PM dispersion patterns from various sources, with an R2 of 0.88. The MLP model accurately predicted NOx dispersion from mobile sources, with an R2 of 0.89.
The scatter plots in Fig. 8 for PM demonstrate a tight clustering of points around the line of perfect agreement, which also supports the statistical measures’ excellent prediction accuracy. The scatter plots for NOx demonstrate a high agreement between observed and anticipated values, but with slightly greater fluctuation than PM. Despite this, the points remain tightly packed around the line of perfect agreement, demonstrating the model’s overall accuracy in forecasting NOx dispersion.
-
Power Plants.
Due to the limited number of power plants (only two), the model cannot be implemented. In this scenario, the pollution produced by the power plants is deemed to be equivalent to the amount of pollution distributed within the impact radius.
Computing the Pollution Dispersion.
Following the construction of the model, the extent of pollution dispersion within the impact radius for each pollution source must be determined. The distance over which pollutants emitted from a source are dispersed is defined as the impact radius. The impact radius is determined using ArcGIS. Following the determination of the impact radius’s extent, regular grids with resolutions of 500 m, 750 m, and 1000 m are formed using GIS within the specified impact radius.
-
Industry and Oil Facilities.
The impact radius for industries and oil facilities is set to be 3 kilometers58,59. Following the determination of the impact radius for industries and oil facilities, model parameters such as temperature, wind speed, wind direction, and CO concentration are calculated within the specified grids with the specified resolutions. Figure 9 depicts the Grid 1000 m created for industries and oil facilities. Following that, these parameters are fed into the model to calculate the concentrations of PM and NOx. within three grids.
Grid created in the specific radius at a resolution of 1000 m for industries and oil facilities/The authors created the maps using ArcGIS 10.8.1 software (https://support.esri.com).
-
Mobility Sources.
The impact radius for mobile sources is considered to be 250 meters60. After computing the model’s parameter, they are inputted into the model, calculating PM and NOx pollutant concentrations from mobility sources across three grids. Figure 10 depicts the Grid 750 m created for mobility sources. It should be noted, Pollution from mobile sources is regarded as a point source in order to facilitate the ultimate integration of pollutant layers from various sources.
Grid created in the specific radius at a resolution of 750 m for mobility sources/The authors created the maps using ArcGIS 10.8.1 software (https://support.esri.com).
-
Power Plants.
The impact radius of power plants is estimated to be around 5 Km61. Based on this assumption, it is assumed that the pollutant produced by power plants remains constant and equal within the impact radius. It is critical to note that pollutant dispersion effects are not limited to the impact radius. However, because the model only addresses a portion of the overall problem, this study assumes that pollutant impacts are restricted to the defined impact radius.
Integration of different pollutant maps
Previously, the concentrations of PM and NOx pollutants originating from diverse sources were determined using the resolutions specified (500 m, 750 m, 1000 m). During this stage, it is imperative to overlay separate pollution layers at resolutions that are relevant to each pollutant. By following this procedure, pollutant contributions from the utilized sources are accounted for in the final model. Figure 11 depicts how to combine different layers at a resolution 500 m. The resulted map presents the concentrations of PM and NOx pollutants from all sources in each pixel. Then, meteorological data such as temperature, humidity, wind speed, wind direction, air pressure, rainfall, altitude, and geographical coordinates are determined at these points. The same combination process is applied to overlay this pollutant in other grids, and a similar combination is performed for the NOx pollutant as well.
Integration of PM pollutants from various resources (spatial resolution of 500 m)/The authors created the maps using ArcGIS 10.8.1 software (https://support.esri.com).
Final modeling and determining better Spatial resolutions
After the preparation of the layers, final grid-based modeling of PM and NOx concentrations at spatial resolutions of 1000 m, 750 m, and 500 m, different MLP architectures were designed based on data complexity and spatial resolution. For PM at 1000 m resolution, the MLP model consisted of five hidden layers with 50 neurons each, using ReLU activations. At 750 m, a slightly deeper network was employed with six hidden layers (40 neurons), while for 500 m, the model used four layers with 60 neurons each to prevent overfitting due to increased spatial granularity. For NOx, the 1000 m model included five layers with 50 neurons, whereas the 750 m and 500 m models used four and three layers respectively (55 neurons), tuned to account for varying emission dispersion patterns at different scales. All models were trained using the Adam optimizer and MSE as the loss function over 200 epochs, with 10 input features.
The model architectures were selected based on iterative trial-and-error combined with preliminary grid search to minimize validation error. Additionally, model complexity was adjusted in relation to spatial resolution and data volume to prevent overfitting and improve generalization.
The modeling results presented in Table 7 were obtained by splitting the dataset into training and testing subsets. The models were trained on the training data and evaluated on the testing set without applying cross-validation. In Fig. 12, Observed and predicted concentrations of PM and NOx were compared by final modeling.
According to the Table 7, for PM at a 500 m resolution, the MLP model has an RMSE of 19.779 kg/year, indicating great accuracy in capturing dispersion patterns. At a resolution of 750 m, the model’s RMSE was 19.324 kg/year, showing a slight performance decline. At 1000 m resolution, the model has an RMSE of 13.509 kg/year. These measures demonstrate the model’s ability to properly describe the dispersion patterns of PM in residential environments at various resolution levels. As a result, the PM pollutant performs better at coarser spatial resolutions (larger grid sizes). Given the problem’s data structure, the modeling accuracy for PM pollutants improves as data resolution increases. In contrast, the RMSE for NOx at a 500 m resolution was 307.496 kg/year, according to the MLP model. This metric is quite accurate in characterizing NOx dispersion patterns at this finer resolution. At 750 m resolution, the model had an RMSE of 461.505 kg/year, showing that performance decreased somewhat as resolution rose. At 1000 m resolution, the model produced an RMSE of 568.380 kg/year, indicating that predicted accuracy decreases with coarser resolution. As a result, for NOx pollutants, lower resolutions improve modeling accuracy. So, when the problem parameters are taken into account, NOx pollutants perform better at lower resolutions.
The scatter plots of Fig. 12 for PM, at 1000 m resolution, reveal a significant alignment between observed and anticipated values, with points tightly placed around the line of perfect agreement, confirming the excellent prediction accuracy. The scatter plots at the resolutions of 500 m and 750 m likewise show satisfactory alignment, but with slightly more fluctuation than the 1000 m resolution. The scatter plots for NOx at 500 m resolution show a tight clustering of dots around the line of perfect agreement, indicating great forecast accuracy based on statistical measures. As the resolution increases to 750 m and 1000 m, the scatter plots for NOx show increased unpredictability and a wider dispersion around the line of perfect agreement, demonstrating that model performance degrades at coarser resolutions.
After developing the models and validating the findings, the spatial distribution map of PM concentration in Grid 1000 m and NOx concentration in Grid 500 is shown, in Fig. 13, Although the modeling was performed at 1000 m for PM and 500 m for NOx, the maps are presented at a 100-meter resolution to give a clearer and more thorough depiction.This greater resolution improves the visual understanding of spatial patterns and pollutant dispersion, making it simpler to detect places with higher concentrations and better comprehend the distribution.
PM and NOx Concentration distribution map in the study area/The authors created the maps using ArcGIS 10.8.1 software (https://support.esri.com).
Figure 13 demonstrates that PM concentrations are highest in the northern section of the research region, with values falling as one moves south. The locations with the greatest concentrations are shown in red, indicating major emission sources in the northern region, most likely due to industrial activity. Also, this figure displays the regional distribution of NOx concentrations. Similar to PM, the greatest NOx concentrations were found in the northern section of the research area, as indicated by the red zones. This trend implies that the majority of NOx emissions come from industrial or high-traffic metropolitan regions in the north. Concentration values drop in the southern areas of the research region, which are highlighted in yellow to indicate lower emission levels.
Accuracy assessment of different ML methods
At this point, we compare various methods for PM pollutants in the 1000 m resolution grid and NOx in the 500 m resolution grid in the final modeling. The approaches being compared are MLP, RF, DT, and SVR. All models were tuned based on trial-and-error and pollutant characteristics. MLP models used 4–6 hidden layers with 25–50 neurons each and ReLU activation; epochs ranged from 150 to 250 depending on convergence. RF models included 60–120 trees with default depth settings. DT models had a maximum depth of 10–15 to prevent overfitting. SVR models used an RBF kernel with optimized C and gamma values. Model settings were adapted to each pollutant and spatial resolution to ensure fair comparison. Table 8 shows the results of PM pollutant modeling using the aforementioned methods.
According to the Table 8, the MLP model outperformed other models for PM at 1000 m resolution, with a R2 of 0.90, MAE of 5.037 kg/year, and RMSE of 13.509 kg/year, showing strong prediction accuracy. The DT model had a slightly lower R2 of 0.81, but produced a lower MAE of 3.881 kg/year compared to MLP, indicating higher average error performance. However, its larger RMSE of 18.824 kg/year shows more unpredictability in predictions than MLP. The RF model demonstrated lower performance than MLP and DT, with a R2 of 0.56, MAE of 8.653 kg/year, and RMSE of 27.040 kg/year. The SVR model performed poorly again, with a R2 of 0.02, MAE of 13.994 kg/year, and RMSE of 43.578 kg/year. At a 500 m resolution for NOx, the MLP model obtained the greatest R2 of 0.90, suggesting good prediction accuracy, with an MAE of 50.528 kg/year and an RMSE of 307.496 kg/year. Despite a strong R2 value, the large RMSE indicates significant fluctuation in NOx concentrations, most likely due to the dataset’s high NOx values. The DT model has an R2 of 0.81, a lower MAE of 44.707 kg/year than MLP, but a higher RMSE of 417.542 kg/year. This suggests that, while the DT model performed better on average errors, it suffered more with bigger variances in NOx values. The RF model performed well, with a R2 of 0.86, MAE of 62.405 kg/year, and RMSE of 367.494 kg/year. The SVR model proved unsuccessful, with a negative R2 of −0.13, MAE of 348.696 kg/year, and RMSE of 1014.953 kg/year.
As a result, the MLP model has the highest predicted accuracy for both NOx and PM. However, it is worth noting that the DT model had higher MAE values for both pollutants, implying that its predictions were, on average, closer to real values. The higher RMSE values for DT models suggest that, while their average predictions were better, they had more mistakes on specific predictions than MLP. When it deals with NOx, the model performs an excellent task of capturing the general trend, but it has trouble with high levels of variability in NOx concentrations, as indicated by the high R2 value and high RMSE for the MLP model. Larger forecast errors may result from the dataset’s intrinsically high NOx values, which is the source of this unpredictability. This emphasizes how important it is to take into account both RMSE and MAE when assessing the effectiveness of a model since they offer distinct viewpoints on prediction accuracy.
Dispersion model performance
In some cases, CO pollutant concentrations are unavailable, necessitating modeling based solely on meteorological data. For preliminary dispersion modeling without CO data, MLP models used 3–4 hidden layers with 20–40 neurons each and ReLU activation. Input features included temperature, wind speed, wind direction, and AOD. Models were trained for 150–200 epochs with Adam optimizer minimizing MSE. These configurations were selected based on iterative tuning to balance accuracy and training time.
The proposed MLP models for PM and NOx pollutants consist of four input neurons and one output neuron. The results of dispersion modeling of PM and NOx pollutants from stationary and mobile sources are shown in Table 9.
Based on the results of modeling without CO pollutants, it can be inferred that this assumption is valid in certain situations, given the acceptable R2 and RMSE values. As a result, even when the CO concentration is unknown, modeling can still be done using meteorological and AOD data.
Discussion
In the following sections, we delve into a detailed study of our findings, assessing the performance of the models and exploring their practical implications for urban planning and policy-making.
In-depth analysis of research results
In the current study, we utilized a variety of ML models to investigate the effect of spatial and temporal resolution on air pollution modeling accuracy, focusing on PM and NOx pollutants. This study’s findings provide light on how varied data configurations and different resolutions might affect these models’ prediction ability.
-
Temporal Modeling.
In order to incorporate different temporal resolutions, this study leveraged the intrinsic properties of time series data, recognizing that pollutant and meteorological measurements are inherently sequential and temporally correlated. By aggregating data at daily intervals, we aimed to capture meaningful short-term variations while maintaining the natural temporal structure of the data. The inclusion or exclusion of autocorrelation in the models was motivated by the fundamental time series concept that past pollutant levels can influence future values, which is essential for improving prediction accuracy at varying temporal resolutions.
The temporal modeling phase, first in the absence of autocorrelation, daily averages of meteorological data and pollution concentrations were utilized to forecast future results. When autocorrelation was not taken into account, the RF technique outperformed the MLP method for PM10 and PM2.5 pollutants. The RF model had decreased RMSE and MAE values, indicating improved forecast accuracy for these pollutants. However, this scenario including autocorrelation offered a different perspective. The MLP model performed better for PM10 and PM2.5 when the link between current and previous pollutant concentrations was considered. The RMSE for PM10 declined from 92.56 to 68.59, and for PM2.5 from 61.10 to 37.30. This finding emphasizes the significance of taking temporal dependencies into account when simulating air quality. Interestingly, autocorrelation did not improve NOx predictions, as the RMSE for NOx rose from 7.90 to 12.10. This anomaly indicates that NOx concentrations may be impacted by reasons other than autocorrelation, such as short-term emission spikes or localized sources of pollution.
Although incorporating AR lag features improved the predictive performance of MLP and RF models for PM10 and PM2.5, it is important to acknowledge that these models are inherently non-temporal and lack mechanisms to directly model time dependencies. The use of lagged pollutant concentrations as static input features allows the models to indirectly benefit from short-term autocorrelation but does not fully capture the sequential dynamics or long-range temporal interactions. As a result, while performance improvements were observed, particularly for PM pollutants, the observed gains may be limited by the models’ inability to learn time-aware representations. several advanced deep learning architectures such as recurrent neural networks (RNNs), temporal convolutional networks (TCNs), or Transformer-based models can be employed in future research to capture temporal dependencies more effectively. For instance, the Geo-STO₃Net model developed by Chen et al.75 successfully integrates spatiotemporal information through a Transformer-based temporal encoder and a ResNet-based spatial encoder, achieving significant accuracy improvements in surface ozone estimation. Furthermore, in a subsequent study, Chen et al.76 proposed the IPMDNN model—a physics-informed deep neural network that jointly estimates multiple air pollutants while enhancing interpretability using a tanh-based self-attention mechanism and layer-wise relevance propagation. These approaches demonstrate the potential of interpretable, sequence-aware deep learning frameworks in modeling spatiotemporal air pollution patterns. However, such models typically require large-scale data and extensive training resources, which were beyond the scope of the current study focused on resolution-based evaluation.
-
Spatial Modeling.
The selection of spatial resolutions at 500 m, 750 m, and 1000 m was carefully motivated by both the nature of the emission data and computational feasibility considerations. The emission inventory data used in this study detailed point sources such as industrial units, oil facilities, and power plants, which are inherently localized. A finer resolution, such as 500 m, allows the model to better capture these discrete, spatially concentrated sources and their immediate dispersion patterns. However, due to the relatively large spatial extent of Ahvaz city and its surrounding areas, along with the significant computational resources required for higher-resolution simulations, coarser grid sizes of 750 m and 1000 m were also evaluated. These coarser resolutions help balance the trade-off between spatial detail and computational efficiency, allowing for a broader regional analysis without prohibitive costs. Moreover, testing these multiple spatial scales enables the identification of the optimal resolution that sufficiently represents pollutant distributions while maintaining manageable computational demands. This approach aligns with previous studies that emphasize the importance of adapting spatial resolution to pollutant source characteristics and study area size to optimize model performance and applicability9,10.
The spatial modeling results demonstrated distinct behaviors for different pollutants across the tested resolutions. Coarser resolution (1000 m) yielded better accuracy for PM, reflected by a lower RMSE value of 13.51 kg/year, which can be attributed to the relatively uniform spatial distribution of PM across the study area. In contrast, NOx, which originate primarily from discrete and localized sources like traffic and industrial facilities, showed improved prediction accuracy at the finer 500 m resolution, achieving an RMSE of 307.50 kg/year. These findings highlight how pollutant-specific emission characteristics influence the effectiveness of spatial resolution choices, reinforcing the importance of customizing modeling parameters according to pollutant type.
-
Model Performance.
ML algorithms including MLP, RF, DT, and SVR were selected for their ability to model complex, nonlinear relationships between pollutants and environmental variables across different spatial resolutions. Among these, MLP and RF demonstrated robust performance, particularly in handling large and complicated datasets with intricate interactions. For instance, in the final modeling phase, the MLP model achieved RMSE values of 13.51 for PM10 at 1000 m resolution and 307.50 for NOx at 500 m resolution, highlighting its adaptability to varying pollutant behaviors and spatial scales. While DT and SVR models showed comparatively lower performance, especially with large datasets, they can still be effective in simpler contexts. Overall, the results suggest that more advanced models like MLP and RF are better suited for comprehensive air quality modeling tasks.
Although traditional spatial statistical models such as GWR and Eigenvector Spatial Filtering (ESF) have been used in various air quality studies, they were not employed in this research due to several methodological limitations. GWR assumes spatial stationarity and local linearity, which may not adequately capture the nonlinear and heterogeneous nature of pollutant dispersion in a highly industrialized and climatically complex urban area like Ahvaz. Likewise, ESF depends on predefined spatial structures that may not be compatible with the multi-source and raster-based emission inventory data used here. In contrast, the ML models applied in this study—particularly MLP and RF—offer higher flexibility in modeling nonlinear spatial interactions, integrating diverse inputs such as AOD, CO, and meteorological rasters. Nevertheless, future research may benefit from hybrid approaches that combine the interpretability of spatial statistical models with the predictive power of ML techniques.
An additional contribution of this study lies in the detailed use of emission inventory data within the spatial modeling framework. Unlike studies that rely solely on ambient measurements, this research incorporates source-specific emission data—covering stationary (industrial, oil facilities, power plants) and mobile (vehicles) sources—into dispersion modeling. These emission data were directly used to compute pollution spread within defined impact radii, which were then mapped to grids of different spatial resolutions. This design enables a structured investigation of how emission distributions influence spatial modeling accuracy. Although temporal variations in emission inventory were not available, this limitation is addressed by fixing temporal resolution and examining the effect of spatial aggregation in emission-driven modeling scenarios. The findings of this study have important practical implications for urban planners and politicians working to enhance air quality and public health.
Optimized Spatial planning
The recent finding that PM are better approximated at a coarser spatial resolution of 1000 m implies that regional air quality control plans should be based on larger spatial scales. This can aid in the efficient allocation of resources and the execution of large-scale pollution controls. In contrast, the necessity for finer spatial resolutions (500 m) for NOx modeling shows the need of targeted treatments. Traffic management, industrial emissions control, and targeted pollution reduction efforts in specific areas can all be more effective.
Improved Temporal modeling
The use of autocorrelation greatly increased forecast accuracy for PM10 and PM2.5, highlighting the relevance of taking into account past pollutant levels in temporal models. This technique can improve the accuracy of air quality forecasts, allowing for more prompt public health alerts and mitigation activities.
Enhanced use of ML models
The superior performance of the MLP model, particularly when autocorrelation was included, demonstrates the advantage of employing sophisticated ML algorithms capable of capturing complex nonlinear relationships in environmental datasets. Such advanced modeling techniques can support urban planners and researchers in developing precise and actionable air quality forecasts.
Resource Allocation and Policy Formulation: By differentiating the spatial and temporal characteristics of various pollutants, these results support a strategic approach for resource allocation and policy formulation. Tailoring spatial resolutions and modeling techniques to pollutant-specific behaviors enhances the effectiveness of pollution control programs and maximizes the utility of available data and computational resources.
Comparative analysis of results with other researchers
The findings of this study were compared to those of earlier studies to validate them and comprehend their importance in the larger context of air pollution modeling. This comparative study took into account many major studies as shown in Table 10.
This study discovers that PM pollutants are better approximated at a coarser spatial resolution of 1000 m, but NOx pollutants are more accurate at a finer resolution of 500 m. This contradicts the findings of Stroh et al.7who noticed 200–400 m as the optimal resolution for urban NOx modeling. The difference might be attributed to varying urban contexts and emission sources, emphasizing the necessity for context-specific modeling methodologies. While Nishikawa and Kannari9, discovered an unexpected association between NH3 at 1*1 km resolution and NO2 at a coarser 3*3 km resolution, the present study’s focus on PM and NOx pollutants especially improves comprehension of their spatial behavior in urban contexts. This uniqueness enables more focused urban planning measures. Also, Fernandes et al.62 and Gariazzo et al.65 assessed air quality at varied spatial resolutions but focused on different pollutants and environments. Fernandes et al. discovered that varying grid sizes produced the same spatial distribution findings for PM10 and NO2, but with significant variations in magnitude and processing time. our research confirms the necessity for high geographic resolution in modeling NOx, but discovers a distinct benefit in utilizing coarser grids for PM, illustrating the need of tailoring model resolutions to individual contaminants for optimal accuracy and computing efficiency.
Additionally, Tan et al.10 employed the WRF/CMAQ system to investigate the influence of spatial resolution on air quality simulations, indicating that finer resolutions offered more accurate forecasts for urban and industrial regions. Our research results are consistent with this in the context of NOx pollutants, which benefit from a 500 m resolution, demonstrating that for pollutants with localized sources, such as NOx, fine spatial information is critical for successful modeling.
The current study stands out from others since it employs sophisticated ML methods such as MLP, RF, DT, and SVR rather than standard statistical approaches or single ML models. Di et al.64 employed comparable sophisticated models to predict daily PM2.5 levels at a 1 km resolution over the contiguous United States, with satisfactory results up to specific concentrations. However, our research takes a step further by using autocorrelation and different spatial resolutions to improve model accuracy, resulting in a more sophisticated strategy to dealing with various pollutant behaviors.
While comparisons with large-scale modeling efforts offer valuable global context, it is also essential to benchmark the results of this study against localized research conducted specifically in Ahvaz. Several studies have previously investigated air pollution in Ahvaz using various methodologies, which provides an opportunity to contextualize and validate the current findings. For instance, Saffar et al.66 employed direct field measurements and GIS-based AQI zoning around oil and gas facilities, identifying extremely unhealthy conditions during the summer. While their study focused on point-based measurements near industrial sites, our approach leveraged ML techniques to capture broader urban patterns, yet the identified pollution hotspots and seasonal variations remain consistent.
Similarly, Jahedi et al.67 applied a hybrid SWOT-AHP framework integrated with emission inventory analysis to assess pollution sources and propose control strategies. Their identification of CO and NOx as major pollutants corroborates the dominant contributors found in our analysis, despite methodological differences in source apportionment.
Asadifard and Masoudi68 used regression-based statistical models to examine CO dynamics in relation to meteorological parameters, revealing temporal patterns (e.g., nighttime peaks, spring maxima) that align with our seasonal results. Finally, Maleki et al.69 utilized artificial neural networks to predict hourly concentrations of multiple pollutants, demonstrating the predictive potential of data-driven approaches. While our method does not rely on ML algorithms, the spatial consistency between their modeled outputs and our mapped results further supports the robustness of the current approach.
Together, these comparisons demonstrate that although the methodologies vary—from field measurements and regression models to decision-support frameworks—the overall findings reinforce the spatial and seasonal characteristics of pollution in Ahvaz, highlighting both the reliability and the complementarity of our mapping outcomes within the existing body of literature.
Conclusion
This study contributes to filling a gap in existing research by thoroughly examining the impact of varying spatial and temporal resolutions on air pollution modeling in Ahvaz, Iran, with a specific focus on PM and NOx pollutants.
The investigation was divided into two phases: temporal and spatial modeling.The study investigated the significance of taking pollutant autocorrelation into account during the temporal modeling phase. It found that the MLP method performed better when autocorrelation was taken into account than other techniques, while the inclusion of autocorrelation had a negative impact on NOx modeling. In temporal modeling, utilizing auto-correlation resulted in better accuracy for the PM10 (3 days) and PM2.5 (6 days), and lower accuracy for NOx (4 days). The spatial modeling phase explored the best spatial resolution for predicting PM and NOx concentrations using emission inventory data. The results showed that lower spatial resolutions (1000 m) increased modeling accuracy for PM pollutants, whereas higher resolutions (500 m) produced superior results for NOx pollutants. Besides, the study compared other ML algorithms, revealing the higher performance of the MLP approach in this situation.
Furthermore, the study provided a thorough comparison with past studies, highlighting the study’s unique contributions and findings. The findings of this study add to the improvement of air pollution modeling approaches and can help policymakers and urban planners make better decisions for sustainable development. As we move forward, continued research in this field is crucial for enhancing our understanding of the complexities of air pollution dynamics, considering the ever-evolving urban environments and the pressing need for effective mitigation strategies.
As a recommendation for future research, it should be noted, one of the drawbacks of our research was that we did not have access to daily and weekly emission inventory data. Since, daily and weekly data offer more options like extracting characteristics such as moving averages, trends, and seasonality indicators, which can improve the model’s prediction potential. On the other side, population density statistics was also unavailable. So, it can be beneficial to utilize population density for the modeling as it usuallycorrelates with other factors in the data to improve the accuracy. Furthermore, regarding the preliminary modeling, it is recommended to employ EPA model like AERMOD and CALPUFF. Because, these models can simulate an extensive variety of scenarios, including many types of emission sources, intricate topographical features, and weather variability.
Data availability
We utilized information from these sources.Air Pollution Monitoring Station: Tehran Air Quality Control Company (Available at: http://airnow.tehran.ir)Emission Inventory: The Iranian Department of Environment (Available at: http://emissioninventory.doe.ir)Meteorological variables: I.R of Iran Meteorological Organization (Available at: https://data.irimo.ir).
References
Jain, S. & Khare, M. Adaptive neuro-fuzzy modeling for prediction of ambient CO concentration at urban intersections and roadways. Air Qual. Atmos. Health. 3 (4), 203–212. https://doi.org/10.1007/s11869-010-0073-8 (2010).
Bai, L., Wang, J., Ma, X. & Lu, H. Air pollution forecasts: an overview. Int. J. Environ. Res. Public Health. 15 (4), 780. https://doi.org/10.3390/ijerph15040780 (2018).
Alimissis, A., Philippopoulos, K., Tzanis, C. & Deligiorgi, D. Spatial Estimation of urban air pollution with the use of artificial neural network models. Atmos. Environ. 191, 205–213. https://doi.org/10.1016/j.atmosenv.2018.07.058 (2018).
Dong, X., Zhao, X., Peng, F. & Wang, D. Population based air pollution exposure and its influence factors by integrating air dispersion modeling with GIS Spatial analysis. Sci. Rep. 10 (1), 479. https://doi.org/10.1038/s41598-019-57385-9 (2020).
Lauriks, T. et al. Application of improved CFD modeling for prediction and mitigation of traffic-related air pollution hotspots in a realistic urban street. Atmos. Environ. 246, 118127. https://doi.org/10.1016/j.atmosenv.2020.118127 (2021).
Motlagh, S. H. B., Pons-Valladares, O. & Hosseini, S. A. City-scale model to assess rooftops performance on air pollution mitigation; validation for Tehran. Build. Environ. 244, 110746. https://doi.org/10.1016/j.buildenv.2023.110746 (2023).
Stroh, E., Harrie, L. & Gustafsson, S. A study of Spatial resolution in pollution exposure modelling. Int. J. Health Geogr. 6, 1–13. https://doi.org/10.1186/1476-072X-6-19 (2007).
Shad, R., Mesgari, M. S. & Shad, A. Predicting air pollution using fuzzy genetic linear membership kriging in GIS. Comput. Environ. Urban Syst. 33 (6), 472–481. https://doi.org/10.1016/j.compenvurbsys.2009.10.004 (2009).
Nishikawa, Y. & Kannari, A. Atmospheric concentration of ammonia, nitrogen dioxide, nitric acid, and sulfur dioxide by passive method within Osaka Prefecture and their emission inventory. Water Air Soil Pollut. 215 (1), 229–237. https://doi.org/10.1007/s11270-010-0472-3 (2011).
Tan, J. et al. Impact of Spatial resolution on air quality simulation: A case study in a highly industrialized area in shanghai, China. Atmospheric Pollution Res. 6 (2), 322–333. https://doi.org/10.5094/APR.2015.036 (2015).
Han, L. et al. Spatial distribution characteristics of PM2. 5 and PM10 in xi’an City predicted by land use regression models. Sustainable Cities Soc. 61, 102329. https://doi.org/10.1016/j.scs.2020.102329 (2020).
Song, X. Y. et al. A machine learning approach to modelling the Spatial variations in the daily fine particulate matter (PM2. 5) and nitrogen dioxide (NO2) of shanghai, China. Environ. Plann. B: Urban Analytics City Sci. 48 (3), 467–483. https://doi.org/10.1177/2399808320975031 (2021).
Saez, M. & Barceló, M. A. Spatial prediction of air pollution levels using a hierarchical bayesian Spatiotemporal model in Catalonia. Spain Environ. Modelling Softw. 151, 105369. https://doi.org/10.1016/j.envsoft.2022.105369 (2022).
Ketu, S. Spatial air quality index and air pollutant concentration prediction using linear regression based recursive feature elimination with random forest regression (RFERF): a case study in India. Nat. Hazards. 114 (2), 2109–2138. https://doi.org/10.1007/s11069-022-05463-z (2022).
Anggraini, T. S., Irie, H., Sakti, A. D. & Wikantika, K. Machine learning-based global air quality index development using remote sensing and ground-based stations. Environ. Adv. 15, 100456. https://doi.org/10.1016/j.envadv.2023.100456 (2024).
Dawar, I., Singal, M., Singh, V., Lamba, S. & Jain, S. Predicting air quality index using machine learning: a case study of the Himalayan City of Dehradun. Nat. Hazards. 121 (5), 5821–5847. https://doi.org/10.1007/s11069-024-07027-9 (2025).
Singh, S. & Suthar, G. Machine learning and deep learning approaches for PM2. 5 prediction: a study on urban air quality in jaipur, India. Earth Sci. Inf. 18 (1), 97. https://doi.org/10.1007/s12145-024-01648-1 (2025).
Kaviani Rad, A. K., Nematollahi, M. J., Pak, A. & Mahmoudi, M. Predictive modeling of air quality in the Tehran megacity via deep learning techniques. Sci. Rep. 15 (1), 1367. https://doi.org/10.1038/s41598-024-84550-6 (2025).
Maleki, H. et al. Air pollution prediction by using an artificial neural network model. Clean Technol. Environ. Policy. 21 (6), 1341–1352. https://doi.org/10.1007/s10098-019-01709-w (2019).
Goudarzi, G. et al. Prediction of airborne pollen concentrations by artificial neural network and their relationship with meteorological parameters and air pollutants. J. Environ. Health Sci. Eng. https://doi.org/10.1007/s40201-021-00773-z (2022).
Goudarzi, G., Hopke, P. K. & Yazdani, M. Forecasting PM2. 5 concentration using artificial neural network and its health effects in Ahvaz. Iran. Chemosphere. 283, 131285. https://doi.org/10.1016/j.chemosphere.2021.131285 (2021).
Chaudhari, K. & Thakkar, A. Neural network systems with an integrated coefficient of variation-based feature selection for stock price and trend prediction. Expert Syst. Appl. 219, 119527. https://doi.org/10.1016/j.eswa.2023.119527 (2023).
Wang, K., Wang, H., Zhao, J. & Wang, L. A transparent and nonlinear method for variable selection. Expert Syst. Appl. 237, 121398. https://doi.org/10.1016/j.eswa.2023.121398 (2024).
Zhang, S., Li, X., Zong, M., Zhu, X. & Cheng, D. Learning k for Knn classification. ACM Trans. Intell. Syst. Technol. (TIST). 8 (3), 1–19. https://doi.org/10.1145/2990508 (2017).
Wu, X. et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 14 (1), 1–37. https://doi.org/10.1007/s10115-007-0114-2 (2008).
Beretta, L. & Santaniello, A. Nearest neighbor imputation algorithms: a critical evaluation. BMC Med. Inf. Decis. Mak. 16, 197–208. https://doi.org/10.1186/s12911-016-0318-z (2016).
Gabr, M. I., Helmy, Y. M. & Elzanfaly, D. S. Effect of missing data types and imputation methods on supervised classifiers: an evaluation study. Big Data Cogn. Comput. 7 (1), 55. https://doi.org/10.3390/bdcc7010055 (2023).
Dridi, N. & Hadzagic, M. Akaike and bayesian information criteria for hidden Markov models. IEEE. Signal. Process. Lett. 26 (2), 302–306. https://doi.org/10.1109/LSP.2018.2886933 (2018).
Tsay, R. & Econometrics, F. Analysis of Financial Time Series. Vol. 543, Wiley, Hoboken, New Jersey. https://doi.org/10.1002/0471746193 (2005).
Amanollahi, J. & Ausati, S. PM2. 5 concentration forecasting using ANFIS, EEMD-GRNN, MLP, and MLR models: a case study of Tehran. Iran. Air Qual. Atmos. Health. 13 (2), 161–171. https://doi.org/10.1007/s11869-019-00779-5 (2020).
Azid, A. et al. Prediction of the level of air pollution using principal component analysis and artificial neural network techniques: A case study in Malaysia. Water Air Soil Pollut. 225 (8), 1–14. https://doi.org/10.1007/s11270-014-2063-1 (2014).
Durao, R. M., Mendes, M. T. & Pereira, M. J. Forecasting O3 levels in industrial area surroundings up to 24 h in advance, combining classification trees and MLP models. Atmospheric Pollution Res. 7 (6), 961–970. https://doi.org/10.1016/j.apr.2016.05.008 (2016).
Ehteram, M., Ahmed, A. N., Khozani, Z. S. & El-Shafie, A. Graph convolutional network–Long short term memory neural network-multi layer perceptron-Gaussian progress regression model: A new deep learning model for predicting Ozone concertation. Atmospheric Pollution Res. 14 (6), 101766. https://doi.org/10.1016/j.apr.2023.101766 (2023).
Zangooei, H., Delnavaz, M. & Asadollahfardi, G. Prediction of coagulation and flocculation processes using ANN models and fuzzy regression. Water Sci. Technol. 74 (6), 1296–1311. https://doi.org/10.2166/wst.2016.315 (2016).
Khojasteh, D. N., Goudarzi, G., Taghizadeh-Mehrjardi, R., Asumadu-Sakyi, A. B. & Fehresti-Sani, M. Long-term effects of outdoor air pollution on mortality and morbidity–prediction using nonlinear autoregressive and artificial neural networks models. Atmospheric Pollution Res. 12 (2), 46–56. https://doi.org/10.1016/j.apr.2020.10.007 (2021).
Jiang, D. et al. Progress in developing an ANN model for air pollution index forecast. Atmos. Environ. 38 (40), 7055–7064. https://doi.org/10.1016/j.atmosenv.2003.10.066 (2004).
Fernando, H. J. et al. Forecasting PM10 in metropolitan areas: efficacy of neural networks. Environ. Pollut. 163, 62–67. https://doi.org/10.1016/j.envpol.2011.12.018 (2012).
Kamigauti, L. Y., Perez, G. M., Martin, T. C., de Fatima Andrade, M. & Kumar, P. Enhancing Spatial inference of air pollution using machine learning techniques with low-cost monitors in data-limited scenarios. Environ. Science: Atmos. 4 (3), 342–350. https://doi.org/10.1039/D3EA00126A (2024).
Arampongsanuwat, S. & Meesad, P. PM10 prediction model by support vector regression based on particle swarm optimization. Adv. Mater. Res., 403, 3693–3698. https://doi.org/10.4028/www.scientific.net/AMR.403-408.3693 (2012).
Lv, L., Wei, P., Li, J. & Hu, J. Application of machine learning algorithms to improve numerical simulation prediction of PM2. 5 and chemical components. Atmospheric Pollution Res. 12 (11), 101211. https://doi.org/10.1016/j.apr.2021.101211 (2021).
Huang, C. et al. Effect of urban morphology on air pollution distribution in high-density urban blocks based on mobile monitoring and machine learning. Build. Environ. 219, 109173. https://doi.org/10.1016/j.buildenv.2022.109173 (2022).
Gardner, M. & Dorling, S. Statistical surface Ozone models: an improved methodology to account for non-linear behaviour. Atmos. Environ. 34 (1), 21–34. https://doi.org/10.1016/S1352-2310(99)00359-3 (2000).
Hosseini, M. R. et al. Comparing classic regression with credit scorecard model for predicting sick Building syndrome risk: A machine learning perspective in environmental assessment. Build. Environ. 253, 111351. https://doi.org/10.1016/j.buildenv.2024.111351 (2024).
Stafoggia, M. et al. Estimation of daily PM10 and PM2. 5 concentrations in italy, 2013–2015, using a Spatiotemporal land-use random-forest model. Environ. Int. 124, 170–179. https://doi.org/10.1016/j.envint.2019.01.016 (2019).
Bozdağ, A., Dokuz, Y. & Gökçek, Ö. B. Spatial prediction of PM10 concentration using machine learning algorithms in Ankara. Turk. Environ. Pollution. 263, 114635. https://doi.org/10.1016/j.envpol.2020.114635 (2020).
Samad, A., Garuda, S., Vogt, U. & Yang, B. Air pollution prediction using machine learning techniques–an approach to replace existing monitoring stations with virtual monitoring stations. Atmos. Environ. 310, 119987. https://doi.org/10.1016/j.atmosenv.2020.118127 (2023).
Khajehali, M., Safavi, H. R., Nikoo, M. R. & Fooladi, M. A fusion-based framework for daily flood forecasting in multiple-step-ahead and near-future under climate change scenarios: a case study of the Kan river. Iran. Nat. Hazards. 120 (9), 8483–8504. https://doi.org/10.1007/s11069-024-06528-x (2024).
Hamid, H. A., Yahaya, A. S., Ramli, N. A., Ul-Saufie, A. Z. & Yasin, M. N. Short term prediction of PM10 concentrations using seasonal time series analysis. MATEC Web Conferences. https://doi.org/10.1051/matecconf/20164705001 (2016).
Fan, J. et al. Evaluating the effect of air pollution on global and diffuse solar radiation prediction using support vector machine modeling based on sunshine duration and air temperature. Renew. Sustain. Energy Rev. 94, 732–747. https://doi.org/10.1016/j.rser.2018.06.029 (2018).
Nieto, P. G., Lasheras, F. S., García-Gonzalo, E., de Juez, C. & F PM10 concentration forecasting in the metropolitan area of Oviedo (Northern Spain) using models based on SVM, MLP, VARMA and ARIMA: A case study. Sci. Total Environ. 621, 753–761. https://doi.org/10.1016/j.scitotenv.2017.11.291 (2018).
Kim, B. Y., Lim, Y. K. & Cha, J. W. Short-term prediction of particulate matter (PM10 and PM2. 5) in seoul, South Korea using tree-based machine learning algorithms. Atmospheric Pollution Res. 13 (10), 101547. https://doi.org/10.1016/j.apr.2022.101547 (2022).
Brunelli, U., Piazza, V., Pignato, L., Sorbello, F. & Vitabile, S. Two-days ahead prediction of daily maximum concentrations of SO2, O3, PM10, NO2, CO in the urban area of Palermo. Italy Atmospheric Environ. 41 (14), 2967–2995. https://doi.org/10.1016/j.atmosenv.2006.12.013 (2007).
Lu, H. C. Estimating the emission source reduction of PM10 in central Taiwan. Chemosphere 54 (7), 805–814. https://doi.org/10.1016/j.chemosphere.2003.10.012 (2004).
Wang, M. et al. Evaluation of land use regression models for NO2 and particulate matter in 20 European study areas: the ESCAPE project. Environ. Sci. Technol. 47 (9), 4357–4364. https://doi.org/10.1021/es305129t (2013).
Ren, M., Sun, W. & Chen, S. Combining machine learning models through multiple data division methods for PM2. 5 forecasting in Northern xinjiang, China. Environ. Monit. Assess. 193 (8), 1–19. https://doi.org/10.1007/s10661-021-09233-5 (2021).
Karatzas, K. D. & Kaltsatos, S. Air pollution modelling with the aid of computational intelligence methods in thessaloniki, Greece. Simul. Model. Pract. Theory. 15 (10), 1310–1319. https://doi.org/10.1016/j.simpat.2007.09.005 (2007).
EPA, U. Air Quality Index (AQI) - A Guide to Air Quality and Your Health. US EPA. 9 December 2011. Retrieved 8 August 2012. (2012).
Afolabi, A., Francis, F. A. & Adejompo, F. Assessment of health and environmental challenges of cement factory on Ewekoro community residents, Ogun state, Nigeria. Am. J. Hum. Ecol. 1 (2), 51–57. https://doi.org/10.11634/21679622150479 (2012).
EPA. Managing Air Quality - Emissions Inventories. (2020). https://www.epa.gov/air-quality-management-process/managing-air-quality-emissions-inventories
EPA. Near Roadway Air Pollution and Health: Frequently Asked Questions. Office of Transportation and Air Quality. EPA-420-F-14-044. 4. (2014). https://www.epa.gov/sites/default/files/2015-11/documents/420f14044_0.pdf
EPA. Power Plants and Neighboring Communities. (2021). https://www.epa.gov/airmarkets/power-plants-and-neighboring-communities
Fernandes, A. et al. The air pollution modelling system URBAIR: how to use a Gaussian model to accomplish high Spatial and Temporal resolutions. Air Qual. Atmos. Health. 14 (12), 1969–1988. https://doi.org/10.1007/s11869-021-01069-9 (2021).
Jiang, X. & Yoo, E. The importance of Spatial resolutions of community multiscale air quality (CMAQ) models on health impact assessment. Sci. Total Environ. 627, 1528–1543. https://doi.org/10.1016/j.scitotenv.2018.01.228 (2018).
Di, Q. et al. An ensemble-based model of PM2. 5 concentration across the contiguous united States with high Spatiotemporal resolution. Environ. Int. 130, 104909. https://doi.org/10.1016/j.envint.2019.104909 (2019).
Gariazzo, C. et al. Impact of different exposure models and Spatial resolution on the long-term effects of air pollution. Environ. Res. 192, 110351. https://doi.org/10.1016/j.envres.2020.110351 (2021).
Saffar, A. K., Norouzi, H., Choobkar, N., Kermanshahi, L. S. & Zoning of air quality index and ambient air pollutants in ahvaz oil and gas factories with geographic information system. seasonal and spatial. Environ. Eng. Manage. J. (EEMJ), 22(5). (2023).
Jahedi, F. et al. Dynamic Evaluation of Air Pollution in Ahvaz: Source Apportionment, SWOT-AHP Analysis, and Innovative Control Strategies. (2025). https://doi.org/10.21203/rs.3.rs-5993611/v1
Asadifard, E. & Masoudi, M. Status and prediction of carbon monoxide as an air pollutant in Ahvaz city, Iran. Casp. J. Environ. Sci. 16 (3), 203–213. https://doi.org/10.22124/CJES.2018.3061 (2018).
Maleki, H. et al. Air pollution prediction by using an artificial neural network model. Clean Technol. Environ. Policy. 21, 1341–1352. https://doi.org/10.1007/s10098-019-01709-w (2019).
Zhalehdoost, A. & Taleai, M. A review of the application of machine learning and Geospatial analysis methods in air pollution prediction. Pollution 8 (3), 904–933. https://doi.org/10.22059/POLL.2022.336044.1300 (2022).
Cortez, P. Sensitivity analysis for time lag selection to forecast seasonal time series using neural networks and support vector machines. 2010 Int. Joint Conf. Neural Networks (IJCNN). https://doi.org/10.1109/IJCNN.2010.5596890 (2010).
Zulfiqar, M., Kamran, M., Rasheed, M., Alquthami, T. & Milyani, A. Hyperparameter optimization of support vector machine using adaptive differential evolution for electricity load forecasting. Energy Rep. 8, 13333–13352. https://doi.org/10.1016/j.egyr.2022.09.188 (2022).
Halabaku, E. & Bytyçi, E. Overfitting in machine learning: a comparative analysis of decision trees and random forests. Intell. Autom. Soft Comput. https://doi.org/10.32604/iasc.2024.059429 (2024).
Zhalehdoost, A. & Taleai, M. Spatial analysis to predict PM10 pollutant in City of Tehran. International Conference of GIScience: Basis and Trans/Interdisciplinary Applications. (2021). https://civilica.com/doc/1383891/
Chen, B. et al. Geo-STO3Net: A deep neural network integrating geographical Spatiotemporal information for surface Ozone Estimation. IEEE Trans. Geosci. Remote Sens. 62, 1–14. https://doi.org/10.1109/TGRS.2024.3358397 (2024).
Chen, B. et al. An interpretable physics-informed deep learning model for estimating multiple air pollutants. GIScience Remote Sens. 62 (1), 2482272. https://doi.org/10.1080/15481603.2025.2482272 (2025).
Ghaemi, Z., Taleai, M., Farnaghi, M. & Javadi, G. Prediction of Tehran air pollution using PCA-ANFIS method. Iranian Journal of Remote Sensing and GIS, 9(3), 45–70. (2017). https://gisj.sbu.ac.ir/article_96377_329c665dfd3c27b385a5a6ba9132962e.pdf
Acknowledgements
This work has been partially supported by the Center for International Scientific Studies & Collaborations (CISSC), Ministry of Science Research and Technology of Iran.
Author information
Authors and Affiliations
Contributions
Alireza Zhalehdoost was responsible for writing the manuscript and performing the modeling work. Mohammad Taleai supervised the study, provided guidance throughout the research process, and reviewed the manuscript.All authors reviewed and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhalehdoost, A., Taleai, M. Unravelling the importance of spatial and temporal resolutions in modeling urban air pollution using a machine learning approach. Sci Rep 15, 27708 (2025). https://doi.org/10.1038/s41598-025-13639-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-13639-3