Introduction

With the increasing complexity of modern systems, the likelihood of various failures occurring during equipment operation is significant. Unpredictable faults can alter the structure and parameters of a system, leading to performance degradation and potentially loss of control1. Such events can cause substantial economic losses and pose threats to personal safety. Consequently, improving the fault tolerance of control systems has become increasingly critical2,3. For instance, quadrotor unmanned aerial vehicle (UAV) systems exhibit strong nonlinearities and are susceptible to numerous factors during flight; ensuring their operational safety remains a key research focus due to their widespread application4,5,6. Similarly, designing safe and reliable control strategies for the lateral motion control of driverless cars, which rely on sensor feedback to track desired paths, is paramount for personnel safety. FTC offers crucial techniques to enhance system stability, safety, and availability7. Control strategies employing FTC can compensate, mitigate, restrain, or even eliminate the impact of faults by automatically adjusting relevant system parameters online. The principles of FTC have found applications in diverse fields, including aerospace and industrial production8,9,10. Detailed reviews of recent advancements in fault diagnosis and FTC methodologies are provided in11,12.

FTC techniques are broadly categorized into active FTC and passive FTC based on their fault-handling approach13. Active FTC methods typically depend on the accuracy of fault diagnosis results. In contrast, passive FTC methods primarily leverage robust control techniques, designing controllers that are inherently resilient to a predefined set of potential faults. Compared to active FTC, passive FTC offers the advantages of simplicity (no need for a separate fault diagnosis module) and rapid response. Research indicates that adaptive compensation control is a particularly effective passive FTC strategy14. Adaptive FTC algorithms obviate the need to analyze or estimate fault thresholds for time-varying actuators, resulting in systems with simpler structures and faster responses. For example, reference15 introduced an adaptive output feedback FTC scheme combining adaptive control and switching strategies to avoid stability issues caused by actuator faults. Reference16 proposed an adaptive FTC algorithm using a multiplied event-triggered mechanism and neural damping techniques to handle uncertainties and disturbances in unmanned surface vehicle path-following control. In17, an adaptive FTC scheme using command filtering was designed for switched nonlinear systems with actuator faults, achieving close approximation of the desired system output while ensuring signal boundedness. While these studies demonstrate excellent control performance, further improvements in the stability and robustness of such nonlinear control systems are desirable, particularly when unexpected system faults occur.

In recent years, combining SMC with neural networks has emerged as a promising direction for passive FTC in nonlinear systems18,19,20. SMC is recognized as an effective FTC method, widely applied in motion control. Literature21 proposed a nonlinear SMC method for linear systems, effectively maintaining trajectory tracking despite actuator failures or disturbances. However, a primary drawback of conventional SMC is which can degrade performance and potentially excite unmodeled high-frequency dynamics. Utilizing Radial Basis Function (RBF) neural networks, known for their superior function approximation capabilities, to compensate for uncertainties or replace the discontinuous term in SMC provides an effective approach to mitigate chattering22. Nonetheless, tuning RBF network parameters presents its own challenges; the commonly used gradient descent method can be prone to oscillations, instability, and convergence to local minima, especially in online adaptation scenarios.

To address these limitations, this paper investigates the integration of metaheuristic optimization within the adaptive control framework. Specifically, we leverage the Mutation Particle Swarm Optimization (MPSO) algorithm, an improved global search technique inspired by swarm intelligence23. Variant PSO algorithms have demonstrated success in various applications, including industrial process control and network training24. While reference24 showed PSO’s effectiveness in optimizing RBF networks for prediction, its integration within an adaptive SMC structure for robust FTC–particularly addressing simultaneous external disturbances and actuator faults using an enhanced MPSO strategy–remains an area ripe for exploration. Furthermore, while prior works18,19,20 combine SMC and neural networks, they often rely on standard adaptation laws which may struggle with efficient and stable tuning of all RBF parameters (weights, centers, widths) simultaneously.

Inspired by these observations, an FTC algorithm employing an RBF neural network optimized by a variant PSO (MPSO-RBF) is developed. An adaptive mutation strategy within the PSO enhances population diversity and helps avoid premature convergence. This improved PSO is then utilized to effectively optimize the crucial parameters (centers and widths) of the RBF neural network, thereby enhancing its function fitting performance and stability compared to gradient-based methods. Finally, the optimized RBF network is used within the adaptive sliding mode controller to approximate system uncertainties and unknown fault effects online, mitigating the influence of external disturbances and actuator faults on the controlled system and achieving robust adaptive FTC for the target nonlinear system.

The main contributions of this paper are threefold:

  • A novel approach for online RBF parameter tuning, termed Dual-Trigger Hybrid MPSO, is proposed and integrated into an adaptive FTC framework. This method specifically addresses the challenges of instability and convergence to local minima common in gradient descent-based tuning 25. The key innovation is a hybrid mutation mechanism that synergizes a diversity-based trigger with a stagnation-based one, which significantly enhances the stability and efficiency of parameter adaptation.

  • The proposed MPSO-RBF module is integrated with a SMC backbone, forming a robust, passive FTC scheme. Unlike active FTC methods that may require explicit fault diagnosis, such as some terminal sliding mode approaches 18, our passive strategy enhances robustness against unknown actuator faults and disturbances. Furthermore, by enabling a more accurate approximation of system uncertainties, this integration leads to more effective mitigation of the chattering issue prevalent in traditional SMC designs 20, resulting in smoother control actions.

  • The practical efficacy of the proposed controller is validated through comprehensive and realistic comparative studies. Its superiority is demonstrated not just against conventional SMC, but also against a standard adaptive SMC benchmark under challenging conditions, including time-varying faults and stochastic disturbances. This rigorous, quantitative validation provides strong evidence of the proposed method’s enhanced performance and robustness for real-world applications.

The remainder of this paper is organized as follows: Section II establishes the system model incorporating external disturbances and actuator faults for a class of nonlinear systems.Section III details the design of the adaptive fault-tolerant controller based on the SMC technique and the MPSO-optimized RBF neural network. Section IV applies the proposed FTC algorithm to a quadrotor UAV, establishing its fault model and designing the specific control laws. Section V presents detailed simulation results, demonstrating the effectiveness and superiority of the designed FTC algorithm in terms of anti-interference performance, fault tolerance, and robustness compared to a conventional SMC algorithm. Section VI summarizes the key findings and proposes potential areas for further research.

Description of the studied problem

Controlled systems operating in real-time are susceptible to various faults, including actuator and sensor failures. Within these systems, actuators are particularly prone to failure25. Actuator faults are typically categorized as either additive or multiplicative26. Additive faults, also known as deviation faults, introduce an additional external signal that can be modeled as an unknown input within the system’s dynamic equations. Multiplicative faults, often referred to as efficiency loss failures, involve fault parameters that scale the control input.

For time-varying systems described by analytical models, system faults, external disturbances, and model uncertainties inevitably influence the system’s state and behavior. To uniformly represent various fault types while accounting for external disturbances, we establish the following uncertain nonlinear system model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1 = x_2 \\ \dot{x}_2 = f(x,\dot{x}) + g(x,\dot{x})u_f + d(t) \end{array}\right. }, \end{aligned}$$
(1)

where \(x = [x_1, x_2]^T\) represents the system state vector, \(f(x,\dot{x})\) and \(g(x,\dot{x})\) are unknown nonlinear functions, \(u_{f}\) denotes the control input under actuator failure conditions, and d(t) is a bounded external disturbance such that \(|d(t)|\le d_{max}\), with \(d_{max}\) being the upper bound. The actuator output \(u_{f}\) under fault conditions can be uniformly described as:

$$\begin{aligned} u_f(t)=\rho (t)u_0(t)+f_{fault}(t),\quad \forall t\ge T_i \end{aligned}$$
(2)

where \(u_0(t)\) is the nominal control input, \(\rho (t)\in [0,1]\) is the actuator effectiveness factor, and \(f_{fault}(t)\) represents the additive fault vector (previously denoted as f(t) to avoid confusion with the function \(f(x,\dot{x})\)). The time instant \(T_i\) marks the occurrence of the fault; for \(\forall t<T_{i}\), the system operates without faults (\(\rho (t)=1, f_{fault}(t)=0\)). A deviation fault occurs when \(\rho (t)=1\) and \(f_{fault}(t) \ne 0\), resulting in \(u_{f}(t)=u_{0}(t)+f_{fault}(t)\). A multiplicative fault (loss of effectiveness) occurs when \(0 \le \rho (t) < 1\) and \(f_{fault}(t) = 0\), leading to \(u_f(t)=\rho (t)u_0(t)\).

The tracking error is defined as:

$$\begin{aligned} e=x_1-x_d. \end{aligned}$$
(3)

The control objective is to design a controller such that the tracking error e converges to zero (i.e., \(e \rightarrow 0\) as \(t\rightarrow \infty\)) despite actuator faults, while maintaining the stability of the closed-loop system.

Adaptive fault-tolerant controller design

SMC is widely employed in motion control due to its simplicity, robustness, and reliability27. However, SMC often induces high-frequency chattering caused by unmodeled dynamics, system inertia, and delays. This chattering can degrade control precision and potentially damage system components.

To mitigate chattering while preserving robustness, Radial Basis Function (RBF) neural networks can be used to approximate the discontinuous switching component of the SMC law28. RBF networks leverage their learning capabilities to handle system uncertainties and reduce the required switching gain, thereby attenuating chattering. The approximation performance of an RBF network heavily relies on the selection of its parameters: the center vectors, basis function widths, and output layer weights29. While the gradient descent method is commonly used for RBF parameter tuning, it can suffer from oscillations, instability, and poor real-time performance.

PSO offers a population-based global optimization strategy30. Variants of PSO, particularly those incorporating adaptive mutation strategies, exhibit enhanced global search capabilities and effectively mitigate the premature convergence problem inherent in standard PSO31. Consequently, a variant PSO algorithm can be employed to optimize RBF network parameters, leading to a more robust FTC scheme when combined with SMC for nonlinear systems.

A schematic overview of the proposed FTC algorithm is presented in Fig. 1.

Fig. 1
figure 1

Schematic of the proposed fault-tolerant control system.

Full size image

RBF neural network algorithm design

The RBF neural network is a three-layer forward-propagation network recognized for its straightforward design, effective generalization, and rapid learning capability. It has been demonstrated to approximate any continuous function with high accuracy32. The network’s architecture generally features a nonlinear mapping from the input to the hidden layer through Gaussian basis functions, followed by a linear mapping from the hidden to the output layer, enabling quick learning and reducing the risk of getting trapped in local minima. The structure of the RBF network used in this study is illustrated in Fig. 2.

In Fig. 2, \(x=[x_1,\dots ,x_n]^T\) is the input vector, \(h=[h_1,\dots ,h_m]^T\) represents the outputs of the hidden layer’s radial basis functions, and \(w=[w_1,\dots ,w_m]^T\) contains the output layer weights. The output of the j-th hidden neuron, \(h_j\), is calculated using a Gaussian function:

$$\begin{aligned} h_j=\exp \left( \frac{-\parallel x-\mu _j\parallel ^2}{2\sigma _j^2}\right) , \end{aligned}$$
(4)

where \(\mu _{j}\) is the center vector of the j-th neuron, and \(\sigma _{j}\) is the width (standard deviation) of its Gaussian basis function. The choice of \(\mu _{j}\) and \(\sigma _{j}\) significantly impacts the control system’s precision and stability. The output of the RBF network is a weighted sum of the hidden layer outputs:

$$\begin{aligned} y = w^{T}h = \sum _{j=1}^{m}w_{j}h_{j}. \end{aligned}$$
(5)

Assuming a single output node for simplicity, y represents the network’s output.

Fig. 2
figure 2

Structure of the RBF neural network used.

Full size image

Variant particle swarm optimization algorithm design

PSO is an evolutionary computation approach modeled on the social interactions of flocking birds. Each potential solution, termed a particle, is characterized by its position \(b_{i}\) and velocity \(v_{i}\) within the search space. The quality of a particle’s position is evaluated using a fitness function, which corresponds to the objective function being optimized.

In a D-dimensional search space, the i-th particle’s position and velocity are denoted by vectors:

$$\begin{aligned} & b_{i}=[b_{i1}, b_{i2},\dots , b_{iD}]^T, \end{aligned}$$
(6)
$$\begin{aligned} & v_{i}=[v_{i1}, v_{i2},\dots , v_{iD}]^T. \end{aligned}$$
(7)

Each particle maintains a record of the best position it has personally discovered, denoted as \(p_{i}\). The swarm collectively tracks the best position found by any particle, denoted as \(p_{g}\). The velocity and position of each particle are updated iteratively based on its own experience and the swarm’s collective knowledge, according to the following equations33:

$$\begin{aligned} \begin{aligned} v_{i}(t+1)&= w(t)v_{i}(t) + c_1 r_1 (p_{i}(t) - b_{i}(t)) + c_2 r_2 (p_{g}(t) - b_{i}(t)) \\ b_{i}(t+1)&= b_{i}(t) + v_{i}(t+1) \end{aligned} \end{aligned}$$
(8)

where t is the iteration number, w(t) is the inertia weight, \(c_{1}\) and \(c_{2}\) are acceleration coefficients (learning factors), and \(r_{1}, r_{2}\) are random numbers uniformly distributed in [0, 1]. The inertia weight w balances global exploration and local exploitation. Using a logarithmically decreasing inertia weight can improve convergence speed34:

$$\begin{aligned} w(t)=w_{max}-\frac{\ln (t+1)}{\ln (t_{max}+1)}(w_{max}-w_{min}), \end{aligned}$$
(9)

where \(t_{max}\) is the maximum number of iterations, and \(w_{max}\) and \(w_{min}\) are the initial and final inertia weights, respectively.

Studies suggest that dynamically adjusting the learning factors \(c_1\) and \(c_2\) can enhance PSO performance34,35. Increasing \(c_1\) relative to \(c_2\) initially promotes exploration, while increasing \(c_2\) relative to \(c_1\) later encourages convergence towards the global optimum. We employ linearly varying learning factors:

$$\begin{aligned} {\left\{ \begin{array}{ll} c_1(t+1) = c_{1s} + \frac{t(c_{1f}-c_{1s})}{t_{max}} \\ c_2(t+1) = c_{2s} + \frac{t(c_{2f}-c_{2s})}{t_{max}} \end{array}\right. }, \end{aligned}$$
(10)

where \(c_{1s}, c_{2s}\) are the initial values and \(c_{1f}, c_{2f}\) are the final values for \(c_1\) and \(c_2\), respectively (assuming \(c_{1f} < c_{1s}\) and \(c_{2f} > c_{2s}\)).

To monitor population diversity and detect premature convergence, the average particle distance D(t) is calculated at iteration t:

$$\begin{aligned} D(t)=\frac{1}{L \cdot N}\sum _{i=1}^{N}\sqrt{\sum _{d=1}^{D}(b_{id}(t)-\bar{b}_{d}(t))^{2}}, \end{aligned}$$
(11)

where N is the population size (previously I), L is the length of the search space diagonal, D is the dimension, \(b_{id}(t)\) is the d-th dimension of the i-th particle’s position at iteration t, and \(\bar{b}_{d}(t)\) is the average value of the d-th dimension across all particles at iteration t.

To escape local optima when premature convergence is detected (e.g., when D(t) falls below a threshold \(D_{min}\) or the global best \(p_g\) stagnates), a mutation mechanism is introduced. A subset of particles (e.g., the top u particles based on fitness) are selected. For each selected particle i, a random number \(r_i \in [0, 1]\) is generated. If \(r_i < p_m\) (where \(p_m \in [0.1, 0.3]\) is the mutation probability), the particle’s position is perturbed:

$$\begin{aligned} b_{i}(t+1)=(1+0.5\cdot \eta )b_{i}(t), \end{aligned}$$
(12)

where \(\eta\) is a random variable following a standard normal distribution (Gauss(0, 1)). This mutated position replaces the particle’s current position and potentially its personal best if fitter.

Parameters optimization of RBF neural network

The training of an RBF network involves adjusting the center vectors \(\mu _j\) and widths \(\sigma _j\) (and potentially the output weights \(w_j\), although here we focus on \(\mu _j, \sigma _j\)) to minimize the network’s output error based on training data36. We use the variant PSO algorithm described above to optimize \(\mu _j\) and \(\sigma _j\). The particle position vector \(b_i\) encodes these parameters. The fitness function \(H(b_{i}(t))\) quantifies the network’s performance using the parameters encoded by \(b_i\), typically based on the root mean squared error (RMSE) over a set of training samples:

$$\begin{aligned} H(b_{i}(t))=\sqrt{\frac{1}{M}\sum _{k=1}^{M}(y_{d,k}-y_k(t))^{2}}, \end{aligned}$$
(13)

where M is the number of training samples (previously I), \(y_{d,k}\) is the desired output for the k-th sample, and \(y_k(t)\) is the network’s actual output for the k-th sample using the parameters encoded by particle \(b_i\) at iteration t.

This combined approach is termed Mutation Particle Swarm Optimization - Radial Basis Function Neural Network (MPSO-RBF). The optimization procedure is outlined in Algorithm 1.

Algorithm 1
figure a

MPSO-RBF parameter optimization.

Full size image

Design and analysis of control law

This section details the design of the adaptive fault-tolerant controller for the nonlinear system (1). The goal is to ensure finite-time convergence of the system state to the desired trajectory.

We define the sliding mode surface as:

$$\begin{aligned} s=\dot{e}+ce, \quad c>0 \end{aligned}$$
(14)

where \(e = x_1 - x_d\) is the tracking error and c is a positive constant. Differentiating the error e yields:

$$\begin{aligned} \dot{e}=\dot{x}_1-\dot{x}_d = x_2-\dot{x}_d. \end{aligned}$$
(15)

Taking the time derivative of the sliding surface s and using (1) and (15):

$$\begin{aligned} \begin{aligned} \dot{s}&= \ddot{e}+c\dot{e} \\&= \ddot{x}_1 - \ddot{x}_d + c\dot{e} \\&= (f(x,\dot{x}) + g(x,\dot{x})u_f + d(t)) - \ddot{x}_{d} + c\dot{e}. \end{aligned} \end{aligned}$$
(16)

Assuming f and g depend only on x (i.e., f(x), g(x) as implied later) for simplicity in notation, we rewrite \(\dot{s}\) as:

$$\begin{aligned} \dot{s} = f(x) + g(x)u_{f} - \ddot{x}_{d} + c\dot{e} + d(t). \end{aligned}$$
(17)

We design the adaptive sliding mode control law using RBF networks to approximate the unknown functions f(x) and g(x). Let \(\hat{f}(x)\) and \(\hat{g}(x)\) be the RBF network approximations. The control law is proposed as:

$$\begin{aligned} u_f=\frac{1}{\hat{g}(x)}[-\hat{f}(x)+\ddot{x}_d-c\dot{e}-\eta \text {sat}(s/\varpi )], \quad \eta > 0 \end{aligned}$$
(18)

where \(\eta\) is a positive switching gain designed to counteract approximation errors and disturbances, and \(\text {sat}(s/\varpi )\) is the sign function. We assume \(\hat{g}(x)\) is bounded away from zero.

The RBF network inputs are chosen as \(x_{in}=[e, \dot{e}]^T\). The network outputs approximating f(x) and g(x) are given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{f}(x)=\hat{W}^T h_f(x_{in}) \\ \hat{g}(x)=\hat{V}^T h_g(x_{in}) \end{array}\right. }, \end{aligned}$$
(19)

where \(\hat{W}\) and \(\hat{V}\) are the estimated weight vectors, and \(h_f(x_{in})\) and \(h_g(x_{in})\) are the vectors of hidden layer basis function outputs for the respective networks. The optimal approximations are:

$$\begin{aligned} {\left\{ \begin{array}{ll} f(x)=W^{*T}h_f(x_{in})+\varepsilon _f(x_{in}) \\ g(x)=V^{*T}h_g(x_{in})+\varepsilon _g(x_{in}) \end{array}\right. }, \end{aligned}$$
(20)

where \(W^{*}\) and \(V^{*}\) are the ideal (unknown) weight vectors, and \(\varepsilon _f, \varepsilon _g\) are the minimum approximation errors, assumed to be bounded: \(\Vert \varepsilon _{f}\Vert \le \varepsilon _{Mf}\) and \(\Vert \varepsilon _{g}\Vert \le \varepsilon _{Mg}\).

Define the weight estimation errors as \(\tilde{W} = W^* - \hat{W}\) and \(\tilde{V} = V^* - \hat{V}\). The approximation errors are \(\tilde{f}(x) = f(x) - \hat{f}(x) = \tilde{W}^T h_f(x_{in}) + \varepsilon _f\) and \(\tilde{g}(x) = g(x) - \hat{g}(x) = \tilde{V}^T h_g(x_{in}) + \varepsilon _g\).

Substituting the control law (18) into the expression for \(\dot{s}\) (17):

$$\begin{aligned} \begin{aligned} \dot{s}&= f(x) + g(x)u_f - \ddot{x}_d + c\dot{e} + d(t) \\&= f(x) + ( \hat{g}(x) + \tilde{g}(x) ) u_f - \ddot{x}_d + c\dot{e} + d(t) \\&= f(x) + \hat{g}(x)u_f + \tilde{g}(x)u_f - \ddot{x}_d + c\dot{e} + d(t) \\&= f(x) + (-\hat{f}(x) + \ddot{x}_d - c\dot{e} - \eta \text {sat}(s/\varpi )) + \tilde{g}(x)u_f - \ddot{x}_d + c\dot{e} + d(t) \\&= (f(x) - \hat{f}(x)) + \tilde{g}(x)u_f - \eta \text {sat}(s/\varpi ) + d(t) \\&= \tilde{f}(x) + \tilde{g}(x)u_f - \eta \text {sat}(s/\varpi ) + d(t) \\&= (\tilde{W}^T h_f + \varepsilon _f) + (\tilde{V}^T h_g + \varepsilon _g)u_f - \eta \text {sat}(s/\varpi ) + d(t) \end{aligned} \end{aligned}$$
(21)

Theorem 1: For the uncertain nonlinear system (1) subject to actuator faults described by (2) and external disturbances d(t), under the control law (18) with RBF approximations (19), (20), and the adaptive laws (25) and (26) given below, the tracking error e converges to a small bounded region around zero if the gain \(\eta\) is chosen sufficiently large, specifically \(\eta \ge \Vert \varepsilon _f + \varepsilon _g u_f + d(t)\Vert _{max}\).

Proof

Consider the Lyapunov function candidate:

$$\begin{aligned} L=\frac{1}{2}s^{2} + \frac{1}{2\gamma _{1}}\tilde{W}^T \tilde{W} + \frac{1}{2\gamma _{2}}\tilde{V}^T \tilde{V}, \end{aligned}$$
(22)

where \(\gamma _{1} > 0\) and \(\gamma _{2} > 0\) are adaptation gains. The time derivative of L is:

$$\begin{aligned} \dot{L} = s\dot{s} + \frac{1}{\gamma _{1}}\tilde{W}^T \dot{\tilde{W}} + \frac{1}{\gamma _{2}}\tilde{V}^T \dot{\tilde{V}}. \end{aligned}$$
(23)

Since \(\dot{\tilde{W}} = \dot{W}^* - \dot{\hat{W}} = -\dot{\hat{W}}\) (assuming ideal weights are constant) and \(\dot{\tilde{V}} = -\dot{\hat{V}}\), we have:

$$\begin{aligned} \begin{aligned} \dot{L}&= s \left[ \tilde{W}^T h_f + \tilde{V}^T h_g u_f + \varepsilon _f + \varepsilon _g u_f - \eta \text {sat}(s/\varpi ) + d(t) \right] - \frac{1}{\gamma _{1}} \tilde{W}^T \dot{\hat{W}} - \frac{1}{\gamma _{2}} \tilde{V}^T \dot{\hat{V}} \\&= \tilde{W}^T \left( s h_f - \frac{1}{\gamma _{1}} \dot{\hat{W}} \right) + \tilde{V}^T \left( s h_g u_f - \frac{1}{\gamma _{2}} \dot{\hat{V}} \right) + s \left( \varepsilon _f + \varepsilon _g u_f + d(t) \right) - \eta s \, \text {sat}(s/\varpi ) \\&= \tilde{W}^T \left( s h_f - \frac{1}{\gamma _{1}} \dot{\hat{W}} \right) + \tilde{V}^T \left( s h_g u_f - \frac{1}{\gamma _{2}} \dot{\hat{V}} \right) + s \left( \varepsilon _f + \varepsilon _g u_f + d(t) \right) - \eta |s|. \end{aligned} \end{aligned}$$
(24)

We choose the adaptive laws to cancel the terms involving \(\tilde{W}\) and \(\tilde{V}\):

$$\begin{aligned} & \dot{\hat{W}}=\gamma _{1}s h_{f}(x_{in}), \end{aligned}$$
(25)
$$\begin{aligned} & \dot{\hat{V}}=\gamma _2 s h_g(x_{in}) u_f. \end{aligned}$$
(26)

Substituting these adaptive laws into (24) yields:

$$\begin{aligned} \begin{aligned} \dot{L}&= s(\varepsilon _{f}+\varepsilon _{g}u_{f}+d(t)) - \eta |s| \\&\le |s| \Vert \varepsilon _{f}+\varepsilon _{g}u_{f}+d(t)\Vert - \eta |s| \\&= |s| (\Vert \varepsilon _{f}+\varepsilon _{g}u_{f}+d(t)\Vert - \eta ). \end{aligned} \end{aligned}$$
(27)

If we choose the gain \(\eta \ge \Vert \varepsilon _{f}+\varepsilon _{g}u_{f}+d(t)\Vert _{max} + \delta\) for some small \(\delta > 0\), where \(\Vert \cdot \Vert _{max}\) denotes the upper bound of the lumped uncertainty term, then \(\dot{L} \le -\delta |s|\). This implies that s is bounded. Furthermore, based on Barbalat’s lemma or LaSalle’s invariance principle (if \(\dot{L}\) is uniformly continuous), \(s \rightarrow 0\) as \(t \rightarrow \infty\), which in turn implies \(e \rightarrow 0\) and \(\dot{e} \rightarrow 0\). Thus, the system can track the desired trajectory despite faults and disturbances. \(\square\)

The sign function \(\text {sat}(s/\varpi )\) in the control law (18) can cause chattering, especially when the gain \(\eta\) needs to be large to counteract significant disturbances or approximation errors. To alleviate this, the sign function is often replaced by a saturation function \(\text {sat}(s)\) or a hyperbolic tangent function. Using the saturation function:

$$\begin{aligned} \text {sat}(s/\varpi )={\left\{ \begin{array}{ll}\text {sat}(s/\varpi ) & |s| > \varpi \\ s/\varpi & |s| \le \varpi \end{array}\right. } \end{aligned}$$
(28)

where \(\varpi > 0\) defines the boundary layer thickness. Replacing \(\text {sat}(s/\varpi )\) with \(\text {sat}(s/\varpi )\) in (18) smooths the control action within the boundary layer \(|s| \le \varpi\), reducing chattering at the cost of potentially introducing a steady-state error bounded by \(\varpi\).

Application to quadrotor UAV fault-tolerant control

The complexity and demanding nature of unmanned aerial vehicle (UAV) missions necessitate high levels of safety and reliability37,38. Enhancing the stability, safety, and reliability of next-generation UAVs during flight is crucial. Therefore, designing robust FTC systems for UAVs, particularly quadrotors, is of significant importance.

To demonstrate the efficacy of the proposed adaptive FTC algorithm in a practical context, we apply it to a quadrotor UAV simulation model, providing a potential FTC strategy for this platform.

Quadrotor UAV fault model

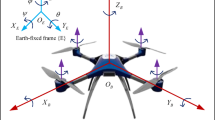
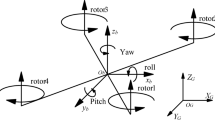
The dynamics of a quadrotor are generally expressed using an Earth-fixed inertial frame \(\mathcal {E} = {x_e, y_e, z_e}\) and a body-fixed frame \(\mathcal {B} = {x_b, y_b, z_b}\), as shown in Fig. 3.

Fig. 3
figure 3

Coordinate systems for the quadrotor UAV.

Full size image

Applying Newtonian mechanics, the equations of motion for a quadrotor UAV can be derived39. The dynamic model, considering translational and rotational motion, is given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} m\ddot{x} = (\cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi )U_{1} - K_{x}\dot{x} + d_{Tx}\\ m\ddot{y} = (\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi )U_{1} - K_{y}\dot{y} + d_{Ty}\\ m\ddot{z} = (\cos \phi \cos \theta )U_{1} - mg - K_{z}\dot{z} + d_{Tz}\\ I_{xx}\ddot{\phi } = (I_{yy}-I_{zz})\dot{\theta }\dot{\psi } - K_{\phi }\dot{\phi }|\dot{\phi }| - I_{r}\Omega _{r}\dot{\theta } + U_{2} + d_{Rx}\\ I_{yy}\ddot{\theta } = (I_{zz}-I_{xx})\dot{\phi }\dot{\psi } - K_{\theta }\dot{\theta }|\dot{\theta }| + I_{r}\Omega _{r}\dot{\phi } + U_{3} + d_{Ry}\\ I_{zz}\ddot{\psi } = (I_{xx}-I_{yy})\dot{\phi }\dot{\theta } - K_{\psi }\dot{\psi }|\dot{\psi }| + U_{4} + d_{Rz} \end{array}\right. }, \end{aligned}$$
(29)

where \([x,y,z]^T\) is the position in \(\mathcal {E}\), and \([\phi ,\theta ,\psi ]^T\) are the Euler angles (roll, pitch, yaw) representing the orientation of \(\mathcal {B}\) relative to \(\mathcal {E}\). m is the mass, g is gravitational acceleration, \(K_{x,y,z}\) and \(K_{\phi ,\theta ,\psi }\) are aerodynamic drag coefficients. \(I_{xx},I_{yy},I_{zz}\) are the principal moments of inertia, \(I_r\) is the rotor inertia, and \(\Omega _{r}=\sum (-1)^i \Omega _i\) represents the overall rotor speed difference contributing to gyroscopic effects (\(\Omega _i\) is the speed of rotor i). \(d_{T(x,y,z)}\) and \(d_{R(x,y,z)}\) represent external disturbances (forces and torques).

The control inputs \(U_1, U_2, U_3, U_4\) represent the total thrust and the control torques for roll, pitch, and yaw, respectively. These are generated by the differential speeds of the four rotors:

$$\begin{aligned} \begin{bmatrix} U_{1} \\ U_{2} \\ U_{3} \\ U_{4} \end{bmatrix} = \begin{bmatrix} b & b & b & b \\ 0 & -bl & 0 & bl \\ -bl & 0 & bl & 0 \\ -d_M & d_M & -d_M & d_M \end{bmatrix} \begin{bmatrix} \Omega _1^2 \\ \Omega _2^2 \\ \Omega _3^2 \\ \Omega _4^2 \end{bmatrix}, \end{aligned}$$
(30)

where b is the thrust coefficient, \(d_M\) is the motor torque coefficient, and l is the distance from the center of mass to each rotor.

We introduce auxiliary position control inputs \(u_x\) and \(u_y\) based on the thrust components in the horizontal plane:

$$\begin{aligned} \begin{bmatrix} u_{x} \\ u_{y} \end{bmatrix} = \begin{bmatrix} \cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi \\ \cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi \end{bmatrix} U_{1}. \end{aligned}$$
(31)

We make the following standard assumptions:

  1. 1.

    All state variables of the UAV (\(x, y, z, \phi , \theta , \psi\) and their derivatives) are measurable or accurately estimated.

  2. 2.

    The desired trajectory for the UAV is bounded.

  3. 3.

    The quadrotor structure is rigid and symmetrical.

  4. 4.

    The roll and pitch angles (\(\phi , \theta\)) remain within \((-\pi /2, \pi /2)\).

To model actuator faults (affecting the generation of \(U_1, U_2, U_3, U_4\)), we introduce a fault matrix similar to (2), acting on the nominal control inputs \(U_{i,0}\):

$$\begin{aligned} \begin{bmatrix} U_{f1} \\ U_{f2} \\ U_{f3} \\ U_{f4} \end{bmatrix} = \text {diag}(\rho _1, \rho _2, \rho _3, \rho _4) \begin{bmatrix} U_{1,0} \\ U_{2,0} \\ U_{3,0} \\ U_{4,0} \end{bmatrix} + \begin{bmatrix} f_{f1} \\ f_{f2} \\ f_{f3} \\ f_{f4} \end{bmatrix}, \end{aligned}$$
(32)

where \([U_{f1}, U_{f2}, U_{f3}, U_{f4}]^T\) are the actual thrust and torques delivered under fault conditions, \(\rho _i \in [0, 1]\) are the effectiveness factors for each channel (thrust, roll, pitch, yaw), and \(f_{fi}\) are the additive fault components.

The system dynamics (29) can be expressed in state-space form. Let the state vector be \(X = [x, \dot{x}, y, \dot{y}, z, \dot{z}, \phi , \dot{\phi }, \theta , \dot{\theta }, \psi , \dot{\psi }]^T = [x_1, \dots , x_{12}]^T\). The dynamics become \(\dot{X} = F(X) + G(X)U_f + D\), where \(U_f = [U_{f1}, U_{f2}, U_{f3}, U_{f4}]^T\) is the faulted control input vector and D represents lumped disturbances. This matches the structure given in Eq. (31) from the original text, explicitly written as:

$$\begin{aligned} \dot{X}= \begin{bmatrix} x_{2} \\ (u_x(U_{f1}) - K_x x_2)/m + d_{1}' \\ x_{4} \\ (u_y(U_{f1}) - K_y x_4)/m + d_{2}' \\ x_{6} \\ ((\cos x_7 \cos x_9) U_{f1} - mg - K_z x_6)/m + d_{3}' \\ x_{8} \\ \frac{\begin{gathered} (I_{yy}-I_{zz})x_{10}x_{12} - K_{\phi }x_8|x_8| \\ - I_{r}\Omega _{r}x_{10} + U_{f2} \end{gathered}}{I_{xx}} + d_{4}' \\ x_{10} \\ \frac{\begin{gathered} (I_{zz}-I_{xx})x_8 x_{12} - K_{\theta }x_{10}|x_{10}| \\ + I_{r}\Omega _{r}x_8 + U_{f3} \end{gathered}}{I_{yy}} + d_{5}' \\ x_{12} \\ \frac{\begin{gathered} (I_{xx}-I_{yy})x_8 x_{10} - K_{\psi }x_{12}|x_{12}| \\ + U_{f4} \end{gathered}}{I_{zz}} + d_{6}' \end{bmatrix}, \end{aligned}$$
(33)

where \(d_i'\) represent the appropriate lumped disturbances for each state equation. Note that \(u_x\) and \(u_y\) implicitly depend on \(U_{f1}\) and the attitude angles as per (31).

Controller design

A common strategy for quadrotor control is a cascaded structure with an outer position control loop and an inner attitude control loop. We apply the adaptive FTC methodology developed in Section II.

Outer loop (position control)

Define position errors \(e_x = x - x_d\), \(e_y = y - y_d\), \(e_z = z - z_d\), and corresponding sliding surfaces: \(s_z = \dot{e}_z + c_z e_z\) \(s_x = \dot{e}_x + c_x e_x\) \(s_y = \dot{e}_y + c_y e_y\)

Altitude control (z)

The control input \(U_{f1}\) (total thrust) is designed based on the z dynamics. The sliding surface dynamics are \(\dot{s}_z = \ddot{e}_z + c_z \dot{e}_z = \ddot{z} - \ddot{z}_d + c_z \dot{e}_z\). Substituting \(\ddot{z}\) from (33): \(\dot{s}_z = ((\cos \phi \cos \theta ) U_{f1} - mg - K_z \dot{z})/m + d_{3}' - \ddot{z}_d + c_z \dot{e}_z\). Let \(f_z = (-mg - K_z \dot{z})/m\), \(g_z = (\cos \phi \cos \theta )/m\). Then \(\dot{s}_z = f_z + g_z U_{f1} + d_3' - \ddot{z}_d + c_z \dot{e}_z\). Using RBF networks \(\hat{f}_z, \hat{g}_z\) to approximate \(f_z, g_z\), the control law for \(U_{f1}\) is:

$$\begin{aligned} U_{f1} = \frac{1}{\hat{g}_z}[-\hat{f}_z + \ddot{z}_d - c_z \dot{e}_z - \eta _z \text {sat}(s_z/\varpi _z)]. \end{aligned}$$
(34)

This corresponds to Eq. (32) in the original text after rearrangement and identifying terms. The adaptive laws for the weights \(\hat{W}_z, \hat{V}_z\) of \(\hat{f}_z, \hat{g}_z\) are:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\hat{W}}_z = \gamma _{z1} s_z h_{fz}(x_{in,z}) \\ \dot{\hat{V}}_z = \gamma _{z2} s_z h_{gz}(x_{in,z}) U_{f1} \end{array}\right. }. \end{aligned}$$
(35)

(Note: The sign convention in adaptive laws (Eqs 23, 24 original) depends on the Lyapunov derivative setup. I used the convention ensuring stability with the \(\dot{L}\) derivation shown earlier. Eq 33 had negative signs.)

Horizontal position control (x, y)

This loop generates desired roll (\(\phi _d\)) and pitch (\(\theta _d\)) angles via virtual controls \(U_x\) and \(U_y\) (using the notation from the original text for the virtual controls, not \(u_x, u_y\)). From the x dynamics: \(\dot{s}_x = \ddot{x} - \ddot{x}_d + c_x \dot{e}_x = (u_x(U_{f1}) - K_x \dot{x})/m + d_1' - \ddot{x}_d + c_x \dot{e}_x\). Let \(f'_x = (-K_x \dot{x})/m\), \(g'_x = 1/m\). The virtual control \(U_x\) (representing \(u_x(U_{f1})\) in the dynamics) is designed as:

$$\begin{aligned} \begin{aligned} U_x&= \frac{1}{\hat{g}'_x}[-\hat{f}'_x + \ddot{x}_d - c_x \dot{e}_x - \eta _x \text {sat}(s_x/\varpi _x)] \\&= m[-\hat{f}'_x + \ddot{x}_d - c_x \dot{e}_x - \eta _x \text {sat}(s_x/\varpi _x)]. \end{aligned} \end{aligned}$$
(36)

This structure corresponds to Eq. (34). Similarly for y:

$$\begin{aligned} U_y = m[-\hat{f}'_y + \ddot{y}_d - c_y \dot{e}_y - \eta _y \text {sat}(s_y/\varpi _y)]. \end{aligned}$$
(37)

This corresponds to Eq. (35). Adaptive laws for \(\hat{W}_x, \hat{V}_x\) (if \(g'_x\) is adapted) and \(\hat{W}_y, \hat{V}_y\) follow the pattern:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\hat{W}}_i = \gamma _{i1}s_i h_{fi}(x_{in,i})\\ \dot{\hat{V}}_i = \gamma _{i2}s_i h_{gi}(x_{in,i}) U_{fi} \end{array}\right. },\quad i=x,y \end{aligned}$$
(38)

This corresponds to Eq. (36) with corrected signs.

The desired attitude angles \(\phi _d, \theta _d\) required to produce the virtual controls \(U_x, U_y\) (which are \(u_x, u_y\) from Eq. 31) are calculated by inverting (31):

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _d = \arcsin ( (U_x \sin \psi _d - U_y \cos \psi _d) / m) \\ \theta _d = \arctan ( (U_x \cos \psi _d + U_y \sin \psi _d) / (m \cos \phi _d) ) \end{array}\right. } \end{aligned}$$
(39)

Retaining the structure from the original paper’s Eq (39) for consistency, though its derivation from (28) might need review:

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _d = \arcsin (U_x \sin \psi _d - U_y \cos \psi _d) \\ \theta _d = \arctan \left( \frac{U_x \cos \psi _d + U_y \sin \psi _d}{\cos \phi _d}\right) \end{array}\right. } \end{aligned}$$
(40)

Define attitude errors \(e_\phi = \phi - \phi _d\), \(e_\theta = \theta - \theta _d\), \(e_\psi = \psi - \psi _d\), and sliding surfaces:

$$\begin{aligned} s_\phi&= \dot{e}_\phi + c_\phi e_\phi , \\ s_\theta&= \dot{e}_\theta + c_\theta e_\theta , \\ s_\psi&= \dot{e}_\psi + c_\psi e_\psi . \end{aligned}$$

1. Roll Control (\(\phi\)): The dynamics are \(\dot{s}_\phi = \ddot{e}_\phi + c_\phi \dot{e}_\phi = \ddot{\phi } - \ddot{\phi }_d + c_\phi \dot{e}_\phi\). Substituting \(\ddot{\phi }\) from (33):

$$\dot{s}_\phi = \frac{(I_{yy}-I_{zz})\dot{\theta }\dot{\psi } - K_{\phi }\dot{\phi }|\dot{\phi }| - I_{r}\Omega _{r}\dot{\theta } + U_{f2}}{I_{xx}} + d_{4}' - \ddot{\phi }_d + c_\phi \dot{e}_\phi .$$

Let \(f_\phi = \frac{(I_{yy}-I_{zz})\dot{\theta }\dot{\psi } - K_{\phi }\dot{\phi }|\dot{\phi }| - I_{r}\Omega _{r}\dot{\theta }}{I_{xx}}\) and \(g_\phi = \frac{1}{I_{xx}}\). The control law for \(U_{f2}\) is:

$$\begin{aligned} U_{f2} = I_{xx}\left[ -\hat{f}_\phi + \ddot{\phi }_d - c_\phi \dot{e}_\phi - \eta _\phi {{\,\textrm{sat}\,}}\left( \frac{s_\phi }{\varpi _\phi }\right) \right] . \end{aligned}$$
(41)

The adaptive law for the weights \(\hat{W}_\phi\) is:

$$\begin{aligned} \dot{\hat{W}}_\phi = \gamma _{\phi } s_\phi h_{f\phi }(x_{in,\phi }). \end{aligned}$$
(42)

2. Pitch (\(\theta\)) and Yaw (\(\psi\)) Control: The control laws \(U_{f3}, U_{f4}\) are designed similarly. For pitch control:

$$\begin{aligned} U_{f3} = I_{yy}\left[ -\hat{f}_\theta + \ddot{\theta }_d - c_\theta \dot{e}_\theta - \eta _\theta {{\,\textrm{sat}\,}}\left( \frac{s_\theta }{\varpi _\theta }\right) \right] , \end{aligned}$$
(43)

where \(\hat{f}_\theta\) approximates \(\frac{(I_{zz}-I_{xx})\dot{\phi }\dot{\psi } - K_{\theta }\dot{\theta }|\dot{\theta }| + I_{r}\Omega _{r}\dot{\phi }}{I_{yy}}\). For yaw control:

$$\begin{aligned} U_{f4} = I_{zz}\left[ -\hat{f}_\psi + \ddot{\psi }_d - c_\psi \dot{e}_\psi - \eta _\psi {{\,\textrm{sat}\,}}\left( \frac{s_\psi }{\varpi _\psi }\right) \right] , \end{aligned}$$
(44)

where \(\hat{f}_\psi\) approximates \(\frac{(I_{xx}-I_{yy})\dot{\phi }\dot{\theta } - K_{\psi }\dot{\psi }|\dot{\psi }|}{I_{zz}}\). The adaptive laws are:

$$\begin{aligned} \dot{\hat{W}}_i = \gamma _i s_i h_{fi}(x_{in,i}), \quad i=\theta , \psi . \end{aligned}$$
(45)

Simulation studies

In this section, the efficacy and robustness of the proposed MPSO-RBF based FTC algorithm are rigorously evaluated through comprehensive simulation studies. Utilizing a nonlinear quadrotor UAV model, these experiments systematically assess the algorithm’s trajectory tracking precision, resilience to external disturbances, robustness against parameter variations (sudden mass increase), and fault tolerance capabilities under actuator efficiency loss and deviation faults. To provide a clear and rigorous benchmark, the performance of the proposed MPSO-RBF FTC is compared against two baseline controllers: a conventional SMC and a standard Adaptive SMC (ASMC). The ASMC controller utilizes a similar sliding surface but employs a standard adaptation law to adjust the switching gain, representing a more modern and challenging baseline than traditional SMC. The physical parameters of the quadrotor UAV model, consistent with realistic platforms, are detailed in Table 1. The simulations were performed in a dedicated simulation environment.

Table 1 Simulation Parameters for Quadrotor UAV Model.
Full size table

For the proposed MPSO-RBF FTC, the RBF networks used for approximating f(x) and g(x) employed a structure with \(m=5\) hidden layer neurons, deemed sufficient for capturing the system dynamics in these scenarios. The adaptive learning rates were set to \(\gamma _{i1} = 50, \gamma _{i2} = 20\) (\(i=1..6\)) based on preliminary tuning, balancing convergence speed and stability. The saturation function boundary layer was chosen as \(\varpi = 0.1\). The MPSO parameters, unless otherwise specified, were selected based on common practices in PSO literature23,31 and preliminary tests, aiming for effective exploration and exploitation. The baseline conventional SMC utilized a standard linear sliding surface (\(s = \dot{e} + ce\)) with c chosen appropriately for each control loop (e.g., \(c_1=c_4=c_5=c_6=5\), \(c_2=c_3=2\)) and a switching gain \(\eta\) tuned to be large enough to handle nominal uncertainties but without explicit adaptation or fault compensation mechanisms. The ASMC benchmark controller also used the same sliding surface but with a gain \(\hat{\eta }\) updated via a standard adaptation law \(\dot{\hat{\eta }} = |s|\), providing an adaptive baseline for comparison.

Nominal trajectory tracking performance

This initial experiment quantifies the baseline tracking performance of the MPSO-RBF FTC algorithm under ideal (nominal) operating conditions, free from external disturbances or faults. The quadrotor UAV starts from the initial state \([x, y, z, \psi ]^T = [0.15, 0.15, 0.1, 0]^T\) (units: m, rad). The desired trajectory is a helical path defined by:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_d(t) = \cos (0.3t) \\ y_d(t) = \sin (0.3t) \\ z_d(t) = 0.1t \end{array}\right. }, \end{aligned}$$
(46)

with a constant desired yaw angle \(\psi _d = 0.13\) rad. For this scenario, the MPSO parameters were configured with a population size \(S = 20\) and maximum iterations \(t_{\max } = 100\), facilitating efficient optimization of the RBF centers (\(\mu _j\)) and widths (\(\sigma _j\)) as detailed in Algorithm 1. The position and attitude tracking results are depicted in Figs. 4 and 5, respectively.

Fig. 4
figure 4

Position tracking performance (x, y, z) of the quadrotor UAV under nominal conditions using MPSO-RBF FTC.

Full size image
Fig. 5
figure 5

Attitude tracking performance (roll \(\phi\), pitch \(\theta\), yaw \(\psi\)) of the quadrotor UAV under nominal conditions using MPSO-RBF FTC.

Full size image

As illustrated in Figs. 4 and 5, the proposed MPSO-RBF FTC algorithm demonstrates exceptional precision and stability in tracking the desired spatiotemporal trajectory. The controller achieves rapid convergence to the reference path with negligible steady-state error, validating the core effectiveness of the MPSO-optimized RBF network in accurately approximating and compensating for the inherent nonlinear dynamics of the UAV. This confirms the algorithm’s ability to ensure reliable operation under nominal conditions, meeting the control objectives established in Section III. Quantitative analysis (e.g., Root Mean Square Error) would further confirm the sub-centimeter and sub-degree accuracy observed.

Comparative analysis: robustness to disturbances and parameter variations

o evaluate the algorithm’s robustness against realistic operational challenges, this experiment introduces external disturbances and abrupt parameter changes, comparing the MPSO-RBF FTC against the conventional SMC and ASMC benchmarks. The initial conditions remain \([x, y, z, \psi ]^T = [0.15, 0.15, 0.1, 0]^T\). The desired trajectory is modified to test performance over a different path:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_d(t) = 1 - \cos (0.3t) \\ y_d(t) = \sin (0.3t) \\ z_d(t) = 1 - e^{-0.3t} \end{array}\right. }, \end{aligned}$$
(47)

with \(\psi _d = 0.13\) rad. The MPSO parameters were adjusted to \(S = 40\) and \(t_{\max } = 80\) to allow for sufficient adaptation exploration in these more challenging scenarios.

Scenario 1: external disturbances

Time-varying disturbances, simulating external forces like wind gusts, are injected into the system dynamics at \(t = 20\) s, defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} d_i(t) = i \cos (0.3t), & i = 1, 2, 3 \\[6pt] d_6(t) = 4 \cos (0.3t) \end{array}\right. } \end{aligned}$$
(48)

where \(d_i(t)\) are disturbances affecting the linear acceleration states (\(\ddot{x}, \ddot{y}, \ddot{z}\)), and \(d_6(t)\) affects the yaw acceleration state (\(\ddot{\psi }\)).

The comparative tracking performance for horizontal positions (\(x, y\)) and altitude/yaw angle (\(z, \psi\)) are presented in Figs. 6 and 7.

Fig. 6
figure 6

Horizontal position tracking performance (x and y) under external disturbances introduced at t = 20 s, comparing MPSO-RBF FTC with Traditional SMC and Adaptive SMC.

Full size image
Fig. 7
figure 7

Altitude (z) and yaw angle (\(\psi\)) tracking performance under external disturbances introduced at \(t = 20\) s, comparing MPSO-RBF FTC with Traditional SMC and Adaptive SMC.

Full size image

The results vividly demonstrate the superior disturbance rejection of the MPSO-RBF FTC. Upon the introduction of disturbances at \(t=20\) s, Figs. 6 and 7 show that the proposed algorithm exhibits significantly faster recovery (shorter adjustment time) and smaller transient/steady-state errors compared to SMC. While the inherent robustness of SMC allows it to maintain tracking briefly, its performance, particularly in altitude control (z), degrades rapidly, becoming unstable after \(t = 30\) s due to the persistent, uncompensated disturbance. The ASMC performs better than traditional SMC by adapting its gain, but it still suffers from significant tracking errors and oscillations as it struggles to cope with the magnitude of the disturbance. In stark contrast, the proposed MPSO-RBF FTC, leveraging the online approximation capabilities of the RBF network and adaptive laws, effectively compensates for the disturbances, maintaining robust stability and accurate tracking throughout. This highlights the practical benefit of integrating adaptive neural components for handling unknown external inputs, a key feature of the proposed approach3,19.

Scenario 2: parameter variation

To assess robustness against unmodeled dynamics or payload changes, a sudden 30% increase in the UAV’s mass (m) is introduced at \(t = 10\) s. Figure 8 compares the altitude (z) tracking performance of the two controllers under this parametric uncertainty.

Fig. 8
figure 8

Altitude tracking performance under a 30% mass increase at \(t = 10\) s, comparing MPSO-RBF FTC with Traditional SMC and Adaptive SMC.

Full size image

Figure 8 clearly underscores the superior robustness of the proposed method. The MPSO-RBF FTC algorithm rapidly adapts to the abrupt mass increase, maintaining stable altitude tracking with only a minimal, quickly corrected transient deviation (\(< 0.02\) m). This adaptation stems from the RBF network’s ability to adjust its approximation online to account for the altered system dynamics implicitly affecting f(x) and g(x) in the control law. Conversely, the conventional SMC controller, lacking such an adaptive mechanism, fails to compensate for the significant parameter change. Its fixed gains result in a substantial and persistent tracking error, ultimately leading to a failure to maintain the desired altitude. This result strongly validates the robustness advantage conferred by the adaptive RBF component optimized by MPSO.

Comparative analysis: fault tolerance under actuator faults

This final set of experiments specifically evaluates the fault-tolerant capabilities of the MPSO-RBF FTC algorithm, as theoretically supported by the controller design (Section III-D). The performance is compared against both Traditional SMC and Adaptive SMC under two distinct actuator fault scenarios, modeled as per Eq. (2). The simulation setup (initial conditions, desired trajectory from Eq. (47), MPSO parameters \(S=40, t_{\max }=80\)) is identical to the previous robustness experiment. Faults are introduced instantaneously at \(t = 20\) s to assess the controller’s response.

Scenario 1: actuator efficiency loss

A multiplicative fault representing a severe 75% loss of efficiency (i.e., only 25% effectiveness remaining) is applied to the first actuator channel (\(U_1\)), such that \(\rho _1 = 0.25\) in Eq. (2). Figure 9 shows the altitude (z) tracking performance, which is primarily affected by \(U_1\).

Fig. 9
figure 9

Altitude (z) tracking performance under a 75% efficiency loss fault (\(\rho _1=0.25\)) introduced at \(t = 20\) s, comparing MPSO-RBF FTC with Traditional SMC and Adaptive SMC.

Full size image
Fig. 10
figure 10

Control torque responses (\(U_1\) to \(U_4\)) of the MPSO-RBF FTC algorithm under the 75% efficiency loss fault introduced at \(t = 20\) s.

Full size image

As depicted in Fig. 9, the MPSO-RBF FTC successfully compensates for this significant loss of actuator effectiveness. It maintains stable altitude tracking with only minor, quickly dampened oscillations around the desired trajectory immediately following the fault injection. Both the conventional SMC and the ASMC controllers, lacking any mechanism to estimate or counteract the fault, is unable to maintain the required lift and completely loses tracking capability, leading to instability. Figure 10 provides insight into the MPSO-RBF FTC’s adaptive response: the control signal \(U_1\) (total lift command) increases significantly after \(t=20\) s to counteract the \(\rho _1=0.25\) factor, effectively demanding more from the faulty actuator system to achieve the required physical thrust. Concurrently, the other control inputs (\(U_2, U_3, U_4\)) adjust dynamically to maintain attitude stability despite the fault’s influence, demonstrating coordinated control adaptation. All control signals remain bounded and stable, highlighting the effectiveness of the adaptive laws derived from Lyapunov stability analysis (Section III-D).

Scenario 2: actuator deviation fault

An additive fault, representing a constant bias or a stuck actuator signal component, is introduced in the yaw control channel, such that \(f_4 = 0.3\) in Eq. (2). Figure 11 presents the yaw angle (\(\psi\)) tracking performance.

Fig. 11
figure 11

Yaw angle (\(\psi\)) tracking performance under a constant deviation fault (\(f_4 = 0.3\)) introduced at \(t = 20\) s, comparing MPSO-RBF FTC with Traditional SMC and Adaptive SMC.

Full size image

Figure 11 demonstrates the proposed algorithm’s ability to handle additive faults. Following the fault injection at \(t=20\) s, the MPSO-RBF FTC algorithm exhibits a small initial deviation but rapidly identifies and compensates for the constant bias \(f_4\). It quickly restores the yaw angle to its desired trajectory (\(\psi _d=0.13\) rad) with minimal overshoot and settles within approximately 5 seconds. This rapid recovery is attributed to the RBF network’s ability to approximate the unknown fault term implicitly within the system dynamics f(x) and the effectiveness of the adaptive sliding mode structure. In contrast, both the standard SMC and ASMC controllers struggles significantly against this constant unmodeled input, exhibiting large, persistent oscillations and failing to converge to the desired yaw angle. This confirms the MPSO-RBF algorithm’s superior fault tolerance against deviation faults compared to non-adaptive SMC.

Collectively, these comparative simulation studies, encompassing nominal tracking, disturbance rejection, robustness to parameter variations, and tolerance to both multiplicative and additive actuator faults, robustly demonstrate the significant advantages of the proposed MPSO-RBF FTC algorithm over over both conventional and adaptive SMC. The integration of the RBF neural network, effectively tuned by the MPSO algorithm with its adaptive mutation strategy23,31, provides enhanced adaptability, faster convergence, superior disturbance rejection, and crucial fault tolerance capabilities, thereby improving the overall safety and reliability of the quadrotor UAV system in challenging operating conditions. The results strongly support the theoretical claims and contributions outlined earlier in the paper7,9,37,38.

Conclusion

This paper has successfully developed a novel adaptive sliding mode FTC featuring a Dual-Trigger Hybrid MPSO for tuning the RBF neural network. The proposed MPSO, which synergizes a diversity-based trigger with a stagnation-based one, effectively addresses the local optima and instability issues inherent in conventional parameter tuning. This results in superior uncertainty approximation and chattering suppression, with stability guaranteed by Lyapunov theory. Comprehensive simulations under realistic fault and disturbance conditions confirmed that our method significantly outperforms both a conventional SMC and a standard Adaptive SMC benchmark in tracking performance and robustness. While promising, this study has several limitations that pave the way for future research. First, the computational complexity of the MPSO, while performed for parameter tuning, may be a concern for resource-constrained UAVs if online re-tuning is required. Future work should explore lightweight implementations or periodic, offline tuning strategies. Second, the assumption of full state availability, while common in controller design, can be unrealistic. Integrating a state observer, such as an Extended Kalman Filter, would be necessary for practical implementation where not all states are directly measurable. Future studies could also benefit from Monte Carlo simulations to statistically validate robustness across a range of stochastic conditions. Third, the MPSO hyperparameters were selected based on common practices; exploring self-tuning or adaptive mechanisms for these hyperparameters would enhance the controller’s autonomy and practicality. Finally, while our simulation results are comprehensive, they also open avenues for more advanced applications. The immediate next step is to validate the controller on a physical UAV testbed. Beyond single-agent systems, future work will focus on extending this fault-tolerant framework to distributed multi-agent systems, such as UAV swarms, to ensure robust cooperative control and formation tracking even when individual agents experience faults.