Novel closed-form travelling wave solutions for space-time fractional coupled Boussinesq–Burger model using extended direct algebraic method

Abstract

The nonlinear fractional partial differential equation known as the space-time fractional coupled Boussinesq-Burger equation (S TFcBBE) is examined in this work. Wave propagation in shallow water, fluid movement in dynamic systems, and wave propagation in nonlinear media are just a few of the physical processes it replicates. We derive new closed-form solutions for travelling waves, including a range of soliton waveforms, such as periodic, bell-type, kink-type, solitary kink, and multiple kink waves, by using the extended direct algebraic technique. The graphical representations of these solutions, created by MAPLE software, provide crucial new insights into the physical behaviour of the system. Our results demonstrate the effectiveness and dependability of the enlarged direct algebraic approach in solving nonlinear fractional partial differential equations, particularly the STFcBBE. The study adds to our understanding of nonlinear wave dynamics and could be used to coastal engineering, fluid dynamics and other fields. The findings show how flexible the extended direct algebraic approach is for reaching exact solutions and how crucial the fractional order is in defining the wave dynamics.

Introduction

Numerous physical issues are regulated by nonlinear evolution equations (NLEEs), such as nonlinear dynamics, fluid dynamics, biological physics, optical engineering, plasma physics, nonlinear phenomena, and many more in the mathematical sciences. Because of this, the precise closed-form solutions of controlled equations are of considerable importance and receive a lot more study attention. These solutions are assessed in order to comprehend the dynamical behaviour of the issue at hand. Even for basic NLPDEs, there are typically no easy methods for figuring out the closed-form solutions from a linear theory perspective. For example, a (4+ 1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili equation employing a newly designed analytical method¹, the Painlevé-integrable (3+ 1) Dimension nonlinear evolution equations using a new extended methodology², and the (3+ 1)-dimensional mKdV–ZK equation using a new modified Sardar sub-equation approach³. In optical fibres, the dynamics of multiple optical soliton solutions of a (3+ 1)-dimensional nonlinear Schrödinger equation with parabolic law⁴, the recently suggested modified approach⁵, the recently developed methodology⁶, the integrable Kuralay equation⁷, the lie symmetry method and unified approach⁸, Lie symmetries, closed-form solutions, and different dynamical profiles of solitons for the variable coefficient (2+ 1)-dimensional KP equations⁹, new wave behaviours of the (3+ 1)-dimensional Date-Jimbo-Kashiwara-Miwa equation¹⁰, Complex solutions to the higher-order nonlinear boussinesq type wave equation transform¹¹, the generalised Hietarinta equation¹², Numerous analytical techniques, such as the OPTIMAL BOUNDARY CONTROL FOR A SCHRODINGER EQUATION¹³ and sin-Gordon expansion approach¹⁴, the generalised exponential rational function approach¹⁵, the Ansatz and sub equation theories¹⁶, the $(G'/G)$-expansion approach¹⁷, the Jacobi elliptic function technique¹⁸, the modified auxiliary expansion technique¹⁹, the Lie symmetry analysis method²⁰, the direct algebraic approach²¹, the stepest descent method^22,23, the improved Bernoulli sub-equation function technique²⁴, the modefoie extended direct algebraic method²⁵, and the residual power series technique²⁶ are all effective ways to solve NLFPDEs. The popular and practical tanh-function approach was first developed by Malfiet²⁷, who established tanh as a new variable for such a dependable solution of nonlinear wave equations. Tanh developed his technique to address issues with moving waves.Wazwaz later introduced the larger tanh technique²⁸. Furthermore, the extended tanh approach has a special set of solutions known as solitons for the equations it can solve. Special travelling waves called soliton waves keep their shape even when they collide with other waves. Numerous situations, such as traffic flow, the internet, turbulence, shock waves, tortoises, Jupiter’s huge red spot, hydrodynamics, and nonlinear optics, are covered by this characteristic. Recent years have seen a significant increase in interest in soliton research in quantum and nanotechnology fields, particularly in nano-hydrodynamics²⁹. Consider the Coupled version of fractional order in space and time Boussinesq (BB) Burger Equation³⁰ which is given as,

$$\begin{aligned} & \frac{\partial ^{\alpha } U}{\partial t^{\alpha }} - \frac{1}{2} \frac{\partial V}{\partial x} + 2U \frac{\partial U}{\partial x} = 0, \end{aligned}$$

(1)

$$\begin{aligned} & \quad \frac{\partial ^{\alpha } V}{\partial t^{\alpha }} - \frac{1}{2} \frac{\partial ^3 U}{\partial x^3} + 2 \frac{\partial (UV)}{\partial x} = 0, \end{aligned}$$

(2)

where $t > 0$ and $0< \alpha < 1$. The variables U(x, t) and V(x, t) in the aforementioned equations represent the following physical quantities:

The symbol U(x, t) represents the field of horizontal velocity, whereas V(x, t) indicates the height of the water’s surface above the lowest horizontal level.

These two equations combine to provide an intriguing mathematical model that shows how waves travel over shallow water. They are crucial to comprehending a number of phenomena pertaining to oceanography, coastal engineering, and water resource management. They arise in the study of fluid flow within vertically well-mixed water bodies.

Model Statement: An essential model in this research is the space-time fractional coupled Boussinesq-Burger equation (STFcBBE), which captures the complex dynamics of numerous physical processes. Specifically, it pertains to fundamental phenomena in fluid dynamics, coastal engineering, and other domains, such as wave propagation in shallow water, fluid flow in complicated systems, and wave propagation in nonlinear media. The STFcBBE’s exceptional capacity to capture the intricacies of nonlinear wave dynamics, combined with its fractional character that effectively represents memory-dependent and non-local effects, makes it an intriguing topic for research. This work examines the STFcBBE to shed light on the behavior of complex systems and contribute significantly to our understanding of nonlinear wave dynamics. We used several alternate methods to explain the space-time fractional order linked type BB equation. Using the Caputo derivative by residual power series, Kumar et al. developed it³². M. H. Heydari and Z. Avazzadeh solved it using the Orthonormal Bernoulli polynomials (OBPs) with a derivative in the Caputo form³¹. Mahmoud S. Alrawashdeh and Shifaa Bani-Issa³³ clarified it using Homotopy polynomials and the Decomposition technique by Caputo derivatives. Khalid K. Ali et al.³⁴ developed the modified extended tanh approach with the modified Riemann-Liouville derivative to solve the space-time fractional order linked type Boussinesq problem. With a conformable derivative and the Exp-function technique, Ayse Girgin and Handan C. Yaslan developed this proposed equation¹⁰. Finding new exact solutions for the NLFPDEs, such as kinks, bells, solitons, and other kinds of solutions, is the primary objective of the work. The extended tanh-function approach was used to solve those equations.

Therefore, it is entirely novel to solve those suggested equations with conformable derivatives using the previously described method. This study employs this methodology to generate more comprehensive and up-to-date solutions that are easier to implement, extensible, adjustable, and faster to simulate. The solutions are shown in 3D, 2D, and contour pattern plots. The physical phenomena described by our proposed models are more accurately explained by those three types of pictographic descriptions.

Definition and basic setup

Recently, Khalil et al.³⁵ introduced the concept of conformable derivatives. Consider a function $\phi : [0, 1) \rightarrow {\mathbb {R}}$ and its $\xi$-order conformable derivative:

$$\begin{aligned} {\mathcal {T}}{\xi }(\phi )(\tau ) = \lim {\epsilon \rightarrow 0} \frac{\phi (\tau + \epsilon \tau ^{1-\xi }) - \phi (\tau )}{\epsilon } \end{aligned}$$

(3)

for all $\tau > 0$, where $\xi \in (0, 1)$. If $\phi$ is $\xi$-differentiable for some $\xi \in (0, 1)$ and $\tau > 0$, and $\lim _{\tau \rightarrow 0^+} {\mathcal {T}}_{\xi }(\phi )(\tau )$ exists, then:

$$\begin{aligned} {\mathcal {T}}{\xi }(\phi )(0) = \lim {\tau \rightarrow 0^+} {\mathcal {T}}_{\xi }(\phi )(\tau ) \end{aligned}$$

(4)

On temporal scales, the conformable derivative is essential for understanding derivatives of quantitative measurements, addition, and products of differentiable functions. As per the given definition, the following theorem satisfies the conformable derivative, offering several noteworthy features.

Investigation of the fractional nonlinear type evolution equation’s soliton propagation

This study investigates by using conformable derivatives. The results provide new insights into the behavior of solitons in fractional nonlinear systems.

Theorem 1

Let $\xi \in (0, 1]$ and suppose $\phi$ and $\psi$ are $\xi$-differentiable at all points $\tau > 0$. Then:

• ${\mathcal {T}}{\xi }(c\phi + d\psi ) = c{\mathcal {T}}{\xi }(\phi ) + d{\mathcal {T}}_{\xi }(\psi )$, as $c, d \in {\mathbb {R}}$.

• ${\mathcal {T}}_{\xi }(\tau ^p) = p\tau ^{p-\xi }$, for all $p \in {\mathbb {R}}$.

• ${\mathcal {T}}_{\xi }(c) = 0$, for all constant functions $\phi (\tau ) = C$.

• ${\mathcal {T}}{\xi }(\phi \psi ) = \phi {\mathcal {T}}{\xi }(\psi ) + \psi {\mathcal {T}}_{\xi }(\phi )$.

• ${\mathcal {T}}{\xi } \left( \frac{\phi }{\psi }\right) = \frac{\psi {\mathcal {T}}{\xi }(\phi ) - \phi {\mathcal {T}}_{\xi }(\psi )}{\psi ^2}$.

• If $\phi$ is differentiable, then ${\mathcal {T}}_{\xi }(\phi )(\tau ) = \tau ^{1-\xi } \frac{d\phi }{d\tau }$.

Theorem 2

The interval of f can be found by assuming g is differentiable and letting f be a $\alpha$-differentiable function. Next, the following is the conformable derivative of the composite function $f \circ g$:

$$\begin{aligned} T_{\alpha }(f \circ g)(t) = t^{1-\alpha } g'(t) f'(g(t)) \end{aligned}$$

EDAM operational procedure

Consider, the PDE^36,37,38

$$\begin{aligned} P(w,\partial ^\alpha _t w,\partial ^\beta _{s_1} w,\partial ^\gamma _{s_2} w,w\partial ^\beta _{s_1} w, \ldots )=0, \ \ 0<\alpha ,\beta ,\gamma \le 1, \end{aligned}$$

(5)

where t, $s_1, s_2, s_3,\ldots , s_r$, and w are the functions respectively. To solve equation (5), follow these steps: Step 1: Transformation of Variables Use a variable transformation of the type $w(s_1, s_2, s_3, \ldots , s_r)=Z(\Phi )$, where $\Phi$ can be written in a variety of ways. With this change, (5) becomes a specific nonlinear ordinary differential equation (ODE), we have

$$\begin{aligned} D(Z,Z',Z'',\dots )=0, \end{aligned}$$

(6)

where the derivatives of Z with respect to $\Phi$ are provided in (6). Integrating (6) any number of times determines the integration constant(s).

Step 2: Solution Form Assume the solution of (6) has the form:

$$\begin{aligned} Z(\Phi )=\sum _{l=-\varsigma }^{\varsigma }d_l(Z(\Phi ))^l, \end{aligned}$$

(7)

$Z(\Phi )$ represents the general solution to the given ODE, whereas $d_l (l=-\varsigma ,\ldots ,0,\ldots ,\varsigma )$ represents the constants to be determined. As an alternative, think about the following solution:

$$\begin{aligned} Z'(\Phi )=ln(\Omega )(n+u Z(\Phi )+v(Z(\Phi ))^2), \end{aligned}$$

(8)

where the constants n, u, andv and $\Omega \ne 0,1$ are used³⁹.

Step 3: Homogeneous Balance determining the solution form in (6) by performing the homogeneous balancing between the largest nonlinear term and the highest order derivative in $\varsigma$.

Step 5: Solving the Algebraic System Use MAPLE to solve the algebraic system of equations.

Step 6: Obtaining Analytical Solutions Identify the unknown values and substitute them into $Z(\Phi )$ of equation (7). This yields the analytical soliton solutions to (5).

Family 1: The situation where $W<0$ and $u\ne 0$

$$\begin{aligned} Z_1(\Phi )= & -{\frac{u}{2v}}+{\frac{\sqrt{-W}\tan _\Omega \left( \frac{1}{2}\,\sqrt{-W}\Phi \right) }{2v}} {,} \\ Z_2(\Phi )= & -{\frac{u}{2\nu }}-{\frac{\sqrt{-W}\cot _\Omega \left( \frac{1}{2}\,\sqrt{-W}\Phi \right) }{2\nu }}, \\ Z_3(\Phi )= & -{\frac{u}{2v}}+{\frac{\sqrt{-W} \left( \tan _\Omega \left( \sqrt{-W}\Phi \right) \pm \left( \sec _\Omega \left( \sqrt{-W}\Phi \right) \right) \right) }{2v}}, \\ Z_4(\Phi )= & -{\frac{u}{2v}}-{\frac{\sqrt{-W} \left( \cot _\Omega \left( \sqrt{-W }\Phi \right) \pm \left( \csc _\Omega \left( \sqrt{-W}\Phi \right) \right) \right) }{2v}}, \end{aligned}$$

and

$$\begin{aligned} Z_5(\Phi )=-{\frac{u}{2v}}+{\frac{\sqrt{-W} \left( \tan _\Omega \left( \frac{1}{4}\, \sqrt{-W}\Phi \right) -\cot _\Omega \left( \frac{1}{4}\,\sqrt{-W}\Phi \right) \right) }{4v}}. \end{aligned}$$

Family 2: As soon as $W>0$ and $u\ne 0$, we have

$$\begin{aligned} Z_6(\Phi )= & -{\frac{u}{2v}}-{\frac{\sqrt{W}\tanh _\Omega \left( \frac{1}{2}\,\sqrt{W} \Phi \right) }{2v}}, \\ Z_7(\Phi )= & -{\frac{u}{2v}}-{\frac{\sqrt{W}\coth _\Omega \left( \frac{1}{2}\,\sqrt{W} \Phi \right) }{2v}}, \\ Z_8(\Phi )= & -{\frac{u}{2v}}-{\frac{\sqrt{W} \left( \tanh _\Omega \left( \sqrt{W}\Phi \right) \pm i \left( \mathrm{sech_\Omega } \left( \sqrt{W}\Phi \right) \right) \right) }{2v}}, \\ Z_9(\Phi )= & -{\frac{u}{2v}}-{\frac{\sqrt{W} \left( \coth _\Omega \left( \sqrt{W}\Phi \right) \pm \left( \mathrm{csch_\Omega } \left( \sqrt{W}\Phi \right) \right) \right) }{2v}}, \end{aligned}$$

and

$$\begin{aligned} Z_{10}(\Phi )=-{\frac{u}{2v}}-{\frac{\sqrt{W} \left( \tanh _\Omega \left( \frac{1}{4}\, \sqrt{W}\Phi \right) -\coth _\Omega \left( \frac{1}{4}\,\sqrt{W}\Phi \right) \right) }{4v}}. \end{aligned}$$

Family 3: When $nv>0$ and $u=0$, then we have

$$\begin{aligned} Z_{11}(\Phi )= & \sqrt{{\frac{n}{v}}}\tan _\Omega \left( \sqrt{nu}\Phi \right) , \\ Z_{12}(\Phi )= & -\sqrt{{\frac{n}{v}}}\cot _\Omega \left( \sqrt{nu}\Phi \right) , \\ Z_{13}(\Phi )= & \sqrt{{\frac{n}{v}}} \left( \tan _\Omega \left( 2\,\sqrt{nu}\Phi \right) \pm \left( \sec _\Omega \left( 2\,\sqrt{v}\Phi \right) \right) \right) , \\ Z_{14}(\Phi )= & -\sqrt{{\frac{n}{v}}} \left( \cot _\Omega \left( 2\,\sqrt{nv}\Phi \right) \pm \left( \csc _\Omega \left( 2\,\sqrt{nv}\Phi \right) \right) \right) , \end{aligned}$$

and

$$\begin{aligned} Z_{15}(\Phi )=\frac{1}{2}\sqrt{{\frac{n}{v}}} \left( \tan _\Omega \left( \frac{1}{2}\,\sqrt{nv}\Phi \right) -\cot _\Omega \left( \frac{1}{2}\,\sqrt{nv}\Phi \right) \right) . \end{aligned}$$

Family 4: When $nv>0$ and $u=0$, then we have

$$\begin{aligned} Z_{16}(\Phi )= & -\sqrt{-{\frac{n}{v}}}\tanh _\Omega \left( \sqrt{-nv}\Phi \right) , \\ Z_{17}(\Phi )= & -\sqrt{-{\frac{n}{v}}}\coth _\Omega \left( \sqrt{-nv}\Phi \right) , \\ Z_{18}(\Phi )= & -\sqrt{-{\frac{n}{v}}} \left( \tanh _\Omega \left( 2\,\sqrt{-nv}\Phi \right) \pm \left( i\mathrm{sech_\Omega } \left( 2\, \sqrt{-nv}\Phi \right) \right) \right) , \\ Z_{19}(\Phi )= & -\sqrt{-{\frac{n}{v}}} \left( \coth _\Omega \left( 2\,\sqrt{-nv}\Phi \right) \pm \left( \mathrm{csch_\Omega } \left( 2\, \sqrt{-nv}\Phi \right) \right) \right) , \end{aligned}$$

and

$$\begin{aligned} Z_{20}(\Phi )=-\frac{1}{2}\sqrt{-{\frac{n}{v}}} \left( \tanh _\Omega \left( \frac{1}{2}\,\sqrt{-vv}\Phi \right) +\coth _\Omega \left( \frac{1}{2}\,\sqrt{-nv}\Phi \right) \right) . \end{aligned}$$

Family 5: The situation where $v=n$ and $u=0$ is

$$\begin{aligned} Z_{21}(\Phi )= & \tan _\Omega \left( n\Phi \right) , \\ Z_{22}(\Phi )= & -\cot _\Omega \left( n\Phi \right) , \\ Z_{23}(\Phi )= & \tan _\Omega \left( 2\,n\Phi \right) \pm \left( \sec _\Omega \left( 2\,n\Phi \right) \right) , \\ Z_{24}(\Phi )= & -\cot _\Omega \left( 2\,n\Phi \right) \pm \left( \csc _\Omega \left( 2\,n\Phi \right) \right) , \end{aligned}$$

and

$$\begin{aligned} Z_{25}(\Phi )=\frac{1}{2}\tan _\Omega \left( \frac{1}{2}\,n\Phi \right) -\frac{1}{2}\,\cot _\Omega \left( \frac{1}{2}\,n\Phi \right) , \end{aligned}$$

Family 6: With $v=-n$ and $u=0$, we get

$$\begin{aligned} Z_{26}(\Phi )= & -\tanh _\Omega \left( n\Phi \right) , \\ Z_{27}(\Phi )= & -\coth _\Omega \left( n\Phi \right) , \\ Z_{28}(\Phi )= & -\tanh _\Omega \left( n,a\Phi \right) \pm \left( i \mathrm{sech_\Omega } \left( 2\,n\Phi \right) \right) , \\ Z_{29}(\Phi )= & -\coth _\Omega \left( 2\,n\Phi \right) \pm \left( { \mathrm csch_\Omega } \left( 2\,n\Phi \right) \right) , \end{aligned}$$

and

$$\begin{aligned} Z_{30}(\Phi )=-\frac{1}{2}\tanh _\Omega \left( \frac{1}{2}\,n\Phi \right) -\frac{1}{2}\,\coth _\Omega \left( \frac{1}{2}\,n\Phi \right) . \end{aligned}$$

Family 7: As soon as $W=0$, we have

$$\begin{aligned} Z_{31}(\Phi )=-2\,{\frac{n \left( u\Phi \,\mathrm{\ln (\Omega )}+2 \right) }{{u}^{2}\Phi \,\mathrm{\ln (\Omega )} }}. \end{aligned}$$

Family 8: When $u=\tau$, $n=m\tau (m\ne 0)$ and $v=0$, then we have

$$\begin{aligned} Z_{32}(\Phi )={\Omega }^{\tau \Phi }- m. \end{aligned}$$

Family 9: $u=v=0$, then we have

$$\begin{aligned} Z_{33}(\Phi )=n\Phi ,\mathrm{\ln (\Omega )}. \end{aligned}$$

Family 10: n $u=n=0$, then we have

$$\begin{aligned} Z_{34}(\Phi )=-{\frac{1}{v\Phi \mathrm{\ln (\Omega )}}}. \end{aligned}$$

Family 11:When $n=0$, $u\ne 0$, and $v\ne 0$ are all equal, we obtain

$$\begin{aligned} Z_{35}(\Phi )=-{\frac{u}{v \left( \cosh _\Omega \left( u\Phi \right) -\sinh _\Omega \left( u\Phi \right) +1 \right) }}, \end{aligned}$$

and

$$\begin{aligned} Z_{36}(\Phi )=-{\frac{u \left( \cosh _\Omega \left( u\Phi \right) +\sinh _\Omega \left( u\Phi \right) \right) }{v \left( \cosh _\Omega \left( u\Phi \right) +\sinh _\Omega \left( u \Phi \right) +1 \right) }}. \end{aligned}$$

Family 12: $u=\tau$, $v=m\tau (m\ne 0)$ and $n=0$, then we have

$$\begin{aligned} Z_{37}(\Phi )={\frac{{\Omega }^{\tau \,\Phi }}{1-m{\Omega }^{\tau \,\Phi }}}. \end{aligned}$$

The following is the definition of the generalised hyperbolic and trigonometric functions, and $W=u^2-4nv$.

$$\begin{aligned} \begin{aligned}&\cos _\Omega \left( \Phi \right) =\frac{{\Omega }^{i\Phi }+{\Omega }^{-i\Phi }}{2}, \quad \sin _\Omega \left( \Phi \right) ={\frac{{\Omega }^{i\Phi }-{\Omega }^{-i\Phi }}{2i}},\\&\cot _\Omega \left( v\Phi \right) =\frac{\cos _\Omega \left( \Phi \right) }{\sin _\Omega \left( v\Phi \right) }, \quad \tan _\Omega \left( \Phi \right) =\frac{\sin _\Omega \left( v\Phi \right) }{\cos _\Omega \left( \Phi \right) },\\&\csc _\Omega \left( \Phi \right) =\frac{1}{\sin _\Omega \left( \Phi \right) }, \quad \sec _\Omega \left( \Phi \right) =\frac{1}{\cos _\Omega \left( \Phi \right) }, \end{aligned} \end{aligned}$$

Similarly,

$$\begin{aligned} \begin{aligned}&\cosh _\Omega \left( \Phi \right) =\frac{{\Omega }^{\Phi }+{\Omega }^{-\Phi }}{2}, \quad \sinh _\Omega \left( \Phi \right) =\frac{{\Omega }^{\Phi }-{\Omega }^{-\Phi }}{2},\\&\coth _\Omega \left( v\Phi \right) =\frac{\cosh _\Omega \left( \Phi \right) }{\sinh _\Omega \left( \Phi \right) }, \quad \tanh _\Omega \left( \Phi \right) =\frac{\sinh _\Omega \left( \Phi \right) }{\cosh _\Omega \left( \Phi \right) },\\&csch_\Omega \left( \Phi \right) =\frac{1}{\sinh _\Omega \left( \Phi \right) }, \quad sech_\Omega \left( \Phi \right) =\frac{1}{\cosh _\Omega \left( \Phi \right) }, \end{aligned} \end{aligned}$$

Implementation of the method

Transformation of the Space-Time Fractional Order Coupled BB Equation We have already shown the space-time fractional order linked BB equation, represented by (1) and 2. We utilise the subsequent nonlinear complex transformation of wave to solve this equation:

$$\begin{aligned} \left\{ \begin{array}{ll} \varsigma =x-\mu \frac{t^\alpha }{\alpha },\\ U(x,t)=U(\varsigma ) \end{array} \right. \end{aligned}$$

(9)

where $\mu$ denotes the speed of the traveling wave. Substituting (9) into (1) and (2)reduces the integration to an ordinary differential equation (ODE):

$$\begin{aligned} & -\mu U' - \frac{1}{2}V' + 2UU' = 0 \end{aligned}$$

(10)

$$\begin{aligned} & \quad -\mu V' - \frac{1}{2}U''' + 2(UV)' = 0 \end{aligned}$$

(11)

Integration of the reduced ODEs where the derivative with respect to $\varsigma$ is symbolized by a prime ($'$) regarding U. Integrating (10) and (11) with respect to $\varsigma$ one time, considering the integrating constant to be zero, we find:

$$\begin{aligned} & -\mu U - \frac{1}{2}V + U^2 = 0 \end{aligned}$$

(12)

$$\begin{aligned} & \quad -\mu V - \frac{1}{2}U'' + 2UV = 0 \end{aligned}$$

(13)

Conclusion from (12) and (13) leads to the following conclusion:

$$\begin{aligned} V = 2(U^2 - \mu U), \end{aligned}$$

(14)

we have:

$$\begin{aligned} - \frac{1}{2}U'' + 4 U^3+2 \mu ^2 U-6 \mu U^2=0 \end{aligned}$$

(15)

Applying the homogeneous balance rule on (7) yields M = 1. Therefore,

$$\begin{aligned} U(\varsigma )=\sum _{i=-1}^{1}d_i(U(\varsigma ))^i. \end{aligned}$$

(16)

When (8) is inserted into (7), all terms with the same orders of $U(\varsigma )$ are collected, and an equation in $U(\varsigma )$ is produced. The formula can be reduced to a system of nonlinear algebraic equations by setting its coefficients to zero. When the resulting problem is tackled with Maple, solutions are obtained: Case. 1

$$\begin{aligned} \begin{aligned}&\mu =-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \left( \alpha \,\beta \,\delta - \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) {\beta }^{2}+2 \, \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \alpha \,\delta \right) }{\beta \, \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) - \alpha \,\delta }},\\ &d_{{-1}}=\frac{1}{2}\ln \left( \Lambda \right) \alpha ,d_{{0 }}=\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) ,d_{{1}}=0. \end{aligned} \end{aligned}$$

(17)

Cluster. 1.1: let $\Omega < 0, \delta \ne 0$, we have

$$\begin{aligned} U_{1,1}(x,t)&= \frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega }\tan _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(18)

$$\begin{aligned} V_{1,1}(x,t)&=2\bigg [\bigg ( \frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega }\tan _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2-\mu \frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega }\tan _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg ] , \end{aligned}$$

(19)

$$\begin{aligned} U_{1,2}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{-\Omega }\cot _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(20)

$$\begin{aligned} V_{1,2}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{-\Omega }\cot _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{-\Omega }\cot _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(21)

$$\begin{aligned} U_{1,3}(x,t)&= \frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega } \left( \tan _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( \sec _\Lambda \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\delta }} \right) ^{-1}+\nonumber \\&\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(22)

$$\begin{aligned} V_{1,3}(x,t)&= 2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega } \left( \tan _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( \sec _\Lambda \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\delta }} \right) ^{-1}+\nonumber \\ &\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2 \nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega } \left( \tan _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( \sec _\Lambda \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\delta }} \right) ^{-1}+\nonumber \\ &\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(23)

$$\begin{aligned} U_{1,4}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega } \left( \cot _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( \csc _\Lambda \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\upsilon }} \right) ^{-1}+\nonumber \\ &\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(24)

and

$$\begin{aligned} V_{1,4}(x,t)&=2\bigg [\bigg (1/2\,\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega } \left( \cot _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( \csc _\Lambda \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\upsilon }} \right) ^{-1}+\nonumber \\ &\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2 \nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{2}{\frac{\sqrt{-\Omega } \left( \cot _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( \csc _\Lambda \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\upsilon }} \right) ^{-1}+\nonumber \\ &\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(25)

$$\begin{aligned} U_{1,5}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{4}{\frac{\sqrt{-\Omega } \left( \tan _\Lambda \left( \frac{1}{4}\sqrt{- \Omega }\varsigma \right) -\cot _\Lambda \left( \frac{1}{4}\sqrt{-\Omega }\varsigma \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) . \end{aligned}$$

(26)

$$\begin{aligned} V_{1,5}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}+\frac{1}{4}{\frac{\sqrt{-\Omega } \left( \tan _\Lambda \left( \frac{1}{4}\sqrt{- \Omega }\varsigma \right) -\cot _\Lambda \left( \frac{1}{4}\sqrt{-\Omega }\varsigma \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\&+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2 \nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2},{\frac{\beta }{ \delta }}+\frac{1}{4}{\frac{\sqrt{-\Omega } \left( \tan _\Lambda \left( \frac{1}{4}\sqrt{- \Omega }\varsigma \right) -\cot _\Lambda \left( \frac{1}{4}\sqrt{-\Omega }\varsigma \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\&+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] . \end{aligned}$$

(27)

Cluster. 1.2: $\Omega > 0, \delta \ne 0$, we have

$$\begin{aligned} U_{1,6}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega }\tanh _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\upsilon }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta + \frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(28)

$$\begin{aligned} V_{1,6}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega }\tanh _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\upsilon }} \right) ^{-1}\nonumber \\ &+\frac{1}{2}\left( \frac{1}{2}\beta + \frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2\nonumber \\&-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2},{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega }\tanh _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\upsilon }} \right) ^{-1}\nonumber \\ &+\frac{1}{2}\left( \frac{1}{2}\beta + \frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(29)

$$\begin{aligned} U_{1,7}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega }\coth _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(30)

$$\begin{aligned} V_{1,7}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-1\frac{1}{2}{\frac{\sqrt{\Omega }\coth _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2\nonumber \\&-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega }\coth _\Lambda \left( \frac{1}{2}\sqrt{-\Omega } \varsigma \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(31)

$$\begin{aligned} U_{1,8}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega } \left( \tanh _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( { sech_\Lambda } \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\upsilon }} \right) ^{-1}+\nonumber \\&\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(32)

$$\begin{aligned} V_{1,8}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega } \left( \tanh _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( { sech_\Lambda } \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\upsilon }} \right) ^{-1}+\nonumber \\&\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2\nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega } \left( \tanh _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( { sech_\Lambda } \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(33)

$$\begin{aligned} U_{1,9}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega } \left( \coth _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( { sech_\Lambda } \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(34)

$$\begin{aligned} V_{1,9}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega } \left( \coth _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( { sech_\Lambda } \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2\nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{2}{\frac{\sqrt{\Omega } \left( \coth _\Lambda \left( \sqrt{- \Omega }\varsigma \right) \pm \left( { sech_\Lambda } \left( \sqrt{-\Omega }\varsigma \right) \right) \right) }{\delta }} \right) ^{-1}\nonumber \\ &+\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(35)

and

$$\begin{aligned} U_{1,10}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{4}{\frac{\sqrt{\Omega } \left( \tanh _\Lambda \left( \frac{1}{4}\sqrt{ \Omega }\varsigma \right) -\coth _\Lambda \left( \frac{1}{4}\sqrt{\Omega }\varsigma \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\ &+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) . \end{aligned}$$

(36)

$$\begin{aligned} V_{1,10}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{4}{\frac{\sqrt{\Omega } \left( \tanh _\Lambda \left( \frac{1}{4}\sqrt{ \Omega }\varsigma \right) -\coth _\Lambda \left( \frac{1}{4}\sqrt{\Omega }\varsigma \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\&+\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2\nonumber \\&-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha \left( -\frac{1}{2}{\frac{\beta }{ \delta }}-\frac{1}{4}{\frac{\sqrt{\Omega } \left( \tanh _\Lambda \left( \frac{1}{4}\sqrt{ \Omega }\varsigma \right) -\coth _\Lambda \left( \frac{1}{4}\sqrt{\Omega }\varsigma \right) \right) }{\upsilon }} \right) ^{-1}\nonumber \\&+\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2},\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] . \end{aligned}$$

(37)

Cluster. 1.3: When $\delta \alpha > 0, \beta = 0$, we have

$$\begin{aligned} U_{1,11}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \tan _\Lambda \left( \sqrt{\delta \,\alpha } \varsigma \right) \right) ^{-1}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(38)

$$\begin{aligned} V_{1,11}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \tan _\Lambda \left( \sqrt{\delta \,\alpha } \varsigma \right) \right) ^{-1}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2 \nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \tan _\Lambda \left( \sqrt{\delta \,\alpha } \varsigma \right) \right) ^{-1}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(39)

$$\begin{aligned} U_{1,12}(x,t)&=-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \cot _\Lambda \left( \sqrt{\delta \,\alpha } \varsigma \right) \right) ^{-1}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(40)

$$\begin{aligned} V_{1,12}(x,t)&=2\bigg [\bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \cot _\Lambda \left( \sqrt{\delta \,\alpha } \varsigma \right) \right) ^{-1}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2 \nonumber \\ &-\mu \bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \cot _\Lambda \left( \sqrt{\delta \,\alpha } \varsigma \right) \right) ^{-1}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(41)

$$\begin{aligned} U_{1,13}(x,t)&=\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \tan _\Lambda \left( 2\,\sqrt{\delta \,\alpha } \varsigma \right) \pm \left( \sec \left( 2\,\sqrt{ \delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ &+\frac{1}{4}\sqrt{ \Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(42)

$$\begin{aligned} V_{1,13}(x,t)&=2\bigg [\bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \tan _\Lambda \left( 2\,\sqrt{\delta \,\alpha } \varsigma \right) \pm \left( \sec \left( 2\,\sqrt{ \delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ &+\frac{1}{4}\sqrt{ \Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ &-\mu \bigg (\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \tan \left( 2\,\sqrt{\delta \,\alpha } \varsigma \right) \pm \left( \sec _\Lambda \left( 2\,\sqrt{ \delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ &+\frac{1}{4}\sqrt{ \Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(43)

$$\begin{aligned} U_{1,14}(x,t)&=-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \cot \left( 2\,\sqrt{\delta \,\alpha } \varsigma \right) \pm \left( \csc \left( 2\,\sqrt{ \delta \,\alpha }\varsigma \right) \right) \right) ^{-1} \nonumber \\ &+\frac{1}{4}\sqrt{ \Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(44)

$$\begin{aligned} V_{1,14}(x,t)&=2\bigg [\bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \cot \left( 2\,\sqrt{\delta \,\alpha } \varsigma \right) \pm \left( \csc \left( 2\,\sqrt{ \delta \,\alpha }\varsigma \right) \right) \right) ^{-1} \nonumber \\&+\frac{1}{4}\sqrt{ \Omega }\ln \left( \Lambda \right) \bigg )^2 \nonumber \\ &-\mu \bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{ \alpha }{\delta }}}}} \left( \cot \left( 2\,\sqrt{\delta \,\alpha } \varsigma \right) \pm \left( \csc \left( 2\,\sqrt{ \delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\&+\frac{1}{4}\sqrt{ \Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(45)

and

$$\begin{aligned} U_{1,15}(x,t)&=\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{\alpha }{ \delta }}}}} \left( \tan \left( \frac{1}{2}\sqrt{\delta \,\alpha }\varsigma \right) -\cot \left( \frac{1}{2}\sqrt{\delta \,\alpha }\varsigma \right) \right) ^{-1}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) . \end{aligned}$$

(46)

$$\begin{aligned} V_{1,15}(x,t)&=2\bigg [\bigg (\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{\alpha }{ \delta }}}}} \left( \tan \left( \frac{1}{2}\sqrt{\delta \,\alpha }\varsigma \right) -\cot \left( \frac{1}{2}\sqrt{\delta \,\alpha }\varsigma \right) \right) ^{-1}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2 \nonumber \\&-\mu \bigg (\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{{\frac{\alpha }{ \delta }}}}} \left( \tan \left( \frac{1}{2}\sqrt{\delta \,\alpha }\varsigma \right) -\cot \left( \frac{1}{2}\sqrt{\delta \,\alpha }\varsigma \right) \right) ^{-1}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] . \end{aligned}$$

(47)

Cluster. 1.4: $\beta = 0, \delta \alpha < 0$, we have

$$\begin{aligned} U_{1,16}(x,t) & =-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \tanh \left( \sqrt{-\delta \,\alpha } \varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(48)

$$\begin{aligned} V_{1,16}(x,t) & =2\bigg [\bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \tanh \left( \sqrt{-\delta \,\alpha } \varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \tanh \left( \sqrt{-\delta \,\alpha } \varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(49)

$$\begin{aligned} U_{1,17}(x,t) & =-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \coth \left( \sqrt{-\delta \,\alpha } \varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(50)

$$\begin{aligned} V_{1,17}(x,t) & =2\bigg [\bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \coth \left( \sqrt{-\delta \,\alpha } \varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \coth \left( \sqrt{-\delta \,\alpha } \varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(51)

$$\begin{aligned} U_{1,18}(x,t) & =-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \tanh \left( 2\,\sqrt{-\delta \,\alpha } \varsigma \right) \pm \left( i{ sech} \left( 2\, \sqrt{-\delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(52)

$$\begin{aligned} V_{1,18}(x,t) & =2\bigg [\bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \tanh \left( 2\,\sqrt{-\delta \,\alpha } \varsigma \right) \pm \left( i{ sech} \left( 2\, \sqrt{-\delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \tanh \left( 2\,\sqrt{-\delta \,\alpha } \varsigma \right) \pm \left( i{ sech} \left( 2\, \sqrt{-\delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(53)

$$\begin{aligned} U_{1,19}(x,t) & =-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \coth \left( 2\,\sqrt{-\delta \,\alpha } \varsigma \right) \pm \pm \left( { csch} \left( 2\, \sqrt{-\delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ & +\frac{1}{2}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(54)

$$\begin{aligned} V_{1,19}(x,t) & =2\bigg [\bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \coth \left( 2\,\sqrt{-\delta \,\alpha } \varsigma \right) \pm \pm \left( { csch} \left( 2\, \sqrt{-\delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (-\frac{1}{2}\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{ \alpha }{\delta }}}}} \left( \coth \left( 2\,\sqrt{-\delta \,\alpha } \varsigma \right) \pm \left( { csch} \left( 2\, \sqrt{-\delta \,\alpha }\varsigma \right) \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(55)

and

$$\begin{aligned} U_{1,20}(x,t) & = -\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{\alpha }{ \delta }}}}} \left( \tanh \left( \frac{1}{2}\sqrt{-\delta \,\alpha }\varsigma \right) +\coth \left( \frac{1}{2}\sqrt{-\delta \,\alpha }\varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) . \end{aligned}$$

(56)

$$\begin{aligned} V_{1,20}(x,t) & = 2\bigg [\bigg (-\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{\alpha }{ \delta }}}}} \left( \tanh \left( \frac{1}{2}\sqrt{-\delta \,\alpha }\varsigma \right) +\coth \left( \frac{1}{2}\sqrt{-\delta \,\alpha }\varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (-\ln \left( \Lambda \right) \alpha {\frac{1}{\sqrt{-{\frac{\alpha }{ \delta }}}}} \left( \tanh \left( \frac{1}{2}\sqrt{-\delta \,\alpha }\varsigma \right) +\coth \left( \frac{1}{2}\sqrt{-\delta \,\alpha }\varsigma \right) \right) ^{-1}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ]. \end{aligned}$$

(57)

Cluster. 1.5: Suppose $\delta = \alpha , \beta = 0$, we have

$$\begin{aligned} U_{1,21}(x,t)&=\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tan \left( \alpha \, \varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(58)

$$\begin{aligned} V_{1,21}(x,t)&=2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tan \left( \alpha \, \varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ &-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tan \left( \alpha \, \varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(59)

$$\begin{aligned} U_{1,22}(x,t)&=-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\cot \left( \alpha \, \varsigma \right) }}+\frac{1}{2}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(60)

$$\begin{aligned} V_{1,22}(x,t)&=2\bigg [\bigg (-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\cot \left( \alpha \, \varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ &-\mu \bigg (-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\cot \left( \alpha \, \varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(61)

$$\begin{aligned} U_{1,23}(x,t)&=\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tan \left( 2\,\alpha \,\varsigma \right) \pm \left( \sec \left( 2\, \alpha \,\varsigma \right) \right) }}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(62)

$$\begin{aligned} V_{1,23}(x,t)&=2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tan \left( 2\,\alpha \,\varsigma \right) \pm \left( \sec \left( 2\, \alpha \,\varsigma \right) \right) }}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ &-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tan \left( 2\,\alpha \,\varsigma \right) \pm \left( \sec \left( 2\, \alpha \,\varsigma \right) \right) }}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(63)

$$\begin{aligned} U_{1,24}(x,t)&=\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\cot \left( 2\, \alpha \,\varsigma \right) \pm \left( \csc \left( 2 \,\alpha \,\varsigma \right) \right) }}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(64)

$$\begin{aligned} V_{1,24}(x,t)&=2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\cot \left( 2\, \alpha \,\varsigma \right) \pm \left( \csc \left( 2 \,\alpha \,\varsigma \right) \right) }}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\cot \left( 2\, \alpha \,\varsigma \right) \pm \left( \csc \left( 2 \,\alpha \,\varsigma \right) \right) }}\nonumber \\ &+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(65)

and

$$\begin{aligned} U_{1,25}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\frac{1}{2}\tan \left( \frac{1}{2}\alpha \,\varsigma \right) -\frac{1}{2}\cot \left( \frac{1}{2}\alpha \,\varsigma \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) . \end{aligned}$$

(66)

$$\begin{aligned} V_{1,25}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\frac{1}{2}\tan \left( \frac{1}{2}\alpha \,\varsigma \right) -1/2\,\cot \left( \frac{1}{2}\alpha \,\varsigma \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\frac{1}{2}\tan \left( \frac{1}{2}\alpha \,\varsigma \right) -\frac{1}{2}\cot \left( \frac{1}{2}\alpha \,\varsigma \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ]. \end{aligned}$$

(67)

Cluster. 1.6: When $\delta = -\alpha , \beta = 0$, we have

$$\begin{aligned} U_{1,26}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tanh \left( {\alpha } ^{2} \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(68)

$$\begin{aligned} V_{1,26}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tanh \left( {\alpha } ^{2} \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\tanh \left( {\alpha } ^{2} \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(69)

$$\begin{aligned} U_{1,27}(x,t) & =-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\coth \left( \alpha \,\varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(70)

$$\begin{aligned} V_{1,27}(x,t) & =2\bigg [\bigg (-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\coth \left( \alpha \,\varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2-\mu \bigg (-\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{\coth \left( \alpha \,\varsigma \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(71)

$$\begin{aligned} U_{1,28}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\tanh \left( 2\, \alpha \,\varsigma \right) \pm \left( i{ sech} \left( 2\,\alpha \,\varsigma \right) \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega } \ln \left( \Lambda \right) , \end{aligned}$$

(72)

$$\begin{aligned} V_{1,28}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\tanh \left( 2\, \alpha \,\varsigma \right) \pm \left( i{ sech} \left( 2\,\alpha \,\varsigma \right) \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega } \ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\tanh \left( 2\, \alpha \,\varsigma \right) \pm \left( i{ sech} \left( 2\,\alpha \,\varsigma \right) \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega } \ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(73)

$$\begin{aligned} U_{1,29}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\coth \left( 2\, \alpha \,\varsigma \right) \pm \left( { cech} \left( 2\,\alpha \,\varsigma \right) \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega } \ln \left( \Lambda \right) , \end{aligned}$$

(74)

$$\begin{aligned} V_{1,29}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\coth \left( 2\, \alpha \,\varsigma \right) \pm \left( { cech} \left( 2\,\alpha \,\varsigma \right) \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega } \ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\coth \left( 2\, \alpha \,\varsigma \right) \pm \left( { cech} \left( 2\,\alpha \,\varsigma \right) \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega } \ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(75)

and

$$\begin{aligned} U_{1,30}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\frac{1}{2}\tanh \left( \frac{1}{2}\alpha \,\varsigma \right) -\frac{1}{2}\coth \left( \frac{1}{2}\alpha \, \varsigma \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) . \end{aligned}$$

(76)

$$\begin{aligned} V_{1,30}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\frac{1}{2}\tanh \left( \frac{1}{2}\alpha \,\varsigma \right) -\frac{1}{2}\coth \left( \frac{1}{2}\alpha \, \varsigma \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \alpha }{-\frac{1}{2}\tanh \left( \frac{1}{2}\alpha \,\varsigma \right) -\frac{1}{2}\coth \left( \frac{1}{2}\alpha \, \varsigma \right) }}\nonumber \\ & +\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ]. \end{aligned}$$

(77)

Cluster. 1.7:When $\Omega = 0$, we have

$$\begin{aligned} U_{1,31}(x,t) & =-\frac{1}{4}{\frac{\ln \left( \Lambda \right) {\beta }^{2}\varsigma \,\ln \left( \mu \right) }{\beta \,\varsigma \,\ln \left( \mu \right) +2}}+ 1/4\,\beta \,\ln \left( \Lambda \right) . \end{aligned}$$

(78)

$$\begin{aligned} V_{1,31}(x,t) & =2\bigg [\bigg (-\frac{1}{4}{\frac{\ln \left( \Lambda \right) {\beta }^{2}\varsigma \,\ln \left( \mu \right) }{\beta \,\varsigma \,\ln \left( \mu \right) +2}}+ \frac{1}{4}\beta \,\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (-\frac{1}{4}{\frac{\ln \left( \Lambda \right) {\beta }^{2}\varsigma \,\ln \left( \mu \right) }{\beta \,\varsigma \,\ln \left( \mu \right) +2}}+ \frac{1}{2}\beta \,\ln \left( \Lambda \right) \bigg )\bigg ]. \end{aligned}$$

(79)

Cluster. 1.7:When $\beta = \rho , \alpha = \pi \rho (\pi \ne 0); \delta = 0$, we have

$$\begin{aligned} U_{1,32}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) \pi \,\rho }{{\Phi }^{\rho \, \varsigma }-\pi }}+\frac{1}{2}\left( \frac{1}{2}\rho +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) . \end{aligned}$$

(80)

$$\begin{aligned} V_{1,32}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \pi \,\rho }{{\Phi }^{\rho \, \varsigma }-\pi }}+\frac{1}{2} \left( \frac{1}{2}\rho +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) \pi \,\rho }{{\Phi }^{\rho \, \varsigma }-\pi }}+\frac{1}{2}\left( \frac{1}{2}\rho +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ]. \end{aligned}$$

(81)

Cluster. 1.8:When $\beta = 0, \delta = 0$,

$$\begin{aligned} U_{1,33}(x,t) & =\frac{1}{2}{\frac{\ln \left( \Lambda \right) }{\varsigma \,\ln \left( \mu \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) . \end{aligned}$$

(82)

$$\begin{aligned} V_{1,33}(x,t) & =2\bigg [\bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) }{\varsigma \,\ln \left( \mu \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2\nonumber \\ & -\mu \bigg (\frac{1}{2}{\frac{\ln \left( \Lambda \right) }{\varsigma \,\ln \left( \mu \right) }}+\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ]. \end{aligned}$$

(83)

Family. 1.11: When $\beta = 0, \alpha = 0$,

$$\begin{aligned} U_{1,34}(x,t) & =\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) , \end{aligned}$$

(84)

$$\begin{aligned} V_{1,34}(x,t) & =2\bigg [\bigg (\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{4}\sqrt{\Omega }\ln \left( \Lambda \right) \bigg )\bigg ], \end{aligned}$$

(85)

Family. 1.12: When $\alpha = 0, \beta \ne 0, \delta \ne 0$, we have

$$\begin{aligned} U_{1,35}(x,t)&=\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(86)

$$\begin{aligned} V_{1,35}(x,t)&=2\bigg [\bigg (\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] , \end{aligned}$$

(87)

$$\begin{aligned} U_{1,36}(x,t)&=\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(88)

$$\begin{aligned} V_{1,36}(x,t)&=2\bigg [\bigg (\frac{1}{2} \left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}\left( \frac{1}{2}\beta +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] . \end{aligned}$$

(89)

Family. 1.11: When $\beta = \rho , \delta = \pi \rho , \alpha = 0$,

$$\begin{aligned} U_{1,37}(x,t)&=\frac{1}{2} \left( \frac{1}{2}\rho +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) , \end{aligned}$$

(90)

$$\begin{aligned} V_{1,37}(x,t)&=2\bigg [\bigg (\frac{1}{2}\left( \frac{1}{2}\rho +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )^2-\mu \bigg (\frac{1}{2}\left( \frac{1}{2}\rho +\frac{1}{2}\sqrt{\Omega } \right) \ln \left( \Lambda \right) \bigg )\bigg ] . \end{aligned}$$

(91)

Results and plots

The results of this study offer important new information about the behaviour of the fractional coupled Boussinesq-Burger equation (STFcBBE) in space time. Solitary waves, kink waves, and rogue waves are among the important system characteristics that we discovered by examining the graphs and travelling wave solutions. In order to comprehend the physical events that the STFcBBE represents, these waves are crucial. In the STFcBBE system, solitary waves are stable waves that retain their amplitude and shape, indicating nonlinear and dispersive behaviour. Kink waves are waves that go across boundaries and may be a sign of system phase changes. - Rogue waves: powerful, erratic waves that can have major effects, indicating the system’s susceptibility to catastrophic events. These results illustrate the possible uses and ramifications of the STFcBBE system while illuminating its intricate behaviour.

Physical explanation of traveling wave solutions

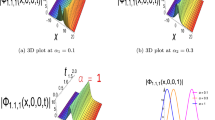
Figure 1: (a) 3D Plot: Displays the wave’s motion throughout time and space while maintaining its localised, stable structure (soliton behaviour). (b) Contour Plot: Shows the location and intensity of the wave by highlighting the regions where its energy is concentrated. (c) 2D Line Plot: Shows the amplitude of the wave at a specific moment, with strong peaks resulting from nonlinear effects.

Figure 1

The contour 2D and three-dimensional soliton solutions given in (18) are plotted for $\beta =.2, \alpha :=.1, \delta =.11, \Lambda = e, r =.5, \mu =. 1$.

Figure 2: (a) 3D Plot: This illustrates how a wave travels and maintains its shape throughout space and time, indicating that it is stable and does not expand out. (b) Contour Plot: This helps visualise how energy is concentrated in specific locations by providing a top-down view of the wave’s strongest points. (c) 2D Line Plot: Because waves are nonlinear, it highlights sharp peaks and displays the wave’s height or intensity at a given moment.

Figure 2

The three-dimensional,2D, contour soliton solution stated in (19) are graphed for $\beta =.2, \alpha =.1, \delta =.11, \Lambda = e, r = 1, \mu = 0.1$.

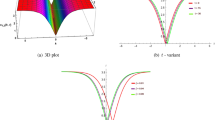
Figure 3: (a) A 3D plot, also known as a surface plot, illustrates how the amplitude of a wave varies with time and space. It shows how a stable wave packet, or soliton, keeps its size and shape while moving. (b) A contour plot shows lines with the same wave amplitude. It displays the distribution of the wave’s energy and identifies regions of significant energy concentration. (c) Real Part of a 2D Line Plot displays the wave’s amplitude at a specific moment in time. The wave’s soliton character is confirmed by the sharp peak, which denotes a powerful, localised pulse.

Figure 3

The three-dimensional, 2D and contour soliton solution stated in (20) are graphed for $\beta =.62, \alpha = 1, \delta = 1, \Lambda = e, r:= 1, \mu =.2$.

Figure 4: (a) 3D Plot: Displays a wave that moves steadily over time and space. This indicates that, like a soliton, the wave remains concentrated rather than dispersing or vanishing. (b) A contour plot shows the area with the highest wave energy. We can understand how energy stays packed by looking at the tight lines, which indicate that the wave is focused in specific places. (c) 2D Line Plot: Displays the height of the wave at a certain point in time or space. The wave maintains its shape because of nonlinear influences, as evidenced by the strong peak, which indicates the wave is intense and localised.

Figure 4

The three-dimensional, 2D and contour soliton solution stated in (21) are graphed for $\beta = 0, \alpha = 11, \delta = 1, \Lambda = e, r = .91, \mu = 0.1$.

Figure 5 Figure (a): 3D Surface Plot. With a localised, steady wave, the 3D plot displays the evolution of waves in both space and time, suggesting soliton-like behaviour. A contour plot shows areas of high energy concentration and gives a top-down view of wave intensity. Strong nonlinear interactions or singularities are indicated by sharp peaks in a 2D line plot, which shows wave amplitude at a fixed time.

Figure 5

The contour, 2D, and three-dimensional soliton solutions given in (28) are plotted for $\beta =.2; \alpha =.11, \delta =.11, \Lambda = e, r = 1, \mu =.6$.

Figure 6: (a) Three-dimensional plot: The wave’s variation throughout time and space is depicted in this plot. Instead of spreading out, the wave takes the shape of a stable point. It is a soliton, which is a wave that moves without altering shape, according to this. A contour plot (b) is a top-down representation of the wave that shows the regions with the highest energy or intensity. The tightly spaced lines show that the wave is localised, indicating that its energy stays in one place while it moves. (c) 2D Line Plot: This shows the wave’s amplitude at a certain point in space or time. Because of its sharp peaks and curves, the wave has significant nonlinear effects and remains concentrated and undistorted.

Figure 6

The contour and three-dimensional soliton solutions given in (29) are plotted for $\beta =.2, \alpha =.1, \delta =.11, \Lambda = e, r = 1, \mu = 1$.

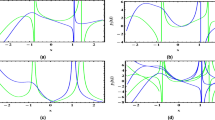
Figure 7: (a) 3D Plot: This illustrates the wave’s motion throughout time and space. The wave is steady and doesn’t expand out since it maintains its shape as it travels. (b) Contour PlotThis illustrates the strongest wave locations, much like a map. The areas with the most energy are shown by the thick or black lines. (c) Line Plot: This displays the wave’s height at a specific point in time. A prominent peak indicates that the wave is concentrated and powerful in one area.

Figure 7

The three-dimensional and contour soliton solution stated in (38) are graphed for $\beta = 2, \alpha = 1, \delta = -.11, \Lambda = e, r =.1, \mu =.9$.

Figure 8: 3D Plot (a): The wave exhibits soliton behaviour (a self-stable wave) with a crisp, stable shape that remains constant as it travels. The contour plot (b) illustrates the wave’s path and strength over time by highlighting the areas where its energy is most concentrated. The sharp peak in the 2D plot (c) indicates that the wave is powerful and localised. It displays a snapshot of the wave’s amplitude at a certain time.

Figure 8

The contour soliton solution and three-dimensional solution given in (39) are plotted for $\beta = 0, \alpha = -61, \delta = 1, \Lambda = e, r =.3, \mu :=.71$.

Conclusion

Several new exact travelling wave solutions for STcBBE were obtained in this study by using the conformable derivative definition and the expanded direct algebraic method. Our findings included closed-form solutions with multiple soliton shapes, double soliton shapes, triple bell shapes, single periodic shapes, kink shapes, singular-kink shapes, and single soliton forms. Following the evaluation of the unknown coefficients using Maple or Mathematica software, all derived solutions were immediately entered into the original equations to guarantee accuracy. The resulting solutions can be applied to the analysis of shallow water wave transmission, vertically well-mixed water body flow, and water body motion. The extended direct algebraic technique offers a variety of unique physical model solutions to nonlinear partial diferential equations (NPDEs) in mathematical physics, engineering, and applied mathematics in a direct, efficient, conformable, and dependable way.