Introduction

Spatiotemporal Series Prediction (SSP) is a field dedicated to predicting conditions in a specified period of time in the future using historically observed spatiotemporal series data (SSD) with continuous spatial attributes and complex spatiotemporal dependence1. SSP is prevalent in various downstream disciplines2,3,4,5, including traffic flow prediction, radar echo extrapolation, human posture estimation, and video prediction. Additionally, the application of SSP is pivotal in constructing smart cities, with applications ranging from intelligent traffic management to weather forecasting. Compared with single-frame images and time series, SSD not only contain complex spatiotemporal features, but also exhibit dynamic spatial and temporal interdependencies. These complexities bring great challenges to model training.

Over the years, a myriad of prediction models have emerged, from traditional Recurrent Neural Networks (RNN) to more contemporary models. Among these, Long Short-Term Memory (LSTM) has been proven to be one of the most effective tools for short-term predictions2,3,4,5. Convolutional Long Short-Term Memory Network(ConvLSTM)6 replaced the fully-connected operations in RNNs with convolutional operations but still retains the architecture of RNN. By stacking multilayered ConvLSTM units, the model is able to efficiently capture rich motion information and higher-order visual features in the spatiotemporal sequences. Nevertheless, most of these meodels are primarily aimed at short-term prediction. Their performance tends to degrade with longer-term predictions, which has been a significant limitation7,8,9.

In response, researchers have introduced a variety of LSTM models specifically tailored for long-term predictions10. Deep learning architectures, represented by CNNs11,12, have demonstrated remarkable predictive performances in various domains. This is mainly due to the unparalleled feature extraction capability. Recognizing this potential, recent efforts been made to integrate CNN into LSTM structures to improve prediction accuracy, especially in 2D frameworks13,14. However,a major shortcoming of most existing models is that they only emphasize the temporal dimension, often ignoring spatial nuances. In time series prediction, these spatial intricacies often contain valuable information that can enhance the predictive power of LSTM. To address this problem, 3D Convolutional Neural Networks(3DCNN) have been introduced to enhance the feature representation capability15,16,17.

Although existing prediction models have made some progress in processing spatio-temporal information, the problem of forgetting in long sequence prediction is still exists. In addition, capturing the non-smooth change process in the spatio-temporal dimension during the evolution of long sequences to improve the quality of image generation is still an urgent problem to be solved.

To solve the aforementioned challenges, we propose a hybrid model called 3DcT-Pred, which combines two-branch 3DCNN and ConvLSTM for spatiotemporal prediction. Specifically, 3DcT-Pred focuses on capturing long-term global spatiotemporal and local non-stationary features, compensating for the limitations of ConvLSTM in dealing with long-range dependencies. First, to enhance the extraction of fine-grained features and mitigate the over-compression of temporal information, We further enhance this with a custom cross-structured spatiotemporal attention module capable of extracting joint attention across both spatial and temporal dimensions. Second, spatiotemporal non-stationary feature extraction module is facilitate to capture the high-order spatiotemporal non-stationarity. Finally, a novel fusion-gate is designed to fuse the local non-smooth and long time global features.We perform comparative experiments with state-of-the-art models on three publicly available datasets, experimental results show that the proposed model achieves excellent results on SSP tasks.

The main contributions of this study are as follows:

  1. 1)

    We introduce a novel architecture that utilizes two-branch 3DCNN to extract comprehensive spatiotemporal information, enhancing the the ability of ConvLSTM in dealing with long-range dependencies. To prevent over-compression of temporal information and enhance the extraction of fine-grained features, we optimizes this with a custom cross-structured spatiotemporal attention module to extract joint attention across both spatial and temporal dimensions.

  2. 2)

    We design a spatiotemporal non-stationary feature extraction module specifically for learning the nonstationary features in the first-order differential input.

  3. 3)

    We design a novel fusion gating strategy to fuse long-term global and non-smooth local spatio-temporal features to improve model prediction performance.

We perform comparative experiments with state-of-the-art models on a variety of SSP tasks, including a synthetic datasets and two real datasets: traffic flow prediction and human pose estimation, experimental results show that the proposed 3DcT-Pred achieves excellent results.

Related work

3DcT-Pred is designed to process long-term global temporal and spatial information through ConvLSTM under the seq-to-seq framework, and capture local non-stationary features through the attention mechanism, so ad to achieve the fine prediction.

3DCNN

Traditional CNN exhibit strong representational learning capabilities due to the sharing of parameters within the convolutional kernel and the inherent sparsity of inter-layer connections. Zhang18 proposed DeepST, a CNN-based prediction model to predict traffic flow. DeepST divides the spatio-temporal data into three different sub-sequences according to temporal proximity, periodicity, and seasonality, and then performs deep convolution operation on the sub-sequences respectively, and then uses the full connectivity for the feature fusion to get the final prediction result. In a similar vein, ST-ResNet19 adopts a novel approach by employing multiple ResNet branches to model the spatiotemporal relationships, periodicities, and trends between two distinct regions. These branches are then fused using a parameter matrix-based technique. Notably, external factors such as inclement weather and holidays are integrated into the model to predict traffic flow. It is important to highlight that these methods predominantly rely on 2D CNNs, which are limited in their capacity to mechanically extract visual features from individual frames. As a result, systematic extraction of motion information is compromised, leading to a significant loss of temporal features. To address these limitations, Du Tran15 pioneered the application of 3DCNN for video understanding. This innovative approach consists of constructing an action recognition network that incorporates 3D convolution layers and 3D maximum pooling layers. Experiments demonstrate that 3DCNN can effectively and accurately extract spatiotemporal features from sequences. Compared to 2D CNN, 3DCNN introduce an additional depth dimension, enabling the representation of continuous frames in video or slices in stereo images. Zhu16 proposed a controllable low light enhancement framework for decoupling non paired learning, which separates lighting and content processing by unfolding the network structure. Liu20 constructed a large-scale rain removal dataset and developed a dual stream ConvLSTM architecture, which for the first time applied spatiotemporal feature fusion to video rain removal. Li21 innovatively introduced rain pattern embedding consistency constraints and hierarchical LSTM to achieve collaborative optimization of rain pattern separation and background restoration in single image rain removal. These works have promoted the development of video enhancement technology in feature decoupling, data construction, and network architecture by improving the spatiotemporal modeling of 3DCNN. Fig.1 provides a visual comparison between 2DCNN and 3DCNN in processing of multi-channel input data.

Fig. 1
figure 1

Comparison between 2DCNN and 3DCNN in multi-channel input.

Full size image

ConvLSTM

In recent years, LSTM has demonstrated excellent performance in various time series prediction tasks. The distinctive architecture of LSTM networks provides it with powerful temporal feature extraction capabilities. However, traditional LSTM implementations require fully-connected operations between input and state updates, which are unsuitable for extracting spatial correlations and high-order visual features from single-frame images. To solve this problem, Shi6 proposed ConvLSTM, which replaces the fully connected operation in LSTM with a convolutional operation. This innovation successfully addresses the limitation of LSTM in capturing spatial information. The integration of stacked ConvLSTM layers allows for the simultaneous modeling of both temporal and spatial features within spatiotemporal sequence. The inherent rigidity of ConvLSTM, characterized by its fixed connection structure and invariant weights, presents challenges in capturing dynamic motion information, such as rotation and scaling. To address this limitation, Shi22 proposed TrajGRU based on ConvLSTM, where conventional convolution operations were replaced with a position-based connection structure.Wang23 recognized that when multiple layers of ConvLSTM units are stacked, the spatial information from a single-frame image can only be encoded at the current step, while fine-grained information from previous spatiotemporal contexts is also important. In response, Wang and colleagues introduced a spatial memory unit (ST-LSTM) to facilitate temporal interactions, and designed a versatile prediction framework known as PredRNN. While Wang24 argued that the spatial memory unit in PredRNN is prone to the problem of gradient disappearance with the increase of prediction step size, and is prone to lose the long-term features of the network, so they cascaded the cell state and spatial memory unit in PredRNN and designed a gradient propagation unit, and the two were combined to effectively capture short-term features and long-term features.Lin25 concluded that existing methods can only capture local spatial dependencies, and the effective sensory field of the model is much smaller than the theoretical value, in order to capture long-term spatial dependencies, they designed a memory-based self-attention module, and experiments have shown that the model is more adept at capturing long-range spatiotemporal dependencies.

Attention mechanisms

In recent years, the application of attention mechanisms has yielded significant results in various deep learning tasks. Some researchers have extended previous work by creating diverse attention mechanism units. Lin25 pointed out that existing methods mainly capture local spatial dependence, with an effective receptive field considerably smaller than the theoretical value. To capture long-term spatial dependence, they introduced a memory-based self-attention module, which was shown to perform well in capturing extended spatiotemporal dependence. Furthermore, Chang26 introduces an innovative spatiotemporal attention gating unit, which applies attention scores to different spatiotemporal states based on the relative importance of these features, providing adaptability and enhancing the quality of spatiotemporal predictions.

Discussion

Unlike previous work, our model firstly captures the higher-order non-smooth features of spatio-temporal data through convolutional network to realize the extraction of local fine features in spatial data. Secondly, the channel attention module is designed to realize the global long-term dependence in temporal data through the process of mutual attention of hidden layers in ConvLSTM. Finally, the local fine features and global long-term dependence are fused by the gated fusion module to realize the fine prediction of spatio-temporal data.

Methods

Overall structure

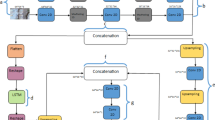
Fig.2 shows an overview of the proposed model with encoder-decoder architecture, which consists of three modules: the Two-branch 3DCNN Based on Attention Mechanism (Att-Conv3d, the Difference-based non-stationary feature extraction module (DF-LSTM) and the Fusion-gate. The overall structure can be divided into two parts. The Encoder is the lower part of theFig.2, which encodes the input moment by moment using a RNN. We use the ConvLSTM and DF_LSTM in the RNN cell, so as to extract the spatial features and enhance the local non-smooth response in the encoder, respectively. Where the downsampling module consists of 2D convolution, normalization and activation functions, so as to reduce the size of the image and extracting preliminary spatial features. The Decoder is the upper part of the Fig.2 designed for the prediction process, with the input of extracted features. DF_LSTM performs feature extraction on the current frame,Att-Conv3d performs global feature extraction on the whole input, and then the Fusion-gate module is utilized for feature fusion, and finally the prediction result is obtained after the upsampling module.

Fig. 2
figure 2

Overall structure.

Full size image

Two-branch 3DCNN based on attention mechanism

Given that 3DCNN has achieved good results in many video tasks, We use 3DCNN to extract the global spatiotemporal dependencies. The traditional 3DCNN is to convolve the length, width and time of the sequence, but the size of the time dimension is much smaller than the length and width. As the network deepens, the information of the time dimension is severely compressed, so the model is unable to learn the rules of motions. We tried to perform padding operation on the time dimension, but it brought a lot of disturbing information to the model, and the result was not satisfactory. Therefore, it is particularly important to realize the long-term dependency extraction of spatio-temporal data so as to alleviate the forgetting problem in long-range data mining. Therefore, it is particularly important to realize the long-term dependency extraction of spatio-temporal data so as to alleviate the forgetting problem in long-range data mining. To solve this problem, we designed a two-branch network module as shown in Fig.3. The left and right branches use the same structure, but the left branch convolves time dimension while the right branch convolves channel dimension. As the number of layers increases, the left and right branches extract multi-scale features in the time dimension and channel dimension respectively. The procedure can be expressed as as eq.(1-5):

$$\begin{aligned} LL= & Conv3d(x_{t})\end{aligned}$$
(1)
$$\begin{aligned} LR= & Conv3d(x_{t}^T)\end{aligned}$$
(2)
$$\begin{aligned} UL= & Conv3d(MLG(LL))\end{aligned}$$
(3)
$$\begin{aligned} UR= & Conv3d(MLG(LR))\end{aligned}$$
(4)
$$\begin{aligned} GF= & ST\_att(LL,LR,UL,UR) \end{aligned}$$
(5)

Where \(x_{t}\) represents the input;\(x_{t}^T\) represents transpose of \(x_{t}\). LL,LR,UL,UR represents Lower Left,Lower Right, Upper Left and Upper Right features respectively; Conv3d represents 3DCNN, MLG represents 3D-MaxPool,Leaky Relu and Group Normal operations.\(ST\_att\) represents Spatial-Temporal Attention Module which will be described in more detail in following parts.

Fig. 3
figure 3

Two-branch 3DCNN Module Based on Spatial-Temporal Attention.

Full size image
Fig. 4
figure 4

Structure of the Spatial-Temporal Attention Module.

Full size image

In order to better extract key features, we design a Spatial-Temporal Attention Module (ST-Attention), as shown in Fig.4, and the calculation is shown as eq.(6-8):

$$\begin{aligned} Att_L= & Softmax(\frac{Q_{LR}K_{LR}^\top }{\sqrt{d_{k_{LR}}}})V_{LL}+Softmax(\frac{Q_{LL}K_{LL}^\top }{\sqrt{d_{k_{LL}}}})V_{LR}\end{aligned}$$
(6)
$$\begin{aligned} Att_R= & Softmax(\frac{Q_{UR}K_{UR}^\top }{\sqrt{d_{k_{UR}}}})V_{UL}+Softmax(\frac{Q_{UL}K_{UL}^\top }{\sqrt{d_{k_{UL}}}})V_{UR}\end{aligned}$$
(7)
$$\begin{aligned} Out= & LeakyReLu(Att_L+Att_R) \end{aligned}$$
(8)

Where the Lower Right and Lower Left come from the shallow spatiotemporal features of the two-branch 3DCNN respectively, and the Upper Right and Upper Left are the deep semantic information. The correlation between both temporal and spatial is attended to by designing cross-structures (red part in the figure) based on self-attention. Finally, the high-level information and low-level information are summed up as the overall output of the two-branch 3DCNN as global features.

Difference-based non-stationary feature extraction module

Temporal series are often non-stationary, and the data are often chaotic and irregular. We can convert them into stationary series by difference and logarithm. The stationary series itself has a certain distribution pattern with some autocorrelation and continuity.

However, SSD is not only non-stationary in time, but also non-stationary in space. Most spatiotemporal task models cannot fully learn spatiotemporal non-stationarity. In order to capture high-order spatiotemporal non-stationarity, we perform first-order difference on the input data, and then use the upsampling module to learn shallow spatial features. We design DF-LSTM based on ConvLSTM, the structural details are shown in Fig.5, and the update formula are shown as eq.(9-15):

$$\begin{aligned} f_{t}^{l}= & \sigma \left( W_{f} *\left[ h_{t}^{l-1}, h_{t-1}^{l-1}\right] +b_{f}\right) \end{aligned}$$
(9)
$$\begin{aligned} i_{t}^{l}= & \sigma \Big (W_{hi}*[h_{t}^{l-1},h_{t-1}^{l-1}]+b_{i}\Big ) \end{aligned}$$
(10)
$$\begin{aligned} d_{t}^{l}= & \sigma [W_{hd}*(h_{t}^{l-1}-h_{t-1}^{l-1})+b_{d}] \end{aligned}$$
(11)
$$\begin{aligned} \tilde{c}_{t}^{l}= & \textrm{tanh}(W_{hc}*[h_{t}^{l-1},h_{t-1}^{l-1}]+b_{c}) \end{aligned}$$
(12)
$$\begin{aligned} c_{t}^{l}= & f_{t}^{l}\otimes c_{t-1}^{l}+i_{t}^{l}\otimes \tilde{c}_{t}^{l}+\left( 1-f_{t}^{l}\right) \otimes d_{t}^{l} \end{aligned}$$
(13)
$$\begin{aligned} o_{t}^{l}= & \sigma (W_{ho}*[h_{t}^{l-1},h_{t-1}^{l-1}]+b_{o}) \end{aligned}$$
(14)
$$\begin{aligned} h_{t}^{l}= & o_{t}^{l}\otimes \textrm{tanh}(c_{t}^{l}) \end{aligned}$$
(15)

Where \(d_{t}\) is a difference unit whose input information is the first order difference between \(h_{t}^{l-1}\) and \(h_{t-1}^{l-1}\),\(h_{t}^{l-1}\) is the output of the previous layer at the current moment, and \(h_{t-1}^{l-1}\) is the output of the previous layer at the previous moment. The forgetting gates, input gates and output gates are the same as the LSTM and will not be repeated here. W is the weight parameter, b is the bias term, * is the convolution operation, and \(\otimes\) is the Hadamard product. The \((1-f_t^l)\) part can play a complementary role in case of negative saturation of the forgetting gate.

Fig. 5
figure 5

(a) Difference-based non-stationary feature extraction module; (b) Fusion-gate Structure.

Full size image

Fusion-gate

Global spatiotemporal features and local spatiotemporal features belong to two perspectives of information. Global spatiotemporal features come from two-branch 3DCNN, whose inputs are the current and all past moments, and this feature implies the overall movement trend of the sequence, which is very important for long-term prediction. It is capable of capturing the future course of spatio-temporal data, thus improving model validity.The local spatiotemporal feature comes from the cyclic cell, whose input is the hidden state of the current and previous moments, and this feature implies more short-range dependencies, which is important for the prediction of sudden changes. However, there are also redundant features between them, and their input sources have cross parts. Therefore, we design the gating unit for feature fusion, as shown in right of Fig.5, and the procedure can be expressed as eq.(16):

$$\begin{aligned} O= & \sigma (W_{A}*A\_3D+B_{A})+ \textrm{tanh}(W_{h}*h+B_{h})\otimes \sigma (W_{A}*A\_3D+B_{A})\\\nonumber+ & (1-\sigma (W_{A}*A\_3D+B_{A})\otimes \textrm{tanh}(W_{h}*h+B_{h}) \end{aligned}$$
(16)

Where \(A\_3D\) is the global spatiotemporal features, h is the local spatiotemporal features, O is the fused output, W is the weight parameter, b is the bias term, and \(\sigma\) and tanh are the activation functions. After this module, not only the two features can be fused, but also the redundant features can be removed.

Experiments and results

Setup

The overall framework adopts the Seq to Seq structure, the encoder and decoder are three-layer CNN and Transpose CNN, respectively, and GroupNorm and LeakyReLU are used uniformly after each convolution.We uniformly use Adam as the optimizer, and the loss function is L2 loss, batch size is 16. The initial learning rate is 0.001, and to avoid overfitting, an early stopping mechanism is used until the learning rate drops to 0.00001. We conduct experiments on one synthetic dataset and three real datasets to measure the effect of our model: the Moving MNIST Dataset27, the TaxiBJ Dataset26, KTH Action Dataset28 and Radar echo dataset. The setup of the fisrt three dataset in the experiments is consistent with the published paper, while the last one is from the National Meteorological Information Center (https://data.cma.cn/). The data source is obtained from the quality control of S-band meteorological radar in East China and after the network mosaic. Detailed information on these datasets is provided in Table1 below:

Table 1 The summary of the datasets used in our work.
Full size table

Consistent with previous work, the experiments used Mean Square Error(MSE),Peak Signal to Noise Ratio(PSNR) and Structural Similarity Index Measure(SSIM)23 as metrics to assess the predictive performance of the model. These measures are defined as eq.(17-19):

$$\begin{aligned} \operatorname {MSE}(y, \tilde{y})= & \frac{\sum _{i=1}^{n}(y-\tilde{y})^{2}}{n}\end{aligned}$$
(17)
$$\begin{aligned} \operatorname {SSIM}(y,\tilde{y})= & \frac{(2\mu _y\mu _{\tilde{y}}+C_1)(2\sigma _{y\tilde{y}}+C_2)}{(\mu _y^2+\mu _{\tilde{y}}^2+C_1)(\sigma _y^2+\sigma _{\tilde{y}}^2+C_2)}\end{aligned}$$
(18)
$$\begin{aligned} \operatorname {PSNR}= & 10 \log _{10}\left( \frac{m^{2}}{\textrm{MSE}}\right) \end{aligned}$$
(19)

Where y is the true frame, \(\tilde{y}\) is the predicted frame, and n is the total number of test samples.\(\mu _{y}\) and \(\mu _{\tilde{y}}\), \(\sigma _{y}\) and \(\sigma _{\tilde{y}}\) are the mean and standard deviation of y and \(\tilde{y}\) respectively, \(\sigma _{y \tilde{y}}\) is the covariance of y and \(\tilde{y}\), \(C_{1}\) and \(C_{2}\) are the stabilization coefficients.max indicates the maximum value of the pixel. MSE refers to the expected value of the square of the difference between the pixel values of all predicted frames and real frames. PSNR is used to measure to difference between predicted and real images. SSIM is used to measure the similarity between two images, the value range is [0,1]. Compared with PSNR, SSIM can better reflect the subjective feeling of human eyes.

In addition to the above metrics, three evaluation metrics commonly used in the meteorological field will be used in the radar echo dataset:

  1. 1)

    Critical success index, CSI:

    $$\begin{aligned} \textrm{CSI}=\frac{T P}{T P+F N+F P} \end{aligned}$$
    (20)
  2. 2)

    Probability of detection, POD:

    $$\begin{aligned} \textrm{POD}=\frac{TP}{TP+FN} \end{aligned}$$
    (21)
  3. 3)

    False alarm rate, FAR:

    $$\begin{aligned} \textrm{FAR}=\frac{FP}{TP+FP} \end{aligned}$$
    (22)

Where TP represents the number of pixels where the true is 1 predicted to also be 1, FP represents the number of pixels where the true is 1 predicted to be 0, and FN represents the number of pixels where the true is 0 predicted to be 1. The results and labels need to be binarized in the calculation.

We use representative models in the field of spatiotemporal sequence prediction in recent years as comparisons, and the experimental results of the comparison models are from published papers:

  1. 1)

    ConvLSTM6 (Convolutional LSTM Networks): a model specialized in capturing spatiotemporal features that the first to incorporate convolutional operations into an LSTM.

  2. 2)

    VPN29 (Video Pixel Network): a probabilistic video model that evaluates the joint distribution of pixel values in videos.

  3. 3)

    ST-ResNet19 (spatiotemporal Residual Networks): a deep spatiotemporal residual network that introduces residual networks to spatiotemporal sequence prediction for the first time.

  4. 4)

    PredRNN23(Predictive RNN): a new spatiotemporal unit is designed to model both spatial and temporal variations, and a new recursive architecture is proposed that allows different memory states of the RNN to interact across layers.

  5. 5)

    E3D-LSTM13 (Eidetic 3D LSTM): 3D convolution is intergrated into LSTM to change the static perception of LSTM to dynamic perception.

  6. 6)

    STAM26(SpatioTemporal Attention based Memory): a spatiotemporal attention based prediction model that jointly utilizes high-level semantic space and low-level texture space to model a global spatial representation.

  7. 7)

    MAU27(Motion-Aware Unit): reliable inter-frame motion information is captured by widening the temporal acceptance domain of the prediction unit.

  8. 8)

    PredRNN-v21: a new curriculum learning strategy to force PredRNN to learn long-term dynamics from context frames, which can be generalized to most sequence-to-sequence model.

  9. 9)

    TC-LIF30(Two-Compartment Leaky Integrate-and-Fire spiking neuron model): a novel biologically inspired model incorporates designed somatic and dendritic compartments that are tailored to facilitate learning long-term temporal dependencies.

  10. 10)

    SimVP28: a novel method that leverages time series decomposition techniques by segregating the convolution operations into distinct temporal and spatial processes to enhance the extraction of spatiotemporal features.

  11. 11)

    STC-LIF31: a novel Spatio-Temporal Circuit (STC) model inspired from the concept of autaptic synapses in biology, integrates two learnable adaptive pathways, enhancing the spiking neurons’ temporal memory and spatial coordination.

  12. 12)

    STMFANet32: a video prediction network based on multi-level wavelet analysis to uniformly deal with spatial and temporal information.

  13. 13)

    SwinLSTM33: a new recurrent cell which integrates Swin Transformer blocks and the simplified LSTM, an extension that replaces the convolutional structure in ConvLSTM with the self-attention mechanism, mainly designed for spatiotemporal prediction.

  14. 14)

    VPTR34: A novel transformer-based video prediction model, available in three variants: fully autoregressive (VPTR-FAR), partially autoregressive (VPTR-PAR), and non-autoregressive (VPTR-NAR).

Results on moving MNIST

Fig. 6
figure 6

Prediction results of different models on Moving MNIST. The two numbers in the left sample do not overlap, and the two numbers in the right sample overlap.

Full size image

Table 2 shows the quantitative results of our model and other advanced models on mnist. The MSE and SSIM columns are averaged over all prediction steps, where− indicates that the result was not provided in the original paper. The overall prediction results outperform the comparison models, with MSE reduced by 4.6 and SSIM improved by 0.011.

In the experimental results, we observed a significant enhancement in performance, primarily attributed to the proposed dual-branch 3D convolutional network structure. Compared to traditional 3D convolutional methods, this network demonstrates exceptional capability in preserving temporal features through its unique dual-branch architecture. This architecture enables the network to more comprehensively capture the dynamic changes in video data, which is crucial for a deep understanding of complex spatiotemporal relationships. To further enhance the extraction of spatiotemporal features, we designed a cross-structured spatiotemporal attention module. This module effectively distills global spatiotemporal features by integrating deep and shallow feature information, providing a richer and more precise data foundation for subsequent analysis and processing.

Additionally, in response to the non-stationary characteristics of spatiotemporal data, we proposed an innovative spatiotemporal non-stationary feature extraction unit, namely Df-LSTM. This unit is specifically designed to capture the heterogeneity in spatiotemporal data, which is particularly important for handling complex datasets with temporal dependencies and spatial correlations. The Df-LSTM unit, through its unique gating mechanisms and memory cells, can adapt to dynamic changes in data, thus maintaining long-term dependencies while rapidly responding to short-term variations. From the results, the proposed Df-LSTM can achieve better results with long-step prediction (e.g. t=16,18,20).

Fig.6 shows the prediction results of our model and comparison models in consecutive frames.The first row is the input to the model, the second row is the label, and the rest of the rows are the prediction results of our model and comparison models. From the figure, it can be clearly seen that the last few frames of the comparison models are blurred, while our model shows clearer prediction results. A recurrent unit for extracting non-smooth features is constructed to capture the non-smooth trend of the hidden state by differential operation, which alleviates the problem of blurring distortion of images predicted by traditional models.Spatiotemporal Attention Module, which effectively correlates spatiotemporal characteristics of the lower and upper levels by means of crossover, thus improving the performance of the relevant metrics. It shows that the proposed model has better prediction results on frames with longer steps and frames with numbers overlapping.

Table 2 Quantitative results of different models on Moving MNIST.
Full size table

Results on TaxiBJ

Table 3 shows the quantitative results of proposed model and and other advanced models. The MSE of each time step is averaged over two channels, and the overall prediction results outperform the comparison models, with each frame reduced by 0.082, 0.064, 0.005 and 0.062 respectively. Fig. 7 shows the qualitative comparison of the prediction results between proposed model and other models (three typical models are chosen to be shown), where the first row is the input, the second row is the label, the left 4 frames are the channel 1, and the right 4 frames are the channel 2.In order to better show the difference between the prediction and the real label, the \(\triangle\) indicate the absolute value of the pixel difference between the prediction and the label, and the smoother it is, the closer the prediction is to the label. From the figure, it can be seen that our model achieves optimal results in every frame, especially in the 4th frame, indicating that the proposed model has strong long-range dependence capture capability.

Fig. 7
figure 7

Prediction results of different models on TaxiBJ, where \(\triangle\) is the difference between prediction and real labels.

Full size image
Table 3 Quantitative results of different models on TaxiBJ.
Full size table

Results on KTH action

Table 4 shows the quantitative results of proposed model and and other advanced models, where − represents this result is not contained in the published paper. Sub-optimal results are achieved with input 10 frames to predict 20 frames, and optimal results are achieved with input 10 frames to predict 40 frames, with SSIM and PSNR improved by 0.006 and 0.04, respectively, which indicates that proposed model has an advantage in the long distance prediction. Fig.8 shows the qualitative comparison of the prediction results between proposed model and other models, the input is 10 frames (only 3 frames are shown) and the prediction is 20 frames (only 9 frames are shown). From the figure, it can be seen that most of the previous work can only predict the fuzzy shadows,while the prediction results of proposed model can clearly distinguish character behavior, which is especially important for the task of video understanding.

Table 4 Quantitative results of different models on KTH action.
Full size table
Fig. 8
figure 8

Prediction results of different models on KTH action.

Full size image

Results on radar echo dataset

Fig.9 demonstrates the qualitative comparison of the prediction results between proposed model and other models on the radar echo dataset, where the first row is the input with a time step of 5, the second row is the label with a time step of 10. The data of the radar echoes take the range of 0-70 (in dBZ), corresponding to the gradual change of the color from blue to violet (blue, green, yellow, orange, red, and violet), which represents that the intensity of echoes from small to large, the rainfall intensity gradually increases. From the figure, it can be seen that our model perfoerms more accurately in predicting the location of strong echoes, which is important for the extreme weather forecasting, and further shows the effectiveness of the spatio-temporal attention mechanism, which makes the model pay more attention to the location of strong echoes. Table5 shows the quantitative comparison results between the proposed model and the comparison models. In the calculation of CSI, POD and FAR, the image is binarized, and three thresholds of 15dbz, 25dbz and 35dbz are set for the calculation, respectively.In the two indexes of CSI and POD, our mosel achieves the highest scores, and preserves the strong echoes to a certain extent compared to the other models, and FAR did not achieve the optimal value, but the difference with the optimal model is very small and within the acceptable range.

Fig. 9
figure 9

Prediction results of different models on Radar echo dataset.

Full size image
Table 5 Quantitative results of different models on Radar echo dataset.
Full size table

Hyper-parametric experimental results and analysis

The hyperparameters in the model have an impact on the performance of the model. In order to better validate the setting of hyperparameters, the Moving mnist dataset was used as an experimental object to analyze the hyperparameters of the model, and the hyperparameters and setting values involved are shown in the following Table6, and the results are shown in the Table7.

Table 6 The hyperparameters and setting values.
Full size table
Table 7 The effect of hyperparameter settings on the experimental results, where the four numbers represent the number of DF-LSTM stacked layers, the number of two-branch 3D convolutional layers, the convolutional kernel size, and the neuron discarding rate, where optimal values are in bold and sub-optimal values are underlined.
Full size table

Table7 shows that the size of the convolution kernel does not have a great impact on the accuracy, and the number of stacked layers has a significant improvement after changing from 2 to 4, but the improvement is limited after changing from 4 to 6. Considering both the accuracy and the number of parameters (the more the number of layers, the larger the number of parameters), the optimal hyperparameter combination is (4, 4, 3, 3).

Ablation experiments and analysis on MNIST

Table 8 Ablation experiment results on Moving MNIST.
Full size table

In order to verify the effectiveness of each module of proposed model, ablation experiments and related analyses is conducted in this section using the Moving MNIST dataset as an example. Ablation experiments are performed on the following three modules respectively: 1) two-branch structure (eq.1-5), 2) attention module (eq.6-8), and 3) non-stationary feature extraction module (eq.9-15). The results are shown in Table 8, where + and - means with or without this module.

Experiment No.1 (Backbone) is without all proposed modules, using ConvLSTM and ordinary deep 3DCNN, the MSE and SSIM are 55.1 and 0.871 respectively. Experiment No.2 only changes the deep 3DCNN to two-branch 3DCNN, MSE decreases by 16.9 and SSIM improves by 0.026, which shows that the two-branch 3DCNN can avoid over-compressing the temporal features. Experiment No.3 adds the spatiotemporal attention module, MSE decreases by 9.9 and SSIM improves by 0.018, indicating that the spatiotemporal attention module is effective and enhances the ability to capture key information. Experiment No.4 adds non-stationary feature extraction module on the basis of Backbone, the effect has some improvement but not as obvious as Experiment No.2. Experiment No.5 is the proposed model with all modules, which achieves optimal results, indicating that each module has an optimization effect on the model capability.

This study introduces a two-branch architecture integrated with an attention mechanism, which enhances the model’s feature extraction capability and improves task performance, albeit at the cost of increased implementation complexity. The two -branch architecture enables complementary feature fusion through parallel hierarchical processing, while it inevitably leads to a a certain increase in the number of model parameters, resulting in higher memory consumption and computational resource demands. Meanwhile, the attention mechanism dynamically focuses on critical information by calculating correlation weights between data elements. In long sequence and high-dimensional data scenarios, the computational complexity increases.

Despite the elevated computational costs, experimental results demonstrate significant improvements in key performance metrics, justifying the increased model complexity through measurable performance gains. To mitigate computational pressure, Depthwise Separable Convolutions can be employed in place of CNN layers within the dual-branch framework. Future research will explore more efficient architectural designs, such as dynamic branch selection mechanisms and adaptive attention allocation strategies, to better balance model complexity with computational efficiency.

Conclusion

In this paper, we propose a 3D Long Time Spatial-Tempral Convolutional for Complex Transfer Sequence Prediction (3DcT-Pred) that incorporates two-branch 3DCNN, spatiotemporal attention, spatiotemporal non-stationary feature extraction and fusion-gate. Specifically, the proposed model addresses the long-range forgetting problem by extracting long-term global features from spatio-temporal sequence data. Additionally, a cross-structured spatio-temporal attention module is introduced during the decoding stage. This module enhances the response of fine features in the image’s convolutional channels, enabling the capture of non-smooth local features. Lastly, a fusion gating module is designed to integrate both global and local features, which improves the overall performance of the model.Experimental results show that the proposed model achieves good results on SSP tasks.