Design of a novel and robust 2-DOF PIDA controller based on enzyme action optimizer for ball position regulation in magnetic levitation systems

Abstract

Magnetic levitation (maglev) systems are characterized by strong nonlinearities and inherent open-loop instability, making precise position regulation of levitating bodies exceptionally challenging. These systems are highly sensitive to model uncertainties, parameter variations, and external disturbances. This demands advanced control strategies beyond conventional PID techniques. To address these challenges, this study introduces a novel two-degree-of-freedom proportional-integral-derivative-acceleration (2-DOF PIDA) controller, specifically designed to stabilize and regulate ball position in magnetic levitation systems. The controller’s structure is augmented with acceleration feedback and reference input weighting, enabling decoupled tuning for transient and steady-state performance and ensuring enhanced damping, disturbance rejection, and tracking accuracy. A core innovation of this work is integration of the controller with the enzyme action optimizer (EAO)—a recently developed bio-inspired metaheuristic algorithm that emulates adaptive catalytic behavior observed in enzymatic reactions. The EAO algorithm balances global exploration and local exploitation to efficiently optimize the 2-DOF PIDA controller parameters, minimizing the integral of absolute error (IAE) as the objective function. This optimization framework is evaluated against two recent metaheuristics: the horned lizard optimization algorithm (HLOA) and the sea-horse optimizer (SHO), using extensive time-domain simulations. Quantitative results confirm the superior performance of the proposed method, achieving 0% overshoot, a rise time of 0.0121 s, and a settling time of 0.0365 s the optimal response speed and stability among all tested algorithms. Additionally, robustness is rigorously validated under multiple scenarios of parameter perturbations, including variations in resistance and inductance, simulating real-world effects such as component aging and thermal drift. The EAO-tuned controller consistently maintains superior regulation and stability across all test cases, exhibiting high resilience to system uncertainties. Furthermore, a comprehensive comparative analysis involving 12 state-of-the-art control strategies, including PID, FOPID, and RPIDD² variants optimized via diverse evolutionary algorithms, confirms the proposed controller’s dominance across all critical performance indices, including IAE, rise time, settling time, and overshoot. These findings underscore the effectiveness of combining 2-DOF control architectures with bio-inspired optimization algorithms for real-time implementation in nonlinear, unstable systems. Overall, the proposed EAO-optimized 2-DOF PIDA controller offers a computationally efficient, auto-tunable, and robust solution for high-precision maglev control.

Introduction

Magnetic levitation systems are characterized by their inherent instability and nonlinear dynamics, presenting significant challenges in achieving precise and robust control of ball position^1,2. Parameter uncertainties due to environmental factors or system aging further complicate effective stabilization and tracking performance^3,4. This paper proposes a novel two-degree-of-freedom proportional-integral-derivative-acceleration (2-DOF PIDA) controller optimized using the enzyme action optimizer (EAO), a bio-inspired metaheuristic algorithm. This approach aims to enhance both transient response and robustness by leveraging the flexible 2-DOF structure and EAO’s efficient parameter tuning.

Conventional control strategies for magnetic levitation systems primarily rely on classical controllers such as proportional-integral-derivative (PID), fractional-order PID (FOPID), and real PID with derivative² (RPIDD²). Özaydİn, et al.⁵, Ekinci, et al.⁶, Dey, et al.⁷, and Maheedhar and Deepa⁸ developed PID controllers for magnetic levitation, while Izci, et al.⁹, Demirören, et al.¹⁰, and Dey, et al.⁷, explored FOPID controllers, and Ekinci, et al.¹¹ proposed RPIDD² controllers. For instance, Roman, et al.¹² proposed a hybrid data-driven active disturbance rejection sliding mode control validated on tower crane systems, demonstrating robustness to external disturbances but requiring complex implementation. Similarly, Wen and Wang¹³ introduced an improved cascade control for single-point levitation systems in maglev trains, achieving stable levitation but with limited adaptability to parameter variations. Additionally, Chi, et al.¹⁴ developed an enhanced P-type control with indirect adaptive learning from set-point updates, offering improved tracking but with increased computational complexity. These controllers are often tuned to balance stability and performance but may struggle with the nonlinear and unstable nature of maglev systems. While PID controllers are simple and widely used^15,16,17, they often lack the flexibility to handle parameter variations effectively^18,19, as noted by Özaydİn, et al.⁵ and Ekinci, et al.⁶. Advanced variants like FOPID and RPIDD² introduce additional degrees of freedom but require sophisticated tuning to achieve optimal performance, particularly under disturbances or uncertainties, as highlighted by Izci, et al.⁹, Demirören, et al.¹⁰, Ekinci, et al.¹¹, and Dey, et al.²⁰.

Recent research has increasingly focused on the integration of advanced metaheuristic optimization algorithms with enhanced control structures to improve stability and dynamic response in nonlinear and uncertain systems. Izci et al.²¹ proposed a refined sinh cosh optimizer for tuning automatic voltage regulation controllers, demonstrating that carefully designed optimizers can significantly improve system robustness. Building on this, Izci et al.²² introduced a fractional-order PID plus double-derivative controller optimized by the mountain gazelle algorithm, highlighting the benefits of combining fractional-order dynamics and higher-order derivative terms to achieve faster convergence and better disturbance rejection. Alrashed et al.²³ developed a control strategy for dynamic voltage restorers that integrated an adaptive notch filter with a PD controller tuned via an improved grey wolf optimizer, emphasizing the importance of disturbance suppression and parameter adaptation. Abualigah et al.²⁴ applied the sinh cosh optimizer to design filtered PID controllers for aircraft pitch control, showing that bio-inspired algorithms can deliver precise tracking in inherently unstable systems. Similarly, Abualigah et al.²⁵ employed an artificial rabbits optimizer to optimize PID-F controllers in pitch regulation applications, further illustrating the capability of metaheuristics to tune complex control schemes. Ekinci et al.²⁶ explored parameter optimization in DC motors and liquid level systems using advanced metaheuristics, demonstrating improvements in transient response and robustness across different process dynamics. Izci et al.²⁷ presented a control scheme for automatic voltage regulators leveraging a modified artificial rabbits optimizer, reinforcing the role of bio-inspired algorithms in achieving high-performance regulation. Abualigah et al.²⁸ proposed a modified elite opposition-based artificial hummingbird algorithm for designing fractional-order PID controllers in cruise control systems, highlighting opposition-based learning as an effective strategy to enhance convergence and avoid local minima. Ekinci et al.²⁹ and Ekinci et al.³⁰ applied the sinh cosh optimizer to optimize controllers in hybrid photovoltaic-thermal power systems and steam condensers, respectively, underlining the relevance of robust tuning techniques in systems with strong nonlinearities and parameter uncertainties. Dei et al.³¹ designed a TID + IDN controller tuned by the coatis optimization algorithm for deregulated hybrid power systems, showcasing how hybrid controller structures can be leveraged to improve dynamic regulation. Ekinci et al.³² developed a quadratic interpolation optimization-based 2-DOF PID controller for continuous stirred-tank heater processes, emphasizing the advantage of two-degree-of-freedom architectures in decoupling transient and steady-state performance. Jabari et al.³³ introduced a TDn (1 + PIDn) controller optimized with the dynamic competitive swarm algorithm to regulate pressure in nonlinear condensers, demonstrating that combining extended derivative terms and novel optimizers can yield significant performance gains. Finally, Davoudkhani et al.³⁴ presented a load-frequency control approach for islanded microgrids using a 1PD-3DOF-PID controller incorporating mobile energy storage, highlighting the potential of multi-degree-of-freedom controllers to enhance resilience against large parameter variations and external disturbances.

Optimization algorithms play a critical role in tuning controllers for magnetic levitation systems³⁵. Common metaheuristic approaches include the enzyme action optimizer (EAO) by Rodan, et al.³⁶, horned lizard optimization algorithm (HLOA) by Peraza-Vázquez, et al.³⁷, and sea-horse optimizer (SHO) by Zhao, et al.³⁸. These algorithms explore the parameter space to minimize performance metrics such as the integral of absolute error (IAE). However, their effectiveness varies depending on the problem’s complexity, with some algorithms suffering from premature convergence or high computational costs. The choice of optimization method significantly impacts the controller’s ability to achieve robust and precise control in real-time applications.

Recent studies on magnetic levitation control have explored diverse approaches to address instability and nonlinearity. Classical PID controllers, optimized using algorithms like the sine cosine algorithm by Özaydİn, et al.⁵, hybrid whale optimization with simulated annealing by Ekinci, et al.⁶, and COOT algorithm by Maheedhar and Deepa⁸ and Deepa and Jayalakshmi³⁹, achieve reasonable stability but often exhibit overshoot and prolonged settling times. Advanced controllers, such as FOPID tuned with grey wolf optimization by Dey, et al.⁷, artificial electric field by Demirören, et al.¹⁰, or hunger games search by Izci, et al.⁹, leverage fractional-order dynamics for improved tracking, though their performance depends heavily on tuning accuracy. RPIDD² controllers optimized with manta ray foraging optimization by Ekinci, et al.¹¹ enhance robustness but may suffer from suboptimal transient responses. Recent studies have also explored novel controller structures, such as 2-DOF PID for continuous stirred tank reactors¹⁸ and FOPID-based controllers optimized with algorithms like pelican optimization for motor control⁴⁰ highlight the trend toward sophisticated tuning, though not specific to maglev systems.

Alternative approaches, such as PD controllers with metaheuristic optimization by Kouvakas, et al.⁴¹ and PID-P controllers by Bizuneh, et al.⁴², offer simpler or variant control structures but often lack the robustness required for precise maglev control. Active disturbance rejection control (ADRC) has also been explored by Blossom and Rao⁴³, though its complexity limits its direct comparability to PID-based methods. Comprehensive reviews by Tewari, et al.⁴⁴ and Abdalhadi and Wahid⁴⁵, highlight the evolution of these strategies, noting persistent challenges like sensitivity to parameter variations and computational complexity in real-time applications. These limitations underscore the need for a control approach that combines robust performance with efficient optimization, motivating the development of the proposed 2-DOF PIDA controller tuned with EAO.

Despite substantial progress in controller design for magnetic levitation systems, existing strategies exhibit notable limitations when subjected to real-world nonlinearities and parameter uncertainties. Classical PID controllers, though widely adopted, offer limited flexibility and tend to underperform in highly unstable conditions, often resulting in overshoot and sluggish responses. Advanced variants like FOPID and RPIDD² provide greater tuning flexibility but require intricate optimization processes and remain sensitive to noise and parameter drift. Moreover, while numerous metaheuristic algorithms—such as SCA, WOA, SHO, and HLOA—have been employed for controller tuning, they often face challenges like premature convergence, high computational overhead, and suboptimal performance consistency. This fragmentation in performance, robustness, and tuning efficiency across existing approaches underscores the need for a control framework that unifies rapid transient response, robustness to uncertainties, and computationally efficient auto-tuning. The absence of a structured integration between advanced control architectures and biologically inspired optimizers further defines the critical gap this work aims to address.

The primary novelty of this work lies in the integration of a two-degree-of-freedom proportional-integral-derivative-acceleration (2-DOF PIDA) controller with the enzyme action optimizer (EAO) a recent bio-inspired metaheuristic algorithm designed to simulate adaptive enzymatic behavior by dynamically balancing exploration and exploitation during optimization. This integration enables the efficient and automated tuning of controller parameters, addressing key limitations observed in conventional PID-based approaches when applied to inherently unstable systems like magnetic levitation. Unlike traditional PID controllers, the proposed method incorporates an acceleration feedback loop and applies reference input weighting, thereby improving damping characteristics and allowing more precise control over the transient and steady-state behavior of the system. These structural enhancements make the controller more responsive to dynamic changes while offering improved tracking accuracy and disturbance rejection. To rigorously validate its performance, the proposed EAO-tuned 2-DOF PIDA controller is compared against 12 state-of-the-art methods, including those developed by Özaydİn, et al.⁵, Ekinci, et al.⁶, and Izci, et al.⁹. Through extensive simulation studies, the proposed controller demonstrates superior dynamic performance, achieving 0% overshoot, a rise time of 0.0121 s, and a settling time of 0.0365 s—clearly outperforming all referenced approaches in terms of response speed and stability. Moreover, robustness analysis under varying system parameters further substantiates the controller’s reliability. Parameter perturbations such as fluctuations in resistance and inductance common in practical maglev environments due to component aging, thermal variation, or manufacturing tolerances were introduced to evaluate controller adaptability. The EAO-optimized controller consistently maintained stable operation and high precision in all cases, demonstrating its effectiveness as a highly robust and application-ready solution for magnetic levitation systems when compared to prior optimization and control strategies. The proposed 2-DOF PIDA controller, optimized by the EAO, surpasses existing methods in maglev control. Unlike PID, FOPID, and RPIDD² controllers, its acceleration feedback and reference input weighting ensure superior damping and tracking accuracy. EAO’s bio-inspired mechanism outperforms metaheuristics like SCA, WOA, and MRFO by balancing exploration and exploitation, achieving zero overshoot, a 0.0121s rise time, and a 0.0365s settling time. Robustness under parameter variations further distinguishes it from methods with notable overshoot or slow response.

This paper is structured as follows. Section 2 introduces the EAO, detailing its bio-inspired mechanism and computational framework. Section 3 presents the mathematical modeling of the magnetic levitation system, including the open-loop dynamics and system parameters. Section 4 describes the structure and implementation of the proposed 2-DOF PIDA controller, along with the objective function used for optimization. Section 5 provides simulation results, comparing the performance of the proposed controller against other metaheuristic-based controllers through statistical analysis, time-domain metrics, robustness testing, and benchmarking with 12 state-of-the-art methods. Finally, Sect. 6 concludes the paper by summarizing the findings, outlining the limitations, and suggesting directions for future work.

Overview of optimization method

Enzyme action optimizer (EOA)

EAO is a novel bio-inspired optimization algorithm that simulates the adaptive catalytic behavior of enzymes in biological systems. Enzymes accelerate chemical reactions by selectively binding to substrates and lowering activation energy under dynamic environmental conditions. This biochemical analogy guides EAO’s mechanism of balancing exploration and exploitation in complex optimization landscapes.

Initialization

Let $\:N$ be the number of substrates (agents), $\:T$ the maximum iterations, $\:dim$ the problem dimension, and $\:f\left(X\right)$ the objective function. Each substrate $\:{X}_{i}^{\left(0\right)}$​ is initialized randomly within the bounds $\:[LB,UB]$:

$$\:{X}_{i}^{\left(0\right)}=LB+(UB-LB)\circ\:{r}_{i}$$

(1)

where $\:{r}_{i}\sim{U\left[\text{0,1}\right]}^{dim}$ and $\:\circ\:$ denotes element-wise multiplication.

Fitness evaluation and best initialization

Each candidate’s quality is evaluated:

$$\:{F}_{0}^{\left(0\right)}=f\left({X}_{i}^{\left(0\right)}\right)$$

(2)

The best candidate is saved as the initial enzyme:

$$\:{X}_{best}^{\left(0\right)}=arg\underset{i}{\underset{⏟}{min}}{F}_{i}^{\left(0\right)},\:{F}_{best}^{\left(0\right)}=f\left({X}_{best}^{\left(0\right)}\right)$$

(3)

Adaptive factor

The adaptive factor dynamically shifts the algorithm from exploration to exploitation:

$$\:{AF}_{t}=\sqrt{\frac{t}{T}}$$

(4)

This gradually shifts the balance from broad search (exploration) to fine-tuned search (exploitation).

Substrate update mechanism

Each substrate generates two candidates in every iteration:

Candidate 1

Sine-based exploitation (local refinement).

$$\:{X}_{i,1}^{\left(t\right)}=\left({X}_{best}^{(t-1)}-{X}_{i}^{(t-1)}\right)+{q}_{i}\circ\:\text{sin}\left({AF}_{t}\times\:{X}_{i}^{(t-1)}\right)$$

(5)

Where, $\:{q}_{i}\sim{\left[\text{0,1}\right]}^{dim}$.

Candidate 2

Difference-based exploration (global search).

$$\:d={X}_{P}^{(t-1)}-{X}_{q}^{(t-1)}$$

(6)

$$\:{X}_{i,2}^{\left(t\right)}={X}_{i}^{(t-1)}+{sc}_{1}\times\:d+{AF}_{t}\times\:{sc}_{2}\times\:({X}_{best}^{\left(t-1\right)}-{X}_{i}^{(t-1)})$$

(7)

Where, $\:{sc}_{1},\:{sc}_{2}\sim U\left[EC,1\right]$. This dual update enhances convergence and prevents stagnation.

Selection of best candidate

Choose the better of the two candidates based on fitness:

$$\:{X}_{i,upd}^{\left(t\right)}=\left\{\begin{array}{c}{X}_{i,1}^{\left(t\right)}\:\:\:\:\:\:\:if\:f\left({X}_{i,1}^{\left(t\right)}\right)<\:f\left({X}_{i,2}^{\left(t\right)}\right)\\\:{X}_{i,2}^{\left(t\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

(8)

Position update

Update the substrate if it improves the previous value:

$$\:{X}_{i}^{\left(t\right)}=\left\{\begin{array}{c}{X}_{i,upd}^{\left(t\right)}\:\:\:\:\:if\:f\left({X}_{i,upd}^{\left(t\right)}\right)<\:f\left({X}_{i}^{(t-1)}\right)\\\:{X}_{i}^{(t-1)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

(9)

Best substrate update

Update the global best solution:

$$\:if\:f\left({X}_{i}^{\left(t\right)}\right)<{F}_{best}^{\left(t-1\right)}\Rrightarrow\:{X}_{best}^{\left(t\right)}={X}_{i}^{\left(t\right)},\:{\:\:\:\:\:F}_{best}^{\left(t\right)}=f\left({X}_{i}^{\left(t\right)}\right)$$

(10)

Boundary control

Ensure all solutions remain inside the search space:

$$\:{X}_{i}^{\left(d\right)}=\text{min}\left({max}\left({X}_{i}^{\left(d\right)},{LB}_{i}\right),{UB}_{i}\right)\:\:\:\:\:\:\:\:\:\:\:\:\vee\:d\in\:\left\{1,\dots\:..,dim\right\}\:$$

(11)

Computational complexity

The total computational cost is:

$$\:O(MnF+Mnd)$$

(12)

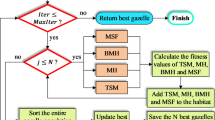
Where, $\:M,n,d\:and\:F$ are the number of iterations, the number of agents, dimensionality and cost of fitness evaluation respectively. EAO is efficient, scalable, and performs well across diverse optimization problems. Figure 1 shows the flowchart for EOA optimization method.

Fig. 1

Flowchart of EOA³⁶.

Description of the magnetic levitation system

The magnetic levitation (maglev) system under study is designed to levitate a steel ball using an electromagnet controlled by a current. The dynamics of the system are nonlinear in nature; however, for controller design and stability analysis, a linearized model around the nominal operating point is considered.

Open-loop transfer function of the system

The linearized open-loop transfer function of the system is derived based on Newton’s second law and the electrical dynamics of the electromagnet. The resulting transfer function from the control voltage input $\:V\left(s\right)$ to the position output $\:Y\left(s\right)$ is given by:

$$\:G\left(s\right)=\frac{m}{(s-{p}_{1})(s-{p}_{2})(s-{p}_{3})}$$

(13)

Definition of system parameters

The physical parameters used in the model are listed below in Table 1, based on references^5,6,9,10,11:

Table 1 Parameters of the examined system.

Using these parameters and linearization around the equilibrium point, the open-loop transfer function is obtained as:

$$\:G\left(s\right)=\frac{-885.9}{{s}^{3}+100{s}^{2}-19.62s-1962}$$

(14)

This transfer function captures the unstable behavior inherent in magnetic levitation systems and is crucial for designing a stabilizing controller.

System gain and poles

The system gain $\:m$ is computed based on the linearization:

$$\:m=\frac{-2\sqrt{kg}}{L\sqrt{M{y}_{0}}}=-885.8894$$

(15)

The poles of the system are:

$$\:{p}_{1}=-\frac{R}{L}=-100$$

(16)

$$\:{p}_{\text{2,3}}=\pm\:\sqrt{g/{y}_{0}}=\pm\:4.4294$$

(17)

Fig. 2

Perspective of magnetic levitation system.

The presence of a positive real pole indicates that the open-loop system is open-loop unstable, which is a well-known characteristic of magnetic levitation systems. This necessitates a robust control strategy to ensure stability and desired performance. General schematic of magnetic levitation system is shown in Fig. 2.

Novel control method proposed for magnetic levitation

Structure of the 2-DOF PIDA controller

To stabilize the inherently unstable magnetic levitation system and enhance its tracking performance, a novel 2-DOF PIDA controller is proposed. The controller structure introduces flexibility by assigning distinct weighting factors to the reference signal for the proportional and derivative actions, while incorporating acceleration feedback for improved damping and robustness.

Transfer function of proposed novel 2-DOF PIDA controller

Transfer function of proposed novel 2-DOF PIDA controller calculated and is given in follows Eq. 

$$\:U\left(s\right)={K}_{P}\left[\alpha\:\times\:R\left(s\right)-Y\left(s\right)\right]+\frac{{K}_{I}}{s}\left[R\left(s\right)-Y\left(s\right)\right]+{K}_{D}\frac{{N}_{D}s}{s+{N}_{D}}\left[\beta\:\times\:R\left(s\right)-Y\left(s\right)\right]+{K}_{A}{\left(\frac{{N}_{A}s}{s+{N}_{A}}\right)}^{2}\left[R\left(s\right)-Y\left(s\right)\right]$$

(18)

Fig. 3

Block diagram of 2-DOF PIDA controller.

where, $\:U\left(s\right),\:R\left(s\right),\:Y\left(s\right)$,$\:\:\alpha\:,\:\beta\:$, $\:{K}_{P},\:{K}_{I},\:{K}_{D},\:{K}_{A}$, $\:{N}_{D}\:$and $\:{N}_{A}$ are controller output, reference input, system output (position of the steel ball), reference input weights for proportional and derivative terms, gains for proportional, integral, derivative, and acceleration terms and filters to regularize the derivative and acceleration terms respectively.

This structure enhances both disturbance rejection and tracking performance by decoupling the transient and steady-state behavior via the 2-DOF configuration. The corresponding block diagram of the controller is illustrated in Fig. 3, which clearly shows the parallel branches for each control term, including the low-pass filtered derivative and acceleration feedback loops.

Objective function

To evaluate and optimize the performance of the magnetic levitation system, the Integral of Absolute Error ($\:IAE$) is selected as the objective function. $\:IAE$ is a widely used performance criterion in control system design as it penalizes the accumulated error over time and ensures fast and accurate convergence to the setpoint⁴⁶. The objective function is mathematically defined as:

$$\:IAE=\underset{0}{\overset{{t}_{f}}{\int\:}}\left|e\left(t\right)\right|dt=\underset{0}{\overset{{t}_{f}}{\int\:}}|r\left(t\right)-y(t\left)\right|dt$$

(19)

where, $\:r\left(t\right),\:y\left(t\right),\:e\left(t\right)$ and $\:{t}_{f}$ are reference input (desired ball position), system output (actual ball position), tracking error and final simulation time, here set to 5 s, respectively.

The goal is to minimize the $\:IAE$, thereby achieving accurate setpoint tracking with minimal overshoot and settling time.

Implementation of the proposed control method to the magnetic levitation system

The implementation framework of the proposed 2-DOF PIDA controller for the magnetic levitation system is illustrated in Fig. 4. The diagram presents the closed-loop structure, where the control parameters are automatically optimized using the EAO algorithm.

Key steps of the control implementation are as follows:

• 1. Initialization Random populations of controller parameters $\:\alpha\:,\:\beta\:$, $\:{K}_{P},\:{K}_{I},\:{K}_{D},\:{K}_{A}$, $\:{N}_{D}\:$and $\:{N}_{A}$ are generated.

• 2. Simulation for each candidate set, the system is simulated under the current controller

• 3. Performance evaluation: The $\:IAE$ is calculated for a fixed time interval ($\:{t}_{f}=5$ s).

• 4. Optimization The EAO algorithm iteratively refines the parameter set to minimize the $\:IAE$.

• 5. Controller update the best-performing parameters are assigned to the 2-DOF PIDA controller

The feedback loop adjusts the electromagnet’s control voltage based on the ball’s position to maintain levitation. The optimized controller ensures system stability and rapid convergence with minimal control effort.

Fig. 4

Implementation of the proposed control method to magnetic levitation system.

Simulation results

To evaluate the effectiveness and robustness of the proposed optimization-based control strategy, simulations were conducted using three metaheuristic algorithms: EOA³⁶, HLOA³⁷, and SHO³⁸. Each algorithm was run 25 independent times to ensure statistical reliability. The population size was set to 30, and the total number of iterations was fixed at 100 for all algorithms.

Statistical analysis

The results of the optimization process were assessed based on the $\:IAE$ objective function. The statistical metrics summarized in Table 2 include the average, standard deviation, best, and worst values of the $\:IAE$ across all runs. The ranking is based on overall performance, with lower IAE values indicating better control performance. Each optimization algorithm EOA, HLOA, and SHO was independently executed 25 times to assess performance consistency and robustness. A population size of 30 was maintained for each run, and the optimization procedure was carried out over 100 iterations. This ensured a balanced trade-off between convergence capability and computational cost.

Table 2 Statistical metrics obtained via compared algorithms.

These results confirm that EOA outperforms both HLOA and SHO in terms of accuracy, stability, and consistency of the obtained solutions.

Obtained controller parameters

The best set of 2-DOF PIDA controller parameters achieved by each algorithm is listed in Table 3. The parameters were bounded within predefined search intervals based on prior tuning heuristics and system limitations.

Table 3 Obtained controller parameters.

The controller parameters obtained by EOA align closely with the theoretical expectations for stabilizing the magnetic levitation system while ensuring fast and smooth tracking. EOA also demonstrates a good balance between aggressive control gains and stable filter coefficients.

Closed-loop response

To assess the dynamic performance of the magnetic levitation system under different controllers, a unit step reference input was applied, and the system’s closed-loop response was observed. The results of the simulation for the EOA, HLOA, and SHO-based 2-DOF PIDA controllers are illustrated in Fig. 5. As shown in the figure, the controller tuned using the EOA achieves the quickest and most precise response, closely tracking the setpoint with no overshoot and the shortest rise and settling times. In contrast, the HLOA and SHO controllers exhibit slightly slower responses, with minor overshoot, particularly in the SHO case.

Fig. 5

Comparative step responses of EOA, HLOA and SHO based 2-DOF PIDA controllers.

The corresponding quantitative time-domain metrics are summarized in Table 4, including percent overshoot, rise time, and settling time. These metrics confirm the superior performance of the EOA-tuned controller in terms of both accuracy and response speed.

Table 4 Comparative transient response metrics for EOA, HLOA and SHO based approaches.

These results clearly demonstrate that the proposed EOA-based tuning not only improves the transient response characteristics but also ensures a faster, overshoot-free convergence to the desired levitation position, which is crucial in magnetic levitation applications requiring precision and stability.

Robustness analysis

To assess the robustness of the proposed controller under parameter uncertainties, four test cases were simulated by perturbing the nominal system parameters $\:R$ and $\:L$. Figures 6, 7, 8 and 9 illustrate the comparative closed-loop step responses obtained using the EOA, HLOA, and SHO-based 2-DOF PIDA controllers under each condition. In this scenario, the system resistance is slightly reduced, potentially accelerating the electrical dynamics. The EOA-based controller demonstrates a fast rise and zero overshoot, whereas HLOA and SHO show noticeable overshoot, with SHO peaking highest. Despite the variation, EOA maintains excellent tracking and settling characteristics. With a slight increase in resistance, the system becomes more sluggish. Here, EOA maintains performance with a minor overshoot (~ 0.07%) and stable convergence. In contrast, HLOA and especially SHO exhibit larger overshoot and slower convergence, highlighting the EOA’s ability to compensate for increased electrical resistance. This test represents a scenario where the system inductance is reduced. As inductance affects the rate of change of current in the electromagnet, this accelerates the system’s magnetic response. EOA again shows zero overshoot and a fast settling response, while both HLOA and SHO become sensitive, leading to increased overshoot and longer settling times, indicating reduced robustness.

Fig. 6

Comparison of step responses for $\:R=0.95$.

Fig. 7

Comparison of step responses for $\:R=1.05$.

Fig. 8

Comparison of step responses for $\:L=0.008$.

Fig. 9

Comparison of step responses for $\:L=0.012$.

Here, with increased inductance, the controller must handle a more sluggish system. The EOA-based controller preserves stability and achieves the best settling performance (~ 0.0217 s), despite a slight increase in overshoot (~ 0.17%). HLOA and SHO suffer more from this change, especially SHO, which shows overshoot exceeding 1.1%.

These observations clearly demonstrate that EOA exhibits superior robustness under all tested parameter deviations, ensuring both stability and high precision in closed-loop control. This makes it well-suited for real-time magnetic levitation applications where system parameters may vary due to heating, aging, or environmental conditions. The time-domain performance under these parameter perturbations is quantitatively summarized in Table 5.

Table 5 Comparative numerical robustness analysis.

The EOA-based controller consistently achieved superior or comparable performance under all test conditions, exhibiting minimal overshoot, shorter rise time, and faster settling time. These results confirm the robustness and adaptability of the EOA-optimized 2-DOF PIDA controller, making it a suitable candidate for practical deployment in magnetic levitation systems where parameter uncertainties cannot be avoided.

Comparison with reported control methods

To comprehensively assess the performance of the proposed EOA-based 2-DOF PIDA controller, it was compared against 12 other recently reported control strategies, including PID, FOPID, and RPIDD² configurations tuned via different metaheuristic optimizers. The benchmarking is based on various time-domain metrics and the $\:IAE$ objective function.

The tested methods, their references, and corresponding method numbers are summarized in Table 6.

Table 6 Comparative performance of the proposed method with respect to proposed approaches.

Figure 10 presents the system response to a unit step input under each of the 13 controllers.

• EOA-based 2-DOF PIDA (Method 1) shows an ideal behavior fast rise, no overshoot, and rapid convergence to the setpoint.

• Other methods, especially Methods 4 and 5 (WOA-based PID and SA-based PID), exhibit large overshoots (over 40%) and oscillations before settling, which are undesirable in sensitive systems like magnetic levitation.

• Several controllers (Methods 7–13) achieve more stable behavior but still fall short of Method 1’s precision and damping quality.

• This figure highlights the superior transient regulation and damping characteristics of the proposed controller, which is critical for stability in highly nonlinear, open-loop unstable systems.

Fig. 10

Comparative step response of the proposed method with respect to reported approaches.

This bar chart in Fig. 11 quantifies how quickly each controller brings the output from 10 to 90% of the setpoint value.

• Method 1 (EOA-based) again leads with the fastest rise time (0.0121 s), significantly better than all other approaches.

• Methods like 4, 5, and 8 require more than 0.03 s, indicating delayed responsiveness.

• A fast rise time is crucial in real-time applications such as magnetic levitation, where quick stabilization directly affects usability and safety. This figure confirms that the EOA-optimized controller ensures rapid action without compromising system stability.

Fig. 11

Comparative rise time with respect to reported approaches.

Settling time in Fig. 12 indicates how quickly the system output stabilizes within a defined tolerance band around the setpoint.

• EOA-based control achieves the shortest settling time of just 0.0365 s, indicating high-speed convergence with minimal oscillations.

• In contrast, Methods 2–5 take over 0.5 s, which is unacceptable in high-precision applications.

• Several RPIDD²-based methods (Methods 10–13) improve on the classical PID methods but still fall behind EOA.

• This chart demonstrates the superiority of EOA not just in speed but also in damping, reinforcing its real-time suitability.

Fig. 12

Comparative settling time with respect to reported approaches.

Percent overshoot in Fig. 13 reflects how much the system output exceeds the desired setpoint during transient response.

• Method 1 is the only one with 0% overshoot, ensuring perfectly critically damped behavior.

• Other methods especially Methods 5 and 9 exhibit substantial overshoot, with Method 5 peaking at 44.07%, indicating poor damping and risk of instability.

• Overshoot is dangerous in magnetic levitation systems as it can lead to loss of levitation or collision with system boundaries. This plot clearly demonstrates the safety and precision advantages of the proposed controller.

Fig. 13

Comparative percent overshoot with respect to reported approaches.

$\:IAE$ evaluates in Fig. 14 the total accumulated tracking error over time a lower $\:IAE$ indicates better long-term tracking accuracy.

• Method 1 outperforms all others with a minimum IAE of 0.0096, compared to 0.0794–0.0959 in Methods 4–5.

• Controllers with high $\:IAE$ are less effective at maintaining precise tracking over time, often due to overshoot, undershoot, or prolonged settling.

• EOA’s low $\:IAE$ result confirms its long-term tracking efficiency and robust setpoint convergence.

Fig. 14

Comparative IAE objective function value with respect to reported approaches.

Advantages and disadvantages of proposed methods

To provide a comprehensive analysis, the advantages and disadvantages of the 2-DOF PIDA controller optimized with the EAO, HLOA, and SHO are discussed. The EAO-based method demonstrates superior performance with 0% overshoot, a rise time of 0.0121 s, and a settling time of 0.0365 s, alongside high robustness against parameter variations (Sect. 5.4). However, its computational complexity may pose challenges in real-time systems with limited hardware resources, and its performance depends on proper initial parameter settings. Additionally, as noted in Sect. 6, it has not been tested in real-world conditions, potentially making it susceptible to sensor quantization noise or hardware delays. The HLOA-based method offers acceptable performance with low overshoot (0.23117%) and a settling time of 0.049113 s but exhibits slower convergence and greater sensitivity to parameter changes (up to 0.36938% overshoot), limiting its stability in demanding applications. The SHO-based method provides simpler implementation but suffers from higher overshoot (up to 1.3938%) and reduced stability under parameter variations, making it less suitable for highly sensitive systems. The following Table 7 summarizes this comparison:

Table 7 Comparison of advantages and disadvantages of proposed Methods.

Conclusion

This This study introduced a novel 2-DOF PIDA controller optimized with the EAO for precise position regulation in magnetic levitation systems. By leveraging acceleration feedback and reference input weighting, the controller achieves independent tuning of transient and steady-state behavior, resulting in 0% overshoot, a rise time of 0.0121 s, and a settling time of 0.0365 s. Extensive simulations demonstrate that the EAO-tuned controller outperforms two recent metaheuristics HLOA and SHO as well as 12 state-of-the-art control strategies, including SCA-, WOA-, and MRFO-tuned PID, FOPID, and RPIDD² controllers, across key metrics such as $\:IAE$, rise time, settling time, and robustness under parameter perturbations (Sect. 5.3–5.5). Robustness testing under variations in coil resistance and inductance further confirms the controller’s adaptability to practical uncertainties like thermal drift and component aging, making it a promising solution for real-time maglev applications.

However, certain limitations must be acknowledged to contextualize the findings. The current validation is simulation-based, which does not account for real-world challenges such as sensor quantization noise, hardware-induced delays, and environmental disturbances. For instance, sensor noise could introduce errors in measuring the steel ball’s position, potentially causing oscillations or degrading the zero-overshoot performance observed in simulations (Table 4). Hardware delays, arising from processing limitations or communication latencies, may increase rise and settling times, compromising the reported 0.0121 s rise time and 0.0365 s settling time. Additionally, the computational complexity of the EAO algorithm (Eq. 12, Sect. 2.1.9), with a population size of 30 and 100 iterations, may pose challenges for real-time implementation on resource-constrained hardware, potentially limiting the controller’s ability to adapt quickly to dynamic changes in system parameters. Furthermore, the study assumes idealized parameter perturbations (± 10% variations in resistance and inductance, Sect. 5.4), whereas real-world systems may experience simultaneous and complex variations due to temperature fluctuations or electromagnetic interference. These unmodeled dynamics could reduce tracking accuracy (e.g., $\:IAE$ of 0.0096, Table 2) or introduce overshoot, particularly if nonlinearities or faults like sensor failures or actuator saturation occur.

To address these challenges, future work will focus on hardware-in-the-loop (HIL) testing to validate the controller under realistic conditions, incorporating sensor noise and hardware delays. Optimizing the EAO algorithm for embedded systems, potentially through reduced population sizes or parallel processing, could mitigate computational constraints. Additionally, exploring adaptive control strategies, such as online parameter estimation, or robust control techniques could enhance resilience to complex parameter variations and unmodeled dynamics. Extending the controller’s application to multi-input multi-output (MIMO) and fault-tolerant maglev systems will further broaden its practical relevance. In summary, the EAO-optimized 2-DOF PIDA controller offers a computationally efficient, self-tunable, and high-precision solution for nonlinear, unstable systems like magnetic levitation platforms. Its superior performance in simulation, combined with its robustness to parameter uncertainties, positions it as a compelling framework for next-generation contactless actuation, smart automation, and maglev transportation systems. Future research addressing the identified limitations will ensure its successful deployment in real-world applications, leveraging the potential of bio-inspired optimization in modern control design.