Knowledge graph convolutional networks with user preferences for course recommendation

Abstract

With the rapid growth of the internet and online education resources, the number of massive open online courses (MOOCs) has increased dramatically, making it difficult for users to find personalized courses that meet their needs. Knowledge graphs (KGs) have been employed in recommendation systems to effectively address the issue of sparse interaction data in the MOOC scenarios for their rich semantic information. Research on KG-enhanced recommendation algorithms has found that the utilization of side information in KGs is crucial for improving accuracy. This paper introduces KGCN-UP (Knowledge Graph Convolutional Networks with User Preferences), a novel model for predicting the likelihood of a user interacting with a course based on user preferences and item relationships within a knowledge graph. The KGCN-UP model consists of two key modules. First, the user preference propagation module refines user preferences by exploring relational chains in the knowledge graph and dynamically adjusting attention to improve user representation. Second, the item neighbor enhancement module enhances item representations by aggregating semantic relationships and assigning attention weights based on the type of relationship between entities. Together, these components address the challenge of data sparsity and improve the quality of recommendations by leveraging high-order structural and semantic information. Empirical results on a real-world dataset demonstrate that KGCN-UP significantly outperforms existing state-of-the-art recommendation models in terms of accuracy.

Introduction

The rapid development of online education platforms has led to a variety of massive open online courses (MOOCs), including Chinese University MOOCs, Xuetang Online, and E-Cloud Classes. These platforms offer rich online learning resources, attract an increasing number of users, and provide fair and open educational opportunities for both college students and lifelong learners.

Fig. 1

Interaction-avg shows the average interaction count in the MOOCs dataset in comparison with the four other commonly used datasets.

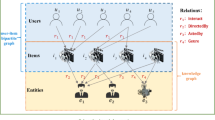
In the vast landscape of online education resources, the way users select courses that meet their specific knowledge needs is crucial, as it directly impacts the completion and dropout rates of learners¹. As illustrated in Fig. 1, the average interaction of user-item (learner-course) for online courses is significantly lower compared to traditional recommendation scenarios, such as those for books, food, and movies. Given that course learning is often a lengthy and somewhat tedious process, this discrepancy has led to a contradiction between the proliferation of online courses and the noticeable lack of interaction. To address the issue of ‘’information overload’’, providing users with personalized courses becomes particularly important^2,47. In light of this challenge, the recommendation algorithms used by online education platforms have increasingly become a focal point in educational research, attracting significant attention from scholars. Traditional recommendation algorithms typically rely on using side information to enhance the accuracy and effectiveness of recommendations⁵⁰. For example, social network data³, image features⁴, contextual information^5,51, and item attributes^6,46 are widely utilized to boost the performance of recommendation systems. The aforementioned recommendation methods, although they improve recommendation performance to some extent, still struggle to effectively address key issues such as data sparsity and the difficulty of providing explainable recommendations in the MOOC environment. In contrast to these information, knowledge graph (KG) inherently offers the advantage of revealing connections between learners and course entities, thus providing implicit feedback on diverse intentions of users. Consequently, many scholars have introduced KG into their recommendation tasks^7,48,49.

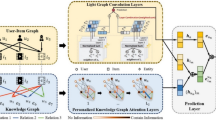
Through research on recommendation algorithms based on KG, improving the utilization of relational information within KGs has become a key factor in enhancing model performance. Based on these considerations, we propose a model named KGCN-UP, short for Knowledge Graph Convolutional Networks with User Preferences, as illustrated in Fig. 2.

Fig. 2

The toy example of a KGCN-UP course recommendation for each user.

This model traverses all courses with which the user has historically interacted and propagates through various relationship chains in the KG to get courses that the user is likely to be interested in. We define this process as the user preference propagation module. Similarly, the model starts with candidate courses and traverses related courses adjacent to these, enhancing the representation of the candidate courses. This forms what we call the item neighbor enhancement module. This approach not only enriches the user representation but also effectively utilizes the relational chain information in the KG, thereby addressing the issue of ‘’information overload’’ and improving the model’s performance.

The main contributions of this work are summarized as follows:

• 1) We systematically analyze the sparsity of user interaction data in MOOCs scenarios. Based on these characteristics, we propose a model named KGCN-UP that enhances user and item representations to predict course click probabilities, addressing data sparsity in MOOCs.

• 2) To address the sparsity problem, a novel user representation method is introduced to propagate user preferences through the knowledge graph by capturing relevant entities connected to previously interacted courses.

• 3) To improve the use of heterogeneous information in the knowledge graph, we design a novel approach to item representation. It traverses entities related to the candidate item and applies message passing to aggregate neighbor information for the final representation.

• 4) Extensive experiments demonstrate that KGCN-UP outperforms leading benchmark models on educational, book, and music recommendation tasks, with ablation studies confirming the effectiveness of both key model components.

The structure of this paper is organized as follows: “PROBLEM DEFINITION” section introduces the purpose of the recommendation task and related definitions. “RELATED WORKS” section introduces the relevant research on recommendation models based on KG. Afterwards, the proposed method is introduced in detail in “METHODS” section. Experimental results and related discussions are then presented in “EXPERIMENT”. we summarize the findings of this paper and outline our plans for future research in “CONCLUSION” section.

Related works

A variety of methods have been developed to introduce KG into recommendation systems. We categorize these methods into four types based on the different uses of additional information from the KG: Embedding-based^8,9,10, Path-based^14,15,16, GNN-based^{18,19,20,21,22} and Contrastive Learning-based^27,28,29.

Embedding-based methods

Embedding-based methods^8,9,10 utilize knowledge graph embeddings (KGE)^11,12 to process KG information, aiming to incorporate both entity and relation embeddings into recommendation systems. CKE⁸ uses the TransR¹¹ algorithm to extract the structured information of items, integrating it into the collaborative filtering module. DKN⁹ aggregates target items by combining entity embeddings and word embeddings through the TransD¹³ algorithm. RippleNet¹⁰ propagates entities from previous user interactions within the KG, modeling the relationships between users and items. These models primarily focus on the semantic relevance between items, but they fall short in capturing complex high-order relationships between users and items, and are more commonly used in prediction tasks.

Path-based methods

Path-based methods^14,15,16 explore potential relationships between users and items in the KG by investigating the paths between them. PER¹⁴ extracts all meta-paths from user-item data to explore the possibilities of user-item interactions. HIN¹⁵ treats the KG as a heterogeneous information network, effectively utilizing its semantic information to represent users and items for personalized recommendations. KPRN¹⁶ extracts paths between users and items from the KG and models entities and relationships by using LSTM¹⁷ to infer user preferences. These models require rigorous domain knowledge and heavily rely on manually set meta-paths, making them a time-consuming and labor-intensive task.

GNN-based methods

Graph Neural Network (GNN) methods^{18,19,20,21,22} establish mechanisms for information aggregation in GNNs, extracting multi-hop information from neighboring nodes and integrate it into node representations to learn user preferences and model long-range connections. Models such as KGCN¹⁸ and KGNN-LS¹⁹ utilize Graph Convolutional Networks (GCN) to synthesize neighbor information, capturing local neighbor structures to obtain item embeddings. KGAT²⁰ combines interaction graph and KG into heterogeneous graph, then recursively uses GCNs for information aggregation, thereby enhancing entity embeddings. CKAN²¹ introduces a novel heterogeneous propagation mechanism to transmit collaborative signals and knowledge-aware information, thus dynamically adjusting the weights of neighboring nodes. Recently, KGIE²² connects KG with user-item interaction matrices to form relational interactive embeddings for users, and then aggregates neighbor information through Convolutional Neural Networks (CNNs). Unlike these models, which make indirect use of relational information in the graph, our proposed method directly leverages the rich relational information within the KG. It places greater emphasis on the types of relationships themselves, rather than just the entities connected by these relationships, resulting in improved recommendation performance.

Contarstive-learning based methods

Contrastive-learning based methods^27,28,29 involve comparing positive and negative samples, positioning the positive samples in the feature embedding space, while further separating the negative samples from the positive ones. The goal is to maximize the distance between different samples, improving node representation learning through supervised learning from the data itself. KGCL²⁷ aims to suppress the noise generated in the information aggregation process of KG by introducing SGL³⁰ into recommendation systems, utilizing self-supervised signals to enhance the representations of users and items. MCCLK²⁸ conducts contrastive learning (CL) from both local and global perspectives, enhancing node representations through multiple views. KGrec²⁹ calculates scores for each triplet, aligning signals from KGs and interaction graphs to mask the KG.

Methods

In this section, we define the recommendation task and introduce related concepts. Following that, we describe our proposed KGCN-UP model, which efficiently captures high-order interaction information between users and items, thereby improving the use of side information in the KG.

Problem definition

In this paper, we follow the general setup of mainstream recommendation systems. We define two types of structured data required by the course recommendation system: the user-course interaction dataset and the KG. Finally, we formulate the problem statement.

1) Interaction Data. Let $\:U\text=\{{}u_{1}, u_{2}, ...u_{n}\}$represent a set of$\:m$ users, and let$\:C=\{{}c_{1}, c_{2}, ...c_{n}\}$ represent a set of$\:n$ courses. Thus, the user-course interaction matrix can be defined as $\:Y=\left\{{\:y}_{uc}\right||u\in\:\:U,\:c\in\:\:C\}$, where $\:U$ and $\:C$ denote the sets of users and courses. In this interaction matrix, if user $\:u$ interacts with course $\:c$, such as by clicking, adding, or purchasing, then $\:{\:y}_{uc}\text{=1}$, otherwise $\:{\:y}_{uc}\text{=0}$.

2) Knowledge Graph. KGs include much side information. We formally define it as $\:G=\{{}(h,r,t)|\:h,t\in\:\epsilon\:,r\in\:R\}$ where $\:h$ and $\:r$ represent the head and the relation of the knowledge triplet, respectively, and $\:t$ represents the tail. A KG is composed of many such knowledge triplets, which are the basic units of the graph. For example, the triplet (Nanjing University. Operating System, course. teacher, Luo Bin) describes the fact that the course on Computer Operating Systems is taught by Professor Luo Bin. To align more closely with real recommendation scenarios, We ensure that each course $\:c\in\:C$ corresponds to one entity $\:e\in\:\epsilon\:$ in the KG, establishing a set of item-entity alignment pairs$\:\:K=\left\{\right(c,e\left)\right|c\in\:C,e\in\:\epsilon\:\}.$This alignment between courses and entities in the KG provides rich semantic information for interaction data.

3) Problem Statement. The primary goal of the online course recommendation problem is to predict whether a user $\:u$ is interested in a course $\:c$ that they have not yet interacted with, using the interaction matrix $\:Y$ and the knowledge graph $\:\text{G}$. The main task of the model is to construct a prediction function $\:{y}_{uc}=F(u,c|G,\varTheta\:)$, where $\:{y}_{uc}$ represents the predicted likelihood of student $\:u$ engaging with course $\:c$,$\:\:F$ denotes the functional form of the model, and $\:\varTheta\:$ represents the parameter of the function $\:F$.

Framework

As illustrated in Fig. 3, the architecture of the KGCN-UP model is structured into three primary components: the User Preference Propagation Module, the Item Neighbor Enhancement Module, and the Prediction Module. The User Preference Propagation Module explores the user’s potential preferences through various relations in the KG, enriching the user’s preference representation. The Item Neighbor Enhancement Module generates the final candidate course list by capturing higher-order neighboring items of the target course and aggregating similarities and correlations among these items. Finally, the Prediction Module integrates the merged user and item representations and outputs the prediction of the user’s selection of candidate courses.

Fig. 3

The proposed KGCN-UP model is illustrated, consisting of three modules: the user preference propagation module, the item neighbor enhancement module, and the prediction module.

User preference propagation module

Similar to the assumptions of traditional collaborative filtering (CF) models^31,32,33, we assume that users’ preferences are mainly reflected in their historical interaction data. Specifically, users tend to choose courses that are similar to items they have engaged with in the past. However, this assumption encounters numerous challenges in practical applications, especially in MOOC scenarios. The number of users usually far exceeds the number of courses, and user behavior often concentrates on popular courses. This leads to extremely sparse historical interaction data, making it difficult to utilize user information to identify potential key users.

The entities in KG contain fruitful facts and connect. For instance, the course ‘’University Physics I’’ is associated with ‘’Tsinghua University’’ (school), the ‘’Maxwell Rate Distribution Law’’ (concept), ‘’Chen Xinyi’’ (teacher), and ‘’Physics’’ (category). However, ‘’Chen Xinyi’’ has a deeper connection with the courses he teaches, such as ‘’University Physics II’’ and ‘’University Physics’’ (Prerequisite). If a user has previously watched Mr. Chen’s courses, he is likely to be interested in physics or other courses taught by Mr. Chen, and may click on ‘’College Physics II (Mechanics, Heat)’’ or ‘’College Physics’’ (Prerequisite) for further learning. Therefore, a user’s personality and preferences should be defined not only by the courses they have previously watched but also by other relevant entities in the KG. To improve recommendation performance, we should enhance user representation to get user-oriented information through user preference sets and KGs. The detailed process is as follows:

User preference propagation set

We consider the set of entities that the user has interacted with as the initial seed in the KG. The initial set is defined as follows:

$$\:\begin{array}{c}{\epsilon\:}_{u}^{0}=\left\{e|\left(e\:,\:c\right)\in\:K\:and\:c\in\:\left\{c|{y}_{uc}=1\right\}\right\}\end{array}$$

(1)

The initial set consists of course entities, with each course entity serving as the head entity. This head entity is explored along the various relationship chains in the KG through $\:{\epsilon\:}_{u}^{0}$ to get the tail entities. These tail entities then serve as new head entities in subsequent rounds. This process iterates $\:l$ times to obtain the $\:l-hop$ propagation entity set. This set can be seen as a natural expansion of the user’s interests. The user preference propagation set is defined as follows:

$$\:\begin{array}{c}{P}_{u}^{l}=\left\{t\right|(h\:,\:r\:,\:t)\in\:G\:and\:h\in\:{P}_{u}^{l-1}\},\:l=\text{1,2},...,L\:\end{array}$$

(2)

The initial set $\:{p}_{u}^{0}$ represents the courses chosen by the user, with the number of courses being equal to $\:{\epsilon\:}_{u}^{0}$. To facilitate the calculation of similarity between courses previously selected by the user and candidate courses, we define a set of triples $\:{S}_{u}^{l}$ as follows:

$$\:\begin{array}{c}\begin{array}{c}{S}_{u}^{l}=\left\{\left(h\:,\:r\:,\:t\right)|\left(h\:,\:r\:,\:t\right)\in\:G\:and\:h\in\:{P}_{u}^{l-1}\right\},\:l=\text{1,2},\dots\:,L\:\end{array}\end{array}$$

(3)

$\:{S}_{u}^{l}$ differs from $\:{p}_{u}^{l}$ in that each element of serves as the head entity in the set of $\:{S}_{u}^{l}$ triples. The set $\:{S}_{u}^{l}$ explore additional related items by traversing various relationship chains in the KG to find other related items, this process is crucial for MOOC recommendations.

Path grouping propagation set

Although the rich semantic information of the KG expands user representation, having either too many or too few elements in each layer set $\:{S}_{u}^{l}$ will degrade the recommendation effect. For example, the course “Data Structures” includes 140 concepts, which constitutes a one-to-many relationship. In contrast, the relationships between the course and the school, and between the course and the teacher, are one-to-one. Mixing these knowledge points into the $\:{S}_{u}^{l}$ set will make it difficult to identify which knowledge points in “Data Structures” user is interested in and also distract the user’s attention. Having too few elements in each layer results in an insufficient number of knowledge entities per connection, which not only reduces the effectiveness of enriching the user’s encoding but also risks failing to iterate to the $\:l-th$ level. Since different relationship chains in the KG can be seen as extensions of various attributes of the same course by the user, they naturally have the advantage of grouping. Based on this, we obtain the path grouping propagation set by traversing through$\:{P}_{u}^{l}$ the relationship chain, as follows:

$$\:\begin{array}{c}\begin{array}{c}{P}_{r}^{l}=t|\left(h,r,t\right)\in\:G,h\in\:{\:P}_{u}^{l-1}andr\in\:R,l=\text{1,2},\dots\:,L\:\end{array}\end{array}$$

(4)

Where $\:r$ is the link which belongs to in the entity alignment set $\:K$. Similarly, for ease of calculation, the user’s path grouping propagation set is extended into a triplet entity set, as follows:

$$\:\begin{array}{c}{S}_{r}^{l}=\left\{\right(h\:,\:r\:,\:t\left)\right|(h\:,\:r\:,\:t)\in\:\:G\:and\:h\in\:\:{P}_{r}^{l-1}\},\:r\in\:R\end{array}$$

(5)

Path preference aggregation set

For a given user $\:u$ and a candidate course $\:c$, tail entities can be expressed by different head entities via various relationship chains. For instance, the course ‘’Bioinformatics’’ may be offered by ‘’Central South University’’ or taught by ‘’Tong Jianbin’’. Therefore, the semantics of tail entities, derived from different head entities and relationship chains, vary across different triples. To more finely represent the relationship between the varying semantics of tail entities and the candidate course $\:c$, it is necessary to perform a weighted representation of the resulting tail entities within the given grouping set $\:{S}_{r}^{l}$ and across different triples. This approach aims to calculate the similarity of candidate courses to the courses that users interact with through different relationship chains.

$$\:\begin{array}{c}{a}_{i}=softmax\left({c}^{T}{R}_{i}{h}_{i}\right)=\frac{exp\left({c}^{T}{R}_{i}{h}_{i}\right)}{{\sum\:}_{(h,r,t)\in\:{S}_{r}^{l}}exp\left({c}^{T}Rh\right)}\end{array}$$

(6)

Where $\:R\in\:{\mathfrak{R}}^{d\times\:d}$ denotes the vector representation of relationship $\:{r}_{i}$, and $\:d$ is the dimension of the embedding. Similarly, $\:h\in\:{\mathfrak{R}}^{d}$ represents the embedding of the head entity in $\:{S}_{r}^{l}$ while $\:{c}^{T}$ is the transpose of the course embedding vector $\:c$. The resulting similarity can be interpreted as the probability that the grouping set $\:{S}_{r}^{l}$ is associated with a particular triple $\:({h}_{i},{r}_{i},{t}_{i})$. We then weight and sum all the tail entities in each hop to get a weighted representation of the different paths:

$$\:\begin{array}{c}{O}_{n}={\sum\:}_{\left({h}_{i},r,{t}_{i}\right)\in\:{S}_{r}^{1}}{a}_{i}{t}_{i}\end{array}$$

(7)

$\:\text{w}\text{h}\text{e}\text{r}\text{e}\:{t}_{i}\in\:{\mathfrak{R}}^{d},n=\left|R\right|.$

The different sets of path grouping in each propagation layer can be regarded as an extension of users’ interests in a certain direction. To reveal the users’ interest hotspots, it is necessary to determine which types of course information attract more user attention by using attention weights. The attention function is defined as follows:

$$\:\begin{array}{c}{z}_{n}=\zeta\:\left({o}_{n\:,}{r}_{n}\right){o}_{n\:}\end{array}$$

(8)

The function $\:\zeta\:\left({o}_{n\:,}{r}_{n}\right)$ determines the weight of each path, reflecting the user’s preference for different relation-links. Inspired by Vaswani’s attention mechanism³⁴, $\:\stackrel{\sim}{\zeta\:}({o}_{n},{r}_{n})$ is defined as follows:

$$\:\begin{array}{c}\stackrel{\sim}{\zeta\:}({o}_{n},{r}_{n})=ReLU\left({W}_{2}\right({W}_{1}\left({o}_{n}\right|\left|{r}_{n}\right)+{b}_{1})+{b}_{2})\end{array}$$

(9)

Here, $\:ReLU$serves as a nonlinear activation function, while $\:W$and $\:b$ are trainable parameters representing linear transformation matrices and bias terms, respectively. The operator ∣∣ denotes the concatenation of two vectors. The subscripts on $\:W$ and $\:b$ indicate that these parameters belong to different layers. By processing in this way, scores for different paths chosen by the user are obtained. Subsequently, to convert attention scores into weights, it is necessary to normalize the coefficients of the entire relationship path. Subsequently, to convert attention scores into weights, it is necessary to normalize the coefficients of the entire³⁶:

$$\:\begin{array}{c}\zeta\:\left({o}_{n},{r}_{n}\right)=\frac{exp\left(\stackrel{\sim}{\zeta\:}\left({o}_{n},{r}_{n}\right)\right)}{{\sum\:}_{i\in\:\left|R\right|}exp\left(\stackrel{\sim}{\zeta\:}\left({o}_{n},{r}_{n}\right)\right)}\end{array}$$

(10)

Therefore, we have determined which type of course knowledge the learners focus on more.

Finally, the attention weights obtained are added to the propagation triples of different paths, resulting in a user embedding representation based on the user preference propagation module as follows:

$$\:\begin{array}{c}{e}^{u}={\sum\:}_{i=1}^{l}{\sum\:}_{n=1}^{\left|R\right|}{z}_{n}^{u}\end{array}$$

(11)

Item neighbor enhancement module

In the recommendation system, we posit that the final representation of candidate items is influenced not only by their own representation but also by the attributes of their neighboring entities in the KG. Specifically, the process begins with the candidate item, from which we construct a set of related entities by iteratively traversing different relational chains within the KG. Subsequently, by calculating the attention weights based on the information in the entity set, we implement message passing based on the attention mechanism, thereby capturing the neighbor information adjacent to the candidate item. This information is subsequently aggregated at the central node to form the final representation of the item. This approach not only captures the potential relationships between different entities but also aggregates neighborhood information of the candidate items, thereby elucidating how relational preferences impact user behavior. The detailed process is as follows:

Obtain first-order neighborhood

By traversing the KG to collect a set $\:{N}_{c}$ of one or more entities directly related to the candidate course $\:c\in\:{\mathfrak{R}}^{d}$, we refer to it as the first-order neighbor set of course $\:c$. In the process of message aggregation, using the relation vector $\:{R}_{i}$ directly as the weight for message passing would obscure the different impacts of relationships on user behavior. For example, consider students who have opted for the course “C + + Programming Design”. Some chose it because they needed a foundation in “C + + Programming Design” for “Data Structures”; some because of the instructor Zheng Li; and others chose it because the course is offered by Tsinghua University. Therefore, we represent each edge with a weight $\:w$:

$$\:\begin{array}{c}{w}_{{r}_{i}}^{u}=q\left({e}^{u},{R}_{i}\right)\end{array}$$

(12)

In this equation, $\:{e}^{u}\in\:{\mathfrak{R}}^{d}$ represents the vector of the user, and $\:{R}_{i}\in\:{\mathfrak{R}}^{d}$ is the relation vector where $\:{e}^{u}$ is connected to the $\:i$th neighbor. The function $\:q$ calculates the correlation score between the user vector and the relation vector through an inner product, resulting $\:{w}_{{r}_{i}}^{u}$​. This score $\:{w}_{{r}_{i}}^{u}$ expresses the target user’s degree of preference for the relation $\:{R}_{i}$, representing the weight of message passing through the edge $\:{R}_{i}.$ Subsequently, the obtained $\:{w}_{{r}_{i}}^{u}$ is normalized:

$$\:\begin{array}{c}{\stackrel{\sim}{w}}_{{r}_{i}}^{u}=Softma{x}_{j}\left({w}_{{r}_{i}}^{u}\right)=\frac{exp\left({w}_{{r}_{i}}^{u}\right)}{{\sum\:}_{j\in\:{N}_{c}}exp\left({w}_{{r}_{j}}^{u}\right)}\end{array}$$

(13)

where $\:{N}_{c}$​ represents the set of first-order neighbors of the candidate course $\:c$.

The final embedding of the candidate course $\:c$, which incorporates user representation, is obtained by weighting the adjacent entities associated with the course:

$$\:\begin{array}{c}{\stackrel{\sim}{e}}_{{N}_{c}}^{c}={\sum\:}_{i\in\:{N}_{c}}{\stackrel{\sim}{w}}_{{r}_{i}}^{u}\cdot\:{e}_{i}\end{array}$$

(14)

where $\:{e}_{i}\in\:\epsilon\:$, represents the vector of the $\:i$-$\:th$ neighbor.

As shown in Fig. 3, inspired by graph sampling^37,45, the message passing process spreads from the outermost to the innermost layer. Through aggregation at each layer, the inner layers near the item $\:c$ aggregates features from outer item entities, ultimately converging at the central node. This process yields the feature vector $\:{\stackrel{\sim}{e}}_{{N}_{c}}^{c}$ for the final candidate course c, capturing the higher-order semantic information from the KG.

Iteration layer

On one hand, it is considered that the actual sizes of $\:{N}_{c}$ in real-world KGs vary; on the other hand, if a candidate item aggregates too many neighbors, it will significantly increase the computational load on the model. Considering these factors, we fixed the number of first-order neighbors sampled randomly for each candidate course. The resulting set of neighbor entities denoted as $\:{e}_{{S}_{c}}^{c}$​, do not include all neighboring entities, thus enabling more efficient and manageable computations. Specifically, the subset $\:{e}_{{S}_{c}}^{c}$​ for a candidate can be defined as $\:{S}_{c}\to\:\left\{e\right|e\sim{N}_{c}\}$, where $\:\left|{S}_{c}\right|=D$ and $\:D$ is a configurable constant, set to 2.

The candidate course vector $\:{e}^{c}$ and the neighborhood set vector $\:{e}_{{S}_{c}}^{c}$ are combined into a single vector using a summing aggregator function $\:{f}_{agg}:{\mathfrak{R}}^{d}\times\:{\mathfrak{R}}^{d}\to\:{\mathfrak{R}}^{d}$. The aggregation process formula is as follows:

$$\:\begin{array}{c}\begin{array}{c}{f}_{agg}\left({e}_{{S}_{c}}^{c},{e}^{c}\right)={e}_{{S}_{c}}^{c}+{e}^{c}\end{array}\end{array}$$

(15)

$$\:\begin{array}{c}{e}^{c}=\sigma\:\left(W\cdot\:{f}_{agg}\left({e}_{{S}_{c}}^{c},{e}^{c}\right)+b\right)\end{array}$$

(16)

The summation aggregator combines two vectors by addition, where $\:\sigma\:\left(\right)$ represents a nonlinear activation function, $\:W$ is the linear transformation matrix, and $\:b$ is the bias term.

With the addition of iterative layers, the model can progressively extract information across multiple hops and integrate it into the course, obtaining the final embedding representation through the item neighbor enhancement module.

Prediction module

As depicted in the Fig. 3, the prediction module processes the resulting user embeddings and candidate course embeddings as input vectors to output the prediction results. The specific steps are as follows:

Given the user embedding $\:{e}^{u}$ and the course embedding $\:{e}^{c}$, we calculate the probability of the user selecting the course by computing the inner product of $\:{e}^{u}$ and $\:{e}^{c}$, as follows:

$$\:\begin{array}{c}\begin{array}{c}{\widehat{y}}_{uc}=sigmod\left({e}^{{u}^{T}},{e}^{c}\right)=\frac{{e}^{{u}^{T}}{e}^{c}}{1+exp\left(-x\right)}\end{array}\end{array}$$

(17)

To balance positive and negative samples and enhance classification performance, negative sampling is typically used to randomly generate an equal number of negative samples for each user. Cross entropy is then employed to quantify the discrepancy between the predicted outcomes and the actual interactions. The loss function is defined as follows:

$$\:\begin{array}{c}\begin{array}{c}\begin{array}{c}{\mathcal{L}}_{CF}={\sum\:}_{u\in\:U}\left({\sum\:}_{c\in\:c|\left(u,c\right)\in\:{\rho\:}^{+}}\iota\:\left({y}_{u,c},{\widehat{y}}_{u,c}\right)-{\sum\:}_{c\in\:c|\left(u,c\right)\in\:{\rho\:}^{-}}\iota\:\left({y}_{u,c},{\widehat{y}}_{u,c}\right)\right)\end{array}\end{array}\end{array}$$

(18)

Where the function $\:\iota\:\left({y}_{u,c},{\widehat{y}}_{u,c}\right)$ represents the cross-entropy loss. $\:{\rho\:}^{+}$ denotes the interactions in which the user actually selects or shows interest, $\:{\rho\:}^{-}$ represents the set of all negative user-course interactions, and $\:\rho\:$ is assumed to follow a uniform distribution.

To capture the potential representation of the relationships between entities as possible, we adopt the approach¹⁰ and utilize KGE method to constrain the embeddings of entities and relationships. The loss function for the KG is defined as follows:

$$\:\begin{array}{c}{\mathcal{L}}_{KG}={\sum\:}_{\left(h,r,t\right)\in\:G}\left|\right|{I}_{r}-{E}^{T}RE|{|}_{2}^{2}\end{array}$$

(19)

Where $\:{I}_{r}$ represents the slice of the tensor $\:I$ corresponding to relation $\:r$ in the KG, and $\:E$ is the embedding matrix of entities.

Finally, to mitigate model overfitting and reduce noise interference, we introduce a regularization loss function:

$$\:\begin{array}{c}{\mathcal{L}}_{reg}={\sum\:}_{r\in\:R}\left|\right|r|{|}_{2}^{2}+{\sum\:}_{c\in\:\epsilon\:}\left|\right|c|{|}_{2}^{2}+{\sum\:}_{e\in\:\epsilon\:}\left|\right|e|{|}_{2}^{2}\end{array}$$

(20)

Therefore, the loss function of the model can finally be expressed as:

$$\:\begin{array}{c}L={\mathcal{L}}_{cf}+{\lambda\:}_{1}{\mathcal{L}}_{kg}+{\lambda\:}_{2}{\mathcal{L}}_{reg}\end{array}$$

(21)

Where $\:{\lambda\:}_{1}$​ and $\:{\lambda\:}_{2}$ are hyperparameters that help prevent overfitting.

Algorithm 1 KGCN-UP

Experiment

In this section, we conducted a series of experiments to verify the effectiveness of the proposed KGCN-UP model in online course recommendations. We aimed to answer the following research questions:

RQ1: How does our proposed model perform compared to other advanced models that also aim to improve recommendation performance?

RQ2: How do hyperparameters impact model performance?

RQ3: How do the user propagation modules and item enhancement modules influence the performance of the model?

RQ4: Can KGCN-UP offer visual case studies to demonstrate the effectiveness of the proposed appr

Datasets prepare

To verify the effectiveness of the proposed model in online course recommendations, we conducted experiments using the MOOCCube open dataset. Additionally, to ensure the fairness of the results, we also performed comparative experiments on two other public datasets, Movielens-1 M and Book-Crossing, to assess the model’s universality in the recommendation scenario.

1)MOOCCube: It is a large-scale and open-source educational dataset that not only includes 706 real courses and nearly 38,000 videos, but also provides additional information for course recommendations.

2)MovieLens-1 M: This dataset, widely used for movie recommendations, includes display ratings from 6,036 users for 2,445 movies, with ratings on a scale of 1 to 5.

3)Book-Crossing: It collects reviews of 2,445 books from 17,860 readers across communities (on a scale of 0 to 1).

We preprocessed the MOOCCube open dataset with specific steps to enhance data quality and relevance. Initially, we filtered the interactive data collected between July 1, 2017, and October 1, 2017. We removed records where learners selected fewer than 10 courses to reduce data sparsity and ensure a sufficient amount of interactive information. Subsequently, we extracted all course names from the dataset, maintaining the historical sequence of learners’ course clicks. Regarding the construction of the sub-KG, we start from the course entity and expand into various course-related knowledge triples through different relationships, until the tail entity points back to the course entity.

For the interaction data from the MovieLens-1 M and Book-Crossing datasets, which exhibit explicit feedback, we adopted the RippleNet¹⁰ approach to convert this data into implicit feedback, thus capturing user-item interactions. For MovieLens-1 M, we set a positive sample threshold of 4; for Book-Crossing, we did not set a specific threshold due to its sparse data. A user’s engagement with an item is quantified such that a positive interaction is assigned a score of 1, whereas the absence of interaction or a low rating is assigned a score of 0. Negative samples are randomly selected from unobserved items for each user, ensuring the number of negative samples equals the number of positive samples. In terms of sub-KG construction, we followed the KGCN¹⁸ methodology and utilized Microsoft’s Satori⁴ business KG to construct the sub-KG for the MovieLens-1 M and Book-Crossing datasets. To create the sub-KG, we first filter out low-confidence triples from the original knowledge graph (KG) by selecting only those with a confidence level greater than 0.9. This pruning step helps eliminate noisy or unreliable data. For the remaining triples, we extract the Satori IDs of all valid movies and books by matching their names with the tail of the triples, such as (head, film.film.name, tail) and (head, book.book.title, tail). To further reduce noise, we exclude items that either match multiple entities or have no valid match at all, ensuring that only clear and unambiguous entities are retained. Table 1 presents the statistics for these three datasets.

Table 1 Statistics settings for the datasets.

Experimental environment and training settings

To ensure the fairness of the experiments, we standardized the model’s dimension at 64 and the batch size at 512. The dataset was randomly divided into training, testing, and validation sets in a 6:2:2 ratio to facilitate hyperparameter tuning. The model parameters were initialized using the Xavier³⁸ method, and the model was optimized with the ADAM optimizer³⁹. The hyperparameters that need to be fine-tuned are as follows: evaluate learning rates among {0.0001, 0.001, 0.01, 0.1}, check regularization coefficients among {10⁻⁷,10⁻⁶,10⁻⁵,10⁻⁴,10⁻³,10⁻²,10⁻¹} explore the maximum number of hops L among {1, 2, 3, 4, 5}, and find the appropriate number of neighbors D among {2, 3, 4, 5, 6, 7, 8}. Training was halted if the model’s loss on the validation set did not improve significantly over five consecutive validation cycles. The final results were averaged from the best outcomes across five model runs. Table 2 lists the specific hyperparameter settings for our model, while the hyperparameters for other baseline models are set based on experience or in accordance with the settings in the original papers to ensure optimal performance. The experiments were conducted on hardware equipped with NVIDIA GeForce RTX 4050 GPUs, with all models implemented in Pytorch and sharing the same hardware for acceleration.

Table 2 Statistics hyper-parameter settings for the datasets.

Evaluation metrics

To evaluate the performance of the proposed method, we predict user clicks by using the trained model and assess the effectiveness of the click-through rate (CTR) prediction by employing two common evaluation metrics: AUC (Area Under Curve) and F1 score. AUC is an evaluation index that measures the performance of a recommendation system on a scale from 0 to 1, with higher values indicating better performance. The F1 score is an indicator that balances precision and recall, also ranging from 0 to 1, where a higher value indicates better performance.

Baselines

To validate the performance of the proposed model KGCN-UP, we compared it with five classical recommendation approaches categorized into different methods: CF-based (LFM, BPRMF), Embedding-based (CKE, MKR, RippleNet), Path-based (PER), GNN-based (KGCN, KGNN-LS, KGAT, CKAN, KGIN, KGIE, CG-KGR), and CL-based (KGCCL, KGRec). Each category is described as follows:

1) LFM⁴⁰: A collaborative filtering (CF) method that utilizes Alternating Least Squares (ALS) decomposition to derive implicit factors for users and items, constructing an interaction matrix that represents user ratings of items.

2) BPRMF⁴¹: A CF approach that employs pairwise matrix decomposition to capture implicit feedback and ranks user preferences using Bayesian Personalized Ranking (BPR) loss optimization.

3) CKE⁴¹: An embedding-based approach that integrates KG into the recommender system using the TransR [] algorithm to extract structured knowledge, which is then fused with CF techniques.

4) MKR⁴²: An embedding-based method that performs recommendation prediction tasks concurrently with knowledge graph embedding (KGE), using cross compression units that are updated synchronously to enhance recommendation outcomes.

5) RippleNet¹⁰: A path-based approach that propagates potential user preferences through various relational links in the KG, culminating in an item representation that incorporates user preferences.

6) PER¹⁴: A path-based method that represents user-item connections by calculating path similarity between items to derive preference scores, forming a user preference diffusion matrix.

7) KGCN¹⁸: A graph neural network (GNN)-based approach that enriches item representations by capturing higher-order semantic information in the KG through recursive message aggregation.

8) KGAT²⁰: The embeddings of neighbor nodes are recursively updated while adopting an attention mechanism to dynamically adjust the weights of each neighbor, thereby distinguishing the importance of different neighbors in node embeddings.

9) CKAN²¹: A GNN-based approach that introduces a novel dissemination strategy combining collaborative and knowledge information, dynamically adjusting the weight of each neighbor node through an attention mechanism to enhance recommendations.

10) KGIN⁴³: A GNN-based method that extracts rich semantic information from the KG by constructing relational path perceptions, refining key user intent features, and enriching the embedded representations of users and items.

11) KGIE²²: A GNN-based method that constructs a user-item interaction matrix and fuses it with item information through GNNs, effectively capturing user information and preferences and considering user context in the recommendation process.

12) KGCCL⁴⁴: A CL-based method that combines interaction graphs and KGs. By contrasting local and global level, it uses noise enhancement to improve the representations of users and items.

13) KGRec²⁹: A CL-based method that calculates high-scoring triplets and then masks the KG by aligning signals from both the KG and the interaction graph.

Table 3 Performance comparison on different datasets.

Preformance comparison (RQ1)

The performance results of all models are shown in Table 3. By analyzing their performance differences, the following observations are obtained:

1) KGCN-UP achieved the best results. Specifically, compared to the strongest benchmark model, KGCN-UP shows significant improvements in AUC on the Book, Movie, and Course datasets respectively by 0.14%, 0.24%, and 4.94%. We attribute these improvements to: (1) the user preference propagation module, which better captures the higher-order preferences of users; (2) the item neighbor enhancement module, which effectively utilizes the higher-order semantic information from the KG.

2) The introduction of KG information not always enhances the recommender system. Compared to traditional recommendation algorithms like LFM and BPRMF, the CKE model, which embeds knowledge information into matrix factorization, shows a notable performance improvement. This indicates the effectiveness of incorporating knowledge information, aligning with conclusions from previous studies⁷.While PER performs worse than BPRMF, this indicates that the model’s performance can only improve by incorporating appropriate knowledge. This highlights the critical role of knowledge sampling and knowledge denoising. This proves that the method we proposed can effectively handle the application of knowledge graph auxiliary information without turning it into a burden that leads to performance degradation.

3) GNN-based methods exhibit stronger performance. Most of the GNN-based methods outperform embedding-based and path-based methods. This highlights the importance of information propagation between graph nodes and suggests that enhancing the representation of users and items can improve model performance, especially in scenarios with sparser interaction data. This also proves that propagating user preference information can achieve good performance in the sparse MOOC scenario.

Parameter analysis (RQ2)

Our proposed KGCN-UP model involves several hyperparameters, as detailed in Fig. 4. We will specifically discuss how these parameters affect the model’s performance.

1) Impact of Embedding Dimension ($\:d$). We investigated the impact of the embedding dimension on the performance of the KGCN-UP model. As shown in Fig. 4, model performance initially tends to increase with an increase in $\:d$. This improvement is mainly because the model can encode more information from users and entities. However, beyond a certain point, an increase in $\:d$ starts to decrease performance, likely due to higher dimensions introducing excessive noise, which leads to model overfitting and adversely affects performance.

2) Impact of Number of Neighbors ($\:n$). We investigated the impact on the performance of the KGCN-UP model by adjusting the size of neighbors. As shown in Fig. 4, the optimal performance of the KGCN-UP model is achieved when n = 8. This may be because if $\:n$ is too small, the model cannot acquire enough neighbor information, while a large $\:n$ may introduce excessive noise, leading to interference in the feature representation of the target entity. Therefore, finding an appropriate number of neighbors is crucial for the effectiveness of the model.

3) Impact of Triplet Size ($\:s$). We further investigated the robustness of the model by varying the size of each triplet in the path grouping propagation ensemble. As shown in Fig. 4, an initial increase in $\:s$ significantly improves model performance, as it allows the model to encode more knowledge from the KG. However, extracting too much information can cause the number of parameters to skyrocket, increasing the training time and potentially reducing model performance when $\:s$ is too large.

4) Impact of Different Hop Numbers ($\:h$). We modified the numbers of hop in our experiments to investigate its impact on model performance. The results, as shown in Fig. 4, indicate that the optimal performance is achieved when $\:h$ is set to 2. Analysis of this phenomenon suggests that a larger $\:h$ enhances the model’s ability to explore information from distant nodes within the KG, but it also introduces a significant amount of noise. This noise can overwhelm valuable signals, thereby negatively affecting the model’s performance. Conversely, setting $\:h$ too small limits the model’s ability to utilize the relevancy between nodes in the graph, which similarly impairs performance.

Fig. 4

Parameter sensitivity of KGCN-UP.

Ablation comparison (RQ3)

To verify the contribution of the main components in the model to the overall performance, we compared KGCN-UP with the following two variants:

• KGCN-UP1: A variant of KGCN-UP that removes the user preference propagation module.

• KGCN-UP2: A variant of KGCN-UP that removes the item neighbor enhancement module.

Figure 5 shows the results for the two variants and KGCN-UP, from which we observed the following:

1) Removing the user preference module significantly decreases model performance, confirming the effectiveness of exploring latent user preferences through traversing the KG.

2) Removing the item neighbor enhancement module also leads to a performance decline, highlighting the importance of capturing high-order semantic information in the KG.

Fig. 5

Effect of ablation study.

Case study (RQ4)

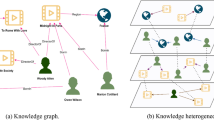
In this section, we demonstrate the effectiveness of the proposed KGCN-UP in a CTR prediction task, as shown in Fig. 6. From the visualization, it’s very clear that the proposed model generates different prediction results for various candidate courses. The user’s preferences are obvious: they have a greater interest in courses related to schools and prefer courses with content that aligns with their interests. For instance, although Software Engineering is also offered by Tsinghua University, the model predicts a low probability of this user selecting it. This is because the content of Software Engineering is less related to Data Structure, which is the user’s main area of interest. On the other hand, courses that are more closely related to computer science, like Data Structure, show a higher chance of being chosen.

Fig. 6

The case study of KGCN-UP. The blue labels indicate the types of entities the user is interested in, while the green labels further refine the focus of attention.

As shown in Fig. 7, the learner selects the Data Structures course on the MOOC platform. Although both Artificial Intelligence and Software Engineering belong to the computer science field and involve algorithm knowledge, the system ultimately recommends the Artificial Intelligence course to the user. This is because the KGCN-UP model, through the extraction of user preferences, identifies that the user prefers courses offered by Tsinghua University. This helps in understanding the patterns in how users select courses and provides a more intuitive visualization of their decision-making process. As a result, the system recommends the Artificial Intelligence course, which is also offered by Tsinghua University.

Fig. 7

The attention-based preference selection of the KGCN-UP model.

Conclusion

In this paper, we propose an end-to-end recommendation system model that effectively integrates with KG. This model not only extends user preferences within the KG through a user preference propagation module, reducing the problem of data sparsity, but also captures high-order structural correlations between entities through a item neighbor enhancement module, enabling it to capture and utilize more complex structural information. Based on these features, the model can balance and optimize user and item representations by using two different structures. Our proposed KGCN-UP model demonstrates astonishing advantages compared to the current state-of-the-art baselines. For future work, we need to introduce Federated learning to store interaction data between users and items in a protected manner, avoiding exposure of private information to local clients.