Introduction

The coronavirus, most commonly introduced as COVID-19 is a global catastrophe which has left millions of people in the lurch1,2,3. The virus was initially emerged in individuals who traveled to a market for seafood in Wuhan City, China, in December 20194. It had affected people badly from normal to the lethal level. The common symptoms of COVID-19 may include but not limited to cough, fatigue, fever, throat soreness and breathing problems5,6,7. COVID-19 urges the world to impose a health emergency and demanded a collective and fruitful efforts to curb this global menace. From the beginning, world health organization (WHO) mainly focused to analyze its symptoms and prepare the effective and accurate vaccines. For the perfect vaccination, WHO gathered the brilliant minds to achieve its landmark target of minimization of lethal impacts of the virus. Vaccination stands as the best effective means to avert and control the disease’s spread. At the end of 2020, The WHO has authorized numerous vaccines for use in emergencies8. Global efforts have been made to launch massive campaign of vaccination which brought down effective results in curbing and stopping the exacerbation of virus9. Some recent publications regarding the efficiency of vaccines can be perceived in10,11,12.

The dynamics of real-world situations can be efficiently analyzed using mathematical models13,14,15,16. Researchers from all over the world develop numerous mathematical models to comprehend the various kinds of diseases and their dynamical aspects. Fractional models offer a more adaptable and practical framework for comprehending and forecasting the evolution of infectious diseases. The transmission of various infectious illnesses has been examined and assessed in17,18,19,20,21,22,23,24,25,26 using mathematical models of fractional order derivatives. The authors performed numerical simulations to validate the theoretical results in addition to analyzing the exact qualitative characteristics of the developed models. Many scholars have established a profound wide range of mathematical models to examine the effectiveness of the vaccines and transmission of COVID-1927,28,29. By applying these models, one can concentrate how an infectious disease extends amongst the masses. The models discussed in30,31,32 may be materialized to amplify all of their sources and execute all control activities more effectively. In33, the authors considered and analyzed COVID-19 mathematical model cobbled with quarantine class and resistive compartment. Because of the quarantine and restive classes, the model is entirely changed from other models that have been developed in the existing works. Peter et al.34 estimated the COVID-19 model by concentrating on actual data that assesses the impacts of several controlling methodologies on the spread of COVID-19 in the human population. The novel COVID-19 has been widely inspected by scholars using mathematical methods from a variety of viewpoints35,36,37. They concentrated on native and sophisticated dynamics, stability theory and numerical tools.

Recently, Keno et al.38 developed and analyzed a deterministic mathematical model for COVID-19 epidemic disease with cost-effectiveness using real data from Ethiopia. The researchers investigated the local and global stability of endemic and disease-free equilibria for the continuous model considering several kinds of criteria. In the present work, three different schemes, which are Euler, RK-4, and NSFD schemes are developed for the original model in order to investigate ecological sustainability and different components of the model. The dynamics of the model are clarified by performing positivity and boundedness properties of solutions. It is revealed that two standard finite difference (SFD) schemes, such as Euler and RK-4 had limitations in capturing the model’s essential dynamics, whereas the third scheme NSFD yields exceptionally accurate and useful findings, and it is suitable for the continuous model. The advanced NSFD technique is being used to better understand the dynamics of COVID-19 transmission and evaluate possible health effects. The NSFD scheme was actually designed for making up over the deficiencies of the RK-4 scheme. The local and global stability of disease-free and endemic equilibria are discussed for the NSFD scheme by employing multiple number of criteria and theories. The results explain that NSFD scheme is unconditionally stable and viable for the continuous model which generates incredible effective results.

The paper is divided into the following categories. In Sect. 2 “SEIHR model”, the COVID-19 mathematical model is presented and its associated parameters are explored. Sect. 3 “COVID-19 model equilibria and basic reproductive number” includess the basic reproduction number and model equilibria. In Sect. 4 “SFD and NSFD numerical schemes”, the conditionally convergent Euler and RK-4 schemes, and unconditionally convergent NSFD scheme are built for the original model. The local and global stability of disease free and endemic equilibria are displayed in the same section for the NFSD scheme. Numerical simulations are given to support our theoretical results. Numerical and theoretical findings portray that the NSFD scheme dominates in every characteristic by controlling the flaws of the RK-4 and Euler schemes. In Sect. 5 “Conclusions”, the conclusions are given.

SEIHR model

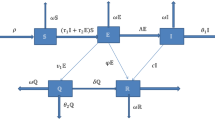
Nonlinear mathematical models that describe the spread dynamics of the deadly COVID-19, are essential in the field of epidemiology. They provide critical insights for public health officials and policymakers. The whole population \(N(t)\) is separated into five different categories in this section: susceptible \(S(t)\), exposed \(E(t)\), infected \(I(t)\), hospitalized \(H(t)\), and recovered \(R(t)\). Then, the nonlinear mathematical model for COVID-1938 is represented as follows.

$$\frac{dS}{{dt}} = q - aSI - u_{1} S + m_{1} R$$
$$\frac{dE}{dt}=aSI-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right) E$$
$$\frac{dI}{dt}={\delta }_{a}E-\left(r+{u}_{1}+\vartheta \right)I$$
(1)
$$\frac{dH}{dt}=rI-\left({t}_{b}+\vartheta +{u}_{1}\right)H$$
$$\frac{dR}{dt}={\tau }_{a}E+{t}_{b}H-\left({m}_{1}+{u}_{1}\right)R.$$

This division is portrayed by the system of ordinary differential equations (ODE’s) represented in Fig. 1. However, the explanation of the parameters is provided in Table 1.

Fig. 1
figure 1

Flowchart for the SEIHR mathematical model, which demonstrates the variations among the model’s compartments.

Full size image
Table 1 The parameters and their description for the suggested SEIHR model (1).
Full size table

In upcoming section, we illustrate the equilibria and basic reproduction number for mathematical model (1).

COVID-19 model equilibria and basic reproductive number

First, we find the equilibria for model (1) as follows.

Disease absence equilibrium point (DAEP)

An equilibrium condition known as disease absence equilibrium point (DAEP) is attained when COVID-19 vanishes. By establishing the model’s (1) right-side equal to 0, it can be attained.

$$q-aSI-{u}_{1}S+{m}_{1}R=0$$
$$aSI-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)E=0$$
$${\delta }_{a}E-\left(r+{u}_{1}+\vartheta \right)I=0$$
(2)
$$rI-\left({t}_{b}+\vartheta +{u}_{1}\right)H=0$$
$${\tau }_{a}E+{t}_{b}H-\left({m}_{1}+{u}_{1}\right)R=0.$$

In order to identify DAEP, we replace \(E=I=H=R=0\) for each differential equation in the system (2) when \(S\ne 0\). Then, we obtain

$$q-{u}_{1}S=0,$$

i.e.

$$S=\frac{q}{{u}_{1}}$$

Thus, if we represent DAEP by \({E}_{0}\)= \(({S}_{0},{E}_{0},{I}_{0},{H}_{0},{R}_{0})\), then it is simple to determine DAEP as \({E}_{0}=\left(\frac{q}{{u}_{1}},\text{0,0},\text{0,0}\right)\).

Endemic equilibrium point (EEP)

The EEP illustrates a situation whereby the disease is persisted in the community rather than being completely eradicated. The quantities for \(S,E,I,H,R\) must be non-zero at the equilibria if the disease present in the population, i.e. if \({E}^{*}\left({S}^{*},{E}^{*},{I}^{*},{H}^{*}, {R}^{*}\right)\) is EEP, then \({E}^{*}\left({S}^{*},{E}^{*},{I}^{*},{H}^{*},{R}^{*}\right)\ne \left(\text{0,0},\text{0,0},0\right)\). The model (2) yields \({S}^{*}=\frac{q-a{S}^{*}{I}^{*}+{m}_{1}{R}^{*}}{{u}_{1}}\), \({E}^{*}=\frac{a{S}^{*}{I}^{*}}{\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}\), \({I}^{*}=\frac{{\delta }_{a}{E}^{*}}{\left(r+{u}_{1}+\vartheta \right)}\), \({H}^{*}=\frac{r{I}^{*}}{\left({t}_{b}+\vartheta +{u}_{1}\right)}\), \({R}^{*}=\frac{{\tau }_{a}{E}^{*}+{t}_{b}{H}^{*}}{\left({m}_{1}+{\tau }_{a}\right)}.\)

The basic reproduction number is provided in the following which is essential for the stability of model (1) equilibria.

Basic reproductive number \({({\varvec{R}}}_{0})\)

The basic reproduction number is the average number of secondary infections that one infectious individual causes in a group of people that are all completely susceptible. It gives an overall assessment of the possibility that an infection will spread throughout a community and is influenced by both the average length of infectiousness and the transmission coefficient. Though, a perfect assessment of secondary infections can’t be given, while studies of epidemiology may yield an average approximation, which is called the basic reproduction number39,40,41. To find \({R}_{0}\), we use the translation \(V(x)\) and transmission \(F\left(x\right)\) matrices, respectively. For model (1), these can be presented as follows.

$$F\left(x\right)=\left[\begin{array}{c}aSI\\ 0\\ 0\end{array}\right]\text{and}V\left(x\right) =\left[\begin{array}{c}\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)E\\ \left(r+{u}_{1}+\vartheta \right)I-{\delta }_{a}E\\ \left({t}_{b}+\vartheta +{u}_{1}\right)H-rI\end{array}\right]$$

Since \({R}_{0}\) is same as the spectral radius, which is determined from the matrix product as \(F{V}^{-1}.\) Therefore, we get.

$${R}_{0}=\frac{a{\delta }_{a}q}{{u}_{1}\left(r+{u}_{1}+\vartheta \right)\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}$$

The following section presents the NSFD scheme and two SFD schemes, namely Euler and RK-4, in order to better comprehend the model (1) dynamics.

SFD and NSFD numerical schemes

An approach for understanding and measuring the dynamics of disease spread is numerical modeling of infectious illnesses. In the current paper, a mathematical model for COVID-19 is proposed and investigated. The goal is to mathematically well understand the spread and behavior dynamics of the disease. To demonstrate the validity and biological animation of mathematical model of COVID-19, we develop two conditionally stable Euler and RK-4 SFD schemes as well as an unconditionally stable NSFD scheme. NSFD schemes are crucial to numerical analysis because they offer better accuracy and stability than standard finite difference techniques, especially for analyzing nonlinear differential equations. The NSFD numerical scheme constructed for model (1) is dynamically credible that retains the positive feature of the solutions. The NSFD scheme guarantees convergence to the model’s equilibria for all time step sizes, however aforementioned SFD schemes break down at large time steps. The findings presented in this research clarify that the previously discussed SFD and NSFD schemes give a clear and detailed picture of the continuous model.

In the following subsection, we first layout Euler scheme for system (1).

Euler scheme

This is one of the earliest and easiest ways to compute the numerical solutions of ODE’s. From model (1), we can write

$$\frac{{S}_{k+1}-{S}_{k}}{h}=q-a{S}_{k}{I}_{k}-{u}_{1}{S}_{k}+{m}_{1}{R}_{k}$$
$${S}_{k+1}-{S}_{k}=hq-ha{S}_{k}{I}_{k}-{hu}_{1}{S}_{k}+{hm}_{1}{R}_{k}$$
$${S}_{k+1}={S}_{k}+hq-ha{S}_{k}{I}_{k}-{hu}_{1}{S}_{k}+{hm}_{1}{R}_{k}.$$

On Similar basis

$$\frac{{E}_{k+1}-{E}_{k}}{h}=a{S}_{k}{I}_{k}-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right){E}_{k}$$
$${E}_{k+1}-{E}_{k}=ha{S}_{k}{I}_{k}-h\left({\delta }_{a}+\vartheta +{\upsilon }_{a}+{\tau }_{a}\right){E}_{k}$$
$${E}_{k+1}={E}_{k}+ha{S}_{n}{I}_{n}-h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right){E}_{k}.$$

Similarly, as

$$\frac{{I}_{k+1}-{I}_{k}}{h}={\delta }_{a}{E}_{k}-\left(r+{u}_{1}+\vartheta \right){I}_{k}$$
$${I}_{k+1}-{I}_{k}={h\delta }_{a}{E}_{n}-h\left(r+{u}_{1}+\varepsilon \right){I}_{n}$$
$${I}_{k+1}={I}_{k}+{h\delta }_{a}{E}_{k}-h\left(r+{u}_{1}+\vartheta \right){I}_{k}.$$

In the same way

$$\frac{{H}_{k+1}-{H}_{k}}{h}=r{I}_{n}-\left({t}_{b}+\vartheta +{u}_{1}\right){H}_{k}$$
$${H}_{k+1}-{H}_{k}=hr{I}_{k}-h\left({t}_{b}+\vartheta +{u}_{1}\right){H}_{n}$$
$${H}_{k+1}={H}_{k}+hr{I}_{k}-h\left({t}_{b}+\vartheta +{u}_{1}\right){H}_{k},$$

and

$$\frac{{R}_{k+1}-{R}_{k}}{h}={\tau }_{a}{E}_{k}+{t}_{b}{H}_{k}-\left({m}_{1}+{u}_{1}\right){R}_{k}$$
$${R}_{k+1}-{R}_{k}={h\tau }_{a}{E}_{k}+h{t}_{b}{H}_{k}-h\left({m}_{1}+{u}_{1}\right){R}_{k}$$
$${R}_{k+1}={R}_{k}+{h\tau }_{a}{E}_{k}+h{t}_{b}{H}_{k}-h\left({m}_{1}+{u}_{1}\right){R}_{k}.$$

Finally, Euler scheme for system (1) becomes

$${S}_{k+1}={S}_{k}+hq-ha{S}_{k}{I}_{k}-{hu}_{1}{S}_{k}+{hm}_{1}{R}_{k}$$
$${E}_{k+1}={E}_{k}+ha{S}_{k}{I}_{k}-h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right){E}_{k}$$
$${I}_{k+1}={I}_{k}+{h\delta }_{a}{E}_{k}-h\left(r+{u}_{1}+\vartheta \right){I}_{k}$$
(3)
$${H}_{k+1}={H}_{k}+hr{I}_{k}-h\left({t}_{b}+\vartheta +{u}_{1}\right){H}_{k}$$
$${R}_{k+1}={R}_{k}+{h\tau }_{a}{E}_{k}+h{t}_{b}{H}_{k}-h\left({m}_{1}+{u}_{1}\right){R}_{k}.$$

Figure 2 (a-d) provides a graphic depiction of the Euler scheme for various step sizes. The Euler scheme produces stable and positive solutions for smaller step sizes, as explained in Fig. 2 (a, b). However, Fig. 2 (c, d) shows the equilibrium point’s instability as the step size grows. This suggests that greater step sizes are not appropriate for Euler scheme.

Fig. 2
figure 2

Graphical illustration of Euler scheme with \(\left({\varvec{a}}\right) h=0.1,\left({\varvec{b}}\right) h=1,\left({\varvec{c}}\right) h=1.7, \text{and} \left({\varvec{d}}\right) h=2.5. \text{The values of fixed parameters are}\) \(q=4.995, a=0.38974,{\tau }_{a}=0.03232,{u}_{1}=0.0301,{m}_{1}=1.2981,{\delta }_{a}=0.000011618,r=0.06813,\vartheta =0.0218,{t}_{b}=0.6450.\).

Full size image

The well-known RK-4 approach is used in the following subsection to solve system (1). The RK-4 scheme is extensively employed method to solve ODE systems. In numerous situations, the RK-4 scheme is frequently employed, unless specified otherwise.

RK-4 scheme

C. V. Runge (1856–1927) and M. W. Kutta (1867–1944), two famous German mathematicians introduced RK–4 method42. It is a commonly used strategy for solving problems and is applied in numerous situations. Let \(S={L}_{1},E={M}_{1},I={N}_{1},H={O}_{1},R={P}_{1},\) then for system (1) the RK-4 scheme can be signified as below.

Stage-1

$${L}_{1}=h\left[q-a{S}_{k}{I}_{k}-{u}_{1}{S}_{k}+{m}_{1}{R}_{k}\right]$$
$${M}_{1}=h\left[a{S}_{k}{I}_{k}-\left(\vartheta ++{u}_{1}+{\tau }_{a}\right){E}_{k}\right]$$
$${N}_{1}=h\left[{\delta }_{a}{E}_{k}-\left(r+{u}_{1}+\vartheta \right){I}_{k}\right]$$
$${O}_{1}=h\left[r{I}_{k}-\left({t}_{b}+\vartheta +{u}_{1}\right){H}_{k}\right]$$
$${P}_{1}=h\left[{\tau }_{a}{E}_{k}+{t}_{b}{H}_{k}-\left({m}_{1}+{u}_{1}\right){R}_{k}\right].$$

Stage-2

$${L}_{2}=h\left[q-a\left({S}_{k}+\frac{{L}_{1}}{2}\right)\left({I}_{k}+\frac{{N}_{1}}{2}\right)-{u}_{1}\left({S}_{k}+\frac{{L}_{1}}{2}\right)+{m}_{1}\left({R}_{k}+\frac{{P}_{1}}{2}\right)\right]$$
$${M}_{2}=h\left[a{(S}_{k}+\frac{{L}_{1}}{2})({I}_{k}+\frac{{N}_{1}}{2})-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\left({E}_{k}+\frac{{M}_{1}}{2}\right)\right]$$
$${N}_{2}=h\left[{\delta }_{a}\left({E}_{k}+\frac{{M}_{1}}{2}\right)-\left(r+{u}_{1}+\vartheta \right)\left({I}_{k}+\frac{{N}_{1}}{2}\right)\right]$$
$${O}_{2}=h\left[r\left({I}_{k}+\frac{{N}_{1}}{2}\right)-\left({t}_{b}+\vartheta +{u}_{1}\right)\left({H}_{k}+\frac{{O}_{1}}{2}\right)\right]$$
$${P}_{2}=h\left[{\tau }_{a}\left({E}_{k}+\frac{{M}_{1}}{2}\right)+{t}_{b}\left({H}_{k}+\frac{{O}_{1}}{2}\right) -\left({m}_{1}+{u}_{1}\right)\left({R}_{k}+\frac{{P}_{1}}{2}\right)\right]$$

Stage-3

$${L}_{3}=h\left[q-a\left({S}_{k}+\frac{{L}_{2}}{2}\right)\left({I}_{k}+\frac{{N}_{2}}{2}\right)-{u}_{1}\left({S}_{k}+\frac{{L}_{2}}{2}\right)+{m}_{1}\left({R}_{k}+\frac{{P}_{2}}{2}\right)\right]$$
$${M}_{3}=h\left[a\left({S}_{k}+\frac{{L}_{2}}{2}\right)\left({I}_{k}+\frac{{N}_{2}}{2}\right)-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\left({E}_{k}+\frac{{M}_{2}}{2}\right)\right]$$
$${N}_{3}=h\left[{\delta }_{a}\left({E}_{k}+\frac{{M}_{2}}{2}\right)-\left(r+{u}_{1}+\vartheta \right)\left({I}_{k}+\frac{{N}_{2}}{2}\right)\right]$$
$${O}_{3}=h\left[r\left({I}_{k}+\frac{{N}_{2}}{2}\right)-\left({t}_{b}+\vartheta +{u}_{1}\right)\left({H}_{k}+\frac{{O}_{2}}{2}\right)\right]$$
$${P}_{3}=h\left[{\tau }_{a}\left({E}_{k}+\frac{{M}_{2}}{2}\right)+{t}_{b}\left({H}_{k}+\frac{{O}_{2}}{2}\right) -\left({m}_{1}+{u}_{1}\right)\left({R}_{k}+\frac{{P}_{2}}{2}\right)\right].$$

Stage-4

$${L}_{4}=h\left[q-a{(S}_{k}+{L}_{3})({I}_{k}+{N}_{3})-{u}_{1}{(S}_{k}+{L}_{3}) +{m}_{1}({R}_{k}+{P}_{3})\right]$$
$${M}_{4}=h\left[a{(S}_{k}+{L}_{4})\left({I}_{k}+{N}_{3}\right)-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right){(E}_{k}+{M}_{3})\right]$$
$${N}_{4}=h\left[{\delta }_{a}{(E}_{k}+{M}_{3})-\left(r+{u}_{1}+\vartheta \right)({I}_{k}+{N}_{3})\right]$$
$${O}_{4}=h\left[r({I}_{k}+{N}_{3})-\left({t}_{b}+\vartheta +{u}_{1}\right)({H}_{k}+{O}_{3})\right]$$
$${P}_{4}=h\left[{\tau }_{a}{(E}_{k}+{M}_{3})+{t}_{b}({H}_{k}+{O}_{3})-\left({m}_{1}+{u}_{1}\right)({R}_{k}+{P}_{3})\right].$$
$${S}_{k+1}={S}_{k}+\frac{1}{6}\left\{{L}_{1}+2{L}_{2}+2{L}_{3}+{L}_{4}\right\}$$
$${E}_{k+1}={E}_{k}+\frac{1}{6}\{{M}_{1}+2{M}_{2}+2{M}_{3}+{M}_{4}\}$$
$${I}_{k+1}={I}_{k}+\frac{1}{6}\{{N}_{1}+2{N}_{2}+2{N}_{3}+{N}_{4}\}$$
$${H}_{k+1}={H}_{k}+\frac{1}{6}\{{O}_{1}+2{O}_{2}+2{O}_{3}+{O}_{4}\}$$
$${R}_{k+1}={R}_{k}+\frac{1}{6}\left\{{P}_{1}+{2P}_{2}+2{P}_{3}+{P}_{4}\right\}.$$

Figure 3 (a-d) shows an example of RK-4 scheme containing different step sizes. The RK-4 method provides solutions that are positive and stable for lower step sizes, as revealed in Fig. 3 (a, b). However, Fig. 3 (c, d) shows the equilibrium point’s instability as the step size grows. This suggests that greater step sizes are not suitable for RK-4 scheme.

Fig. 3
figure 3

Graphical illustration of RK-4 scheme with\(\left({\varvec{a}}\right) h=0.1,\left({\varvec{b}}\right) h=1,\left({\varvec{c}}\right) h=2.2, \text{and} \left({\varvec{d}}\right) h=2.4\). The values of fixed parameters are \(q=4.995, a=0.38974,{\tau }_{a}=0.03232,{u}_{1}=0.0301,{m}_{1}=1.2981,{\delta }_{a}=0.000011618,r=0.06813,\vartheta =0.0218,{t}_{b}=0.6450\)Generally.

Full size image

In the following, we build the NSFD scheme for model (1) which is independent of the step size, guaranteeing the boundedness of the solutions and provide better outcomes in all aspects.

The NSFD scheme

The primary goal of this section is to develop a discrete, smoothly changing NSFD scheme for model (1). The Mickens43,44 approach is remarkable for producing a discrete model that has similarities to the continuous model. For both partial and ordinary differential equations, the NSFD scheme provides a flexible way for discrete model creation and numerical solution findings. According to Shokri et al.45, discretizing the derivative and accurately estimating nonlinear terms are the two key components that make the NSFD scheme effective. \(\text{The standard notation for the first order derivative }df/dx\) is written as \(\frac{f\left(y+h\right)-f\left(y\right)}{h}\), where \(h\) represents the step size. Mickens specified that, this term can be written as \(\frac{f\left(y+h\right)-f\left(y\right)}{\varphi \left(h\right)}\), where \(\varphi \left(h\right)\) is a rising denominator function. For model (1), \({S}_{k}, {E}_{k},{I}_{k}, {H}_{k}{\text{and} R}_{k}\) are the numerical estimates of \(S\left(t\right)\),\(E\left(t\right)\),\(I(t)\), \(H\left(t\right)\text{ and }R\left(t\right)\) at \(t=kh\), where \(h\) denotes the step size and \(k\) is a nonnegative integer. Therefore, from model (1) we can express

$$\frac{{S}_{k+1}-{S}_{k}}{h}=q-a{S}_{k+1}{I}_{k}-{u}_{1}{S}_{k+1}+{m}_{1}{R}_{k}$$
$$\frac{{E}_{k+1}-{E}_{k}}{h}=a{S}_{k+1}{I}_{k}-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right){E}_{k+1}$$
$$\frac{{I}_{k+1}-{I}_{k}}{h}={\delta }_{a}{E}_{k+1}-\left(r+{u}_{1}+\vartheta \right){I}_{k+1}$$
(4)
$$\frac{{H}_{k+1} -{H}_{k}}{h}=r{I}_{k+1}-\left({t}_{b}+\vartheta +{u}_{1}\right){H}_{k+1}$$
$$\frac{{R}_{k+1}-{R}_{k}}{h}={\tau }_{a}{E}_{k+1}+{t}_{b}{H}_{k+1}-\left({m}_{1}+{u}_{1}\right){R}_{k+1}$$

After simplifying, the explicit form of NSFD scheme (4) can be given as

$${S}_{k+1}=\frac{{(S}_{k}+hq+h{{m}_{1}R}_{k})}{\left(1+ha{I}_{k}+h{u}_{1}\right)}$$
$${E}_{k+1}=\frac{{E}_{k}+ha{S}_{k+1}{I}_{k}}{\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}$$
$${I}_{k+1}=\frac{{I}_{k}+h{\delta }_{a}{E}_{k+1}}{\left(1+h\left(r+{u}_{1}+\vartheta \right)\right)}$$
(5)
$${H}_{k+1}=\frac{{H}_{k}+hr{I}_{k+1}}{\left(1+h\left({t}_{b}+\vartheta +{u}_{1}\right)\right)}$$
$${R}_{k+1}=\frac{{R}_{k}+{h\tau }_{a}{E}_{k+1}+h{t}_{b}{H}_{k+1}}{\left(1+h\left({m}_{1}+{u}_{1}\right)\right)}.$$

The numerical solutions of epidemic models must persist positive in order to guarantee validity and applicability. However, it is crucial to make sure that the total population is never greater than the sum of the populations in each compartment. The positivity and boundedness are successfully addressed in the subsection that follows.

The NSFD scheme’s positivity and boundedness

Let the starting values of scheme (5) are positive, i.e. \({S}_{0},{E}_{0},{I}_{0},{H}_{0},{R}_{0}\ge 0\). Due to the expectancies, the predicted outcomes for these variables are also nonnegative., i.e. \({S}_{k}{, E}_{k},{I}_{k},{H}_{k},{R}_{k}\ge 0\). Hence, the NSFD scheme (5) is positive, i.e. \({S}_{k+1},{E}_{k+1},{I}_{k+1},{H}_{k+1},{R}_{k+1}\ge 0\). To find the boundedness of solutions for NSFD system (5), we write \({P}_{k}={S}_{k}+{E}_{k}+{I}_{k}+{H}_{k}+{R}_{k},\). Then

$$\frac{{P}_{k+1}-{P}_{k}}{h}=q-{u}_{1}{P}_{k+1}-\vartheta \left({E}_{k+1}+{I}_{k+1}+{H}_{k+1}\right)-{m}_{1}\left({R}_{k+1}-{R}_{k}\right),$$
(6)

From (6), we can write.

$$\frac{{P}_{k+1}-{P}_{k}}{h}\le q-{u}_{1}{P}_{k+1}$$

I.e.

$$(1+h{u}_{1}){P}_{k+1}\le hq+{P}_{k}.$$
$${P}_{k+1}\le \frac{hq}{(1+h{u}_{1})}+\frac{{P}_{k}}{(1+h{u}_{1})}\Leftrightarrow {P}_{k}\le hq{\sum }_{j=1}^{k}{\left(\frac{1}{1+h{u}_{1}}\right)}^{j}+{P}_{0}{\left(\frac{1}{1+h{u}_{1}}\right)}^{k}.$$

If \(0<P\left(0\right)<\frac{q}{{u}_{1}}\), then Gronwall’s inequality permits us to establish

$${P}_{k}\le \frac{q}{{u}_{1}}\left(1-\frac{1}{{\left(1+h{u}_{1}\right)}^{k}}\right)+{P}_{0}{\left(\frac{1}{1+h{u}_{1}}\right)}^{k}=\frac{q}{{u}_{1}}+\left({P}_{0}-\frac{q}{{u}_{1} }\right){\left(\frac{1}{1+h{u}_{1}}\right)}^{k}.$$

As \(\frac{1}{1+h{u}_{1}}<1\), therefore we acquire \({P}_{k}\to \frac{q}{{u}_{1}}\) whenever \(k\to \infty .\) This shows that the system (5)’s solutions are bounded, and the reasonable region turns into

$$B=\left\{\left({S}_{k}+{E}_{k}+{I}_{k}+{H}_{k}+{R}_{k}\right):0\le {S}_{k}+{E}_{k}+{I}_{k}+{H}_{k}+{R}_{k}\le \frac{q}{{u}_{1}}\right\}.$$

The following subsection discusses the local stability of DAEP and EEP for NSFD scheme (5).

Local stability of equilibria

For local asymptotic stability (LAS) of equilibria, assume

$${S}_{k+1}=\frac{hq+{S}_{k}+{m}_{1}{R}_{k}}{1+h\left(a{I}_{n}+{u}_{1}\right)}={s}_{1}$$
$${E}_{k+1}=\frac{ha{S}_{k+1}{I}_{k}+{E}_{k}}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}={s}_{2}$$
$${I}_{k+1}=\frac{h{\delta }_{a}{E}_{k+1}+{I}_{k}}{1+h\left(r+{u}_{1}+\vartheta \right)}={s}_{3}$$
(7)
$${H}_{k+1}=\frac{hr{I}_{k+1}+{H}_{k}}{1+h\left({t}_{b}+\vartheta +{u}_{1}\right)}={s}_{4}$$
$${R}_{k+1}=\frac{h\left({\tau }_{a}{E}_{k+1}+{t}_{b}{H}_{k+1}\right)+{R}_{k}}{1+h\left({m}_{1}+{u}_{1}\right)}={s}_{5}.$$

We will implement the Schur-Cohn criterion46,47 as stipulated in the subsequent Lemma 1 to establish that DAEP is LAS.

Lemma 1

The solutions to \({\Gamma }^{2}-E\Gamma +F=0\) ensure that \(\left|{\Gamma }_{k}\right|<1 \text{for} k=\text{1,2}\) \(\iff\) the prerequisites are met.

  1. 1.

    \(F<1,\) 

  2. 2.

    \(1+E+F>0,\) 

  3. 3.

    \(1-E+F>0.\) 

where \(F\) concerns to the J-matrix’s determinant and \(E\) specifies the trace.

Theorem 1

For all \(h>0\), the DAEP of the NSFD scheme (5) for model (1) is LAS whenever \({R}_{0}<1\)

Proof

The above-mentioned data can be employed to get the J-matrix as follows.

$$J(S,E,I,H,R)=\left[\begin{array}{ccccc}\frac{\partial {s}_{1}}{\partial S}& \frac{\partial {s}_{1}}{\partial E}& \frac{\partial {s}_{1}}{\partial I}& \frac{\partial {s}_{1}}{\partial H}& \frac{\partial {s}_{1}}{\partial R}\\ \frac{\partial {s}_{2}}{\partial S}& \frac{\partial {s}_{2}}{\partial E}& \frac{\partial {s}_{2}}{\partial I}& \frac{\partial {s}_{2}}{\partial H}& \frac{\partial {s}_{2}}{\partial R}\\ \frac{\partial {s}_{3}}{\partial S}& \frac{\partial {s}_{3}}{\partial E}& \frac{\partial {s}_{3}}{\partial I}& \frac{\partial {s}_{3}}{\partial H}& \frac{\partial {s}_{3}}{\partial R}\\ \frac{\partial {s}_{4}}{\partial S}& \frac{\partial {s}_{4}}{\partial E}& \frac{\partial {s}_{4}}{\partial I}& \frac{\partial {s}_{4}}{\partial H}& \frac{\partial {s}_{4}}{\partial R}\\ \frac{\partial {s}_{5}}{\partial S}& \frac{\partial {s}_{5}}{\partial E}& \frac{\partial {s}_{5}}{\partial I}& \frac{\partial {s}_{5}}{\partial H}& \frac{\partial {s}_{5}}{\partial R}\end{array}\right]$$
(8)

where \({s}_{1},{s}_{2},{s}_{3},{s}_{4}\) and \({s}_{5}\) are provided in (7). The list of derivatives involved in (8) can be found as follows.

$$\begin{array}{*{20}{l}} {\frac{{\partial {s_1}}}{{\partial S}} = \frac{1}{{1 + h\left( {a{I_k} + {u_1}} \right)}},} \\ {\frac{{\partial {s_1}}}{{\partial E}} = 0,\frac{{\partial {s_1}}}{{\partial I}} = \frac{{ - \left( {hq + {m_1}{R_k} + {S_k}} \right)ha}}{{{{\left( {1 + h\left( {a{I_k} + {u_1}} \right)} \right)}^2}}},} \\ {\frac{{\partial {s_1}}}{{\partial H}} = 0,\frac{{\partial {s_1}}}{{\partial R}} = \frac{{{m_1}}}{{1 + h\left( {a{I_k} + {u_1}} \right)}},} \\ {\frac{{\partial {s_2}}}{{\partial S}} = \frac{{ha{I_k}}}{{1 + h\left( {{\delta _{a11}} + \vartheta + {u_1} + {\tau _{a3}}} \right)}},} \\ {\frac{{\partial {s_2}}}{{\partial E}} = \frac{1}{{1 + h\left( {{\delta _{a11}} + \vartheta + {u_1} + {\tau _{a3}}} \right)}},} \\ \begin{gathered} \frac{{\partial {s_2}}}{{\partial I}} = \frac{{ha{S_{k + 1}}}}{{1 + h\left( {{\delta _{a11}} + \vartheta + {u_1} + {\tau _{a3}}} \right)}}, \hfill \\ \frac{{\partial {s_2}}}{{\partial H}} = 0,\frac{{\partial {s_2}}}{{\partial R}} = 0,\frac{{\partial {s_3}}}{{\partial S}} = 0, \hfill \\ \end{gathered} \\ {\frac{{\partial {s_3}}}{{\partial E}} = \frac{{h{\delta _{a11}}}}{{1 + h\left( {r + {u_1} + \vartheta } \right)}},} \\ {\frac{{\partial {s_3}}}{{\partial I}} = \frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}},} \\ {\frac{{\partial {s_3}}}{{\partial H}} = 0\frac{{\partial {s_3}}}{{\partial R}} = 0,\frac{{\partial {s_4}}}{{\partial S}} = 0} \\ {\frac{{\partial {s_4}}}{{\partial E}} = 0,\frac{{\partial {s_4}}}{{\partial I}} = \frac{{hr}}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}}} \\ \begin{gathered} \frac{{\partial {s_4}}}{{\partial H}} = \frac{1}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}}, \hfill \\ \frac{{\partial {s_4}}}{{\partial R}} = 0 \hfill \\ \end{gathered} \\ {\frac{{\partial {s_5}}}{{\partial S}} = 0,\frac{{\partial {s_5}}}{{\partial E}} = \frac{{h{\tau _{a3}}}}{{1 + h\left( {{m_1} + {u_1}} \right)}};} \\ {\frac{{\partial {s_5}}}{{\partial I}} = 0,\frac{{\partial {s_5}}}{{\partial H}} = \frac{{h{\tau _b}}}{{1 + h\left( {{m_1} + {u_1}} \right)}},} \\ {\frac{{\partial {s_5}}}{{\partial R}} = \frac{1}{{1 + h\left( {{m_1} + {u_1}} \right)}}} \\ {} \end{array}$$

By inserting all of the aforementioned derivatives in (8), we obtain

$$J=\left[\begin{array}{ccccc}\frac{1}{1+h\left(a{I}_{k}+{u}_{1}\right)}& 0& \frac{-\left(hq+{m}_{1}{R}_{k}+{S}_{k}\right)ha}{{\left(1+h\left(a{I}_{k}+{u}_{1}\right)\right)}^{2}}& 0& \frac{{m}_{1}}{1+h\left(a{I}_{k}+{u}_{1}\right)}\\ \frac{ha{I}_{k}}{1+h\left({\delta }_{a11}+\vartheta +{u}_{1}+{\tau }_{a3}\right)}& \frac{1}{1+h\left({\delta }_{a11}+\vartheta +{u}_{1}+{\tau }_{a3}\right)}& \frac{ha{S}_{k+1}}{1+h\left({\delta }_{a11}+\vartheta +{u}_{1}+{\tau }_{a3}\right)}& 0& 0\\ 0& \frac{h{\delta }_{a11}}{1+h\left(r+{u}_{1}+\vartheta \right)}& \frac{1}{1+h\left(r+{u}_{1}+\vartheta \right)}& 0& 0\\ 0& 0& \frac{hr}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}& \frac{1}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}& 0\\ 0& \frac{h{\tau }_{b}}{1+h\left({m}_{1}+{u}_{1}\right)}& 0& \frac{h{\tau }_{b}}{1+h\left({m}_{1}+{u}_{1}\right)}& \frac{1}{1+h\left({m}_{1}+{u}_{1}\right)}\end{array}\right]$$
(9)

At DAEP \({E}_{0}=\left(\frac{q}{{u}_{1}},\text{0,0},\text{0,0}\right)\), the matrix (9) becomes.

$$J = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{1 + h\left( {a{I_k} + {u_1}} \right)}}}&0&{\frac{{ - \left( {hq + {m_1}{R_k} + {S_k}} \right)ha}}{{{{\left( {1 + h\left( {a{I_k} + {u_1}} \right)} \right)}^2}}}}&0&{\frac{{{m_1}}}{{1 + h\left( {a{I_k} + {u_1}} \right)}}} \\ {\frac{{ha{I_k}}}{{1 + h\left( {{\delta _{a11}} + \vartheta + {u_1} + {\tau _{a3}}} \right)}}}&{\frac{1}{{1 + h\left( {{\delta _{a11}} + \vartheta + {u_1} + {\tau _{a3}}} \right)}}}&{\frac{{ha{S_{k + 1}}}}{{1 + h\left( {{\delta _{a11}} + \vartheta + {u_1} + {\tau _{a3}}} \right)}}}&0&0 \\ 0&{\frac{{h{\delta _{a11}}}}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}}&{\frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}}&0&0 \\ 0&0&{\frac{{hr}}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}}}&{\frac{1}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}}}&0 \\ 0&{\frac{{h{\tau _b}}}{{1 + h\left( {{m_1} + {u_1}} \right)}}}&0&{\frac{{h{\tau _b}}}{{1 + h\left( {{m_1} + {u_1}} \right)}}}&{\frac{1}{{1 + h\left( {{m_1} + {u_1}} \right)}}} \end{array}} \right]$$

To find the eigenvalues, we adopt.

$$\left|J\left({E}_{0}\right)-\Gamma I\right|=0,$$

I.e.

$$\left|\begin{array}{ccccc}\frac{1}{1+h{u}_{1}}-\Gamma & 0& \frac{-\left(hq+\frac{q}{{u}_{1}}\right)ha}{{\left(1+h{u}_{1}\right)}^{2}}& 0& \frac{{m}_{1}}{1+h{u}_{1}}\\ 0& \frac{1}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}-\Gamma & \frac{haq}{{u}_{1}\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}& 0& 0\\ 0& \frac{h{\delta }_{a}}{1+h\left(r+{u}_{1}+\vartheta \right)}& \frac{1}{1+h\left(r+{u}_{1}+\vartheta \right)}-\Gamma & 0& 0\\ 0& 0& \frac{hr}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}& \frac{1}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}-\Gamma & 0\\ 0& \frac{h{\tau }_{a}}{1+h\left({m}_{1}+{u}_{1}\right)}& 0& \frac{h{\tau }_{b}}{1+h\left({m}_{1}+{u}_{1}\right)}& \frac{1}{1+h\left({m}_{1}+{u}_{1}\right)}-\Gamma \end{array}\right|=0$$

Easy calculations produce outcomes

$$\left(\frac{1}{1+h{u}_{1}}-\Gamma \right)\left(\frac{1}{1+h\left({m}_{1}+{u}_{1}\right)}-\Gamma \right)\left(\frac{1}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}- \Gamma \right)\left|\begin{array}{cc}\frac{1}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}-\Gamma & \frac{haq}{{u}_{1}\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}\\ \frac{h{\delta }_{a}}{1+h\left(r+{u}_{1}+\vartheta \right)}& \frac{1}{1+h\left(r+{u}_{1}+\vartheta \right)}-\Gamma \end{array}\right|=0.$$
(10)

The Eq. (10) provides \({\Gamma }_{1}=\frac{1}{1+h{u}_{1}}<1,{\Gamma }_{2}=\frac{1}{1+h\left({m}_{1}+{u}_{1}\right)}<1.\) and \({\Gamma }_{3}=\frac{1}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}<1\).To look for remaining eigenvalues, we use.

$$\left|\begin{array}{cc}\frac{1}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}-\Gamma & \frac{haq}{{u}_{1}\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}\\ \frac{h{\delta }_{a}}{1+h\left(r+{u}_{1}+\vartheta \right)}& \frac{1}{1+h\left(r+{u}_{1}+\vartheta \right)}-\Gamma \end{array}\right|=0,$$

I.e.

$$\begin{array}{*{20}{l}}\begin{gathered}{\Gamma ^2}{\kern 1pt} - \Gamma \left( {\frac{1}{{1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)}} + \frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}} \right) \hfill \\\frac{1}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)\left( {1 + h\left( {r + {u_1} + \vartheta } \right)} \right)}} \hfill \\- \frac{{h{\delta _a}}}{{\;\;\;\;1 + h\left( {r + {u_1} + \vartheta } \right)}}\frac{{haq}}{{{u_1}\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}} = 0 \hfill \\ \end{gathered} \\ {\;\;} \\ {} \\ {} \\ {} \\ \begin{gathered}\hfill \\\hfill \\ \end{gathered} \\ \begin{gathered}\hfill \\\hfill \\ \end{gathered} \\ \end{array}$$
(11)

Comparing Eq. (11) with \({\Gamma }^{2}-E\Gamma +F=0\), we get.

$$\begin{array}{*{20}{l}}\begin{gathered} E = \frac{1}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}} + \frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}and \hfill \\ F = \frac{1}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)\left( {1 + h\left( {r + {u_1} + \vartheta } \right)} \right)}} \hfill \\- \frac{{h{\delta _a}}}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}\frac{{haq}}{{{u_1}\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}}\;Ifthen{R_0} < 1,then\; \hfill \\\hfill \\ \end{gathered} \\ {\;\;} \\ {} \\ {} \\ {} \\ \begin{gathered}\hfill \\\hfill \\ \end{gathered} \\ {} \\ {} \\ {} \\ {} \\ \begin{gathered}\hfill \\\hfill \\ \end{gathered} \\ {} \\ {} \\ {} \\ {} \end{array}$$
  1. 1.

    \(F=\frac{1}{\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)\left(1+h\left(r+{u}_{1}+\vartheta \right)\right)}-\frac{h{\delta }_{a}}{1+h\left(r+{u}_{1}+\vartheta \right)}\frac{haq}{{u}_{1}\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}<1\) 

  2. 2.

    \(1+E+F=1+\frac{1}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}+\frac{1}{1+h\left(r+{u}_{1}+\vartheta \right)}+\frac{1}{\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)\left(1+h\left(r+{u}_{1}+\vartheta \right)\right)}- \frac{h{\delta }_{a}}{1+h\left(r+{u}_{1}+\vartheta \right)}\frac{haq}{{u}_{1}\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}>0\) 

  3. 3.

    \(1-E+F=1-\frac{1}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}-\frac{1}{1+h\left(r+{u}_{1}+\vartheta \right)}+\frac{1}{\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)\left(1+h\left(r+{u}_{1}+\vartheta \right)\right)}- \frac{h{\delta }_{a}}{1+h\left(r+{u}_{1}+\vartheta \right)}\frac{haq}{{u}_{1}\left(1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)\right)}>0\) 

Therefore, the Schur-Cohn condition met whenever \({R}_{0}<1\). The DAEP \({E}_{0}\) of the discrete NSFD scheme (5) then turn LAS when \({R}_{0}<1\).

To discuss LAS of EEP, substitute \({R}_{k}\) by \(\left(\frac{q}{{u}_{1}}-{S}_{k}-{E}_{k}-{I}_{k}-{H}_{k}\right)\) in Eq. (4). The system (4) will be reduced to

$$\frac{{S}_{k+1}-{S}_{k}}{h}=q-a{S}_{k+1}{I}_{k}-{u}_{1}{S}_{k+1}+{m}_{1}\left(\frac{q}{{u}_{1}}-{S}_{k}-{E}_{k}-{I}_{k}-{H}_{k}\right)$$
$$\frac{{E}_{k+1}-{E}_{k}}{h}=a{S}_{k+1}{I}_{k}-\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right){E}_{k+1}$$
$$\frac{{I}_{k+1}-{I}_{k}}{h}={\delta }_{a}{E}_{k+1}-\left(r+{u}_{1}+\vartheta \right){I}_{k+1}$$
$$\frac{{H}_{k+1} -{H}_{k}}{h}=r{I}_{k+1}-\left({\tau }_{b}+\vartheta +{u}_{1}\right){H}_{k+1}.$$

Now the above system becomes

$${S}_{k+1}=\frac{hq+{S}_{k}+h{m}_{1}\left(\frac{q}{{u}_{1}}-{S}_{k}-{E}_{k}-{I}_{k}-{H}_{k}\right)}{1+h\left(a{I}_{k}+{u}_{1}\right)}$$
$${E}_{k+1}=\frac{ha{S}_{k+1}{I}_{k}+{E}_{k}}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)}$$
(12)
$${I}_{k+1}=\frac{h{\delta }_{a}{E}_{k+1}+{I}_{k}}{1+h\left(r+{u}_{1}+\vartheta \right)}$$
$${H}_{k+1}=\frac{hr{I}_{k+1}+{H}_{k}}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}.$$

Let

$${S}_{k+1}=\frac{hq+{S}_{k}+{hm}_{1}\left(\frac{q}{{u}_{1}}-{S}_{k}-{E}_{k}-{I}_{k}-{H}_{k}\right)}{1+h\left(a{I}_{k}+{u}_{1}\right)}={k}_{1}$$
$${E}_{k+1}=\frac{ha{S}_{k+1}{I}_{k}+{E}_{k}}{1+h\left({\delta }_{a}+\vartheta +{u}_{1}+{\tau }_{a}\right)} ={k}_{2}$$
$${I}_{k+1}=\frac{h{\delta }_{a}{E}_{k+1}+{I}_{k}}{1+h\left(r+{u}_{1}+\vartheta \right)}={k}_{3}$$
(13)
$${H}_{k+1}=\frac{hr{I}_{k+1}+{H}_{k}}{1+h\left({\tau }_{b}+\vartheta +{u}_{1}\right)}={k}_{4}.$$

Theorem 2

For all \(h>0\), the EEP of the NSFD scheme (12) for model (1) is LAS whenever \({R}_{0}>1\).

Proof

We find the derivatives of (13) as follows.

$$\frac{\partial {k}_{1}}{\partial S}=\frac{1-h{m}_{1}}{\left(1+h\left(a{I}_{k}+{u}_{1}\right)\right)},\frac{\partial {k}_{1}}{\partial E}=\frac{-h{m}_{1}}{1+h\left(a{I}_{k}+{u}_{1}\right)},\frac{\partial {k}_{1}}{\partial I}=\frac{-{hm}_{1}}{1+h\left(a{I}_{k}+{u}_{1}\right)}-\frac{\left(hq+{S}_{k}+h{m}_{1}\left(\frac{q}{{u}_{1}}-{S}_{k}-{E}_{k}-{I}_{k}-{H}_{k}\right)\right)ha}{{\left(1+h\left(a{I}_{k}+{u}_{1}\right)\right)}^{2}},$$
$$\begin{array}{*{20}{l}} {\frac{{\partial {k_1}}}{{\partial H}} = \frac{{ - h{m_1}}}{{1 + h\left( {a{I_k} + {u_1}} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial S}} = \frac{{ha{I_k}}}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial E}} = \frac{1}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial I}} = \frac{{ha{S_{k + 1}}}}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},frac\partial {k_2}\partial H = 0,\frac{{\partial {k_3}}}{{\partial S}} = 0,} \\ \begin{gathered} \frac{{\partial {k_3}}}{{\partial E}} = \frac{{h{\delta _a}}}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}, \hfill \\ \frac{{\partial {k_3}}}{{\partial I}} = \frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}}, \hfill \\ \end{gathered} \\ {\frac{{\partial {k_4}}}{{\partial I}} = \frac{{hr}}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}},} \\ {\frac{{\partial {k_4}}}{{\partial H}} = \frac{1}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}},} \\ \end{array}$$

By putting EEP \({E}^{*}\) in above derivatives, we get

$$\frac{\partial {k}_{1}}{\partial {S}^{*}}=\frac{1-{hm}_{1}}{\left(1+h\left(a{I}^{*}+{u}_{1}\right)\right)}, \frac{\partial {k}_{1}}{\partial {E}^{*}}=\frac{-h{m}_{1}}{1+h\left(a{I}^{*}+{u}_{1}\right)},\frac{\partial {k}_{1}}{\partial {I}^{*}}=\frac{-h{m}_{1}}{1+h\left(a{I}^{*}+{u}_{1}\right)}-\frac{\left(hq+{S}^{*}+h{m}_{1}\left(\frac{q}{{u}_{1}}-{S}^{*}-{E}^{*}-{I}^{*}-{H}^{*}\right)\right)ha}{{\left(1+h\left(a{I}^{*}+{u}_{1}\right)\right)}^{2}},$$
$$\begin{array}{*{20}{l}} {\frac{{\partial {k_1}}}{{\partial H}} = \frac{{ - h{m_1}}}{{1 + h\left( {a{I_k} + {u_1}} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial S}} = \frac{{ha{I_k}}}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial E}} = \frac{1}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial I}} = \frac{{ha{S_{k + 1}}}}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {\frac{{\partial {k_2}}}{{\partial H}} = 0,\frac{{\partial {k_3}}}{{\partial S}} = 0,\frac{{\partial {k_3}}}{{\partial E}} = \frac{{h{\delta _a}}}{{1 + h\left( {r + {u_1} + \vartheta } \right)}},} \\ {\frac{{\partial {k_3}}}{{\partial I}} = \frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}},} \\ {\frac{{\partial {k_3}}}{{\partial H}} = 0,\frac{{\partial {k_4}}}{{\partial S}} = 0,\frac{{\partial {k_4}}}{{\partial E}} = 0,} \\ {\frac{{\partial {k_4}}}{{\partial I}} = \frac{{hr}}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}},} \\ {\frac{{\partial {k_4}}}{{\partial H}} = \frac{1}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}}} \end{array}$$

Let

$${g}_{1}=\frac{1-h{m}_{1}}{\left(1+h\left(a{I}^{*}+{u}_{1}\right)\right)},{g}_{2}=\frac{-h{m}_{1}}{1+h\left(a{I}^{*}+{u}_{1}\right)},{g}_{3}=\frac{-h{m}_{1}}{1+h\left(a{I}^{*}+{u}_{1}\right)}-\frac{\left(hq+{S}^{*}+{hm}_{1}\left(\frac{q}{{u}_{1}}-{S}^{*}-{E}^{*}-{I}^{*}-{H}^{*}\right)\right)ha}{{\left(1+h\left(a{I}^{*}+{u}_{1}\right)\right)}^{2}},$$
$$\begin{array}{*{20}{l}} {{g_4} = \frac{{ - h{m_1}}}{{1 + h\left( {a{I^*} + {u_1}} \right)}}} \\ {{g_5} = \frac{{ha{I^*}}}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {{g_6} = \frac{1}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {{g_7} = \frac{{ha{S^*}}}{{\left( {1 + h\left( {{\delta _a} + \vartheta + {u_1} + {\tau _a}} \right)} \right)}},} \\ {{g_8} = \frac{{h{\delta _a}}}{{1 + h\left( {r + {u_1} + \vartheta } \right)}},} \\ {{g_9} = \frac{1}{{1 + h\left( {r + {u_1} + \vartheta } \right)}},} \\ {{g_{10}} = \frac{{hr}}{{1 + h\left( {\left( {{\tau _b} + \vartheta + {u_1}} \right)} \right)}}} \\ {{g_{11}} = \frac{1}{{1 + h\left( {{\tau _b} + \vartheta + {u_1}} \right)}}.} \\ \end{array}$$

Following the same steps as in Theorem 1, the J-matrix can be described as.

$$J\left({E}^{*}\right)=\left[\begin{array}{cccc}{g}_{1}& {g}_{2}& {g}_{3}& {g}_{4}\\ {g}_{5}& {g}_{6}& {g}_{7}& 0\\ 0& {g}_{8}& {g}_{9}& 0\\ 0& 0& {g}_{10}& {g}_{11}\end{array}\right].$$

For eigenvalues, we study

$$\left|J\left({E}^{*}\right)-\Gamma I\right|=0,$$

i.e.

$$\left|\begin{array}{cccc}{g}_{1}-\Gamma & {g}_{2}& {g}_{3}& {g}_{4}\\ {g}_{5}& {g}_{6}-\Gamma & {g}_{7}& 0\\ 0& {g}_{8}& {g}_{9}-\Gamma & 0\\ 0& 0& {g}_{10}& {g}_{11}-\Gamma \end{array}\right|=0.$$
(14)

The Eq. (14) gives the characteristic equation as follows.

$${\Gamma }^{4}+{U}_{1}{\Gamma }^{3}+{U}_{2}{\Gamma }^{2}+{U}_{3}\Gamma +{U}_{4}=0,$$

Where.

$${U}_{1}=-{g}_{1}-{g}_{6}-{g}_{9}-{g}_{11},$$
$${U}_{2}={g}_{1}{g}_{11}+{g}_{1}{g}_{6}+{g}_{6}{g}_{11}+{g}_{6}{g}_{9}+{g}_{1}{g}_{9}+{g}_{9}{g}_{11}-{g}_{7}{g}_{8}-{g}_{2}{g}_{5},$$
$${U}_{3}={g}_{1}{g}_{7}{g}_{8}+{g}_{7}{g}_{8}{g}_{11}+{g}_{2}{g}_{5}{g}_{9}+{g}_{2}{g}_{5}{g}_{11}-{g}_{1}{g}_{6}{g}_{11}-{g}_{1}{g}_{9}{g}_{11}-{g}_{1}{g}_{6}{g}_{9}-{g}_{3}{g}_{5}{g}_{8}-$$
$${g}_{6}{g}_{9}{g}_{11},$$
$${U}_{4}={g}_{1}{g}_{6}{g}_{9}{g}_{11}+{g}_{3}{g}_{5}{g}_{8}{g}_{11}-{g}_{1}{g}_{7}{g}_{8}{g}_{11}-{g}_{2}{g}_{5}{g}_{9}{g}_{11}-{{g}_{4}g}_{5}{g}_{8}{g}_{10}.$$

By employing Routh–Hurwitz criteria48,49, the EEP \({E}^{*}\) of system (12) is LAS if \({U}_{i}>0\) for \(i=\text{1,2},\text{3,4}\) and \({U}_{1}{U}_{2}{U}_{3}>\) \({U}_{3}\)2+\({U}_{1}\)2 \({U}_{4}\). Therefore, whenever \({R}_{0}>1\), the EEP for the discrete NSFD scheme (12) is LAS. Consequently, the EEP \({E}^{*}\) of the discrete NSFD scheme (5) is LAS.

The following subsection examines DAEP and EEP global asymptotic stability (GAS) for NSFD scheme (5).

Global stability of equilibria

Theorem 3

For all \(\text{h}>0\), the DAEP of the NSFD scheme (5) for the model (1) is GAS whenever \({\text{R}}_{0}<1\) and the EEP is GAS whenever \({\text{R}}_{0}>1\).

Proof

Let \({\left({\text{X}}_{\text{k}}\right){=(\text{S}}_{\text{k}}, {\text{E}}_{\text{k}},{\text{I}}_{\text{k}}, {\text{H}}_{\text{k}},{\text{ R}}_{\text{k}})}^{\text{T }}\epsilon {R}^{5}\) denote the bounded sequence provided by the NFSD scheme (5). Our goal is to show that \({\text{X}}_{k} \to {\text{X}}^{\prime}\) as \(\text{k}\to \infty ,\) where \({\text{X}}^{\prime}\) is either DAEP or EEP. Since, the sequence \(\left({\text{X}}_{\text{k}}\right)\) is bounded, the Bolzano-Weierstrass theorem ensures the existence of a convergent subsequence \(\left( {{\text{X}}_{{{\text{K}}_{{\text{n}}} }} } \right)\) such that \(\left( {{\text{X}}_{{{\text{K}}_{{\text{n}}} }} } \right) \to {\text{Y}}^{\prime}\) as \({\text{n}} \to \infty\).

Due to the structure of NSFD scheme (5) and assumption made above, the limit point \({\text{Y}}^{\prime}\) must coincide with \({\text{X}}^{\prime}\), which is either DAEP or EEP. It is already proved in Theorem 1 and 2 that both the equilibria are LAS. Thus, there exists \(\updelta>0\) such that for an initial condition \({\text{X}}_{0}\) satisfies

$${\text{X}}_{0} - {\text{X}}^{\prime} \le {\updelta }, \,{\text{then}}\mathop {\lim }\limits_{{{\text{k}} \to \infty }} {\text{X}}_{{\text{k}}} - {\text{X}}^{\prime} = 0$$
(15)

Suppose \({\text{X}}_{0}\) be any arbitrary initial value. For instance \(\mathop {\lim }\limits_{j \to \infty } {\text{ X}}_{{{\text{k}}_{{\text{j}}} }} = {\text{X}}^{\prime}\), it follows that there exists an integer \({\text{j}}_{0}\) for which.

$${\text{X}}_{{{\text{k}}_{{{\text{j0}}}} }} - {\text{X}}^{\prime} \le \updelta$$
(16)

From (15) and (16), we conclude that.

$$\mathop {\lim }\limits_{{{\text{k}} \to \infty ,\;{\text{k}} \ge 1}} \left\| {{\text{X}}_{{\text{k}}} - {\text{X}}^{\prime}} \right\| = \mathop {\lim }\limits_{{{\text{k}} \to \infty ,\;{\text{k}} \ge {\text{k}}_{{{\text{j}}_{{0}} }} }} \left\| {{\text{X}}_{{\text{K}}} - {\text{X}}^{\prime}} \right\|$$
(17)

This completes the proof that \({\text{X}}^{\prime}\) is GAS.

An illustration of NSFD scheme with various step sizes can be found in Fig. 4 (a–d) and Fig. 5 (a–d). The numerical assessment offered in Fig. 4 (a-d) displays that NSFD scheme (5) is convergent to DAEP, however Fig. 5 (a-d) shows that NSFD scheme (5) is convergent to EEP for all step sizes.

Fig. 4
figure 4

Graphical illustration of NSFD scheme with \(\left({\varvec{a}}\right) h=0.1,\left({\varvec{b}}\right) h=1,\left({\varvec{c}}\right) h=10, \text{and} \left({\varvec{d}}\right) h=20\). The values of fixed parameters are \(q=4.995, a=0.38974,{\tau }_{a}=0.03232,{u}_{1}=0.0301,{m}_{1}=1.2981,{\delta }_{a}=0.000011618,r=0.06813,\vartheta =0.0218,{t}_{b}=0.6450.\).

Full size image
Fig. 5
figure 5

Graphical illustration of NSFD scheme with \(\left(\mathbf{a}\right)\text{ h}=0.1,\left(\mathbf{b}\right)\text{ h}=1,\left(\mathbf{c}\right)\text{ h}=10,\text{ and }\left(\mathbf{d}\right)\text{ h}=20\). The values of fixed parameters are \(q=4.995, a=0.38974,{\tau }_{a}=0.03232,{u}_{1}=0.0301,{m}_{1}=1.2981,{\delta }_{a}=0.11618,r=0.06813,\vartheta =0.000218,{t}_{b}=0.6450\).

Full size image

Conclusions

This paper develops and investigates a mathematical model for COVID-19. The intent is to study mechanisms of COVID-19 disease and reducing or preventing its transmission amongst people. The basic reproduction number is calculated which serves as essential tool in analyzing the local and global stability of both DAEP and EEP. Two different approaches, such as SFD which include Euler as well as RK-4 and NSFD schemes, are used to discuss the dynamical properties of the model. Conditional convergence and step-size dependency were both validated by the RK-4 and Euler systems, which means that when the step size increases, they diverge. In addition, to produce exact results that are both mathematically and biologically consistent with the corresponding continuous model, the discrete NSFD scheme is designed for the model which is unconditionally convergent. The aim of developing NSFD scheme for system is to ensure its dynamical reliability. The NSFD scheme is a useful method for confirming that outputs from discrete and continuous models act similarly and are mathematically steady. The local and global stability of both the equilibria for NSFD scheme are determined using multiple theories and criteria. Numerical solutions are applied to ensure the accuracy of all theoretical conclusions. The results indicate that the COVID-19 epidemic disease transmission can be effectively monitored using NSFD scheme. The evidences provided in this study are beneficial to both humanity and the field of health sciences. The outcomes provided in the current work can also be employed as a suitable tool to estimate the development of the COVID-19 epidemic disease.

In our future work, we will explore various comprehensive epidemic models with properties analogous to the one being measured in order to get an enhanced understanding of the dynamics of disease spread. We will examine the fluctuating behavior of the epidemic models employing the Euler, RK-4, and NSFD numerical approaches.