Introduction

Motivation and literature review

As one of the seven key pillars of China’s “new infrastructure” initiative, the data center industry continues to expand rapidly1. Driven by the Three-year Action Plan for the Development of New Data Centers (2021–2023), China’s data center rack capacity had established a multi-tiered infrastructure—encompassing national cloud hubs, provincial nodes, and edge computing—by the end of 2023, maintaining a compound annual growth rate (CAGR) of approximately 20% over this period2,3. Concurrently, explosive growth in critical technology markets (e.g., 5G, artificial intelligence, and big data), alongside deepening demands for industrial internet and smart manufacturing transformation, continues to drive large-scale computing infrastructure expansion4. Guided by national “dual-carbon” goals, the industry is accelerating its transition toward green practices, with energy-efficient data centers adopting renewable energy sources and liquid cooling technologies to advance carbon-neutral digital infrastructure. Further, China’s release of the Guideline on Building a Unified National Data Market underscores efforts to integrate multi-level resources through data centers, fostering deeper convergence between the digital and real economies. This rapid rack-capacity scaling and sustained service demand growth have intensified energy consumption challenges and escalated operational costs. Consequently, mitigating rising energy expenses has become critical to ensuring data centers’ sustainable development5.

In July 2021, China’s National Development and Reform Commission released the Notice on Further Refining the Time-of-Use Tariff Mechanism6, aiming to guide users toward optimizing electricity consumption and shifting load away from peak periods. The workloads in the DC can be categorized into interactive loads (requiring real-time processing) and batch-processing loads (delay-tolerant and schedulable). By deferring or rescheduling batch-processing loads to off-peak periods, data centers can reduce electricity demand during peak tariff hours and improve operational efficiency7,8. For example, in Ref.9, an electric adjustable potential model for coordinating the operation of distributed large-scale data centers, which optimizes the expected electricity payment minus the revenue from participating into the day-ahead martet. Considering the adjustable potential of data centers, literature10 proposes flexible dispatch strategies of data centers to improve the operational flexibility of power system. In Ref.11, the adjustable potential model in deregulated electricity markets for data centers that often have significant flexibility in workload scheduling to reduce the average contract payment of data centers and increase the revenue of the utility companies. A data-driven flexibility assessment scheme for data centers is proposed by12 investigating the adjustable potential of periodic batch workloads, which are the major flexibility source in the workload scheduling and execution process. While these studies focus on adjustable potential of data centers through IT equipment adjustments—such as delaying batch-processing loads, relocating tasks, or shutting down servers—the adjustable potential of data center cooling systems (e.g., computer room air conditioning) remains underexplored. Specifically, the energy consumption of air conditioning systems is influenced by cooling capacity adjustments. By dynamically optimizing cooling levels in alignment with TOU pricing, while ensuring server stability, data centers can further reduce peak-time electricity demand.

In addition to leveraging in-house infrastructure for participation in demand responseto reduce electricity costs, some studies have explored the integration of external energy storage devices to enhance economic efficiency. For example, literature13 proposes an integrated planning scheme that optimally determines the locations and capacities of interconnected Internet data centers and energy storage systems in a smart grid to improve the computational performance metrics of Internet data centers and operational criteria of the grid. By taking heterogeneous service delay guarantees and energy storage systems management into consideration, literature14 formulate a stochastic optimization problem to minimize the total energy cost. literature15 focuses on the optimal dispatch and design of energy storage systems in data centers, particularly in the context of progressive workloads to enhance the economic benefits. However, the high investment costs of energy storage equipment and limited capital allocation for data centers have intensified the conflict of low utilization16. Recently, driven by national policies advocating for intensive, large-scale, and green data center development and the emergence of shared energy storage business models17,18, shared energy storage system (SESS) planning for data center clusters has emerged as a promising approach to improve economic efficiency. By exploiting the complementary energy storage needs of diverse data centers, this model enhances energy storage system utilization and reduces system operation costs, offering an economical, efficient, and green low-carbon operational paradigm.

In terms of the operation of shared energy storage, Reference16 optimized the charging and discharging power of shared energy storage for industrial users to achieve optimal daily operating costs for user groups. To further improve energy utilization efficiency and reduce electricity costs, a optimization scheduling strategy for multi-RIES with electrical energy interaction is proposed by17 to reflect the fact of rental prices with related to the demand for energy storages, to reduce carbon dioxide emissions, and to promote the efficient utilization of energy storage devices. a master-slave game schedule strategy is constructed by18 for distribution network based on microgrid group and shared energy storage to improve the operational efficiency of the entire system. In order to reduce the impact of wind power output and electricity price uncertainty on the income of wind power participating in the electricity market, Reference19 proposes a day-ahead and real-time market bidding and scheduling strategy for wind power participation based on shared energy storage. Reference20 studies a representative scene of shared energy storage in a residential area and proposes a new method for service pricing and load dispatching in such a circumstance. References21 employed the Shapley value method to redistribute joint operational benefits among multiple agents. Currently, while numerous achievements exist in shared energy storage optimization and configuration, existing research predominantly focuses on sharing energy storage power across time periods within a single scenario. Few studies explore cross-scenario energy storage sharing or leverage the differences and complementarity of users’ resource requirements under varying operational environments for shared energy storage planning, thereby maximizing shared storage efficiency.

Contributions

In order to overcome the knowledge gaps as stated above, this paper proposes a data center alliance shared energy storage planning method that fully considers the adjustable potential of IT equipment and computer room air conditioners. First, the shared energy storage operation mode for the data center alliance is studied, including capacity allocation of shared energy storage across scenarios, a cost-sharing model, and a Nash bargaining-based benefit allocation method to ensure fairness among data center users. Then, a shared energy storage planning model for the data center alliance is established, integrating data center adjustable potential. This model determines the optimal shared energy storage capacity during the planning stage and allocates storage power and energy capacities in real-time across different operational scenarios. For each data center, a room-level energy management model is developed to precisely regulate IT device power consumption and air conditioning operations while providing adjustable potential. To address the computational burden caused by a large number of generated scenarios, a improved L-shaped algorithm is proposed to solve the two-stage stochastic optimization problem, reducing computational complexity through problem decomposition. Finally, case studies validate the effectiveness of the proposed shared energy storage planning method and data center energy management model.

The main contributions of this paper are in threefold, as highlighted below:

  1. (1)

    Developing of a holistic adjustable potential model of data center to explore the benefits of harnessing data center flexibility to the economy and operational benefit of system. In this study, we present a composite model to characterize the adjustable potential of data center during operation. Unlike previous works (Refs.7,8,9,10,11,12. only focus on adjustable potential of data centers through IT equipment adjustments, Refs.13,14,15,16. only considers the integration of external energy storage devices to enhance economic efficiency in data center.), the proposed formulation considers data center adjustable potential in terms of both their time-shifting and energyswitching effects to the system, which are created from workloads transferring and computer room air conditioners management, collectively. Through these considerations, the proposed model could allow a comprehensive and realistic representation for the data center characteristics as they occur in real world.

  2. (2)

    Proposing a shared energy storage planning model based on the two-stage stochastic optimization model for the data center alliance. In this paper, a shared energy storage planning model based on the two-stage stochastic optimization model for the data center alliance to determine the optimal shared energy storage capacity and allocates storage power and energy capacities in real-time across different operational scenarios, where the capacity allocation of shared energy storage across scenarios, a cost-sharing model, and a Nash bargaining-based benefit allocation method to ensure fairness among data center users. For the previous works, Refs.16,17,18,19,20. do not consider cross-scenario energy storage sharing combined with adjustable potentials. Through these consideration, the comprehensive cost of data center alliance under the shared energy storage mode is reduced by at least 3% compared with that under the energy storage mode of each data center, and the reduction ratio increases with the increase of data center scale.

  3. (3)

    Developing a improved L-shaped algorithm to solve the two-stage stochastic optimization problem. Unlike previous works (Refs.7,8,9,10,11,12,13,14,15,16,17,18,19,20. consider solve the model through the commercial solver and intelligent optimization algorithm), in this study, we develop a improved L-shaped algorithm instead of commercial solver to deal with the proposed two-stage stochastic optimization problem, which includes the multicut strategy into the L-shaped algorithm. Therefore, this algorithm could fully address the computational burden caused by a large number of generated scenarios. Through these considerations, in the face of larger-scale instances (e.g., cases with more than 200 scenarios), the solution speed of the proposed improved L-shaped algorithm could be improved by at least 11 times compared with the traditional commercial solver.

Operation mode of SESS in the data center alliance

Operation framework of SESS in the data center alliance

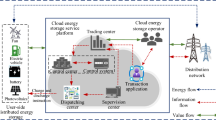
The proposed operation framework of SESS for data center alliances is illustrated in Fig. 1, comprising multiple data centers, shared energy storage facilities, and the main grid. Each data center can be powered by self-built Wind turbine (WT)/Photovoltaic (PV) generation, main grid, or SESS. Its energy consumption primarily comes from IT equipment and computer room air conditioner system (CRACS).

Due to the intermittent and fluctuating nature of renewable energy output and temporal variations in user request demands across data centers, the internal supply-demand balance of each data center dynamically changes, leading to corresponding fluctuations in their energy storage requirements. For instance, in scenarios with low renewable energy output and high user demand, data centers require larger energy storage capacities to shift energy consumption temporally and reduce peak electricity purchases. Conversely, in scenarios with high renewable energy output, the demand for energy storage diminishes significantly. If data centers individually configure energy storage, this may result in scenarios where storage resources are insufficient in some cases and underutilized in others. This presents opportunities for multi-data-center collaboration: multiple data centers can form an alliance to jointly invest in energy storage infrastructure. By leveraging differences and complementarities in energy storage requirements across operating scenarios, the alliance can reallocate storage capacities, improve utilization efficiency, and enhance the operational economics of all participating data centers.

Fig. 1
figure 1

Operation framework of shared energy storage for data center alliances.

Full size image

Capacity allocation and cost-sharing model of SESS in DC alliance

Under the SESS co-construction model of the DC alliance, this study considers one day as the scheduling cycle, during which the shared energy storage capacity allocation is conducted once per scheduling cycle. Each data center can obtain the right to use a certain power capacity and energy capacity of the SESS according to its own demand:

$$\sum\limits_{{n=1}}^{{{N_{DC}}}} {{P_{BS,n,s}}} \leq P_{{BS}}^{{\hbox{max} }}$$
(1)
$$\sum\limits_{{n=1}}^{{{N_{DC}}}} {{E_{BS,n,s}}} \leq E_{{BS}}^{{\hbox{max} }}$$
(2)

where \({P_{BS,n,s}}\) and \({E_{BS,n,s}}\) are the allocated power capacity and energy capacity of energy storage for data center n under scenario s ; \(P_{{BS}}^{{\hbox{max} }}\) and \(E_{{BS}}^{{\hbox{max} }}\) are the total installed power capacity and energy capacity of the shared energy storage; NDC is the number of data centers in the alliance.

After determining the allocated power and energy capacities of SESS for each data center in a specific scenario, the investment cost is distributed proportionally based on their usage ratios:

$${C_{P,n,s}}=\frac{{{P_{BS,n,s}}}}{{\sum\limits_{{\delta =1}}^{{{N_{DC}}}} {{P_{BS,\delta ,s}}} }} \cdot \frac{{\gamma {{(1+\gamma )}^{{T_{LT}}}}{\kappa _P}P_{{BS}}^{{{\text{max}}}}}}{{365[{{(1+\gamma )}^{{T_{LT}}}} - 1]}}$$
(3)
$${C_{E,n,s}}=\frac{{{E_{BS,n,s}}}}{{\sum\limits_{{\delta =1}}^{{{N_{DC}}}} {{E_{BS,\delta ,s}}} }} \cdot \frac{{\gamma {{(1+\gamma )}^{{T_{LT}}}}{\kappa _E}E_{{BS}}^{{{\text{max}}}}}}{{365[{{(1+\gamma )}^{{T_{LT}}}} - 1]}}$$
(4)

where \({C_{P,n,s}}\) and \({C_{E,n,s}}\) are the allocated power capacity cost and energy capacity cost for data center n under scenario s; \(\gamma\) is the discount rate; \({T_{LT}}\) is the design lifespan of the energy storage system; \({\kappa _P}\) and \({\kappa _E}\) represent the unit power capacity cost and unit energy capacity cost of the energy storage equipment.

SESS benefit allocation method in the DC alliance

To ensure the long-term stable cooperation within the data center alliance, it is essential to reasonably allocate the benefits obtained by the alliance. This paper employs the Nash bargaining method20 to distribute the benefits to each data center:

$$\hbox{max} \prod\limits_{{n=1}}^{{{N_{DC}}}} {({C_{DC,n,0}} - {C_{DC,n}})}$$
(5)
$$\begin{gathered} \hfill \\ {\text{s}}.{\text{t}}.\;\;\;{\kern 1pt} {C_{DC,n}} \leq {C_{DC,n,0}} \hfill \\ \end{gathered}$$
(6)
$${C_{{\text{DC}},n}}{\text{ }}={C^{\prime}_{{\text{DC}},n}} - {\pi _n}$$
(7)
$${C^{\prime}_{{\text{DC}},n}}{\text{ }}={p_s}\left( {\sum\limits_{{t=1}}^{T} {{\alpha _t}} {P_{{\text{buy}},t,n,s}}+{C_{{\text{P}},n,s}}+{C_{{\text{E}},n,s}}} \right)$$
(8)

where \({C_{DC,n,0}}\) denotes the comprehensive cost of data center when individually configuring energy storage; \({C_{{\text{DC}},n}}{\text{ }}\) and \({C^{\prime}_{{\text{DC}},n}}\) represent the post-bargaining and pre-bargaining comprehensive costs of data center under the shared energy storage cooperation mode; \({\pi _n}\) is the subsidy received by data center from the alliance post-bargaining; \({p_s}\) is the probability of scenario ;\({\alpha _t}\) is the grid electricity price at time ;\({P_{{\text{buy}},t,n,s}}\) is the power purchased by data center n from the grid at time t in scenario s; T is the total number of time periods.

The objective of bargaining is to achieve a fair and reasonable distribution of the coalition’s total benefits among the data centers, which implies that the total benefits of the data center coalition must remain unchanged before and after the bargaining process:

$$\sum\limits_{{n=1}}^{{{N_{{\text{DC}}}}}} {{\pi _n}} =0$$
(9)

SESS planning based on the spatial-temporal adjustable potential of DC

To comprehensively integrate shared energy storage planning with data center alliance operation under uncertain environments (e.g., renewable energy output, workloads, and ambient temperature), a two-stage stochastic optimization model is proposed for shared energy storage planning considering the spatial-temporal adjustable potential of DC to minimize the total costs. As shown in Fig. 2, the first stage is the planning and decision-making stage, aiming at minimizing the investment cost of SESS, and determining the allocated capacity of SESS, which consider shared energy storage configuration constraints. The second stage is the operation simulation stage under uncertainties, in which the decision-making aims at minimizing the system operation costs, and determines the optimal scheduling strategy of data center alliance and SESS, which considers adjustable potential of the room-level energy management for IT equipment, adjustable potential of cooling system model, shared storage capacity operating constraints, and other operational constraints.

Fig. 2
figure 2

Structure of two-stage stochastic optimization model.

Full size image

Objective function

The objective function of the shared energy storage planning model is to maximize the collective interests of the DC alliance, i.e., minimize the sum of SESS investment costs and electricity procurement costs of all data centers, which ensures that shared energy storage capacity is allocated more economically in typical scenarios:

$$\hbox{min} f{\text{ }}=\frac{{\gamma {{(1+\gamma )}^{{T_{{\text{LT}}}}}}}}{{365({{(1+\gamma )}^{{T_{{\text{LT}}}}}} - 1)}}({\kappa _P}P_{{{\text{BS}}}}^{{{\text{max}}}}+{\kappa _E}E_{{{\text{BS}}}}^{{{\text{max}}}})\;{\kern 1pt} +\sum\limits_{{s=1}}^{{{N_s}}} {{p_s}} \sum\limits_{{n=1}}^{{{N_{{\text{DC}}}}}} {\sum\limits_{{t=1}}^{T} {{\alpha _t}} } {P_{{\text{buy}},I,n,s}}$$
(10)

where \({N_s}\) is the total number of scenarios.

SESS configuration constraints

The constraints for SESS configuration aim to determine the capacity of energy storage devices invested by the DC alliance. It is noteworty that excessive SESS capacity may lead to low resource utilization and poor economic benefits, while insufficient capacity limits the optimization potential for dispatch operations.

The power and energy capacity constraints for SESS are as follows:

$$0 \leqslant {P_{{\text{BS}}}} \leq {P_{{\text{BS,max}}}}$$
(11)
$${E_{{\text{BS}}}}={T_{{\text{BS}}}} \cdot {P_{{\text{BS}}}}$$
(12)

where \({P_{{\text{BS}}}}\) and \({E_{{\text{BS}}}}\) represent the planned power and energy capacity of the SESS, respectively; \({T_{{\text{BS}}}}\) denotes the charge/discharge duration of the SESS.

Adjustable potential of CRACS

Unlike previous models that estimate cooling system energy consumption using Power Usage Effectiveness (PUE)21 or empirical fitting22, the proposed adjustable potential of CRACS model takes the thermal effects of IT equipment and ambient temperature while enabling pre-cooling during off-peak hours (e.g., aggressive cooling to lower server room temperatures) into accout to reduce air conditioning power consumption during peak pricing periods.

Server room temperature constraints

Based on a first-order equivalent thermal parameter model23, the relationship between initial and final temperatures in a time interval is:

$${T_{{\text{in}},t+1,i,n,s}}={T_{{\text{out}},t,n,s}} - {Q_{t,i,n,s}}R - ({T_{{\text{out}},t,n,s}} - {Q_{t,i,n,s}}R - {T_{{\text{in}},t,i,n,s}}){e^{ - \frac{{\Delta t}}{{RC}}}}$$
(13)
$${Q_{t,i,n,s}}={Q_{{\text{co}},t,i,n,s}} - \varsigma {P_{{\text{IT}},t,i,n,s}}$$
(14)
$${T_{{\text{min}}}} \leqslant {T_{{\text{in}},L,n,s}} \leqslant {T_{{\text{max}}}}$$
(15)

where \({T_{{\text{in}},t,i,n,s}}\) is the indoor temperature of server room i in data center n at time t under scenario s; \({T_{{\text{out}},t,n,s}}\) is the ambient temperature of data center n at time t; R and C represent the equivalent thermal resistance and capacitance of the cooling load; \({Q_{t,i,n,s}}\) is the cooling capacity provided to server room ; \({Q_{{\text{co}},t,i,n,s}}\) is the cooling output of the variable-frequency air conditioner; \(\varsigma\) is the heat-to-power ratio of servers; \({T_{{\text{max}}}}\) and \({T_{{\text{min}}}}\) are the upper and lower temperature limits for normal server operation, where 18–27 °C is recommended by American Society of Heating, Refrigeration and Air Conditioning Engineers as the optimum interval for IT equipment operation24; \({P_{{\text{IT}},t,i,n,s}}\) is the IT equipment power consumption.

CRACS power consumption constraints

For variable-frequency air conditioners23, the relationship between power consumption and cooling output is:

$${P_{{\text{co}},t,i,n,s}}{\text{ }}=\frac{{{k_1}}}{{{k_2}}}{Q_{{\text{co}},t,i,n,s}}+\frac{{{k_2}{k_1} - {k_1}{k_2}}}{{{k_2}}}$$
(16)
$$0{\text{ }} \leq {P_{{\text{co}},t,i,n,s}} \leq {P_{co,{\text{max}}}}$$
(17)
$${P_{{\text{co}},t,n,s}}=\sum\limits_{{i=1}}^{{{N_{{\text{comb}}}}}} {{P_{{\text{co}},t,i,n,s}}}$$
(18)

where k1, k2, l1, l2 are constant coefficients; \({P_{{\text{co}},t,n,s}}\) and \({P_{{\text{co}},t,i,n,s}}\) represent the total air conditioning power consumption of data center n and that of server room i, respectively; \({P_{co,{\text{max}}}}\) is the rated power consumption of the air conditioner; and \({N_{{\text{comb}}}}\) is the number of server rooms in data center .

Adjustable potential of IT equipment

The energy consumption model of IT equipment considering adjustable potential of primarily adjusts the execution volume of batch-processing loads across time periods based on fluctuations in electricity prices, aiming to reduce power demand during peak pricing periods. The constraints include Service Level Agreement (SLA) constraints, data center capacity and server quantity constraints, CPU utilization constraints, and IT equipment energy consumption constraints.

Service level agreement constraints

Considering the immediate process for interactive loads, the workloads processed by data center n in period t under scenario s:

$${\mu _{t,n,s}}={a_{t,n,s}}+{d_{t,n,s}}$$
(19)

where \({\mu _{t,n,s}}\) is the total data load processed by data center n in period t under scenario ; \({a_{t,n,s}}\) is the interactive load arriving at data center n in period t; \({d_{t,n,s}}\) is the batch-processing load processed by data center n in period t.

Unprocessed batch loads arriving in the current period are queued chronologically:

$${q_{t,n,s}}={B_{t,n,s}} - {D_{t - 1,n,s}}=\sum\limits_{{\tau =1}}^{t} {{b_{\tau ,n,s}}} - \sum\limits_{{\tau =1}}^{{t - 1}} {{d_{\tau ,n,s}}}$$
(20)

where \({q_{t,n,s}}\) is the pending batch load in the queue of data center n in period t under scenario s; \({b_{\tau ,n,s}}\) is the batch load arriving at data center n in period t; \({B_{t,n,s}}\) and \({D_{t - 1,n,s}}\) are the cumulative batch loads arriving at data center n under scenario s and processed by data center n up to period t under scenario s.

To ensure batch loads are completed within the maximum allowable delay time :

$${B_{t - (T_{{{\text{max}}}}^{\prime } - 1),n,s}} \leq {D_{t,n,s}} \leq {B_{t,n,s}}$$
(21)

Capacity constraints of DC and servers

$$0{\text{ }} \leq {\mu _{t,n,s}} \leq {U_n}$$
(22)
$$0{\text{ }} \leq {m_{t,i,n,s}} \leq {\overline {M} _n}$$
(23)
$${U_n}{\text{ }}={\overline {M} _n}{N_{{\text{room}},n}}F$$
(24)

where \({U_n}\) is the capacity of data center n; \({\overline {M} _n}\) is the number of servers per room in data center n; \({m_{t,i,n,s}}\) is the number of active servers in room i of data center n during period t under scenario s; F is the number of servers.

CPU utilization constraints

CPU utilization must maintain a capacity margin:

$${u_{t,n,s}}{\text{ }} \leq 1 - \sigma$$
(25)
$${u_{t,n,s}}{\text{ }}=\frac{{{\mu _{t,n,s}}}}{{F\sum\limits_{{i=1}}^{{{N_{{\text{room}},n}}}} {{m_{t,i,n,s}}} }}$$
(26)

where \({u_{t,n,s}}\) is the CPU utilization of active servers in data center n during period t under scenario s; \(\sigma\) is the server capacity margin.

IT equipment energy consumption constraints

$${P_{{\text{TT}},t,i,n,s}}{\text{ }}={m_{t,i,n,s}}[{p_{{\text{idle}}}}+({p_{{\text{peak}}}} - {p_{{\text{idle}}}}){u_{t,n,s}}]$$
(27)
$${P_{{\text{TT}},t,n,s}}{\text{ }}=\sum\limits_{{i=1}}^{{{N_{{\text{room}},n}}}} {{P_{{\text{TT}},t,i,n,s}}}$$
(28)

where \({P_{{\text{TT}},t,n,s}}\) is the total IT equipment energy consumption of data center n in period t under scenario s; \({p_{{\text{peak}}}}\) and \({p_{{\text{idle}}}}\) are the idle and peak power consumption of servers, respectively.

Other constraints

SESS operation constraints

SESS operation constraints include charging/discharging power constraints, as shown in (28)–(29), state-of-charge constraints (30), energy level constraints (31) and (32), and terminal energy constraints (33):

$$0{\text{ }} \leq {P_{{\text{dis}},t,n,s}} \leqslant {Z_{{\text{dis}},t,n,s}}{P_{{\text{BS}},n,s}}$$
(29)
$$0{\text{ }} \leq {P_{{\text{ch}},t,n,s}} \leqslant {Z_{{\text{ch}},t,n,s}}{P_{{\text{BS}},n,s}}$$
(30)
$$0{\text{ }} \leq {Z_{{\text{ch}},t,n,s}}+{Z_{{\text{dis}},t,n,s}} \leq 1$$
(31)
$${E_{{\text{BS}},t+1,n,s}}{\text{ }}={E_{{\text{BS}},t,n,s}}+{\varphi _{{\text{BS}}}}{P_{{\text{ch}},t,n,s}} - \frac{{{P_{{\text{dis}},t,n,s}}}}{{{\varphi _{{\text{BS}}}}}}$$
(32)
$$0.1{E_{{\text{BS}},n,s}}{\text{ }} \leq {E_{{\text{BS}},t,n,s}} \leq {E_{{\text{BS}},n,s}}$$
(33)
$${E_{{\text{BS}},T,n,s}}{\text{ }}={E_{{\text{BS}},0,n,s}}$$
(34)

where \({P_{{\text{dis}},t,n,s}}\) and \({P_{{\text{ch}},t,n,s}}\) are discharging/charging power of SESS for data center in scenario at time. \({Z_{{\text{ch}},t,n,s}}\) and \({Z_{{\text{dis}},t,n,s}}\) denote Binary variables indicating discharging/charging states. \({E_{{\text{BS}},t,n,s}}\) is the energy level of the SESS allocated to data center at time in scenario. \({\varphi _{{\text{BS}}}}\) represent the charge/discharge efficiency of the SESS.

Power balance constraints

The power supply and demand within each data center must satisfy power balance constraints:

$${P_{{\text{IT}},t,n,s}}+{P_{{\text{co}},t,n,s}}+{P_{{\text{ch}},t,n,s}}{\text{ }}={P_{{\text{wind}},t,n,s}}+{P_{{\text{solar}},t,n,s}}+{P_{{\text{dis}},t,n,s}}+{P_{{\text{buy}},t,n,s}}$$
(35)
$$0 \leq {P_{{\text{wind}},t,n,s}}{\text{ }} \leq P_{{{\text{wind}},t,n,s}}^{{\text{a}}}$$
(36)
$$0 \leq {P_{{\text{solar}},t,n,s}}{\text{ }} \leq P_{{{\text{solar}},t,n,s}}^{{\text{a}}}$$
(37)

where \({P_{{\text{wind}},t,n,s}}\) are \({P_{{\text{solar}},t,n,s}}\) are the actual output of WT and PV in data center n in scenario s at time t. \(P_{{{\text{wind}},t,n,s}}^{{\text{a}}}\) and \(P_{{{\text{solar}},t,n,s}}^{{\text{a}}}\) are the predicted power generation of WT and PV in data center n in scenario s at time t.

Solution algorithm

The uncertainties in renewable energy output, workloads, and ambient temperature lead to significant variations in operational states across different time periods, resulting in diverse energy storage demands. Therefore, it is essential to account for the diversity of operational scenarios in planning. This study utilizes historical annual output data from renewable energy stations as the basis. Wind power scenarios are generated using the Markov Chain Monte Carlomethod to model duration and volatility characteristics, while photovoltaic output scenarios are generated via a vector autoregressive time series model to simulate potential renewable energy output scenarios. Considering that the workload has a strong daily pattern28, the typical daily curves29 of different workloads are used for Monte Carlo generation to describe the randomness of workloads.

However, obtaining a large number of scenarios to simulate the actual uncertain operation scenarios would be reformulated as a deterministic equivalent problem with these scenarios and each constraint in the subproblem is duplicated for each scenario data. Generally, The resulting problem can be solved by any Commercial solver, e.g., IBM ILOG CPLEX, Gurobi. which will lead to large calculation scale and difficult solution. Typically, the mixed-integer programming models with high-dimensional scenario spaces exhibit computational intractability, particularly when incorporating binary variables. To address the computational burden caused by a large number of generated scenarios, a improved L-shaped algorithm is proposed, effectively reducing computational complexity through problem decomposition. In order to facilitate the introduction of the algorithm, a compact form of the model is given:

$$\hbox{min} {\text{ }}{{\mathbf{c}}^ \top }{\mathbf{x}}+\sum\limits_{{s=1}}^{S} {p({\xi _s}) \cdot f} ({\mathbf{x}},{\mathbf{u}},{\xi _s})$$
(38)
$$s.t.{\text{ }}{\mathbf{Ax}}+{\mathbf{{\rm B}u}} \geq {\mathbf{q}}$$
(39)
$${\text{ }}{\mathbf{x}},{\mathbf{u}} \in \left\{ {0,1} \right\}$$
(40)

where for each scenario\({\xi _s}\):

$$f({\mathbf{x}},{\mathbf{u}},{\xi _s})=\hbox{min} {\text{ }}{\mathbf{h}}{({\xi _s})^ \top }{\mathbf{y}}({\xi _s})$$
(41)
$${\text{s}}.{\text{t}}.{\text{ }}{\mathbf{W}} \cdot {\mathbf{y}}({\xi _s}) \geq {\mathbf{l}}({\xi _s}) - {\mathbf{Gx}} - {\mathbf{Pu}}$$
(42)

where \({\mathbf{x}}\) is the variable matrix related to the planning Case, \({\mathbf{u}}\) is binary variable matrix for system operation, \({\mathbf{y}}({\xi _s})\) is the continuous variable matrix related to system operation. \({\mathbf{c}}\) and \({\mathbf{h}}({\xi _s})\) are the coefficient matrix in the objective function. \({\mathbf{A}}\), \({\mathbf{{\rm B}}}\), \({\mathbf{W}}\), \({\mathbf{l}}({\xi _n})\), \({\mathbf{G}}\), \({\mathbf{P}}\) are the coefficient matrix in the constraint condition.

The main problem (43)–(47) is the planning and decision-making problem, aiming at minimizing the investment cost of SESS, and determining the allocated capacity of SESS, which consider shared energy storage configuration constraints.

$$\hbox{min} {\text{ }}{{\mathbf{c}}^ \top }{\mathbf{x}}+\eta$$
(43)
$$s.t.{\text{ }}{\mathbf{A}}({\mathbf{x}},{\mathbf{u}}) \geq {\mathbf{b}}$$
(44)
$$\beta _{t}^{ \top }{\mathbf{x}}+\gamma _{t}^{ \top }{\mathbf{u}}+\eta \geq {\alpha _t}{\mkern 1mu} {\text{ }}\forall t \in {\theta _k}$$
(45)
$$\beta _{t}^{ \top }{\mathbf{x}}+\gamma _{t}^{ \top }{\mathbf{u}} \geq {\alpha _t}{\mkern 1mu} {\text{ }}\forall t \notin {\theta _k}$$
(46)
$${\text{ }}{\mathbf{x}},{\mathbf{u}} \in \left\{ {0,1} \right\}$$
(47)

While solving the above master problem interatively, Benders optimality cuts (9c) and feasibility cuts (9d) are added to approximate the expected recourse cost defined as η. Note that in the first iteration, let η take -∞, and the feasible cut and the optimal cut are all empty sets. \({\theta _k}\) is the iteration index set for which all subproblems are feasible. Benders optimality and feasibility cuts can be generated from the solution of the dual subproblem (48)–(50).

The subproblem (48)–(50) is the operation problem under uncertainties, in which the decision-making aims at minimizing the system operation costs, and determines the optimal scheduling strategy of data center alliance and SESS. Through the dual transformation, the dual form of the subproblem is as follows:

$$g({\mathbf{x}},{\mathbf{u}},{\xi _s})=\hbox{max} {\text{ }}\pi {({\xi _s})^ \top }({\mathbf{l}}({\xi _s}) - {\mathbf{Gx}} - {\mathbf{Pu}})$$
(48)
$$s.t.{\text{ }}\pi {({\xi _s})^ \top }{\mathbf{W}} \leq {\mathbf{h}}({\xi _s})$$
(49)
$$\pi ({\xi _s}) \geq 0$$
(50)

where \(\pi ({\xi _s})\) are the dual variable.

At each iteration m: if the dual subproblem is feasible for all scenarios s with optimal solutions \({\pi ^*}({\xi _s})\), an optimality cut is generated and added to the master problem, as shown in (51).

$$\beta _{t}^{ \top }{\mathbf{x}}+\gamma _{t}^{ \top }{\mathbf{u}}+\eta \geq {\alpha _t}{\mkern 1mu} {\text{ }}\forall t \in {\theta _k}$$
(51)
$${\alpha _t}=\sum\limits_{{s=1}}^{S} P ({\xi _s}){(\pi (\xi _{s}^{*}))^ \top }{\mathbf{l}}({\xi _s})$$
(52)
$$\beta _{k}^{ \top }=\sum\limits_{{s=1}}^{S} {p({\xi _s}){{(\pi (\xi _{s}^{*}))}^ \top }{\mathbf{G}}}$$
(53)
$$\gamma _{k}^{ \top }={\text{ }}\sum\limits_{{s=1}}^{S} p ({\xi _s}){(\pi (\xi _{s}^{*}))^ \top }{\mathbf{P}}$$
(54)

If the dual subproblem is unbounded for any scenario with extreme rays \(\xi _{s}^{*}\), a feasibility cut (55) is generated from the subproblem with the corresponding scenario and added to the master problem.

$$\beta _{t}^{ \top }{\mathbf{x}}+\gamma _{t}^{ \top }{\mathbf{u}} \geq {\alpha _t}{\mkern 1mu} {\text{ }}\forall t \notin {\theta _k}$$
(55)
$${\alpha _t}=\sum\limits_{{s=1}}^{S} P ({\xi _s}){(v(\xi _{s}^{*}))^ \top }{\mathbf{l}}({\xi _s})$$
(56)
$$\beta _{k}^{ \top }=\sum\limits_{{s=1}}^{S} {p({\xi _s}){{(v(\xi _{s}^{*}))}^ \top }{\mathbf{G}}}$$
(57)
$$\gamma _{k}^{ \top }={\text{ }}\sum\limits_{{s=1}}^{S} p ({\xi _s}){(v(\xi _{s}^{*}))^ \top }{\mathbf{P}}$$
(58)

There are options for adding feasibility cuts and we choose to generate feasibility cuts from all the scenarios that result in infeasibility and add the cuts to the master problem at each iteration. Depending on the master problem solution, either feasibility cut(s) or an optimality cut is generated and added to the master problem. In addition, the multicut strategy is proposed to apply on the L-shaped algorithm by adding multiple optimality cuts to the master problem instead of adding a single aggregated cut. The improved L-shaped algorithm are demonstrated as follows. The schematic diagram and the flow chart of solution are shown in Figs. 3 and 4.

Step 1: Load the model parameters, set the number of iterations t = 1, the lower bound of the objective function LB = − ∞ and the upper bound of the objective function UB = + ∞.

Step 2: Solve the main problem MP, obtain the optimal planning Case x*(t), and update LB = \({\eta ^*}\)

$$\hbox{min} {\text{ }}{{\mathbf{c}}^ \top }{\mathbf{x}}+\eta$$
(59)
$$s.t.{\text{ }}{\mathbf{A}}({\mathbf{x}},{\mathbf{u}}) \geq {\mathbf{b}}$$
(60)
$$p({\xi _s}){(\pi (\xi _{{s,t}}^{*}))^ \top }{\mathbf{Gx}}+p({\xi _s}){(\pi (\xi _{{s,t}}^{*}))^ \top }{\mathbf{Pu}}+\eta \geq P({\xi _s}){(\pi (\xi _{{s,t}}^{*}))^ \top }{\mathbf{l}}({\xi _s}){\text{ }}\forall t \in {\theta _k},s \in S$$
(61)
$$p({\xi _s}){(v(\xi _{{s,t}}^{*}))^ \top }{\mathbf{Gx}}+p({\xi _s}){(v(\xi _{{s,t}}^{*}))^ \top }{\mathbf{Pu}}+\eta \geq P({\xi _s}){(v(\xi _{{s,t}}^{*}))^ \top }{\mathbf{l}}({\xi _s}){\mkern 1mu} {\text{ }}\forall t \notin {\theta _k},s \in S$$
(62)
$${\text{ }}{\mathbf{x}},{\mathbf{u}} \in \left\{ {0,1} \right\}$$
(63)

Step 3: For s = 1,…,S, Solve the dual subproblem (48)-(50), if the dual subproblem is feasible for all scenarios obtain the optimal results \({\pi ^*}({\xi _s})\), and update UB =\(\sum\limits_{{s=1}}^{S} {p({\xi _s})} \cdot {\pi ^*}{({\xi _s})^ \top }({\mathbf{l}}({\xi _s}) - {\mathbf{G}}{{\mathbf{x}}^*} - {\mathbf{P}}{{\mathbf{u}}^*})\). Optimality cut is generated and added to the master problem, as shown in (64).

$$p({\xi _s}){(v(\xi _{{s,t}}^{*}))^ \top }{\mathbf{Gx}}+p({\xi _s}){(v(\xi _{{s,t}}^{*}))^ \top }{\mathbf{Pu}}+\eta \geq P({\xi _s}){(v(\xi _{{s,t}}^{*}))^ \top }{\mathbf{l}}({\xi _s}){\mkern 1mu} {\text{ }}\forall t \notin {\theta _k},s \in S$$
(64)

Step 4: If the dual subproblem is unbounded for any scenario with extreme rays \(\xi _{s}^{*}\), a feasibility cut (65) is generated from the subproblem with the corresponding scenario and added to the master problem.

$$p({\xi _s}){(\pi (\xi _{{s,t}}^{*}))^ \top }{\mathbf{Gx}}+p({\xi _s}){(\pi (\xi _{{s,t}}^{*}))^ \top }{\mathbf{Pu}}+\eta \geq P({\xi _s}){(\pi (\xi _{{s,t}}^{*}))^ \top }{\mathbf{l}}({\xi _s}){\text{ }}\forall t \in {\theta _k},s \in S$$
(65)

Step 5: judge whether the upper and lower bounds satisfy |UB-LB|<1e− 5. If yes, continue; otherwise, make t = t + 1 and return to Step 2) .

Fig. 3
figure 3

Flow chart of solution.

Full size image
Fig. 4
figure 4

Flow chart of solution.

Full size image

Case study

Parameter setting

Based on the structure shown in Fig. 1, a data center alliance consisting of three geographically adjacent data centers is considered. Referring to the scale of an actual data center in21,22,23,24, the following assumptions are made: Data centers-1, 2, and 3 have 12, 12, and 16 computer rooms, respectively, where each computer room contains 20 cabinets, and each cabinet holds 20 servers. The peak power consumption and idle power consumption of each server are 0.2 kW and 0.12 kW, respectively. The proportion of batch processing workloads to the total workloads for data centers-1, 2, and 3 is 40%, 50%, and 60%, respectively. Each data center has a self-built WT with an installed capacity of 1 MW and a PV station with an installed capacity of 800 kW. For the configuration parameters, the data center alliance can configure shared energy storage ranging from 0 to 2 MW × 6 h. The unit power cost and unit energy capacity cost of energy storage are 3500 yuan/kW and 350 yuan/(kWh)32, respectively. The energy storage system has a design lifespan of 10 years, a charge/discharge efficiency of 0.9, and a discount rate of 8%25. The time-of-use (TOU) tariff follows the pricing Case implemented in Beijing in February 202215, as shown in Fig. 5. The ambient temperature is based on the real data in the Beijing, as shown in Fig. 6.

This study utilizes annual historical output data from RES power stations at Shenzhen as the original dataset. A Markov Chain Monte Carlo method26, which incorporates duration and fluctuation characteristics, is applied for wind power scenario generation. Concurrently, a time series generation method based on a vector autoregressive model27 is employed for photovoltaic power output scenario generation, thereby simulating potential RES output profiles. Considering that workloads exhibit strong daily patterns28,29,30,31,32, typical daily profiles of different workloads are generated via Monte Carlo simulations to depict the stochastic nature of workloads demand. Based on the research requirements of this study, the initial number of scenarios is set to 200.

To validate the effectiveness and superiority of the proposed shared energy storage planning method, four cases are designed based on energy storage construction modes and demand response participation:

Case 1: Each data center is equipped with its own energy storage and does not participate in demand response.

Case 2: Each data center is equipped with its own energy storage and participates in demand response.

Case 3: The data center alliance jointly constructs and shares energy storage but does not participate in demand response.

Case 4 (Proposed): The data center alliance jointly constructs and shares energy storage and participates in demand response.

The simulation is conducted on the MATLAB platform. The YALMIP toolbox is utilized to invoke the commercial solver Gurobi for solving the formulated optimization problem, with an optimization error tolerance of 0.01%.

Fig. 5
figure 5

time-of-use price from main grid.

Full size image
Fig. 6
figure 6

Ambient temperature.

Full size image

Case study

The energy storage configuration results and cost details under each Case are listed in Table 1. It is evident that Case 4 (the proposed Case) achieves the lowest total cost for the data center alliance. Comparing Case 1 and Case 3 (or Case 2 and Case 4), although the alliance configures slightly more storage capacity in the shared energy storage mode compared to individual configurations, its grid electricity purchase cost significantly decreases. This indicates that shared energy storage improves utilization efficiency and provides higher economic benefits. Additionally, comparing Case 1 with Case 2 (or Case 3 with Case 4), it is observed that incorporating adjustable potential reduces the demand for energy storage by data centers, effectively lowering total costs.

Table 1 Optimization results under cases.
Full size table

To further analyze the impact of shared energy storage on improving utilization and the collective costs of data centers, the total costs of each data center under Cases 2 and 4 are calculated and summarized in Table 2. The shared energy storage power and energy capacity allocation under different scenarios under Case 4 is illustrated in Figs. 7 and 8.

Table 2 shows that before Nash bargaining, the total cost of each data center in the shared energy storage mode is lower than that under individual configurations. However, the cost reductions vary significantly across data centers. For instance, in Case 4, data center 1 only reduces its costs by 28.1 yuan per day, while data center 3 achieves a reduction of 123.3 yuan per day. Such uneven cost savings would lead to imbalanced profit distribution.

Besides, as seen, the subsidy from the alliance after bargaining by data center 1 is 1.1 yuan, while the subsidy from the alliance after bargaining by data center 2 is 47.1 yuan, and after bargaining, data center 3 has to pay 48.2 yuan to the alliance. This illustrate Data Center 1 and 2 receive subsidies for contributing more adjustable potential. Through the above conclusions, it can be shown that the income from the alliance is distributed to all data centers fairly and reasonably to ensure that the total income of the data center alliance should remain unchanged before and after bargaining. This demonstrates that the Nash bargaining method ensures fair profit distribution while maintaining collective benefits, thereby enhancing the willingness of data centers to participate in the alliance.

Table 2 Total cost of each data center.
Full size table
Fig. 7
figure 7

Optimal power capacity allocation of shared energy storage under different scenario.

Full size image
Fig. 8
figure 8

Optimal energy capacity allocation of shared energy storage under different scenario.

Full size image

From Fig. 7, taking data center 3 as an example, its power capacity requirements exceed 200 kW in scenarios 1, 2, 7, and 9 but drop to nearly zero in scenarios 6 and 10. This highlights the variability in energy storage demand across different scenarios. If configured individually, the underutilization of energy storage would lead to poor economic returns. Furthermore, data center 1 requires significantly different energy-to-power ratios in scenarios 2 and 4 (e.g., 218 kW/1860 kWh vs. 412 kW/2166 kWh), confirming the heterogeneous demands for shared storage capacity among alliance members. Consequently, the shared storage planning method efficiently leverages complementarities in power and energy capacity needs across diverse scenarios, maximizing storage utilization.

To analyze the specific effects of data centers participating in adjustable potential of data center, the batch processing load execution status and room temperature curves of data center 2 under Scenario 2 in Case 3 and Case 4 are shown in Figs. 9 and 10 (room temperatures represent initial values for each time period), respectively. From Figs. 9 and 10, it can be observed that before electricity price increases or after price reductions (e.g., at t = 10 h or t = 20 h), data centers regulating their power consumption tend to process as many batch workloads as possible to avoid handling them during peak electricity price periods (e.g., t = 11–12 h or t = 15–19 h). For computer room air conditioners, when data centers do not participate in demand response, room temperatures remain at the permissible maximum level, as shown in Fig. 9; whereas participating data centers precool rooms intensively before peak price periods, leveraging thermal inertia to reduce air conditioning energy demand during peak hours.

Fig. 9
figure 9

Temperature variation curve in computer rooms under case 3.

Full size image
Fig. 10
figure 10

Temperature variation curve in computer rooms under case 4.

Full size image

The power supply and consumption profiles of data center 2 under Scenario 2 for Cases 3 and 4 are illustrated in Figs. 11 and 12, respectively.

From the operation of energy storage in Fig. 11, it is evident that compared to Case 3 (without demand response), Case 4 (with demand response) requires significantly less energy storage during operation. This is because the participation of demand-responsive batch processing loads and computer room air conditioners can be regarded as “virtual energy storage,” thereby reducing the demand for physical energy storage. Furthermore, combining Figs. 11, 12 and 13, under Case 4, the batch processing loads handled during peak electricity price periods (e.g., t = 15–19 h) are reduced. Consequently, the power consumption of IT equipment decreases, as does the heat generated by these devices. Given that the ambient temperature in Scenario 2 is generally low, the computer room air conditioners only need minimal cooling or even no cooling to meet temperature requirements. This reduces the electricity demand of data centers during peak price periods, thereby decreasing their reliance on grid purchases and energy storage. Therefore, when data centers participate in demand response, their operational dependence on energy storage can be reduced, thereby lowering energy storage investment costs and total costs, and improving the economic efficiency of data center operations.

Fig. 11
figure 11

Batch workloads distribution.

Full size image
Fig. 12
figure 12

Optimal power supply circumstance.

Full size image
Fig. 13
figure 13

Optimal power consumption circumstance.

Full size image

To analyze the impact of the peak-valley price difference on the planning results, based on the electricity price in Fig. 5, we will gradually change the peak-valley difference level of electricity price from − 20% to + 20%. with a step-size of 10%. The corresponding results under different settings of peak-valley price difference are illustrated in Fig. 14. We find that with the increase of peak-valley price difference, investors have the incentive to allocate more shared energy storage. This is because with the increase of peak-valley price difference, the investment in shared energy storage will gain more benefits through peak-valley arbitrage, thus reducing the cost while investing more energy storage. On the contrary, with the decrease of peak-valley price difference, investors are more reluctant to invest in shared energy storage because of the decrease of expected profits from charging and discharging. In this case, a lower investment tendency can be observed.

Fig. 14
figure 14

Impact of the peak-valley price difference on the planning results.

Full size image

Algorithm performance comparison

To address the computational burden caused by a large number of generated scenarios, this paper propose a improved L-shaped algorithm to reduce computational complexity through problem decomposition effectively. To demonstrate the effectiveness of improved L-shaped algorithm in solving the proposed two-stage stochastic program, we compare the performance of improved L-shaped algorithm with directly solving the deterministic equivalent problem by Commercial solver (i.e., Gurobi) in terms of objective function values (including optimality gaps) and computational time. Based on Benders decomposition, this study implements the improved L-shaped algorithm using Gurobi 9.5.1. For comparison, the deterministic equivalent problem is solved using Gurobi 9.5.1 with default settings. To evaluate performance, instances with varying numbers scenarios are considered, and the computational time is limited to 3600 s (1 h). The numerical results are summarized in Table 3. The results indicate that improved L-shaped algorithm outperform the direct solution of Commercial solver in both objective value and computational time. Due to complexity constraints, Commercial solver fails to solve larger-scale instances (e.g., cases with more 200 scenarios) within 3600 s, prompting the termination of problem size expansion when solution by Commercial solver becomes intractable. This highlights that the L-shaped algorithm aligns better with the problem structure and significantly reduces the solution complexity through decomposition. Furthermore, the multi-cut strategy demonstrates higher efficiency than the L-shaped algorithm, suggesting that non-aggregated multiple Benders cuts provide stronger approximation than a single aggregated cut.

Table 3 Performance comparison.
Full size table

To further compare the performance between the L-shaped algorithm and the proposed improved L-shaped algorithm, we also investigate their convergence behavior toward the optimal solution, with results summarized in Figs. 15 and 16. In Figure, the upper bound represents the objective function value of the best feasible solution, while the lower bound corresponds to the objective value of the best LP relaxation problem. Note that an upper bound of “0” indicates no feasible solution is found. As expected, we observe that the L-shaped algorithm requires more iterations than the proposed algorithm to converge to the optimal solution.

Fig. 15
figure 15

Convergence to optimal solution by L-shaped algorithm.

Full size image
Fig. 16
figure 16

Convergence to optimal solution by the proposed improved L-shaped algorithm.

Full size image

To verify the proposed algorithm’s actual effectiveness, simulations based on larger-scale system are presented in this revision. The related system is refers to the scale of an actual data center in reference31, where there are eight data centers (DC1–DC8). It is assumed that the number of computer rooms in eight data centers are 25, and each computer room has 50 cabinets, and each cabinet can hold 40 servers. The numerical results are summarized in Table 4. The results indicate that improved L-shaped algorithm outperform the direct solution of Commercial solver and the traditional L-shaped algorithm in both objective value and computational time. Due to larger-scale system and scenarios, Commercial solver fails to solve all circumstances within 3600 s. And the traditional L-shaped algorithm fails to solve the problems with more than 200 scenarios. While the improved L-shaped algorithm could solve all problem within limited solution times, which highlights that the improved L-shaped algorithm significantly reduces the solution complexity through decomposition and utilizes the multi-cut strategy to provide stronger approximation than a single aggregated cut.

Table 4 Performance comparison in the larger-scale system.
Full size table

In addition, the impact of the choice of algorithm parameters on the results is analyzed. To analyze the impact of convergence tolerance on the results, we change the convergence tolerance(1e− 5 in this study). The corresponding results under different settings of the convergence tolerance are illustrated in Fig. 17. We find that with the increase of convergence tolerance, the optimal cost value increases, and the calculation speed accelerates. However, for convergence tolerances 1e− 5 and 1e− 6, there is almost no difference between the two optimal cost results, and the solution time is much longer under 1e− 6.

Fig. 17
figure 17

Impact of the convergence tolerance on the results.

Full size image

Conclusion

To address the challenges of low utilization and poor economic benefits caused by individual energy storage deployment in data centers, this study proposes a shared energy storage planning method for data center alliances that incorporates demand response. By leveraging the heterogeneity and complementarity of energy storage requirements across different operational scenarios, the proposed approach enhances storage utilization while minimizing investment costs. The following conclusions are drawn:

Compared to individual energy storage deployment, a shared energy storage framework within a data center alliance allows dynamic allocation of storage capacity (power and energy) based on diverse operational scenarios, thereby improving utilization efficiency and economic outcomes. After Nash bargaining for equitable profit distribution, the daily comprehensive costs for Data Centers 1, 2, and 3 decreased by 2.8%, 3.1%, and 1.9%, respectively, demonstrating higher cost-effectiveness compared to standalone configurations.

By integrating demand response, batch processing loads and HVAC systems act as generalized energy storage resources. Adjusting batch load scheduling and implementing pre-cooling strategies during off-peak electricity pricing periods reduce energy demand during peak hours, thereby diminishing reliance on physical storage and lowering overall operational costs.

This study focuses on cooperative shared energy storage planning for data centers, while conflicts of interest among participants in non-cooperative scenarios remain to be explored. Future work will investigate operational mechanisms for shared energy storage under non-cooperative conditions.