Introduction

Out of many power quality issues in the distribution network, harmonics are the major issue1. The tremendous use of non-linear loads generates integral multiples of fundamental frequency either in voltage and current waveform that leads to huge deterioration of waveform from its ideal sinusoidal2. This deterioration causes overheating of generator and transformer windings, undesired operation of circuit breaker and relay, overburden on generators and transformers and deterioration of true power factor1,2,3,4. In some cases, harmonics are alleviated by adjusting or modifying the network topologies without using harmonic compensators. As an example, voltage harmonics gets rid of by resizing the source impedance5. Alleviating the harmonics by internal network modifications is not possible many times due to dynamic changes in load and supply6. The resonance conditions in the network also change dynamically, which results in excessive generation of harmonics1,2,3,4,5,6,7. Harmonic Compensators are required where network modification and resizing will not workout in reducing the harmonic distortion8. Harmonic compensators are connected either in series or parallel with network at the Point of Common Coupling (PCC) to reduce voltage and current distortion9. Based on the requirement and need either series or parallel or both series and parallel connected harmonic compensators are preferred9,10. Harmonic compensators are categorized into passive, active and hybrid compensators11,12. Passive compensators are either tuned or unturned in nature13. Depends on the application and requirement any one will be preferred14. As an example, in induction motor, untuned LC filter is preferred to compensate the voltage due to high starting torque. Tuned Passive Filters (TPFs) are preferred at HVDC converters to eliminate the most dominant lower order current or voltage harmonics15. Passive compensators mainly work based on resonance condition. Resonance condition changes with respected to supply and loading conditions. The major drawback with passive harmonic filtering is that, these are not suitable under dynamic supply and load conditions but the cost of implementing is less16. Other side, active harmonic compensators are proved to ideal in reducing the harmonic distortion irrespective of changes in supply, load and fault conditions17. The cost and complex control techniques are the major shortcomings of active filtering. As like passive filtering, active filtering also applied to reduce voltage or current distortion or both18. Active filtering mainly works on harmonic cancelation technique18. It is done by generating anti harmonics so that harmonics at the load side gets rid of from the network. SAHC is connected in shunt or series or both and is most commonly used to reduce the current distortion19. Typically, SAHC is just a voltage source inverter (VSI) with IGBT switches. Unlike passive harmonic compensators, these are most efficient and alleviate multiple harmonics at a time19. Designing a control scheme for SAHC to meet al.l practical abnormalities is a challenging task. The SAHC control is divided into three, reference current extraction, DC bus voltage control and pulse generation20. Traditional frequency domain techniques were slow in response. In direct method, the controller will be fed on error between actual and reference VSI capacitor voltages21. Here the controller has to maintain constant VSI capacitor voltage and also generate the required reference currents (180 degrees out of phase) at the same time22. Hence the designing and tuning of VSI capacitor voltage may be difficult. Hence, the direct method of reference current extraction technique will not reduce harmonic distortion as per requirement of IEEE 519-2022 standards23. The traditional indirect time domain reference techniques such as PQ, SRF, Unit Vector, I cosθ were failed to meet practical conditions24,25,26,27. The DC bus voltage controls such as PI, PID, Type-1 and 2 fuzzy, PI-Fuzzy, ANFIS controllers are not capable in maintaining stiff voltage under all practical conditions28,29,30,31. PWM, SPWM, SVPWM, Hysteresis, adaptive hysteresis, adaptive fuzzy hysteresis pulse generating techniques were failed to track the reference currents accurately as a result misfiring of switches and overshooting may takes place27,28,32,33. The coordination between these three sub controls is much important to get the desired output from SAHC.

In order to design SAHC under all practical conditions, the following conditions are considered.

  1. 1.

    Designing a novel reference current extraction technique by averaging the unit vector, PQ and SRF control techniques i.e. AUV-PQ-SRF technique.

  2. 2.

    Designing a DC bus voltage control using sliding mode control (SMC).

  3. 3.

    Elimination of pulse width control (emulator) by implementing a novel optimal switching vector – model predictive control (OSV-MPC).

An idea of combining the three reference current extraction techniques with the matrix average is a novel solution and is not existed anywhere in the literature. In this paper, unit vector reference current extraction technique, PQ control technique and SRF control technique are combined and averaged to calculate the proposed Unit Vector-PQ-SRF (AUV-PQ-SRF) reference current extraction technique. The model predictive control has been widely used as an industrial controller due to the elimination external emulator or pulse generator. In this paper Optimal Switching Sequence-Model Predictive Controller (OSV-MPC) technique has been used in association with AUV-PQ-SRF reference current extraction technique34,35,36. A Sliding Mode Controller (SMC) offers significant advantages over traditional PI/PID/fuzzy/ANN controllers in maintaining a constant DC link voltage for a SAHC37. One of the key benefits of SMC is its robustness against parameter variations and external disturbances, ensuring stable performance even under fluctuating loads and grid conditions33. Unlike traditional controllers, which require precise tuning and may struggle with uncertainties, SMC exhibits fast dynamic response due to its discontinuous control action, quickly driving the system to the desired state27. Additionally, SMC is well-suited for nonlinear and time-varying systems, making it ideal for SAHC applications where load conditions frequently change27. Another advantage is its reduced sensitivity to modelling inaccuracies, allowing effective control without needing an exact system model24. While traditional controllers often experience steady-state errors and require compensators, SMC inherently minimizes such deviations, ensuring better voltage regulation38. Furthermore, advanced SMC techniques, such as Super Twisting Sliding Mode Control (ST-SMC), help mitigate chattering while retaining robustness38. Overall, SMC provides superior performance in maintaining DC link voltage stability, making it a more reliable and adaptive choice for power quality improvement in modern power systems. This paper is well sectioned into introduction, modelling of AUV-PQ-SRF reference current extraction technique, designing of a DC bus control with SMC, implementing OSV-MPC controller, Results and discussions, conclusions and references.

The comparison of proposed method with existing works along with strengths and weaknesses are tabulated in Table 1.

Table 1 Comparison of proposed method with existing works.
Full size table

Modelling of AUV-PQ-SRF reference current extraction technique

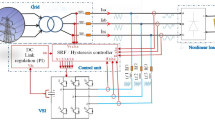
The pictorial diagram of the proposed AUV-PQ-SRF reference current extraction is as shown in Fig. 1. These current references were takeout independently from each reference current extraction technique and then converged with matrix average relationship.

The reference currents from unit vector control technique are given by (1)39,40.

$$\left[ {\begin{array}{*{20}{c}} {{i^*}_{{Ca}}} \\ {{i^*}_{{Cb}}} \\ {{i^*}_{{Cc}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{I_{max}}}&0&0 \\ 0&{{I_{max}}}&0 \\ 0&0&{{I_{max}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {sin\theta } \\ {sin\left( {\theta +120^\circ } \right)} \\ {sin\left( {\theta - 120^\circ } \right)} \end{array}} \right]$$
(1)

The reference currents from PQ control technique are given by (2)40.

$$\left[ {\begin{array}{*{20}{c}} {{i^*}_{{Ca}}} \\ {{i^*}_{{Cb}}} \\ {{i^*}_{{Cc}}} \end{array}} \right]=\sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt 2 }}}&1&0 \\ {\frac{1}{{\sqrt 2 }}}&{ - \frac{1}{2}}&{\frac{{\sqrt 3 }}{2}} \\ {\frac{1}{{\sqrt 2 }}}&{ - \frac{1}{2}}&{ - \frac{{\sqrt 3 }}{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - {i_0}} \\ {{i_{C\alpha }}} \\ {{i_{C\beta }}} \end{array}} \right]$$
(2)

The reference currents from SRF control technique are given by (3)41.

$$\left[ {\begin{array}{*{20}{c}} {{i^*}_{{Ca}}} \\ {{i^*}_{{Cb}}} \\ {{i^*}_{{Cc}}} \end{array}} \right]=\sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }&1 \\ {\cos \left( {\theta - 120} \right)}&{ - \sin \left( {\theta - 120} \right)}&1 \\ {\cos \left( {\theta +120} \right)}&{ - \sin \left( {\theta +120} \right)}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde {i}}_d} - {i_{loss}}} \\ {{i_q}} \\ {{i_0}} \end{array}} \right]$$
(3)

The matrix averaging of (1), (2) & (3) gives the proposed AUV-PQ-SRF reference current extraction technique and is given by (4)

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {{\text{i}}_{{{\text{Ca}}}}^{*} } \\ {{\text{i}}_{{{\text{Cb}}}}^{*} } \\ {{\text{i}}_{{{\text{Cc}}}}^{*} } \\ \end{array} } \right] &= \frac{1}{3}\left[ {\begin{array}{*{20}c} {I_{{\max }} \sin \theta } \\ {I_{{\max }} \sin (\theta + 120^\circ )} \\ {I_{{\max }} \sin (\theta - 120^\circ )} \\ \end{array} } \right] + \frac{1}{3}\sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}c} {\frac{1}{{\sqrt 2 }}\left( { - {\text{i}}_{0} } \right) + {\text{i}}_{{{\text{C}}\alpha }} } \\ {\frac{1}{{\sqrt 2 }}\left( { - {\text{i}}_{0} } \right) - \frac{1}{2}{\text{i}}_{{{\text{C}}\alpha }} + \frac{{\sqrt 3 }}{2}{\text{i}}_{{{\text{C}}\beta }} } \\ {\frac{1}{{\sqrt 2 }}\left( { - {\text{i}}_{0} } \right) - \frac{1}{2}{\text{i}}_{{{\text{C}}\alpha }} - \frac{{\sqrt 3 }}{2}{\text{i}}} \\ \end{array} } \right] \\ & \quad + \frac{1}{3}\sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}c} {\cos \theta ({\tilde{\text{i}}}_{{\text{d}}} - {\text{i}}_{{{\text{loss}}}} - \sin \theta {\text{i}}_{{\text{q}}} + {\text{i}}_{0} } \\ {\cos (\theta - 120^\circ )\left( {{\tilde{\text{i}}}_{{\text{d}}} - {\text{i}}_{{{\text{loss}}}} } \right) - \sin (\theta - 120^\circ ){\text{i}}_{{\text{q}}} + {\text{i}}_{0} } \\ {\cos (\theta + 120^\circ )\left( {{\tilde{\text{i}}}_{{\text{d}}} - {\text{i}}_{{{\text{loss}}}} } \right) - \sin (\theta + 120^\circ ){\text{i}}_{{\text{q}}} + {\text{i}}_{0} } \\ \end{array} } \right] \end{aligned}$$
(4)
Fig. 1
figure 1

Block diagram of the proposed AUV-PQ-SRF technique.

Full size image

Modelling of SMC DC voltage regulator

The modelling of DC voltage regulator plays an important role in perfect tracking of references with actual compensating current. In general, PI controller was being used for this purpose41. However, the tuning of PI controller is very difficult. Zigler and Nocholas method of approximation failed to achieve tuning under practical conditions41. Type-1 fuzzy and Type-2 fuzzy logic controllers were also used for this purpose but the system response is slow and more computational burden. Combination of PI and fuzzy also used to reduce the computational burden. The automatic tuning of PI controller leads to more complex42. Sliding mode control (SMC) is a robust control strategy and is well-suited for systems with uncertainties and non-linearities, such as maintaining a constant DC link voltage in a shunt active filter43. The block diagram of the SMC integrated with OSV- MPC and AUV-PQ-SRF technique is as shown in Fig. 2. SMC is a non-linear control method that forces the system states to “slide” along a predetermined surface (called the sliding surface) by applying a discontinuous control signal44. SMC operates in two phases. In reaching phase, the system state moves toward a predefined sliding surface5,44. Whereas, in sliding phase, the system state stays on the surface, ensuring stable regulation45.

The SMC design is based on the DC link voltage error dynamics. The mathematical modelling of DC link voltage is given by (5)

$$~{{\text{C}}_{{\text{dc}}}}\frac{{{\text{d}}{{\text{V}}_{{\text{dc}}}}}}{{{\text{dt}}}}={{\text{I}}_{{\text{dc}}}} - {{\text{I}}_{{\text{load}}}}$$
(5)

where \({V_{dc}}\) = DC link voltage, \({C_{dc}}\)= DC link capacitance, \({I_{dc}}\) = Current drawn from the DC bus, \({I_{load}}\)= Load current.

Fig. 2
figure 2

Sliding mode controller integrated with OSV-MPC Technique and AUV-PQ-SRF technique.

Full size image

The sliding surface is given by (6)

$${\text{S}}\left( {\text{t}} \right)={\text{ev}}+{\text{\varvec{\uplambda}}}\smallint {\text{evdt}}$$
(6)

Where \(ev={V_{dc,ref}}~ - {V_{dc}}\), \(\lambda {\text{~}}\)= positive number.

The control law ensures that the system state reaches and remains on the sliding surface and is given by (7)

$$\frac{{{\text{dS}}}}{{{\text{dt}}}}+{\text{\varvec{\upeta}S}}=0$$
(7)

where η is a positive constant for convergence.

The discontinuous switching control law is given by (8)

$$I_{{dc}}^{*}={I_{{\text{dc}},{\text{eq}}}} - {K_s}{\text{sign}}\left( {\text{S}} \right)$$
(8)

where \(I_{{dc}}^{*}\)= Reference current for the SAHC, \({I_{dc,~eq}}\)= Equivalent control ensuring steady-state operation, \({K_s}\) = Switching gain, sign(S)= Sign function inducing switching behavior.

To reduce chattering, a smooth approximation of the sign function can be used. It is given by (9).

$$sign\left( S \right)=\frac{S}{{ \in +\left| S \right|}}$$
(9)

where \(\in\) is a small boundary layer to smooth the control signal.

Design of OSV-MPC technique

The design of OSV-MPC requires three of the following steps.

  1. 1.

    Prediction of compensating currents.

  2. 2.

    Extrapolation of predicted and actual reference currents.

  3. 3.

    Minimizing the cost function thereby to produce required pulses.

Prediction of compensating currents

The circuit diagram of the shunt active filter is as shown in Fig. 3. Basically, it is a three-phase voltage source inverter (VSI).

Fig. 3
figure 3

Circuit diagram of a shunt active filter.

Full size image

In each leg of three phase VSI, there will be two switches complements each other46. The potentials in each leg are given by (10).

$$\begin{gathered} {v_{aN}}={S_a}{V_{dc}} \hfill \\ {v_{bN}}={S_b}{V_{dc}} \hfill \\ {v_{cN}}={S_c}{V_{dc}} \hfill \\ \end{gathered}$$
(10)

The voltage vector at the output side is given by (11)

$$v=\frac{2}{3}\left( {{v_{aN}}+a{v_{bN}}+{a^2}{v_{cN}}} \right)$$
(11)

From Fig. 2, The load current may be written as (12)

$${i_l}={i_s}+{i_c}$$
(12)

The capacitor current that is responsible for charging and discharging is given by (13)

$${i_{dc}}={i_{ca}}{S_a}+{i_{cb}}{S_b}+{i_{cc}}{S_c}$$
(13)

Applying KVL to Fig. 2 that yields (14)

$${L_c}\frac{{dic}}{{dt}}=v - {V_s} - {R_c}{i_c}$$
(14)

The output voltages of the inverter may rewrite as (15)

$$v={V_{dc}}.H.{S_{abc}}$$
(15)

Where Vdc is the DC link voltage and H is the constant matrix as shown in (16)

$$H=\left[ {\begin{array}{*{20}{c}} {\frac{2}{3}}&{\frac{{ - 1}}{3}}&{\frac{{ - 1}}{3}} \\ {\frac{{ - 1}}{3}}&{\frac{2}{3}}&{\frac{{ - 1}}{3}} \\ {\frac{{ - 1}}{3}}&{\frac{{ - 1}}{3}}&{\frac{2}{3}} \end{array}} \right]$$
(16)

There are eight possible switching combinations, each producing a corresponding voltage vector. In switching sequence-1 (0, 0, 0) and switching sequence-8, the inverter’s output voltage in each phase is zero. Since switching sequence-1 and sequence-6 result in the same output, sequence-6 is not considered. Among these, the switching sequence (1, 1, 0) provides an optimized voltage vector with minimal error between the reference and compensating SAHC currents47. Table 2 presents the possible switching states and their associated voltage vectors.

Table 2 Switching states and vectors.
Full size table

The two steps ahead predicted SAHC compensating currents are obtained by the forward Euler approximation and is given by (17)48,49,50.

$$\frac{{d{i_c}}}{{dt}} \approx \frac{{{i_c}\left( {k+1} \right) - {i_c}\left( k \right)}}{{{T_s}}}$$
(17)

From (14)

$$\frac{{d{i_c}}}{{dt}}=\frac{{v - {V_s} - {R_c}{i_c}}}{{{L_c}}}$$
(18)

Substitute (18) in (17), gives the one step ahead predicted SAHC compensating current and is given by (19)

$${i_c}\left( {k+1} \right)={T_s}\frac{{v\left( k \right) - {V_s}\left( k \right)}}{{{L_c}}}+\left( {1 - \frac{{{R_c}{T_s}}}{{{L_c}}}} \right){i_c}\left( k \right)$$
(19)

Similarly, the two steps ahead predicted SAHC compensating current is given by (20)

$${i_c}\left( {k+2} \right)={T_s}\frac{{v\left( {k+1} \right) - {V_s}\left( {k+1} \right)}}{{{L_c}}}+\left( {1 - \frac{{{R_c}{T_s}}}{{{L_c}}}} \right){i_c}\left( {k+1} \right)$$
(20)

Extrapolation of reference and compensating currents

For small sampling intervals, the predicted reference currents closely match the actual currents. However, for larger sampling times, extrapolation is used to estimate the current values of one or two steps ahead49,50. A straightforward approach is to apply linear extrapolation, using the current and previous reference values to predict the reference current for the next two sampling instants51. The block diagram of the linear extrapolation technique is as shown in Fig. 4.

Fig. 4
figure 4

Extrapolation of reference currents.

Full size image

The error vector is given by (21)

$$\begin{gathered} \Delta \left( {{i_q}+{i_{c\beta }}} \right)/2= - \mathop \sum \limits_{{m=1,2}} \left[ {2C{'_m}{C_m}\left( {{i_q}+{i_{c\beta }}} \right)/2+2S{'_m}{S_m}\left( {{i_q}+{i_{c\beta }}} \right)/2} \right] \hfill \\ \Delta \left( {{i_d}+{i_{c\alpha }}} \right)/2=\mathop \sum \limits_{{m=1,2}} \left[ {2C{'_m}{C_m}\left( {{i_d}+{i_{c\alpha }}} \right)/2+2S{'_m}{S_m}\left( {{i_d}+{i_{c\alpha }}} \right)/2} \right] \hfill \\ \end{gathered}$$
(21)

The one step ahead predicted reference currents are given by (22)

$$i{*_{c\left( {k+1} \right)}}=\frac{{\left( {{i_q}+{i_{c\beta }}} \right)/2\Delta \left( {{i_q}+{i_{c\beta }}} \right)/2++\left( {{i_d}+{i_{c\alpha }}} \right)/2\Delta \left( {{i_d}+{i_{c\alpha }}} \right)/2}}{2}$$
(22)

The two step ahead horizon predicted reference currents are given by (23)

$$i{*_{c\left( {k+2} \right)}}=i{*_{c\left( {k+1} \right)}}+\Delta {i_{c\left( {k+1} \right)}}$$
(23)

where \({C_m}=\cos 6m\theta\), \({S_m}=\sin 6m\theta\), \(C{'_m}=\cos 6m\theta - \cos 6m\left( {\theta +{\theta _s}} \right)\), \(S{'_m}=\sin 6m\theta - \sin 6m\left( {\theta +{\theta _s}} \right)\), \(\theta =\omega {T_s},{T_s}=1/{f_s}\)

Cost function

The block diagram of the proposed two step ahead cost function is represented in Fig. 5.

For OSV-MPC control strategy, the best suitable two step ahead cost function is given by (24)

$$g={\left( {{i_c}\left( {k+2} \right) - {i_c}^{*}\left( {k+2} \right)} \right)^2}+\lambda {n_c}$$
(24)

where g—cost function, \({i_c}\left( {k+2} \right)\)—two step ahead SAHC compensating currents, \({i_c}^{*}\left( {k+2} \right)\)—two step ahead reference compensating currents, λ—weighting factors

Fig. 5
figure 5

Cost minimization function.

Full size image

For OSV-MPC control strategy, the best suitable two step ahead cost function is given by (25)

$$g={\left( {{i_c}\left( {k+2} \right) - {i_c}^{*}\left( {k+2} \right)} \right)^2}+\lambda {n_c}$$
(25)

\({i_c}\left( {k+2} \right)\)—two step ahead SAHC compensating currents, \({i_c}^{*}\left( {k+2} \right)\)—two step ahead reference compensating currents, \(\lambda\)—weighting factors.

Weighting factors are combination of remaining variables apart from predicted and reference currents involved in the SAHC operation. Hence, the cost function is divided into two types one is cost function to optimize the references (g1) i.e. zero error between actual and references compensating currents and second is the cost function to optimize the remaining parameters (g2) [82-84]. The cost function is given by (26)

$$g={g_1}+{g_2}$$
(26)

Where g1 is represented as (26) and g2 is represented as (27) & (28)

$${g_1}={\left( {\widehat {{{i_c}\left( {k+2} \right)}} - {i_c}^{*}\left( {k+2} \right)} \right)^2}$$
(27)
$${g_2}=\lambda {n_c}$$
(28)
$${g_2}={\lambda _1}{n_{c1}}+{\lambda _2}{n_{c2}}+{\lambda _3}{n_{c3}}$$
(29)

\({\lambda _1},{\lambda _2}\& {\lambda _3}\) are the weighting factors. \({\lambda _3}=1\); This is always constant. \({\lambda _2}\& {\lambda _3}\) Values are adjusted according to the system conditions and variations, where

$${n_{c1}}=\frac{1}{{{V_{dc,reted}}}}\left| {{V^*}_{{dc}}\left( {k+2} \right) - {V_{dc}}\left( {k+2} \right)} \right|$$
(30)
$${n_{c2}}=\frac{1}{{{P_{s,rated}}}}\left| {{P_s}^{*}\left( {k+2} \right) - {P_s}\left( {k+2} \right)} \right|$$
(31)
$${n_{c3}}=\frac{1}{{{P_{s,rated}}}}\left| {{Q_s}^{*}\left( {k+2} \right) - {Q_s}\left( {k+2} \right)} \right|$$
(32)

The proposed method aims to enhance the performance of the Shunt Active Harmonic Compensator (SAHC) by integrating three innovative control strategies that address key limitations in existing techniques. The core components of the proposed method are:

AUV-PQ-SRF reference current extraction

This novel technique combines three established methods—Unit Vector Template (UVT), Instantaneous Power Theory (PQ), and Synchronous Reference Frame (SRF)—to accurately determine the reference compensating currents. Each method contributes uniquely:

  • UVT ensures phase synchronization,

  • PQ handles instantaneous power variations,

  • SRF efficiently separates harmonics under dynamic conditions.

By averaging the outputs of these methods through a matrix-based approach, the AUV-PQ-SRF technique ensures robust and accurate harmonic detection, even under fluctuating load and grid conditions.

Sliding mode controller (SMC) for DC link voltage regulation

To maintain a stable DC bus voltage, a Sliding Mode Controller (SMC) is used instead of conventional PI or fuzzy controllers. SMC offers strong robustness against system disturbances and parameter uncertainties. It operates in two phases:

  • Reaching Phase, where the system states are driven toward the sliding surface, and.

  • Sliding Phase, where the system states remain on the surface, ensuring consistent regulation.

The SMC’s discontinuous control law ensures rapid dynamic response and precise voltage tracking without the tuning complexity associated with linear controllers.

Optimal switching vector-model predictive control (OSV-MPC)

Traditional PWM techniques suffer from misfiring and poor tracking under dynamic conditions. The proposed OSV-MPC approach eliminates the need for a separate pulse-width modulator by directly predicting the inverter’s switching states.

The process involves:

  • Predicting compensating currents for two-time steps ahead using system dynamics,

  • Extrapolating reference currents for alignment,

  • Minimizing a custom-designed cost function that ensures optimal tracking and system stability.

OSV-MPC achieves high precision by evaluating all possible switching combinations and selecting the one that minimizes the deviation between reference and predicted currents.

Key advantages

  • Accurate harmonic extraction under varying conditions.

  • Fast, stable, and robust DC link voltage regulation.

  • Reduced total harmonic distortion (THD) to < 2%, meeting IEEE-519-2022 standards.

  • Enhanced power factor and improved real/reactive power compensation.

Together, these modules synergistically improve the SAHC’s performance across various operating conditions, making the system well-suited for modern nonlinear and dynamic power networks.

The proposed SAHC system integrates three innovative control techniques to enhance power quality in distribution networks. First, the AUV-PQ-SRF method accurately extracts reference currents by averaging Unit Vector, PQ, and SRF techniques. These references guide a Sliding Mode Controller (SMC), which robustly regulates the DC link voltage under varying conditions. Then, the Optimal Switching Vector–Model Predictive Controller (OSV-MPC) predicts compensating currents, minimizes a cost function, and selects the best switching states for the inverter. The IGBT-based VSI injects compensating currents to cancel harmonics. This closed-loop system ensures low Total Harmonic Distortion, improved power factor, and IEEE-519-2022 compliance as shown in Fig. 6.

Fig. 6
figure 6

Flow chart of the proposed technique.

Full size image

The internal control diagram of the proposed SAHC system illustrates the coordinated operation of three main modules: AUV-PQ-SRF, SMC, and OSV-MPC is as shown in Fig. 7. The AUV-PQ-SRF block extracts accurate reference compensating currents by combining unit vector, PQ, and SRF methods. These references are fed into the Sliding Mode Controller (SMC), which regulates the DC link voltage with high robustness against disturbances. The regulated voltage and predicted compensating currents are then processed by the OSV-MPC, which generates optimal switching pulses for the VSI. This internal control loop ensures accurate tracking, low THD, and stable operation under dynamic and nonlinear load conditions.

Fig. 7
figure 7

Internal control diagram of the proposed technique.

Full size image

Results

The load current without the SAHC connected is depicted in Fig. 8. It appears highly distorted and non-sinusoidal. Under a fixed loading condition, the total harmonic distortion (THD) of the load current is 28.03%. Under dynamic loading conditions, when a second load is switched on at 0.5 s, the THD increases slightly to 28.12%.

Fig. 8
figure 8

Phase A load current without SHAF.

Full size image

When the SAHC is activated at 0.1 s, the load or source current becomes sinusoidal, as shown in Fig. 9. The SAHC injects compensating currents in a counterclockwise direction relative to the harmonics present in the load current, as illustrated in Fig. 10. As a result, the load current is effectively shaped into a sinusoidal waveform. The SAHC successfully mitigates current harmonics under both fixed and dynamic loading conditions.

Fig. 9
figure 9

The source current when SAHC is on at t = 0.1 s.

Full size image
Fig. 10
figure 10

SAHC compensating currents.

Full size image

The SAHC is designed to achieve multiple objectives simultaneously. It effectively reduces oscillations in real power demand, as illustrated in Fig. 11, and minimizes reactive power demand, as shown in Fig. 12. Additionally, the SAHC contributes to power factor correction, as depicted in Fig. 13.

Fig. 11
figure 11

Reduction of real power oscillations by SAHC.

Full size image
Fig. 12
figure 12

Reduction of reactive power demand by SAHC.

Full size image
Fig. 13
figure 13

Power factor correction by SAHC.

Full size image

The SAHC effectively maintains a constant DC link voltage, as shown in Fig. 14, ensuring it remains approximately equal to its reference level. As a result, the error is nearly zero. The cost function in SAHC optimizes the voltage vectors using a two-step-ahead horizon prediction, ensuring minimal deviation between the actual and reference DC link voltage.

Fig. 14
figure 14

DC link voltage across the VSI capacitor.

Full size image

The key advantage of OSV-MPC is its ability to precisely track the reference and actual compensating currents with zero error and its result is shown in Fig. 15. This ensures optimal performance of the SAHC.

Fig. 15
figure 15

Reference and actual SAHC compensating currents tracking.

Full size image

The source voltage of phase A is depicted in Fig. 16. It remains sinusoidal throughout the operation of the SAHC.

Fig. 16
figure 16

Source voltage of phase A.

Full size image

The THD of the source current with SAHC compensation under the fixed loading is 1.80% is as shown in Fig. 17 and under dynamic loading is 1.84 is as shown in Fig. 18.

Fig. 17
figure 17

THD of source current with SAHC compensation under fixed loading condition.

Full size image
Fig. 18
figure 18

THD of source current with SAHC compensation under dynamic condition.

Full size image

The comparison of the proposed methodology with the other existing techniques are shown in Table 3. It has been observed that, the proposed method of shunt active filter is giving superior performance as compared with other techniques. The proposed AUV-PQ-SRF reference current extraction method was evaluated using various DC link voltage controllers—including PI, Type-1 fuzzy, Type-2 fuzzy, and Sliding Mode Controller (SMC)—as well as model predictive controllers such as GPC, EMPC, OSS-MPC, and OSV-MPC. In all cases, the AUV-PQ-SRF technique demonstrated effective performance and complied with IEEE 519–2022 standards. Among the tested combinations, the integration of AUV-PQ-SRF with the SMC voltage controller and the OSV-MPC yielded superior results compared to the others.

Table 3 %THD comparison of the proposed AUV-PQ-SRF with the various DC link controllers and MPCs.
Full size table

The simulation parameters for the proposed SAHC are shown in Table 4.

Table 4 Simulation parameters.
Full size table

Conclusions and future scope

The proposed Optimal Switching Vector-Model Predictive Controller (OSV-MPC) technique, integrated with the Unit Vector-PQ-SRF (AUV-PQ-SRF) reference current extraction method, effectively enhances the performance of the Shunt Active Harmonic Compensator (SAHC). The results demonstrate that the OSV-MPC approach achieves precise reference tracking, significantly reducing harmonic distortion while optimizing real and reactive power compensation. The system maintains a stable DC link voltage, ensuring efficient and reliable operation under both steady-state and dynamic load conditions. The achieved Total Harmonic Distortion (THD) levels are well within the IEEE-519-2022 standards, validating the robustness of the proposed methodology.

The study can be extended in the following ways: Testing Under Unbalanced and Distorted Supply Conditions: Future research can explore the performance of OSV-MPC under unbalanced and distorted voltage scenarios to validate its effectiveness in real-world grid conditions. Application to Various Nonlinear Loads: While this study considered diode bridge rectifiers as nonlinear loads, further evaluation can be performed on different types of nonlinear loads, such as arc furnaces, fluorescent lamps, and elevator systems. Implementation in Multilevel Inverters: The OSV-MPC and AUV-PQ-SRF techniques can be extended to multi-level Shunt Active Filters (SAHCs) with reduced switch count for enhanced efficiency and reduced power losses. Hardware Implementation and Experimental Validation: The proposed method can be tested on hardware prototypes to validate simulation results, ensuring practical feasibility for industrial applications. This work provides a strong foundation for future advancements in harmonic mitigation, power quality enhancement, and optimized control strategies for active power filters in modern power systems.