EPRSA: interference resource scheduling algorithms for air-ground communication networks

Abstract

In recent years, the rapid development of air-ground communication networks has posed challenges to traditional interference methods. However, existing research rarely involves joint air-ground distributed communication interference, and there is a lack of the ability to schedule jammers with limited energy, a limited quantity, and different types. Based on this, this paper proposes the interference link margin in the mathematical model and normalizes and quantifies the optimization objectives. Strategies such as cycle and initial quantity selection, elastic initialization, double tabu power scheduling, and jammer conversion are designed to improve the scheduling ability of the Elastic Parallel Random Search Algorithm (EPRSA) in terms of system operation duration and interference cost. The experimental results show that EPRSA can increase the success rate of searching for interference schemes by 15.4%, reduce the number of jammers by 26.4%, enhance the type scheduling ability significantly, decrease the cost by 31%, and increase the system operation duration by 45.3%.

Introduction

The air-ground communication network, which is composed of low-altitude communication equipment and ground communication equipment, takes advantage of the rapid deployment and high elevation gain of aerial platforms such as UAV. References^1,2,3 illustrate that it effectively expands the communication relay range in complex electromagnetic environments. A large number of scattered communication devices are interconnected to form a network. The application of the centerless ad-hoc network technology enhances the communication anti-jamming ability, as shown in References^4,5. The traditional “one-to-one” suppression jamming over long distances, whether from the ground or in the air, has difficulty covering the entire low-altitude communication network. Moreover, an excessively high jamming power increases the risk of exposing the jamming source, as discussed in References^6,7,8. Air-ground joint distributed communication jamming has received attention due to its advantages such as flexibility, high efficiency, low cost, and the ability to effectively suppress air-ground communication networks, as presented in Reference⁹.

Interference resource scheduling is a non-convex and non-deterministic polynomial-hard (NP-hard) problem, and existing research mainly focuses on mathematical models and algorithm design. In terms of mathematical models, the main targets of distributed radar jamming include ground-based radars^{10,11,12,13,14,15}UAV-borne radars¹⁶underwater acoustic sensors¹⁷and airborne missiles¹⁸. The jamming equipment includes airborne jammers^10,11,12,13ground-based jammers^14,15,16underwater jammers¹⁷and sea-surface jammers¹⁸with a wide variety of application scenarios. The optimization objectives are diverse. However, apart from a few aspects similar to the background of communication jamming, such as the ratio of the echo power to the jamming signal power at the radar receiver¹¹ and the jamming power¹²a large amount of the content in mathematical modeling has no direct relation to communication interference resource scheduling. Regarding optimization methods, the resource allocation method under random selection conditions¹⁰the method of joint path planning and jamming power allocation optimization¹¹and the method of establishing an interference resource matrix¹⁵ provide ideas for the optimization of communication interference resource scheduling. Nevertheless, due to the differences in the practical backgrounds of the optimization problems, it is difficult to directly refer to these methods.

In terms of the mathematical models of distributed communication jamming, in the air-sea joint monitoring system described in Reference¹⁹the objective function is to maximize the total eavesdropping rate, and the optimization targets are the UAV jamming power and the trajectories of air and sea carriers. Reference²⁰ constructs a model of a distributed jamming system for the downlink of low-orbit satellites, with the jamming parameters such as power, time domain, and frequency domain as the optimization objectives. Reference²¹ constructs a model of ground-based distributed communication jamming, taking the number, location, and power of jammers as the optimization objectives. Currently, there is relatively little research on mathematical models, which mostly rely on a single type of jammer. The main optimization objectives are jamming power and jamming frequency bands, and these models belong to relatively simple linear combination optimizations. In response to the jamming problem in the fixed-frequency communication network between aircraft, Reference²² sets the constraints for jammer link selection and jamming power allocation, and proposes an objective function that includes the target importance and the jamming-to-signal ratio.

In terms of optimization algorithms, Reference¹⁹ decomposes the problem to be solved into three sub-problems and proposes an iterative algorithm to find its suboptimal solution. References^20,21 use the Pareto ranking of multi-objective genetic algorithms and the combination of objective function weights of single-objective genetic algorithms to optimize multiple interference resource objectives. References^22,23,24 adopt the strategy of central training and decentralized execution, as well as the multi-agent reinforcement learning method in deep learning, to achieve intelligent decision-making for a single jammer. References^25,26,27,28 use strategies such as hierarchical methods, orthogonal matching pursuit (OMP), multi-armed bandit (MAB), the experience replay mechanism of expert trajectories, and embedding expert incentives in the reward function to improve the reinforcement learning algorithm and enhance the quality and efficiency of interference decision-making training. Reference²⁹ applies machine learning to the model data analysis based on the Criteria Importance Through Intercriteria Correlation (CRITIC) weighting and improved grey correlation theory for multi-UAV swarm jamming. Reference³⁰ uses a deep learning algorithm with spectrum sensing, offline training, and learning functions for frequency-hopping communication. Reference³¹ introduces a priority experience replay mechanism based on temporal difference errors and an adaptive exploration strategy into the deep learning algorithm to achieve dynamic adaptive scheduling of jamming power. The above-mentioned heuristic optimization algorithms focus on solving problems in specific jamming scenarios and do not have strategies for scheduling air-ground joint distributed interference resources. Reinforcement learning algorithms generally have a long training period, rely on prior interference resources and communication targets, and are not flexible enough to use. Deep learning algorithms, on the other hand, rely heavily on datasets, but in fact, it is difficult to obtain datasets for communication jamming and adversarial games.

In summary, existing research lacks algorithms for the scheduling of air-ground joint distributed communication interference resources aimed at air-ground communication networks. The problems are mainly reflected in the following four aspects:

• 1. Most of the distributed jamming targets are radar systems, with few being communication devices, and almost none of them focus on air-ground communication networks.

• 2. Communication jamming parties mostly use long-distance high-power jammers with fixed positions and fixed quantities. There are almost no cases of using airborne and ground-based jammers with characteristics such as flexible quantity, uncertain positions, limited power, and cost differences. Moreover, there are almost no mathematical models that are highly adaptable to the scenarios in this paper.

• 3. Communication interference resource scheduling algorithms mostly focus on the selection of jamming power and frequency bands. However, when scheduling airborne and ground-based jammers, they lack scheduling strategies for the number, position, type, and operating duration of jammers.

• 4. In simulation experiments, the amount of interference resources that can complete the jamming target is set, and there are many restrictive conditions. The setting of the initial quantity of jammers has not been explained. In the actual deployment of communication jamming environments, it is difficult to effectively estimate the initial quantity of interference resources.

Therefore, in response to the above problems, the contributions of this paper are as follows:

• 1. A mathematical model of air-ground communication networks is established. The communication parties include airborne communication devices, ground communication stations, and handheld communication terminals, and the types of communication devices can be further enriched.

• 2. A mathematical model of air-ground joint distributed communication jamming is established. The concepts of interference link margin and the jamming-to-signal ratio of air-ground joint jamming are proposed. The system operation duration and interference cost are normalized and quantified, and the proposed objective function can complete the screening of interference schemes.

• 3. Strategies such as cycle and initial quantity selection, elastic initialization, double tabu power scheduling, and jammer conversion are designed. An Elastic Parallel Random Search Algorithm is proposed to efficiently schedule interference resources, solving the problems of low efficiency of simple random search algorithms and low solution rates of clustering optimization algorithms.

• 4. In the simulation experiments, the initial number of jammers is the same as the number of communication devices, which meets the requirements of having the worst interference scheme.

Mathematical model

Air-ground joint distributed communication jamming scenarios

Fig. 1

Air-Ground Joint Distributed Communication Jamming Scenarios.

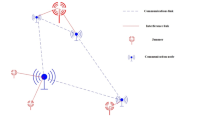
The air-ground communication network is composed of airborne communication devices and various types of ground communication devices. In Fig. 1, air-ground joint distributed communication jamming aims to schedule parameters such as the quantity, location, and power of airborne jammers and ground-based jammers, so as to achieve overall jamming of the communication receiving parties. It is characterized by limited interference resources, sparse scenarios, a large number of parameters, and high dimensionality.

The path loss between airborne devices, as well as between airborne devices and ground-based devices, follows line-of-sight (LOS) propagation. In Formula (1), the path loss of the LOS propagation model is ${L_s}$. The electromagnetic wave frequency is f, with the unit of ${\text{MHz}}$. The environmental factor is ${n_1}$, which varies according to different propagation environments. The LOS transmission distance is R, with the unit of km.

$${L_s}=32.5+20\text{l}\text{g}f+10{n_1}\text{l}\text{g}R$$

(1)

The path loss between ground-based devices follows the two-ray propagation model. In Eq. (2), the path loss of the two-ray propagation model is denoted as ${L_d}$. The terrain influence index is ${n_2}$, and its value varies depending on the differences in the propagation environment. The two-ray transmission distance is $R^{\prime}$, with the unit of km. The height of the electromagnetic wave transmitting end is ${h_t}$, and the height of the electromagnetic wave receiving end is ${h_r}$, both with the unit of meters (m).

$${L_d}=120+10{n_2}\lg R^{\prime} - 20\lg {h_t} - 20\lg {h_r}$$

(2)

Mathematical model of air-ground joint distributed communication jamming

Constraints

The air-ground distributed communication jammers are deployed in close proximity to save jamming power. To avoid exposure due to being too close to the communication devices, it is necessary to set the minimum distance between the jammers and the communication devices. As shown in Eq. (3), when the total number of jammers is I and the total number of communication devices is J, where ${x_i}$, ${y_i}$, and ${h_i}$ are the coordinates of the i-th jammer, and ${x_j}$, ${y_j}$, and ${h_j}$ are the coordinates of the j-th communication device, ${r_{\hbox{min} }}$ represents the minimum distance, with the unit of m.

$$\sqrt {{{({x_i} - {x_j})}^2}+{{({y_i} - {y_j})}^2}+{{({h_i} - {h_j})}^2}} \geqslant {r_{\hbox{min} }},(i \in (1,I),j \in (1,J))$$

(3)

If the i-th jammer is an airborne jammer, to meet the restrictive conditions of the Fresnel zone under line-of-sight propagation and avoid being visually detected, it is necessary to set a lower flight limit ${\text{h}_{\text{m}\text{i}\text{n}}}$,and due to the performance limitations of the flight carrier, it is necessary to set an upper height limit ${{\text{h}}_{{\text{max}}}}$, as shown in Eq. (4), with the unit of m.

$${{\text{h}}_{{\text{max}}}} \geqslant {h_i} \geqslant {{\text{h}}_{{\text{min}}}}, (i \in (1,I))$$

(4)

The air-ground communication network is equipped with anti-jamming measures such as multi-hop forwarding. The jamming party needs to impose effective interference on the received signals of all communication devices. As shown in Eq. (5), where $JS{R_j}$ is the quantized jamming-to-signal ratio of the j-th communication device, and $\text{J}$ is the total number of communication devices. If the constraints are satisfied, the equation holds; otherwise, it does not hold.

$$\sum\limits_{{j=1}}^{\text{J}} {JS{R_j}=\text{J}}$$

(5)

Calculation scope of jamming

Distributed communication jamming exhibits a power superposition effect. In order to reduce the calculation of weak interference signals that are of little significance, an upper limit of the interference spacing, denoted as ${\text{D}}^{\prime } _{{\text{s}}}$, is set based on the environmental conditions and device performance for inclusion in the calculation.

Communication interference signals need to meet the requirements regarding height and distance for line-of-sight propagation. In Eq. (6), ${D_s}$ represents the line-of-sight propagation distance, with the unit being km. ${h_t}$ is the height of the signal transmitting party, and ${h_r}$ is the height of the signal receiving party, both having the unit of m.

$${D_s}=4.12(\sqrt {{h_t}} +\sqrt {{h_r}} )$$

(6)

System Fade Margin ($SFM$) is the actual received signal power of the communication device, referring to the power value that is in excess of its receiving sensitivity, with the unit of ${\text{dB}}$. In Eq. (7), $RSS$ represents the received signal strength, and ${\text{RS}}$ represents the device receiving sensitivity, both with the unit of ${\text{dBW}}$.

$$SFM=RSS - {\text{RS}}$$

(7)

Assume that the received strength of the communication signal exactly meets the requirements of the communication link margin. A new concept, System Jammer Margin ($SJM$), is defined. It represents the margin by which the power of the jamming signal from the j-th jammer received by the i-th communication device and the power of the environmental noise exceed the receiving sensitivity of the communication device. In Eq. (8), ${P_{rj}}$ is the power of the jamming signal received by the communication device, and ${\sigma ^2}$ represents the power of the environmental noise, both with the unit of ${\text{dBW}}$.

$$SJM {\text{= }}{P_{rj}}+{\sigma ^2} - 2{\text{RS}}$$

(8)

As shown in Eq. (9), if $SJM$ is equal to the communication link margin, and the distance between the jammer and the communication device is less than ${D_s}$ and ${\text{D}^{\prime}_\text{s}}$, then ${x_{ij}}$ can be set to 1. That is, it is considered that the communication device is within the jamming range.

$${x_{ij}}=\left\{ \begin{gathered} 0, SJM <SFM{\text{ and }}{{\text{d}}_{ij}}<\hbox{min} ({D_S},{{\text{D}^{\prime}}_\text{s}}) \hfill \\ 1, SJM \geqslant SFM{\text{ and }}{{\text{d}}_{ij}}<\hbox{min} ({D_S},{{\text{D}^{\prime}}_\text{s}}) \hfill \\ \end{gathered} \right.$$

(9)

Quantized jamming-to-signal ratio

In Eq. (10), $P_{c}^{r}$ is the communication signal receiving power, and $P_{c}^{t}$ is the communication signal transmitting power, both with the unit of ${\text{dBW}}$. ${{\text{G}}_{{\text{tc}}}}$ is the antenna gain of the communication transmitting antenna in the direction of the communication receiving antenna, and ${{\text{G}}_{{\text{rc}}}}$is the antenna gain of the communication receiving antenna in the direction of the communication transmitting antenna. ${L_c}$ is the path loss of communication transmission, and ${{\text{L}}_{{\text{pc}}}}$ is the attenuation of the cables and cable connectors at the communication receiving end, all with the unit of ${\text{dB}}$.

$$P_{c}^{r}=P_{c}^{t}+{{\text{G}}_{{\text{tc}}}}+{{\text{G}}_{{\text{rc}}}} - {L_c} - {{\text{L}}_{{\text{pc}}}}$$

(10)

In Eq. (11), $P_{j}^{r}$ is the communication interference signal receiving power, and $P_{j}^{t}$ is the communication interference signal transmitting power, both with the unit of ${\text{dBW}}$. ${{\text{G}}_{{\text{tj}}}}$ is the antenna gain of the communication interference transmitting antenna in the direction of the communication receiving antenna, and ${{\text{G}}_{{\text{rj}}}}$ is the antenna gain of the communication receiving antenna in the direction of the communication interference transmitting antenna. ${L_j}$ is the path loss of communication interference transmission, and ${{\text{L}}_{{\text{pc}}}}$ is the attenuation of the cables and cable connectors at the communication receiving end, all with the unit of ${\text{dB}}$.

$$P_{j}^{r}=P_{j}^{t}+{{\text{G}}_{{\text{tj}}}}+{{\text{G}}_{{\text{rj}}}} - {L_j} - {{\text{L}}_{{\text{pc}}}}$$

(11)

The ratio of the sum of the power of the airborne and ground-based interference signals received by the communication device to the maximum communication receiving power is ${k_{j2}}$. In Eq. (12), within the calculable interference range, if the i-th jammer is an airborne jammer, its jamming power is $P_{{ia}}^{{rj}}$; if the i-th jammer is a ground-based jammer, its jamming power is $P_{{is}}^{{rj}}$. $P_{{j^{\prime}a}}^{{rj}}$ represents the maximum power received by the j-th communication device from airborne communication devices, and $P_{{j^{\prime}s}}^{{rj}}$ represents the maximum power received by the j-th communication device from ground-based communication devices, both with the unit of ${\text{dBW}}$.

$$k_{{j2}} = \sum\limits_{{i = 1}}^{I} {(P_{{ia}}^{{rj}} + P_{{is}}^{{rj}} )x_{{ij}} + \sigma ^{2} - \max \left( {P_{{j^{\prime}a}}^{{rj}} ,P_{{j^{\prime}s}}^{{rj}} } \right)} ,j^{\prime} \in (1,j) \cup (j,J)$$

(12)

As shown in Eq. (13), if the power ratio of the interference signal to the communication signal of the communication device is not less than the jamming-to-signal ratio ${k_j}$ required for successful jamming, it is considered that the jamming is successful, that is, the quantized jamming-to-signal ratio j of the $JS{R_j}$ communication device is 1.

$$JS{R_j}=\left\{ \begin{gathered} 0,{k_{j2}}<{k_j} \hfill \\ 1,{k_{j2}} \geqslant {k_j} \hfill \\ \end{gathered} \right.$$

(13)

System operating duration

When the jamming system is in operation, if the power of a certain jammer is insufficient, it will lead to the inability to release the predetermined jamming power. Without adjusting the jamming scheme, it may be impossible to jam and suppress the entire air-ground communication network system. That is to say, the operating duration of the jamming system is limited by the jammer with the maximum jamming power.

In Eq. (14), for the i-th jammer, ${T_i}$ is its effective system operating duration, with the unit of hours (H). ${{\text{\varvec{\upeta}}}_{\text{s}}}$ is the battery power limit required for normal jamming. ${{\text{U}}_{{\text{out}}}}$ is the operating voltage of the battery, with the unit of volts (V). ${{\text{E}}_{{\text{es}}}}$ is the battery capacity of the jammer, with the unit of ampere-hours (AH). ${P_i}$ is the jamming output power of the i-th jammer, and ${{\text{P}}_{\text{x}}}$ is the power consumed by the jammer to maintain other functions, both with the unit of watts (W).

$${T_i}={{\text{\varvec{\upeta}}}_{\text{s}}}\frac{{{{\text{U}}_{{\text{out}}}}{{\text{E}}_{{\text{es}}}}}}{{{P_i}+{{\text{P}}_{\text{x}}}}}$$

(14)

After the initial deployment of the air-ground distributed communication jamming system, no mid-course scheduling is performed. The system operating duration for maintaining the expected jamming effect is constrained by the shortest working time of any single ground or airborne jammer, denoted as $\hbox{min} ({T_i})$. Facing large differences in value ranges under multiple jamming schemes $\hbox{min} ({T_i})$, the system operating duration is normalized to facilitate the fitness comparison of the algorithm objective function. In Eq. (15), it is assumed that there exists an optimal jamming scheme for the air-ground distributed communication jamming system, where ${{\text{T}}_{{\text{min}}}}$ is the minimum value of the system operating duration and ${{\text{T}}_{{\text{max}}}}$ is the maximum value.

$$T=\frac{{\hbox{min} ({T_i}) - {{\text{T}}_{{\text{min}}}}}}{{{{\text{T}}_{{\text{max}}}} - {{\text{T}}_{{\text{min}}}}}},i \in (1,I)$$

(15)

Jamming cost

The costs of airborne jammers and ground-based jammers are different. For the convenience of comparison, it is necessary to carry out normalization and quantization processing on the total cost of the jammers.

$$Q={N_s}{C_s}+{{\text{N}}_{\text{a}}}{C_a}$$

(16)

$$Q^{\prime}=1 - \frac{{Q - {{\text{Q}}_{{\text{min}}}}}}{{{{\text{Q}}_{{\text{max}}}} - {{\text{Q}}_{{\text{min}}}}}}$$

(17)

In Eqs. (16) and (17), ${C_s}$ is the cost of the ground-based jammer, ${C_a}$ is the cost of the airborne jammer, and Q is the cost of all jammers. When the preset number of jammers is equal to the number of communication devices, ${{\text{Q}}_{{\text{min}}}}$ is the minimum cost, ${{\text{Q}}_{{\text{max}}}}$ is the maximum cost, and $Q^{\prime}$ is the normalized and quantized jamming cost.

Objective Function.

In Eq. (18), in order to optimize the system operating duration and jamming cost, a linear combination method is used to transform them into a single-objective optimization function. ${a_1}$ and ${a_2}$ are the weight indices, which represent the degrees of emphasis on the system operating duration and jamming cost.

$$\left\{ \begin{gathered} F = \arg \max (a_{1} T + a_{2} Q^{\prime}),(1) \hfill \\ a_{1} + a_{2} = 1,(2) \hfill \\ \end{gathered} \right.$$

(18)

Three types of air-ground communication network systems

Table 1 Parameters of the Air-Ground communication network System.

In an environment with a relatively high level of electromagnetic environmental noise, compared with ground-based communication devices, airborne communication devices have the advantage of elevation gain. They also have a larger communication relay support range, which can improve the communication quality and anti-interference ability of the wireless ad-hoc network communication system. Based on the changes in the number of airborne communication devices and ground communication stations, three types of air-ground communication network systems have been designed. The number of communication devices is shown in Table 1, and the communication layout is illustrated in Fig. 2.

Fig. 2

Layout of the Air-Ground Communication Network System.

Algorithm

EPRSA

The Simple Random Search Algorithm³² (SRSA) is an algorithm that explores the search space completely randomly. It does not rely on any prior knowledge or mathematical models. It is simple and easy to implement, but its search efficiency is relatively low.

Fig. 3

Flow Chart of EPRSA.

The joint air-ground distributed communication jamming resource scheduling involves deploying a small number of jammers in a sparse scenario. With a large number of involved variables and a vast search space, it belongs to a high-dimensional non-convex optimization problem. Traditional clustering search algorithms do not perform well. Based on the structure of this problem, this paper designs the EPRSA, and the overall block diagram is shown in Fig. 3a.

The EPRSA is designed with short-period and long-period search strategies as well as an escape and termination strategy, which can efficiently utilize the number of search iterations. Based on the bisection method, the initial number search strategy of jammers is used. The short-period search is employed to find the optimal initial number of jammers, and the long-period search is carried out to conduct a large number of searches for the optimal initial number of jammers. The parallel search strategy shares and updates the optimal jamming scheme, which can accelerate the convergence speed. Real number encoding is adopted, where the serial number, type, location, and power of jammers are represented by numerical values, resulting in relatively high efficiency. The elastic initialization strategy improves the pertinence of the algorithm to the problems in the search space. The dual tabu power scheduling strategy can reduce redundant jamming power and the number of jammers. The jammer conversion strategy can give full play to the advantages of airborne and ground-based jammers respectively.

Period and initial quantity selection strategies

In Fig. 3b, after inputting the number of communication devices ${N_c}$, the first search period is a short period, and the initial number of jammers ${N_j}$ is the integer value of 0.5 times the number of communication devices. After the end of each round of parallel search, according to the number of solutions in this search, the upper limit ${N_{ju}}$ or the lower limit ${N_{jl}}$ of the initial jammer search interval is updated. The bisection method is adopted to obtain a new ${N_j}$, as shown in Eqs. (19, 20).

$$\left\{ \begin{gathered} {N_{ju}}={N_j} \hfill \\ {N_j}={N_{jl}}+({N_{jl}}+{N_j})//2 \hfill \\ \end{gathered} \right.$$

(19)

$$\left\{ \begin{gathered} {N_{jl}}={N_j} \hfill \\ {N_j}={N_j}+({N_{jl}}+{N_j})//2 \hfill \\ \end{gathered} \right.$$

(20)

In Eq. (21), the number of long-period iterations is ${T_l}$, the number of short-period iterations is ${T_s}$, the number of executions of the short period is ${n_s}$, and the total number of algorithm iterations is ${T_{total}}$.

$${T_l}={T_{total}} - {T_s} \times {n_s}$$

(21)

If the long-period search is executed, or the number of times the period is executed reaches the upper limit ${T_{up}}$, then the optimal jamming scheme $Pl{a_{best}}$ is output.

Elastic initialization strategy

$$\left\{ \begin{gathered} {D_{L\hbox{max} }}={N_c} \times {D_1}/{N_j} \hfill \\ {{\text{x}}_{ij}}{\text{and }}{y_{ij}} \in ({D_{L\hbox{min} }},{D_{L\hbox{max} }}) \hfill \\ \end{gathered} \right.$$

(22)

$$\left\{ \begin{gathered} {D_{A\hbox{max} }}={N_c} \times {D_2}/{N_j} \hfill \\ {{\text{x}}_{ij}}{\text{and }}{y_{ij}} \in ({D_{A\hbox{min} }},{D_{A\hbox{max} }}) \hfill \\ \end{gathered} \right.$$

(23)

In Fig. 3c, the search interval of the coordinate distance between the jammers and the communication devices is adaptively scheduled according to the initial number of jammers. In Eqs. (22, 23), ${D_{L\hbox{max} }}$, ${D_{A\hbox{max} }}$, ${D_1}$, ${D_{L\hbox{min} }}$, ${D_{A\hbox{min} }}$ ${D_2}$ are successively the upper limit, lower limit, and reference value of the distance search for ground-based jammers and airborne jammers.

The power of the jammers is randomly searched within the user-defined discretized airborne jamming power ${P_{Agrid}}$ and ground-based jamming power ${P_{Lgrid}}$, which increases the success rate of jamming and reduces the computational load. In Eq. (24), ${P_{A\hbox{max} }}$ and ${P_{L\hbox{max} }}$ are the maximum jamming powers of airborne and ground-based jammers, respectively.

$$\left\{ \begin{gathered} {P_{Lgrid}} \in (0.5,0.75,1){P_{L\hbox{max} }} \hfill \\ {P_{Agrid}} \in (0.33,0.66,1){P_{A\hbox{max} }} \hfill \\ \end{gathered} \right.$$

(24)

For the scheduling of jammer types, when selecting ground-based jammers, the fixed probability depends on the costs of airborne and ground-based jammers. The adaptive probability increases as the number of search iterations in the cycle increases, so that the generation probability of airborne jammers gradually rises with the number of iterations. In Eq. (25), ${R_L}$ represents the probability of selecting a ground-based jammer, and ${I_{now}}$, ${I_{sum}}$ represent the real-time number of iterations and the total number of iterations in each search cycle, respectively.

$${R_L}<{C_s}/({C_s}+{C_a}) - {I_{now}}{C_a}/{I_{sum}}{C_s}$$

(25)

Dual Tabu power scheduling strategy

In Fig. 3e, with the positions of the jammers fixed, a strategy is adopted to schedule the power of the jammers. Jammers with zero power are removed to reduce the number of jammers. Tabu List 1 is designed to avoid the dead loop in the increase and decrease of power. Tabu List 2 aims to record all the jammers whose jamming power values cannot be further reduced.

Jammer conversion strategy

In Fig. 3d, airborne jammers with power values lower than ${P_{a1}}$ are adjusted to ground-based jammers, and the jamming power is increased to ${P_{s2}}$ to take advantage of the low cost of ground-based jammers. Ground-based jammers with power greater than ${P_{s1}}$ are adjusted to airborne jammers, and the jamming power is reduced to ${P_{a2}}$ to take advantage of the elevation gain of airborne jammers.

Algorithm flow

Combining the above strategies, the pseudocode of the EPRSA is as follows. Among them, the fitness of the objective function of the optimal jamming scheme is ${F_{best}}$, the number of times a solution is found is ${N_{ans}}$, and the number of searches is ${N_{search}}$.

EPRSA employs a parallel random search strategy. Its time complexity is ${{\text{N}}_{{\text{search-up}}}}{\text{/}}{{\text{N}}_{{\text{group}}}}$, where ${{\text{N}}_{{\text{search-up}}}}$ represents the upper limit of the number of random searches, and ${{\text{N}}_{{\text{group}}}}$ is the number of parallel search groups. During the operation of EPRSA, it mainly incurs a fixed space overhead for storing $Pl{a_{best}}$, ${F_{best}}$, and other local variables. After disregarding factors such as $Pl{a_{best}}$, the overall space complexity can be approximately regarded as being at the constant level $O(1)$.

Algorithm 1

The proposed EPRSA with the four strategies.

Results and discussion

Simulation parameter settings

In the experiment, an Intel(R) Core(TM) i5-8300 H CPU @ 2.30 GHz processor with 16.0 GB of RAM and an NVIDIA GTX1080Ti graphic card were used, and an environment of anaconda 23.7.4 was selected for verification.

Table 2 Table of simulation scenario parameter Settings.

In the case of obtaining the information of the communication network system through preliminary exploration and without conducting secondary interference resource scheduling during the process, power suppression interference is applied to the maximum received power that each communication device can receive. It is necessary to achieve effective interference on the receiving functions of all communication devices. An algorithm is used to obtain the interference scheme. The parameters of the experimental simulation scenario are shown in Table 2.

Due to the different values of the weight settings in the objective function of this paper, different feasible solutions can be screened out. Based on the experience of simulation experiment tests, two modes of the objective function have been designed, and the weight settings are shown in Table 3.

Table 3 Settings of the objective Function.

Experimental results of the comparative algorithms

The proposed EPRSA was simulated and compared with the SRSA, the Adaptive Grid Particle Swarm Optimization Algorithm³³ (AGPSOA) and the Improved Artificial Bee Colony Algorithm³⁴ (IABCA).

In distributed communication jamming resource scheduling, SRSA uniformly and randomly generates all parameters of jamming schemes within the selectable range. After screening by constraint conditions and objective function fitness, the optimal jamming scheme is recorded. AGPSOA rasterizes the scene spatial coordinates, initializes jamming schemes by randomly selecting in each population, evaluates the fitness of each population, records the optimal fitness and the best population, and iteratively updates the velocity and position of all populations according to adaptive formulas until reaching the upper limit of iterative search.

In the initialization phase of IABCA, the initial solution set randomly generates jamming schemes with a quantity twice that of the population. After calculating the objective function fitness, the better half is selected. In each iteration:

During the “employed bee” phase, a neighboring solution directional search mechanism is adopted to generate neighboring solutions within the solution space for all solutions, and the solution with higher fitness is greedily selected between the new and old solutions.

During the “onlooker bee” phase, the parameters of jamming schemes in all populations are mutated and updated with probability, and the solution with higher fitness is greedily selected between the new and old solutions.

During the “scout bee” phase, solutions that have not been replaced for consecutive iterations reaching the threshold are re-initialized.

In distributed communication jamming, if the number of jammers is the same as that of communication devices, close-range jamming can be carried out, where one jammer is targeted at one communication device. Since the three comparative algorithms do not have a jammer quantity scheduling strategy, 32 jammers are taken as the initial value of the number of jammers to ensure the existence of a solution. In the combined air-ground communication jamming, the different costs of ground jammers and airborne jammers will affect the formulation of the jamming scheme. The two modes of the objective function will also generate different jamming schemes. Based on this, this paper designs four comparative experiments, as shown in Table 4.

Table 4 Simulation experiment Settings.

In Experiments 1–4, each algorithm was run 30 times, and the average values and standard deviations of various comparative indicators were obtained, as shown in Tables 5, 6, 7 and 8.

Table 5 Exp. 1 (The data are presented as the mean ± standard deviation).

Table 6 Exp. 2.

Table 7 Exp. 3.

Table 8 Exp. 4.

Analysis of simulation experiments

Fig. 4

Schematic Diagram of Experimental Analysis.

In Fig. 4a, as the number of airborne communication devices increases, the number of solutions obtained by the comparative algorithms drops significantly, while EPRSA always has solutions. Compared with IABCA, the solution availability rate of EPRSA is 15.4% higher in Scenario 2 and 233.3% higher in Scenario 3, which reflects that the comparative algorithms are not suitable for the interference resource scheduling facing the air-ground communication network system. The elastic initialization strategy of EPRSA first adaptively adjusts the coordinate spacing of communication nodes for jammers within a certain range to narrow the search scope, and second gradually increases the proportion of airborne jammers to enhance the jamming effect. The period and initial quantity selection strategies increase the number of jammers when the solution success rate is low, which improves the solution success rate of the algorithm.

In Fig. 4b, EPRSA can complete the jamming task with a relatively small number of jammers. The comparative algorithms use 32 jammers, and the number of jammers used by EPRSA in Scenario 1, Scenario 2, and Scenario 3 decreases successively by 48.3%, 31.1%, and 26.4%. In the period and initial quantity selection strategies of EPRSA, if the number of successful solutions exceeds the threshold, the number of jammers is reduced. The dual tabu power scheduling strategy gradually reduces the redundant jamming power of jammers and removes jammers with zero jamming power, which decreases the number of jammers.

In Fig. 4c, the ratio of the number of airborne jammers to the number of ground jammers is defined as the ratio of the number of types, which can be used to measure the usage of different types of jammers. After the cost ratio of jammers is adjusted from 2:1 to 4:1, the maximum value of the ratio of the number of types of EPRSA is adjusted from 1.14 to 0.48, and the minimum value of the ratio of the number of types of the comparative algorithms is adjusted from 1.28 to 1.13. The scheduling range of EPRSA is 340% of that of the comparative algorithms. The jammer conversion strategy of EPRSA adjusts airborne and ground jammers based on a threshold. The elastic initialization strategy adaptively schedules jammer types, gradually increasing the proportion of airborne jammers as the number of searches increases.

In Fig. 4d, compared with the comparative algorithms, the jamming costs of EPRSA are reduced by 31%, 31.7%, 50.7%, and 46.5% respectively. Through scheduling the number and type of jammers, EPRSA effectively controls the jamming cost.

In Fig. 4e, compared with the comparative algorithms, the system operating durations of EPRSA are increased by 64.2%, 78.3%, 48.4%, and 45.3% respectively. In the elastic initialization strategy of EPRSA, jamming power is randomly selected from user-defined discretized values to balance power redundancy and jamming effect. The dual tabu power scheduling strategy gradually reduces jamming power; if reduction is impossible, it increases the power of other jammers and retries, using Tabu List 1 to store jammers with non-reducible power. The jammer conversion strategy transforms high-power ground jammers into low-power airborne jammers. These strategies reduce the maximum jamming power and extend the system operating duration.

In Fig. 4f, the cycle selection strategy of EPRSA plays a role. Without using the long-cycle search, the convergence speed of the algorithm is accelerated. If the long cycle is used, the algorithm achieves better results with a relatively small time cost.

In the original literature, IABCA was designed for a small number of jammers targeting a small number of jamming objectives, lacking consideration for a larger number of jammers and objectives, as well as mechanisms for parallel computing and saving fitness values of each population. During the initialization, “employed bee”, “onlooker bee”, and “scout bee” phases, IABCA repeatedly applies constraint conditions and fitness calculations to jamming schemes, significantly increasing the algorithm’s time cost.

Conclusion and future scope

This paper constructs a mathematical model for the joint air-ground distributed communication jamming resource scheduling aimed at the air-ground ad-hoc network system. Four optimization variables are utilized to optimize the jamming cost and the system operating duration. The constraints for the deployment of jamming devices and the receiving failure of all communication devices are defined. The jamming link margin is proposed, and the jammer-to-signal ratio suitable for the complex air-ground jamming scenarios is determined. By adjusting the weights of the objective function, the jamming schemes that prioritize either the jamming cost or the system operating duration are screened out. Finally, the EPRSA with four strategies is proposed.

The simulation experiment results show that compared with the SRSA, the AGPSOA, and the IABCA, EPRSA has a stronger ability to search for feasible solutions. It reduces the number of jammers, schedules the types of jammers according to cost differences, lowers the jamming cost, extends the system operating time, and the time cost of algorithm operation is controllable. The four scheduling strategies concerning quantity, location, power, type, and the number of iterations meet the requirements for solving multi-dimensional non-convex optimization problems with limited resources in sparse scenarios.

In the future, research can be conducted on the game confrontation of communication jamming, focusing on situations such as incomplete prior information of the communication side, frequency hopping, power adjustment, etc., to improve the accuracy of jamming. In addition, research on the joint air-ground distributed communication jamming resource scheduling in complex terrains such as mountainous areas and urban areas can also be considered³⁵. Reinforcement learning and multi-agent technologies can be introduced to enhance the ability of jammers to make decentralized decisions, so as to adapt to intense and unknown communication game scenarios³⁶.