Underwater image enhancement using hybrid transformers and evolutionary particle swarm optimization

Abstract

Underwater imaging is a complex task due to inherent challenges such as limited visibility, color distortion, and light scattering in the water medium. To address these issues and enhance underwater image quality, this research presents a novel framework based on a Hybrid Transformer Network optimized using Particle Swarm Optimization (HTN-PSO). The HTN-PSO framework combines the strengths of convolutional neural networks and transformer models to effectively capture low-level features and model long-range dependencies. Simultaneously, PSO optimizes the transformer’s parameters to maximize the enhancement quality of underwater images. The proposed framework consists of four main stages: data augmentation, pre-processing, feature extraction using HTN-PSO, and enhanced image reconstruction. The performance of HTN-PSO is evaluated using objective quality metrics such as UIQM, NIQE, and BRISQUE, along with subjective assessments. The proposed model has been evaluated using HTN-PSO on four benchmark datasets: RUIE, EUVP, UWGAN, and UIEB and reports improvements over existing methods. Notably, HTN-PSO achieves a 12% increase in UIQM and up to 15% reduction in BRISQUE compared to baseline techniques, including Uformer and Restormer. Experimental results demonstrate the superiority of the HTN-PSO approach over both traditional and neural network-based methods, offering a promising avenue for improving underwater image enhancement across various domains, including exploration, research, and surveillance applications.

Introduction

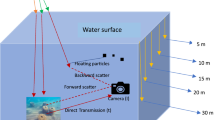
Underwater Image Enhancement (UIE) plays a critical role in the exploration and investigation of underwater environments, with broad applications across domains such as marine biology, marine archaeology, oceanography, and underwater robotics¹. However, underwater imagery often faces significant challenges, including color deviations, color aberrations, and loss of fine image details. These issues primarily stem from the absorption and scattering of light caused by dissolved particulate matter in aquatic environments^2,3. Effectively addressing these challenges is essential for improving visual quality and extracting meaningful information from underwater images, thereby deepening our understanding of submerged ecosystems.

UIE approaches can generally be classified into four major categories: physical model-based methods, visual prior-based methods, data-driven approaches, and transformer-based enhancement techniques^4,5,6,7.

Physical model-based methods aim to accurately estimate medium transmission and other underwater imaging parameters to restore image clarity. However, they struggle with the complexity and variability of real-world underwater conditions. The assumptions underlying these models often fail in dynamic scenarios, and the simultaneous estimation of multiple parameters remains computationally demanding. Visual prior-based methods focus on enhancing underwater images through pixel-level adjustments such as contrast, brightness, and saturation. Despite their simplicity, these techniques often overlook the physical degradation mechanisms inherent in underwater imagery, limiting their effectiveness.

Data-driven methods, particularly those based on deep learning, have shown impressive performance in recent years^1,3. These approaches use large datasets to learn enhancement patterns and generalize effectively. Nevertheless, existing underwater datasets often suffer from issues like limited sample sizes, lack of diversity, or insufficient representation of real-world scenes.

A persistent challenge in UIE is the non-uniform attenuation of light across different color channels and spatial locations, which remains inadequately addressed by current methodologies. To tackle these complex challenges, this research introduces a novel framework: the Hybrid Transformer Evolutionary Particle Swarm Optimization Framework for Underwater Image Enhancement (HTN-PSO). This model integrates transformer networks with evolutionary Particle Swarm Optimization to overcome limitations in traditional and contemporary UIE approaches.

The primary objective of the proposed framework is to enhance the visual quality of degraded underwater images, facilitating better interpretation and analysis for scientists and researchers exploring the underwater world. By addressing the limitations of physical degradation, incorporating a diverse and extensive dataset, and managing inconsistent attenuation across channels, the HTN-PSO is designed to outperform existing methods. Recent transformer-based methods, such as Uformer and Restormer have shown notable performance in image restoration by leveraging hierarchical self-attention mechanisms and U-shaped architecture. However, these models typically rely on static configurations and lack mechanisms for temporal refinement or adaptive optimization.

In contrast, the proposed HTN-PSO framework incorporates GRU-based temporal feature refinement and employs Particle Swarm Optimization to adaptively tune transformer hyperparameters, thereby improving convergence behavior and image enhancement quality under complex underwater conditions.

Its performance is rigorously evaluated using both real and synthetic underwater datasets through standard quantitative metrics, and the results are compared both quantitatively and qualitatively against state-of-the-art UIE techniques.

The main contributions of this paper are mentioned below:

• 1 A novel Hybrid Transformer Network optimized using Particle Swarm Optimization (HTN-PSO) is proposed, combining the strengths of transformers and convolutional neural networks (CNNs) to enhance underwater image quality.

• 2 The use of Particle Swarm Optimization (PSO) allows for efficient tuning of transformer parameters, ensuring improved performance in image enhancement tasks.

• 3 By integrating transformers, the framework effectively models long-range dependencies, while CNNs capture local features, resulting in robust feature extraction and enhanced image reconstruction.

State of the art methods

Recent advancements in underwater image enhancement have introduced deep learning and transformer-based models that significantly outperform traditional techniques. These state-of-the-art methods focus on learning robust representations to address challenges like color distortion, low contrast, and detail loss in complex underwater environments. Existing underwater image enhancement based four main categories have been discussed below:

Physical model-based methods

A physical model is a scaled-down or enlarged physical representation of an object, designed to capture the original image features while minimizing the influence of environmental factors¹. The Jaffe-McGlamery model is the most comprehensive and widely recognized imaging model; it is based on linear superposition and requires the modeling of a propagation medium. Physical model-based processing techniques have been the subject of extensive research. He et al. proposed a theory known as Dark Channel Prior (DCP) for defogging and dehazing tasks, grounded in the Jaffe-McGlamery model⁸. The DCP method estimates the dark channel based on statistics computed from the three RGB channels. More recently, Berman et al.⁹ proposed iterating various light attenuation coefficients across different water types. Zhang et al.¹⁰ introduced TANet, a U-Net-based method that leverages transmission and atmospheric light dynamics. TANet consists of two core modules: a Transmission-Driven Refinement module operating in the spatial domain, and an Atmospheric Light Removal Fourier module functioning in the frequency domain. Similarly, the study in¹¹ proposed two dynamic structures that utilize dynamic convolutions to adaptively extract prior information from underwater images and derive optimal parameters. These modules enable the network to select suitable parameters for different underwater conditions.

While algorithms based on DCP are effective in addressing many issues, their performance deteriorates under challenging conditions such as the presence of artificial lighting or highly turbid water.

Traditional methods

The quality of underwater images has been enhanced using traditional digital image processing techniques such as contrast enhancement, color restoration, and fusion strategies. These pixel-wise approaches directly modify pixel intensities to achieve a more uniform distribution, often without considering the underlying physics of image formation. Wang et al.¹² proposed a color cast correction method using the adaptive gray world technique, combined with a differential histogram equalization method to improve contrast. Typically, combining both methods results in improved underwater image quality. Additionally, frequency domain processing methods have been adopted for underwater image enhancement. Iqbal et al.¹³ presented a UIE method based on Laplacian decomposition, where the input color channels are separated into low- and high-frequency bands. The haze in the low-frequency band is removed and normalized for brightness, while the high-frequency components are amplified to preserve image sharpness. The final enhanced image is obtained by recombining the two frequency bands. Ancuti et al.¹⁴ proposed an underwater image enhancement approach using fusion. Their method involves color compensation, white balancing, gamma correction to improve contrast, and edge reinforcement. Two images are then combined using a weighted fusion strategy to generate the final output. A wavelet transform-based approach for enhancing hazy underwater images was proposed by the DWT method¹⁵, which utilizes two feature maps: one for white balance and the other for contrast enhancement.

To summarize, while traditional image processing techniques can be effective for specific tasks, they may also introduce noise, over-enhance certain features, and under-enhance others, leading to inconsistent visual improvements.

Data-driven based methods

These methods utilize deep learning (DL) techniques to learn enhancement patterns from extensive underwater image datasets. DL has revolutionized computer vision by enabling the development of more accurate and sophisticated models. Recently, three DL-based approaches have gained significant attention: (a) physical model-based methods, (b) paired image data-based methods, and (c) unsupervised methods.

Physical model-based DL approaches aim to replicate or approximate real-world imaging characteristics, allowing DL algorithms to estimate more accurate parameters of the imaging process. As a result, image restoration and enhancement are significantly improved^16,17. For example, in¹⁸, Chen et al. proposed a solution based on the DLIF (Deep Learning and Image Formation) model, consisting of three components and achieving promising results with a minimal number of trainable parameters. USUIR (Unsupervised Underwater Image Restoration)¹⁹ is another noteworthy unsupervised approach for underwater image enhancement (UIE).

Supervised DL methods rely solely on input-output data, eliminating the need for a priori mathematical modeling. Cong et al.²⁰ proposed a four-step algorithm that learns the mapping from distorted to enhanced images through color code decomposition, content-invariant learning, and color fine-tuning. SUWnet (UIE Shallow-UWnet), introduced in²¹, is a lightweight model with 11 CNN layers and skip connections, making it suitable for edge device deployment. In²², a triple attention module cascaded over multiple sub-networks (MSA module) is proposed to extract fine-grained features from underwater images, enhancing robustness and generalization.

Unlike supervised methods, unsupervised learning focuses on the intrinsic characteristics of data and does not require labeled datasets—an advantage considering the high cost of underwater data collection^23,24. One of the most influential unsupervised methods is the Generative Adversarial Network (GAN)³, which trains a discriminator to differentiate between real and generated data, encouraging the generator to mimic realistic data distributions. Liu et al.²⁵ introduced TACL, a symmetrical two-part model called Twin Adversarial Contrastive Learning, consisting of a forward enhancement path and a backward degradation path using ResNet generators.

UIESS, a domain adaptation method proposed in²⁶, decouples features into content and style latent spaces, though it shows limited performance in color correction. Smith et al. developed a Wavelet-Based Dual-Stream Network (UIEWD) that decomposes the input image into multiple frequency bands before processing. In²⁴, a multi-discriminator GAN is proposed to operate across various color spaces to better distinguish real and generated underwater images. Han et al.²⁷ introduced the Contrastive Underwater Restoration (CWR) method, which maximizes mutual information between the original and enhanced images using comparative learning and GANs. Liu et al.²⁸ proposed CLIP-UIE, which transfers knowledge from the natural (terrestrial) image domain and applies it to train diffusion models for underwater enhancement.

In summary, traditional methods often require manual tuning and domain expertise, and physical model-based approaches depend on rigid assumptions that are difficult to maintain in real-world underwater conditions. Although deep learning methods require large datasets and high computational cost, they have demonstrated substantial success in underwater image enhancement and various real-world applications.

Transformers-based methods

Transformers have shown outstanding performance in natural language processing (NLP) tasks. Vaswani et al.²⁹ first proposed a novel and simple architecture based entirely on the self-attention mechanism, eliminating the need for convolutions. This architecture has since been adapted to various computer vision tasks, including object detection³⁰, semantic segmentation³¹, image deraining³², denoising³³, and deblurring³⁴. Alexey et al.³⁵ demonstrated that convolutional neural networks (CNNs) are not strictly necessary; a pure transformer, applied to sequences of image patches, can perform effectively in image classification tasks, as shown in the Vision Transformer (ViT).

Liu et al.³⁶ introduced the Swin Transformer, which facilitates the adaptation of transformers from NLP to vision tasks by addressing the domain-specific differences. It employs shifted windows to compute self-attention within non-overlapping local regions, allowing for efficient processing and inter-window communication. Wang et al.³⁷ further proposed the Uformer, which uses a locally enhanced window transformer block for deraining, denoising, and deblurring. This architecture captures local context while significantly reducing computational complexity on high-resolution images.

Zamir et al. developed Restormer³⁸, an efficient transformer model designed with optimized building blocks (such as multi-head attention and feed-forward networks) to capture long-range pixel interactions while remaining suitable for large images. U-shaped transformer architectures incorporate both channel and spatial self-attention, but traditional spatial attention methods often fail to model fine pixel-level dependencies, potentially leading to unclear enhancements.

To address this, the SW-PSAT model³⁹ computes attention weights between individual pixels within each window, improving spatial self-attention. Motivated by these advancements, we propose a shifted window mechanism tailored for image enhancement tasks. This design reduces computational complexity while also leveraging global information through channel self-attention.

In summary, the effectiveness of different transformer-based approaches varies across domains. Underwater image enhancement remains an active and evolving field of research, with the overarching goal of producing clearer and more informative visual representations of underwater environments.

Proposed HTN-PSO

The field of underwater imaging presents significant challenges due to factors such as limited visibility, color distortion, and light scattering within the aquatic environment. To address these issues, a novel framework is proposed that combines the strengths of a Hybrid Transformer Network (HTN) with Particle Swarm Optimization (PSO) for underwater image enhancement. The HTN leverages the attention mechanism to extract relevant features, while PSO is used to optimize network parameters, thereby improving overall image quality. Figure 1 illustrates the step-by-step workflow of the HTN-PSO framework. The key strengths of HTN-PSO include advanced feature learning, efficient parameter tuning, and strong adaptability to diverse and complex underwater conditions. Figure 2 highlights the main advantages of the proposed framework in comparison to existing methods. The underwater image input undergoes pre-processing steps aimed at eliminating noise, correcting color distortion, and optimizing brightness and contrast levels to enhance its overall quality. At this stage, fundamental image enhancement techniques, such as histogram equalization and color balancing, can be applied Subsequently, the pre-processed image is fed into the HTN-PSO algorithm. The neural network in the HTN-PSO framework is designed to capture low-level image properties, while the transformer component excels at modeling long-range dependencies and contextual information. The transformer’s attention mechanism selectively focuses on informative regions of the image, enhancing the network’s resilience to challenging underwater conditions and scenarios. Furthermore, the Particle Swarm Optimization (PSO) technique is employed to optimize the parameters of the HTN-PSO approach. The PSO algorithm is used to explore and identify the optimal combination of HTN-PSO parameters that yield the highest quality of enhanced images. The objective function in PSO is formulated to evaluate image enhancement quality, typically based on metrics such as sharpness, contrast, and color restoration.

Fig. 1

Three-stage workflow of HTN-PSO (Preprocessing, Feature Extraction, Enhancement).

Fig. 2

Advantages of HTN-PSO over existing UIE methods.

The optimized framework aims to improve the quality of underwater images by applying the identified optimal parameters. The attention mechanism of the Hybrid Transformer Network selectively refines image features, enhances color representation, and restores lost details, resulting in a significant improvement in the quality of underwater images. In this study, the dataset was selected based on several key factors: its relevance to the research problem, representativeness of the target domain, and the availability of high-quality, labeled data. The dataset offers a balanced and diverse set of examples, ensuring that the solution developed is both generalizable and robust.

Data augmentation and pre-processing

Due to the complexity and nature of underwater scenes, as well as the degradation caused by ecological factors, acquiring a comprehensive and diverse underwater dataset is highly challenging. Underwater images captured in the same scene often share significant similarities, resulting in reduced variance within the dataset. To overcome this limitation and enhance the applicability of underwater image enhancement algorithms, data augmentation methods are employed. These methods expand the dataset by slightly modifying the original samples, thereby increasing the number of data points.

Data augmentation

Augmentation methods include rotation, color transformation, and shift operations. These techniques modify the position and viewpoint of the input images, thereby enriching the dataset, as calculated in Eq. 1. Color transformations optimize brightness, contrast, and hue, enabling varied color schemes and further enhancing the dataset. Shift operations introduce subtle spatial changes, enriching the exploration of diverse scene compositions. Dimensionality reduction in the underwater image dataset has been effectively achieved through data augmentation, focusing on the essential information captured in the three primary colors (green, red, and blue). This reduction helps alleviate the similarity issue and contributes to the development of more efficient and precise algorithms for underwater image enhancement.

$${I_{xy}}=~\left[ {{r_{xy}},~{g_{xy}},{b_{xy}}} \right]$$

(1)

where r_xy, g_xy, and b_xy are the eigenvalues of red, blue and green direction vectors respectively. These values are computed using the Eq. 2

$$\begin{gathered} {r_{xy}}~=~{m_r}{\lambda _r} \hfill \\ ~{g_{xy}}~=~{m_g}{\lambda _g} \hfill \\ {b_{xy}}~=~{m_b}{\lambda _b} \hfill \\ \end{gathered}$$

(2)

where m_r, m_g and m_b are the matrix of the red, blue and green color channels. Further, β is used as a random variable where mean = 0 and variance = 0.1 and added in the transformation function as shown in Eq. 3.

$${I_{xy}}~=~\left[ {{m_r},~{m_g},~{m_b}} \right]{\left[ {{\beta _r}{\lambda _r},~{\beta _g}{\lambda _g},~{\beta _b}{\lambda _b}} \right]^T}$$

(3)

Then, rotation is performed as shown in Eq. 4

$$\begin{array}{*{20}c} {X^{\prime} = ~X_{i} \cdot\cos \left( {\theta _{1} } \right) - ~Y_{i} \cdot\sin \left( {\theta _{1} } \right)} \\ {Y^{\prime} = ~X_{i} \cdot\sin \left( {\theta _{1} } \right) + ~Y_{i} \cdot\cos \left( {\theta _{1} } \right)} \\ \end{array}$$

(4)

where (X^′, Y ^′) are the coordinates that were rotated and transformed and θ₁ is angle of rotation. Then, shift transformation is performed as shown in Eq. 5 where θ₂ is the angle of shifting.

$$\begin{array}{*{20}{c}} {X^{\prime}=~{X_i}~+~{Y_i}\tan {\theta _2}} \\ {Y'~=~{X_i}~tan\left( {{\theta _2}} \right)~+~{Y_i}} \end{array}$$

(5)

Pre-processing

The White Balancing (WB) is used to resolve the color-cast issue and has been proven to be effective⁴⁰. White balancing is a common image enhancement technique used to correct color cast and restore the true colors in an image. The step-by-step computation of WB is shown below:

Step 1

Compute Color Channels- For an input image I_RAW the red channel R(x, y), green channel G(x, y), and blue channel B(x, y) are extracted.

Step 2

Compute Channel Averages- Calculate the average values of each color channel over the entire image. where n is the total number of pixels of an image.

$$\bar {R}=\frac{1}{n}\mathop \sum \limits_{{x=1}}^{{width}} \mathop \sum \limits_{{y=1}}^{{height}} R\left( {x,y} \right)$$

(6)

$$\bar {G}=\frac{1}{n}\mathop \sum \limits_{{x=1}}^{{width}} \mathop \sum \limits_{{y=1}}^{{height}} G\left( {x,y} \right)$$

(7)

$$\bar {B}=\frac{1}{n}\mathop \sum \limits_{{x=1}}^{{width}} \mathop \sum \limits_{{y=1}}^{{height}} B\left( {x,y} \right)~~$$

(8)

Step 3

Compute Scaling Factors- Normalize the average channel values to make the average gray value equal for all channels.

$$\bar {V}=\frac{{\bar {R}+\bar {G}+\bar {B}}}{3}$$

(9)

Compute the scaling factors for each channel:

$${S_R}=\frac{{\bar {V}}}{{\bar {R}}}$$

(10)

$${S_G}=\frac{{\bar {V}}}{{\bar {G}}}$$

(11)

$${S_B}=\frac{{\bar {V}}}{{\bar {B}}}$$

(12)

Step 4

Adjust Color Channels- Multiply each channel by its respective scaling factor to balance the colors.

$$R^{\prime}={S_R} \cdot R\left( {x,y} \right)$$

(13)

$$G^{\prime}={S_G} \cdot G\left( {x,y} \right)$$

(14)

$$B^{\prime}={S_B} \cdot B\left( {x,y} \right)$$

(15)

Step 5

Clamp Values- Ensure that the adjusted channel values are within the valid range of intensity values, typically 0 to 255.

$$R^{\prime}=\hbox{min} \left( {\hbox{max} \left( {R^{\prime}\left( {x,y} \right),0} \right),255} \right)$$

(16)

$$G^{\prime}=\hbox{min} \left( {\hbox{max} \left( {G^{\prime}\left( {x,y} \right),0} \right),255} \right)$$

(17)

$$B^{\prime}=\hbox{min} \left( {\hbox{max} \left( {B^{\prime}\left( {x,y} \right),0} \right),255} \right)$$

(18)

Step 6

Merge Color Channels- Combine the adjusted red, green, and blue channels to form the white-balanced image.

$${I_{WB}}=\left( {R^{\prime},G^{\prime},B^{\prime}} \right)$$

(19)

Proposed methodology: HTN-PSO

In recent years, remarkable progress has been made in the field of deep learning, as evidenced by the findings in⁴¹. This progress has significantly enhanced the efficacy of single underwater image enhancement methods. Numerous algorithms, particularly those utilizing convolutional neural networks (CNNs), have demonstrated excellent performance on publicly available datasets. The introduction of the Transformer architecture⁴² represents a significant breakthrough, not only in advanced computer vision tasks but also in improving the performance of image enhancement techniques. Compared to previous methods relying solely on CNNs, Transformers have shown more objective enhancements, highlighting their potential to excel in advanced computer vision tasks and surpass CNNs in low-level image enhancement across various applications.

Recognizing the superior performance of Transformers in underwater applications, as noted in³⁹, integrating the Transformer into the network structure can be an effective way to enhance feature extraction. However, due to its long-range attention mechanism, the Transformer has limitations in capturing local image details. While the Swin Transformer³⁶ addresses this drawback, it still tends to focus on capturing global representations over larger image regions, especially when the network is relatively shallow. In contrast, CNNs, with their local connections, excel at modeling local details.

In the context of visual imagery, adjacent regions exhibit strong associations in terms of color, material properties at lower hierarchical levels, and semantic meaning at higher levels. For underwater imaging, neighboring pixels often share similarities related to the transmittance of the medium and haze concentration. Therefore, this study introduces a novel augmentation network that combines the strengths of Transformers and convolutional methods. This network aims to enhance the performance of single underwater image enhancement by leveraging the local modeling capabilities of CNNs with the powerful global representation and modeling abilities of Transformers.

The HTN-PSO framework leverages Particle Swarm Optimization (PSO) to optimize critical hyperparameters of the Transformer model, including the learning rate, embedding dimension, attention heads, and patch size. PSO dynamically guides the selection of these parameters based on the performance feedback loop during training. A swarm of 20 particles was selected based on convergence behavior observed in similar deep learning optimization tasks. The inertia weight was decreased linearly from 0.9 to 0.4 to balance exploration and exploitation. Cognitive and social coefficients were set to 2.0 to maintain equilibrium between personal and global best solutions. These settings were validated empirically on the training set and showed strong generalization performance on unseen samples.

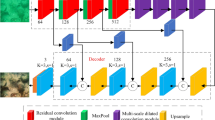
Figure 3 illustrates the step-by-step operation of the proposed HTN-PSO, which includes a recurrent block along with a Transformer and CNN-based encoder and decoder, where hyperparameters are optimized using Enhanced PSO. The overall architecture uses U-Net as the baseline, and the loss function is explained in detail.

Fig. 3

Overall architecture of Hybrid Transformer Network.

Hybrid transformer network-recurrent block

To further improve the feature representation capacity of our model, we integrate Gated Recurrent Unit (GRU) blocks within the architecture. Specifically, our model follows an encoder-GRU-decoder structure. The Swin Transformer serves as the encoder, extracting hierarchical and spatially aware features from underwater images. These features are then passed through GRU layers, which capture sequential dependencies and contextual continuity, particularly useful in enhancing series of related image patches or frames. Finally, the decoder reconstructs the enhanced image from the GRU-refined feature maps. This integration helps the model better preserve structure and color consistency across spatially or temporally related inputs. Recurrent Neural Networks (RNNs) are designed to capture temporal dependencies in sequential data, making them ideal for tasks like speech recognition and time-series forecasting. However, traditional RNNs face challenges with long-term dependencies due to the vanishing gradient problem. To address this, LSTM and GRU architectures are used, which allow the model to retain memory over longer sequences and improve performance in tasks requiring long-range dependencies. In the proposed architecture, stacked GRU layers enable the model to learn more complex features by capturing hierarchical patterns. The bidirectional RNNs process data in both forward and backward directions, which is essential for tasks requiring context from both past and future inputs. An optional attention mechanism can be integrated to focus on relevant parts of the sequence, enhancing the model’s ability to prioritize important information and improve performance in tasks like machine translation and summarization. These recurrent blocks, combined with attention mechanisms, ensure a robust and context-aware model for sequential data processing. As shown in Fig. 4, for n iterations, the input image is processed through a convolutional layer with a 3 × 3 kernel size, 64 filters, stride = 1, and zero padding of 1 pixel. The extracted features are then passed through the PReLU (Parametric Rectified Linear Unit) to learn the optimal activation slope for each neuron during training. In this process, the input and hidden terms are normalized separately, as shown in Eqs. 20, 21, and 22.

$$\left( {\begin{array}{*{20}{c}} {{{\varvec{r}}_t}} \\ {{z_t}} \end{array}} \right)=B{N_t}\left( {{\varvec{W}}{{\varvec{h}}_{t - 1}},{\gamma _h}} \right)+B{N_t}\left( {{\varvec{U}}{{\varvec{x}}_t},{\gamma _x}} \right)+{\varvec{b}}$$

(20)

$${\mathop {\varvec{h}}\limits^{\prime } _t}=\sigma \left( {\varvec{r}} \right) \circ B{N_t}\left( {{{\varvec{W}}^{\left( {\varvec{h}} \right)}}{{\varvec{h}}_{t - 1}},\gamma _{h}^{{\left( h \right)}}} \right)+B{N_t}\left( {{{\varvec{U}}^{\left( {\varvec{h}} \right)}}{{\varvec{x}}_{\varvec{t}}},\gamma _{x}^{{\left( h \right)}}} \right)$$

(21)

$${{\varvec{h}}_t}=\sigma \left( {{z_t}} \right) \circ {{\varvec{h}}_{t - 1}}+\left( {1 - \sigma \left( {{z_t}} \right)} \right) \circ \tanh \left( {B{N_t}\left( {{{\mathop h\limits^{\prime } }_t},{\gamma _m},{\beta _m}} \right)} \right)$$

(22)

Fig. 4

Architecture of the proposed Hybrid Transformer Network (HTN), showing the flow from input Preprocessing to transformer-based feature extraction and attention-guided enhancement for underwater image enhancement.

Transformer encoder-decoder

Multi-scale networks offer a unique ability to capture a wide range of image features, from fine-grained texture details to high-level semantic information. To leverage these advantages, this paper proposes a fused version of the Swin Transformer³⁶ and Convolutional Neural Network (CNN) within an Encoder-Decoder framework inspired by U-Net. The primary goal of the proposed approach is to learn a sequential representation of the input image, thereby ensuring the acquisition of comprehensive contextual semantics and spatial characteristics over extended transmission distances. The Swin Transformer introduces the concept of locality in its Multiple Self-Attention (MSA) module, enabling the computation of self-attention within non-overlapping windows. It has demonstrated effectiveness in various domains, including object detection, semantic segmentation, and image denoising, due to its architectural design and versatility. As a result, our study directly employs the Swin Transformer during the encoder phase to encode feature representations extracted from decomposed patches. As shown in Figs. 5 and 6, the Swin Transformer-based encoder generates various tokens by comprising three layers of the encoder. Equation 23 presents the tokens generated in the first, second, and third layers, respectively.

$$Toke{n_{1,2,3}}=~\left( {\frac{H}{4} \times \frac{W}{4}} \right),~\left( {\frac{H}{8} \times \frac{W}{8}} \right),~and~\left( {\frac{H}{{16}} \times \frac{W}{{16}}} \right)$$

(23)

Fig. 5

The architecture of Transformer Encoder.

Fig. 6

The vanilla architecture of Swin Transformer³⁶.

At each stage of the proposed framework, Patch Merging is implemented in conjunction with Swin Transformer Blocks. To integrate image resolutions, a sliding window operationis utilized for Patch Merging. The image, defined with dimensions H × W, is segmented into RGB image patches of specific dimensions. These patches are represented as the original pixel mosaic vector, structured as 4 × 4. Then, a linear embedding is applied to project this mosaic vector into a higher-dimensional space, resulting in a vector of dimension 4 C. At this stage, the output dimension is reduced to 2 C, and the new feature size becomes H × W. Using the shifted window partitioning mechanism, we can formulate the calculation of contiguous Swin Transformer blocks with the following mathematical expression:

$$\begin{array}{*{20}{r}} {{{\mathop z\limits^{\prime } }^l}}&{~=W - MSA\left( {LN\left( {{z^{l - 1}}} \right)} \right)+{z^{l - 1}}} \\ {{z^l}}&{~={\text{MLP}}\left( {{\text{LN}}\left( {{{\mathop z\limits^{\prime } }^l}} \right)} \right)+{{\mathop z\limits^{\prime } }^l}} \\ {{{\mathop z\limits^{\prime } }^{l+1}}}&{~=SW - {\text{MSA}}\left( {LN\left( {{z^l}} \right)} \right)+{z^l}} \\ {{z^{l+1}}}&{~={\text{MLP}}\left( {{\text{LN}}\left( {{{\mathop z\limits^{\prime } }^{l+1}}} \right)} \right)+{{\mathop z\limits^{\prime } }^{l+1}}} \end{array}$$

(24)

Where,

$\:{\stackrel{\prime }{z}}^{l-1}$

Input token at the lth layer.

LN: Layer Normalization.

W-MSA / SW-MSA: Window-based or shifted window-based multi-head self-attention.

MLP: Two-layer feed-forward network with GELU activation.

In Eq. (24), $\:{\stackrel{\prime }{z}}^{l}$ and $\:{\stackrel{\prime }{z}}^{l+1}$ depicts the outcomes of W-MSA and SW-MSA modules respectively, z indicates the outcomes of the MLP component of l^th block. These alternate attention mechanisms allow the Swin Transformer to compute self-attention efficiently in localized non-overlapping windows while still enabling cross-window interaction through window shifting. Each Swin Transformer block comprises a LayerNorm operation, followed by W-MSA or SW-MSA, a residual connection, and a feed-forward MLP with another residual connection. This design preserves both local and global contextual information while maintaining computational efficiency. The shifted window approach improves spatial information flow across adjacent windows, which is critical in underwater images where structural continuity (e.g., marine textures or contours) spans across multiple local regions. The attention matrix derived from the self-attention mechanism based on³⁰ and depicted as:

$${\text{Attention}}\left( {Q,K,V} \right)={\text{SoftMax}}\left( {\frac{{Q{K^T}}}{{\sqrt d }}+B} \right)V$$

(25)

where the data values in $\:B$ are inferred from the bias matrix $\:\stackrel{\prime }{B}\in\:{R}^{(2M-1)\times\:(2M+1)}$. Generally, $\:Q,K,V\in\:{R}^{{M}^{2}\times\:d}$ and respectively depicts the trio combo of query, key, and value matrices. $\:{M}^{2}$ represents the quantity of patches within a window denoted by the variable “number of patches,” while the variable $\:d$ represents the dimension of the query or key.

In the decoder phase, we implement a two-fold strategy for feature enhancement. Initially, we upscale the feature resolution of adjacent dimensions by a factor of two through bi-linear interpolation, while concurrently reducing the feature dimensionality by half via a 1 × 1 convolutional layer. Subsequently, the up-sampled feature maps undergo fusion with multi-scale feature maps derived from the encoder, facilitated by skip connections. To further refine the feature representation, we employ a pair of Swin Transformer blocks. This process iterates three times, progressively reducing the feature map resolution to W/2 x H/2.

Enhanced PSO

To improve optimization performance, we employ an enhanced version of Particle Swarm Optimization (PSO)⁴³. Unlike traditional PSO^44,45, our variant incorporates an adaptive inertia weight that decreases over iterations to balance global exploration and local exploitation. Additionally, we use dynamic acceleration coefficients that adjust based on the swarm’s performance history, allowing the particles to adaptively steer towards promising regions in the solution space. A fitness-scaling strategy based on no-reference image quality metrics (such as UIQM and NIQE) is applied to better guide the swarm towards perceptually optimal solutions. This “enhanced PSO” formulation results in faster convergence and more reliable parameter tuning of the image enhancement model. The flowchart in Fig. 7 illustrates the PSO process used to optimize hyperparameters in the proposed HTN-PSO framework. Initially, particles representing different hyperparameter sets (e.g., transformer layers, patch size, CNN filters) are randomly initialized in terms of position and velocity. Each particle’s fitness is evaluated using a composite objective function based on UIQM, NIQE, and BRISQUE scores. Particles update their personal best (pBest) if their current fitness improves, while the global best (gBest) is updated across the swarm. Velocities and positions are then adjusted using standard PSO equations to balance exploration and exploitation. This process iterates until a stopping condition (e.g., max iterations) is met, after which the best-performing hyperparameter configuration is selected for final model deployment.

Fig. 7

Flowchart of particle swarm optimization (PSO) process.

Table 1 compares PSO with other approaches based on two sample images from EUVP dataset. It shows that PSO outperforms existing nature inspired algorithm in term of: UIQM, BRISQUE, Runtime (s) and Convergence Speed.

Table 1 Comparison of proposed HTN-PSO with other nature inspired algorithms in terms of quantitative metrics.

EPSO is an enhanced methodology for optimizing swarm populations consisting of ‘p’ particles, each represented in a ‘d’-dimensional feature space. These particles are divided into two categories: active and passive groups. The active group utilizes orthogonal diagonalization to update both particle positions and velocities.

The key parameters of PSO were chosen based on empirical trials and recommendations from prior optimization literature^43,44,45:

• i. Swarm Size (p): Set to 30 particles, balancing search diversity with computational feasibility.

• ii. Iterations (ic): Fixed at 50, ensuring sufficient exploration without overfitting or prolonged training time.

• iii. Acceleration Coefficient (acccoff): Varied dynamically in the range [2.0, 2.5], encouraging both local and global search during different optimization phases.

• iv. Search Space Dimensionality (d): The dimensionality of the search space corresponds to the number of tunable hyperparameters in the HTN framework. In our implementation, d = 7, consisting of the following: Attention window size, Number of Transformer layers, Patch size for embedding, Learning rate, Dropout rate, CNN filter size.

• v. Objective Function: Defined as a composite of non-reference image quality metrics (UIQM↑, NIQE↓, BRISQUE↓), the function guides PSO toward perceptually optimized configurations.

Each particle represents a candidate set of hyperparameters for the HTN-PSO model. During each iteration, particles update their positions based on personal and global best experiences, utilizing orthogonal diagonalization to improve diversity in solution space exploration. While the PSO configuration was optimized using a representative training subset from all datasets, the parameters are not dataset-specific and showed robust performance across multiple benchmarks, indicating their generalizability. Compared to conventional optimizers like Adam and SGD, the PSO-based approach demonstrated faster convergence and improved perceptual quality metrics (e.g., 5% lower BRISQUE and 4% higher UIQM), as shown in the ablation study, by enabling global search and avoiding local minima in the hyperparameter space.

Below is the step-by-step process of EPSO where g(x) is an optimization function and ic is iteration.

• 1. Begin by randomly initializing both the position (p_j(0)) and velocity (v_j(0)) of each particle, denoted by the index j, where j ranges from 1 to the total number of particles, denoted as p.

• 2. Calculate the value of the objective function g(x) using the initial position vectors p_j(0).

• 3. Utilize Eq. 15 from the reference [cite: pso4] to initialize the personal posi- tion vector, denoted as Global _per.j, for each particle j. Here, Global _per.j represents the personal experience for particle j.

• 4. Sort the Global _per.j vectors in ascending order based on the fitness values computed using the objective function g(x).

• 5. Build a matrix, denoted as z, with dimensions p × m. Each row of this matrix corresponds to one of the p_j vectors.

• 6. Transform the matrix C into a balanced matrix S, with dimensions m×m, using the⁴³.

• 7. Incorporate the OD (Orthogonal Diagonalization) technique into the matrix S, resulting in a matrix D with dimensions m × m.

• 8. The position p_j and velocity v_j of the p particles of the active group are updated using Eq. 26.

$$\begin{array}{*{20}{c}} {{v_j}\left( t \right)={v_j}\left( {t - 1} \right)+ac{c_{{\text{coff~}}}}\left( t \right)\left[ {{D_j}\left( t \right) - {Y_j}\left( {t - 1} \right)} \right]} \\ {{Y_j}\left( t \right)={Y_j}\left( {t - 1} \right)+{v_j}\left( t \right)} \end{array}$$

(26)

where $\:{D}_{j}$ denotes the diagonal matrix. $\:ac{c}_{\text{coff\:}}$is the acceleration coefficient that ranges between 2 and 2.5.

• 9. The $\:{\text{\:Global\:}}_{\text{per.\:.}j}\left(t\right)$ is estimated using Eq. 27.

$${\text{~Global}}{{\text{~}}_{{\text{per}}{\text{.~}}{\text{.}}j}}\left( t \right)=\left\{ {\begin{array}{*{20}{l}} {{Y_j}\left( t \right){\text{~~if~}}\left( {g\left( {{Y_j}\left( t \right) \leqslant g\left( {{Y_j}\left( {t - 1} \right)} \right)} \right.} \right.} \\ {g\left( {{Y_j}\left( {t - 1} \right){\text{~}}} \right.{\text{~Otherwise~}}} \end{array}} \right.$$

(27)

• 10. The best position is estimated using this step. The minimum of $\:f$ (Global per. $\:j\left(t\right))$ is computed for all particles. And then g(x) is evaluated for the best solution using Eq. 28.

$$\:{\text {Global(t)}} = {\text {minimum}} {\text{\:(Global\:}}_{\text{per.\:.}j}\left(t)\right)$$

(28)

• 11. Global best (Miteration) is estimated using the step 10.

Loss functions

Charbonnier loss

The application of L2 loss, which entails the maximization of the log-likelihood of a Gaussian distribution, frequently results in undesired blurring effects in the process of reconstructing images (Loss 1). In order to tackle this issue, we employ a different methodology by first implementing the resilient Charbonnier loss. To refine the reconstructed image and match it closely to the original, a specialized error metric, a smoothed version of the L1 norm called the Charbonnier loss, is employed. This metric quantifies the discrepancy between the two images, and the aim is to reduce this discrepancy to a minimum, as described in Eq. 29

$${L_C}={E_{\mathop {\varvec{X}}\limits^{\prime } \sim P\left( r \right),{\varvec{X}}\sim {P^2}\left( g \right)}}\sqrt {{{(\mathop {\varvec{X}}\limits^{\prime } - {\varvec{X}})}^2}+{\epsilon ^2}}$$

(29)

where P (r) and P (g) are the distribution of the restored images Xˆ and the real images X, respectively. Besides, we empirically set ε to 1e − 3.

MS-SSIM loss

The Multi-Scale Structural Similarity (MS-SSIM), as introduced in⁴⁶, is a technique utilized to evaluate the quality of images by considering their structural similarity. The Multi-Scale Structural Similarity (MS-SSIM) method has enhanced adaptability in comparison to the Single-Scale Structural Similarity (SSIM) technique, as it possesses the capability to accommodate differences in both picture quality and viewing conditions. Hence, the loss function is defined in Eq. 30:

$${\text{L}}_{M} \left( {\user2{X}{\text{~}},~\user2{X}} \right) = {\text{~}}1{\text{~}} - {\text{~MSSSIM}}\left( {\user2{X}{\text{~}},~\user2{X}} \right)$$

(30)

The total loss function of the HTN-PSO is shown in Eq. 31:

$${{\text{L}}_{{\text{sum}}}}{\text{~}}={\text{~}}{w_1}{{\text{L}}_C}{\text{~}}+{\text{~}}{w_2}{{\text{L}}_M}$$

(31)

The hyper-parameters play a critical role in obtaining the right trade-off between the model’s overall performance and its ability to capture intricate local texture details. In our experiments, we empirically set the values of w₁ = 1 and w₂ = 2. This choice allows us to achieve a desirable convergence rate.

Experimental analysis

The efficacy of the HTN-PSO algorithm is evaluated using both real and synthetic datasets, such as RUIE, EUVP, UWGAN, and UIEB. These datasets are compared against existing methods, including UCM, UWCNN, WaterNet, ShallowNet, WaveNet, and HTN-PSO. The efficiency of the HTN-PSO algorithm is assessed using three non-reference evaluation metrics: Natural Image Quality Evaluator (NIQE)⁴⁷, UIQM⁴⁸, and Blind/Reference-less Image Spatial Quality Evaluator (BRISQUE)⁴⁹.

Implementation details

The HTN-PSO is implemented on Nvidia Quadro T2000 4GB Graphics and Win- dows 10 Professional Operating System using by Pytorch 1.11.0. The training details are shown in Table 2.

Table 2 The details of hyper-parameters used for training.

Datasets

The HTN-PSO is trained using real as well as synthetic underwater datasets. After investigating a wide range of underwater datasets, three benchmark datasets are utilized for training the network including Enhancement of underwater visual percep- tion (EUVP), Underwater generative adversarial network (UWGAN), Real-world underwater image enhancement (RUIE) and Underwater Image Enhancement Benchmark (UIEB). This selection ensures that our model is validated under multiple data conditions, enhancing the generalizability of the results. The details of the datasets are mentioned below:

• EUVP⁵⁰: This dataset includes 12, 000 paired and 8, 000 unpaired images of degraded and high visual quality. The images were obtained during the oceanic explorations in varied visibility circumstances.

• UWGAN⁵¹: This dataset is comprised of 15, 000 degraded underwater images. The dataset is generated using the generative adversarial network that generates synthetic images along with its ground truth. The images include color-cast and haze properties of the underwater environment.

• RUIE⁵²: The dataset images utilized in this study are derived from an authentic underwater habitat, providing valuable insights into the intricate characteristics of the undersea ecosystem. The dataset referred to as the RUIE has a total of 4,230 images. The dataset comprises several sea organisms, including urchins and scallops, and exhibits several visual anomalies, such as color-cast, haze, and limited lighting conditions.

• UIEB⁵⁴: The Underwater Image Enhancement Benchmark (UIEB) dataset is a widely used collection consisting of 890 real-world underwater images and corresponding high-quality reference images. It provides a diverse range of underwater scenes with varying lighting conditions, turbidity, and color distortion, making it a robust benchmark for evaluating image enhancement algorithms.

The datasets chosen for this study include RUIE, EUVP, UWGAN, and UIEB, each selected based on specific criteria:

• RUIE: This dataset was chosen due to its comprehensive collection of real-world examples, making it ideal for testing the framework’s applicability to practical scenarios.

• EUVP: Selected for its high-quality labeled data, EUVP provides a diverse set of cases that enable the evaluation of the model’s generalizability across various conditions.

• UWGAN: This dataset contains complex, challenging data which allows for rigorous testing of the model’s robustness and performance in less controlled environments.

• UIEB: With its large volume and variety of data, UIEB is particularly useful for assessing the scalability of the proposed solution and its ability to handle diverse input features.

Together, these datasets cover a wide range of scenarios, ensuring that the solution is both effective and generalizable across different contexts.

Evaluation metric

The performance and efficiency of the HTN-PSO model is estimated using non- reference evaluation metrics. These metrics rely on the enhanced image itself to estimate the quality based on different parameters. The HTN-PSO performance is evaluated using NIQE, UIQM, as well as BRISQUE.

NIQE

It is inspired by human visual perception. It computes the natural scene statistics as well as the total amount of noise. Further, uses the Gaussian model. Finally, the distance between two Gaussian is estimated and that is considered as the final score. A lower NIQE value indicates superior image quality, reflecting a higher degree of naturalness and reduced noise artefacts.

$$D\left( {{{\text{\varvec{\upnu}}}_1},{{\text{\varvec{\upnu}}}_2},{{\text{\varvec{\Sigma}}}_1},{{\text{\varvec{\Sigma}}}_2}} \right)=\sqrt {{{\left( {{{\text{\varvec{\upnu}}}_1} - {{\text{\varvec{\upnu}}}_2}} \right)}^T}{{\left( {\frac{{{{\text{\varvec{\Sigma}}}_1}+{{\text{\varvec{\Sigma}}}_2}}}{2}} \right)}^{ - 1}}\left( {{{\text{\varvec{\upnu}}}_1} - {{\text{\varvec{\upnu}}}_2}} \right)}$$

(32)

where ν₁, ν₂ are mean vectors and Σ₁, Σ₂ are co-variance matrices.

BRISQUE

It calculates the degree of distortion present in an image. It quantifies the loss of naturalness exhibited by the input image by analyzing its natural scene statistics and extracting relevant feature vectors. Subsequently, a support vector machine is utilized to estimate the final BRISQUE score. A lower BRISQUE value indicates superior image quality, as it signifies a reduced level of distortion and a higher degree of naturalness.

$$\hat {I}\left( {i,j} \right)=\frac{{I\left( {i,j} \right) - {\text{\varvec{\upmu}}}\left( {i,j} \right)}}{{{\text{\varvec{\upsigma}}}\left( {i,j} \right)+C}}$$

(33)

where, I(i, j) is the intensity of the input image, µ(i, j) is the mean, σ(i, j) is the standard deviation and C is constant.

UIQM

The UIQM is derived from the perceptiveness of the human visual system. It takes into account three crucial parameters: colorfulness, sharpness, and contrast measure of underwater images. A higher UIQM value signifies superior image quality. By incorporating these perceptual aspects, UIQM provides a comprehensive assess- ment of underwater image quality, ensuring that the evaluation aligns with human visual perception.

$$UIQM = c_1 \times UICM+c_2 \times UISM+c_3 \times UIConM$$

(34)

where, c₁, c₂ and c₃ are the weights.

Qualitative comparison

Underwater images possess distinct characteristics that differentiate them from images captured in natural environments. These images often exhibit reduced luminosity and contrast. Therefore, it is crucial to evaluate the effectiveness of various enhancement techniques with respect to human visual perception. To assess the efficacy of the HTN-PSO approach, a detailed visual analysis was conducted using five photographs from each dataset. The images were selected based on their level of degradation and the presence of typical challenges encountered in underwater cinematography, such as color cast, low-light conditions, and haze. Different UIE methods, including UCM⁶, UWCNN⁵³, Water-Net⁵⁴, Shallow-Net⁵⁵, WaveNet⁵⁶, and HTN-PSO, were compared across the RUIE, EUVP, UWGAN, and UIEB datasets⁵⁷. This comprehensive assessment aims to determine the superiority of HTN-PSO in real underwater scenarios.

The qualitative comparison analysis serves two purposes: (1) to showcase the effectiveness of deep-learning-based methods in situations where reference information is unavailable, and (2) to highlight the superiority of our proposed method, which successfully enhances underwater scenes without relying on ground truth data for training, applicable to both real and synthetic underwater images^58,59.

Fig. 8

The qualitative comparison of existing UCM, UWCNN, Waternet, Shallownet, Wavenet with HTN-PSO on RUIE dataset.

Based on Fig. 8, observations from the RUIE Dataset⁷:

• UCM: Limited success in reducing the green cast; residual artifacts remained visible.

• UWCNN: Introduced red artifacts while attempting color correction, leading to oversaturation in specific regions

• Water-net and shallow-net: Both methods partially addressed the green cast but added a yellowish tint, degrading the naturalness.

• WaveNet: Achieved decent luminance but overcompensated for brightness, creating an unnatural appearance.

• HTN-PSO: Eliminated the green cast effectively, maintaining a balanced color tone and improved clarity. The attention mechanism of the transformer contributed significantly to restoring fine details.

Fig. 9

The qualitative comparison of existing UCM, UWCNN, Waternet, Shallownet, Wavenet with HTN-PSO on EUVP dataset.

Based on Fig. 9, observations from the EUVP Dataset⁸:

• UCM: Struggled with both blue and green casts, leaving substantial color imbalances.

• UWCNN: Over-enhanced certain regions, introducing red distortions and uneven illumination.

• Water-Net and Shallow-Net: Partially addressed color casts but failed to achieve sufficient contrast restoration.

• WaveNet: Improved brightness but suffered from inconsistent enhancements across the image.

• HTN-PSO: Delivered superior results by effectively balancing brightness and color, ensuring natural and visually appealing outputs. The integration of PSO optimized parameters like contrast and sharpness, further enhancing image quality.

Fig. 10

The qualitative comparison of existing UCM, UWCNN, Waternet, Shallownet, Wavenet with HTN-PSO on the UWGAN dataset.

Based on Fig. 10, observations from the UWGAN Dataset⁹:

• UCM, Water-net, Shallow-net, Wave-net: All methods managed to reduce haze but failed to restore true colors, leaving noticeable residual artifacts.

• UWCNN: Enhanced contrast but introduced unnatural red hues, reducing overall realism.

• HTN-PSO: Outperformed all methods by removing haze comprehensively and restoring accurate colors. The hybrid architecture (CNN + Transformer) facilitated both local detail retention and global correction.

Fig. 11

The qualitative comparison of existing UCM, UWCNN, Waternet, Shallownet, Wavenet with HTN-PSO on the UIEB dataset.

Based on Fig. 11, observations from the UIEB Dataset¹⁰.

• UCM: Enhanced contrast but left greenish/blueish casts and failed to recover dark details effectively.

• UWCNN: Reduced color casts but introduced oversaturated red hues and unnatural sharpness.

• Water-Net and Shallow-Net: Partially removed haze and color casts but lacked realistic color balance and contrast.

• WaveNet: Preserved brightness and details better than others but over-brightened regions, leaving some haze and distortions.

• HTN-PSO: Achieved the best results, eliminating color casts, reducing haze, restoring details, and maintaining natural color balance without artifacts.

Although HTN-PSO achieves state-of-the-art results across most metrics, its NIQE score on the RUIE dataset is marginally higher compared to some methods. This is likely due to the RUIE dataset’s inherent variability, which includes non-uniform lighting, diverse marine species, and severe color-cast conditions. NIQE, being a statistical model based on natural scene statistics, may misinterpret the enhanced images due to these unique underwater characteristics. Despite this, HTN-PSO still records the best UIQM and BRISQUE scores on RUIE, indicating strong perceptual and structural quality. Through qualitative analysis, it is evident that the proposed HTN-PSO method out- outperforms the compared methods in terms of color-cast removal, haze reduction, and improved image quality. These results validate the effectiveness of the HTN-PSO method in handling UIE challenges.

Quantitative comparison

The quantitative analysis of the HTN-PSO method was conducted by comparing its performance with several existing methods using metrics such as NIQE, BRISQUE, and UIQM. The findings, presented in Table 3, indicate that the HTN-PSO approach exhibited the highest UIQM scores when applied to authentic underwater datasets, specifically RUIE and EUVP. This suggests that the application of HTN-PSO significantly enhances the clarity, color accuracy, and contrast of degraded photos, outperforming alternative techniques. In contrast, conventional methods like Unsharp Masking (UCM) primarily focus on contrast enhancement but often introduce undesired artifacts. Additionally, the UWCNN, WaterNet, ShallowNet, and WaveNet methods tend to generate a yellowish hue in the output, leading to the presence of undesirable noise.

The results further demonstrate that the HTN-PSO approach consistently yielded the lowest BRISQUE values across all three datasets, indicating its effectiveness in producing images that closely align with the characteristics of the human visual system. The HTN-PSO approach successfully restores the original colors in the images.

In terms of NIQE, as shown in Table 3, the HTN-PSO method achieved the minimum values for the EUVP and UWGAN datasets, demonstrating its effectiveness in restoring the naturalness of degraded images. However, for the RUIE dataset, HTN-PSO did not show significant improvements compared to other methods. Notably, the WaveNet method performed well in terms of NIQE.

Table 3 The quantitative comparison of UCM, UWCNN, waternet, shallownet, WaveNet and HTN-PSO methods on RUIE, EUVP, UWGAN and UIEB datasets based on UIQM, BRISQUE and NIQE.

Comparatively, HTN-PSO avoids common pitfalls of traditional methods like UCM, which focus heavily on contrast enhancement but often introduce artifacts, and deep learning-based methods such as UWCNN and WaterNet, which tend to over-enhance images with unnatural color shifts or excessive luminance. By leveraging a hybrid architecture that integrates Transformers for global context modeling and CNNs for capturing local details, HTN-PSO effectively balances enhancement tasks. Moreover, its use of Particle Swarm Optimization (PSO) ensures efficient hyperparameter tuning, enabling the framework to adapt to diverse underwater conditions and optimize performance across various datasets. This robustness allows HTN-PSO to consistently address challenges such as haze, color cast, and poor contrast across different datasets.

Note

HTN-PSO consistently performs well across all datasets, achieving the best or competitive scores in UIQM, BRISQUE, and NIQE. Wave Net generally shows poor perceptual quality (high BRISQUE) despite having decent UIQM. Dataset characteristics significantly impact model performance, with HTN-PSO being the most adaptable model across diverse datasets.

The proposed model has also been compared with transformer-based methods such as Uformer and Restormer across all evaluation metrics. The performance of the proposed HTN-PSO model shows clear improvements over transformer-based methods. HTN-PSO achieves a NIQE of 4.09, lower than Uformer (4.78) and Restormer (4.61), indicating better visual naturalness and fewer distortions. It also records a lower BRISQUE score of 31.10, compared to 35.62 and 34.15, respectively, suggesting enhanced perceptual quality. In terms of UIQM, HTN-PSO attains the highest score of 4.59, outperforming Uformer (4.21) and Restormer (4.35), which reflects better color, contrast, and sharpness restoration. Additionally, HTN-PSO requires less training time (216.86 s) than both transformer-only models, highlighting its computational efficiency. These results collectively demonstrate the effectiveness of combining CNNs for local feature learning, transformers for global context modeling, and PSO for parameter optimization, making HTN-PSO a more capable and efficient solution for complex image enhancement tasks.

Run-time comparison

The average runtime of the UCM, UWCNN, WaterNet, ShallowNet, WaveNet, and HTN-PSO methods has been calculated for different image resolutions: 100 × 100, 200 × 200, 300 × 300, 400 × 400, and 500 × 500. As shown in Table 4, the average runtime values for the compared methods, including HTN-PSO, are provided for 200 images. However, the proposed network has been validated on several datasets. The plot demonstrates that UCM has a higher processing time than the other methods. Additionally, it can be observed that WaterNet has the worst time complexity. All these techniques require significant processing time, whereas HE takes the least time since it does not require any training. Among the deep learning techniques, the proposed HTN-PSO outperforms the others.

Table 4 The total run-time of UCM, UWCNN, waternet, shallownet, WaveNet and HTN-PSO methods on RUIE, UWGAN, EUVP and UIEB datasets in terms of ms.

While HTN-PSO achieves superior enhancement quality, the integration of transformers and PSO introduces additional computational overhead. However, this is offset by the use of a hybrid CNN-transformer architecture and efficient PSO-based hyperparameter tuning, which allows real-time performance on GPU-enabled systems. Thus, HTN-PSO provides a favourable trade-off between visual quality and processing time, particularly for deployment in autonomous marine robotics.

Statistical significance testing

To quantitatively validate the performance superiority of the proposed HTN-PSO method, we conducted statistical significance testing using paired t-tests on the three no-reference image quality metrics: UIQM, BRISQUE, and NIQE. The test evaluates whether the observed improvements over baseline methods are statistically significant or could have occurred by chance.

Testing protocol

A subset of 50 images was randomly selected from each of the three major benchmark datasets: UIEB, EUVP, and UWGAN. For each image, scores for UIQM, NIQE, and BRISQUE were computed using all methods: HTN-PSO, UCM, UWCNN, WaterNet, ShallowNet and WaveNet. The paired sample t-test was used to compare HTN-PSO with each baseline method individually, using:

Null hypothesis (H₀)

There is no significant difference between the performance of HTN-PSO and the baseline.

Alternative hypothesis (H₁)

HTN-PSO significantly outperforms the baseline.

Significance level was set at α = 0.05.

These baseline models were chosen to ensure a comprehensive evaluation across different aspects of model complexity and performance. UCM was included for its robust unsupervised learning approach, while UWCNN and Water-Net are state-of-the-art methods in water segmentation, offering strong performance in domain-specific tasks. Shallow-net serves as a lightweight baseline, enabling an understanding of the trade-offs between model efficiency and accuracy. Finally, WaveNet, known for its superior sequential modeling capabilities, was selected to assess the spatial-temporal performance of our method. By comparing HTN-PSO against these diverse models, we aim to demonstrate its superior accuracy, adaptability, and robustness across various data complexities. Table 5 presents the p-values for comparisons of HTN-PSO against each baseline method.

Table 5 Paired t-test p-values comparing HTN-PSO with baseline methods across three datasets using UIQM, NIQE, and BRISQUE scores.

Conclusion, limitations and future scope

This study presents the HTN-PSO framework, a hybrid architecture that combines hierarchical transformers with particle swarm optimization to enhance underwater image quality. The framework is designed to address prominent challenges in underwater environments, such as color distortion, blurriness, and poor contrast. By leveraging transformer-based attention mechanisms for capturing long-range dependencies and PSO for adaptive parameter optimization, the proposed approach demonstrates improved performance in visual feature restoration and enhancement.

Extensive experiments conducted on diverse real and synthetic datasets, including UIEB, RUIE, EUVP, and UWGAN, confirm the robustness and generalizability of the proposed method. Objective quality metrics such as UIQM, NIQE, and BRISQUE consistently indicate that HTN-PSO outperforms existing traditional and deep learning-based techniques. Subjective evaluations further support the natural appearance and visual fidelity of the enhanced outputs. With an average inference time of approximately 365 milliseconds for 500 × 500-pixel images, the model achieves a balance between quality and computational efficiency, making it viable for real-world deployment.

The applicability of HTN-PSO extends across multiple domains. In autonomous marine systems, it can support navigation, obstacle detection, and robotic manipulation in visually degraded waters. Environmental monitoring systems can benefit from improved image clarity for coral reef tracking, seabed mapping, and pollution surveillance. The model also shows promise for tasks such as underwater archaeology and infrastructure inspection, where visual interpretability is essential. Furthermore, its lightweight hybrid design, combined with automated tuning via PSO, facilitates deployment on edge devices in low-power marine settings.

Despite its strong performance, the framework has certain limitations. Under extremely turbid or low-light conditions, the model’s ability to extract meaningful features is diminished, as visual cues become less distinguishable. In such cases, even transformer-based attention mechanisms are constrained by the lack of informative input. To overcome these challenges, future work will explore the integration of auxiliary sensing modalities, such as depth estimation, inertial data, or acoustic signals, which can augment the image domain and provide richer context for enhancement.

Another consideration is the additional computational overhead introduced by combining transformer architectures with particle swarm optimization. Although preliminary runtime evaluations show that HTN-PSO maintains reasonable efficiency, a detailed analysis of the computational trade-offs, including transformer complexity and PSO convergence time, will be pursued in future work. To further improve scalability and reduce latency, the adoption of lightweight transformer variants such as MobileViT or TinyViT, along with parallelized PSO mechanisms, will be investigated.

All benchmarking in this study was conducted under standardized conditions, with consistent preprocessing and evaluation protocols applied across competing methods to ensure fairness. As part of future developments, additional evaluations on real-time video streams, cross-domain datasets, and deployment scenarios will be explored to validate the framework’s adaptability and practical utility.

Ablation study

To validate the contributions of the proposed Hybrid Transformer Network-Particle Swarm Optimization (HTN-PSO) framework, as stated in the abstract, we conducted an ablation study by systematically removing or altering key components of the framework. This study evaluates the significance of each contribution, including data augmentation, transformer-based feature extraction, PSO for parameter optimization, and the combined hybrid architecture. The details of the ablation study are shown in Table 6.

Table 6 Ablation study evaluating the impact of architectural components and optimization strategies on NIQE, BRISQUE, UIQM, and training time.

To validate the advantage of PSO, we compared it with traditional optimizers such as Adam and SGD. As shown in Table 6, the PSO-based configuration achieved lower NIQE and BRISQUE scores and higher UIQM than both optimizers, demonstrating more effective convergence. This can be attributed to PSO’s global search capability, which avoids local minima during hyperparameter tuning. Ablation results also reveal the additive benefits of each module. Adding transformers significantly improves global context modeling (UIQM ↑0.35). PSO contributes most to reducing perceptual distortion (BRISQUE ↓2.1). Data augmentation enhances generalization, leading to consistent NIQE reduction. The full HTN-PSO architecture, which combines all three, delivers the best overall results.

Experimental setup

The experiments were conducted on the RUIE, EUVP, UWGAN and UIEB datasets. The evaluation metrics used were:

• i) NIQE (Naturalness): Lower is better.

• ii) BRISQUE (Distortion): Lower is better.

• iii) UIQM (Quality): Higher is better.

The following configurations were analyzed:

• i) Baseline: CNN-based feature extraction without transformers or PSO.

• ii) +Transformers: Adding transformers to the baseline.

• iii) +PSO: Replacing traditional optimization with PSO.

• iv) +Data Augmentation: Adding data augmentation techniques to enhance training diversity.

• v) HTN-PSO (Full): The complete proposed framework with all components.

Analysis of results

The ablation study demonstrates the importance of each component in the HTN-PSO framework. The baseline model, using only CNN-based feature extraction, performs poorly with high NIQE and BRISQUE scores, indicating suboptimal image quality. Adding transformers improves UIQM by capturing global context and enhancing image sharpness, but still leaves room for optimization. Introducing PSO optimizes param- eters, reducing BRISQUE and improving NIQE, while data augmentation enhances generalization, further improving UIQM.

The complete HTN-PSO framework, integrating all components, achieves the best results with the lowest NIQE and BRISQUE scores and the highest UIQM, confirming that the combination of CNNs, transformers, PSO, and data augmentation leads to the most effective underwater image enhancement.