A comprehensive analysis of digital inclusive finance’s influence on high quality enterprise development through fixed effects and deep learning frameworks

Abstract

In the context of global economic transformation, high-quality enterprise development (HQED) is crucial for driving economic growth, particularly through enhancing Total Factor Productivity (TFPLP). Digital Inclusive Finance (DIF), as a classical financial model, plays an important role in promoting high-quality enterprise development. To explore the relationship between TFP and DIF, we first applied traditional double fixed-effects models, along with robustness and heterogeneity tests, for modeling experiments. This series of tests effectively revealed the theoretical linear relationships between economic variables. However, the double fixed-effects model has limitations in capturing nonlinear relationships and making predictions. Given the growing body of research on existing hybrid models, we acknowledge the importance of exploring and contributing to this evolving area. To address this issue, based on the results of traditional economic analysis, we introduced improved time series models. These advanced deep learning models allow us to better capture the complex nonlinear relationship between DIF and TFP. The experiment initially explored the preliminary structural relationship between DIF and TFP using double fixed-effects models combined with robustness and heterogeneity tests. Then, based on the results of these tests, we selected deep learning features and combined Kolmogorov–Arnold Neural Network (KAN), Graph Neural Network (GNN) models with classic time series deep learning models (Transformer, LSTM, BiLSTM, GRU) to capture the latent nonlinear features in the data for prediction. The results show that, compared to traditional time series forecasting methods, the improved deep learning models perform better in capturing the nonlinear relationships of economic variables, improving prediction accuracy, and reducing prediction errors. Finally, paired t-tests and Cohen’s d effect size tests were used to evaluate error metrics, and the results indicate that the introduction of KAN and GNN models significantly improved the performance of time series forecasting models.

Introduction

In the current global economic context, high-quality enterprise development (HQED) has become a key goal for economic growth¹, especially in China, where the economy is transitioning from rapid growth to quality-focused development². Improving internal efficiency and innovation is critical². Total Factor Productivity (TFPLP, we use Levinsohn and Petrin’s (2003) LP approach to assess enterprise development quality versus Total Factor Productivity)³ is a key measure of business efficiency and innovation, calculated using LP methods to estimate the marginal output of production factors⁴, reflecting output levels under specific technological and managerial conditions⁵. Digital Inclusive Finance (DIF) has emerged as a major financial innovation, transforming the traditional financial system⁶, improving resource sharing, and providing businesses with better access to funding⁷. By leveraging technologies like the internet⁸, big data, and AI⁹, DIF reduces financing costs, enhances transparency⁹, and makes financial services more inclusive, making it increasingly important for HQED¹⁰.

This research choses companies listed in China from 2011 to 2022 as the research sample. The data can be obtained in supporting material. By analyzing data from this period, the study investigates the relationship between DIF and TFPLP of enterprises. To guarantee the precision and robustness of the results, this research incorporates multiple control variables when analyzing the impact of DIF. These variables reflect the basic characteristics and operational conditions of the enterprises, which may also influence their TFPLP. Furthermore, the study performs heterogeneity tests, examining the distinctions between state-controlled and non-state-controlled enterprises, enterprises in different life cycle stages, and technology-based enterprises, to guarantee the universality and reliability of the conclusions. Additionally, to get rid of potential interference from the COVID-19 pandemic, robustness checks are conducted to account for its impact on enterprise operations. These control variables and heterogeneity tests help us gain a more thorough understanding of the mechanisms through which digital inclusive finance affects the HQDE. However, as the volume of data increases and relationships become more complex, traditional linear models are clearly insufficient to understand the potential complex nonlinear relationships between DIF and enterprise total factor productivity. Considering the extensive research already conducted on existing hybrid models, we recognize the value in further exploring and building upon this area of study. After completing the empirical analysis in economics, this study has fully understood the relationship between explanatory variables and explained variables through multicollinearity, robustness, heterogeneity, and endogeneity tests. These assumptions, control variables, and heterogeneity tests provide a solid foundation to clearly explain the relationships between different variables. The control variables and heterogeneity tests help in gaining a deeper understanding of the impact of DIF on TFPLP of enterprises. However, with the increase in data volume and complexity, traditional linear models are insufficient to reveal the potential nonlinear relationships between DIF and TFPLP. Therefore, this study transforms the empirical results into features for deep learning models to better perform nonlinear prediction. In the empirical analysis, the results of the two-way fixed effects model regression confirm that DIF, three mediating variables, and nine control variables are significantly correlated with TFPLP (the regression results are statistically significant). These variables show strong predictive power, so we selected them as input features for the deep learning model. Specifically, DIF as the core explanatory variable, three mediating variables, and nine control variables have been identified as key factors strongly correlated with TFPLP. These variables not only have an economic theoretical background but also provide necessary features for the deep learning model, helping it capture the potential nonlinear relationships. In the selection of deep learning models, this study employs Long Short-Term Memory (LSTM)¹¹, Bidirectional Long Short-Term Memory (BiLSTM)¹², and Gated Recurrent Unit (GRU)¹³, and Transformer¹⁴ as baseline models, which demonstrate significant advantages in processing economic time-series data. Specifically, LSTM¹¹ and BiLSTM, with their unique gating mechanisms¹¹, effectively capture long-term dependencies in time-series data¹², aligning well with the inherent dynamic characteristics of economic data. GRU, as a more parameter-efficient variant of recurrent neural networks¹³, maintains strong predictive performance while significantly reducing computational complexity. The Transformer model¹⁵, leveraging its self-attention mechanism and parallel computing capabilities, exhibits outstanding performance in modeling complex temporal patterns. The adoption of these four models as baselines ensures both prediction accuracy and computational efficiency.

However, traditional multilayer perceptrons (MLPs) exhibit notable limitations in handling complex nonlinear relationships in economic data. Although models such as LSTM¹⁶ and BiLSTM effectively model temporal dependencies, the fully connected layers (MLPs) in their core structures still suffer from inherent drawbacks: First, traditional MLPs rely on linear transformations and fixed activation functions, making it difficult to fully represent complex nonlinear interactions in high-dimensional economic data. Second, MLP layers require predefined neuron counts, and this rigid structure often leads to overfitting or underfitting when dealing with dynamic cross-enterprise and cross-temporal relationships in panel data. These limitations highlight the urgent need for novel nonlinear modeling approaches.

To overcome these constraints, this study introduces the Kolmogorov-Arnold Network¹⁷ (KAN) as an alternative solution¹⁸. The theoretical foundation of KAN stems from the Kolmogorov-Arnold representation theorem¹⁹, which rigorously proves that any multivariate continuous function can be represented as a finite composition of univariate functions. By replacing the fixed activation functions in traditional MLPs with learnable nonlinear basis functions, KAN achieves two key improvements²⁰: First, it enables dynamic high-dimensional nonlinear mappings to explicitly model complex interactions among variables. Second, it employs a hierarchical function composition strategy to significantly enhance parameter efficiency²¹, thereby improving the model’s generalization capability for panel data. In the experimental design, we systematically validate KAN by substituting it for the MLP layers in the baseline models.

Furthermore, while traditional temporal models effectively handle time-dependent features, they generally overlook the topological relationships among firms in economic data (e.g., supply chain connections, industry competition). In reality, firms in panel data are not independent but interact through complex network structures. To address this, the study further incorporates a graph neural network (GNN) framework²², specifically adopting Graph convolutional networks (GCN)²³ and Graph attention networks (GAT)²⁴. GCN aggregates neighborhood information through convolutional operations, effectively capturing static dependencies among firms (e.g., industry classification). GAT, on the other hand, dynamically learns node association weights via attention mechanisms²⁵, precisely identifying the influence propagation of key firms (e.g., the ripple effects of leading firms on upstream and downstream entities). By integrating GNN-extracted topological features²¹ with temporal models, this study achieves systematic modeling of complex cross-firm²⁴ and cross-temporal relationships²⁶.

In the experiments, this study adopted five-fold cross-validation to make full use of the data and conducted ablation experiments on these model variants. We used R², RMSE, MAE, and MSE as evaluation metrics to assess model performance. To further validate the significant improvement of the modified models compared to the original models, statistical methods such as paired t-tests and Cohen’s d tests were conducted to confirm the effectiveness and performance enhancement of the improved models. The main innovations of this study are as follows:

• (1) This paper systematically explores how DIF promotes high-quality enterprise development through intermediary variables such as innovation, financing constraints, and internal control.

• (2) This paper employs the traditional economic fixed effects model to provide a linear explanation of economic variables. However, due to its limitations in nonlinear prediction, it fails to effectively capture the nonlinear relationships within economic data. To overcome this limitation, deep learning models are introduced to improve predictive performance.

• (3) The paper combines the KAN with four traditional time series models, replacing the fully connected layer (MLP layer) in traditional models. This significantly improves the model’s predictive accuracy.

• (4) The paper also combines GNNs with time series models, utilizing GNNs to understand complex dependencies in the data and integrating it with time series modeling, which the model’s predictive performance.

In conclusion, by combining traditional empirical analysis with advanced deep learning technologies, this study comprehensively explores how DIF affects the high-quality development of enterprises, especially by revealing the nonlinear relationship between DIF and enterprise TFP. The introduction of innovative models addresses the shortcomings of traditional empirical analysis in capturing complex nonlinear relationships, offering a new methodology for financial research and providing important decision-making references for policymakers and business managers. The two experimental models are illustrated in Fig. 1.

Fig. 1

Structural overview of traditional economic and deep learning models.

The remainder of this paper is structured as follows: Section "Literature review" provides a comprehensive review of existing research on DIF and high-quality development and applications of the deep learning models, after which Section "Theoretical hypothesis analysis" presents the theoretical hypothesis analysis. Next, Section "Empirical strategies of empirical analysis and data sources of basic regression" reviews the research design of empirical analysis of basic regression in detail. Section "Empirical results and analysis" focuses on experimental results and Section "Further discussion: heterogeneity analysis" presents analysis of heterogeneity test. Section "The application of deep learning models in prediction of TFPLP" shows the experimental process and results of prediction in deep learning models. Finally, Section "Conclusion" concludes the research with a key finding’s summary, current limitations and future research recommendations.

Literature review

The rapid development of DIF has provided rich data resources for economic research^27,28, and at the same time²⁹, it has put forward higher requirements for analytical models and the relationship between DIF and TFPLP³⁰ has attracted increasing attention in recent years, with deep learning models being applied to better understand and predict the dynamics between these two variables^30,31. Traditional econometric models, such as fixed effects and dynamic panel models, have been useful for analyzing the impact of DIF on TFPLP by controlling for unobserved heterogeneity³² and temporal dynamics³³. These methods have provided valuable insights into the link between financial inclusion³⁴ and productivity growth³⁵. However, they often rely on linear assumptions and fail to capture the complexity³⁶ and nonlinearity inherent in the data³⁷.

In contrast, deep learning models like LSTM networks and Transformer models have shown significant potential in handling the dynamic, high-dimensional nature of financial and productivity data. These models excel at capturing temporal dependencies and nonlinear relationships, making them well-suited for analyzing the evolving nature of DIF and TFPLP. Despite their advantages, current deep learning models face certain limitations when it comes to addressing the intricate interactions within economic systems and handling the complex dependencies between different economic factors.

While time series models offer greater flexibility than traditional econometric approaches, they still struggle with generalizing to complex economic data³⁸. These models often face difficulties in capturing the intricate spatial and temporal relationships that exist between multiple entities, time periods, and variables, especially in panel data settings. The inherent complexity of economic systems, where multiple firms, time dynamics, and various influencing factors interact simultaneously³⁹, can overwhelm the capacity of conventional time series models to capture their underlying connections fully. As a result, these models may fail to account for the rich interdependencies between entities and time periods, leading to a limitation in their predictive accuracy and explanatory power.

Theoretical hypothesis analysis

This section introduces four hypotheses, along with detailed descriptions for each.

Direct pathways of DIF in promoting high-quality enterprise development

DIF has become a key factor in promoting HQDE by directly affecting several internal mechanisms within businesses. First, DIF helps traditional industries become more productive and transform faster, making the real economy more sustainable over the long term. Second, DIF improves the efficiency of production processes, leading to better quality results. This boost in productivity directly supports overall business growth, enhances competitive advantage, and maximizes corporate performance, all of which contribute to high-quality development. From this analysis, we derive the first hypothesis of this study.

Hypothesis 1

The development of DIF promotes HQDE.

Indirect paths of DIF affecting the HQDE

This section looks at how DIF affects three key factors: alleviating corporate financing constraints, enhancing internal control, and boosting innovation capacity. We will look at how these impacts indirectly promote HQDE.

Addressing financing constraints in enterprises through DIF

Financing is a major issue for Chinese businesses, mainly due to problems in the financial market and banks’ unfair lending policies. DIF helps solve this problem by playing a crucial role in expanding access to credit, especially for vulnerable businesses, providing them with better opportunities to secure long-term loans and supporting their ongoing development.

As a result, easing financing constraints through DIF indirectly improves the overall development quality of businesses. Based on this analysis, we derive the following hypothesis:

Hypothesis 2

Digital inclusive finance alleviates financing constraints to boost the HQDE.

Enhancing internal control level of enterprises through DIF

DIF is an effective way to help businesses improve their internal control mechanisms by using digital tools to make data more transparent and monitor processes in real time. These technologies allow businesses to identify mistakes, automate tasks, and ensure compliance with rules. This reduces the risk of errors, fraud, and rule violations. Based on this analysis, we derive the following hypothesis:

Hypothesis 3

Digital inclusive finance enhances internal control level to boost the HQDE.

Facilitating innovation of enterprises through DIF

Innovation is a crucial factor for sustaining long-term enterprise success and maintaining a competitive edge in the market. By granting enterprises access to digital financial services, DIF enables them to invest more effectively in research and development (R&D), improving products and services. Based on this analysis, we derive the following hypothesis:

Hypothesis 4

DIF facilitates innovation of enterprises to boost the HQDE.

Empirical strategies of empirical analysis and data sources of basic regression

The experimental design of this paper concentrates on exploring the impact of DIF on high-quality enterprise development, employing rigorous modeling and diverse empirical analysis methods. The traditional economic research design’s overall framework is presented in Fig. 2.

Fig. 2

The overall framework of research design.

Overall, the experimental design emphasizes the rigor of model construction and employs a variety of analytical methods to comprehensively examine the impact pathways and mechanisms of DIF on high-quality enterprise development.

Index selection and data description

In this study, 22,291 enterprise annual observations for the period of 2011–2022 were selected as the analyzed sample, covering a wide range of industries and regions to guarantee the representativeness and breadth of the research outcomes. The sample data were strictly screened and processed. Firstly, financial enterprises were removed from the sample to avoid the interference of financial industry specificity on the research results. Secondly, ST and *ST enterprises, which often face financial difficulties or operational abnormalities that may bias the analysis results, are removed from the sample as well. Finally, enterprises with more missing values in the data were removed to make sure the completeness and reliability of the data. In order to further minimize the impact of extreme values on the results of the study, the continuous variables have been reduced-tailed at the upper and lower 1% quartiles. All company data are sourced from CSMAR database (shown in Table 1).

Table 1 The result of descriptive statistics for the variables.

The measurement of variable

This section introduces the specifics of various economic variables, including explained variables, explanatory variables, mediating variables, and control variables.

Explained variable: High-quality development of enterprises

In this study, total factor productivity is used as a key indicator for measuring HQDE. TFPLP, as the explanatory variable, reflects the efficiency and overall production capability of an enterprise in relation to the input of production factors. Specifically, Total Factor Productivity represents the actual level of output that an enterprise can achieve, considering the input of capital, labor, and other production factors. By analyzing changes in TFP, we can evaluate the performance of enterprises in improving production efficiency, innovation capability, and resource allocation, thereby indirectly measuring the progress in high-quality development. It is worth noting that the Chinese government has stressed that the key to high-quality development is to improve TFP and achieve innovation-driven development. For businesses and enterprises, total factor productivity is not only an indicator to measure the overall resource allocation of enterprises, but also an important indicator to reflect the technological innovation level of enterprises. Therefore, on the basis of keeping consistent with the methods followed by most scholars, this paper chooses total factor productivity as an indicator to measure HQDE. For our benchmark specification, we use Levinsohn and Petrin’s (2003) LP approach to assess enterprise development quality versus TFP. In a follow-up analysis, we used Wooldridge’s (2009) one-step OP-based estimation method to recalculate TFP to demonstrate the robustness of our preliminary results.

Explanatory variable: digital inclusive finance

In this study, DIF is used as an explanatory variable to explore its impact on financial development and economic performance. DIF refers to financial services provided through digital technologies, aiming to make financial services more accessible, convenient, and affordable. We consider DIF as an explanatory variable because it may influence changes in other economic or financial indicators. To comprehensively analyze the role of DIF, we decompose it into three key sub-indexes:

• (1) Depth: This refers to the extent of digital inclusive financial services’ penetration among different social groups.

• (2) Breadth: This pertains to the coverage of digital inclusive financial services, including the types of services provided and the diversity of financial products.

• (3) Degree of digitization: This indicates the level of digitalization of financial services, i.e., whether services are provided fully or partially through digital channels.

Control variables

In the study, control variables are used to isolate the effect of the primary explanatory variable to ensure that the observed results are attributable to the explanatory variable and not confounded by other factors. Here’s an explanation of these eight control variables:

• (1) Firm size (SIZE): Represented by the natural logarithm of total assets. Firm size often influences financial and market performance. Larger firms may have more resources, stronger market positions, and greater economic stability. Controlling firm size helps to avoid confounding effects on the results.

• (2) Financial leverage (LEV): The ratio of total debt to total assets. Financial leverage reflects the level of debt in the firm’s capital structure. Higher financial leverage can increase financial risk and affect investment decisions and operational performance. Controlling financial leverage helps to understand the impact of capital structure on firm performance.

• (3) Cash flow level (CFO): The ratio of net cash flow from operating activities to total assets. Cash flow level reflects the firm’s cash generation capacity. A higher cash flow level typically indicates sufficient cash to support operations and investment activities. Controlling cash flow level helps to distinguish the effects of cash flow from other financial factors.

• (4) Firm growth (GROWTH): The growth rate of operating revenue. Firm growth measures the expansion capability and market opportunities of the firm. Growth can impact financial conditions and market performance. Controlling growth helps to understand the influence of expansion speed on overall performance.

• (5) Firm age (AGE): The time difference between the firm’s founding year and the observation year. Firm age can affect market experience, stability, and reputation. Older firms may have more market experience and stability, so controlling for firm age helps to exclude its impact on the results.

• (6) Ownership concentration (TOP): The proportion of shares held by the largest shareholder. Ownership concentration reflects the shareholder structure of the firm. Firms with high ownership concentration might face different governance structures and decision-making processes, so controlling this variable helps understand its influence on performance.

• (7) Board size (BSIZE): The natural logarithm of the number of board members. Board size can affect corporate governance and decision-making efficiency. Controlling board size helps isolate the impact of governance structure on firm performance.

• (8) Management shareholding (MSR): The proportion of shares held by the management team. Management shareholding can align the interests of management with those of shareholders and affect strategic decisions. Controlling management shareholding helps to account for its effect on firm performance.

Mediating variables

Intermediary variables are used to explore the mechanisms or pathways through which the explanatory variable affects the explanatory variable. Here’s an explanation of Innovation, Financing Constraints (FC), and Internal Control Level (ICL) as intermediary variables:

• (1) Innovation: Innovation typically refers to new developments and improvements in products, services, or processes within a firm. As an intermediary variable, innovation can help explain how the explanatory variable influences the explanatory variable through driving technological advancements, product development, or business model improvements. For example, DIF may indirectly affect financial performance or market competitiveness by enhancing a firm’s innovation capabilities.

• (2) Financing constraints (FC): Financing constraints refer to the difficulties and limitations a firm faces in obtaining external funding. As an intermediary variable, financing constraints can reveal how the explanatory variable influences the explanatory variable through its impact on the firm’s ability to obtain and conditions of financing. For instance, firm size or financial leverage might affect financing constraints, which in turn influences the firm’s innovation capacity and growth potential.

• (3) Internal control level (ICL): The internal control level refers to the effectiveness of measures in place for financial reporting, operations, and compliance within a firm. As an intermediary variable, the internal control level can help explain how the explanatory variable impacts financial stability and operational efficiency through improving internal control. For example, effective internal control can reduce operational risks and financial irregularities, enhancing overall performance and decision-making quality.

Reference model specification

Dual fixed-effect model

In order to more intuitively analyze the impact of DIF on enterprise high-quality development, the following regression model is established based on existing literature:

$$TFPLP_{i,t} = \alpha_{0} + \alpha_{1} DIF_{i,t} + \alpha control_{i,t} + \delta_{i} + \rho_{t} + \varepsilon_{i,t}$$

(1)

where $i$ represents the individual, $t$ represents the year, enterprise high-quality development (TFPLP) is the explanatory variable, digital financial inclusion (DIF), breadth (BRE), depth (DEP), digitization degree (DIG) is the core explanatory variable, and $control$ is the relevant control variable:enterprise scale (SIZE), financial leverage (LEV), cash flow level (CFO), Enterprise Growth (Growth), enterprise age (AGE), ownership concentration (TOP), Board size (BSIZE),management shareholding (MSR). ${\delta }_{i}$ represents individual fixed effects, ${\rho }_{t}$ expressed fixed time effect, ${\varepsilon }_{i,t}$ is the random disturbance term.

Mediating effect model

To explore possible intermediary variables in the transmission mechanism of DIF on enterprise high-quality development, this section adopts the Stepwise Regression for Mediation Effect (Baron and Kenny’s mediation test) model and takes financing constraint (FC), Innovation and Internal Control Level (ICL) as the intermediary variable ${M}_{i,t}$ for empirical analysis and the mediating effect mechanism overview is presented in Fig. 3.

Fig. 3

The overview of mediating effect model.

The three-step method is a classic approach to testing mediation effects, typically divided into three steps as follows:

Step 1: Total effect test: First, test whether the total effect of the independent variable (DIF) on the dependent variable (TFPLP) is significant. Establish the regression model:

$$TFPLP_{i,t} = \gamma_{0} + \gamma_{1} DIF_{i,t} + \gamma control_{i,t} + \delta_{i} + \rho_{t} + \varepsilon_{i,t}$$

(2)

If the regression coefficient c is significant, it demonstrates that the independent variable has a significant impact on the dependent variable, allowing for further mediation effect testing.

Step 2: Mediator Variable Effect Test: Test whether the independent variable (DIF) has a significant effect on the mediator variable (M). Establish the regression model:

$$M_{i,t} = \beta_{0} + \beta_{1} DIF_{i,t} + \beta Control_{i,t} + \delta_{i} + \rho_{t} + \varepsilon_{i,t}$$

(3)

If the regression coefficient a is significant, it indicates that the independent variable significantly affects the mediator variable, suggesting that the independent variable may influence the dependent variable through the mediator.

Step 3: Mediation effect and direct effect test: Test the impact of the mediator variable (M) on the dependent variable (TFPLP), while controlling for the independent variable (DIF). Establish the regression model:

$$TFPLP_{i,t} = \gamma_{0} + \gamma_{1} DIF_{i,t} + \theta M_{i,t} + \gamma control_{i,t} + \delta_{i} + \rho_{t} + \varepsilon_{i,t}$$

(4)

where the above three equations test whether there is a conduction relationship between explanatory variable, intermediary variable and explanatory variable, and whether the intermediary variable is an important influence path. ${M}_{i,t}$ is an intermediary variable, First, the intermediary variable is not included in Eq. (2). Suppose that coefficient ${\alpha }_{1}$ indicates that the impact of DIF on enterprise high-quality development (TFPLP) is significant. In that case, regression is carried out based n Eq. (3) to evaluate the effect of DIF on ${M}_{i,t}$ and further bring the intermediary variables into the regression framework to form Eq. (4). If these variables are significant, it implies that a mediating effect is evident. If ${\gamma }_{1}$ is significant, it implies that ${M}_{i,t}$ has a partial mediating effect. If ${\gamma }_{1}$ is not significant, it implies that ${M}_{i,t}$ has a complete mediating effect.

Estimation methods for Endogeneity concerns

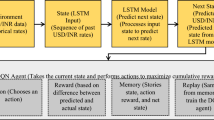
In analyzing the impact of DIF on TFPLP, there may be a reciprocal causal relationship between the two, leading to endogeneity issues. Additionally, using a fixed effects model for panel data regression may result in bias due to endogeneity. To estimate the model, the lagged value of the core explanatory variable is selected as an instrument to reduce estimation bias coming from the empirical regression. We use the lagged value (${DIF}_{i,t-1}$) of the core explanatory variable (${DIF}_{i,t}$). The process is shown in Fig. 4. This is because the lagged variable is generally uncorrelated with the current random disturbance term but may be correlated with the current explanatory variable, meeting the requirements for an instrument.

Fig. 4

The overview of endogeneity estimation.

First stage regression: Use the instrumental variable ${DIF}_{i,t-1}$ to perform a regression on and obtain the predicted value $\widehat{I}{F}_{i,t}$ , The model can be structured as follows:

$$D\hat{I}F_{i,t} =\uplambda _{0} +\uplambda _{1} DIF_{i,t - 1} +\uplambda _{2} {\text{control}}_{i,t} + \delta_{i} + \rho_{t} + \varepsilon_{i,t}$$

(5)

where $D\widehat{I}{F}_{i,t}$ is the predicted value obtained from the first stage regression.

Second stage regression: In the second stage, substitute the predicted value $D\widehat{I}{F}_{i,t}$ obtained from the first stage regression into the original baseline regression model:

$$TFPLP_{i,t} = \phi_{0} + \phi_{1} D\hat{I}F_{i,t} + \phi control_{i,t} + \delta_{i} + \rho_{t} + \varepsilon_{i,t}$$

(6)

where by using $D\widehat{I}{F}_{i,t}$ instead of the original ${DIF}_{i,t}$, the model effectively addresses the endogeneity issue.

Estimation methods for robustness concerns

To assess the robustness of the empirical results from the previously constructed fixed effects regression model Eq. (2) and make sure the rigor of the study’s outcomes, this paper opts to modify the regression model to an Ordinary Least Squares (OLS) regression, which is applied to verify the validity of the original model.

$$TFPLP_{i,t} = \beta_{0} + \beta_{1} DIF_{i,t} + b{\text{control}}_{i,t} + \varepsilon_{i,t}$$

(7)

where individual fixed effects ${\delta }_{i}$ and fixed time effect ${\rho }_{t}$ are not included.

Additionally, this study further validates the model’s robustness by excluding the impact of the 2020 COVID-19 pandemic from the original fixed effects model and by replacing the dependent variable (TFPLP) with a variable calculated using the OP method (TFPOP) and the process of robustness estimation illustrated in Fig. 5.

Fig. 5

The process of robustness estimation.

Empirical results and analysis

This section presents the results and the analysis process of the Multicollinearity analysis, Correlation analysis, Baseline regression analysis, and Robustness tests. The results are discussed in detail to evaluate the relationship between DIF and TFPLP.

Multicollinearity analysis

Table 2 presents the Variance Inflation Factor (VIF) and its reciprocal (1/VIF) for various variables in the regression model, used to assess the degree of multicollinearity among the explanatory variables. In general, a VIF value less than 10 indicates that multicollinearity is not a serious problem. From Table 2, we can see that the VIF values for SIZE, LEV, MSR, AGE, Growth, CFO, TOP, and BSIZE are all well below 10, with the highest VIF being 1.60 for SIZE. The corresponding 1/VIF values are all above 0.1, further confirming that multicollinearity is not a significant issue in this model. Specifically, SIZE has a VIF of 1.60 and 1/VIF of 0.626817, indicating almost no multicollinearity. LEV has a VIF of 1.49 and 1/VIF of 0.672060, indicating a low level of multicollinearity. The VIF values for MSR, AGE, Growth, CFO, TOP, and BSIZE range from 1.01 to 1.24, with corresponding 1/VIF values between 0.805599 and 0.985874, indicating almost no multicollinearity. The mean VIF value is 1.21, with a corresponding mean 1/VIF of 0.848432, further supporting the conclusion that multicollinearity is not an issue in this dataset.

Table 2 The result of VIF test.

Correlation analysis

Tables 3, 4 and Fig. 6 reveal several strong relationships among the variables ("***", "**" and "*" respectively indicate that the indicators are significant at the level of 1% , 5% and 10% in the following Tables 3, 6, 7, 8, 9, 10, 11), such as a positive correlation between TFPLP and FC (0.81) and between SIZE and BSIZE (0.83), indicating that these pairs move in tandem. Conversely, there are strong negative correlations, such as between Innovation and FC (− 0.82) and between LEV and SIZE (− 0.69), suggesting that as one variable increases, the other tends to decrease. Most other variables, such as Growth, TOP, and CFO, show weak correlations, indicating limited linear relationships among them. Overall, the matrix highlights key variable interactions that may warrant further investigation.

Table 3 Correlation analysis result.

Table 4 Correlation analysis result.

Fig. 6

The correlation matrix heatmap.

Overall, the analysis shows robust relationships between the key variables and TFPLP, emphasizing the significant role of firm size, financial indicators, and internal control in driving productivity. The significant positive and negative correlations highlight the complex interplay of these factors in determining firm performance.

Baseline regression analysis

This section analyzes the impact of DIF on the high-quality development of enterprises by comparing the results before and after adding control variables.

From Table 5, it can be seen that in Model 1, DIF has a significant positive impact on high-quality development of enterprises (TEPLP), with a coefficient of 0.00204 and a t-value of 5.16, significant at the 1% level (***). This indicates that the improvement of DIF significantly promotes the high-quality development of enterprises. Model 1 does not include other control variables and only demonstrates the direct impact of DIF on the high-quality development of enterprises.

Table 5 Regression results for testing the role of DIF.

In Model 2, with the introduction of multiple control variables, the impact of DIF) on high-quality development of enterprises (TEPLP) remains significant, with a coefficient of 0.00076 and a t-value of 2.59, significant at the 1% level (). The introduced control variables include firm size (SIZE, coefficient of 0.55284, t-value of 97.53), financial leverage (LEV, coefficient of 0.17039, t-value of 7.84***), firm growth (GROWTH, coefficient of 0.24830, t-value of 47.37***), and cash flow level (CFO, coefficient of 0.76915, t-value of 21.54***), all of which significantly affect the high-quality development of enterprises. Other control variables including ownership concentration (TOP), firm age (AGE), board size (BSIZE), and manager’s shareholding ratio (MSR) are also considered in Model 2, but their impacts are relatively small or insignificant.

Comparing Model 1 and Model 2, the impact of DIF is significant in both models, but the coefficient decreases from 0.00204 to 0.00076, indicating that the influence of DIF weakens after introducing control variables, yet it remains positively significant. Control variables such as firm size (SIZE), financial leverage (LEV), firm growth (GROWTH), and cash flow level (CFO) show high significance in Model 2, demonstrating their crucial impact on the high-quality development of enterprises. After introducing control variables, the explanatory power of Model 2 has a significant improvement, with R² increasing from 0.389 to 0.669, indicating that Model 2 can more comprehensively explain the factors influencing the high-quality development of enterprises. Overall, the results are more robust after introducing control variables, further confirming the key role of DIF in promoting high-quality development of enterprises, while also highlighting the importance of firm size, financial leverage, growth rate, and cash flow level.

Robustness tests

As shown in Fig. 7, it presents the results of heatmap and distribution of T value in robustness test. The regression results of Model 1 in Table 6 after applying the first-order lagging show that the coefficients of the year variables are all significant, indicating that these years have a significant impact on the high-quality development of enterprises (TFPLP). The regression coefficient for DIF remains positive and significant, suggesting that even after controlling for the effects of lagged years, DIF still has a positive impact on high-quality enterprise development, which supports the positive role of DIF in business growth. Additionally, control variables such as SIZE, LEV, and GROWTH remain significant in the model after applying the first-order lagging, implying that their influence is not diminished by the lagging process. Overall, the model’s R² value is relatively high (0.77), indicating strong explanatory power, and the lagging process has not significantly reduced the model’s fit. This further demonstrates the effectiveness of first-order lagging in controlling endogeneity and improving the accuracy of the model’s estimates.

Fig. 7

The heatmap and distribution of T value in robustness test.

Table 6 Robustness check and dealing with endogeneity concerns.

As shown in Table 6, Model 2 changes the explanatory variable from TFPLP to TFPOP. The results of this model indicate that the coefficient for DIF remains significant and positive, which means that DIF has a positive impact not only on high-quality enterprise development (TFPLP) but also on total factor productivity (TFPOP) as an alternative measure. This further demonstrates that the positive effect of DIF on enterprise development is robust and does not depend on a specific explanatory variable.

Model 3 uses Ordinary Least Squares (OLS) for regression, and the results show that most variables have significant coefficients and consistent directions. This indicates that, even without considering fixed effects and time effects, the relationship between the explanatory variables and the dependent variable is robust. The R-squared value of the OLS model is 0.774, suggesting strong explanatory power, with most variables having a significant and positive impact on the outcome. However, since the OLS model does not account for individual and time fixed effects, there might be omitted variable bias, which could affect the robustness of the results. Model 4 is a fixed effects model that excludes the impact of the 2020 COVID-19 pandemic. It shows coefficients with similar directions to those in Model 3, although some coefficient values differ. After excluding the 2020 data, the R-squared value slightly decreases (to 0.663) but remains high, indicating that the model still has strong explanatory power. The fixed effects model, by controlling for individual and time effects, effectively reduces potential biases. Although some coefficients are smaller compared to Model 3, their significance remains high, indicating that the model results are still robust after controlling for more potential influencing factors. Excluding the 2020 data also helps test the impact of the pandemic on the results, enhancing the credibility of the findings.

Furthermore, the results of above analysis have significant economic implications for both policymakers and business managers. From a policy perspective, the positive impact DIF on enterprise development and productivity underscores the importance of promoting digital financial services, particularly for small and medium-sized enterprises (SMEs). Policymakers should focus on expanding digital infrastructure and enhancing financial inclusion to improve resource allocation and business competitiveness. For managers, these findings suggest that integrating DIF into business strategies can drive growth, improve productivity, and help navigate economic uncertainties. By leveraging digital financial solutions, enterprises can optimize capital access and resource use, ensuring long-term success in a dynamic market environment.

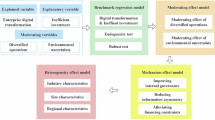
Mechanism verification

This section further assesses the transmission path between DIF and HQDE from the perspectives of enterprise FC, innovation and ICL.

The mediating effect in financing constraint (FC)

In the study, introducing Financing Constraint (FC) as an intermediary variable is both necessary and beneficial. By incorporating FC, the study can better understand how DIF promotes high-quality enterprise development by alleviating financing constraints. This mediating effect helps uncover the internal mechanisms through which DIF influences enterprise development, providing a more comprehensive explanatory framework.

We can see that, from Table 7, DIF has a significant direct effect on high-quality enterprise development (coefficient 0.00076, p < 0.01), indicating that DIF effectively enhances enterprise quality. In the second step, DIF has a significant negative impact on financial constraint (FC) (coefficient − 0.00098, p < 0.01), suggesting that DIF reduces financial constraints for enterprises. In the third step, after introducing FC into the model, DIF’s positive effect on high-quality development remains significant (coefficient 0.00162, p < 0.01), while FC also has a significant negative impact on high-quality development. This indicates that FC plays a partial mediating role in the relationship between DIF and high-quality development. In other words, DIF not only directly promotes enterprise high-quality development but also indirectly contributes by reducing financial constraints. This dual impact shows that DIF influences enterprise development through a complex network of pathways, rather than merely through simple capital injection. Therefore, the mediating effect of DIF in reducing financing constraints reveals its fundamental role in enhancing resource allocation efficiency, which is crucial for improving enterprise competitiveness and long-term growth.

Table 7 The results of mediating effect in FC.

Innovation

By including innovation as an intermediary variable, the study can explore how DIF indirectly promotes high-quality development by fostering corporate innovation. Analyzing this mediating effect helps reveal the role of DIF in the innovation process, providing a deeper understanding of how financial inclusion policies influence corporate innovation behaviors and high-quality development, thereby offering theoretical support for policy formulation.

From Model 1 of Table 8, This table applies the three-step method to verify the mediating effect of DIF on high-quality enterprise development. First, Column 1 shows that the direct effect of DIF on high-quality development (TFPLP) is significant, with a regression coefficient of 0.00076 and a t-value of 2.59, indicating that DIF has a major beneficial impact on advancing high-quality development. Second, Column 2 demonstrates that DIF also has a strong impact on innovation, with a regression coefficient of 0.00326 and a t-value of 12.70, suggesting that DIF significantly promotes innovation within enterprises. Finally, Column 3 further reveals that innovation serves as a partial mediating role between DIF and high-quality development. After controlling for innovation, the indirect effect of DIF on high-quality development through innovation remains significant, with a regression coefficient of 0.00164 and a t-value of 19.42. This means that DIF not only directly promotes high-quality development but also indirectly enhances it by fostering innovation. Therefore, the mediating effect of innovation between DIF and high-quality development is confirmed, indicating that DIF contributes to enterprise development through both direct and innovation-driven pathways By fostering innovation, DIF gives companies greater flexibility and creativity, allowing them to not only survive in the current market but also excel in future competition. Therefore, the mediating effect of DIF in promoting innovation strengthens its core role in the strategic development of enterprises.

Table 8 The results of mediating effect in Innovation.

Internal control level (ICL)

Table 9 illustrates the mediating role of internal control in the impact of different variables on corporate performance. First, DIF (institutional ownership) has a direct effect on corporate performance (TFPLP) with a coefficient of 0.00076 in the first column, which is significant at the 1% level (***), indicating a positive effect of institutional ownership on corporate performance. The second column shows that FI significantly influences the internal control level (ICL) with a high coefficient of 0.44758, also significant at the 1% level, suggesting that institutional ownership greatly enhances internal control within a company. In the third column, the effect of DIF on corporate performance slightly increases to 0.00077, indicating that although internal control as a mediating variable reduces some of the direct effect, its positive impact remains significant. Moreover, the direct impact of SIZE (company size) on corporate performance is 0.55284, and after considering the mediating role of internal control, the coefficient changes from 17.82246 to 0.55006, highlighting the significant moderating role of internal control in large companies. Thus, the data suggests that strengthening internal control helps optimize resource allocation and management efficiency, thereby improving corporate performance. Thus, the mediating effect of DIF in enhancing internal control further solidifies its strategic role as a pillar of comprehensive enterprise development.

Table 9 The results of mediating effect in ICL.

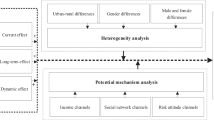
Further discussion: heterogeneity analysis

This section will examine heterogeneity from the perspectives of enterprise life cycle, region, enterprise ownership and whether it is a technology enterprise.

Heterogeneity test analysis for DIF sub-index

This section analyzes the impact of DIF depth, breadth, and digitalization on the HQDE. Through regression analysis of these dimensions, we explore their specific roles in enhancing enterprise development, incorporating control variables into the analysis. This analysis helps confirm the influence of various aspects of DIF while also revealing the roles of other important factors in HQDE.

From the results shown in Table 10, The first sub-index, BRE, shows a significant positive effect on TFPLP, with a coefficient of 0.00162, indicating that broader digital financial inclusion is positively associated with higher-quality firm development. The negative t-value (− 19.25) suggests a robust result, significant at the 1% level, highlighting the importance of financial inclusiveness breadth in fostering firm performance.

Table 10 Heterogeneity: Digital inclusive finance sub-index.

For the second sub-index, DEP, the coefficient of 0.00108 also shows a positive and significant impact on TFPLP, indicating that greater depth in digital financial inclusion enhances high-quality firm development. The corresponding t-value (− 19.3) confirms the statistical significance at the 5% level, reinforcing the finding that a deeper penetration of digital financial services correlates with improved firm outcomes.

The third sub-index, DIG, representing the degree of digitalization, shows an insignificant effect on TFPLP, with a coefficient close to zero (− 0.00005) and a t-value of  − 0.38. This result implies that the degree of digitalization alone may not significantly impact high-quality firm development. The lack of significance suggests that while the breadth and depth of digital financial inclusion are important, the mere presence of digitalization may not be sufficient to influence firm performance outcomes.

Heterogeneity test analysis for state-owned and private enterprises

State-controlled and non-state- controlled enterprises differ significantly in terms of resource access, policy support, and market orientation, making it essential to conduct a heterogeneity test between these two types of enterprises.

According to the analysis of columns 1–2 in Table 11, the impact of DIF on state- controlled and non-state- controlled enterprises shows significant differences. Non-state-owned enterprises are more sensitive to DIF, with an impact coefficient of 0.00131 and a t-value of 3.30, indicating that DIF significantly promotes their high-quality development. In contrast, state- controlled enterprises have an impact coefficient of − 0.00020 and a t-value of − 0.45, showing that the impact of DIF on them is not significant. Non-state-controlled enterprises face greater financing pressure in market competition and can better leverage DIF to acquire resources and drive growth, whereas state-owned enterprises, with stable financing channels and government support, experience a relatively small marginal effect from DIF.

Table 11 Heterogeneity: ownership, life circles of enterprises and technical level.

Heterogeneity test analysis for different life circles of enterprises

Enterprises face different challenges and development needs at different stages of their lifecycle (growth, maturity, decline), making it necessary to conduct a heterogeneity test across these stages.

The data of columns 3–5 in Table 11 reveals that DIF’s impact on high-quality development varies across different stages of the corporate lifecycle. Growing companies (coefficient 0.00147, t-value 2.88) and mature companies (coefficient 0.00135, t-value 10.89) are significantly promoted by DIF, likely because these companies are at critical stages of expansion or market consolidation and thus have a greater need for external funds and resources. In contrast, declining companies have an impact coefficient of 0.00164 and a t-value of 1.34, which is not statistically significant, indicating that DIF’s effectiveness in aiding company transformation or recovery is limited.

Heterogeneity test analysis for high and low technical enterprises

Conducting a heterogeneity test between high-tech and low-tech enterprises is necessary because DIF may have different impacts on companies with varying levels of technological sophistication. High-tech enterprises, which often rely more on innovation and R&D, may more easily obtain the funding and resources they need for innovation through digital finance, thereby promoting high-quality development. In contrast, low-tech enterprises may face more technological bottlenecks, and even with financial support, their ability to translate that into high-quality development might be limited. This test helps to clarify the differential impact of digital finance on enterprises at various technology levels.

According to the analysis of columns 6–7 in Table 11, DIF has a significant and positive impact on high-tech enterprises, with an impact coefficient of 0.00141 and a t-value of 13.95, suggesting that DIF effectively supports innovation and market expansion in these companies. For low-tech enterprises, however, the impact coefficient is 0.00068 and the t-value is 1.41, indicating that DIF does not significantly promote their high-quality development. This could be because high-tech enterprises have greater innovation needs and market potential, enabling them to significantly enhance their competitiveness with DIF support, whereas low-tech enterprises, with limited overall development potential, see relatively minimal benefits from DIF even with financial support.

Summary of traditional economic empirical analysis

In the above experiment, we analyzed the linear relationship between DIF and TFPLP using traditional econometric methods like the dual fixed-effects model, mediation effect model, and heterogeneity robustness checks. We found that DIF has a positive effect on TFPLP. This shows that changes in DIF can help improve TFPLP in traditional economic models. But traditional models have limits in explaining complex nonlinear relationships. To explore the possible nonlinear links between DIF and TFPLP, we will use deep learning time series models. Deep learning methods are better at finding nonlinear patterns in data, giving us clearer predictions for understanding the complex relationship between the two. Therefore, we will use deep learning models in the next experiments to look deeper into this relationship.

The application of deep learning models in prediction of TFPLP

This chapter first introduces four benchmark time series models, providing a foundation for the subsequent experimental analysis. Next, we present a detailed description of the experimental methods and the datasets used. The main body of the chapter is divided into two sections: one focuses on the introduction and result analysis of the KAN framework, while the other discusses the GNNs framework and provides a comparative analysis of the results. Through these sections, we aim to present a comprehensive evaluation of the performance of different models in time series forecasting.

The overview of four classical time series models

In this section, based on the double fixed-effects model used in performing the linear regression analysis of DIF and TFPLP, their deeper nonlinear relationship is explored with four classic time series models: LSTM, BiLSTM, GRU, and Transformer (as illustrated in Figs. 8, 9, 10 and 11), for prediction. The KAN, GCN and GAT methods are employed to improve the accuracy of the four models for the prediction and explanation of nonlinear relationships between DIF and TFPLP. It begins the chapter with a review of four classic models and presents the experiments. Basic concepts are then introduced regarding KAN, GCN and GAT on how they enhance the models. Four evaluation metrics are used for analysis, containing R², RMSE, MSE, MAE, to demonstrate the improvements in predictive performance for enhanced models and further probe into the complicated nonlinear relationship between DIF and TFPLP.

Fig. 8

The architecture of LSTM model.

Fig. 9

The architecture of BiLSTM model.

Fig. 10

The architecture of GRU model.

Fig. 11

The architecture of Transformer model.

Experimental methods and data

• Overall experimental design: This experiment improves respectively traditional time series prediction models using KAN, GNNs. KAN network replaces the MLP layer in LSTM, BiLSTM, GRU, and Transformer, enhancing the model’s prediction accuracy and generalization ability. For GNN models, GCN and GAT are used to extract high-dimensional features from the data, which are then passed to the traditional models to form a hybrid model, thus improving the model’s ability to handle complex time series data. Finally, the experiment uses five-fold cross-validation with an 8/2 split between the training and testing sets, ensuring the reliability and stability of model evaluation. This study further processes the experimental data (Table 1) by selecting corporate annual observation data from the complete period of 2011 to 2022, covering a wide range of industries and regions to ensure the representativeness and breadth of the research results.

• The process of data preparing: Data preprocessing includes the following steps: First, the time series data is cleaned and denoised, with missing values handled through interpolation or mean imputation, outliers removed using Z-scores, and the data standardized or normalized to enhance model training stability and performance. Then, the data is split into training and testing sets with an 8:2 ratio, ensuring that the majority of the data is used for training while a portion is reserved for model evaluation.

• Ablation and comparison study design: In this experiment, we conducted three ablation studies to evaluate the effectiveness of the KAN, GCN, and GAT improved models. First, in the ablation study of the KAN improved model, we removed the KAN network and restored the traditional MLP layer to assess the impact of replacing the MLP layer with the KAN network on model performance. In the ablation study of the GNN improved model, first, we directly fed the raw data into four traditional time series models to obtain preliminary results. Then, we incorporated a GCN network for feature extraction, and the extracted features were fed back into the time series models to obtain results after adding the GCN layer, thus examining the contribution of GCN feature extraction to model performance. Next, in the experiment comparing GAT and GCN, we removed the feature extraction part of the GCN network and replaced it with GAT for feature extraction, comparing the effects of adding GCN and GAT in time series prediction. In the final comparative experiment, we separately applied GCN and GAT to improve four traditional time series models (LSTM, BiLSTM, GRU, Transformer). First, GCN aggregates information from neighboring nodes through graph convolutions to capture local graph structure features in the time series data. We combined it with LSTM, BiLSTM, GRU, and Transformer to explore the effect of GCN on improving the prediction performance of these models.

• Similarly, GAT introduces an attention mechanism that dynamically adjusts the weights of neighboring nodes based on their importance in the sequence. Based on this mechanism, we combined GAT with the above four traditional time series models and evaluated its effect on improving these models.

• In conclusion, both GCN and GAT can effectively enhance the prediction performance of traditional time series models, but they exhibit different advantages. In this experiment, GAT showed more significant improvement, particularly when applied to economic data. Its adaptive weighting mechanism allows it to more accurately capture the relationships between key nodes, thus improving prediction accuracy..

• Statistical analysis methods: In this experiment, we used paired t-tests, effect size calculations, and MAE (Mean Absolute Error) from five-fold cross-validation as evaluation metrics to perform statistical analysis of the comparison models. The paired t-test was used to compare the prediction performance of different models on the same dataset, assessing whether the improved models were statistically significantly better than the original models. Additionally, a comparison was made between the GAT-improved model and the GCN-improved model to evaluate their relative advantages in feature extraction and model optimization. To quantify the performance differences between the models, we calculated the effect size (e.g., Cohen’s d), which reveals the magnitude of the difference beyond statistical significance. All models were evaluated using five-fold cross-validation to ensure the reliability and stability of the results. Through paired t-tests, effect size calculations, and MAE evaluations, we comprehensively compared the performance of different models in time series prediction tasks and validated the improvements made by KAN, GCN, and GAT.

Performance valuation metrics

To comprehensively assess the effectiveness of models on time series data, this section employs three commonly used metrics to compare and analyze the effectiveness of each model. These metrics are R² (coefficient of determination), RMSE (root mean square error), and MSE (mean square error). By integrating these three metrics, the evaluation provides a well-rounded assessment of each model’s performance in time series forecasting tasks, ensuring the objectivity and reliability of the results.

• R²: R² represents the proportion of variance in the dependent variable that is explained by the independent variables. Its value ranges from 0 to 1, with higher values indicating that the model captures a larger portion of the variance, reflecting stronger predictive power.

  $$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {y_{i} - \overline{y} } \right)^{2} } }}$$

  (8)

  where ${y}_{i}$ stands for the actual value, ${\widehat{y}}_{i}$ stands for the predicted value, $\overline{y}$ stands for the average value of the actual values, and n denotes the sample size.

• RMSE: The RMSE on the test set assesses the model’s ability to generalize to new data. A strong model should not only perform well on training data but, more importantly, maintain consistent performance on previously unseen data.

  $$RMSE_{test} = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {(Y_{test,i} - Y_{pred,test,i} )^{2} } }$$

  (9)

  where $N$ stands for the quantity of samples within the test set, and the formula uses ${Y}_{train, i}$ and ${Y}_{pred, train, i}$ to calculate the mean value of squared discrepancies between the actual and predicted values for each sample in the test set, evaluating the model’s capability of generalization.

• MSE: MSE is the average of the squared differences between predicted and actual values, reflecting the overall prediction error in the model. Like RMSE, MSE is sensitive to large errors, making it an effective metric for identifying significant prediction deviations. Smaller MSE values suggest better prediction accuracy.

  $$MSE = \frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} }$$

  (10)

  where ${y}_{i}$ represents the actual value, ${\widehat{y}}_{i}$ represents the predicted value, and n denotes the sample size.

• MAE: MAE calculates the average magnitude of errors in predictions, disregarding their direction. It is the mean of the absolute differences between predicted and actual values across the test sample, offering a simple interpretation of the average error size.

  $$MAE = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left| {y_{i} - \hat{y}_{i} } \right|}$$

  (11)

  where ${y}_{i}$ represents the actual value, ${\widehat{y}}_{i}$ represents the predicted value, and n denotes the sample size.

The Enhanced Deep Learning Framework Based on KAN

To better understand the application of KAN in enhancing the four previously mentioned models, this chapter first introduces the KAN model and compares it with the traditional MLP model in neural networks. Then, it presents the mechanisms and methods of the four modified models individually.

The KAN and MLP models

Kolmogorov–Arnold Neural Network (KAN)¹⁷ is built upon the Kolmogorov-Arnold representation theorem, which decomposes a multivariable continuous function into a superposition and composition of univariate functions, enabling the approximation of any continuous function. The theorem states that any continuous function f (x₁, x₂, …, x_n) can be represented as:

$$f(x) = \sum\limits_{q = 1}^{2n + 1} {\Phi_{q} } \left( {\sum\limits_{p = 1}^{n} {\phi_{q,p} } (x_{p} )} \right)$$

(12)

where ${\phi }_{q,p}$ are nonlinear transformation functions applied to the input ${x}_{p}$, and ${\Phi }_{q}$ are nonlinear functions for final aggregation. In KAN, this decomposition can replace the fully connected layers (MLP), with the implementation process as follows:

• (1) First layer (Transformation Layer): Each input variable ${x}_{p}$ undergoes an independent nonlinear transformation through the univariate functions ${\phi }_{q,p} (xp ).$

• (2) Second layer (Aggregation Layer): The outputs from the first layer are summed and passed through nonlinear functions ${\Phi }_{q}$ to construct the final function representation.

As presented in Fig. 12, learnable activation function of KAN applied to the edges: The activation function is dynamically learnable and acts on the weights of the edges, while each node performs a simple summation operation. Furthermore, the KAN structure, from Fig. 13, is closer to the implementation of mathematical theory, using learnable activation functions. The activation functions apply to the non-linear mapping part of the deep structure, while the linear transformation part is fixed.

Fig. 12

The shallow architecture of KAN.

Fig. 13

The deep architecture of KAN.

Multi-Layer Perceptron (MLP) is based on the Universal Approximation Theorem. As shown in Fig. 14 the activation function fixed at the node: Each node (neuron) in the network has a fixed activation function (such as ReLU, Sigmoid, etc.), while the edges (connection weights) are learnable parameters and we can see that from Fig. 15, MLP consists of alternating linear transformations (weight matrices) and fixed non-linear transformations (activation functions), with parameters at each layer being learnable. This ultimately enables complex feature extraction and mapping.

Fig. 14

The shallow architecture of MLP.

Fig. 15

The deep architecture of MLP.

This KAN structure avoids the redundant fully connected operations of traditional MLPs, improves representation efficiency, reduces parameter count, and still retains the ability to approximate any continuous function.

The experimental methods of the enhanced deep learning models based on KAN and MLP and the process of hyperparameter optimization

This section introduces the mechanisms of the four improved models. Figure 16 clearly illustrates the experimental process in which KAN replaces the fully connected layer in each of the four models, ultimately generating the final output.

Fig. 16

The experimental flowchart of improved KAN series models.

The process of hyperparameter optimization: During the model optimization phase, we performed systematic manual hyperparameter tuning for four baseline architectures (LSTM, BiLSTM, GRU, and Transformer) and their KAN/MLP-enhanced variants. Initial configurations were set based on domain expertise: recurrent models used a 128-dimensional hidden layer, 2-layer architecture, dropout rate of 0.2, and learning rate of 1e-3, while Transformer-based models employed 4 attention heads, a 256-dimensional feedforward layer, and an attention dropout rate of 0.1. Throughout the tuning process, we dynamically adjusted key parameters—learning rate (1e−4 to 5e−3, based on training stability), hidden layer dimensions (64–256), and dropout rate (0.1–0.5, guided by overfitting severity)—while closely monitoring training loss and validation performance.

Incorporating the Kolmogorov–Arnold Networks (KAN) theorem into the model, we replaced the MLP layer just before the output with a KAN-enhanced layer. According to the KAN theorem, any continuous function can be approximated by a finite-dimensional neural network with sufficient depth, making it ideal for modeling complex, nonlinear dependencies in time series data. By substituting the traditional MLP layer with the KAN network, we allowed the model to capture higher-order dependencies between the input features, effectively enhancing its ability to make predictions. During the optimization process, the KAN-enhanced layer impacted the weight updating mechanism by refining the learning of these complex relationships. The optimization procedure, therefore, involved dynamically adjusting the learning rate, hidden layer dimensions, and dropout rate while utilizing KAN’s capacity to map complex dependencies into a more efficient representation for the neural network. Each parameter update was evaluated on one-fold of a five-fold cross-validation scheme, with the best configuration (lowest validation MAE) further verified on an independent test set.

Comparison analysis of ablation study of KAN/MLP-models

Based on the results of the ablation experiment in Table 12, we can observe that the KAN structure generally brings performance improvements when replacing the traditional MLP architecture. In time series modeling, the traditional MLP-Transformer model demonstrated superior predictive performance, achieving the lowest error metrics (RMSE = 0.2758, MAE = 0.1864) and the highest R² score (0.8263). However, its computational efficiency was relatively low, requiring 25.36 s per run. These results indicate that, for economic data processing, the Transformer model based on the MLP architecture outperforms the other three comparative models. Notably, when the KAN structure replaced the traditional MLP, the KAN-Transformer model further improved prediction accuracy, with the five-fold cross-validation MAE mean significantly decreasing from 0.1864 to 0.1692. Similarly, other models exhibited comprehensive performance enhancements after the architectural upgrade. For example, KAN-LSTM reduced its RMSE from 0.3102 to 0.2931 and increased its R² from 0.7809 to 0.8024, KAN-BiLSTM improved its MAPE from 851.1093 to 1014.9150, KAN-GRU rose its R² from 0.7799 to 0.7984, although the KAN-Transformer achieves the best performance across all metrics, the improvement from replacing the MLP with the KAN model is relatively small, with the RMSE only decreasing from 0.2758 to 0.2657. Nevertheless, the prediction performance of the KAN-Transformer is the best among all the models. However, these improvements came at the cost of increased computational overhead—KAN-LSTM’s runtime rose from 2.96 to 7.72 s. Overall, the KAN architecture delivered notable performance gains across different model variants, particularly in prediction accuracy and stability. Nevertheless, the increased computation time remains an important factor to consider in practical applications, as presented in Fig. 17, it shows the results of the scatter plot of improved MLP and KAN in Transformer model. These results suggest that while the KAN structure enhances model performance, it may require more computational resources, which should be weighed carefully in practical.

Table 12 The outcomes of ablation study of KAN/MLP-models.

Fig. 17

The scatter plot of improved MLP and KAN series models of Transformer.

Analysis of effect size estimation and T-test analysis for KAN/MLP-models

According to the T-test results of Table 13 and Fig. 18, the KAN structure significantly outperforms the traditional MLP model in most cases. Specifically, BiLSTM-KAN, LSTM-KAN, and Transformer-KAN show significant performance improvements in MAE, with p-values less than 0.05, indicating a notable advantage in accuracy. However, the difference between GRU-KAN and GRU-MLP is not significant, with a p-value greater than 0.05, suggesting similar performance in MAE for both models. Therefore, the KAN structure demonstrates significant improvements in certain models, especially in the BiLSTM, LSTM, and Transformer variants.

Table 13 The outcomes of t-test for KAN/MLP-models.

Fig. 18

The results of radar plot in effect size estimation and T-test for KAN vs MLP-models.

In the effect size analysis of Table 13 and Fig. 19, the KAN models show significant performance improvements over the traditional MLP models across various variants. Specifically, BiLSTM-KAN and Transformer-KAN demonstrate strong effects with Cohen’s d values of 1.3769 and 0.8176, and improvement rates of 9.6053% and 9.1865%, respectively, indicating significant performance gains. LSTM-KAN also shows a moderate effect size with an improvement rate of 7.1904%. In contrast, GRU-KAN shows a smaller improvement with a Cohen’s d value of 0.3972 and an improvement rate of 2.7655%. Overall, the KAN structure leads to notable performance improvements in most models, especially in the BiLSTM and Transformer variants.

Fig. 19

The results of forest plot in effect size estimation and T-test for KAN/MLP-models.

The enhanced deep learning framework based on GNNs

In addition to using KAN to improve the four models mentioned, we also employ Graph Convolutional Networks (GCN) to enhance these models. This section will first introduce the basic concept of GCN, followed by a detailed explanation of the mechanisms of the four GCN-based modified models.

GCN/GAT model

GCN, are one of deep learning models designed for graph-structured data. In the context of this study, we leverage GCN to model multi-enterprise digital financial data (DIF), where nodes represent variables such as DIF, eight control variables (including Company Size, Leverage Ratio, Ownership Concentration, Business Growth, Company Age, Board Size, and Management Shareholding), and the target variable TFPLP. Edges in this graph represent the relationships between these variables, capturing both statistical correlations and domain-specific prior knowledge. The primary target of GCN⁴⁰ in this context is to capture the representation of each variable (node) by aggregating information from its related variables (neighboring nodes) in the graph. In GCN, the feature information of each node is updated by not only considering its own value (e.g., a variable’s time-series data at a specific time step) but also by propagating the features from neighboring nodes that share relationships with it. This propagation allows GCN to explicitly capture the dependencies between input variables (DIF and control variables) and their combined impact on the output variable TFPLP.

This information propagation is done through convolution operations, similar to those in traditional Convolutional Neural Networks (CNNs). However, instead of working with grid-structured data like images, GCN works on nodes and their connections in a graph. The main idea of GCN is to update the feature representation of each node by applying a convolution operation using the adjacency matrix, which shows the relationships between nodes. This adjacency matrix can include both statistical relationships⁴¹ (like correlation or mutual information) and prior knowledge about variable dependencies, making GCN well-suited for modeling the complex interactions in digital financial data. Assume the graph has N nodes, and each node has a feature vector of dimension D. The node feature matrix is $X \in R^\{N \times D\}$ and the adjacency matrix of the graph is $A \in R^\{N \times N\}$. The update formula for GCN is as follows:

$$H^{(l + 1)} = \sigma \left( {\hat{A}H^{(l)} W^{(l)} } \right)$$

(13)

where H^(l) represents the node feature matrix at the l-th layer, and H^(l) = X is the input feature matrix of the nodes. Â = D^−1/2, A D^−1/2 is the normalized adjacency matrix, where A is the original adjacency matrix⁴², and D is the degree matrix. W^(l) is the weight matrix at the l-th layer. σ is the activation function, typically ReLU or another nonlinear function.

With this formula, GCN updates the node features by aggregating information from neighboring nodes via the normalized adjacency matrix Â. The output of each layer serves as the input to the next layer, allowing the model to aggregate information from progressively larger neighborhoods of each node⁴³.

The Graph Attention Network (GAT) is a graph neural network based on the attention mechanism, which captures local feature relationships in graph structures by dynamically computing attention weights between nodes. Unlike traditional graph convolutional networks, GAT does not rely on a fixed adjacency matrix but instead employs learnable attention mechanisms to assign varying importance weights to each node’s neighbors, enabling more flexible processing of heterogeneous and dynamic graphs. Specifically, GAT first applies a linear transformation to node features, then computes attention coefficients between node pairs, normalizes them via softmax to obtain weights, and finally aggregates neighbor information through weighted summation to update node representations. The model supports multi-head attention mechanisms to enhance expressive power and possesses inductive learning capabilities, making it applicable to unseen graph structures or new nodes. GAT has demonstrated outstanding performance in tasks such as social network analysis, recommendation systems, and molecular property prediction, and has become a pivotal method in the field of graph neural networks due to its efficiency and adaptability.

The experimental methods of the enhanced deep learning models based on GCN and GAT and the process of hyperparameter optimization

In the GCN/GAT improved model series, we propose combining GCN and GAT with traditional time series models, using graph-structured data to extract features that further improves the model’s prediction capability and the process is provided in Fig. 20.

Fig. 20

The experimental flowchart of improved GCN series models.

When tuning the model parameters, the learning rate can be adjusted first to optimize the training process. For example, different learning rates (such as 0.001, 0.0005, 0.01) can be tested, and a learning rate scheduler can be used to dynamically adjust the learning rate. Next, the layers and the number of neurons in the GCN and GAT models can be tuned by adjusting the number of nodes per layer (such as 32, 64, 128) and the number of attention heads (by increasing or decreasing the number of heads). In the combination of LSTM, BiLSTM, GRU, and Transformer, the number of hidden units (such as 32, 64, 128) and the depth of the architecture can be adjusted. For LSTM and BiLSTM, different dropout rates and sequence lengths can be explored to prevent overfitting and improve generalization, while for GRU and Transformer, different layer numbers and learning rates can be tested, along with attention mechanisms to enhance the model’s expressive power. Finally, cross-validation can be used to evaluate the performance of various model architectures and parameter combinations, selecting the optimal configuration to improve prediction accuracy and stability.

Comparison analysis of ablation study of GCN/GAT-models

Based on the results of the ablation study in Table 14, when comparing the original models with the GCN-improved models, we observe that GCN improves prediction accuracy across all four models. In BiLSTM, GCN reduces RMSE from 0.3102 (Original) to 0.2429 (GCN) and MAE from 0.2163 to 0.1519. Similarly, for LSTM and GRU, GCN reduces RMSE (Original-LSTM: 0.3102, GCN-LSTM: 0.2609; Original-GRU: 0.312, GCN-GRU: 0.2614) and MAE (Original-LSTM: 0.2192, GCN-LSTM: 0.1565; Original-GRU: 0.217, GCN-GRU: 0.1544). In terms of R², GCN improves fit, with GCN-BiLSTM at 0.8468, GCN-LSTM at 0.8235, and GCN-GRU at 0.8228, all showing significant improvements. However, the cost is a higher computation time, with GCN models taking substantially longer (GCN-BiLSTM: 66.39 s, GCN-LSTM: 65.37 s, GCN-GRU: 60.37 s) compared to the original models (Original-BiLSTM: 6.11 s, Original-LSTM: 2.96 s, Original-GRU: 3.34 s). Comparing GCN with GAT, GAT significantly outperforms GCN in terms of prediction accuracy. In BiLSTM, GAT-BiLSTM achieves an RMSE of 0.0995, MAE of 0.0496, and R² of 0.9658, outperforming GCN-BiLSTM’s RMSE of 0.2429, MAE of 0.1519, and R² of 0.8468. Similarly, GAT-LSTM (RMSE: 0.2444, MAE: 0.1501, R²: 0.8775) and GAT-GRU (RMSE: 0.2511, MAE: 0.1481, R²: 0.8365) show superior performance compared to their GCN counterparts. However, GAT models require significantly more computation time, with GAT-BiLSTM taking 101.93 s, GAT-LSTM 97.61 s, and GAT-GRU 97.85 s, all much higher than the GCN models. Thus, while GAT offers improved accuracy, it comes with a trade-off in computational efficiency.

Table 14 The outcomes of Ablation study of GCN/GAT-models.

In Fig. 21, it shows the results of the scatter plot of improved GCN and GAT of BiLSTM model. However, while the GAT model provides higher prediction accuracy and stability, the computation time increases significantly, especially for GAT-Transformer, which has an average run-time of 121.07 s, notably higher than other models. Although the GAT model offers better prediction precision and stability, its longer computation time should also be considered in practical applications, particularly in scenarios where runtime efficiency is a higher priority.

Fig. 21

The comparison of true value and prediction of models in GCN and GAT of BiLSTM.

Analysis of effect size estimation and T-test analysis for GCN/GAT-models

Based on the results of the T-test of Table 15 and Fig. 22, most GCN and GAT model variants show significant performance differences when compared with the original. Specifically, the GCN and GAT models show significant performance improvements compared to the original models. In the BiLSTM architecture, the T-value between GCN-BiLSTM and Original-BiLSTM is 5.3124 with a P-value of 0.0060, and the mean difference is 0.0645, resulting in a 29.80% performance improvement. The T-value between GAT-BiLSTM and Original-BiLSTM is 4.9100 with a P-value of 0.0080, and the mean difference is 0.1668, leading to a 77.08% performance improvement. In the LSTM and GRU models, the T-value between GCN-LSTM and Original-LSTM is 10.5228 with a P-value of 0.0005, and the mean difference is 0.0627, yielding a 28.59% improvement. The T-value between GAT-LSTM and Original-LSTM is 10.6047 with a P-value of 0.0004, and the mean difference is 0.0690, resulting in a 31.49% improvement. For GCN-GRU and Original-GRU, the T-value is 7.2396 with a P-value of 0.0019, and the mean difference is 0.0625, leading to a 28.81% improvement. The T-value for GAT-GRU and Original-GRU is 10.6855 with a P-value of 0.0004, and the mean difference is 0.0689, resulting in a 31.74% improvement. In the Transformer architecture, the T-value between GCN-Transformer and Original-Transformer is 18.7487 with a P-value of 0.0000, resulting in a 77.89% performance improvement, while GAT-Transformer shows a T-value of 14.0360 with a P-value of 0.0001, achieving an 80.94% improvement. In the comparison between GAT and GCN models, GAT shows significant improvements over GCN in BiLSTM and LSTM architectures. The T-value between GAT-BiLSTM and GCN-BiLSTM is 4.5961 with a P-value of 0.0101, resulting in a 67.35% improvement, and for GAT-LSTM and GCN-LSTM, the T-value is 7.1438 with a P-value of 0.0020, leading to a 4.06% improvement. This indicates that, in these architectures, the models with GAT outperforms the models with GCN in time series models.

Table 15 The outcomes of t-test for GCN/GAT-models.

Fig. 22

The results of forest plot in effect size estimation and T-test for KAN/MLP-models.

However, in the GRU and Transformer architectures, the differences between GAT and GCN are not significant. The T-value between GAT-GRU and GCN-GRU is 1.5485 with a P-value of 0.1964, and between GAT-Transformer and GCN-Transformer, the T-value is 1.6396 with a P-value of 0.1764, showing that the performance improvements in these architectures are similar for both GAT and GCN. Overall, most time series models with GAT and models with GCN show significant performance improvements when compared with the original models, particularly in the BiLSTM, LSTM, and GRU architectures, while the differences between the models with GAT and models with GCN are not significant, likely due to inherent performance of these architectures, sample variability, and the extent of improvements between the models.

Conclusion

This study explores the impact of DIF on TFPLP, revealing how DIF drives high-quality development in enterprises. Given the significant amount of work already done in the field of hybrid models, we appreciate the relevance of advancing this research and exploring new avenues. The research first applies the traditional Fixed Effects (DFE) model to analyze the linear relationship between DIF and TFPLP, and then incorporates KAN and GNN to improve four classical time-series models (LSTM, BiLSTM, GRU, Transformer) for nonlinear prediction, achieving superior results. We replaced the MLP layer in the four models with KAN for prediction and compared it with the original models. For the GNN models, we used GCN and GAT to extract features from the economic data, and then input these extracted features into the time series models for prediction. Subsequently, we compared these improved models with the original time series models and further compared the performance of the GCN and GAT improved models, finally we test the metrics in pair T test and Cohen’s test. This series of analyses provides empirical support for understanding the role of DIF in promoting innovation, improving resource allocation efficiency, and enhancing managerial effectiveness. The contribution of this study lies in systematically revealing how DIF influences enterprise long-term sustainable development by affecting total factor productivity, through the combination of traditional economic models and advanced deep learning methods. However, there are some limitations in this study. First, while we focus on more stable, intrinsic economic patterns, real-world economic data are often influenced by various external factors, such as regional policies, geographical characteristics, and other heterogeneous factors. These exogenous variables often involve complex nonlinear interactions, which may obscure fundamental economic relationships, thus limiting the generalizability of the model. Second, although deep learning models, especially hybrid models, have strong predictive capabilities, they come with high computational complexity and require complex parameter tuning, which can be challenging when applied to large-scale datasets. Moreover, when facing heterogeneous data in different economic environments, the generalizability and adaptability of the model may be constrained.

To address these limitations, future research can explore several directions: first, integrating reinforcement learning to optimize the model’s adaptability, enabling it to better handle changes in dynamic economic environments, thereby improving prediction accuracy and stability. Second, future studies could delve into the specific impacts of DIF across different sectors, analyzing sectoral differences and tailoring the model’s application to each sector’s characteristics. Lastly, to further validate the model’s generalizability, future research could test the model on international datasets, assessing its applicability across various global contexts and exploring the effects of different economic environments on model performance. These improvements would help enhance the model’s accuracy, flexibility, and applicability, providing deeper theoretical support and practical guidance for the application of DIF.