Introduction

There is little doubt that the Covid-19 pandemic has challenged the way in which the health sector has deployed its resources across space to address sudden peaks in demand for services. As the emergency has given way to a ‘new normal’, a review on how to respond to health crises in a timely and effective manner has become a strategic priority for government and the private health sector alike.

We contribute to the literature by testing alternative models to predict the short-term demand for health services, with a focus on mental health, in Australia by combining daily data on internet searches on keywords related to emotions and monthly Medicare expenditures on medical visits and anti-depressants. Our aim is to determine whether:

  1. 1.

    it is possible to gain relevant timely information on imminent spikes in health demand from high frequency (daily) search data on engines such as Google; and whether

  2. 2.

    nowcasting, a technique that combines data of different frequencies, and machine learning, which uses algorithms capturing non-linear relationships in the data, can improve forecasts relative to traditional autoregressive models.

The answers to these questions will clarify if such data and techniques can be used as additional planning tools to improve the efficiency, and lower the cost, of deploying finite medical resources across territories experiencing uneven demand and dynamics for health services.

Empirically, we use Google daily searches on words that indicate depressive symptoms across Australia’s eight states and territories, which we map onto corresponding monthly aggregate administrative data on visits to general practitioners (GPs) and expenditures on antidepressant for the period 2020–2022. In this study, we use visits to general practitioners (GPs) as a proxy for mental health service demand. While GPs provide care for a wide range of health issues, they also serve as the first point of contact for individuals experiencing mental health concerns, particularly in primary care settings. As such, GP visitation patterns may reflect underlying changes in community mental health needs, especially for conditions like depression that often first present in general practice1. We then apply the benchmark forecast for visits and expenditures in the following 30–60 days using individual time series for each state and panel vector-autoregressive techniques (AR1 and AR2). Finally, we compare such forecasts with the ones obtained from nowcasting techniques and machine learning algorithms.

The results show that nowcasting enhances the precision of the forecast by reducing the mean square error of the model estimated—a standard measure of efficiency. In addition, we find that machine learning models produce forecasts with lower root mean square error than traditional econometric models.

From a policy perspective, the results suggest that daily search data contain valuable information to predict short-term health demand, which can be exploited to improve the planning of health inventories and resources catering for a locale.

Literature

Nowcasting, a term originally coined in meteorology, and machine learning algorithms have become increasingly influential among central banks to predict key macro-economic indicators such as Gross Domestic Product in narrower intervals than what traditionally occurring (e.g.2,3,4). A growing body of research also explores the integration of mixed-frequency data with machine learning techniques to improve nowcasting accuracy (e.g. 5,6). Applications focusing on individual economic behaviours are rare and limited to forecast the demand of particular items such as vehicles of a given brand (e.g.7,8).

With respect to the health sector, nowcasting and machine learning have been used to predict the epidemic trends of Covid-19 (e.g.9,10). Additionally, high-frequency indicators such as Google Trends have been used for nowcasting unemployment insurance claims during the pandemic (e.g.11,12). However, we are not aware of any use of either technique to forecast the demand for health services for specific conditions, such as depression, across locations where demand may actually differ, such as across towns in a given jurisdiction or branches of a health providers.

Notwithstanding that the potential for forecasting such future demand is exciting, the main drawback to the unquestioned adoption of these new techniques is a general lack of full knowledge about the algorithms that are applied to produce forecasts. In essence, they are akin to a ‘black box’. This is especially true in the case of machine learning models like deep learning, which provide little, if any, information about how the relationships between variables are built and hence can be interpreted13,14. This problem is less common among nowcasting models, which tend be built within well-known statistical and economic and behavioural theories15. In our study, the use of a nowcasting framework allows for a more transparent examination of the temporal relationship between search interest in depressive symptoms and mental health service demand. By specifying lag structures and incorporating fixed effects at the state level, we are able to observe and interpret how changes in online search behaviour precede shifts in general practitioner visits and antidepressant expenditures, offering both timely insights and theoretical interpretability—for instance, it can help health administrators to better anticipate hospitals’ and medical centres’ expected use of medical stocks in the near future, and policy-makers to better manage health resources based on future demand across heterogeneous locales.

The limited understanding of the architecture and in-built algorithms underpinning these new approaches to data analysis, risks adopting models that overfit historical information while having lower performance on unseen data16. They also require more training resources than traditional methods, as tuning machine learning models are generally computationally intensive17.

The objective of this paper is to advance the understanding of nowcasting models by comparing their predictions of health demand relative to established parametric approaches. In doing so, we combine information from health expenditures with more frequent information obtained from daily Google searches of words that identify a well-known psychological status, such as negative emotions.

Methodology

Approaches to forecast

The simplest way to forecast is to use past values of these variables and estimate a univariate autoregressive model. In the case of the demand for health services, the forecast for each variable and for each state yields the one-step ahead forecast (see Appendix A – Eq. 1 and 2).

It is possible to augment this model by taking advantage of cross-sectional information from other states in forecasting state s’s health demand (see Appendix A – Eq. 3 and 4). This approach is consolidated practice in forecasting.

In recent times, machine learning models have also been used to generate forecasts by building up, in an iterative process, new models from the residuals of the existing models to capture complex non-linear relationships. This feature sets apart machine learning model from traditional time-series models18. The intuition behind Gradient Boosting Machines (GBM) is rooted in the idea of building on mistakes. At each stage, a weak learner is introduced to correct the errors and shortcomings of the existing ensemble. As a result, this iteration combines the predictions of multiple weak learners (individual trees) to generate a final prediction.

The combination of weak models to form a stronger ensemble is akin to the concept of Bayesian Model Averaging (BMA) in that both methods involve aggregating the predictions of multiple models. However, two alternatives are possible, and we use them both. The first one focuses on decision trees and employs a boosting approach, where each tree is trained to address the shortcomings of its predecessors, enhancing the model’s overall performance through sequential refinement.

The second approach involves combining predictions from different models using a weighted average, considering them as parallel rather than sequentially improved models. Parameters of the model are iteratively estimated by minimizing the prediction error (difference between predicted and actual values)—a procedure called gradient descent optimization technique19. In each iteration, a new decision tree is added to the ensemble, focusing on capturing the remaining errors from the combined predictions of the existing models. The model assigns weights to each tree based on its performance, allowing more accurate trees to contribute more to the final prediction. While gradient boosting is often associated with large datasets, it uses regularization techniques that are efficient in fitting non-linear relationships for small datasets20.

Using a machine learning model

We use a nonlinear machine learning model that is referred to as XGBoost (eXtreme Gradient Boostin), an implementation of gradient boosting machines (GBMs), a category of ensemble learning methods, which is efficient in handling large-scale dataset or a large number of variables. The efficiency stems from several key features. First, XGBoost employs a scalable and parallelized implementation of gradient boosting, allowing it to efficiently process and analyze massive amounts of data. It introduces regularization techniques such as L1 and L2 regularization, which mitigate overfitting and enhance generalization, crucial factors when dealing with extensive datasets. Second, XGBoost utilizes a tree-based ensemble approach, where decision trees are added sequentially to correct errors made by previous models. This not only enables the model to capture complex non-linear relationships but also facilitates the handling of a large number of variables, as it can naturally select and prioritize features. The combination of these features, along with its ability to handle missing data and provide insights into variable importance, makes XGBoost a versatile and efficient choice for a variety of tasks, especially in scenarios involving large and complex datasets.

XGBoost uses the gradient descent optimization technique to minimize an objective function

$$\hat{y}_{t} = \Sigma_{k = 1}^{K} f_{k} \left( {x_{t} } \right),f_{k} \in F$$

with respect to the model’s parameters. This approach is formalized in Eqs. 5 and 6 in Appendix A.

Gradient descent and well-established gradient methods like BFGS (Broyden-Fletcher-Goldfarb-Shanno) share the common goal of optimizing a function by iteratively adjusting parameters. However, they differ in their approaches. Gradient descent is a first-order optimization algorithm that relies solely on the first-order derivative (gradient) of the objective function. It updates parameters in the direction opposite to the gradient, aiming to minimize the function step by step. In contrast, BFGS belongs to the family of quasi-Newton methods and is a second-order optimization algorithm. It not only considers the gradient but also incorporates information about the curvature of the function through the Hessian matrix. BFGS tends to converge faster than simple gradient descent methods since it utilizes additional information about the local curvature, making it more suitable for optimizing complex and non-linear objective.

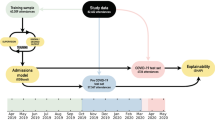
Figure 1 illustrates the full forecasting pipeline described above. The process begins with the loading of both daily and monthly data, followed by iteration across eight states and territories. Daily sentiment data are aggregated to the monthly level and merged with target variables. We then construct various feature sets with Machine learning approach (ML) and apply three forecasting models which are Autoregression (AR), Vector Autoregression (VAR), and XGBoost within a rolling-window cross-validation framework (18-month training, 1-month testing, over 12 windows). Forecast performance is evaluated using Root Mean Square Errors (RMSE) and results are aggregated across states and time windows. The details are presented in section “Results”.

Fig. 1
figure 1

Forecasting pipeline overview. Note: This flowchart outlines the end-to-end forecasting procedure used in the study. The process begins with loading daily sentiment and monthly health data, followed by state-level aggregation and feature construction.

Full size image

Combining data collected at different frequencies (nowcasting)

Nowcasting model is the model to predict current events, nearby events in the past or future21,22. We applied Mixed Data Sampling (MIDAS) regression as one of common method in nowcasting model23 to utilize higher frequency data in direct predicting lower frequency data:

$$y_{t}^{s} = \beta _{0} + \beta _{1} B(L^{{1{ / }d}} ;\theta )x_{{t - h}}^{d} + \varepsilon _{t}$$

where \(B(L^{{1{ / }d}}\);\(\theta )\) is a lag polynomial that fits h-lags of the daily explanatory variable \(x_{t - h}^{d}\) as a function of a small parameter space \(\theta\) in predicting the monthly health demand \(y_{t}^{s}.\)

Therefore, we use a parametric MIDAS regression with an exponential Almon lag structure to relate daily sentiment indicators to monthly health outcomes. This structure imposes a smooth weighting across high-frequency lags using a low-dimensional parameter space. An alternative specification is the unrestricted MIDAS approach, which relaxes functional constraints on lag coefficients, enabling greater flexibility and compatibility with machine learning models. While U-MIDAS can enhance forecasting accuracy in large datasets, our approach favors parsimony and interpretability, which is important given our explanatory focus and relatively short time span of data.

Data

Expenditure on mental health service for each of the eight Australian states are sourced from administrative data collected by the Department of Health. It consists of information on the number of doctor visits in the previous month across a given state (hitherto ‘services’) and the corresponding dollar value of the government rebates on expenditure for anti-depressant pharmaceuticals resulting from those visits (‘benefits’). We focus on depression as a condition that is reflective of anxiety and uncertainty, as experienced during the recent pandemic.

Figures 2 and 3 display the services and benefits on depression healthcare values across eight Australian states from July 2019 to December 2021. The data reveal a distinct trend: three states (New South Wales (NSW), Victoria (VIC), and Queensland (QLD)), which include the most populous parts of the country, consistently have values approximately four times higher than those observed in other states. Perhaps unsurprisingly, the three least populated states (Tasmania (TAS), the Australian Capital Territory (ACT), and the Northern Territory (NT)), report the lowest values during the period.

Fig. 2
figure 2

Monthly service benefit value in eight States in Australia from July 2019 – December 2021.

Full size image
Fig. 3
figure 3

Monthly service benefit value in 8 States in Australia from July 2019 – December 2021.

Full size image

We use Google daily search data for specific words that are classified as representing ‘negative’ and ‘sad’ emotions based on established sentiment analysis and psychological research (e.g.24). Linguistic Inquiry and Word Count (LIWC) is widely used in existing literature because it has achieved the level of reliability and validity as a measurement of sentimental categories such as emotions, cognition and pronouns25.

We then construct an indicator using Google trend scores (between 0 and 100) for each word in the list. Google trend data represents the total number of searches as a measurement of popularity for a specific keyword. It is normalized in a range [0,100] over times and locations. In which, 0 means no search or very few searches while 100 is the highest number of searches.

Finally, we calculate the sum as the final scores for negative, positive and sad indicators. Negative and sad indexes are calculated using a sum rather than an average to capture the total activity or presence of these emotions over time. This approach ensures that every instance, whether big or small, is fully accounted for, reflecting the complete scope of how often and how intensely these emotions are expressed. By summing up all occurrences, we can see the true scale of negativity or sadness during a given period, which helps in understanding trends and patterns. Although daily Google Trends data can exhibit weekly seasonal patterns, we mitigate this effect by summing normalized search scores across a list of validated emotion-related keywords. This aggregation across multiple terms inherently smooths out day-of-week effects, capturing the broader emotional tone of the population while preserving the temporal granularity necessary for real-time nowcasting. This method avoids the issue of averaging, where high peaks of emotion could be diminished by periods with lower activity, thereby providing a more accurate and comprehensive measure of emotional expression.

Table B1 in Appendix B shows the descriptive statistics of the underlying information. Our daily dataset ranges from 1/7/2019 to 31/12/2019, and contains 915 daily data points (this is available from the authors upon request). As this period covers COVID-19 lockdowns in some parts of the country, we construct COVID-19 lockdown dummies. These are sourced from Government announcements and depicted in Figure B1 in Appendix B.

Results

Benchmark results

We use the monthly number of services (doctor visits) and benefits (expenditure) as the dependent variable of two distinct sets of estimations. In the benchmark comparison, we apply two approaches: a state-by-state time series analysis, in which an AR model is used, which only includes the autoregressive components to produce the forecast. A panel approach, where the eight states are followed at once, which uses a VAR model. We augment these specifications with a set of ML models that use google search sentiment and a binary indicator of lockdown in addition to the autoregressive component. In particular, we use extensions of the ML model (ML) with daily Google search data (ML-T), a panel of monthly health demand from other states (ML-S), and both daily Google search data and the panel of monthly health demand from other states (ML-TS).

We conduct forecasts using a rolling window with 18 months as the initial sample. Hence, we estimate the respective models and produce a month ahead forecast for each remaining 12 months. We then calculate the RMSE, aggregated over 12 months, and present the results in Table 1.

Table 1 Forecasting results (18-month window, aggregate by mean daily variables).
Full size table

Comparing the RMSE of VAR and ML models, the machine learning model emerges as better in forecasting the number of doctor visits across all states. Since we use identical independent variables for the VAR and ML models, the machine learning model seems to better use the information from independent variables in predicting health demand.

Adding information by using the machine learning model

The superior performance of the ML model over AR and VAR models lies on the fact that the ML model is ‘flexible’ in exploring nonlinear relationships. In other words, it can combine different variables non-linearly regardless of whether such combination reflects true economic and behavioural relations.

Does this apparent advantage imply that more data is preferable to more parsimonious settings and specifications? We explore two dimensions by adding: (i) more data along the time dimension sourced from daily Google search data (ML-T); (ii) more cross-sectional dimension by incorporating contiguous states (ML-S); and (iii) both dimensions (ML-TS).

Comparing the ML and ML-T models, the results suggest that the machine learning model can utilize the daily Google search data in forming better forecasts in most cases. In comparison, the gain in the forecasting performance is more substantive when the panel of monthly health demand from contiguous states are included (ML-S). Adding both daily Google search data and the monthly panel of health demand does not necessarily produce better forecasts, as the ML-TS model has the least RMSE for only three states: the most populous (NSW), the least populous (NT), and one state in between (SA).

Overall, the forecasting results suggest that machine learning models can be very useful in forecasting health demand, and that adding additional information generally improves it, but with diminishing improvements in precision.

Nowcasting results

Table 2 shows the nowcasting performance for three models:

  • M-AR: Autoregressive model Midas model

  • M-VAR: VAR model with optimal lags are selected based on the likelihood

  • M-ML: Machine learning (Xgboost) model

Table 2 Nowcasting results.
Full size table

As can be seen in Table 2, M-ML model produces the best nowcasting results in comparison with other models for both the number of doctor visits and the value of service. The superior performance of the machine learning model is consistent with the forecasting results, highlighting a strong case of adapting such models in nowcasting and forecasting health demand at regional and local levels.

Concluding remarks

In this paper we ‘horse race’ traditional time-series models in nowcasting and forecasting health demands in Australia during the COVID 19 pandemic to ascertain if using Google searches can enhance forecasting heterogeneous health demand across Australia states—a clear advantage when resources are finite and needs are different across locales. Our results suggest machine learning models out-perform traditional time-series models in both nowcasting and forecasting exercise. This superior performance is likely to arise from exploiting non-linearity in the data, which reflect the choice of algorithms implemented by the developers of machine learning programmes. The results invite to include non-traditional information sources such as Google searches to identify near-future trends in demand, and to apply various approaches (not just machine learnings) to identify improvements in the ability to make forecasts and their likely sources. The results are significant as improved forecast performance can enable operators such as hospitals to minimize wastage at critical times, such as during the pandemic. A key limitation of this study is the use of general practitioner visits as a proxy for mental health service utilization. Although GPs play a central role in diagnosing and managing depressive symptoms, they are not mental health specialists, and our outcome measure may also capture unrelated healthcare needs. Future research should aim to incorporate more specific indicators of mental health service use, such as visits to psychologists or psychiatrists, to more precisely capture the relationship between online search behaviour and mental health care demand.