Experimental study of tunnel effects on deformation mitigation in soft clay excavation using centrifuge and PIV

Abstract

In soft clay, deep excavations adjacent to tunnels cause complex soil–structure interactions. We conducted centrifuge tests with Particle Image Velocimetry (PIV) to simulate a staged deep-pit excavation near a model tunnel. A scaled retaining wall and tunnel lining were instrumented in a strongbox; the soil was consolidated and excavated in four stages under 60 g. PIV tracked soil and structure displacements while pore-pressure sensors recorded stresses. Tunnel position (beside vs. below the pit) and lining stiffness were varied to isolate their effects. The results reveal a shielding effect: the tunnel acts as a rigid strut that redistributes stresses and mitigates excavation-induced settlement. Surface settlement and retaining-wall deflection were lower than in a no-tunnel case. This shielding depends on tunnel stiffness and proximity: a stiffer tunnel provides greater soil restraint, whereas a flexible lining allows more movement. A tunnel close to the excavation (within roughly one to two pit depths) bears higher internal load but yields the largest reduction of far-field displacement. PIV shows soil arching: settlement above the tunnel is reduced, while heave develops at the pit base. Three characteristic uplift patterns emerge: a symmetric “hill”, a central “groove”, and an asymmetric “triangle” toward the tunnel. These patterns reflect how soil arching is altered by the adjacent tunnel and wall. We define a critical interaction depth where the tunnel’s role shifts from passive inclusion to an active structural element. When the tunnel lies in this vertical zone near the pit bottom, it markedly alters stress paths and uplift geometry. By highlighting the tunnel’s dual role—reducing wall deformation while sustaining higher internal stress—and by categorizing uplift shapes and the depth threshold of interaction, this study advances understanding of tunnel–excavation interaction. These contributions (quantified shielding metrics, uplift-pattern classification, and the critical-depth concept) provide a basis for design and deformation prediction in deep excavations near tunnels.

Introduction

Rapid urbanization and scarce land availability have compelled cities to expand downward, transitioning urban growth from two-dimensional surface development to a three-dimensional approach utilizing subsurface space^1,2,3,4. Deep foundation pit projects for underground infrastructure (such as transit lines and multi-level basements) are increasingly prevalent, effectively unlocking new urban space below ground. However, such excavations inevitably disturb the surrounding soil and nearby structures. The removal of soil (unloading) relieves stress in the ground, which can trigger ground movements beyond the excavation site and raise concerns about potential damage to adjacent buildings, utilities, and tunnels.

In soft clay deposits, excavation-induced stress relief and construction disturbances can markedly weaken the soil’s short-term strength and stiffness. This often leads to ground settlements and lateral displacements that pose settlement^5,6,7 , posing risks to nearby structures. Extensive studies have been undertaken to characterize and mitigate these movements, as excessive ground deformation can crack foundations or disrupt the serviceability of structures.

One key indicator of excavation performance is the lateral deformation of the retaining wall, which is closely monitored because it correlates with ground settlement and overall stability. Prior research shows that increasing the stiffness of the retaining structure or support system generally reduces the maximum wall deflection, although beyond a certain point additional stiffness yields diminishing returns⁸. Nevertheless, even with robust support, deep excavations in clay cannot entirely eliminate movement, necessitating careful control of wall deflection to safeguard adjacent facilities.

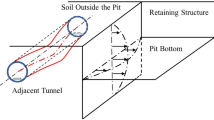
While numerous studies have examined soil deformation patterns around deep excavations and developed empirical guidelines for expected settlement and wall deflection^9,10,11, relatively few have focused on the combined effects on nearby tunnels and buildings. In dense urban environments, a deep excavation rarely exists in isolation—it often lies in proximity to existing tunnels (e.g., metro or utility tunnels) and surface structures, shallow foundations, and subway tunnels^12,13,14. The presence of these adjacent elements alters the stress and deformation fields, making the soil–structure interaction more complex¹⁵.

Among these interactions, the influence of an adjacent tunnel is particularly noteworthy due to its capacity to both resist and redirect excavation-induced soil movements. However, the role of tunnels in modifying deformation patterns has not been systematically quantified in most conventional studies. In this context, the ‘shielding effect’ refers to the phenomenon where the presence of an adjacent tunnel alters the stress redistribution and displacement field induced by the excavation¹⁶. Quantitatively, the shielding effect can be characterized by a relative reduction in horizontal wall displacement or ground settlement in the zone adjacent to the tunnel, typically expressed as a percentage decrease compared to an equivalent scenario without a tunnel. For example, a shielding effect ratio ηₛ = ((Δ_ref − Δ_shielded)/Δ_ref) × 100% can be used, where Δ_ref is the reference deformation without a tunnel, and Δ_shielded is the measured deformation with a tunnel present. Physically, this effect manifests as a redistribution of earth pressure around the tunnel boundary, which modifies the local stiffness and deformation pattern of the surrounding soil mass¹⁷. The magnitude and extent of the shielding effect are sensitive to several factors, including the tunnel’s horizontal offset distance from the excavation, its burial depth, the relative stiffness between the tunnel lining and the surrounding soil, and the stage of excavation. In some cases, the tunnel acts as a barrier that inhibits ground movement toward the excavation, whereas in others it may cause stress concentration or redirection that amplifies local deformation¹⁸.

For instance, an excavation near a tunnel can impose asymmetric loads on the tunnel lining, with one side of the tunnel experiencing stress relief and potential heave while the opposite side remains confined by the intact soil^19,20. This differential loading may lead to ovaling distortion or other damage in the tunnel if not properly accounted for^21,22,23. Field reports underscore the severity of such interactions: in cities like Shenzhen, numerous deep pits have been built adjacent to operational subway tunnels, sometimes even on both sides of a tunnel (twin-pit scenarios)^24,25. These twin-pit excavations have been found to significantly amplify tunnel lining pressures and distortions compared to single-side excavations, reinforcing the need to study multi-structure and multi-sided excavation effects in depth.

Despite these challenges, current design codes and guidelines offer limited provisions for assessing and mitigating excavation-induced tunnel deformation, especially under conditions involving multiple adjacent structures and nonuniform soil properties²⁶. Conventional analysis methods often assume simplified boundary conditions and fail to capture the highly nonlinear and spatially variable stress redistribution that occurs in soft clay when excavations interact with nearby tunnels²⁷. The limitations of existing empirical approaches become particularly evident in complex urban contexts, where asymmetry in structural layouts and excavation stages introduce significant uncertainties into predicted deformation patterns and internal tunnel responses²⁸.

In response to the rising complexity of urban underground development, particularly in the presence of closely spaced structures and adjacent tunnels, there is a pressing need to understand the mechanisms governing soil–structure interaction in multi-structure environments²⁹. Existing models often fall short in accurately capturing the intricate interactions between excavations and neighboring tunnels, especially under conditions involving staged excavation, anisotropic soil properties, and spatial heterogeneity typical of soft clay environments^30,31. Studies that comprehensively account for excavation-induced effects on nearby tunnels, especially under staged excavation sequences in soft soils, remain scarce. Additionally, the influence of factors such as tunnel geometry, burial depth, stiffness contrast between tunnel lining and surrounding soil, and their coupled effects with excavation staging has not been systematically investigated³². This knowledge gap poses risks for the reliability of current design practices and highlights the necessity for controlled experimental studies that simulate realistic excavation–tunnel configurations under urban settings. Bridging this gap is essential for improving prediction accuracy, ensuring construction safety, and optimizing mitigation measures in increasingly congested underground spaces³³.

To address these challenges, researchers are adopting advanced analysis and monitoring techniques^7,34,35,36. On the project management side, emerging digital twin frameworks have been proposed to integrate real-time field monitoring data with numerical simulations for deep excavations^14,37,38. Such data-driven virtual models enable continuous tracking of excavation-induced changes and improved risk prognosis^39,40. Meanwhile, geotechnical centrifuge modeling provides a powerful experimental approach to investigate excavation–soil–structure interaction under realistic stress conditions^{41,42,43,44,45,46}. By testing small-scale models under elevated gravity, centrifuge experiments replicate in-situ stress distributions in soft clay and allow staged excavation sequences to be simulated with proper scaling of loads and deformations^{47,48,49,50,51}. When combined with high-resolution image analysis techniques like Particle Image Velocimetry (PIV), centrifuge tests can capture the evolution of soil and structural displacements throughout each excavation stage in great detail. Insights from these physical model tests not only advance understanding of soil–wall–tunnel interaction but also furnish valuable benchmarks for validating numerical and digital twin predictions^52,53,54.

Furthermore, consideration of long-term effects is essential. Soft clay sites may continue to deform after construction, due to consolidation and creep of the soil. Indeed, field observations have reported that a substantial portion of the total displacement can occur post-excavation; for example, about 36% of a deep excavation’s final wall deflection and 44% of surface settlement were observed to develop after the pit was fully excavated in one case study. Such findings underscore that both the immediate and time-dependent responses of the ground must be addressed to ensure the protection of adjacent infrastructure over the project’s lifespan^55,56,57,58.

In this study, a centrifuge model of a staged deep excavation in soft clay is employed to investigate the interactions between the excavated soil, the retaining wall, and an adjacent tunnel. The excavation sequence is simulated under enhanced gravity in a stepwise manner, while PIV is used to continuously monitor displacement fields around the wall and tunnel. This controlled experimental framework captures the complex soil–structure interaction behavior as the excavation progresses through multiple stages. The findings provide new insights into how staged excavation-induced unloading in soft clay affects nearby tunnel stability and ground movements. Ultimately, these results contribute to improved design guidelines and risk management strategies for deep excavations in urban settings.

Centrifuge experimental system and model

Experiment setup

During the pre-consolidation phase, a rectangular aluminium alloy test box (790 mm × 180 mm × 470 mm; Fig. 1) was used. An extension of matching cross-section was attached on top of the box to attain the target clay depth. Initially, the front of the box was closed with a 60 mm thick aluminium panel (Fig. 1a). After the model tunnel and retaining wall were installed, this front panel was replaced by a 140 mm thick aluminium frame fitted with a Perspex plate (Fig. 1c).

Fig. 1

Centrifuge test box: (a) test box during the pre-consolidation stage; (b) back of the test box; (c) front elevation with 2-D actuator assembled and side view of the 2-D actuator.

Strategically placed holes at the container’s back facilitated the insertion of Pore Pressure Transducers (PPTs). Additionally, these holes were pivotal for threading the wires associated with the model tunnel’s instruments during the centrifuge tests (Fig. 1b). The experimental ground was a blend of a sand drainage base and Speswhite Kaolin clay. All tests employed the laboratory-grade Speswhite Kaolin clay sourced from Lam⁴⁴. This specific clay’s permeability was ideal as it allowed model consolidation within an acceptable timeframe and enabled in-flight excavation in an almost undrained state.

Figure 2 depicts the model layout, with the tunnel located on the active (retained soil) side of the retaining wall. All components—the tunnel, retaining wall, excavation, and soil strata—were assembled under 1 g (normal gravity) conditions prior to testing. To approximate plane-strain conditions, the interfaces between the clay and the rigid boundaries (the tunnel lining, retaining wall, and Perspex sidewall) were made as stiff and low-friction as possible. A thin layer of silicone grease was applied at these interfaces to minimize friction. According to Clough and O’Rourke²⁴, the zone of influence in soft-to-medium clay extends approximately twice the excavation depth. For a 90 mm deep model excavation, this implies a minimum of 180 mm of clay behind the wall (to the container boundary) is required to capture the full influence zone. In this study, 315 mm of clay was provided behind the wall, exceeding this requirement and effectively eliminating boundary effects.

Fig. 2

Scale diagram of model setup for tunnel in active side.

Model retaining wall and tunnel

The model retaining wall, constructed from a 2 mm thick aluminium alloy plate, measured 375 mm in length. When buried in the clay, the wall had a depth of 295 mm. This wall was positioned into a groove in a PTFE sheet, ensuring that the wall’s toe sat at the clay layer’s base.

The model tunnel lining was fabricated from seamless aluminium tubing (Fig. 3a). Two tunnel liners were prepared, each with an outer diameter of 63.5 mm (approximately a 3.81 m prototype diameter at 60 g scale), but with different wall thicknesses (1.65 mm and 0.825 mm) to represent different lining stiffnesses. The assembled tunnel was 176 mm long, slightly shorter than the container’s 180 mm internal width, leaving a 2 mm gap at each end to accommodate silicone end seals. The water table in the model was set at the clay surface, meaning the clay was fully saturated up to ground level. To prevent seepage into the tunnel, both ends of the lining were capped with silicone rubber seals. These seals were cast using a three-piece PTFE mold, ensuring a uniform contact surface and allowing nondestructive removal after curing. Strain gauges attached to the central portion of the tunnel lining were coated with epoxy for waterproofing and protection. Additionally, the exterior of the central tunnel section was coated with a uniform layer of silicone rubber to eliminate any small gaps and ensure full contact between the clay and the tunnel surface. Four Perspex markers (black dots on a white backing for contrast) were also affixed to the inside of the tunnel lining (Fig. 3b). These internal targets enabled precise tracking of lining displacements using Particle Image Velocimetry (PIV), while minimizing the influence of any end-seal deformations on the measurement results.

Fig. 3

Model tunnel: (a) aluminium alloy tube; (b) cross section of the model tunnel lining.

Centrifuge test methodology and procedure

Centrifuge spin-up and excavation procedure

This section begins by detailing the experimental configuration and tunnel layout, followed by a description of the staged excavation procedure, aiming to provide a clear understanding of the test setup. Figure 4 provides an overview of the tunnel configurations used in the four centrifuge tests, including both tunnel position and stiffness. As labeled, “F5” and “F7” refer to flexible tunnel cases (adjacent and beneath pit center, respectively), while “S6” and “S8” denote stiff tunnel cases. Each configuration is aligned with a specific test. Table 1 summarizes the key parameters and setup details for each test, including tunnel placement, lining thickness, stiffness category, and excavation sequence type.

Fig. 4

Tunnel locations and stiffness for test. Note S for stiff tunnel and F for flexible tunnel.

Table 1 Test parameters and details.

The centrifuge model tests were performed using a 60 g geotechnical centrifuge facility to simulate deep excavation behavior in soft clay under realistic in-situ stress conditions. A rectangular strongbox was used to house the model ground and excavation system, which included an embedded tunnel lining made of aluminum or plastic and a staged excavation sequence simulating the removal of soil layers. Pore pressure transducers, linear displacement sensors, and high-resolution cameras were installed to monitor responses during each excavation stage.

To ensure similarity between the model and the full-scale prototype, standard centrifuge scaling laws were applied. In this approach, the length scale is defined as L* = 1/N and the gravity field is scaled by g* = N. Under these conditions, effective stress scales as σ* = 1, meaning that the increased gravity in the model (e.g., 60 g) compensates exactly for the geometric reduction in scale (1/60), allowing the model to replicate prototype stress states accurately. Strains (e.g., displacement gradients or deformation ratios) remain identical between model and prototype.

In terms of time scaling, two regimes are important: for undrained or inertial processes (e.g., dynamic loading), time scales as T* = L*, while for diffusion-controlled processes such as consolidation and pore pressure dissipation, time scales as T* = L², i.e., 1/N² in model time. This implies that drainage and consolidation in the model occur N² times faster than in the field, allowing settlement and pore-pressure response to be captured within feasible experimental durations. These relationships ensure that the observed displacement, stress redistribution, and soil–structure interactions in the centrifuge tests are representative of real-world field conditions.

Centrifugal acceleration was gradually increased from 1 to 60 g in stages (10 g, 30 g, 60 g) to ensure a stable consolidation process before excavation. The standard excavation was carried out in four sequential stages (Fig. 5 illustrates the excavated area after each stage). The total excavation depth was 90 mm, corresponding to about 5.4 m at prototype scale. The four stages were defined as follows:

• 1. Cantilever stage: The first-level props were fully retracted, and the excavator’s first-level blade was used to knock out the top section of the gate wall. Excavation then proceeded in 4 mm increments to reach a depth of 16 mm (Fig. 5a).

• 2. Single-propped excavation: Next, the first-level props were deployed to press against the retaining wall, after which the second-level props were retracted. The second-level gate wall elements were then removed. Excavation continued with support from the top props until a depth of 52 mm was reached (Fig. 5b).

• 3. Multi-propped excavation: At the start of this stage, the second-level props were deployed against the retaining wall. The third-level props were subsequently retracted, and the final section of the gate wall was removed. Excavation was continued to the full depth of 90 mm (Fig. 5c).

• 4. Final stage: The third-level props were finally deployed, and the model was then left in this state for an additional five hours to observe any long-term effects (Fig. 5d).

Fig. 5

Standard excavation sequence in the centrifuge tests. Note the red areas to be excavated in each stage.

This four-stage excavation procedure was used in Tests 5, 7, and 8. However, in Test 6 a malfunction occurred: at the beginning of Stage 2, the first-level props failed to deploy properly and never made contact with the retaining wall. As a result, the second stage of excavation in Test 6 was performed without any support against the wall (Fig. 6).

Fig. 6

Excavation sequences Type 2 for Test 6.

Re-consolidation stage

Prior to the in-flight excavation, the model was allowed to reconsolidate for approximately 7 h to ensure at least 90% consolidation of the clay layer. This prolonged consolidation was critical for achieving a uniform stress distribution in the clay, thereby ensuring consistent undrained soil conditions across all tests. Before spinning up the centrifuge, water was added to the model from the prop side until it reached just below the lowest gate wall level (stopping when water began to overflow from the standpipes). This water-filling step helped to balance the weight of the model package against the centrifuge’s counterweight prior to testing. Once the centrifuge was accelerated to 60 g, the increased self-weight of the clay induced a rise in pore water pressures. Approximately 7 h were required under these conditions to achieve 90% consolidation, as illustrated in Fig. 7. (In Fig. 7, the pore pressure dissipation curves correspond to the locations of the Pore Pressure Transducers, PPTs, installed in the model.)

Fig. 7

Dissipation of excess pore water pressure/square rot time at model scale.

In the centrifugal acceleration field, the water table in the model assumes a sloped profile (approximately linear with respect to distance from the rotation center). To ensure the water table remained above the entire clay surface, the standpipe water level was maintained about 10 mm higher than the clay surface. Figure 8 compares the pore pressure measurements taken just before excavation (Tests 5–8) with the corresponding theoretical hydrostatic profiles. The measured pore pressures show excellent agreement with the expected hydrostatic values on the active side of the excavation. Moreover, the consolidation outcomes from each test group were highly consistent, indicating that the post-consolidation stress state (pore pressures and soil conditions) was virtually identical across all experiments. Having established a uniform initial condition through consolidation, the study then proceeded to examine the system behavior during the foundation pit excavation stage.

Fig. 8

Pore Pressure reading comparison with Hydrostatic target.

In summary, the experimental methodology employed in this study successfully integrates physical modeling under elevated gravity with rigorous control of boundary conditions, stress scaling, and pore pressure equilibrium. The stepwise excavation process, conducted under 60 g conditions with high-fidelity instrumentation, allows the capture of both instantaneous and time-dependent responses of the soil and structure system. The inclusion of tunnel variants and support system anomalies (e.g., prop malfunction in Test 6) introduces valuable complexity that reflects real-world uncertainty. These centrifuge tests form the backbone of the subsequent analysis and discussion, offering a robust dataset to evaluate ground deformation patterns, soil–structure interaction phenomena, and the influence of shielding effects caused by adjacent tunnels. The following chaper presents detailed results on soil movement characteristics observed during the staged excavation process.

Settlement and displacement response in sectional excavation

For a deep foundation pit excavated in sections through soft clay, the surrounding soil exhibited characteristic settlement and displacement behaviors. The analysis of field measurements reveals how excavation depth, nearby tunnels, and unloading processes influence the deformation patterns. Key trends include the evolution of surface settlement with excavation progress, the mitigating “shielding” effect of existing tunnels, and the distinct active versus passive side responses due to staged construction.

Soil settlement behavior during re-consolidation stage in deep excavation with tunnels

The centrifuge results show that significant settlement occurs during the initial re-consolidation stage, even before any excavation begins. Figures 9 and 10 demonstrate that ground movement initiates as soon as consolidation loading is applied, indicating that the soft clay is adjusting its volume under the changed stress state in the pre-excavation phase. Under greenfield conditions (Fig. 9, no tunnel), the settlement profile is nearly symmetric between the active (excavation) side and the passive side of the wall. The soil on both sides settles by similar amounts and follows the same pattern, as evidenced by the equal contour lines on each side of Fig. 9. This symmetry arises because without an embedded structure, both sides of the model respond equally to the stress increase, and no side is “shielded” from settlement.

Fig. 9

Soil movement during consolidation stage in green field condition.

Fig. 10

Soil settlement during re-consolidation stage (a) Test 5; (b) Test6.

By contrast, when a tunnel is present on one side (Fig. 10), the settlement on the tunnel side is substantially reduced. This asymmetry reflects the shielding effect: the rigid tunnel structure carries part of the load, reducing stress and movement in the adjacent soil. The data show that whichever side hosts the tunnel (whether originally designated passive or active), its settlement is lower than on the opposite side. For example, in Test 6 the tunnel was placed on the passive side. The settlement recorded on that passive side closely matches the active-side settlement of the greenfield (no-tunnel) case. In other words, adding the tunnel on the passive side lowered its settlement to the level seen on the opposite side without a tunnel. This confirms that the tunnel’s presence redistributes stresses and mitigates ground movement on its side of the excavation.

Figure 11 focuses on the displacements measured in Test 8, detailing both the tunnel structure and the surrounding soil. The contours indicate that the tunnel is carried along with the adjacent clay mass—it moves as part of the settling soil. However, the measured vertical displacement of the tunnel is distinctly smaller than the settlement of soil farther away. In other words, the tunnel settles less than the more distant clay layers. This pattern suggests that the tunnel is effectively “floating” in the clay. The heavy clay around the tunnel sinks more, while the lighter tunnel structure descends by a smaller amount.

Fig. 11

Tunnel and soil settlement at mid-depth of tunnel in Test 8.

The reduced settlement of the tunnel is explained by a buoyancy effect. Because the tunnel (and any air or lightweight fill it contains) is much lighter than an equivalent volume of clay, it experiences an upward buoyant force as it displaces soil. By analogy to Archimedes’ principle, the tunnel displaces a volume of clay whose weight produces an upward force equal to the weight of that displaced soil. If the tunnel’s own weight is less than this displaced weight, the net effect is an upward lift that counteracts part of the clay’s downward pull. In simple terms, the soil “supports” the lighter tunnel, so the tunnel descends less than the surrounding clay. Mathematically, one can think of the buoyant force as ${F}_{b}={\gamma }_{clay}{V}_{tunnel}$ (where ${\gamma }_{clay}$​ is the clay’s unit weight and ${V}_{tunnel}$ is the volume displaced), and when this exceeds the tunnel’s weight, the tunnel effectively floats upward relative to the settling soil. This buoyancy effect thus explains why the tunnel’s settlement is smaller in Fig. 11.

In addition to buoyancy, frictional restraint from the retaining wall and surrounding soil provides a dampening effect that further limits movement. As the soil settles, shear stresses develop along the interfaces with the anchored excavation wall (and along the tunnel lining), resisting further motion. These frictional forces dissipate deformation energy and “smooth” the settlement pattern. For example, the anchored diaphragm wall effectively clamps the adjacent clay, spreading out the deformation and slowing its progression. Similarly, any soil–structure interaction around the tunnel lining resists the tunnel’s movement. This interface friction thus reduces the net settlement transfer to the tunnel and nearby soil.

Together, these observations confirm that the buried tunnel actively moderates ground settlement during re-consolidation. The reduction in settlement on the tunnel side (Fig. 10) and the lower absolute settlement of the tunnel itself (Fig. 11) are consistent with the combined buoyancy and dampening effects. In summary, the tunnel moves largely with the settling clay but is uplifted by buoyant forces and held by interfacial friction. These mechanisms cause the tunnel to settle less than the far-field soil, producing the deformation patterns observed in the centrifuge tests.

Soil settlement during sectional excavation

Building on the tunnel‐excavation interactions discussed previously, this section examines the vertical ground movements induced by the staged excavation of the pit. Figure 12 shows the soil settlement profiles for Stages 2 and 3 of excavation, while Fig. 13 compares the final settlement troughs for Tests 5–8 under different tunnel/support conditions. The key settlement metrics for each test are summarized in Table 2. In all cases the excavation produces a downward deflection of the clay behind the wall, but the magnitude and distribution of that subsidence vary according to excavation sequence and the presence of rigid structures (such as existing tunnels) in the soil. In Stage 2, the settlement trough is shallow and the maximum settlement is very small and located near the retaining wall. According to Table 2, the peak settlement in Stage 2 remains low, indicating that the early excavation stage produces negligible ground movement in the soft clay. The lateral extent of significant settlement in Stage 2 is limited, reflecting the relatively minor influence of this shallow excavation. In contrast, Stage 3 excavation induces substantially larger settlement. As shown in Fig. 12, the Stage 3 settlement trough is much deeper and wider than that of Stage 2. The maximum settlement during Stage 3 is significantly higher and occurs at a greater distance from the wall.

Fig. 12

Ground settlement during excavation: (a) Test 5; (b) Test 6; (c) Test 7; (d) Test 8.

Fig. 13

Horizontal distance and settlement value of maximum settlement point for each test. Note the settlement value shown in the figure is 10 times the actual value.

Table 2 Demonstrate ground settlement parameters for each test.

Figure 12 shows that the maximum vertical displacement occurs immediately adjacent to the excavation (nearest the retaining wall and tunnel opening) and then decays monotonically with horizontal distance. This behavior is consistent with the expected attenuation of stress release in soft clay: the steepest subsidence occurs where the soil is first unloaded, with smaller deformations spreading outward. Notably, the settlement trough in Fig. 12 exhibits a smooth, nearly symmetric shape that can be approximated by a Gaussian curve, reflecting the idealized spread of undrained settlement beneath the pit. In each case, the settlement magnitude decays with distance: it falls to about half its peak value at roughly three times the distance of the peak and becomes negligible by around five times that distance. This uniform decay is evident in Figs. 12 and 13, indicating a predictable settlement envelope. Understanding this decay pattern is useful for estimating the affected zone around the excavation.

Across these tests, the settlement trough extends roughly one to two tunnel diameters beyond the pit, in agreement with prior centrifuge studies which found that excavation‐induced ground movements typically decay exponentially with distance. In other words, the “zone of influence” of the excavation is limited: beyond a few meters the clay is hardly affected. Comparing the measured settlements to theoretical expectations shows both consistency and clear effects of three-dimensional behavior. The peak-at-face and decay-with-distance pattern matches classical solutions (e.g. Mindlin or Boussinesq models) for a line load or stepped excavation: the undrained response tends to follow an approximately Gaussian or exponential attenuation curve.

The data in Fig. 13 indeed lie close to such smooth curves, confirming that the overall trend is captured. However, small deviations from the ideal curve are evident, reflecting the real soil plasticity and spatial complexity. In particular, the presence of the tunnel introduces additional soil arching and 3D interaction that pure 2D theory does not capture. The induced deformation is not purely vertical: as noted in recent three-dimensional analyses, unloading above a tunnel causes the lining to heave and bend in both longitudinal and transverse directions. Such 3D effects can produce slight asymmetry or inflection in the settlement profile that would be absent in a simpler 2D model. In practice, this means the observed settlement trough may be skewed or have a “bulge” near the tunnel due to upward displacement (heave) of the tunnel invert—a phenomenon also seen in centrifuge tests of excavation above tunnels. Nevertheless, the overall scale of settlement remains close to theory: in all tests the maximum subsidence was only a few tenths of a percent of the pit depth, comparable to field cases of deep excavations in soft ground. This agreement suggests that, despite the complexities, the experimental results are in line with expectations for a properly designed excavation. In summary, the staged excavation tests produced relatively small soil settlements that attenuated rapidly away from the pit, but the details were significantly influenced by the tunnel conditions. Test 5 (the baseline) generated the largest settlement trough, while Tests 6–8 (with stiffer tunnel support or different excavation order) showed modestly reduced subsidence. These findings corroborate the concept that existing tunnels or rigid liners act to stiffen the ground and mitigate settlement. The decay of settlements with distance was also consistent with known attenuation “laws” (exponential/Gaussian) observed in both analytical models and centrifuge experiments. Overall, the results are coherent with theory: excavations in soft clay produce only minor surface settlements (Zone I behavior) but the exact displacement field depends on 3D factors.

Influence of an existing tunnel on soil settlement in deep foundation pit excavation

The soil settlement measured adjacent to the excavation (deep foundation pit) varied significantly depending on the presence and type of an existing tunnel. As summarized in Table 2, Tests 5–6 were carried out with a flexible (lightweight) tunnel lining, while Tests 7–8 used a rigid (stiffer) tunnel under otherwise comparable geometry. Figure 12 illustrates the settlement contours for each case, and Fig. 13 plots the settlement versus distance from the retaining wall. In all cases the settlement peaked on the side of the pit nearest the tunnel and decayed toward the far field. Notably, the rigid-tunnel tests (7 and 8) consistently showed lower maximum settlements and slightly different shapes than the flexible-tunnel tests (5 and 6). For example, the peak settlement occurred at roughly the same distance from the wall in each pair of tests, but its magnitude was noticeably smaller for the rigid lining. This indicates that the stiffer tunnel lining more effectively restrains soil movement compared to the lighter flexible lining. Regardless of tunnel type, the settlements attenuated rapidly with distance—the ground displacement diminished to near zero beyond roughly 1–1.5 m from the wall in all tests.

In detail, the flexible-tunnel cases (Tests 5 and 6) exhibited the largest surface settlements close to the retaining wall. The settlement trough was relatively broad, with the maximum values occurring near the wall and tapering off gradually. In Test 5 the peak settlement was somewhat higher than in the corresponding rigid case (Test 7) located at the same depth (see Table 2). Similarly, Test 6’s flexible tunnel (at a different depth or offset) produced a higher peak settlement than Test 8’s rigid tunnel under the same geometry. This suggests that the more compliant, lightweight tunnel allows more soil deformation near the pit. However, one must note the “buoyancy effect” in these flexible cases: because the flexible tunnel lining (or empty tunnel section) has a lower effective density than the surrounding soil, the tunnel tends to experience an upward buoyant force as the ground settles. In practice this buoyancy counteracts some of the vertical displacement—the lightweight tunnel can “float” slightly as adjacent soil moves, which moderates the settlement near the tunnel. In Tests 5–6 this effect manifests as the flexible tunnel moving upward relative to soil (a positive displacement within the tunnel), partially offsetting the larger soil settlements around it¹².

By contrast, the rigid-tunnel cases (Tests 7 and 8) produced the smallest ground movements overall. The peak settlements in these tests were lower in magnitude and sometimes occurred slightly closer to the wall. The settlement profile under the rigid lining was more sharply attenuated: the deformation dropped off more rapidly with distance than in the flexible cases. In practical terms, the stiff tunnel acts like a structural beam within the soil. Its high flexural rigidity imposes an “inhibition effect” on soil movement³⁵, meaning the tunnel resists bending and effectively holds up the soil mass. As a result, the ground surface settles less when the tunnel is rigid. In our tests, this produced a noticeably flatter settlement curve in Fig. 13 for the rigid-tunnel scenarios. For example, Test 7 had a peak settlement only about two-thirds of the value in Test 5 (same offset but different lining stiffness), and Test 8’s settlement curve lies consistently below that of Test 6. These reductions are consistent with literature findings that stiffer buried linings mitigate soil deformation around them.

Across all four tests, the general attenuation pattern was similar: maximum settlement near the wall, decreasing roughly exponentially with distance. The presence of the tunnel altered this pattern quantitatively but not qualitatively. In each case the settlement contours in Fig. 12 show that the influence zone of the excavation extended about 0.8–1.0 m from the pit wall, beyond which surface settlement became very small. The shape of the settlement trough was mildly asymmetric only in that the tunnel lining changed the slope of the decline, but no new peaks or inflection points appeared. In other words, both flexible and rigid tunnels reduced the overall settlement, but did not fundamentally change where the settlement was concentrated. It is also worth noting that the peak settlement distances from the wall did not shift dramatically between tests: the first peak remained within a few tens of centimeters of the wall in all cases. This suggests that while tunnel stiffness affects magnitude, the mechanics of excavation govern the location of maximum soil movement. These observed behaviors can be understood through simple physical mechanisms.

The buoyancy effect arises because the tunnel lining (especially when empty or made of light material) effectively replaces soil with a lighter medium. As a result, the net vertical stress in the soil is slightly reduced, and the tunnel tends to “float” upward relative to the settling ground. This explains why the flexible tunnel tests (5 and 6) showed larger surrounding settlements but the tunnel itself moved upward. By contrast, the inhibition effect of a rigid tunnel means that the tunnel lining carries some of the load and resists bending, acting like an internal buttress for the excavation. The stiff tunnel pushes up against the soil (or holds it up), which directly diminishes the downward displacement. This duality of effects has been noted in previous studies^12,24—a light tunnel lining can exhibit a buoyant response that reduces effective soil weight, whereas a stiff lining inhibits ground movement by structural support. In our experiments, the net result is that both effects help lower the measured settlement, but the inhibition (rigidity) mechanism proved stronger than buoyancy: the rigid-lining tests consistently had the lowest settlements.

In summary, the comparative analysis of Tests 5–8 shows that the presence of an existing tunnel reduces excavation-induced settlement, and that a rigid tunnel lining has a greater mitigating effect than a flexible lining. The peak settlements were significantly smaller in Tests 7–8 (rigid tunnel) than in Tests 5–6 (flexible tunnel), even though the distance of the peak from the wall remained almost the same. Figures 12 and 13 thus confirm that increased tunnel stiffness translates directly into an inhibition of soil settlement, whereas reduced tunnel density yields a buoyancy contribution that is less pronounced. These findings align with the trends reported in the literature and help clarify the roles of tunnel weight and rigidity in controlling ground deformation adjacent to deep excavations.

Section "Settlement and displacement response in sectional excavation" has demonstrated how staged deep excavation in soft clay leads to well-defined and measurable ground movements, which are significantly influenced by the presence, location, and rigidity of nearby tunnels. The observed deformation patterns, including settlement attenuation, asymmetric displacement profiles, and variations between flexible and rigid tunnel cases, highlight the complex interplay of buoyancy, arching, and structural interaction mechanisms. These findings validate the shielding effect introduced in earlier discussions and underscore the critical role of existing subsurface infrastructure in shaping excavation-induced responses. The results in this section provide a necessary foundation for the interpretation of soil–structure interaction phenomena and form the basis for the more detailed deformation mode classification and pattern analysis that follows in section "Soil heave characteristics at the excavation surface".

Soil heave characteristics at the excavation surface

Particle-image velocimetry (PIV) analysis of the centrifuge test data revealed three distinct surface uplift patterns under the deep pit: “hill”, “groove”, and “triangle”. These describe the shape of the soil heave across the pit floor (Figs. 14, 15, 16, 17). The hill pattern is a symmetric mound of uplift peaking at the center of the pit. The groove pattern shows a trough or lowered segment at mid-span with raised zones toward the edges. The triangle pattern is distinctly asymmetric, with the uplift skewed toward one side. These forms emerged consistently in Tests 5–8. PIV provides a fine-mesh, full-field measurement of soil displacement, capturing these shapes with high precision. For example, in a freely developing (unconstrained) heave, the maximum uplift occurs at the pit center—corresponding to the hill profile. Constraining elements (walls or tunnels) then modify this ideal pattern into the groove or triangle forms observed.

Fig. 14

Displacement of each group of foundation pit soil mass collected by PIV.

Fig. 15

The maximum uplift starting point of excavation surface at different stages in Test 5.

Fig. 16

The maximum uplift starting point of excavation surface at different stages in Test 6.

Fig. 17

The maximum uplift starting point of excavation surface at different stages in Test 7.

These deformation patterns can be conceptually linked to classical earth pressure and soil arching theories. The hill pattern aligns with a uniform basal rebound under plane strain conditions, similar to what Terzaghi’s theory of passive pressure predicts under symmetric stress release. The groove profile suggests arching action near the pit walls, where side resistance channels stress away from the center, akin to Marston’s load transfer mechanism in narrow trenches. The triangular pattern reflects eccentric stress redistribution, similar to the non-uniform arching observed when rigid inclusions (e.g., tunnels) disturb the symmetry of the passive pressure field.

Moreover, these profiles also correspond to well-established theoretical arching models. The groove pattern resembles an active earth-pressure condition where the central soil yields downward while side zones remain supported, forming a concave arch. This is consistent with classical interpretations of active failure surfaces in retaining systems. The hill pattern reflects a passive state, with the soil arching upward in a convex form between support points (e.g., tunnel and wall), analogous to the observations of Gao et al.⁵⁹. The triangle profile can be interpreted using Carlson’s triangular arching model⁶⁰ and Sweeney et al.’s wedge model⁶¹, in which a portion of the soil mass yields while another remains stationary, resulting in a triangular deformation zone with a distinct load-transfer direction.

Hill pattern: A single symmetric “dome” of uplift. The peak heave is at the pit center, and displacement decays toward the edges. This often occurs when the soil can rebound relatively uniformly, consistent with the case of unconstrained basal heave and symmetric arching.

Groove pattern: An “inverted” uplift with a central depression. Heave is concentrated near the pit walls, leaving a low or neutral zone at the center. This resembles the outcome of side-wall arching, where load transfer to lateral supports increases vertical heave near edges.

Triangle pattern: An asymmetric uplift lobe, typically peaking on the side of the pit nearest the tunnel. One edge of the pit heaves much more than the other, producing a tilted profile. This was seen when a stiff tunnel resisted movement on one side and transferred heave to the opposite side. Such asymmetric arching is well-documented in soil-structure interaction studies involving underground inclusions.

Influence of tunnel position (passive-side vs active-side)

The location of the tunnel relative to the retaining wall had a strong effect on the heave pattern. In Test 5 the tunnel lay on the passive side (outside the wall, farther from the excavation). Here the surface heave was relatively moderate and often exhibited a broad, symmetric hill profile. In contrast, Test 6 had the tunnel on the active side (within the excavation boundary, closer to the wall), and produced a larger, skewed uplift. Specifically, the PIV data for Test 6 showed a pronounced heave lobe shifted toward the tunnel side of the pit, giving a triangular shape. This difference arises because the active-side tunnel lies in the zone of soil unloading. In that case the excavation stress release directly influences the tunnel, intensifying soil rebound under the pit. By comparison, a passive-side tunnel lies farther out; its influence on the pit bottom is weaker. In fact, centrifuge studies have shown that tunnel-induced heave decays rapidly with distance: Huang et al.⁶². reported that excavation effects are essentially confined within about 2.5 × the pit width, and become negligible once the tunnel is more than ~ 1.5 × the excavation depth away. In our tests, the active-side tunnel (closer to the pit) triggered significantly more heave than the passive-side case, consistent with these findings.

Passive-side tunnel (Test 5): Uplift at the pit base was relatively uniform (often a hill profile). The tunnel’s distance from the pit meant that soil arching under the wall dominated the heave, yielding a broad, centered mound. Amplitudes were smaller, since much of the load could “arch” into the nearby rigid wall without disturbing the tunnel.

Active-side tunnel (Test 6): Uplift became asymmetric (often triangle shaped). The soil between the wall and tunnel formed a soil wedge that unloaded strongly toward the tunnel, causing a one-sided heave. The proximity effect was clear: closer position amplified uplift and shifted its peak toward the tunnel side. The heave magnitude and eccentricity were higher than in Test 5.

Influence of tunnel stiffness (flexible vs rigid)

Tunnel stiffness altered the surface heave patterns by changing how load is transferred between soil and structure. In the flexible-tunnel tests (Tests 5 and 6, with a compliant lining), the tunnel deformed somewhat with the soil, allowing load to be shared along its length. The resulting heave tended to be more distributed (favoring the hill or gently sloped patterns). In the rigid-tunnel test (Test 7), the stiff lining acted like a fixed strut, constraining soil movement on its side. The PIV data from Test 7 showed a sharper, more localized uplift lobe (often a clear triangle or groove shape) even if the tunnel was on the same side as a flexible case. The rigid tunnel resisted deformation, so the soil arching pattern sharpened. In essence, a flexible tunnel “absorbs” some of the heave by deforming, whereas a rigid tunnel blocks it and forces a different arch geometry.

Flexible tunnel (Tests 5–6): The lining flexes with the soil mass. Heave was broader and generally smoother. For example, Test 5 (flexible, passive side) showed nearly uniform uplift (hill). Test 6 (flexible, active side) still leaned toward a triangle shape, but with a gentler gradient compared to the rigid case. The flexibility allowed some settlement transfer along the tunnel, mitigating abrupt soil arching.

Rigid tunnel (Test 7): The lining remained nearly undeformed. Soil on the tunnel side could not move downward easily, so more upward rebound occurred at the pit surface, especially on the opposite side. The PIV data exhibited a pronounced asymmetric peak (triangle) or sometimes a dual-lobe (groove) if the wall and tunnel pinched the soil block. The rigid structure thus intensified the channeling of heave.

Mechanisms of observed heave

Physically, the observed behaviors can be attributed to stress relief and arching effects in the clay. Excavation removal of load causes an upward rebound (heave) of the soft clay, which naturally tries to expand toward areas of lower stress. This rebound is shaped by any rigid boundaries or stress transfers. When the tunnel is far away, the soil primarily arches between the side walls, pushing upward uniformly (hill). As a nearby tunnel comes into play, a second arch develops between the wall and tunnel. If the tunnel is compliant, this second arch is gentle; if the tunnel is stiff, the arch is sharp and concentrated. Thus, stiffer or closer tunnels tend to drive localized heave on one side, while flexible or distant tunnels yield a more even uplift. In summary, the centrifuge PIV results show that soil heave at the pit bottom is highly sensitive to tunnel proximity and stiffness. The characteristic hill–groove–triangle classification captures how the shape of uplift changes. A passive (distant) tunnel and/or a flexible lining promotes a symmetric hill-shaped rebound, whereas an active (nearby) tunnel and/or a rigid lining causes one-sided or grooved uplift. These findings highlight the need to consider tunnel stiffness and placement in excavation design—consistent with Zhang⁵¹ and other studies. The clear transitions between uplift patterns reflect the underlying mechanics of soil arching: as constraints change, so does the path of load transfer and soil flow under the pit.

Furthermore, it can be observed that the shielding effect becomes particularly pronounced when the vertical offset between the excavation base and the tunnel top is within the critical depth range. The experimental results indicate that when this depth difference is approximately 0.5 to 1.2 times the tunnel diameter (or roughly 0.6 to 1.0 times the excavation depth), the soil–structure interaction intensifies, producing observable alterations in deformation mode and uplift profiles. Within this window, the tunnel intersects a zone of active stress redistribution and arching, leading to distinctive “triangle” or “groove” patterns in surface heave. In contrast, when the tunnel is located well above or below this zone, the soil tends to follow a more uniform or symmetric rebound (hill profile), indicating minimal tunnel involvement.

This finding points to the existence of a critical interaction depth, analogous to the well-known “zone of influence” in foundation and retaining wall design. Conceptually, this is the vertical distance at which a tunnel transitions from passive background inclusion to an active structural participant in excavation-induced deformation. When within this zone, the tunnel exerts dual influence: it alters vertical stress pathways through its structural stiffness (inhibition effect), and modifies arching geometry between itself and the retaining wall. These combined mechanisms shape the direction and magnitude of soil uplift at the excavation base.

Furthermore, the tunnel’s role in this critical zone is conditional on its stiffness. A flexible tunnel deforms with the soil and reduces concentrated arching, while a rigid tunnel creates a stronger rebound shift and localized stress rerouting. Therefore, the critical interaction depth is not a fixed value, but rather a functional range influenced by tunnel geometry, material stiffness, burial depth, and excavation sequence.

From a geotechnical design perspective, identifying whether a tunnel lies within this range is crucial. If so, measures should be taken to predict asymmetric heave, adjust support systems, and possibly reinforce zones of amplified displacement. Our findings emphasize that proper assessment of tunnel proximity—not only laterally but vertically—is essential in excavation adjacent to underground infrastructure. Incorporating the concept of a critical interaction depth improves predictive accuracy for soil movement and enhances the resilience of both new and existing structures.

Analysis of retaining wall deformation during deep foundation pit excavation in soft clay

Figures 14, 18, and 19 illustrate the lateral displacement of the excavation retaining wall at various stages of pit deepening. In all cases, the wall deflects outward toward the excavation, exhibiting the typical curved (“bowed”) profile of a cantilevered wall in soft clay. The maximum displacement occurs near mid-height of the wall and grows steadily with increasing excavation depth. Importantly, the plots reveal that the wall deformation is strongly influenced by the presence and properties of an adjacent tunnel: the curves for the stiff (rigid) tunnel lining consistently lie above those for the flexible lining, indicating larger wall deflections when the tunnel is rigid. This trend is most pronounced when the tunnel is located deep below the pit (Fig. 14), and becomes less marked as the tunnel is placed higher (Figs. 18 and 19).

Fig. 18

Retaining wall deflection during excavation: (a) Test 5; (b) Test 6; (c) Test 7; (d) Test 8.

Fig. 19

Maximum deformation point depth and maximum deformation value of retaining wall each test.

Effect of tunnel rigidity

The comparison of rigid versus flexible tunnel conditions shows that a stiffer tunnel lining amplifies the wall deflection. In each figure, the curve for the rigid-case wall (solid line) is higher than that for the flexible-case wall (dashed line) at every excavation stage. For example, in Fig. 14 the rigid-lined tunnel case produces roughly 2.40 times the maximum wall displacement of the flexible-lined case. Similarly, Fig. 18 shows the rigid case reaching about 3.95 times the displacement of the flexible case at the same stage. These visual gaps between curves demonstrate that adding tunnel stiffness causes the soil-structure interaction to transfer more load to the wall, resulting in larger deflections. The rigid lining thus aggravates wall deformation relative to a more compliant tunnel, as quantified by the pronounced vertical separation of the curves in the figures.

Effect of tunnel position

The influence of tunnel rigidity also depends on the tunnel’s depth. When the tunnel is nearer the bottom of the excavation, the wall deflections are greatly amplified; the rigid case can be nearly four times the flexible case. In contrast, when the tunnel is located higher (Fig. 19), the difference shrinks—the rigid case reaches only about 1.30 times the displacement of the flexible case, as seen by the closely spaced curves. Figure 18 (intermediate tunnel depth) yields an intermediate effect (≈240% difference). Thus, as the tunnel moves upward away from the pit base, its stiff lining has diminishing influence on the wall. This positional trend is evident in the shapes of the three plots: the lowest tunnel produces the steepest (most separated) deflection curves, while the highest tunnel yields nearly overlapping curves. In every case, however, the rigid-tunnel condition leads to a consistently larger wall deflection than the flexible-tunnel condition, confirming that tunnel proximity and stiffness jointly govern the deformation magnitude.

Quantitative results

Table 3 compiles the key numerical results for each scenario, confirming the trends seen in the graphs. The table shows that the maximum wall lateral displacement and bending moment occur for the rigid-lined, deep-tunnel case. For instance, the rigid/deep case’s peak displacement is about 2.40 times that of the reference flexible case, and its peak bending moment is roughly 3.95 times larger. When the tunnel is raised to an intermediate level, the amplification drops to about 240%, and at a shallow level the amplification is only about 130%. These figures in Table 3 underline the visual trends: the wall deflection (and internal moment) increases markedly with tunnel stiffness, and the effect is strongest when the tunnel is at or below the excavation base. In every case, the rigid tunnel condition yields the highest values, while the flexible tunnel shows more moderate values. In summary, the quantitative comparisons in Table 3 confirm that both tunnel rigidity and tunnel location have a first-order impact on wall deformation patterns and magnitudes.

Table 3 Maximum deformation point and maximum deformation of retaining wall.

Analysis of deformation and displacement characteristics of existing tunnels during excavation of deep foundation pit

Characteristics of tunnel deformation and displacement

Deep excavation adjacent to existing tunnels produces significant tunnel deformation. As noted in the literature, foundation pit excavation “disrupts the equilibrium of the surrounding soil, causing deformation and displacement, particularly in tunnels parallel to the pit”⁶³. In our tests, the tunnel cross-section expanded markedly: Fig. 20 shows the tunnel diameter increased by about 12% at the side nearest the pit. This localized bulging indicates substantial circumferential strain in the lining. Likewise, Fig. 21 reveals a large lateral shift of the tunnel: the maximum horizontal displacement toward the excavation reached approximately 0.624 m. The vertical profile also shows pronounced settlement (on the order of ~ 0.5 m in our case) with a clear inflection near the pit. The primary directions of tensile and compressive forces on the tunnel’s diameter shift in a counterclockwise manner, leading to a transformation in its cross-sectional shape from a “circle” to a more “elongated oval” or "horizontal duck egg" configuration. Taken together, the deformed shape is highly non-uniform—the side of the tunnel facing the pit moved outward and downward most, while the far side moved much less.

Fig. 20

Deformation of existing tunnel during excavation in Test 5.

Fig. 21

Displacement of existing tunnel during excavation in Test 5.

Quantitatively, these movements are considerably larger than those reported in smaller-scale studies. For example, Han et al. found a “spoon-shaped” settlement profile along a subway tunnel adjacent to an excavation and recorded only ~ 13 mm maximum vertical and ~ 21 mm maximum horizontal displacement. In contrast, our measured horizontal displacement (624 mm) is over an order of magnitude greater, reflecting the deeper, more aggressive excavation in our experiment. Despite the difference in magnitude, both our results and those of Han et al.⁶³. share a similar pattern: the greatest deformations occur near the limits of the excavation, forming a longitudinal “spoon” or trough in the tunnel vault. This pattern highlights how excavation-induced soil movements concentrate toward the pit edges.

The detailed deformation of the tunnel lining can be inferred from these values. The 12% increase in diameter suggests the tunnel was driven into the post-elastic range at the pit face, as load redistribution caused one side of the lining to flex outward. The combination of substantial lateral shift (0.624 m) and large settlement (~ 0.5 m) implies a complex distortion: the vault and sidewalls were deformed by both bending and shear. Importantly, the deformations on the near side of the pit are much larger than on the far side, indicating an asymmetric loading condition. These observed characteristics—large magnitude of deformation, localization near the excavation, and asymmetric distortion of the tunnel ring—set the stage for understanding why the tunnel behaved as a “shield” under load.

Mechanism of existing tunnel shielding effect

The asymmetric deformation pattern above suggests a classic soil–structure interaction effect: the excavation-induced stresses are redistributed by the stiff tunnel lining, producing a shielding effect. In soil mechanics terms, this is akin to the arching effect first described by Terzaghi: when soil is removed, the remaining soil forms an arch that carries load across the void. In our case, the existing tunnel lining effectively becomes part of this load-bearing arch. Because the tunnel lining is much stiffer than the surrounding soil, it supports a significant portion of the load that would otherwise have transferred through the soil. Consequently, the vertical and lateral soil movements are “shielded”—i.e. reduced—on the side of the tunnel opposite the excavation, and transferred to other areas.

This mechanism is evident in both our data and prior analyses. Li et al.⁵⁷ demonstrated that “the stiffness of the existing tunnel is much larger than that of the surrounding soil, which results in the shielding effect and reduces the surface settlement” above the tunnel. In other words, the rigid tunnel lining forces the excavation-induced ground unloading to spread outward, alleviating some of the settlement directly over the tunnel. In our experiment, this explains why the far wall of the tunnel moved relatively little while the near wall and vault deformed substantially. The stiff lining and soil arching carry load from the roof into the lining, so the excavation has a smaller impact on the portion of soil behind (downstream of) the tunnel.

In practical terms, the shielding effect means the tunnel behaves like a stiff inclusion within the soil. As the excavation deepened, the soil between the pit and tunnel tended to arch over the tunnel (enhanced by the tunnel’s rigidity), thereby limiting deformation directly above it. Conversely, once the excavation progresses past the tunnel crown, this arch is lost and settlement increases rapidly (consistent with classical arching theory). The net result is that the existing tunnel causes a non-uniform stress field: one side of the tunnel (nearest the pit) “sees” most of the deformation while the other side remains relatively supported. This interpretation is consistent with both our measurements and previous findings.

In summary, the experimental data are best explained by the interaction of soil arching and structural stiffness. The tunnel’s rigid lining re-distributes excavation-induced loads, creating a shielding effect that concentrates deformation toward the excavation face. This mechanism accounts for the large diameter expansion and 0.624 m lateral shift we observed, and mirrors the behavior reported in other studies of tunnel–excavation interaction. These insights link the observed deformation characteristics (Sect. 7.1) to fundamental mechanics, and will inform the design of tunneling near existing structures.

The deep foundation pit sectional excavation system

Building on the findings from Sections "Settlement and displacement response in sectional excavation", "Soil heave characteristics at the excavation surface", "Analysis of retaining wall deformation during deep foundation pit excavation in soft clay", and "Analysis of deformation and displacement characteristics of existing tunnels during excavation of deep foundation pit", it becomes evident that the existing tunnel exerts a shielding effect on both soil movement and retaining wall deformation. Instead of analyzing the soil layer, retaining wall, and tunnel separately, envisioning them as a cohesive unit—termed the deep foundation pit sectional excavation system—provides a clearer perspective. Within this unified system, the shielding effect can be conceptualized as the deformation and displacement of a rigid, non-uniform body (the existing tunnel) superseding the deformation and displacement of the surrounding soil. In this context, the soil is regarded as the least rigid and most uniform component.

Section "Settlement and displacement response in sectional excavation" concludes that a tunnel’s ability to restrict the movement of nearby soil is directly proportional to its rigidity: the more rigid the tunnel, the greater its inhibitory effect. This implies that a highly rigid, heterogeneous structure (like a rigid tunnel) possesses a stronger shielding effect than a slightly less rigid one (like a flexible tunnel). Moreover, both these effects are substantially more pronounced than that of a completely consistent structure with minimal rigidity (like soil). Drawing from insights in Section "Analysis of retaining wall deformation during deep foundation pit excavation in soft clay", when juxtaposed against the tunnel, the adjacent soil exhibits significant displacement and deformation. Specifically, the soil, affected by disturbances and unloading from excavation, undergoes far greater shifts and changes than the most rigid, heterogeneous structure (rigid tunnel). In summary, as depicted in Fig. 22, when external conditions remain unchanged, minimal deformations and displacements in a more rigid, heterogeneous structure (like the tunnel) compensate for the more dramatic changes in a less rigid, consistent structure (like soil). This dynamic showcases interactions between entities with varying rigidity, resulting in clear reciprocal feedback. The more pronounced the disparity in their rigidity, the more evident the shielding effect becomes.

Fig. 22

Shielding effect: (a) displacement part; (b) deformed part.

Engineering implications and design recommendations

The findings from this study offer several important insights for engineering practice, particularly in the context of deep excavation projects in urban environments where existing metro tunnels or underground structures are present. The observed deformation behaviors, soil–structure interactions, and surface uplift mechanisms provide a foundation for developing practical design guidelines to improve safety, minimize disturbance, and enhance structural performance.

• 1. Optimize spatial arrangement: increase structural separation: The results highlight the significant influence of tunnel proximity on both settlement and uplift. As such, increasing the vertical and horizontal clearance between new excavations (e.g., diaphragm walls or pile systems) and existing tunnels can effectively reduce mutual interference. A conservative design practice would maintain a minimum vertical separation of at least 1.5 times the tunnel diameter, especially if the tunnel lies within the identified critical interaction depth. Laterally, a clearance of one to two tunnel diameters is advisable where space allows.

• 2. Sequence control and pre-support measures: Construction sequence plays a critical role in stress redistribution. It is recommended to complete tunnel lining construction (especially rigid linings) before initiating adjacent excavation activities. This ensures the tunnel behaves as a load-bearing structural element during nearby excavation and reduces differential movements. For pile-supported retaining systems, it is vital to avoid excessive load transfer during early stages of excavation by carefully staging support activation (e.g., propping levels).

• 3. Reinforcement of soft ground and tunnel linings: In regions with soft or compressible soils, proactive ground improvement techniques—such as grouting, preloading, or jet mixing—should be considered to increase stiffness and minimize deformation. Likewise, tunnels within the interaction zone should incorporate enhanced linings, potentially with double shells or additional reinforcement layers, to resist bending and provide better confinement. These measures improve deformation control and extend service life under combined stress from excavation and soil rebound.

• 4. Monitoring and real-time feedback systems: The variability in observed heave patterns across tests emphasizes the need for robust monitoring. Installing dense arrays of settlement markers, inclinometers, and pore pressure transducers provides early warning of unexpected soil movement. It is particularly important to monitor zones above and adjacent to the tunnel crown, as these are most sensitive to asymmetric uplift. Based on monitoring data, adaptive construction control (e.g., adjusting excavation rates or sequencing) can be implemented to mitigate risks.

• 5. Design adaptations for critical interaction zones: The study introduces the concept of a critical interaction depth, within which tunnel–excavation interactions become significant. If a tunnel lies within this zone, designers should anticipate nonuniform arching and uplift patterns, particularly the transition to triangle or groove profiles. Structural adaptations—such as reinforced pit bottoms or stiffer retaining systems—can help accommodate and redistribute these deformation modes. Consideration should also be given to potential uplift-induced damage, particularly for rigid tunnels or utilities located close to the pit base.

• 6. Integration with urban metro planning: For large metro networks, where future excavations may occur near existing tunnels, city planners and design teams should incorporate geotechnical interaction models into early-stage design. Risk assessments should simulate possible deformation envelopes using centrifuge-derived data or numerical back-analysis. This proactive approach allows selection of tunnel alignments, burial depths, and support types that minimize interference.

In summary, the centrifuge study provides not only valuable mechanistic insights but also a practical framework for design. By integrating considerations of tunnel stiffness, depth, position, and interaction thresholds, engineers can reduce excavation-induced risks and enhance structural resilience. These recommendations serve as a bridge between experimental findings and real-world geotechnical challenges in densely built urban environments.

Conclusion

• 1. Employing centrifuge testing and Particle Image Velocimetry (PIV) technology, this study accurately replicates the segmented excavation process in a soft clay layer proximate to an existing tunnel. The results consistently showed that the tunnel provided a shielding effect, reducing both surface settlements and wall displacements compared to the no-tunnel case. The results of the experiment were satisfactory, affirming the precision of the model parameters and the efficacy of the experimentation process.

• 2. Excavating the foundation pit prominently increases soil settlement on the pit’s passive side and uplift on the active side. Depending on the existing tunnels, three distinct excavation surface uplift patterns can occur: hill, trough, and triangle. The existing tunnel acts as a shield, limiting soil movement and consequently reducing settlement and uplift induced by the excavation. The existing tunnels can reduce the required support stiffness and expected settlements of new excavations. Design and analysis should therefore account for the tunnel’s presence: ignoring nearby tunnels could lead to overprediction of wall deflections and settlements, while including them could improve prediction accuracy and enable more economical support designs.

• 3. The shielding efficacy of the existing tunnel notably fluctuates, depending on its relative position and stiffness during the foundation pit excavation. This effect diminishes as the distance between the soil and the tunnel increases, signaling a limit to its effectiveness. A tunnel with greater rigidity offers more pronounced shielding to the surrounding soil. Under rigid tunnel conditions, the maximum soil settlement point is more distant from the retaining wall, and the settlement curve is smoother and more stable than in flexible tunnels.

• 4. Throughout the foundation pit excavation, pronounced lateral shifts in the retaining wall towards the excavated surface are observable, intensifying as excavation deepens, and causing the peak deformation point to migrate downward. The manifestation of shielding effects varies with the tunnel’s relative positions, unfolding in sequence. Remarkably, tunnels on the active side showcase a deferred shielding response, leading to unique retaining wall deformations under diverse tunnel conditions. If the existing tunnel is on the passive side of the excavation pit, an arch shape is formed in the retaining wall; if on the passive side, a “bow” shape is evident.

• 5. During the excavation of the foundation pit, the existing tunnel is subjected to deformation and displacement, both demonstrating a continual increase. Specifically, the tunnel on the passive side mainly experiences horizontal expansion and vertical compression. The horizontal diameter expands by approximately 12%, while the vertical diameter contracts about 14%. In essence, the shielding effect implies that the slight deformations and displacements of a structure with higher rigidity and non-uniformity, such as the existing tunnel, are more significant than the pronounced deformations and displacements of a softer, uniform structure like soil. The more marked the contrast in rigidity between these structures, the more noticeable the shielding effect is. Overall, the quantitative results provided here can guide engineers in adjusting excavation support parameters and predictive models when working in soft clay with adjacent tunnels.