Introduction

Turbulence is one of the most complex phenomena in classical physics, occurring in both natural environments and industrial applications. It is characterized by its chaotic multiscale nature and a complex interplay of structures of different sizes. A distinctive feature of turbulent flows is their intermittent behavior, where quantities undergo long periods of low intensity, interrupted by sudden bursts, during which variables deviate several standard deviations (SDs) away from the mean1. These extreme events lead to non-Gaussian probability density functions (PDFs) and, despite their low probability, can have important effects on flow phenomena and dynamics. For example, in atmospheric and oceanic turbulence, extreme events manifest as severe weather phenomena, including storms, hurricanes, and rogue waves, which can occur as isolated events or in rapid succession2. Beyond atmospheric turbulence, extreme events have also been linked to abrupt transitions between quasi-stable flow configurations3, such as quasi-relaminarization events4,5. The dissipation rate, a highly intermittent quantity in wall-bounded shear flows, is another example of extreme behavior in turbulence. Extreme dissipation events are associated with phenomena like local flame extinction6, enhanced particle concentration or clustering7,8, and an increased likelihood of particle collisions9. Moreover, these events produce smaller-than-expected instantaneous Kolmogorov scales compared to those typically used in mesh requirement estimations. This suggests that a finer computational mesh may be necessary to accurately estimate the probabilities and intensities of extreme events10.

Extreme events in turbulent flows have a significant impact on the performance and reliability of many systems, making accurate early predictions essential for effective control and mitigation. The predictability of a dynamical system is typically quantified using Lyapunov exponents, which measure the average exponential rate of separation between trajectories that start from nearby points under the action of the deterministic dynamics. In turbulent flows, the presence of positive Lyapunov exponents indicates chaotic behavior, meaning that two initially close trajectories will diverge exponentially over time. This sensitivity to initial conditions, often referred to as the butterfly effect, imposes a fundamental limit to predictability11, as any small perturbation or uncertainty in measurements will inevitably lead to exponential divergence within a finite time frame, rendering long-term predictions inherently unreliable. However, Lyapunov exponents are typically not reliable enough indicators of the predictability of extreme events in intermittent dynamical systems11,12. In addition to the sensitivity of chaotic dynamical systems to fully known initial conditions, uncertainty in the initial state, the influence of unobserved or hidden variables, and inaccuracies in the underlying physical model further hinder the accurate forecasting of extreme events13.

Recent studies have explored various machine learning techniques for predicting turbulent flows and chaotic signals, including recurrent neural networks, autoencoders, and reservoir computing. For instance, in the works of Eivazi and Borrelli et al.14,15, long short-term memory networks are employed to predict the evolution of space proper orthogonal decomposition (POD) coefficients, which effectively represent large-scale, long-duration coherent structures. These strongly nonlinear methods have shown particular effectiveness in capturing and reproducing long-term turbulent dynamics, but they can struggle with accurate short-term predictions16. Moreover, since POD retains the most energetic modes, it is unable to accurately capture fast, spatially localized extreme events that, despite their intensity, do not significantly contribute to the overall ensemble of snapshots. Works such as Racca and Magri17 and Ahmed et al.18 have shown success in predicting signals containing extreme events. They use echo state networks to forecast extreme events in the Moehlis-Faisst-Eckhardt model, a nine-dimensional representation of the self-sustaining process in turbulence. However, due to the large amount of training data required for parameter estimation19, these methods might face difficulties as such extreme events become less frequent. Physics-informed machine learning approaches may have the potential to reduce the data requirements, as explored in Doan et al.4. Concurrently, Koopman-based methods have emerged as a promising avenue for predicting dynamical systems20. This rise in popularity can be attributed to advances in methods such as dynamic mode decomposition (DMD), which allow for the approximation of the Koopman operator from data. Variants like Hankel-DMD21 and Higher-Order-DMD22 have been successfully employed for univariate time signal predictions. In the work of Mezić et al.23, Hankel-DMD is employed to predict black swan events in epidemiology. However, these methods rely heavily on the choice of observables and face challenges in systems with a continuous part of the Koopman spectrum, which is the case in turbulent flows24,25. Recent advancements aim to address these limitations, using artificial neural networks to learn tailored dictionaries of functions26 and autoencoders to identify mappings onto lower-dimensional invariant manifolds27. Simultaneously, Schmidt and Schmid28 presented a conditional space-time POD approach to analyze extreme acoustic bursts in turbulent jets. This method constructs a realization matrix, where each column comprises snapshots from the moments preceding and following an extreme event. Applying space-time POD to this matrix reveals modes that are coherent in space and over a finite time horizon, effectively capturing the evolution of extreme events from their onset through their progression. Subsequently, Hack and Schmidt1 used this approach to investigate the mechanisms responsible for the formation of extreme dissipation events in wall-bounded flows. Later, Stahl et al.29 applied this methodology to predict extreme negative pressure fluctuations on the walls of a channel containing an offset bluff body. Using conditional space-time POD on snapshots leading to extreme negative pressure fluctuations on the top wall, the method identified the origin of these events in the bluff body and tracked their downstream propagation through the wake. This analysis led to the development of a forecasting framework that leverages the upstream-to-downstream progression of extreme events: once an extreme event is observed at the bluff body, it serves as a precursor for predicting the corresponding future event at the wall. The lead time for this prediction corresponds to the time it takes for the event to propagate from the bluff body to the wall.

A major challenge in many real-world applications, especially those involving complex multiscale flow phenomena, is the limited availability of spatially-resolved data, where measurements are often restricted to a few time-resolved probes. The absence of spatial data to integrate into models, especially for high-dimensional dynamical systems, significantly limits the time horizon over which extreme events can be effectively predicted. Given these constraints, this work proposes a conditional time-only POD method for predicting extreme events in the limit of considering a single time signal of a turbulent flow system. In this work, following a similar criterion to Ahmed et al.18, extreme events are defined as the highest-intensity dissipation rate occurrences in turbulent flow signals that surpass a predefined threshold, and inherently result from the deterministic nonlinear dynamics described by the equations of fluid motion30. Given a time signal containing extreme events, a realization matrix of time segments leading up to these events is constructed. Applying POD to this matrix yields a set of modes that optimally capture the variance of the ensemble of time segments, with the first mode representing the average growth of signals prior to an extreme event. The similarity between incoming real-time signals and this mode is used as an indicator of an upcoming extreme event. The proposed approach does not leverage spatial information, and its low computational complexity enables on-the-fly prediction of extreme events. Additionally, the method is designed to operate with less data than conventional, data-intensive approaches19. It remains effective even when only a short time signal containing a few extreme events is available for training, where the data may not fully represent the underlying distribution. This completely data-driven methodology is highly versatile and applicable to other systems where extreme events have similar growth dynamics.

The primary objective of this paper, thus, is to develop a robust data-driven framework that given a predefined threshold, predicts extreme events in univariate time signals, even under conditions of limited data. The proposed methodology is applied to time signals of the dissipation rate from wall-bounded turbulence, with the method’s robustness tested across different wall distances and Reynolds numbers, capturing a wide range of intermittent behavior. The rest of the paper is structured as follows: the “Materials and methods” section introduces the flow physics modeling framework based on the incompressible equations of fluid motion, details the computational experiments, and presents the conditional time-only POD methodology. The “Results and discussion” section begins with a characterization of flow intermittency to contextualize the signals, followed by an evaluation of the method’s performance, and concludes with a comparison of the lead times given by the method with the duration over which Hankel-DMD predictions remain accurate. Finally, the key findings of the work are summarized in the “Conclusions” section, along with potential directions for future research.

Material and methods

This Section outlines the methods used in the study, including the flow physics modeling, the setup of the numerical cases, and the methodology used to predict extreme events.

Flow physics modeling

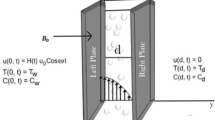
The flow motion of isothermal incompressible turbulence is described by the conservation of mass and momentum, which, in dimensionless form, are written as

$$\begin{aligned}&\nabla ^\star \cdot \textbf{u}^\star = 0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial \textbf{u}^{\star }}{\partial t^{\star }} + \nabla \cdot \left( \textbf{u}^{\star } \otimes \textbf{u}^{\star } \right) = - \nabla ^{\star } p^{\star } + \frac{1}{Re_c} {\Delta }^{\star } \textbf{u}^{\star }, \end{aligned}$$
(2)

where the superscript \(\star\) denotes normalized quantities, \(\textbf{u}\) is the velocity vector, t is the time, p is the hydrodynamic pressure, and \(\otimes\) denotes the outer product. The derivation of these dimensionless equations is based on the following set of inertial scalings31,32

$$\begin{aligned}&\textbf{x}^{\star } = \frac{\textbf{x}}{\delta }, \quad \textbf{u}^{\star } = \frac{\textbf{u}}{U_{c}},\quad t^{\star } = \frac{t U_c}{\delta }, \quad p^{\star } = \frac{p}{\rho U_{c}^{2}}, \end{aligned}$$
(3)

with \(\textbf{x}\) the position vector, \(\delta\) the half-channel height, and \(U_c\) the centerline velocity of an equivalent laminar case with the same volumetric flux33. The dimensionless form of the equations showcases the dependence on a unique dimensionless number, the centerline Reynolds number \(Re_c = \rho U_c \delta / \mu\), with \(\rho\) and \(\mu\) the density and dynamic viscosity of the fluid, respectively, which characterizes the ratio of inertial to viscous forces.

The equations of fluid motion are computationally solved by means of the in-house flow solver RHEA34. A standard semi-discretization procedure is adopted, in which they are first discretized in space and then integrated in time. In particular, spatial operators are treated using second-order central-differencing schemes, and time-advancement is explicitly performed by means of a third-order strong-stability preserving (SSP) Runge–Kutta approach35. The convective terms are expanded according to the Kennedy–Gruber–Pirozzoli (KGP) splitting36,37. The method preserves kinetic energy by convection and is locally conservative for mass, momentum, and total energy. This numerical framework provides stable computations without the need for any form of artificial dissipation or stabilization procedures.

Computational experiments

Direct numerical simulations of channel flows with significantly smaller domains, known as minimal flow units (MFUs)33,38, are conducted. A constant volumetric flux \(\dot{V} = (2/3)U_c L_y L_z\) is imposed in the x-direction, following the work of Jiménez and Moin33, which results in a slightly varying friction Reynolds number \(Re_\tau\). To evaluate the robustness of the method across different flow regimes, simulations are performed at three distinct Reynolds numbers: \(Re_c=2000\), 3000, and 5000, while considering multiple wall distances. At \(Re_c=2000\), the flow undergoes quasi-relaminarization events, where the flow near one wall becomes laminar, while the flow near the opposite wall remains turbulent. Figure 1a–c show the evolution of the flow field during a switch of the turbulent wall. After a period in which the flow near the top wall is laminar, the system briefly transitions to a fully turbulent state. However, this state is inherently unstable, and turbulence near one of the walls decays after a short period33. Figure 1 presents a time signal of (d) the streamwise velocity and (e) the dissipation rate measured at a point in the buffer layer of the top and bottom walls, showing that high-intensity dissipation events are often associated with the laminar wall. As the Reynolds number increases, quasi-relaminarization events become less frequent. However, the flow exhibits more rapid temporal variations, with greater intensity and a higher frequency of extreme events.

Fig. 1
figure 1

Quasi-relaminarization events for the MFU at \(Re_c=2000\)Isocontours of normalized Q-criterion, \(Q^{\star }= (\Vert {\varvec{\Omega }}^{\star }\Vert ^2 - \Vert \textbf{S}^{\star }\Vert ^2)/2 =0.2\) with rate-of-rotation tensor \({\varvec{\Omega }}^{\star } = [\nabla ^{\star } \textbf{u}^{\star }- (\nabla ^{\star } \textbf{u}^{\star })^T]/2\) and rate-of-strain tensor \(\mathbf {S^*} = [\nabla ^{\star } \textbf{u}^{\star }+ (\nabla ^{\star } \textbf{u}^{\star })^T]/2\), during a switch of the turbulent wall, with color indicating the streamwise velocity. Time signals of (d) the streamwise velocity and (e) dissipation rate from probes located at a distance of \(y^+ = 10\) from the top and bottom walls.

Full size image

For the three Reynolds numbers considered, the domain is set to \((L_x/\delta , L_y/\delta , L_z/\delta ) = (\pi , 2, 0.35 \pi )\), with a computational mesh of \(64\times 128 \times 64\) grid points in the streamwise, wall-normal and spanwise directions, respectively. This domain size is chosen based on prior works of MFUs at comparable Reynolds numbers33,39,40,41. For the computationally most restrictive case considered, \(Re_c = 5000\) (with mean \(Re_{\tau } = \rho u_{\tau } \delta / \mu\) approximately 200, friction velocity \(u_{\tau }=\sqrt{\tau _w/\rho }\), wall shear \(\tau _{w} = \mu \left( \partial {\langle u \rangle }/{\partial y} \right) _{y=0, L_y}\), and \(\langle u \rangle\) the mean streamwise velocity), the mesh employed results in the following grid-spacings: \(\Delta x^+ \approx 9.79\), \(\Delta y^+ \approx 3.12\), and \(\Delta z^+ \approx 3.42\). The first grid-point in the wall-normal direction is located at \(y^+ = \rho u_{\tau } y /\mu \approx 1.56\), ensuring that the viscous sublayer is properly resolved. Compared to previous studies39,41, a higher-resolution is employed in the z-direction to properly capture the roll-streak structures42. The normalized local dissipation rate \(\varepsilon ^* = 2 \nu S_{ij}S_{ij} \delta / U_c^3\), where \(\nu =\mu /\rho\) is the kinematic viscosity of the fluid and \(S_{ij}= \left( {\partial u_i}/{\partial x_j} + {\partial u_j}/{\partial x_i}\right) /2\) is the ij-th component of the strain rate tensor, is recorded for \(1000 t^{\star }\).

Conditional POD for extreme event identification

The conditional time-only POD formulation for predicting extreme events in time signals is presented here. First, the inner product over a predefined time-interval \(\Delta t^{\star }\) for two general complex-valued functions of time \(\textbf{a}_1(t)\) and \(\textbf{a}_2(t)\) is defined as

$$\begin{aligned} \langle \textbf{a}_1,\textbf{a}_2 \rangle _{\Delta t^{\star }} = \int _{\Delta t^{\star }} \textbf{a}_1^{{\textsf{H}}}(t) \textbf{a}_2(t) dt, \end{aligned}$$
(4)

where superscript \(\textsf{H}\) denotes the Hermitian or complex conjugate. Using this inner product for a generic function \(\textbf{q}(t)\) (e.g., streamwise velocity, turbulent kinetic energy, dissipation rate), the time-only eigenfunctions \({\varvec{\phi }}\), conditioned on the occurrence of an arbitrary event \(\mathscr {H}\), are obtained by maximizing

$$\begin{aligned} \lambda = \frac{ \mathbb {E}\{ \Vert \langle \textbf{q}(t), {\varvec{\phi }}(t) \rangle _{\Delta t^{\star }} \Vert ^2 \mid \mathscr {H} \} }{\langle {\varvec{\phi }}(t), {\varvec{\phi }}(t) \rangle _{\Delta t^{\star }}}, \end{aligned}$$
(5)

with \(\mathbb {E}\{\cdot \mid \mathscr {H}\}\) being the conditional expectation given \(\mathscr {H}\). These eigenfunctions \({\varvec{\phi }}\) and their corresponding eigenvalues \(\lambda\) are solutions to the Fredholm eigenvalue problem

$$\begin{aligned} \int _{\Delta t^{\star }} \textbf{C}(t, t') {\varvec{\phi }}(t') dt' = \lambda {\varvec{\phi }}(t), \end{aligned}$$
(6)

where \(\textbf{C}(t, t') = E \{ \textbf{q}(t) \textbf{q}^{{\textsf{H}}}(t') \mid \mathscr {H} \}\) represents the correlation tensor conditioned on an event \(\mathscr {H}\). The problem of extracting a set of discrete dominant modes is formulated as an eigendecompositon of the form \(\textbf{QQ}^{{\textsf{H}}}\pmb {\mathcal {W}} {\varvec{\Phi }} = {\varvec{\Phi \Lambda }}\), where \(\textbf{Q} \in \mathbb {R}^{M\times N}\) is the matrix of realizations with \(M>N\), the columns of \({\varvec{\Phi }} = \begin{bmatrix}{\varvec{\phi }}^{(1)}, {\varvec{\phi }}^{(2)}, \dots , {\varvec{\phi }}^{(N)} \end{bmatrix}\) correspond to the conditioned POD modes, while the diagonal entries of \({\varvec{\Lambda }} = \text {diag}\begin{bmatrix}\lambda ^{(1)}, \lambda ^{(2)}, \dots , \lambda ^{(N)} \end{bmatrix}\) are the associated eigenvalues. The matrix \(\pmb {\mathcal {W}}\) is a diagonal, positive-definite matrix that incorporates the quadrature weights used to approximate the correlation matrix from discrete measurements. This eigendecomposition problem can be reformulated as a singular value decomposition (SVD) problem, which is numerically better conditioned43, in the form

$$\begin{aligned} \pmb {\mathcal {F}}\textbf{Q} = \pmb {\mathcal {U}}_r {\varvec{\Sigma }}_r \pmb {\mathcal {V}}_r^T, \end{aligned}$$
(7)

with \(\pmb {\mathcal {F}}\) being the Cholesky factor of \(\pmb {\mathcal {W}}\). The columns of \(\pmb {\mathcal {U}}_r\) contain the first r POD modes, \(\pmb {\mathcal {U}}^{(i)} = {\varvec{\phi }}^{(i)}, \quad i = 1, 2, \dots , r\) with \(r \le N\). The eigenvalues can be recovered from the entries of \({\varvec{\Sigma }}_r = \text {diag}\begin{bmatrix} \sigma ^{(1)}, \sigma ^{(2)}, \dots , \sigma ^{(r)} \end{bmatrix}\) as \(\lambda ^{(i)} = (\sigma ^{(i)})^2\).

In this work, an extreme event is defined as a local maximum that exceeds a specified threshold, determined by a given percentile of the training data. From a training signal \(q_{trng}(t)\), the extreme event realization matrix \(\textbf{Q}_{EE}\) is constructed from non-overlapping time segments of duration \(\Delta T^{\star }\) leading up to these extreme events. The objective is to extract optimal time-only modes that effectively capture the variance of an ensemble of time signals that result in an extreme event, and then use them for prediction tasks. From \(q_{trng}(t)\), a total of \(N_{peaks}\) time segments of duration \(\Delta T^{\star }\) sampled at a rate \(\Delta t^{\star }\) are identified, each ending in a local peak that exceeds the threshold at time \(t_{EE}^{(i)}, \quad i = 1,2,\dots N_{peaks}\). This process is depicted schematically in Fig. 2a. These segments are organized as columns of the matrix \(\textbf{Q}_{EE} \in \mathbb {R}^{M \times N_{peaks}}\)

$$\begin{aligned} \textbf{Q}_{EE} = \begin{bmatrix} q_{trng}\left( t_{EE}^{\star (1)} - \Delta T^{\star } \right) & q_{trng}\left( t_{EE}^{(2)} - \Delta T^{\star } \right) & \dots & q_{trng}\left( t_{EE}^{(N_{peaks})} - \Delta T^{\star } \right) \\ q_{trng}\left( t_{EE}^{\star (1)} - \Delta T^{\star } + \Delta t^{\star } \right) & q_{trng}\left( t_{EE}^{\star (2)} - \Delta T^{\star } + \Delta t^{\star } \right) & \dots & q_{trng}\left( t_{EE}^{\star (N_{peaks})} - \Delta T^{\star } + \Delta t^{\star } \right) \\ \vdots & \vdots & \ddots & \vdots \\ q_{trng}\left( t_{EE}^{\star (1)} \right) & q_{trng}\left( t_{EE}^{\star (2)} \right) & \dots & q_{trng}\left( t_{EE}^{\star (N_{peaks})} \right) \end{bmatrix} \in \mathbb {R}^{M \times N_{peaks}}, \end{aligned}$$
(8)

with \(M = 1 + \Delta T^{\star }/\Delta t^{\star }\). To analyze the relative signal growth leading up to extreme events, the shifted realization matrix \(\textbf{Q}_{EE}'\) is computed by subtracting the final row, which corresponds to the value at the peak, from each row of \(\textbf{Q}_{EE}\). This corresponds to \(\textbf{Q}_{EE}' = \textbf{Q}_{EE} - \textbf{1}_M \otimes \textbf{Q}_{EE}[M,:]^T\), where \(\textbf{1}_M\) is a vector of ones of size M and \(\textbf{Q}_{EE}[M,:]\) is the last row of matrix \(\textbf{Q}_{EE}\). The conditioned time-only POD modes are then obtained from the SVD of \(\textbf{Q}_{EE}'\). Because the columns of the realization matrix are conditioned to exhibit similar strong growth dynamics, the POD decomposition robustly extracts the dominant growth mode, even when a few number of segments are used. This makes the method particularly well-suited for infrequent extreme events. Further discussion on its robustness to the number of extreme events is provided in section “Sensitivity to the number of extreme events and training window duration” of the supplementary information.

To detect early signs of extreme events, a time segment of duration \(\Delta T^\star\), defined as

$$\begin{aligned} \textbf{s}(t) = \left[ q(t - \Delta T^{\star }), q(t - \Delta T^{\star } + \Delta t^{\star }), \dots , q(t) \right] \in \mathbb {R}^{M}, \end{aligned}$$
(9)

is considered. The projection of the signal’s relative growth onto the most energetic mode, \({\varvec{\phi }}^{(1)}\) (shown in Fig. 2b), serves as a measure of the alignment between the current signal evolution and the dominant growth pattern identified by the conditional time-only POD. Using the training time signal, projections are computed for both known extreme-event segments and local peaks that do not surpass the threshold. Based on these projections, an indicator threshold can be selected to classify incoming real-time signals as extreme event precursors or not. Given the significant impact of extreme events on the system, the threshold can be chosen to prioritize early detection and maximize true positives, at the cost of more false positives. Nonetheless, to automate the classification process, a support vector machine (SVM) with a radial basis function (RBF) kernel is fitted based on the projections of the training data to define the decision boundary. To address the natural class imbalance between extreme and non-extreme events, a balanced weighted SVM44 is used, assigning class weights inversely proportional to their frequencies in the training set, which improves classification performance. The trained SVM is then used to classify the projection of the relative growth of the testing signals as either indicative of an impending extreme event or not.

Fig. 2
figure 2

Extraction of the conditioned POD modes for the MFU \(Re_c=3000\) case. (a) Normalized dissipation rate \(\varepsilon ^\star\) of a probe in the buffer region \((y^+= 10)\). The dashed line marks the extreme event threshold used. Time segments leading to extreme events, which are used to compute the conditioned POD time modes, are highlighted in red. (b) The leading POD mode of the realization matrix is shown in red, with the remaining POD modes displayed in gray.

Full size image

Results and discussion

In this section, the results of applying the conditional time-only POD to detect extreme dissipation events in wall-bounded turbulence are presented. The method’s efficacy is evaluated for signals at various wall-normal distances and Reynolds numbers, demonstrating its robustness across a range of flow regimes and levels of intermittency. First, the intermittency of the signals for \(Re_c=3000\) is characterized at different wall distances. Then, the results for the predictions of extreme events at \(Re_c=3000\) across different wall distances are presented. Results for the signals in the buffer region for \(Re_c=2000\) and 5000 are also shown to corroborate the robustness of the method for different Reynolds numbers. Finally, the advance time provided by the method is compared with the duration for which the predictions of the Hankel-DMD remain accurate.

Flow intermittency characterization

The intermittency for the MFU is quantified here, which exhibits additional challenges compared with low dimensional models. In systems like the Moehlis-Faisst-Eckhart model, modes exhibit similar frequency content15, and extreme events tend to have comparable magnitudes, with time intervals that are neither excessively short nor too long. In contrast, the MFU displays more complex behavior, with extreme events exhibiting different intensities among themselves, and sometimes occurring in rapid succession, making their prediction more challenging.

The intermittency of the dissipation rate for the \(Re_c = 3000\) case is characterized across different wall distances. Figure 3a shows the PDF, adjusted to have zero mean and unit standard deviation, for different \(y^+\) distances. To assess deviations from Gaussian behavior, the skewness and excess kurtosis

$$\begin{aligned}&\operatorname {Skew}[\varepsilon ] =\mathbb {E}\left[ \left( \frac{\varepsilon -\mu _{\varepsilon }}{\sigma _{\varepsilon }}\right) ^3\right] = \frac{\mathbb {E}\left[ (\varepsilon - \mu _{\varepsilon })^3\right] }{\sigma _{\varepsilon }^3}, \ \qquad \operatorname {Excess\ Kurt}[\varepsilon ]=\mathbb {E}\left[ \left( \frac{\varepsilon -\mu _{\varepsilon }}{\sigma _{\varepsilon }}\right) ^4\right] - 3 = \frac{\mathbb {E}\left[ (\varepsilon - \mu _{\varepsilon })^4\right] }{\sigma _{\varepsilon }^4} - 3, \end{aligned}$$
(10)

are computed, where \(\mu _{\varepsilon }\) and \(\sigma _{\varepsilon }\) are the mean and standard deviation of the dissipation rate, respectively. Skewness quantifies the asymmetry of the distribution, while excess kurtosis quantifies the presence of extreme events compared to a Gaussian distribution. The PDFs reveal significantly different levels of intermittency across the wall-normal direction. For the time signal at \(y^+ = 10\) (buffer region, \(5< y^+ < 30\)), where root-mean-square velocity fluctuations peak, the distribution exhibits relatively low skewness and excess kurtosis, despite dissipation values occasionally deviating approximately 9 SDs from the mean. For the signal at \(y^+ = 100\), (logarithmic layer, \(y^+ > 30\)), the distribution becomes highly skewed, exhibiting significant extreme events (\(\operatorname {Excess\ Kurt} \approx 60\)), with deviations reaching up to 30 SDs. For a signal near the wall, \(y^+=1\) (viscous sublayer, \(y^+ < 5\)), the distribution exhibits an intermediate degree of skewness and heavy-tailed behavior compared to the buffer and logarithmic layers.

The temporal autocorrelations for the signals at different wall distances are shown in Fig. 3b. A probe measurement at each wall distance is shown in Fig. 4a,c,e. Notably, the signal at the viscous sublayer exhibits an extremely slow background flow mechanism, with return times between extreme events on the order of \(\mathscr {O}(10^2) t^{\star }\). As a result, weak correlations persist up to a lag time of \(100 t^{\star }\), before the signal fully decorrelates around \(150 t^{\star }\). For all wall distances, a peak is observed at a lag time approximately equal to the flow-through-time (FTT), which represents the average time it takes the fluid to travel through the domain; \(\text {FTT} = L_x/U_b \approx 4.71\), where \(U_b\) is the bulk velocity (\(U_c/U_b = 3/2\)). This peak at lag-time of approximately one FTT is a result of extreme events being measured as they are convected through the periodic domain, reaching the same location repeatedly. As the \(Re_c\) increases, this periodic effect diminishes quickly as more complex structures emerge, with additional frequencies contributing to the signal. The duration of the segment used to compute the mode is shorter than the FTT, ensuring that no periodicity is exploited for predictions.

Fig. 3
figure 3

(a) PDF of the scaled dissipation rate \(\varepsilon ^{\star }\), centered and scaled to have zero mean and a unit standard deviation, at various wall distances for \(Re_c = 3000\). (b) Temporal autocorrelation of the dissipation rate \(\varepsilon ^{\star }\) for the same time signals.

Full size image

Performance of the method

For each time signal, extreme events from the initial \(300 t^{\star }\) of the dissipation rate signal [\(q(t)=\varepsilon (t)\)] are used to construct the realization matrix and fit the support vector machine. Here, extreme events are defined as local peaks exceeding the 99th percentile of the training data. As shown in section “Sensitivity to the extreme event definition threshold” of the supplementary material, moderate variations to this percentile do not significantly impact the results. Depending on the signal’s intermittency and frequency, this results in between 2 and 12 extreme events being used during training, demonstrating that the method remains effective without requiring a large dataset containing many rare events. Increasing or decreasing the length of the training window (while keeping the threshold fixed) slightly alters the number of extreme events considered. However, as shown in section “Sensitivity to the number of extreme events and training window duration” of the supplementary information, these variations have minimal impact on the resulting POD mode and subsequent predictions. The duration of the time modes, \(\Delta T^{\star }\), should be selected based on the typical timescale of the coherent growth leading to an extreme event. For consistency, however, a fixed segment duration of \(\Delta T/\text {FTT} = 0.2\) (\(\Delta T^{\star }/t^{\star } \approx 0.94\)) is used across all \(Re_c\) and wall distances. While the segment duration should roughly match the signal’s temporal dynamics, the method is not highly sensitive to moderate variations of this parameter. Its influence on prediction accuracy and anticipation time is discussed in section "Sensitivity to the segment duration" of the supplementary information. For each signal, the most energetic time POD mode is computed, and the corresponding projections of segments that lead to extreme and non-extreme events are evaluated using the training data. A SVM with a RBF kernel is then fitted to classify incoming real-time signals as either preceding extreme events or not. The performance of SVMs is known to depend on the choice of hyperparameters45. Here, the same SVM setup (\(C = 10\) and \(\gamma =1\)) is maintained across all \(Re_c\) values and wall distances. The influence of these parameters on the results, particularly on the precision and recall (defined later), is analyzed in section "Sensitivity to parameters of the support vector machine" of the supplementary information. For the remaining \(700 t^\star\) from each signal, segments of duration \(\Delta T^{\star }\) are continuously projected onto the first POD mode and classified using the SVM.

Fig. 4
figure 4

Results for the \(Re_c = 3000\) case. Normalized dissipation rate of a probe located at (a) \(y^+ = 1\), (c) \(y^+ = 10\), and (e) \(y^+ = 100\). The dashed horizontal line denotes the threshold used to label an extreme event. The values of the signal when the model predicts an incoming extreme event are marked both for true positives and false positives. The PDF of the training and testing signal for the signals \(y^+ = 1, 10\) and 100 are displayed in subplots (b), (d) and (e), respectively. Vertical dashed blue lines denote the value at the moment of flagging for true positives.

Full size image

Figure 4 presents the method’s predictions for parts of the signals at different wall distances for \(Re_c = 3000\). In testing parts of the signals, the times when the indicator is activated are marked for both true and false positives. The PDFs for both the training and testing data are also shown, highlighting a clear difference in the tails, which is a fundamental issue when dealing with intense events that are rare. It is worth noting that false positives often occur during instances where the signal still experiences significant growth but happens to fall short with respect to the threshold. The proposed method tends to perform better for signals with higher skewness and kurtosis, such as those at \(y^+ = 1\) and 100. In these cases, there is a clearer separation between extreme events and the more regular behavior, facilitating the classification task. In contrast, the \(y^+=10\) signal constantly approaches the threshold without necessarily crossing it. This makes it more challenging to distinguish between extreme and non-extreme events, leading to a higher rate of misclassifications. This limitation is a consequence of the fixed-threshold definition of extreme events when applied to signals with moderate intermittency. The trend where the buffer region signals exhibit less intermittency, resulting in frequent fluctuations around the threshold without crossing it, persist for \(Re_c = 2000\) and 5000. Figure 5 presents the results for these more challenging signals for \(Re_c = 2000\) and 5000. For Reynolds numbers higher than those considered in this study, the faster time scales and increased nonlinearity are expected to make the prediction of extreme events more challenging, both for the proposed method and for existing approaches in the literature. However, the enhanced intermittency associated with higher Reynolds numbers improves the contrast between extreme events and background fluctuations. As a result, the method is still expected to deliver reasonably accurate predictions, although the effect on achievable lead time remains to be explored.

Fig. 5
figure 5

Results for a probe located in the buffer region (\(y^+ = 10\)) at (a) \(Re_c = 2000\) and (b) \(Re_c=5000\). The dashed horizontal line denotes the threshold used to label an extreme event. The values of the signal when the model predicts an incoming extreme event are marked both for true positives and false positives.

Full size image

The method’s performance is quantified using precision, recall, and F-score. Precision \([p=\text {TP}/(\text {TP}+\text {FP})]\) measures the proportion of correctly identified extreme events among all flagged instances, while recall \([r = \text {TP}/(\text {TP}+\text {FN})]\) quantifies the fraction of actual extreme events that were successfully detected. The F-score \([F=2/(p^{-1}+r^{-1})]\), which is the harmonic mean of precision and recall, provides an overall performance measure. These metrics are based on true positives (TP), false positives (FP), and false negatives (FN) from the model’s predictions on the testing data. In addition to accuracy metrics, the method’s advance time capabilities are reported for the true positives using the time-to-threshold (T2T) and time-to-peak (T2P), defined as the average time from when an event is flagged to when the signal crosses the extreme event threshold and the average time between flagging and the signal’s peak, respectively. To further quantify the predictive performance, the deviation of the average predicted dissipation rate value at the time of flagging relative to the extreme event threshold \((\varepsilon _{\text {threshold}}^{\star } - \overline{\varepsilon _p^{\star }})/\sigma _{\varepsilon ^{\star }}\) is reported, where \(\varepsilon _{\text {threshold}}^{\star }\) is the threshold value used and \(\overline{\varepsilon _p^{\star }}\) is the mean dissipation rate value at the time of flagging. Table 1 summarizes these quantities for \(Re_c=3000\) at different wall-normal distances, as well as for the buffer region signals at \(Re_c = 2000\) and 5000.

Table 1 Precision (p), recall (r), F-score (F), time-to-threshold (T2T), time-to-peak (T2P), and the normalized deviation between the threshold and the average value at the moment of flagging \([(\varepsilon _{\text {threshold}}^{\star } - \overline{\varepsilon _p^{\star }})/\sigma _{\varepsilon ^{\star }}]\), computed from multiple \(1000 t^\star\)-long signals at different Reynolds and wall distances.
Full size table

To contextualize the lead times given by the conditional time-only POD method, the advance warning time provided is compared to the time window in which the Hankel-DMD approach remains accurate. The Hankel-DMD methodology is a data-driven approach that predicts the evolution of time signals based on past observations. Using one or more measurements of the dynamical system, time delay embeddings are used to lift the signals into a higher-dimensional space, where the system’s temporal dynamics can be approximated with a set of DMD modes, each associated with a frequency and a growth or decay rate. The Hankel-DMD methodology is included as a comparison due to its similar low-data requirements and minimal computational cost, especially relative to more data-intensive approaches19. This is particularly relevant given the variability of signal statistics and extreme event characteristics across Reynolds numbers and wall-normal distances. Additionally, the method was recently employed to predict black swan events in epidemiological signals23. A more detailed discussion of the Koopman operator, as well as numerical algorithms for its discrete approximation, is provided in section "Koopman framework" of the supplementary information. One challenge with the DMD methodology is the selection of key parameters, such as the number of delay embeddings and the size of the training window. While the choice of these parameters is influenced by the signal’s characteristics, such as turbulence timescale or intermittency level, it remains unclear how to scale them to account for varying conditions, such as changes in Reynolds number or wall distance. Consequently, multiple combinations of parameters are tested, including the use of recent improvements, such as eigenvector and eigenvalue refinement46, which enhances the accuracy of the eigendecomposition of the underlying Koopman operator, and has been used to detect black swan events in epidemiology23. For all the predictions, the time window duration is set to be larger than the FTT, allowing the exploitation of the small periodicity present, especially in the lower Reynolds number cases. Further details on the Hankel-DMD predictions and the parameter ranges used are provided in section "Predictions of Time Signals using Hankel-DMD" of the supplementary information.

Figure 6 presents an extreme event for the signal at (a) \(y^+=1\) for \(Re_c=3000\), and (b) \(y^+=10\) for \(Re_c=5000\). Both of these extreme events are correctly predicted by the conditional POD method, with the times at which the events are forecasted indicated in the figure. From this point onward, predictions are made using the Hankel-DMD method with several combinations of parameters. The mean prediction and the 25-75th percentiles are shown for the predictions where the relative reconstruction error in the \(\ell _2\)-norm is smaller than 0.01. For \(Re_c = 3000\), the signal exhibits low-amplitude variations over an extended period before the extreme event occurs. While the Hankel-DMD predictions initially capture the local trend, their accuracy is only maintained for really short durations. The absence of similar events in the training data results in either uncontrolled growth in the predicted signal or forecasts that fail to capture the extremity of the event. At higher Reynolds numbers, even when extreme events are present in the training window, the Hankel-DMD method remains unable to predict them because of enhanced nonlinear effects and instabilities in the dynamical system. In contrast, the proposed conditional POD method shows robustness across varying Reynolds numbers and wall distances, offering competitive forecasting capabilities that often meet or exceed the warning times provided by the Hankel-DMD method.

Fig. 6
figure 6

Comparison of the lead time given by the conditional POD method and the time for which the Hankel-DMD method remains accurate. An extreme event is shown for both (a) \(Re_c=3000\) and \(y^+=1\), and (b) \(Re_c=5000\) and \(y^+=10\). For each case, an ensemble of trajectories is plotted starting from the point where the conditional POD method correctly flags an incoming extreme event.

Full size image

Conclusions

This work introduces a novel data-driven method for predicting extreme events that operates on-the-fly and requires minimal training data, making it particularly well-suited for significantly rare events. The method is applied to predict extreme dissipation events in turbulent flows across a range of wall distances and Reynolds numbers, ensuring its robustness across varying levels of intermittency and demonstrating its applicability to turbulent flow systems. From a short training signal, time segments leading to extreme events are used to compute the most energetic conditional time-only POD mode that captures the relative growth of the ensemble. Incoming real-time signals are compared to this mode, with similarities serving as indicators of approaching extreme events. Due to the severity of extreme events, the classification could be biased towards a higher recall and an earlier warning time, at the cost of more false positives. The classification of these segments as leading to extreme events is done automatically with a weighted SVM with a RBF kernel.

The method is tested on turbulent signals from a high-dimensional dynamical system, with different levels of intermittency. For signals in the viscous and logarithmic layers, which exhibit extreme dissipation events that deviate substantially from the more typical behavior, the method performs consistently well. Predicting the highest-intensity events in the buffer region is more challenging due to the less distinguishable behavior from the lower-intensity ones. The false positives given by the method tend to precede parts of the signals where substantial growth is observed, but the signal ultimately fails to cross the specified threshold. Nevertheless, the method demonstrates a strong performance across a range of Reynolds numbers and wall distances, both in terms of F-scores and lead times. The lead time of the predictions for extreme events is quantified through time-to-threshold and related metrics. A Hankel-DMD method is applied with a similar forecasting horizon. However, Hankel-DMD predictions show limitations when no extreme events are present in the immediate previous time window. In such cases, the Hankel-DMD method may fail to predict incoming extreme events, and once an extreme event is observed, the forecast can overestimate their frequency, making it generally ineffective for predicting rare events.

In this work, extreme events were labeled using a “hard” threshold based on the 99th percentile of the signal. However, this threshold is arbitrary, and some signals come very close to crossing it but just fall short. The utilization of alternative definitions of extreme events could offer a more complete characterization for signals with moderate intermittency, and address the potential ambiguity of fixed-threshold approaches in such cases. The use of alternative classifiers could also be explored to improve robustness and adaptability across different signal characteristics. Another avenue for future work is integrating the conditioned POD method with approaches that predict time signal evolution. In this regard, due to its low computational complexity, the conditional POD method could complement techniques like the Hankel-DMD. The conditional POD method could be used to identify instances when an impending extreme event is likely to occur, indicating when Hankel-DMD predictions may be unreliable. If an extreme event is anticipated, the forecast horizon of the Hankel-DMD could be shortened for improved accuracy, or its predictions could be discarded altogether. An additional extension of the current approach could involve incorporating more than just the leading POD mode into the analysis, potentially improving accuracy at the cost of increased complexity. This could be particularly valuable in fields where extreme events exhibit diverse growth dynamics, which may make a single mode insufficient to fully capture the variability in precursors. Finally, the application of the proposed methodology to higher Reynolds number flows and other flow configurations will be investigated, with particular attention to its predictive accuracy and the impact on achievable lead times.