Introduction

Recently, there has been a surge of interest among researchers and scientists in the resolution of nonlinear partial differential equations (NLPDE) and the soliton solutions obtained for these equations1,2,3,4,5,6. The nonlinear Schrödinger equation (NLSE) is a fundamental dispersive nonlinear partial differential equation that has been extensively studied for over four decades across various fields of physics. The search for soliton solutions in NLSEs has long been a crucial and fascinating area of research in engineering and applied sciences.7,8,9,10. Solitons play a pivotal role in advancing new theories in mathematical physics, particularly in applied physics. These solitary wave solutions provide valuable insights into the complex dynamics of various physical systems, spanning from fluid mechanics to optics and beyond11,12,13. To facilitate the investigation of soliton solutions, it is essential to apply suitable transformations that reduce nonlinear partial differential equations (NPDEs) to ordinary differential equations (ODEs). The reliability and precision of the derived analytical solutions are highly contingent upon the judicious choice of parameters and coefficients within these transformations. These elements are critical in assessing the physical relevance and applicability of the resulting mathematical models to real-world phenomena14,15,16,17.

Solitons are self-reinforcing wave packets that maintain their shape and speed during propagation, due to a delicate balance between dispersion and nonlinearity. In the context of optical systems, soliton solutions play a crucial role in describing stable light pulses traveling through nonlinear media, such as optical fibers. These optical solitons can take various forms bright, dark, and mixed types each characterized by unique amplitude, width, and localization properties18,19,20,21. Bright solitons represent localized peaks of intensity, commonly observed in focusing media, while dark solitons correspond to localized dips on a continuous wave background, typically found in defocusing media. Mixed solitons and wave-like structures offer even more complex dynamics, especially in systems governed by higher-order effects or fractional calculus. These optical soliton solutions are fundamental in advancing high-speed communication, signal processing, and laser technology, where stable, distortion-free transmission is essential22,23.

This study investigates the time-fractional improved (2+1)-dimensional nonlinear Schrödinger equation (NLSE), incorporating power-law nonlinearity, group-velocity dispersion, and spatio-temporal dispersion. This equation provides an effective model for pulse propagation in optical fibers. To analyze this system, we employ a novel technique introduced by the Russian mathematician Kudryashov, known as Kudryashov’s approach. This method has been instrumental in obtaining exact solutions to the differential equations governing the system, and has since been modified and further developed by Kudryashov and other researchers24,25,26,27,28,39,40,41. Using this approach, we derive a diverse range of optical solutions, including bell-shaped, bright, singular, and wave soliton solutions. These solutions exhibit distinct characteristics, offering valuable insights into nonlinear phenomena in optics. The application of this method allows researchers to explore and analyze complex nonlinear optical systems with greater confidence, contributing to a deeper understanding of their behavior and opening avenues for practical applications in optical communication, signal processing, and nonlinear optics. Unlike the Hirota method, which typically requires the construction of a bilinear form and dependent variable transformations, the Kudryashov method offers a more straightforward application by employing a direct ansatz, thereby reducing algebraic complexity an advantage particularly useful in nonlinear and fractional-order partial differential equations (PDEs). While the inverse scattering transform is a powerful technique, it is generally confined to integrable models and classical derivatives. In contrast, the Kudryashov method can be effectively adapted to fractional derivatives such as the conformable or Caputo types, making it especially suitable for the class of fractional models considered in this study. This study aims to explore the influence of the fractional order and nonlinear parameters on the behavior of localized wave structures, thereby enhancing our understanding of ultrashort pulse propagation in advanced optical environments. This model incorporates essential physical phenomena such as power-law nonlinearity, group-velocity dispersion, and spatiotemporal dispersion, all within a fractional-order framework. In particular, the presence of the second-order spatial derivative term represents group-velocity dispersion, which plays a vital role in the propagation and shaping of optical pulses in nonlinear media. The main aim and motivation of the present work are to construct and analyze a variety of exact optical solutions to the time-fractional improved (2+1)-dimensional nonlinear Schrödinger equation. The time-fractional improved (2+1)-dimensional NLSE, including those involving power-law nonlinearity, group-velocity dispersion, and spatio temporal dispersion:

$$\begin{aligned} i\frac{{{\partial }^{\tau }}p}{\partial {{t}^{\tau }}}+{{c}_{1}}{{p}_{xx}}+{{c}_{2}}{{p}_{yy}}+{{c}_{3}}\frac{{{\partial }^{\tau }}{{p}_{x}}}{\partial {{t}^{\tau }}}+{{c}_{4}}\frac{{{\partial }^{\tau }}{{p}_{y}}}{\partial {{t}^{\tau }}}+{{c}_{5}}{{\left| p \right| }^{2m}}p=0, \end{aligned}$$
(1)

where the complex function p(x, t) describes the wave profile. The real values \({{c}_{1}}\) and \({{c}_{2}}\) are the group-velocity dispersion coefficients, \({{c}_{3}}\) and \({{c}_{4}}\) are the spatio-temporal dispersions coefficients, \({{c}_{5}}\) is the power law nonlinearity coefficient, and the condition\(m\ne 2n,\,\forall \,n\in N\)should take in consideration to avoid self-focusing singularity29. Now, Eq. (1) is reduced to the (1+1)-dimensional case where \({{c}_{3}}={{c}_{4}}=0\)as follows:

$$\begin{aligned} i\frac{{{\partial }^{\tau }}p}{\partial {{t}^{\tau }}}+{{c}_{1}}{{p}_{xx}}+{{c}_{3}}\frac{{{\partial }^{\tau }}{{p}_{x}}}{\partial {{t}^{\tau }}}+{{c}_{5}}{{\left| p \right| }^{2m}}p=0,\,\,0<\tau \le 1, \end{aligned}$$
(2)

Due to the presence of the spatio-temporal dispersions terms\(\frac{{{\partial }^{\tau }}{{p}_{x}}}{\partial {{t}^{\tau }}}\)and \(\frac{{{\partial }^{\tau }}{{p}_{y}}}{\partial {{t}^{\tau }}}\), Eq. (1) is considered as a well-posted nonlinear Schrödinger equation30. The power law nonlinearity is commonly observed in various materials, such as semiconductors, and is also applicable to media where higher-order photon processes occur at different intensities. Additionally, the perturbed nonlinear Schrödinger equation with spatiotemporal dispersion and quadratic-cubic nonlinearity in (2+1) dimensions was studied in31. The optical soliton solutions to the (1+1)-dimension NLSE applying the functional variable and first integral methods are obtained by Mirzazadeh and Biswas32. By means of the semi-inverse variational principle and ansatz approach several optical soliton solutions to the (2+1)-dimension NLSE are studied by Xu et al. in28. The present model is studied by Matinfar and Hosseini in33 when \({{c}_{1}}={{c}_{2}}\)and \(m=1\), using the new Kudryashov method. Later, Akinyemi et al. in34 used the same technique to study the present model and find several bright and singular soliton solutions of the model with the condition \(m\ne 2n,\,\forall \,n\in N\).

The conformable fractional derivative of order \(\beta\) is defined as follows35:

$$\begin{aligned} {{L}_{\tau }}\left( z \right) (x)=\underset{r\rightarrow 0}{\mathop {\lim }}\,\frac{z(x+r{{x}^{1-\tau }})-z(x)}{r}, z:(0,\infty )\rightarrow R, \tau \in (0,1]. \end{aligned}$$

Description of the method

In this section, we employ the Kudryashov method, a recently developed analytical technique introduced by the Russian mathematician Nicolay Kudryashov in 202036. This method is particularly effective for obtaining exact solutions to nonlinear partial differential equations (NPDEs), as it leverages the structure of the logistic function to construct analytical solutions37,38. On the other hand, the current methodologies developed by Kudryashov for generating optical soliton solutions using the logistic function are found to be insufficient when applied to the extended Schrödinger equations in non-linear partial differential equations due to their unique structural characteristics. This novel technique is designed to overcome the challenges posed by the complexities inherent in obtaining optical soliton solutions. Specifically, we propose the utilization of an alternative function that is tailored to meet the specific requirements of addressing these complexities. Consider the following function:

$$\begin{aligned} R(\gamma )=\frac{2\eta K}{\left( {{K}^{2}}{{e}^{\eta \rho \gamma }}\mp s{{e}^{-\eta \rho \gamma }} \right) }. \end{aligned}$$
(3)

The hyperbolic function of (3) is as follows:

$$\begin{aligned} R(\gamma )=\frac{2\eta K}{\left( {{K}^{2}}\mp s \right) \cosh (\rho \gamma )+\left( {{K}^{2}}\pm s \right) \sinh (\rho \gamma )}, \end{aligned}$$
(4)

where \(\rho ,s,\) and K are real numbers, \(\eta =\mp 1\), and the functions \(R(\gamma )\) fulfills the following equation:

$$\begin{aligned} {{\left( \frac{dR(\gamma )}{d\gamma } \right) }^{2}}-{{\rho }^{2}}{{R}^{2}}(\gamma )\left( 1\pm s{{R}^{2}}(\gamma ) \right) =0. \end{aligned}$$
(5)

By employing the Kudryashov method and utilizing the corresponding base function, the following series representation is derived to express the solution of the studied model:

$$\begin{aligned} V(\gamma )=\sum \nolimits _{i=0}^{L}{{{q}_{i}}}{{\left( R(\gamma ) \right) }^{i}},\,{{q}_{L}}\ne 0, \end{aligned}$$
(6)

where L is the balancing value and the values \({{q}_{0}},\,{{q}_{1}},\,{{q}_{2}},...\) are the unknown constants need to be found.

Formulation of problem

Here, we utilized the present technique for solving the time-fractional improved (2+1)-dimensional nonlinear Schrödinger equation with the presence of the spatio-temporal dispersions, which enables us to obtain optical solutions with diverse forms. To initiate the analysis, we introduce the following transformations:

$$\begin{aligned} \begin{aligned}&p(x,y,t)=V(\gamma ){{e}^{i\vartheta (x,y,t)}},\, \\&\,\gamma =\,{{a}_{1}}x+{{b}_{1}}y+{{n}_{1}}\,\frac{{{t}^{\tau }}}{\tau }+w,\,\,\vartheta (x,t)=\,{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\,\frac{{{t}^{\tau }}}{\tau }+u, \\ \end{aligned} \end{aligned}$$
(7)

where \({{a}_{1}},{{b}_{1}},{{n}_{1}},{{a}_{2}},{{b}_{2}},{{n}_{2}},u,\) and w are the arbitrary constants. The above transformations are used to achieve the following nonlinear ordinary differential equation:

$$\begin{aligned} \begin{aligned}&({{a}_{1}}{{n}_{1}}{{c}_{3}}+a_{1}^{2}{{c}_{1}}+{{b}_{1}}{{n}_{1}}{{c}_{4}}+b_{1}^{2}{{c}_{2}}){V}''+i({{a}_{2}}{{n}_{1}}{{c}_{3}}+{{a}_{1}}{{n}_{2}}{{c}_{3}}+2{{a}_{1}}{{a}_{2}}{{c}_{1}}+{{b}_{2}}{{n}_{1}}{{c}_{4}}+{{b}_{1}}{{n}_{2}}{{c}_{4}}+2{{b}_{1}}{{b}_{2}}{{c}_{2}}+{{n}_{1}}){V}' \\&-({{a}_{2}}{{n}_{2}}{{c}_{3}}+a_{2}^{2}{{c}_{1}}+{{b}_{2}}{{n}_{2}}{{c}_{4}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}})V+{{c}_{5}}{{V}^{2m+1}}=0, \end{aligned} \end{aligned}$$
(8)

we can decompose the Eq. (7) into the following real and imaginary parts:

$$\begin{aligned} ({{a}_{1}}{{n}_{1}}{{c}_{3}}+a_{1}^{2}{{c}_{1}}+{{b}_{1}}{{n}_{1}}{{c}_{4}}+b_{1}^{2}{{c}_{2}}){V}''-({{a}_{2}}{{n}_{2}}{{c}_{3}}+a_{2}^{2}{{c}_{1}}+{{b}_{2}}{{n}_{2}}{{c}_{4}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}})V+{{c}_{5}}{{V}^{2m+1}}=0. \end{aligned}$$

and

$$\begin{aligned} ({{a}_{2}}{{n}_{1}}{{c}_{3}}+{{a}_{1}}{{n}_{2}}{{c}_{3}}+2{{a}_{1}}{{a}_{2}}{{c}_{1}}+{{b}_{2}}{{n}_{1}}{{c}_{4}}+{{b}_{1}}{{n}_{2}}{{c}_{4}}+2{{b}_{1}}{{b}_{2}}{{c}_{2}}+{{n}_{1}}){V}'=0. \end{aligned}$$
(9)

Solving the above equation, we obtain

$$\begin{aligned} {{n}_{1}}=\frac{{{a}_{1}}{{n}_{2}}{{c}_{3}}+2{{a}_{1}}{{a}_{2}}{{c}_{1}}+{{b}_{1}}{{n}_{2}}{{c}_{4}}+2{{b}_{1}}{{b}_{2}}{{c}_{2}}}{1+{{a}_{2}}{{c}_{3}}++{{b}_{2}}{{c}_{4}}}. \end{aligned}$$
(10)

To make the balance between \({{V}^{2m+1}}\) and \({V}''\) in Eq. (8), we obtain \(L=\frac{1}{m}\). Thus, we use this transform \(V(\gamma )=U{{(\gamma )}^{\frac{1}{m}}}\)in Eq. (8), the following equation is obtained:

Fig. 1
figure 1

The bell-shapes plots of \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\), where \(a_{1} = 0.4,a_{2} = 0.5,b_{1} = c_{1} = y = w = 0.3,\) \(c_{2} = c_{3} = 2,b_{2} = c_{4} = 1,c_{5} = 0.2,s = - 0.2,\)\(u = n_{1} = \rho = 0.1,K = 2\) and \(\tau =1\).

Full size image
Fig. 2
figure 2

The wave plots of \(\operatorname {Re}({{p}_{1}}(x,t))\) and \(\operatorname {Im}({{p}_{1}}(x,t))\) where \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\), where \(a_{1} = 0.4,a_{2} = 0.5,\)\(\:b_{1} = c_{1} = y = w = 0.3,\)\(\: c_{2} = c_{3} = 2,b_{2} = c_{4} = 1,\)\(\:c_{5} = 0.2,s = - 0.2,\)\(\: n_{1} = u = \rho = 0.1,K = 2\) and \(\tau =1\).

Full size image
Fig. 3
figure 3

The bell-shape and dark plots of \({{\left| {{p}_{14}}(x,t) \right| }^{2}}\) and \(\operatorname {Im}({{p}_{14}}(x,t))\) where \(a_{1} = b_{2} = 1,b_{1} = c_{1} = y = w = 0.3,\)\(\: c_{2} = 0.2,c_{3} = - 26.57,c_{4} = a_{2} = 0.1,c_{5} = 0.2,s = - 0.2,n_{1} = - 1.58,u = \rho = 0.1,K = 2\) and \(\tau =1\).

Full size image
Fig. 4
figure 4

The dark-bright plot of \(\operatorname {Im}({{p}_{6}}(x,t))\) where \(a_{1} = b_{2} = 1,b_{1} = c_{1} = y = w = 0.3,c_{2} = 0.2,\)\(\: c_{3} = - 26.57,c_{4} = a_{2} = 0.1,c_{5} = 0.2,s = - 0.2,n_{1} = - 1.5,u = \rho = 0.1,K = 2\) and \(\tau =1\).

Full size image
Fig. 5
figure 5

The bright plot of \({{\left| {{p}_{17}}(x,t) \right| }^{2}}\) where \(a_{1} = 2,b_{2} = - 1,b_{1} = c_{1} = ,c_{3} = y = w = 0.3,\)\(\: c_{2} = 0.2,a_{2} = 0.149,c_{5} = 2,s = - 0.2,n_{1} = 0.669,n_{2} = - 0.1,u = c_{4} = \rho = 1,\) and \(K=2\).

Full size image
$$\begin{aligned} \begin{aligned}&({{a}_{1}}{{n}_{1}}{{c}_{3}}+a_{1}^{2}{{c}_{1}}+{{b}_{1}}{{n}_{1}}{{c}_{4}}+b_{1}^{2}{{c}_{2}})(mU{U}''+(1-m){{{{U}'}}^{2}})-{{m}^{2}}({{a}_{2}}{{n}_{2}}{{c}_{3}}+a_{2}^{2}{{c}_{1}}+{{b}_{2}}{{n}_{2}}{{c}_{4}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}}){{U}^{2}} \\&+{{m}^{2}}{{c}_{5}}{{U}^{4}}=0. \\ \end{aligned} \end{aligned}$$
(11)

Here, balancing \(U{U}''\) with \({{U}^{4}}\) in this equation, we can have \(L=1\) and the solution (5) is set up as

$$\begin{aligned} U(\gamma )={{q}_{0}}+{{q}_{1}}R(\gamma ),\,{{q}_{1}}\ne 0. \end{aligned}$$
(12)

Now, inserting Eq. (12) along with Eq. (4) into (11) and setting the coefficients of \({{R}^{j}}(\gamma )(j=0,1,...)\) to be zero, we obtain the following nonlinear equations:

$$\begin{aligned} {{\left( R(\gamma ) \right) }^{0}}\,\,:\,-{{m}^{2}}a_{2}^{2}{{c}_{1}}q_{0}^{2}-{{m}^{2}}b_{2}^{2}{{c}_{2}}q_{0}^{2}-{{m}^{2}}{{n}_{2}}q_{0}^{2}-{{m}^{2}}{{a}_{2}}{{c}_{3}}{{n}_{2}}q_{0}^{2}-{{m}^{2}}{{b}_{2}}{{c}_{4}}{{n}_{2}}q_{0}^{2}+{{m}^{2}}{{c}_{5}}q_{0}^{4}=0,~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \begin{aligned}&{{\left( R(\gamma ) \right) }^{1}}:\,m{{\rho }^{2}}a_{1}^{2}{{c}_{1}}{{q}_{0}}{{q}_{1}}-2{{m}^{2}}a_{2}^{2}{{c}_{1}}{{q}_{0}}{{q}_{1}}+m{{\rho }^{2}}b_{1}^{2}{{c}_{2}}{{q}_{0}}{{q}_{1}}-2{{m}^{2}}b_{2}^{2}{{c}_{2}}{{q}_{0}}{{q}_{1}}+m{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}{{q}_{0}}{{q}_{1}}+m{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}{{q}_{0}}{{q}_{1}} \\&-2{{m}^{2}}{{n}_{2}}{{q}_{0}}{{q}_{1}}-2{{m}^{2}}{{a}_{2}}{{c}_{3}}{{n}_{2}}{{q}_{0}}{{q}_{1}}-2{{m}^{2}}{{b}_{2}}{{c}_{4}}{{n}_{2}}{{q}_{0}}{{q}_{1}}+4{{m}^{2}}{{c}_{5}}q_{0}^{3}{{q}_{1}}=0, \\ \end{aligned}\\ \begin{aligned}&{{\left( R(\gamma ) \right) }^{2}}:{{\rho }^{2}}a_{1}^{2}{{c}_{1}}q_{1}^{2}-{{m}^{2}}a_{2}^{2}{{c}_{1}}q_{1}^{2}+{{\rho }^{2}}b_{1}^{2}{{c}_{2}}q_{1}^{2}-{{m}^{2}}b_{2}^{2}{{c}_{2}}q_{1}^{2}+{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}q_{1}^{2}+{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}q_{1}^{2}-{{m}^{2}}{{n}_{2}}q_{1}^{2}-{{m}^{2}}{{a}_{2}}{{c}_{3}}{{n}_{2}}q_{1}^{2} \\&-{{m}^{2}}{{b}_{2}}{{c}_{4}}{{n}_{2}}q_{1}^{2}+6{{m}^{2}}{{c}_{5}}q_{0}^{2}q_{1}^{2}=0, \\ \end{aligned}\\ {{\left( R(\gamma ) \right) }^{3}}:\,2ms{{\rho }^{2}}a_{1}^{2}{{c}_{1}}{{q}_{0}}{{q}_{1}}+2ms{{\rho }^{2}}b_{1}^{2}{{c}_{2}}{{q}_{0}}{{q}_{1}}+2ms{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}{{q}_{0}}{{q}_{1}}+2ms{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}{{q}_{0}}{{q}_{1}}+4{{m}^{2}}{{c}_{5}}{{q}_{0}}q_{1}^{3}=0,\\ \begin{aligned}&{{\left( R(\gamma ) \right) }^{4}}:\,s{{\rho }^{2}}a_{1}^{2}{{c}_{1}}q_{1}^{2}+ms{{\rho }^{2}}a_{1}^{2}{{c}_{1}}q_{1}^{2}+s{{\rho }^{2}}b_{1}^{2}{{c}_{2}}q_{1}^{2}+ms{{\rho }^{2}}b_{1}^{2}{{c}_{2}}q_{1}^{2}+s{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}q_{1}^{2}+ms{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}q_{1}^{2}+s{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}q_{1}^{2} \\&+ms{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}q_{1}^{2}+{{m}^{2}}{{c}_{5}}q_{1}^{4}=0. \\ \end{aligned} \end{aligned}$$

This system of nonlinear equations yields the following results:

Result 1.

$$\begin{aligned} \begin{aligned}&{{q}_{1}}=\frac{\sqrt{s\left( 1+m \right) }\rho \sqrt{a_{2}^{2}b_{1}^{2}{{c}_{1}}-b_{2}^{2}\left( a_{1}^{2}{{c}_{1}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}} \right) +{{a}_{2}}b_{1}^{2}{{c}_{3}}{{n}_{2}}+b_{1}^{2}\left( 1+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}}}}{\sqrt{{{c}_{5}}\left( -{{\rho }^{2}}b_{1}^{2}+{{m}^{2}}b_{2}^{2} \right) }} \\&{{c}_{2}}=\pm \frac{{{\rho }^{2}}a_{1}^{2}{{c}_{1}}+{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}+{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}-{{m}^{2}}\left( a_{2}^{2}{{c}_{1}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }{-{{\rho }^{2}}b_{1}^{2}+{{m}^{2}}b_{2}^{2}},{{q}_{0}}=0. \end{aligned} \end{aligned}$$
(13)

By using (2), (4), (6), (10), and (13) The following solutions can be obtained:

$$\begin{aligned} {{p}_{1}}(x,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{\pm 2K\rho \sqrt{s+sm}{{\mu }_{1}}}{\left( {{\text {e}}^{-\rho \gamma }}{{K}^{2}}-{{\text {e}}^{\rho \gamma }}s \right) \sqrt{\left( {{\rho }^{2}}b_{1}^{2}-{{m}^{2}}b_{2}^{2} \right) {{c}_{5}}}} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(14)

where \(\gamma =w+{{a}_{1}}x+{{b}_{1}}y+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau },\phi (x,y,t)=u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau }\) and \({{\mu }_{1}}=\sqrt{b_{2}^{2}\left( a_{1}^{2}{{c}_{1}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}} \right) -a_{2}^{2}b_{1}^{2}{{c}_{1}}-\left( {{a}_{2}}b_{1}^{2}{{c}_{3}}{{n}_{2}}+b_{1}^{2}\left( 1+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }\).

The following solutions is the hyperbolic forms of (14):

$$\begin{aligned} {{p}_{2}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{\pm 2K\rho \sqrt{s(1+m)}{{\mu }_{1}}}{\left( \left( {{K}^{2}}-s \right) \cosh \left( \rho \gamma \right) +\left( {{K}^{2}}+s \right) \sinh \left( \rho \gamma \right) \right) \sqrt{\left( {{\rho }^{2}}b_{1}^{2}-{{m}^{2}}b_{2}^{2} \right) {{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(15)

Plugging \(s=-{{K}^{2}}\) in (15), the below optical solutions are acquired:

$$\begin{aligned} {{p}_{3}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{\left| K \right| \rho {{\mu }_{2}}\operatorname {sech}\left( \rho \gamma \right) }{\pm K\sqrt{\left( {{\rho }^{2}}b_{1}^{2}-{{m}^{2}}b_{2}^{2} \right) {{c}_{5}}}} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(16)

where \({{\mu }_{2}}=\sqrt{\left( 1+m \right) \left( a_{2}^{2}b_{1}^{2}{{c}_{1}}-b_{2}^{2}\left( a_{1}^{2}{{c}_{1}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}} \right) -{{a}_{2}}b_{1}^{2}{{c}_{3}}{{n}_{2}}-b_{1}^{2}\left( 1+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }\).

Plugging \(s={{K}^{2}}\) in (15), the below singular soliton solutions are acquired:

$$\begin{aligned} {{p}_{4}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{\left| K \right| \rho {{\mu }_{2}}\operatorname {csch}\left( \rho \gamma \right) }{\pm K\sqrt{\left( {{\rho }^{2}}b_{1}^{2}-{{m}^{2}}b_{2}^{2} \right) {{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(17)

Result 2.

$$\begin{aligned} \begin{aligned}&{{q}_{0}}=0,{{q}_{1}}=\pm \frac{\sqrt{-s}\sqrt{\left( 1+m \right) \left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }}{\sqrt{{{c}_{5}}}},{{b}_{1}}=\frac{{{m}^{2}}{{b}_{2}}{{n}_{2}}}{{{\rho }^{2}}{{n}_{1}}},{{c}_{4}}=free, \\&{{a}_{1}}=\pm \frac{{{\rho }^{4}}{{c}_{3}}n_{1}^{3}+\sqrt{4{{m}^{2}}{{\rho }^{6}}{{c}_{1}}\left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}} \right) n_{1}^{4}+{{\rho }^{8}}c_{3}^{2}n_{1}^{6}+4{{m}^{2}}{{\rho }^{6}}{{c}_{1}}\left( 1+{{a}_{2}}{{c}_{3}} \right) n_{1}^{4}{{n}_{2}}-4{{m}^{4}}{{\rho }^{4}}b_{2}^{2}{{c}_{1}}{{c}_{2}}n_{1}^{2}n_{2}^{2}}}{2{{\rho }^{4}}{{c}_{1}}n_{1}^{2}}. \end{aligned} \end{aligned}$$
(18)

The optical soliton solutions to the Eq. (1) utilizing (2), (4), (6), (10), and (18) are as follows:

Fig. 6
figure 6

The mixed dark-bright plots of \(\operatorname {Re}({{p}_{17}}(x,t))\) where \(a_{1} = 2,b_{2} = - 1,b_{1} = c_{1} = ,c_{3} = y = w = 0.3,\)\(\:c_{2} = 0.2,a_{2} = 0.149,c_{5} = 2,s = - 0.2,n_{1} = 0.669,n_{2} = - 0.1,u = c_{4} = \rho = 1,\) and \(K=2\).

Full size image
Fig. 7
figure 7

The singular plots of \({{\left| {{p}_{20}}(x,t) \right| }^{2}}\) and \(\operatorname {Im}({{p}_{20}}(x,t))\), where \(a_{1} = 2,b_{2} = - 1,b_{1} = c_{1} = ,c_{3} = y = w = 0.3,\)\(\: c_{2} = 0.2,a_{2} = 0.149,c_{5} = 2,n_{1} = 0.669,n_{2} = - 0.1,u = c_{4} = \rho = 1,K = 2\), and \(\tau =1\).

Full size image
Fig. 8
figure 8

The bright plot of \({{\left| {{p}_{1}}(x) \right| }^{2}}\) and wave plot of \(\operatorname {Re}({{p}_{1}}(x))\) with the effect of \(\tau\), where \(a_{1} = 0.4,a_{2} = 0.5,\)\(\: b_{1} = c_{1} = y = w = 0.3,c_{2} = 1.482,c_{3} = 2,b_{2} = c_{4} = 1,c_{5} = 0.2,s = - 0.2,n_{1} = - 0.3731,u = \rho = 0.1,\) and \(K=2\).

Full size image
Fig. 9
figure 9

The bright plot of \({{\left| {{p}_{18}}(x) \right| }^{2}}\) and dark-bright of \(\operatorname {Im}({{p}_{18}}(x))\) with the effect of \(\tau\), where \(a_{1} = 2,b_{2} = - 1,b_{1} = c_{1} = ,\)\(\:c_{3} = y = w = 0.3,c_{2} = 0.2,a_{2} = 0.149,c_{5} = 2,n_{1} = 0.669,n_{2} = - 0.1,u = c_{4} = \rho = 1,\) and \(K=2\).

Full size image
Fig. 10
figure 10

The bright plot of \({{\left| {{p}_{1}}(x) \right| }^{2}}\) and wave plot of \(\operatorname {Re}({{p}_{1}}(x))\) with the effect of m, where \(a_{1} = 0.4,a_{2} = 0.5,\)\(\: b_{1} = c_{1} = y = w = 0.3,c_{2} = 1.482,c_{3} = 2,b_{2} = c_{4} = 1,c_{5} = 0.2,s = - 0.2,n_{1} = - 0.3731,u = \rho = 0.1,\) and \(K=2\).

Full size image
$$\begin{aligned} {{p}_{5}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{\pm K\sqrt{-s}\sqrt{\left( 1+m \right) \left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }}{\sqrt{{{c}_{5}}}\left( {{\text {e}}^{-\rho \left( w+t{{n}_{1}}+\frac{{{m}^{2}}y{{b}_{2}}{{n}_{2}}}{{{\rho }^{2}}{{n}_{1}}}+{{a}_{1}}x \right) }}{{K}^{2}}-{{\text {e}}^{\rho \left( w+t{{n}_{1}}+\frac{{{m}^{2}}y{{b}_{2}}{{n}_{2}}}{{{\rho }^{2}}{{n}_{1}}}+{{a}_{1}}x \right) }}s \right) } \right) }^{\frac{1}{m}}}. \end{aligned}$$
(19)

The following solutions is the hyperbolic forms of (19):

$$\begin{aligned} {{p}_{6}}(x,y,t)={{\text {e}}^{\text {i}\left( u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{\left( \frac{\pm 2K\sqrt{-s}\sqrt{\left( 1+m \right) \left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }}{\left( \left( {{K}^{2}}-s \right) \cosh \left( \rho \gamma \right) +\left( {{K}^{2}}+s \right) \sinh \left( \rho \gamma \right) \right) \sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(20)

where \(\gamma =w+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau }+\frac{{{m}^{2}}{{b}_{2}}{{n}_{2}}}{{{\rho }^{2}}{{n}_{1}}}y+{{a}_{1}}x.\)

Plugging \(s=-{{K}^{2}}\) in (20), the below optical solutions are acquired:

$$\begin{aligned} {{p}_{7}}(x,y,t)={{\text {e}}^{\text {i}\left( u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{\left( \frac{\mp \left| K \right| \sqrt{\left( 1+m \right) \left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }\operatorname {sech}\left( \rho \gamma \right) }{K\sqrt{-{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(21)

Plugging \(s={{K}^{2}}\) in (20), the below singular soliton solutions are acquired:

$$\begin{aligned} {{p}_{8}}(x,y,t)={{\text {e}}^{\text {i}\left( u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{\left( \mp \frac{\text {i}\left| K \right| \operatorname {csch}\left( \rho \gamma \right) \sqrt{\left( 1+m \right) \left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) }}{K\sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(22)

Result 3.

$$\begin{aligned} \begin{aligned}&{{q}_{1}}=\frac{\pm \rho \sqrt{s\left( 1+m \right) }\sqrt{a_{1}^{2}{{a}_{2}}{{c}_{1}}{{n}_{2}}+{{a}_{2}}{{b}_{1}}\left( {{b}_{1}}{{c}_{2}}+{{c}_{4}}{{n}_{1}} \right) {{n}_{2}}-{{a}_{1}}{{n}_{1}}\left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}}+{{b}_{2}}{{c}_{4}}{{n}_{2}} \right) }}{\sqrt{{{c}_{5}}\left( {{\rho }^{2}}{{a}_{1}}{{n}_{1}}-{{m}^{2}}{{a}_{2}}{{n}_{2}} \right) }} \\&{{c}_{3}}=\frac{{{\rho }^{2}}a_{1}^{2}{{c}_{1}}+{{\rho }^{2}}{{b}_{1}}\left( {{b}_{1}}{{c}_{2}}+{{c}_{4}}{{n}_{1}} \right) -{{m}^{2}}\left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}}+{{b}_{2}}{{c}_{4}}{{n}_{2}} \right) }{-{{\rho }^{2}}{{a}_{1}}{{n}_{1}}+{{m}^{2}}{{a}_{2}}{{n}_{2}}},{{q}_{0}}=0. \\ \end{aligned} \end{aligned}$$
(23)

The optical soliton solutions to the Eq. (1) utilizing (2), (4), (6), (10), and (23) are as follows:

$$\begin{aligned} {{p}_{9}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{2K\rho \sqrt{s\left( 1+m \right) }{{\mu }_{3}}}{\pm \left( {{\text {e}}^{-\rho \left( w+x{{a}_{1}}+y{{b}_{1}}+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{K}^{2}}-{{\text {e}}^{\rho \left( w+x{{a}_{1}}+y{{b}_{1}}+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau } \right) }}s \right) \sqrt{{{c}_{5}}\left( {{\rho }^{2}}{{a}_{1}}{{n}_{1}}-{{m}^{2}}{{a}_{2}}{{n}_{2}} \right) }} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(24)

where \({{\mu }_{3}}=\sqrt{a_{1}^{2}{{a}_{2}}{{c}_{1}}{{n}_{2}}+{{a}_{2}}{{b}_{1}}\left( {{b}_{1}}{{c}_{2}}+{{c}_{4}}{{n}_{1}} \right) {{n}_{2}}-{{a}_{1}}{{n}_{1}}\left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}}+{{b}_{2}}{{c}_{4}}{{n}_{2}} \right) }\) and \(\phi (x,y,t)=u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau }\).

The following solutions is the hyperbolic forms of (23):

$$\begin{aligned} {{p}_{10}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{2K\rho \sqrt{s\left( 1+m \right) }{{\mu }_{3}}}{\pm \left( \left( {{K}^{2}}-s \right) \cosh \left( \rho \gamma \right) +\left( {{K}^{2}}+s \right) \sinh \left( \rho \gamma \right) \right) \sqrt{{{c}_{5}}\left( {{\rho }^{2}}{{a}_{1}}{{n}_{1}}-{{m}^{2}}{{a}_{2}}{{n}_{2}} \right) }} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(25)

where \(\gamma =w+{{a}_{1}}x+{{b}_{1}}y+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau }.\) Plugging \(s=-{{K}^{2}}\) in (25), the below optical solutions are acquired:

$$\begin{aligned} {{p}_{11}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{{{\mu }_{4}}\left| K \right| \rho \operatorname {sech}\left( \rho \gamma \right) }{\pm K\sqrt{{{c}_{5}}\left( -{{\rho }^{2}}{{a}_{1}}{{n}_{1}}+{{m}^{2}}{{a}_{2}}{{n}_{2}} \right) }} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(26)

where \({{\mu }_{4}}=\sqrt{\left( 1+m \right) \left( a_{1}^{2}{{a}_{2}}{{c}_{1}}{{n}_{2}}+{{a}_{2}}{{b}_{1}}\left( {{b}_{1}}{{c}_{2}}+{{c}_{4}}{{n}_{1}} \right) {{n}_{2}}-{{a}_{1}}{{n}_{1}}\left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+{{n}_{2}}+{{b}_{2}}{{c}_{4}}{{n}_{2}} \right) \right) }\).

Plugging \(s={{K}^{2}}\) in (25), the below singular soliton solutions are acquired:

$$\begin{aligned} {{p}_{12}}(x,y,t)={{\text {e}}^{\text {i}\phi (x,y,t)}}{{\left( \frac{i\left| K \right| \rho {{\mu }_{4}}\operatorname {csch}\left( \rho \gamma \right) }{\mp K\sqrt{{{c}_{5}}\left( -{{\rho }^{2}}{{a}_{1}}{{n}_{1}}+{{m}^{2}}{{a}_{2}}{{n}_{2}} \right) }} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(27)

Result 4.

$$\begin{aligned} \begin{aligned}&{{q}_{0}}=0,{{q}_{1}}=\pm \frac{\sqrt{-s\left( 1+m \right) }\sqrt{a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}}}}{\sqrt{{{c}_{5}}}}, \\&{{b}_{1}}=\pm \frac{\sqrt{{{\rho }^{4}}c_{4}^{2}n_{1}^{2}-4{{\rho }^{2}}{{c}_{2}}\left( {{\rho }^{2}}a_{1}^{2}{{c}_{1}}+{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}-{{m}^{2}}\left( a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}} \right) \right) }-{{\rho }^{2}}{{c}_{4}}{{n}_{1}}}{2{{\rho }^{2}}{{c}_{2}}}. \\ \end{aligned} \end{aligned}$$
(28)

The optical soliton solutions to the Eq. (1) utilizing (2), (4), (6), (10), and (28) are as follows:

$$\begin{aligned} {{p}_{13}}(x,y,t)={{\left( \frac{\pm K\sqrt{-s\left( 1+m \right) }\sqrt{a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}}}}{\left( {{\text {e}}^{-\rho \left( w+x{{a}_{1}}+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau }-\frac{y\left( {{\rho }^{2}}{{c}_{4}}{{n}_{1}}\pm {{b}_{1}} \right) }{2{{\rho }^{2}}{{c}_{2}}} \right) }}{{K}^{2}}-{{\text {e}}^{\rho \left( w+x{{a}_{1}}+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau }-\frac{y\left( {{\rho }^{2}}{{c}_{4}}{{n}_{1}}\pm {{b}_{1}} \right) }{2{{\rho }^{2}}{{c}_{2}}} \right) }}s \right) \sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(29)

The following solutions is the hyperbolic forms of (29):

$$\begin{aligned} {{p}_{14}}(x,y,t)={{\text {e}}^{\text {i}\left( u+{{a}_{2}}x+{{b}_{2}}y+\frac{{{t}^{\tau }}}{\tau }{{n}_{2}} \right) }}{{\left( \frac{\pm 2K\sqrt{-s\left( 1+m \right) }\sqrt{a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}}}}{\left( \left( {{K}^{2}}-s \right) \cosh \left( \rho \gamma \right) +\left( {{K}^{2}}+s \right) \sinh \left( \rho \gamma \right) \right) \sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(30)

where \(\gamma =w+x{{a}_{1}}+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau }-\frac{y\left( {{\rho }^{2}}{{c}_{4}}{{n}_{1}}\pm {{b}_{1}} \right) }{2{{\rho }^{2}}{{c}_{2}}}.\) Plugging \(s=-{{K}^{2}}\) in (30), the below optical solutions are acquired:

$$\begin{aligned} {{p}_{15}}(x,y,t)={{\text {e}}^{\text {i}\left( u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{\left( \frac{\pm \left| K \right| \sqrt{1+m}\operatorname {sech}\left( \rho \gamma \right) \sqrt{a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}}}}{K\sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(31)

Plugging \(s={{K}^{2}}\) in (20), the below singular soliton solutions are acquired:

$$\begin{aligned} {{p}_{16}}(x,y,t)={{\text {e}}^{\text {i}\left( u+{{a}_{2}}x+{{b}_{2}}y+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{\left( \frac{\pm i\left| K \right| \sqrt{1+m}\operatorname {csch}\left( \rho \gamma \right) \sqrt{a_{2}^{2}{{c}_{1}}+b_{2}^{2}{{c}_{2}}+\left( 1+{{a}_{2}}{{c}_{3}}+{{b}_{2}}{{c}_{4}} \right) {{n}_{2}}}}{K\sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(32)

Result 5.

$$\begin{aligned} \begin{aligned}&{{q}_{0}}=0,{{q}_{1}}=\pm \frac{\rho \sqrt{-s\left( 1+m \right) }\sqrt{a_{1}^{2}{{c}_{1}}+b_{1}^{2}{{c}_{2}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}}}}{m\sqrt{{{c}_{5}}}}, \\&{{a}_{2}}=\mp \frac{\pm {{m}^{2}}{{c}_{3}}{{n}_{2}}+\sqrt{{{m}^{4}}c_{3}^{2}n_{2}^{2}+4{{m}^{2}}{{c}_{1}}\left( {{\rho }^{2}}a_{1}^{2}{{c}_{1}}+{{\rho }^{2}}b_{1}^{2}{{c}_{2}}+{{\rho }^{2}}{{a}_{1}}{{c}_{3}}{{n}_{1}}+{{\rho }^{2}}{{b}_{1}}{{c}_{4}}{{n}_{1}}-{{m}^{2}}\left( b_{2}^{2}{{c}_{2}}+{{n}_{2}}+{{b}_{2}}{{c}_{4}}{{n}_{2}} \right) \right) }}{2{{m}^{2}}{{c}_{1}}}. \end{aligned} \end{aligned}$$
(33)

The optical soliton solutions to the Eq. (1) utilizing (2), (4), (6), (10), and (33) are as follows:

$$\begin{aligned} {{p}_{17}}(x,y,t)={{\text {e}}^{\text {i}\left( u+y{{b}_{2}}+t{{n}_{2}}\pm {{a}_{2}}x \right) }}{{\left( \frac{\pm \text {2}K\rho \sqrt{-s\left( 1+m \right) }\sqrt{a_{1}^{2}{{c}_{1}}+b_{1}^{2}{{c}_{2}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}}}}{m\left( {{\text {e}}^{-\rho \left( w+{{a}_{1}}x+{{b}_{1}}y+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau } \right) }}{{K}^{2}}-{{\text {e}}^{\rho \left( w+{{a}_{1}}x+{{b}_{1}}y+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau } \right) }}s \right) \sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(34)

The following solutions is the hyperbolic forms of (33):

$$\begin{aligned} {{p}_{18}}(x,y,t)={{\text {e}}^{\text {i}\left( u+y{{b}_{2}}+t{{n}_{2}}\pm {{a}_{2}}x \right) }}{{\left( \frac{K\sqrt{1+m}\rho \sqrt{a_{1}^{2}{{c}_{1}}+b_{1}^{2}{{c}_{2}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}}}}{m\left( \left( {{K}^{2}}-s \right) \cosh \left( \rho \gamma \right) +\left( {{K}^{2}}+s \right) \sinh \left( \rho \gamma \right) \right) \sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}, \end{aligned}$$
(35)

where \(\gamma =w+{{a}_{1}}x+{{b}_{1}}y+{{n}_{1}}\frac{{{t}^{\tau }}}{\tau }.\) Plugging \(s=-{{K}^{2}}\) in (34), the below optical solutions are acquired:

$$\begin{aligned} {{p}_{19}}(x,y,t)={{\text {e}}^{\text {i}\left( u+y{{b}_{2}}+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau }\pm {{a}_{2}}x \right) }}{{\left( \frac{\pm \sqrt{1+m}\rho \operatorname {sech}\left( \rho \gamma \right) \sqrt{a_{1}^{2}{{c}_{1}}+b_{1}^{2}{{c}_{2}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}}}}{Km\sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(36)

Plugging \(s={{K}^{2}}\) in (34), the following singular soliton solutions are obtained:

$$\begin{aligned} {{p}_{20}}(x,y,t)={{\text {e}}^{\text {i}\left( u+y{{b}_{2}}+{{n}_{2}}\frac{{{t}^{\tau }}}{\tau }\pm {{a}_{2}}x \right) }}{{\left( \frac{\text {i}\left| K \right| \rho \sqrt{1+m}\operatorname {csch}\left( \rho \gamma \right) \sqrt{a_{1}^{2}{{c}_{1}}+b_{1}^{2}{{c}_{2}}+\left( {{a}_{1}}{{c}_{3}}+{{b}_{1}}{{c}_{4}} \right) {{n}_{1}}}}{Km\sqrt{{{c}_{5}}}} \right) }^{\frac{1}{m}}}. \end{aligned}$$
(37)

Results and discussion

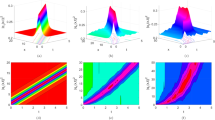
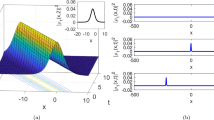
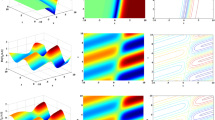
In this section, appropriate physical parameter values were chosen to demonstrate the scope and behavior of the proposed model. A series of graphical representations were provided to examine the features of the newly derived optical soliton solutions and to gain insights into their physical significance. To investigate the effects of key parameters, two-dimensional plots were constructed, illustrating how the fractional-order derivative \(\tau\), the temporal variable, and the polynomial degree m influence the soliton dynamics discussed in this study. Additionally, contour, 2D, and 3D plots are used to visualize several novel soliton solutions. Figures 1-10 (graphs a and b) depict these solutions in detail.

It is clear that the optical soliton solution \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\) and \({{\left| {{p}_{10}}(x,t) \right| }^{2}}\) are bell-shapes from Figure 1. graph (a) and Figure 3. graph (a), respectively. Bell-shaped and bright optical solitons proved to be highly suitable for long-distance communication within optical fibers. Their inherent ability to preserve both shape and amplitude throughout propagation ensured minimal signal distortion, thereby maintaining data fidelity over extended transmission ranges. This remarkable stability underpinned their practical effectiveness in optical communication systems. The real part and imaginary part of the optical soliton solution \({{p}_{1}}(x,t)\) are wave solutions from Figure 2. graph (a) and graph (b), the real part and imaginary part of solution \({{p}_{10}}(x,t)\) are dark-bright soliton solutions from Fig. 3. graph (b) and Fig. 4. graph (a), respectively. The bright soliton solutions of square modulus solution \({{p}_{17}}(x,t)\) for \(\tau =1\) and \(\tau =0.5\) are plotted in Fig. 5. graph (a) and graph (b), respectively. The real part of the solution \({{p}_{17}}(x,t)\) is mixed dark-bright soliton solution which is depicted for both cases \(\tau =1\) and \(\tau =0.9\) from Fig. 6. graph (a) and graph (b), respectively. A decrease in the conformable parameter \(\tau\) can significantly affect the soliton’s characteristics, potentially modifying its amplitude, shape, and the balance between its dark and bright components. Such alterations may influence the soliton’s propagation speed and stability, possibly resulting in new interaction dynamics between the dark and bright regions or even reshaping the overall soliton profile. Mixed dark-bright soliton solutions represent the coexistence of both dark and bright soliton features within a single wave structure where the dark soliton appears as a localized dip in intensity, and the bright soliton emerges as a localized peak. This coexistence gives rise to regions of varying amplitude, facilitating intricate interactions between the dark and bright components and influencing the overall wave dynamics. The singular soliton solutions of \(|{{p}_{20}}(x,t)|^2\) and \(Im({p}_{20}(x,t))\) are depicted from Fig. 7. graphs (a) and (b), respectively. However, the impact of degree m , parameter of time, and \(\tau\) on the two-dimensional plots are given in this paper. In Fig. 8. and 9. graph (a) and (b) the influence of various values of fractional order \(\tau\) on the square modulus and imaginary part of \({{p}_{1}}(x,t)\) and the square modulus and real part of the exact solution \({{p}_{18}}(x,t)\) is illustrated, respectively. The influence of time parameter on \(|{{p}_{1}}(x,t)|^2\) and of \(Re({{p}_{10}}(x,t))\) is shown in Fig. 1. graph (b) and Fig. 4. graph(b). Finally, in Fig. 10. graph(a) and graph(b) the effect of several values of m on the square modulus and imaginary part of \({{p}_{1}}(x,t)\) is illustrated.

By manipulating the parameters of the soliton solution (such as \(\tau\)), you can control the pulse width and shape. This is crucial for ensuring that the pulse has the right characteristics for efficient transmission through optical fibers. The mixed dark-bright soliton could be engineered to have specific properties, such as low dispersion or optimal peak power for long-distance propagation. One of the most valuable aspects of solitons in optical fibers is their ability to resist dispersion. In systems where high-power pulses are required, maintaining the shape and amplitude of the pulse as it travels down the fiber is key. The present solitons may offer improved resilience to dispersion and other nonlinear effects, making them suitable for high-bandwidth communication.

Modulation instability analysis

Modulation instability (MI) analysis leads to dispersion and nonlinear effects in various nonlinear system. We use linear stability investigation to study the MI analysis of the governing Eq. (1). The stability or instability of the system is determined through the analysis of the dispersion relation and gain spectrum. This analysis provides insight into how various parameters influence wave evolution, which is crucial for understanding the dynamic stability of solitons in practical applications, such as nonlinear optical systems. Modulation instability can lead to the formation of new wave structures or impact signal transmission. Steady state solution of the Eq.(1) is as follows:

$$\begin{aligned} p(x,y,t)= \left( Q(x,y,t)+\sqrt{\varpi }\right) e^{(i x \varpi )} \end{aligned}$$
(38)

Where \(\varpi\) is a sensitivity parameter. By inserting the Eq. (38) into Eq. (1), and by linearization we get the following result.

$$\begin{aligned} \left( Q^*+Q\right) \left( c_5 \varpi -c_1 \varpi ^2\right) +i c_3 \varpi \left( Q_t+\left( Q_t\right) {}^*\right) +i c_1 \varpi \left( Q_x+\left( Q_x\right) {}^*\right) +c_3 Q_{\text {xt}}+c_1 Q_{\text {xx}}+c_4 Q_{\text {yt}}+c_2 Q_{\text {yy}}+i Q_t=0 \end{aligned}$$
(39)

Now, supposing the solution Eq. (39) is given by

$$\begin{aligned} Q(x,y,t)=a_1 e^{(i (a x+b y-t \Psi ))} +a_2 e^{(-i (a x+b y-t \Psi )) } \end{aligned}$$
(40)

Here a is the normalized wave number and b is angular frequency. By substituting the Eq. (40) into Eq.(39), collecting the coefficeint of \(e^{(i (a x+b y-t \Psi ))}\) and \(e^{(-i (a x+b y-t \Psi )) }\), we get the following dispersion relation by solving the determinant of coefficient matrix.

$$\begin{aligned} -2 a^3 c_1^2 \varpi +4 a^2 c_1 c_3 \Psi \varpi -2 a b^2 c_1 c_2 \varpi +2 a b c_1 c_4 \Psi \varpi -2 a c_3^2 \Psi ^2 \varpi +2 b^2 c_2 c_3 \Psi \varpi -2 b c_3 c_4 \Psi ^2 \varpi -2 c_1 \Psi \varpi ^2 +2 c_5 \Psi \varpi =0 \end{aligned}$$
(41)

Solving the Eq. (41), by finding the dispersion relation \(\Psi\) of the MI, we obtain as follows

$$\begin{aligned} \Psi = \frac{-4 a^2 c_1 c_3-2 a b c_1 c_4-2 b^2 c_2 c_3+2 c_1 \varpi -2 c_5 \pm \sqrt{D}}{2 \left( -2 a c_3^2-2 b c_4 c_3\right) } \end{aligned}$$
(42)

Where \(D = \left( {4a^{2} c_{1} c_{3} + 2abc_{1} c_{4} + 2b^{2} c_{2} c_{3} - 2c_{1} \varpi + 2c_{5} } \right)^{2}\)\(- 4\left( { - 2a^{3} c_{1}^{2} - 2ab^{2} c_{1} c_{2} } \right)\left( { - 2ac_{3}^{2} - 2bc_{4} c_{3} } \right)\) In a scenario where \(\left( {4a^{2} c_{1} c_{3} + 2abc_{1} c_{4} + 2b^{2} c_{2} c_{3} - 2c_{1} \varpi + 2c_{5} } \right)^{2}\)\(- 4\left( { - 2a^{3} c_{1}^{2} - 2ab^{2} c_{1} c_{2} } \right)\left( { - 2ac_{3}^{2} - 2bc_{4} c_{3} } \right) \ge 0\), \(\Psi\) is real for any real value of \(\varpi\) and the steady state is stable against small perturbations. In contrast, the steady state is unstable, when \(\left( 4 a^2 c_1 c_3+2 a b c_1 c_4+2 b^2 c_2 c_3-2 c_1 \varpi +2 c_5\right) {}^2- 4 \left( -2 a^3 c_1^2-2 a b^2 c_1 c_2\right) \left( -2 a c_3^2-2 b c_4 c_3\right) <0\), that is \(\Psi\) is imaginary and hence the perturbation grows exponentially leading to a MI.

Fig. 11
figure 11

Visualization of gain spectrum \(\varpi\) of modulation instability.

Full size image

Conclusion

This study examined the time-fractional improved (2+1)-dimensional nonlinear Schrödinger equation incorporating spatio-temporal dispersion effects within the framework of nonlinear optics. A range of novel optical soliton solutions such as bright, bell-shaped, wave, and singular solitons were obtained through the application of exponential and hyperbolic function methods. To illustrate their behavior, we provide comprehensive visual representations, including two-dimensional, three-dimensional, and contour plots, which depict the magnitude of the time-fractional improved (2+1)-dimensional nonlinear Schrödinger equation. By appropriately choosing the physical parameters, we revealed a diverse spectrum of solutions, including bright, bell-shaped, wave-like, and singular forms. In addition, we examined how variations in the temporal parameter and the conformable fractional-order derivative influenced the behavior and structure of these solutions. The findings emphasize the effectiveness and practicality of the new Kudryashov approach in studying both integer and fractional order differential equations, providing valuable analytical solutions that contribute to our understanding of complex optical systems and their dynamics. In the future, the present method can be applied to other forms of nonlinear Schrödinger equations with integer and fractional orders.