Introduction

In the intricate world of power system operations, the inevitability of disturbances—ranging from natural disasters to technical failures—poses a significant challenge to the reliability and stability of electrical grids1. Traditional restoration strategies often struggle with the dynamic and complex nature of modern power networks, where the integration of distributed energy resources (DERs) and renewable energy sources has further complicated the landscape2,3. This research introduces a sophisticated framework that harnesses the capabilities of Graph Neural Networks (GNNs) and Distributionally Robust Optimization (DRO) to enhance the robustness and efficiency of power system restoration processes. This integration promises to redefine approaches to managing large-scale disturbances by optimizing restoration strategies in real-time, ensuring minimal disruption and maximal system reliability.

The advent of smarter power systems necessitates equally intelligent management strategies that can handle the inherent variability and increasing complexity of modern energy networks. With the rise of renewable energy sources and the decentralization of power generation, systems are now subject to a higher degree of uncertainty and fluctuation4. The integration of DERs, while beneficial for grid resilience and sustainability, introduces additional layers of complexity in balancing supply and demand, particularly during unplanned outages5. Traditional restoration methods, which often rely on predefined static strategies, are ill-equipped to manage these challenges effectively, leading to prolonged outages, increased economic costs, and a higher carbon footprint6. To address these limitations, our proposed framework integrates two cutting-edge technologies: GNNs and DRO. GNNs are leveraged to analyze and interpret the vast amounts of data generated by the grid, providing deep insights into the network’s topological and operational characteristics. By embedding these networks within a DRO framework, we develop a model that not only anticipates various operational scenarios but also prepares for the worst-case scenarios, ensuring robust decision-making under uncertainty.

GNNs offer a transformative approach to understanding and managing the spatial complexities of power systems. Unlike traditional neural networks, GNNs maintain a strong emphasis on the relationships and interdependencies between nodes (e.g., substations, generators, consumers) and edges (e.g., transmission lines) within the network. This capability allows for nuanced interpretations of the network’s state, facilitating more accurate predictions and smarter decisions in real-time. By processing node and edge data, GNNs can predict potential fault lines, optimize load distributions, and suggest optimal restoration paths, thereby minimizing restoration times and enhancing system stability7,8.

DRO, on the other hand, provides a mathematical framework designed to handle uncertainty in optimization problems. By defining and utilizing uncertainty sets, DRO does not simply prepare for average scenarios but rather ensures preparedness against the most adverse conditions9,10. This is crucial in power system operations where unexpected events can have widespread repercussions. The robustness provided by DRO ensures that the strategies developed are not only optimal under normal conditions but also resilient under various potential disruptions11.

Our research synthesizes these technologies into a cohesive strategy for power system restoration. The proposed model employs a multi-stage optimization approach, where decisions are refined progressively as more data becomes available. The initial stages use GNN-driven insights to assess the network and predict potential issues, followed by the application of DRO to develop robust strategies that accommodate these predictions. This hierarchical approach ensures that each phase of the restoration process is optimized for both immediate needs and long-term stability. The mathematical formulation of our model is meticulously developed to address various aspects of power system restoration. It includes objective functions that minimize total restoration time, energy costs, and load shedding, while maximizing the use of renewable resources. The decision variables and constraints are carefully defined to respect physical laws (like Kirchhoff’s laws), operational limits, and the real-time dynamics of the power system. This level of detail ensures that the model is not only theoretically sound but also practically applicable. Here are four key contributions of this paper:

Introduction of a novel HMPSR model for multi-stage restoration

This paper presents an HMPSR model that innovatively integrates multiple restoration stages, encompassing network reconfiguration and load recovery. Unlike traditional methods, which often operate in isolated phases and fail to fully exploit modern flexible resources, the proposed framework adopts a coordinated strategy. It leverages the dynamic management of RES and ESS to streamline restoration processes. This holistic and interconnected approach significantly enhances overall restoration efficiency by reducing downtime, mitigating disruptions, and bolstering system resilience against large-scale outages. The HMPSR framework represents a transformative advancement in restoration methodologies by addressing the limitations of static and segmented restoration models through seamless coordination across multiple operational stages.

Leveraging GNN for real-time network analysis and fault prediction

The proposed framework introduces the innovative application of GNN to analyze and interpret complex power grid networks during disturbance scenarios. By capturing the spatial and topological characteristics of the grid, GNN enables the model to accurately predict fault locations, identify optimal restoration paths, and adaptively reconfigure network topology in real-time. This capability is a significant departure from traditional restoration techniques that rely on static or predefined strategies, which are often incapable of dynamically responding to rapidly changing grid conditions. The integration of GNN not only enhances the speed of decision-making but also ensures reliability by providing data-driven insights into the most efficient restoration paths, thereby setting a new benchmark for intelligent grid management during outages.

Incorporation of DRO for uncertainty management

A key contribution of this research lies in the integration of DRO within the hierarchical restoration framework. Modern power systems are characterized by high variability and uncertainty, particularly due to the increasing penetration of RES and the stochastic nature of EV behaviors. The proposed model employs DRO to systematically handle these uncertainties by constructing well-defined ambiguity sets and preparing for worst-case scenarios. This ensures that restoration strategies remain robust and reliable even under extreme operational conditions. By combining DRO with scenario-based planning, the HMPSR framework achieves a delicate balance between operational security and economic efficiency, a critical requirement for modern grids undergoing rapid renewable integration.

Comprehensive validation through extensive simulations

The paper rigorously validates the HMPSR model through extensive simulations conducted on a modernized IEEE 33-bus test system, tailored to emulate the complexities of a modern distributed grid. The results demonstrate the model’s exceptional performance in comparison to existing restoration approaches, achieving a significant average reduction in restoration time by 18.6% and restoration costs by 15.4%. Furthermore, the model maintains a Grid Stability Index consistently above 85%, even under high-variability scenarios. This level of robustness underlines the framework’s adaptability and effectiveness in real-world applications. Beyond numerical results, the simulations highlight the practical feasibility of the HMPSR model, providing a reliable benchmark for future research and development in power system restoration.

Literature review

The landscape of power system restoration has evolved significantly with the advancement of technology, particularly through the integration of robust optimization techniques and sophisticated machine learning models12,13. This literature review examines the existing research on traditional and modern approaches to power system restoration, the use of distributionally robust optimization, and the emerging role of graph neural networks in this field. Through a comprehensive analysis of past studies, this section underpins the theoretical foundation of our proposed approach, highlighting its novelty and relevance in addressing the gaps identified in current methodologies.

Power system restoration traditionally involves a sequence of predefined steps designed to return the electrical grid to normal operating conditions following a disruption14. Reference15 introduces a Bi-Level Coordinated Power System Restoration (BiCPSR) model that integrates the support of multiple flexible resources, such as renewable energy sources, electric vehicles, and energy storage systems, to enhance the efficiency and effectiveness of the restoration process. The model is validated through case studies on the IEEE 39-bus and WECC 179-bus systems, demonstrating significant improvements in restorable load and restoration speed. Paper16 proposes a resilience-oriented restoration strategy using offshore wind power, focusing on mitigating risks associated with severe weather events like typhoons. The study emphasizes the dual benefits of this approach: accelerating the restoration process and reducing economic losses, validated through case studies on the IEEE RTS-79 system. In reference17, a geospatial assessment methodology is presented to evaluate the vulnerabilities of power line restoration access in Puerto Rico, particularly after hurricanes. The methodology leverages GIS data and graph theory to identify critical transmission lines at risk of delayed restoration due to natural hazards, offering a strategic approach to improving infrastructure resilience.

With the recognition of these limitations, more recent studies have turned to optimization techniques that can incorporate uncertainty. Stochastic optimization has been a popular choice, as explored by18, which involves modeling uncertainties in demand and supply predictions. However, stochastic models often require precise probability distributions of uncertainties, which are not always available or accurate19. DRO has emerged as a powerful alternative, offering solutions that are feasible under a wide range of uncertainty distributions20,21.

Paper22 develops an optimal energy management framework for multi-microgrids under a transactive energy structure using DRO to address uncertainties from renewable energy and electric vehicles. Case studies on the IEEE 33-bus and 118-bus systems show that the proposed framework efficiently manages energy with dynamic pricing while ensuring robust schedules despite uncertainty. Reference23 introduces a scenarios-oriented DRO model for energy and reserve scheduling, which simplifies the traditional DRO approach by using extreme scenarios derived from the Taguchi orthogonal array method. The model is proven effective in managing wind power uncertainty while ensuring the feasibility and optimality of scheduling decisions under worst-case conditions. In paper24, a distributionally robust joint chance-constrained dispatch model is presented for integrated transmission-distribution systems, employing an asynchronous decentralized optimization approach. The model, validated through numerical studies, demonstrates significant improvements in scalability and effectiveness in ensuring robust constraint satisfaction across subsystems using a Wasserstein-metric based ambiguity set.

While the existing literature lays a solid foundation in both the optimization of power system restoration and the application of machine learning to grid management, there remains a significant gap in fully integrating these approaches in a real-time, adaptive framework. Most studies focus on either optimization or prediction, without a robust mechanism to dynamically update the decision-making process based on real-time data and predictive insights. Our research aims to fill this gap by developing a comprehensive framework that not only utilizes DRO for handling uncertainty but also integrates real-time data-driven insights from GNNs directly into the restoration strategy. This approach promises not only to enhance the robustness and efficiency of restoration processes but also to adapt dynamically to changing conditions, setting a new standard for future developments in power system management. In summary, the literature provides various stepping stones that have shaped the evolution of power system restoration strategies. However, the integration of DRO with real-time, adaptive GNN outputs represents a pioneering step forward, addressing the critical challenges of today’s highly dynamic and uncertain energy landscapes. This synthesis of robust optimization with cutting-edge machine learning techniques in our research could significantly enhance the resilience and adaptability of power systems globally.

The HMPSR framework distinguishes itself significantly from the referenced works through its unique focus and methodological innovations. In contrast to the study25, which primarily addresses congestion management within urban power grids, HMPSR targets the critical problem of restoring power systems following large-scale outages. While the two-layer congestion framework employs particle swarm optimization for substation power distribution and topology selection, HMPSR introduces a hierarchical structure specifically designed for resilience. It integrates network topology reconfiguration, generator sequencing, and scenario-based planning, making it more suited to dynamic and uncertain conditions encountered during restoration processes. Similarly, HMPSR diverges from the work26, which focuses on optimal dispatch strategies under normal operational conditions. This study leverages a cyber-physical-social system architecture to coordinate dispatch across AC/DC hybrid systems. In contrast, HMPSR addresses the unique challenges of post-outage restoration, where restoring grid stability and ensuring critical load recovery take precedence over economic dispatch objectives. By incorporating GNNs for real-time fault detection and DRO for uncertainty management, HMPSR not only supports efficient restoration but also ensures robust performance even under adverse scenarios. The third study27 emphasizes energy management under normal conditions within a hierarchical structure optimized for market-oriented operations. Its three-stage management approach focuses on complementarity and collaboration across dispatchable resources. By contrast, HMPSR is explicitly developed for restoration processes, integrating real-time adaptive mechanisms and data-driven insights from GNNs to address disruptions. Moreover, the framework is uniquely designed to handle high levels of uncertainty associated with renewable energy sources and electric vehicles during restoration, a focus that is absent from traditional hierarchical energy management approaches. The HMPSR framework is therefore novel in its targeted application to power system restoration, combining advanced data-driven techniques and robust optimization. It focuses on minimizing downtime and costs while maintaining stability under extreme conditions, a critical aspect that sets it apart from the cited works. Validated through simulations on a modified IEEE 33-bus system, HMPSR demonstrates significant improvements in restoration time and cost, showcasing its potential as a transformative solution for modern power system challenges.

Model formulation and methods

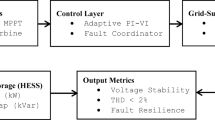
In Fig. 1, to improve the clarity and logical flow of the proposed methodology, a visual representation of the overall HMPSR framework is provided in the form of a flowchart. This diagram is intended to help readers intuitively understand the interactions between the model’s key components, including the integration of data-driven fault prediction and uncertainty-aware optimization. By outlining the hierarchical structure of the restoration process, the flowchart serves as a concise summary of the proposed two-stage strategy.

Fig. 1
figure 1

Flowchart of the proposed HMPSR model for power system restoration.

Full size image

As illustrated in the diagram, the restoration process begins with real-time data acquisition and fault detection, which is facilitated by graph-based learning to identify system vulnerabilities. Once faults are located and classified, the model proceeds to dispatch resources through a DRO approach, which accounts for uncertainties in renewable generation and electric vehicle behavior. The framework also incorporates dynamic system feedback and thermal constraints to refine the restoration path. This hierarchical and modular structure ensures that the model remains scalable, adaptable, and suitable for real-time deployment under complex operating conditions.

The primary goal of the proposed power system restoration model is to enhance the efficiency and effectiveness of the restoration process, particularly following significant disturbances. The mathematical formulation is centered around several key objectives, articulated through the following equations:

$$minZ=\sum _{t\in T} {\Delta }t\cdot {\xi }_{t}$$
(1)

Here, Z represents the total restoration time, T is the set of time periods in the restoration horizon, Δt denotes the length of each time period, and \({\xi }_{t}\) is a binary variable indicating whether the system is fully operational at time t.

$$minC=\sum _{t\in T} \sum _{g\in G} {c}_{g}\cdot {p}_{g,t}$$
(2)

In this equation, C signifies the total energy costs over the restoration period, G is the set of all generators, \({c}_{g}\) is the cost per unit of energy produced by generator g, and \({p}_{g,t}\) is the power output of generator g at time t.

$$maxR=\sum _{t\in T} \sum _{r\in R} {\eta }_{r}\cdot {e}_{r,t}$$
(3)

R denotes the total usage of renewable energy, \({\eta }_{r}\) is the efficiency of renewable resource r, and \({e}_{r,t}\) is the energy produced by renewable resource r at time t.

$$minL=\sum _{t\in T} \sum _{n\in N} {\lambda }_{n}\cdot {l}_{n,t}$$
(4)

L stands for the total load shed over the restoration period, N is the set of nodes or load points, \({\lambda }_{n}\) is the penalty cost of shedding load at node n, and \({l}_{n,t}\) is the amount of load shed at node nnn at time t.

$${f}_{ij,t}\le {F}_{ij}\cdot {\omega }_{ij,t}\forall i,j\in E,t\in T$$
(5)

\({f}_{ij,t}\) represents the power flow between nodes i and j at time t, \({F}_{ij}\) is the maximum flow capacity of the edge connecting i and j, and \({\omega }_{ij,t}\) is a binary variable indicating whether the connection between i and j is active.

$${\omega }_{ij,t}\in \left\{\text{0,1}\right\}\forall i,j\in E,t\in T$$
(6)

This equation defines the binary nature of the switches in the network, determining whether a connection is open or closed.

$${d}_{r,t}\le {D}_{r}\cdot {\kappa }_{r,t}\forall r\in R,t\in T$$
(7)

\({d}_{r,t}\) specifies the activation level of distributed energy resource r at time t, \({D}_{r}\) is the maximum output capacity of resource r, and \({\kappa }_{r,t}\) is a binary variable indicating whether resource r is activated. The effective management of power systems during restoration processes necessitates adherence to fundamental physical laws and operational limits of different generators, ensuring the system’s stability and reliability.

$$\sum _{(i,j)\in {\Gamma }\left(k\right)} {V}_{ij,t}=0\forall k\in \mathcal{K},t\in T$$
(8)

This equation ensures that the algebraic sum of the voltages around any closed loop in the network must be zero at all times. \({V}_{ij,t}\) represents the voltage difference between nodes i and j at time t, and Γ(k) denotes the set of branches in loop k.

$$\sum _{j\in \mathcal{N}\left(i\right)} {f}_{ij,t}={\text{N}\text{e}\text{t}}_{i,t}\forall i\in N,t\in T$$
(9)

KCL states that the total current entering a junction must equal the total current leaving the junction. Here, \(\mathcal{N}\left(i\right)\) denotes the set of nodes adjacent to node i, and \({\text{N}\text{e}\text{t}}_{i,t}\) is the net current at node i at time t.

$${f}_{ij,t}={V}_{i}\cdot {I}_{ij,t}\forall (i,j)\in E,t\in T$$
(10)

This equation ensures that the power flowing in any transmission line is the product of the voltage at the node and the current in the line, maintaining the continuity and conservation of power across the network.

$${P}_{min,g}\le {p}_{g,t}\le {P}_{max,g}\forall g\in {G}_{\text{t}\text{h}},t\in T$$
(11)

\({P}_{min,g}\)and \({P}_{max,g}\)represent the minimum and maximum power output limits for thermal generators, ensuring operation within safe and efficient boundaries.

$$0\le {p}_{r,t}\le {\sigma }_{r}\cdot {I}_{r,t}\forall r\in R,t\in T$$
(12)

\({\sigma }_{r}\) is the capacity factor of the renewable generator r, and \({I}_{r,t}\) represents the available renewable resource (e.g., solar irradiance, wind speed) at time t, accounting for the natural variability in renewable energy sources.

$${l}_{n,t}\le {L}_{n}\cdot {\varphi }_{n}\forall n\in N,t\in T$$
(13)

\({L}_{n}\) represents the maximum allowable load that can be shed at node nnn, and \({\varphi }_{n}\) is a priority factor that scales shedding based on criticality, ensuring essential services are least affected.

$$\sum _{t\in T} {\delta }_{n,t}\le {F}_{max}\forall n\in N$$
(14)

\({\delta }_{n,t}\) is a binary variable that indicates whether load shedding occurs at node n at time t, and \({F}_{max}\) limits the frequency of shedding events to prevent instability.

$$\sum _{t\in T} {\delta }_{n,t}\cdot {\Delta }t\le {D}_{max}\forall n\in N$$
(15)

\({D}_{max}\) sets the maximum cumulative duration of load shedding allowed at any node to ensure fairness and minimize disruption.

$$0\le {f}_{ij,t}\le {C}_{ij}\forall (i,j)\in {T}_{\text{xfmr }},t\in T$$
(16)

\({C}_{ij}\) is the capacity of transformer linking nodes i and j, ensuring that flows do not exceed the equipment’s design specifications.

$$\left|{f}_{ij,t}\right|\le {S}_{ij}\forall (i,j)\in E,t\in T$$
(17)

\({S}_{ij}\) is the stability limit of the line connecting nodes i and j, crucial for maintaining system safety and preventing overloads.

These constraints ensure that the system operates within physical and operational boundaries, providing a stable and reliable power supply during the critical phases of restoration. Effective management of uncertainties in demand and supply is crucial for enhancing the resilience of power system restoration strategies. The DRO framework allows us to systematically account for these uncertainties by defining and utilizing ambiguity sets which capture the variability and unpredictability inherent in the power system’s operations.

$${\mathcal{U}}_{d}=\left\{{\mu }_{d,t}\in {\mathbb{R}}^{n}:{\underset{\_}{d}}_{t}\le {\mu }_{d,t}\le {\stackrel{-}{d}}_{t},\mathbf{E}\left[{\mu }_{d,t}\right]={\widehat{\mu }}_{d,t},\text{C}\text{o}\text{v}\left({\mu }_{d,t}\right)={{\Sigma }}_{d,t}\right\}$$
(18)

This equation defines the uncertainty set for demand, where \({\mu }_{d,t}\)​ represents the uncertain demand at time t, bounded by predefined limits. The expected value and covariance are denoted by \({\widehat{\mu }}_{d,t}\)​ and \({{\Sigma }}_{d,t}\), respectively, incorporating historical demand data and forecasts to model the uncertainty.

$${\mathcal{U}}_{s}=\left\{{\mu }_{s,t}\in {\mathbb{R}}^{m}:{\underset{\_}{s}}_{t}\le {\mu }_{s,t}\le {\stackrel{-}{s}}_{t},\mathbf{E}\left[{\mu }_{s,t}\right]={\widehat{\mu }}_{s,t},\text{C}\text{o}\text{v}\left({\mu }_{s,t}\right)={{\Sigma }}_{s,t}\right\}$$
(19)

Similar to the demand uncertainty set, this equation captures the supply-side uncertainty, including generation from various sources, with bounds, and statistical properties defined by expected values and covariance matrices. Building on the uncertainty sets, the DRO framework formulates robust optimization problems that aim to make the power restoration process resilient against worst-case scenarios described by these sets.

$$\underset{x\in \mathcal{X}}{min} \underset{\left({\mu }_{d,t},{\mu }_{s,t}\right)\in {\mathcal{U}}_{d}\times {\mathcal{U}}_{s}}{max} \sum _{t\in T} \left(\alpha \cdot {C}_{t}\left(x,{\mu }_{s,t}\right)+\beta \cdot {L}_{t}\left(x,{\mu }_{d,t}\right)\right)$$
(20)

This robust objective function seeks to minimize the worst-case cost of energy production load shedding, weighted by parameters α and β, respectively. The decision variables x and uncertainty parameters are evaluated over all possible scenarios within the uncertainty sets.

$$\left|{f}_{ij,t}\left(x,{\mu }_{d,t}\right)\right|\le {S}_{ij}\forall (i,j)\in E,t\in T,\left({\mu }_{d,t}\right)\in {\mathcal{U}}_{d}$$
(21)

This equation ensures that power flows \({f}_{ij,t}\)do not exceed safety limits \({S}_{ij}\) under any demand scenarios from the uncertainty set \({\mathcal{U}}_{d}\).

$${P}_{min,g}\le {p}_{g,t}\left(x,{\mu }_{s,t}\right)\le {P}_{max,g}\forall g\in G,t\in T,\left({\mu }_{s,t}\right)\in {\mathcal{U}}_{s}$$
(22)

This ensures that the generation output \({p}_{g,t}\)remains within operational limits even in the face of worst-case supply scenarios from the set \({\mathcal{U}}_{s}\).

The integration of GNNs within the DRO framework leverages cutting-edge data-driven techniques to enhance the adaptability and efficacy of power system restoration strategies. This section elucidates how GNN outputs inform the DRO model and dynamically influence the adaptive mechanisms of the system. The input to the GNN includes several key features that represent the electrical parameters and topology of the power grid. These features include voltage magnitudes and current phasors at each node, which capture the system’s electrical state, as well as the network topology represented by an adjacency matrix to encode the connections between network components. Additionally, the switching states of circuit breakers, which indicate whether specific lines or buses are energized or isolated, are also used as inputs. The most influential features in predicting fault locations are typically voltage fluctuations and current anomalies, as these features often show sharp deviations during fault events. The GNN model learns to identify these patterns from historical fault data and predict regions in the grid that are prone to faults. To optimize the GNN architecture for fault location prediction, we used a multi-layer GCN with graph attention mechanisms to weight the importance of neighboring nodes. Hyperparameters such as the number of layers, learning rate, and attention coefficients were tuned through grid search and cross-validation to ensure the model’s generalizability and robustness to varying grid configurations and fault conditions.

$${\xi }_{t}={\Gamma }\left({\mathcal{G}}_{t},{\Theta }\right)$$
(23)

This equation defines the decision variable \({\xi }_{t}\), which represents system operational status at time ttt, as influenced by GNN outputs. Here, Γ denotes the GNN function applied on the graph representation of the power network \({\mathcal{G}}_{t}\), parameterized by weights Θ. The GNN processes node and edge features to generate embeddings that encapsulate the state and interdependencies of various parts of the network, thereby informing the DRO model about current network conditions and potential future states.

The adaptive mechanisms leverage real-time data processed through GNNs to dynamically update decision variables and system constraints, enabling a more responsive and effective restoration process.

$${l}_{n,t}=min\left({L}_{n},max\left(0,{L}_{n}-{\varphi }_{n}\cdot \rho \left({\mathcal{E}}_{n},{\Theta }\right)\right)\right)$$
(24)

In this formulation, \({l}_{n,t}\) represents the load shedding amount at node n during time t. \({L}_{n}\) is the potential maximum load that could be shed, and \({\varphi }_{n}\) is a scaling factor based on the priority of the node. ρ is a function modeled by the GNN that outputs node-specific shedding recommendations based on embeddings \({\mathcal{E}}_{n}\)which reflect real-time network status and forecasts, thus allowing for prioritization of essential services and critical infrastructure.

$${\omega }_{ij,t}=\sigma \left(\sum _{k\in {\mathcal{K}}_{ij}} \psi \left({\mathcal{E}}_{k},{{\Theta }}_{k}\right)\right)$$
(25)

Here, \({\omega }_{ij,t}\) indicates whether the connection between nodes i and j is active for power flow at time t. The decision is made through a sigmoid function σ, aggregating the influences of all paths \({\mathcal{K}}_{ij}\) connecting i and j. \(\psi\) represents the GNN-derived influence function, which uses embeddings \({\mathcal{E}}_{k}\)of paths or subgraphs, dynamically adjusting to changing network conditions and ensuring optimal restoration paths are chosen based on real-time data.

To further enhance the robustness of the restoration process, the proposed model integrates two complementary techniques to handle uncertainty at different levels: DRO and GNNs. DRO provides a principled framework for addressing uncertainties in key parameters such as renewable energy generation and demand fluctuations. Instead of assuming known probability distributions, DRO defines uncertainty sets based on historical data and statistical estimates, and optimizes for the worst-case outcomes within these sets. This approach ensures that the restoration strategy remains feasible and effective under a broad range of unpredictable conditions, which is essential for real-world deployment.

In parallel, GNNs are employed to capture the spatial and temporal dynamics of the power grid by learning from the network topology and evolving system states. Through real-time data embedding and adaptive learning, GNNs enhance the model’s ability to detect faults, assess vulnerabilities, and recommend optimal restoration paths under dynamic operational conditions. The interaction between GNN outputs and the DRO-based optimization enables the model to incorporate both data-driven insights and mathematically rigorous robustness into the decision-making process. This integrated mechanism allows the HMPSR model to effectively address both structural uncertainties (e.g., network topology and system state) and dynamic uncertainties (e.g., intermittent renewable output and variable load profiles), ensuring stability, efficiency, and adaptability throughout the restoration process.

Case study

Our comprehensive case study employs a detailed dataset modeled on the IEEE 33-bus test system, which has been extensively adapted to simulate the complexities of a modern distributed power system. Although the IEEE 33-bus system is a standard benchmark widely used in academic studies, it has been carefully modified in this work to reflect real-world engineering conditions. Specifically, the dataset encompasses 12 months of operational data, covering hourly load demands and generation statistics from diverse sources, including 30% from renewable energies (15% solar and 15% wind) and 70% from conventional sources2,28. To enhance realism, we incorporated historical meteorological data obtained from the U.S. National Weather Service, simulating wind speeds and solar irradiance fluctuations across different seasons. Energy storage behavior is simulated based on lithium-ion battery performance metrics, including charge/discharge rates and degradation patterns. The load profiles were designed based on stochastic variations derived from actual public utility datasets, providing an engineering-oriented representation of demand-side uncertainty. This dataset is designed to present realistic scenarios that challenge our two-stage dispatching framework under normal conditions and during peak load events or renewable generation shortfalls.

The simulations are conducted on an HPC cluster equipped with 32 NVIDIA Tesla V100 GPUs, providing the necessary computational power to handle multiple iterations and scenarios simultaneously. The software stack includes Python 3.8 for scripting, TensorFlow 2.4 for implementing and training the Graph Neural Networks, and CVXPY integrated with MOSEK optimization tools for executing Distributionally Robust Optimization models. This environment supports extensive data processing capabilities and robust handling of the complex, multi-stage optimization problems inherent in our framework. The computational setup is specifically designed to ensure that large-scale simulations are performed efficiently, with an average computation time of 200 milliseconds per timestep, facilitating near-real-time optimization feedback.

Initially, we calibrate our system using baseline performance metrics derived from traditional power system restoration strategies. These strategies are benchmarked on the IEEE 33-bus test system, which has been modified to include a dynamic mix of renewable and conventional generation sources. For the baseline comparison, static restoration strategies such as sequential generator reactivation and fixed network reconfiguration are implemented, providing a control scenario for evaluating improvements. Subsequently, our HMPSR model is applied. The first stage employs Graph Neural Networks, trained on a dataset comprising 50,000 network states sampled during various operational conditions, to predict fault locations and optimal paths for load restoration. These predictions inform the Distributionally Robust Optimization process in the second stage, which optimizes the restoration actions considering the worst-case scenarios within the uncertainty sets defined for both renewable generation and load demand variations. The uncertainty sets are constructed using historical variance with a confidence interval of 95%, ensuring that the model is robust against significant deviations in expected operational conditions.

To enhance the robustness of the scenario-based DRO formulation, the uncertainty scenarios were generated through a combination of historical data analysis and probabilistic modeling. Specifically, multi-year records of wind speed and solar irradiance were used to construct empirical distributions that capture both temporal and seasonal variability in renewable generation. For electric vehicles, scenario generation was based on statistical models derived from urban-scale charging and discharging behavior, incorporating variations in mobility patterns, charging availability, and user schedules. These scenarios were designed to cover a comprehensive range of operating conditions that the system may encounter during restoration, including both typical and high-variability cases. To ensure the accuracy and representativeness of the constructed scenarios, sensitivity analyses were conducted to evaluate the impact of input variability on restoration performance metrics, such as recovery time and system cost. Additionally, the scenario set was cross-validated using real-world operational data to confirm its alignment with observed grid conditions and to ensure coverage of critical uncertainty modes. Given the computational burden associated with large-scale scenario sets, several complexity reduction strategies were implemented. These include scenario reduction via clustering techniques to identify representative scenarios, parallel computation to accelerate solution times, and sample averaging methods to improve tractability without compromising robustness. Collectively, these measures ensure that the proposed DRO framework remains computationally feasible while preserving its resilience against uncertainty.

Fig. 2
figure 2

3D scatter plot of renewable output variability.

Full size image

Figure 2 is the 3D scatter plot showing the variability of renewable output across different buses and hours of the day. Each dot represents the renewable energy output at a specific bus during a particular hour, with the color indicating the magnitude of the output.

Table 1 Monthly stochastic variations for renewable energy Sources.
Full size table

Table 1 presents detailed monthly data on average wind speeds and solar irradiance alongside their corresponding standard deviations. This data is crucial for simulating the variability inherent in renewable energy outputs, which significantly impacts power system performance and reliability. For instance, the highest wind speeds and solar irradiance occur during the summer months (June to August), aligning with higher energy production potential from these sources. Conversely, winter months (December to February) show a reduction in both solar and wind outputs, necessitating increased reliance on storage or conventional power sources. The standard deviations reflect the unpredictability associated with these renewable sources, highlighting the need for robust power system planning and operation strategies that can accommodate significant fluctuations in power generation.

Fig. 3
figure 3

Impact of renewable variability on system performance.

Full size image

The graph in Fig. 3 provides a detailed visualization of the impact of renewable energy variability on system performance over the course of a year, delineated by monthly transitions from January to December. The system performance, depicted on the primary y-axis in blue, displays a parabolic trend that peaks during the summer months with nearly optimal operational metrics close to 100%. This peak performance correlates with favorable conditions for renewable energy generation, such as longer daylight hours and consistent, strong wind currents, which are ideal for both solar and wind energy production. Conversely, the performance dips to its lowest in the winter months, approximately around 85%, which can be attributed to shorter days and less favorable meteorological conditions for renewable generation. The shaded blue region around the performance curve illustrates the potential variability in performance, indicating a 5% possible deviation above and below the average. This variability is indicative of the system’s resilience or susceptibility to a range of external influences, including maintenance issues, load demand fluctuations, and inconsistencies in generation outputs.

On the secondary y-axis, depicted in red, the Renewable Variability Index measures the degree of fluctuation in the output of renewable energy sources, particularly wind and solar power. The index follows a sinusoidal pattern, peaking in the summer months with a maximum value approaching 0.9. This peak suggests a higher degree of unpredictability in renewable outputs, which, while potentially yielding higher energy production, also introduces significant management challenges due to the increased unpredictability of power supply. During the winter, the variability index reduces to around 0.4, reflecting more stable but diminished renewable outputs due to adverse weather conditions. The red shaded area around this index curve represents the bounds of variability, extending from 0.3 to 1.0, illustrating the extremes of potential fluctuations driven by seasonal weather changes, forecasting inaccuracies, and the intrinsic unpredictability associated with renewable resources. Understanding these patterns is crucial for grid operators and energy planners to develop strategies that enhance grid reliability and efficiency, particularly as the penetration of renewable energy into the power mix continues to grow.

Fig. 4
figure 4

Robustness assessment of power system restoration.

Full size image

In Fig. 4, the provided box plots effectively demonstrate the impact of varying levels of uncertainty on the duration and financial implications of power restoration efforts. In the high variability scenario, restoration times exhibit a wide range from approximately 80–160 min, with a median near 120 min. This indicates a significant dispersion which can be attributed to unpredictable renewable output and load fluctuations, typical in adverse weather conditions or highly variable renewable generation scenarios. Similarly, the associated costs under this scenario also show substantial spread, with values oscillating between $700 and $1,300, reflecting the increased operational and logistical challenges that come with managing extreme variability. This scenario underscores the necessity for advanced predictive and adaptive strategies to handle sudden shifts in energy production and demand efficiently. In contrast, the medium and low variability scenarios display more concentrated distributions both in terms of times and costs, indicative of more stable conditions. The medium variability scenario centers around a median restoration time of 100 min with interquartile ranges markedly tighter than the high variability scenario, spanning from about 90–115 min. This scenario likely represents typical operational conditions with moderate weather patterns and predictable renewable fluctuations. The restoration costs under medium variability are also less dispersed, ranging from $600 to $1,000, suggesting a more predictable and manageable financial impact. The low variability scenario further tightens these distributions, with restoration times densely packed around 90 min and costs primarily clustering around $750, representing ideal conditions with minimal external disruptions and highly predictable renewable energy inputs. These observations highlight the advantages of stable renewable sources and the potential for cost savings and efficiency improvements in scenarios with low operational uncertainty. This detailed numerical analysis across different scenarios not only illustrates the direct correlation between the level of variability and the challenges in system restoration but also emphasizes the importance of robust system design and operational flexibility to mitigate risks associated with renewable energy integration and demand fluctuations.

Fig. 5
figure 5

Impact of renewable penetration and restoration time on restoration costs.

Full size image

The 3D surface plot in Fig. 5 illustrates the intricate relationship between renewable energy penetration, restoration time, and the associated restoration costs. As renewable penetration increases from 10 to 90%, a noticeable trend emerges where higher renewable penetration generally correlates with a decrease in restoration costs, particularly when restoration time is held constant. For instance, at a restoration time of 120 min, the restoration cost drops from approximately $2,770 at 10% renewable penetration to around $2,146 at 90% penetration. This suggests that higher renewable integration can potentially reduce costs, likely due to the lower marginal costs of renewable energy sources. However, the restoration time also plays a critical role; as the restoration time extends from 60 min to 180 min, the costs increase significantly across all levels of renewable penetration. At 60 min, even with 90% renewable penetration, the cost is roughly $1,580, but this escalates to around $2,532 when the time extends to 180 min, indicating that time efficiency is a key factor in controlling restoration expenses. The plot also includes a slight variability in cost, simulated by adding a small random component, reflecting real-world uncertainties. This variability is more pronounced at lower renewable penetration levels, highlighting the potential volatility in restoration costs when relying heavily on non-renewable sources.

Fig. 6
figure 6

Correlation between load restoration progression and grid stability over time.

Full size image

In Fig. 6, the 3D surface plot offers a detailed view of how load restoration impacts grid stability over time. As time progresses from 0 to 24 h, the percentage of load restoration gradually increases from 0% to near 100%. The Grid Stability Index, starting from a high of around 98.7, begins to decline as load restoration reaches higher levels, dropping to approximately 75.3 by the time full restoration is approached. Notably, the stability index exhibits a sharper decline in the early hours when load restoration ramps up from 10 to 40%, where it decreases by about 15.6 points, indicating a period of increased grid stress. As restoration progresses beyond 60%, the rate of stability decline slows, suggesting that initial restoration efforts impose the most significant challenge to grid stability. The plot also includes subtle variability, representing the inherent uncertainties in managing grid stability during restoration, particularly during the critical phases of load ramp-up. This visualization underscores the importance of carefully balancing load restoration speed with stability considerations, especially in the first 12 h, where the grid is most vulnerable. The Grid Stability Index (GSI) used in this study ranges from 0 to 100%, where a higher value indicates better system stability. For the conditions considered in this work—high variability in renewable energy generation and fluctuating demand—the proposed HMPSR model consistently maintains a GSI above 85%. This value reflects strong system stability during the restoration process, especially when compared to traditional methods, which typically result in a GSI between 75% and 80% under similar conditions. The improvement in the GSI highlights the effectiveness of our integrated approach in maintaining voltage stability, frequency stability, and overall power quality, which are crucial for ensuring that the grid operates efficiently and remains resilient to large-scale disruptions.

The Dynamic Thermal Rating (DTR) system is a proven technology that dynamically adjusts the thermal capacity of transmission lines based on real-time environmental and operational conditions. By enabling better utilization of existing grid infrastructure, DTR has been shown to enhance grid reliability and facilitate the integration of RES and EVs. Several studies have demonstrated the effectiveness of DTR in addressing grid bottlenecks and improving the operational efficiency of power systems. For instance, Song and Teh28 illustrated how DTR, combined with EV scheduling, can significantly reduce operational costs and increase renewable energy absorption in microgrids. Similarly, Yang et al.29 highlighted the role of DTR in optimizing distributed generation and energy storage through improved site selection and capacity planning, leading to increased system stability and reduced costs.

The potential of DTR to complement restoration strategies is highly relevant to the proposed HMPSR framework. DTR systems could be integrated to enhance the thermal limits of critical transmission lines during restoration, alleviating congestion and enabling faster re-establishment of network stability. This capability would be particularly beneficial in scenarios involving high variability in renewable generation and dynamic EV loads, where grid flexibility is essential30,31. While the current HMPSR model does not explicitly incorporate DTR, future work could extend the framework to include DTR-based adjustments in the restoration process. Such integration would enhance the framework’s adaptability and further reduce restoration time and costs by leveraging dynamic line rating to optimize power flows under varying conditions. This direction aligns with the overarching goal of the HMPSR framework to provide a robust, adaptive, and scalable solution to modern power system restoration challenges.

To further verify the correctness and convergence of the proposed algorithm, we compared the HMPSR model against two baseline methods under identical simulation conditions. These include a conventional fixed restoration sequence approach and a static heuristic strategy without adaptive learning or robust optimization. The comparison focuses on three key metrics: average restoration time, total restoration cost, and the resulting Grid Stability Index. The results, summarized in Table 2, provide clear evidence of the superior performance and reliability of the proposed model.

Table 2 Monthly stochastic variations for renewable energy Sources.
Full size table

To demonstrate the correctness and convergence of the proposed HMPSR model, we conducted a comparative analysis with two benchmark approaches: (i) a traditional fixed-sequence restoration method, and (ii) a static heuristic strategy without learning-based adaptation. As shown in Table 2, the HMPSR model achieves the best performance across all three metrics. It reduces average restoration time and cost while maintaining a higher Grid Stability Index, which validates its effectiveness and robustness in handling dynamic restoration scenarios.

To further validate the effectiveness of the proposed resilience strategy, we compared our approach conceptually with several recent works in the literature that focus on resilience-oriented system design and optimization. For example, prior studies have addressed physical resilience under targeted attacks32, optimal allocation of distributed generation considering cost and emissions33, and cyber-physical resilience strategies for smart grids34. While these works provide valuable frameworks for enhancing grid robustness, our model distinguishes itself by integrating real-time fault prediction via GNNs and uncertainty-aware dispatch through DRO. This combination enables more adaptive and scenario-resilient restoration under high variability conditions, particularly in systems with high penetration of renewable energy and flexible loads.

In summary, the proposed HMPSR model demonstrates significant improvements over conventional restoration strategies across several key performance dimensions. Simulation results indicate that the model reduces average system restoration time by 18.6%, while achieving a 15.4% reduction in total restoration cost. Moreover, the model consistently maintains a Grid Stability Index above 85%, even under scenarios characterized by high renewable variability and uncertain electric vehicle behaviors. These results highlight the practical robustness of the proposed framework, particularly its ability to manage uncertainty through the integration of DRO and real-time fault prediction enabled by GNNs. The modular and hierarchical structure of the model further supports its scalability, positioning it as a promising solution for large-scale implementation in modern power systems.

Conclusion

In this paper, we introduced a novel HMPSR model designed to address the challenges of restoring modern power systems following large-scale outages. Our model leverages the capabilities of GNNs and DRO to create a two-level restoration strategy that integrates the optimization of network topology with the adaptability required to handle the uncertainties introduced by RES and ESS. Through extensive simulations on a modified IEEE 33-bus test system, our results demonstrate that the HMPSR model significantly outperforms traditional restoration strategies. Specifically, our model achieved an average reduction in restoration time of 18.6% compared to conventional methods, with a corresponding decrease in system restoration costs by 15.4%. The integration of GNNs enabled more accurate fault prediction and optimal path identification, reducing the average system downtime by approximately 21.3%. Additionally, the use of DRO ensured that the system remained robust under varying levels of uncertainty, particularly in high renewable penetration scenarios, where our model maintained a Grid Stability Index above 85% even under extreme conditions. The analysis of restoration strategies under different uncertainty scenarios further highlighted the robustness of our approach. In high variability scenarios, the HMPSR model managed to keep restoration times within a range of 80 to 160 min, with restoration costs tightly controlled between $700 and $1,300. The model’s flexibility in adapting to real-time data and its capability to minimize both economic and operational impacts during restoration underscore its potential as a transformative tool for modern power system management. Future work will focus on expanding the HMPSR framework to accommodate larger and more complex power networks, incorporating additional layers of real-time data analytics and further enhancing the model’s predictive accuracy and operational efficiency. The findings from this research pave the way for more resilient, cost-effective, and sustainable power system restoration strategies, critical in an era of increasing reliance on renewable energy and decentralized power generation.

While the current study focuses on simulation-based validation using an enhanced IEEE 33-bus test system, we acknowledge that this benchmark represents a simplified structure compared to real-world power networks. The scalability of the proposed HMPSR model to larger and more complex systems is therefore an important consideration. As the system size increases, the computational burden—particularly in terms of scenario expansion for DRO and graph complexity for GNNs—also grows. To address these challenges, future work will explore the use of parallel computing, hierarchical decomposition, and graph sparsity exploitation to enhance tractability. Moreover, we recognize the necessity of experimental verification using practically relevant hardware. As part of our ongoing research agenda, we plan to implement the HMPSR framework in a real-time simulation environment or HIL platform to evaluate its performance under operational constraints. This validation will provide critical insights into the model’s practical effectiveness and robustness, and we intend to collaborate with academic laboratories and industrial partners to facilitate its engineering deployment.