Nonlocal complex short pulse equation in ${\mathcal{P}\mathcal{T}}$-symmetry like symmetry breaking, breather–grammian interactions and soliton solutions

Abstract

Research on ${\mathcal{P}\mathcal{T}}$-symmetry and spontaneous symmetry breaking captivates contemporary scholars due to its extensive applicability in several fields, including microwave propagation and nonlinear optics. This article studies the nonlocal complex short pulse (NL-CSP) equation in which we discuss how under certain symmetry reduction general complex short pulse equation turns into NL-CSP equation. We construct the binary Darboux transformation for the reverse space-time NL-CSP equation and derive its quasi-grammian solutions. Further, we obtain explicit expressions for spontaneous symmetry-breaking and symmetry-preserving breather, interaction of breather with grammian and also the soliton solutions. It is concluded that the existence of both symmetry-breaking and symmetry-preserving solutions for NL-CSP equation. Finally, to verify the theoretical results, we illustrate the dynamics of these solutions using surface and contour plots.

Introduction

The short pulse (SP) equation is well known equation used for describing the propagation of ultra-short optical pulses in quartz fibers by Schafer and Wayneo^1,2. The SP equation is

$$\begin{aligned} \beta _{xt}=\beta +\frac{1}{6}\left( \beta ^{3}\right) _{xx}, \end{aligned}$$

(1)

initially, arise during the study of pseudo-spherical surfaces³. The integrability of SP equation is its key feature, also it possesses infinite many conservation laws^4,5, the Wadati-Konno-Ichikawa (WKI) type Lax pair⁶ and bi-Hamiltonian structure^7,8. The transformation of SP equation into sine-Gorden equation is studied through hodograph transformation in^6,7,8,9. Also by using Riemann Hilbert method long-term asymptotic behaviors of SP equation were calculated in^10,11. Its breather solutions, periodic solutions and multi-soliton solutions have been explored in^9,12,13.

Parity-time (${\mathcal{P}\mathcal{T}}$) symmetry means the system remains invariant under space and time transformation. Basically, the theory of ${\mathcal{P}\mathcal{T}}$-symmetry promoted the advancement of quantum mechanics by improving the concept of non-Hermitian Hamiltonians. Bender and Boettcher introduced that a non-Hermitian Hamiltonian contains real eigenvalues only if the system remains invariant under ${\mathcal{P}\mathcal{T}}$ symmetry¹⁴. This theory has also been extended to complex systems by assuming potential V(x) is complex and has to satisfy $V^{*}(-x)=V(x)$, also non-Hermitian Hamiltonian $H=p+V(x)$ is ${\mathcal{P}\mathcal{T}}$-symmetric, here p is a momentum operator. ${\mathcal{P}\mathcal{T}}$-symmetric system plays a vital role in mathematical physics^15,16,17.

Now, we discuss about nonlocal problems which is consequence of ${\mathcal{P}\mathcal{T}}$- symmetry. Nonlocal systems remain invariant under reverse space-time transformation. In few years back, many researchers have explored nonlocal systems. Ablowitz and Musslimani¹⁵ proposed the first ${\mathcal{P}\mathcal{T}}$-symmetric nonlocal Schrodinger equation which was solved by technique inverse scattering transform. Some of the well-familiar nonlocal integrable models include nonlocal Schrodinger equation¹⁸, nonlocal short pulse equation¹⁹, nonlocal Manakov system²⁰.

The Darboux transformation (DT) for NL-CSP is studied and presented soliton solutions¹⁹ but in this article, our main focus is to study binary Darboux transformation (BDT) of NL-CSP equation for the first time which has not been studied in literature. Further, we present our solutions in terms of quasi-grammians instead of writing in determinants. We present naturally occurring quasi-grammian solutions from BDT here. At the end, we present novel characteristics solutions such as symmetry breaking and preserving interaction of breather with grammian, breather also one and two soliton solutions for NL-CSP equation for vanishing background seed solution. For non-vanishing background seed solution we compute lump solution of NL-CSP equation.

Now for NL-CSP equation, we initiate from the general coupled nonlinear evolution system

$$\begin{aligned} \alpha _{xt}+\alpha -\frac{1}{2}\left( \alpha \beta \alpha _{x}\right) _{x}= & 0, \end{aligned}$$

(2)

$$\begin{aligned} \beta _{xt}+\beta -\frac{1}{2}\left( \beta \alpha \beta _{x}\right) _{x}= & 0{,} \end{aligned}$$

(3)

where $\alpha (x,t)$ and $\beta (x,t)$ are the scalar complex-valued functions. The consistency condition ($\partial _{x}\partial _{t}\Phi =\partial _{t}\partial _{x}\Phi$) and equating the coefficient of $\zeta$ leads Eqs. (2) and (3) of the following WKI scheme⁶,

$$\begin{aligned} \Phi _{x}\equiv & E\Phi =\left( -i\zeta \sigma _{3}+\zeta K_{x}\right) \Phi , \end{aligned}$$

(4)

$$\begin{aligned} \Phi _{t}\equiv & F\Phi =\left( -\frac{i}{4\zeta }\sigma _{3}+F_{0}+\zeta F_{1}\right) \Phi , \end{aligned}$$

(5)

where

$$\begin{aligned} K= & \left( \begin{array}{cc} 0 & \beta \\ \alpha & 0 \end{array} \right) , \\ F_{0}= & \left( \begin{array}{cc} 0 & \frac{i\beta }{2} \\ -\frac{i\alpha }{2} & 0 \end{array} \right) , \\ F_{1}= & \left( \begin{array}{cc} -\frac{i\alpha \beta }{2} & \frac{\beta \alpha \beta _{x}}{2} \\ \frac{\alpha \beta \alpha _{x}}{2} & \frac{i\alpha \beta }{2} \end{array} \right) , \\ \sigma _{3}= & \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) . \end{aligned}$$

For $\beta =-\alpha ^{*}$ which is the local symmetry reduction, Eqs. (2), (3) transform to classical CSP equation as

$$\begin{aligned} \alpha _{xt}+\alpha +\frac{1}{2}\left( \left| \alpha \right| ^{2}\alpha _{x}\right) _{x}=0. \end{aligned}$$

(6)

Further, for $\alpha ^{*}=\alpha$, we get short pulse equation. Now, for the nonlocal symmetry reduction $\beta (x,t)=-\alpha ^{*}(-x,-t)$ we get NL-CSP equation from (2), (3) as

$$\begin{aligned} \alpha _{xt}(x,t)+\alpha (x,t)+\frac{1}{2}\left( \alpha (x,t)\alpha ^{*}\left( -x,-t\right) \alpha _{x}\left( x,t\right) \right) _{x}= & 0, \end{aligned}$$

(7)

$$\begin{aligned} \alpha _{xt}^{*}(-x,-t)+\alpha ^{*}(-x,-t)+\frac{1}{2}\left( \alpha ^{*}\left( -x,-t\right) \alpha (x,t)\alpha _{x}^{*}\left( -x,-t\right) \right) _{x}= & 0. \end{aligned}$$

(8)

If we replace $\alpha ^{*}\left( -x,-t\right)$ by $\alpha ^{*}\left( x,t\right)$ then (7), (8) can be converted to classical CSP (6). By applying symmetry reduction $t\rightarrow -t$, $x\rightarrow -x$ and complex conjugation, it can be easily verified that the Eqs. (7), (8) remians invariant, also the potential $V\left( x,t\right) =-\alpha \left( x,t\right) \alpha ^{*}\left( -x,-t\right)$ obeys reverse space time symmetry i.e., $V^{*}\left( -x,-t\right) =V\left( x,t\right)$. It is to be noted, that the dynamics of quasi-grammian solutions of NL-CSP equation has never been under discussion in past years. We present in this article quasi-grammain solutions of NL-CSP equation for the first time which is the novelty of this work.

In this work, we calculate both the symmetry preserving and symmetry breaking solutions for NL-CSP equation. Modern researchers are more rigrous to study nonlocal systems as compared to local evolution systems because at the same time nonlocal systems contain both type of solutions like symmetry breaking and preserving simultaneously unlike that of their counter local parts. In (7), (8), the varaiables $\alpha (x,t)$ and $\alpha ^{*}(-x,-t)$ separately evolving i.e., if $\alpha (x,t)$ is calculated at (x, t), so $\alpha ^{*}\left( -x,-t\right)$ has to be calculated at $\left( -x,-t\right)$. It means both have particularly different eigenvalues so we cannot deduce the solutions $\alpha \left( x,t\right)$ and $\beta \left( x,t\right) =-\alpha ^{*}\left( -x,-t\right)$ from one another. Such kind of solutions are termed as symmetry breaking (non-preserving) solutions and also the potential in that case must have the complex-valued function. But if the eigenvalues are selected having specific coherence, then $\alpha$, $\alpha ^{*}$ will no longer independent also we can deduce solutions $\alpha \left( x,t\right)$ and $\beta \left( x,t\right) =-\alpha ^{*}\left( -x,-t\right)$ from one another under specific symmetry transformations. Such type of solutions are termed as symmetry preserving solution having real-valued potential function.

Particularly, nonlocal systems have been shown to study the systems with balanced gain and loss, non-reciprocal media and bidirectional wave propagation which are vital characteristics of modern optical systems such as ${\mathcal{P}\mathcal{T}}$-symmetric waveguides or metamaterials. Thus, the NL-CSP equation investigated in our manuscript can be interpreted as a theoretical model for such non-Hermitian nonlinear systems, where the spatial and time reversal symmetry plays a crucial role in the system dynamics. The NL-CSP equation has potential applications in explaining ultra-short pulse dynamics in engineered optical settings having nonlocal response characteristics whereas our primary focus in this work is to explore the mathematical structure and exact solutions of the given equation.

In this paper, we study BDT for NL-CSP equation and have the following pattern. Section 1 describes the information about nonlocal systems and also presents the linear system for NL-CSP equation. In Section 2, we study briefly DT for the system. In Section 3, we develops BDT for NL-CSP equation. In Section 4, we calculate the general form of quasi-grammian solutions of the system in terms of dynamical variables by using BDT. In Section 5, the dynamics of solutions like interaction of symmetry preserving and non-preserving breather with grammian, breather and one and two solitons are expressed. Section 6 consists of discussion of calcculated results. Concluding remarks would be summarized in Section 7.

Darboux transformation

One of the most important and widely used solution generating technique is DT. It is basically the gauge transformation of linear problem (for detail see^21,22,23. Now, we define DT on matrix solution $\Phi$ as

$$\begin{aligned} \Phi {[1]}=D({\zeta })\Phi , \end{aligned}$$

(9)

where $D(\zeta )$ is the Darboux matrix. Under the action of DT, new transformed solution $\Phi {[1]}$ has to satisfy the following linear system (4), (5) as

$$\begin{aligned} \Phi _{x}{[1]}= & E{[1]}\Phi {[1]}, \nonumber \\ \Phi _{t}{[1]}= & F{[1]}\Phi {[1]}, \end{aligned}$$

(10)

where E[1] and F[1] are

$$\begin{aligned} E[1]= & -i\zeta \sigma _{3}+\zeta K_{x}[1], \nonumber \\ F[1]= & -\frac{i}{4\zeta }\sigma _{3}+F_{0}[1]+\zeta F_{1}[1], \end{aligned}$$

(11)

having

$$\begin{aligned} K[1]= & \left( \begin{array}{cc} 0 & \beta [1] \\ \alpha [1] & 0 \end{array} \right) , \nonumber \\ F_{0}[1]= & \left( \begin{array}{cc} 0 & \frac{i\beta [1]}{2} \\ -\frac{i\alpha [1]}{2} & 0 \end{array} \right) , \nonumber \\ F_{1}[1]= & \left( \begin{array}{cc} -\frac{i\alpha [1]\beta [1]}{2} & \frac{\beta [1]\alpha [1]\beta _{x}[1]}{2} \\ \frac{\alpha [1]\beta [1]\alpha _{x}[1]}{2} & \frac{i\alpha [1]\beta [1]}{2} \end{array} \right) . \end{aligned}$$

(12)

The new transformed solution $\Phi [1]$ is defined as

$$\begin{aligned} \Phi [1]\equiv D\left( \zeta \right) \Phi =\left( \zeta ^{-1}I-R\right) \Phi , \end{aligned}$$

(13)

where $R=S\Xi ^{-1}S^{-1}$ and $I=diag(1,1)$ matrix also $S=\left( \left| s^{\left( 1\right) }\right\rangle ,\left| s^{\left( 2\right) }\right\rangle \right)$ is a distinct matrix solution of Lax pair (4)-(5). At $\zeta =\zeta _{i}$, each column $\left| s^{\left( i\right) }\right\rangle$ is a solution of Lax pair (4)-( 5). Under the action DT, the invariance of Lax pair (4)-( 5), implies

$$\begin{aligned} K[1]= & K-S\Xi ^{-1}S^{-1},{ \ \ \ } \end{aligned}$$

(14)

$$\begin{aligned} F_{0}[1]= & F_{0}-\frac{i}{4}\left[ \sigma _{3},S\Xi ^{-1}S^{-1}\right] , \end{aligned}$$

(15)

$$\begin{aligned} \partial _{x}R= & \left[ K_{x},S\Xi ^{-1}S^{-1}\right] \left( S\Xi ^{-1}S^{-1}\right) ^{-1}+i\left[ \sigma _{3},S\Xi ^{-1}S^{-1}\right] \left( S\Xi ^{-1}S^{-1}\right) ^{-1}, \end{aligned}$$

(16)

$$\begin{aligned} \partial _{t}R= & \left[ F_{1},S\Xi ^{-1}S^{-1}\right] \left( S\Xi ^{-1}S^{-1}\right) ^{-1}+\left[ F_{0},S\Xi ^{-1}S^{-1}\right] \nonumber \\ & -\frac{i}{4} \left[ \sigma _{3},S\Xi ^{-1}S^{-1}\right] S\Xi ^{-1}S^{-1}. \end{aligned}$$

(17)

Now by using equation (15), we calculate transformations on dynamical variables as

$$\begin{aligned} \alpha \left[ 1\right] \left( x,t\right)= & \alpha \left( x,t\right) -R_{21}, \end{aligned}$$

(18)

$$\begin{aligned} \beta \left[ 1\right] \left( x,t\right)= & \beta \left( x,t\right) -R_{12}. \end{aligned}$$

(19)

The result (13) can be expressed in the form of quasideterminants as

$$\begin{aligned} \Phi {[1]}= & \left( \zeta ^{-1}I-S\Xi ^{-1}S^{-1}\right) \Phi , \nonumber \\= & \left| \begin{array}{cc} S & \Phi \\ S\Xi ^{-1} & {\zeta ^{-1}I} \end{array} \right| . \end{aligned}$$

The N-fold DT on $\Phi {[N]}$ is given as

$$\begin{aligned} \Phi {[N]}=\left| \begin{array}{ccccc} S_{1} & S_{2} & \cdots & S_{K} & \Phi \\ S_{1}\Xi _{1}^{-1} & S_{2}\Xi _{2}^{-1} & \cdots & S_{N}\Xi _{N}^{-1} & \zeta ^{-1}\Phi \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ S_{1}\Xi _{1}^{-(N-1)} & S_{2}\Xi _{2}^{-(N-1)} & \cdots & S_{N}\Xi _{N}^{-(N-1)} & \zeta ^{-(N-1)}\Phi \\ M_{1}\Xi _{1}^{-N} & M_{2}\Xi _{2}^{-N} & \cdots & M_{N}\Xi _{N}^{-N} & {\zeta ^{-N}\Phi } \end{array} \right| . \end{aligned}$$

(20)

The equation (15) can also be written as for expressing in terms of quasideterminants as

$$\begin{aligned} F_{0}\left[ 1\right]= & F_{0}+\frac{i}{4}\left[ \sigma _{3},\left( O-S\Xi ^{-1}S^{-1}\right) \right] , \nonumber \\= & F_{0}+\frac{i}{4}\left[ \sigma _{3},\left| \begin{array}{cc} S & I \\ S\Xi ^{-1} & {O} \end{array} \right| \right] . \end{aligned}$$

(21)

The result can be generalized to N-times DT as

$$\begin{aligned} F_{0}[N]=F_{0}+\frac{i}{4}\left[ \sigma _{3}, \begin{vmatrix} S_{1}&S_{2}&\cdots&S_{N}&O \\ S_{1}\Xi _{1}^{-1}&S_{2}\Xi _{2}^{-1}&\cdots&S_{N}\Xi _{N}^{-1}&O \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ S_{1}\Xi _{1}^{-(N-1)}&S_{2}\Xi _{2}^{-(N-1)}&...&S_{N}\Xi _{N}^{-(N-1)}&I \\ M_{1}\Xi _{1}^{-K}&M_{2}\Xi _{2}^{-K}&\cdots&M_{K}\Xi _{K}^{-K}&{O} \end{vmatrix} \right] . \end{aligned}$$

(22)

Binary Darboux transformation

In this section we will compute general mechanism of BDT. So for BDT, we first define adjoint spectral problem by taking adjoint of linear system (4), (5), we get

$$\begin{aligned} \Psi _{x}= & \Psi \left( -i\mu \sigma _{3}+\mu K_{x}^{\dag }\right) , \nonumber \\ \Psi _{t}= & \Psi \left( -\frac{i}{4\mu }\sigma _{3}+F_{0}^{\dag }+\mu F_{1}^{\dag }\right) . \end{aligned}$$

(23)

where

$$\begin{aligned} K^{\dag }= & \left( \begin{array}{cc} 0 & \beta ^{\dag } \\ \alpha ^{\dag } & 0 \end{array} \right) , \nonumber \\ F_{0}^{\dag }= & \left( \begin{array}{cc} 0 & \frac{i\beta ^{\dag }}{2} \\ -\frac{i\alpha ^{\dag }}{2} & 0 \end{array} \right) , \nonumber \\ F_{1}^{\dag }= & \left( \begin{array}{cc} -\frac{i\alpha ^{\dag }\beta ^{\dag }}{2} & \frac{\beta ^{\dag }\alpha ^{\dag }\beta _{x}^{\dag }}{2} \\ \frac{\alpha ^{\dag }\beta ^{\dag }\alpha _{x}^{\dag }}{2} & \frac{i\alpha ^{\dag }\beta ^{\dag }}{2} \end{array} \right) . \end{aligned}$$

(24)

Now, for BDT, consider the copied version of direct space known as hat space i.e., ${\widehat{\Phi }}\in {\widehat{W}}$ (for detail see^24,26). The linear system for hat space is defined as

$$\begin{aligned} {\widehat{\Phi }}_{x}= & \left( -i\zeta \sigma _{3}+\zeta {\widehat{K}} _{x}\right) {\widehat{\Phi }}, \end{aligned}$$

(25)

$$\begin{aligned} {\widehat{\Phi }}_{t}= & \left( -\frac{i}{4\zeta }\sigma _{3}+{\widehat{F}} _{0}+\zeta {\widehat{F}}_{1}\right) {\widehat{\Phi }}. \end{aligned}$$

(26)

where ${\widehat{K}}$, ${\widehat{F}}_{0}$ and ${\widehat{F}}_{1}$ are define as

$$\begin{aligned} {\widehat{K}}= & \left( \begin{array}{cc} 0 & {\widehat{\beta }} \\ {\widehat{\alpha }} & 0 \end{array} \right) , \nonumber \\ {\widehat{F}}_{0}= & \left( \begin{array}{cc} 0 & \frac{i{\widehat{\beta }}}{2} \\ -\frac{i{\widehat{\alpha }}}{2} & 0 \end{array} \right) , \nonumber \\ {\widehat{F}}_{1}= & \left( \begin{array}{cc} -\frac{i{\widehat{\alpha }}{\widehat{\beta }}}{2} & \frac{{\widehat{\beta }} {\widehat{\alpha }}{\widehat{\beta }}_{x}}{2} \\ \frac{{\widehat{\alpha }}{\widehat{\beta }}{\widehat{\alpha }}_{x}}{2} & \frac{i {\widehat{\alpha }}{\widehat{\beta }}}{2} \end{array} \right) . \end{aligned}$$

(27)

In order to define BDT, consider two standard DT’s ${\widehat{D}}(\zeta )$ and $D(\zeta )$ whose action is to transform matrix solutions ${\widehat{\Phi }}$ and $\Phi$ respectively onto a same matrix solution $\Phi$¹, we can write as

$$\begin{aligned} D(\zeta )\Phi ={\widehat{D}}(\zeta ){\widehat{\Phi }}. \end{aligned}$$

(28)

Now, we can write operator of BDT as $\widehat{\mathcal {B}}={\widehat{D}} ^{-1}(\zeta )D(\zeta )$ which is the definition of BDT. Now operate $\widehat{\mathcal {B}}$ on matrix solution, ${\widehat{\Phi }}=$ ${\widehat{D}} ^{-1}(\zeta )D(\zeta )\Phi$. For detail discussion of BDT, assume $i( {\widehat{S}})$ and $\Psi$ belongs to the adjoint space, we can write

$$\begin{aligned} i({\widehat{S}})=D^{(-1)\dag }(\zeta )\Psi . \end{aligned}$$

Also, we get $iS=S^{(-1)\dag }$ from the condition $D^{\dag }(\zeta )(iS)=0$ . Similarly, $i{\widehat{S}}={\widehat{S}}^{(-1)\dag }$, so we can write transformation on ${\widehat{S}}$ as

$$\begin{aligned} {\widehat{S}}=SG^{-1}(S,\Psi ), \end{aligned}$$

(29)

where G is the eigenfunction potential defined as

$$\begin{aligned} G(S,\Psi )=(\Psi ^{\dagger }S)(\zeta ^{-1}I-\Xi ^{-1})^{-1}. \end{aligned}$$

(30)

Similar results can be obtained for adjoint space

$$\begin{aligned} {\widehat{P}}=PG^{(-1)\dag }(\Phi ,P), \end{aligned}$$

where

$$\begin{aligned} G(\Phi ,P)=-(\zeta ^{-1}I-\digamma ^{(-1)\dagger })^{-1}(P^{\dagger }\Phi ). \end{aligned}$$

(31)

Please note that, S and P are distinct matrix solutions for direct and adjoint spaces. We write Eqs. (30), (31) in terms of matrix and get the result

$$\begin{aligned} \digamma ^{(-1)\dagger }G(S,P)-G(S,P)\Xi ^{-1}=P^{\dagger }S. \end{aligned}$$

(32)

where G(S, P) is eigen potential matrix given by

$$\begin{aligned} G(S,P)_{ij}=\frac{\left\langle P|S\right\rangle _{(i\;j)}}{\digamma ^{(-1)\dagger }-\Xi ^{(-1) }}. \end{aligned}$$

(33)

In order to get the general expression of BDT, putting the values of $D(\zeta )$,$\ {\widehat{D}}(\zeta )$ and also using (29), (32) in the definition of ${\widehat{B}}_{n}$, we get

$$\begin{aligned} \widehat{\mathcal {B}}=I+SG^{-1}(S,\Psi )(\zeta ^{-1}I-\digamma ^{(-1)\dag })^{-1}P^{\dag }. \end{aligned}$$

Now, we are able to write BDT for eigenfunctions $\Phi$ and $\Psi$ as

$$\begin{aligned} {\widehat{\Phi }}= & \Phi -SG^{-1}(S,P)G(\Phi ,P), \\ {\widehat{\Psi }}= & \Psi -PG^{^{(-1)\dag }}(S,P)G^{^{\dag }}(S,\Psi ). \end{aligned}$$

In terms of quasideterminants

$$\begin{aligned} {\widehat{\Phi }}= & \begin{vmatrix} G(S,P)&G(\Phi ,P) \\ S&{\Phi } \end{vmatrix}, \\ {\widehat{\Psi }}= & \begin{vmatrix} G^{\dag }(S,P)&G^{\dag }(S,\Psi ) \\ P&{\Psi } \end{vmatrix}. \end{aligned}$$

Through the applications of the properties of quasideterminants, these results can be generalized to N-times of BDT.

Quasi-Grammian solutions of nonlocal complex short pulse equation

Now, we derive the quasi-grammian solution for NL-CSP equation. For this operating BDT on matrix solution $F_{0}$ as

$$\begin{aligned} {\widehat{F}}_{0}-\frac{i}{4}\left[ \sigma _{3},{\widehat{R}}\right] =F_{0}- \frac{i}{4}\left[ \sigma _{3},R\right] , \\ {\widehat{F}}_{0}=F_{0}+\frac{i}{4}\left[ \sigma _{3},{\widehat{S}}\digamma ^{(-1)\dagger }{\widehat{S}}^{-1}\right] -\frac{i}{4}\left[ \sigma _{3},S\Xi ^{-1}S^{-1}\right] . \end{aligned}$$

Using the result (29), we get

$$\begin{aligned} {\widehat{F}}_{0}=F_{0}+\frac{i}{4}\left[ \sigma _{3},SG^{-1}\digamma ^{(-1)\dagger }GS^{-1}\right] -\frac{i}{4}\left[ \sigma _{3},S\Xi ^{-1}S^{-1} \right] . \end{aligned}$$

Now, using the value of $\digamma ^{(-1)\dag }G$ from (32), after solving we have

$$\begin{aligned} {\widehat{F}}_{0}= & F_{0}+\frac{i}{4}\left[ \sigma _{3},SG^{-1}P^{\dag } \right] , \nonumber \\= & F_{0}-\frac{i}{4}\left[ \sigma _{3}, \begin{vmatrix} G&P^{\dagger } \\ S&{O} \end{vmatrix} \right] . \end{aligned}$$

(34)

Using Eq. (34), we write results of BDT for dynamical scalar variables

$$\begin{aligned} {\widehat{\alpha }}\left( x,t\right)= & \alpha \left( x,t\right) -\widehat{ \mathcal {R}}_{21}, \end{aligned}$$

(35)

$$\begin{aligned} {\widehat{\beta }}\left( x,t\right)= & \beta \left( x,t\right) -\widehat{ \mathcal {R}}_{12}\equiv -{\widehat{\alpha }}^{*}\left( -x,-t\right) , \end{aligned}$$

(36)

where $\widehat{\mathcal {R}}=SG^{-1}P^{\dag }$. Through iteration of BDT, we can derive N-times iteration of ${\widehat{F}}_{0}$ expressed as

$$\begin{aligned} {\widehat{F}}_{0}[N]=F_{0}-\frac{i}{4}\left[ \sigma _{3}, \begin{vmatrix} G(S_{1},P_{1})&\cdots&G(S_{N},P_{1})&P_{1}^{\dag } \\ \vdots&\cdots&\vdots&\vdots \\ G(S_{1},P_{N})&\cdots&G(S_{N},P_{N})&P_{N}^{\dag } \\ S_{1}&\cdots&S_{N}&{O} \end{vmatrix} \right] . \end{aligned}$$

(37)

We express quasi-grammians in the form of matrix having $2\times 2$ order, as

$$\begin{aligned} {\widehat{F}}_{0}=F_{0}-\frac{i}{4}\left[ \sigma _{3},\left( \begin{array}{cc} \left| \begin{array}{cc} G & P_{1}^{\dag } \\ S_{1} & {O} \end{array} \right| & \left| \begin{array}{cc} G & P_{2}^{\dag } \\ S_{1} & {O} \end{array} \right| \\ & \\ \left| \begin{array}{cc} G & P_{1}^{\dag } \\ S_{2} & {O} \end{array} \right| & \left| \begin{array}{cc} G & P_{2}^{\dag } \\ S_{2} & {O} \end{array} \right| \end{array} \right) \right] . \end{aligned}$$

Now, we can write the quasi-grammian for the dynamical scalar variables as

$$\begin{aligned} {\widehat{\alpha }}\left( x,t\right)= & \alpha \left( x,t\right) -\left| \begin{array}{cc} G & P_{1}^{\dag } \\ S_{2} & {O} \end{array} \right| , \end{aligned}$$

(38)

$$\begin{aligned} {\widehat{\beta }}\left( x,t\right)= & \beta (x,t)-\left| \begin{array}{cc} G_{n} & P_{2}^{\dag } \\ S_{1} & {O} \end{array} \right| . \end{aligned}$$

(39)

These are the quasi-grammian solutions for the dynamical variables of NL-CSP equation. Therefore, through BDT we can derive quasi-grammian solutions of NL-CSP equation in the form of quasideterminants which are not identical with the solutions as derived by using classical DT¹⁹. Although the quasi-grammian form is structurally unconventional and nonlocal, inherits certain robustness from its determinantal nature. In general, small perturbations in the seed solution or spectral parameters leads the proportionally small variations in the quasideterminant, thereby preserving the qualitative shape of the solution. Specifically, for the class of solutions obtained via DT and BDT, such perturbations do not break the integrability structure, allowing the system to evolve in a stable and controlled manner.

Exact solution

In this section, we derive expressions for the grammian, breather and soliton solutions of NL-CSP equation. In order to obtain the explicit expression, we take the seed solution $\alpha \left( x,t\right) =\beta \left( x,t\right) =0$. The linear system (4), (5) has the following form

$$\begin{aligned} \Phi _{x}= & i\zeta \left( \begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array} \right) \Phi , \end{aligned}$$

(40)

$$\begin{aligned} \Phi _{t}= & \frac{i}{4\lambda }\left( \begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array} \right) \Phi . \end{aligned}$$

(41)

The linear system (40), (41) yields the matrix solution

$$\begin{aligned} \Phi (x,t;\zeta )=\left( \begin{array}{cc} e^{\lambda } & 0 \\ 0 & e^{-\lambda } \end{array} \right) , \end{aligned}$$

(42)

where $\lambda =-i\zeta x-\frac{i}{4\zeta }t$. The distinct matrix solution S is defined as

$$\begin{aligned} S=\left( \begin{array}{cc} e^{\lambda } & -e^{-\overline{\lambda }} \\ e^{-\lambda } & e^{\overline{\lambda }} \end{array} \right) . \end{aligned}$$

(43)

Similarly, distinct matrix solution P is expressed as

$$\begin{aligned} P=\left( \begin{array}{cc} e^{\eta } & -e^{-\overline{\eta }} \\ e^{-\eta } & e^{\overline{\eta }} \end{array} \right) , \end{aligned}$$

(44)

where $\eta =-i\mu x-\frac{i}{4\mu }t$. Using (43), (44), we get the form of G(S, P), i.e.,

$$\begin{aligned} G(S,P)=\left( \begin{array}{cc} \frac{\cosh (\eta +\lambda )}{-\zeta +\mu } & \frac{\sinh (\eta -\overline{ \lambda })}{-\overline{\zeta }+\mu } \\ \frac{\sinh (-\overline{\eta }+\lambda )}{-\zeta +\overline{\mu }} & \frac{ \cosh (\overline{\eta }+\overline{\lambda })}{-\overline{\zeta }+\overline{ \mu }} \end{array} \right) . \end{aligned}$$

(45)

Now, consider

$$\begin{aligned} \widehat{\mathcal {R}}=SG^{-1}(S,P)P^{\dagger }=\frac{1}{L}\left( \begin{array}{cc} \widehat{\mathcal {R}}_{11} & \widehat{\mathcal {R}}_{12} \\ \widehat{\mathcal {R}}_{21} & \widehat{\mathcal {R}}_{22} \end{array} \right) . \end{aligned}$$

(46)

So, the solutions (35), (36) are

$$\begin{aligned} {\widehat{\alpha }}\left( x,t\right)= & -\widehat{\mathcal {R}}_{21}, \nonumber \\= & \frac{1}{L}\left( \begin{array}{c} \left( \frac{\cosh (\overline{\eta }+\overline{\lambda })}{\overline{\mu }- \overline{\zeta }}\right) e^{(\eta -\lambda )}-\left( \frac{\sinh (\eta - \overline{\lambda })}{\mu -\overline{\zeta }}\right) e^{(-\overline{\eta } -\lambda )} \\ +\left( \frac{\cosh (\eta +\lambda )}{\mu -\zeta }\right) e^{(-\overline{ \eta }+\overline{\lambda })}+\left( \frac{\sinh (-\overline{\eta }+\lambda ) }{\overline{\mu }-\zeta }\right) e^{(\eta +\overline{\lambda })} \end{array} \right) , \end{aligned}$$

(47)

$$\begin{aligned} -{\widehat{\alpha }}\left( -x,-t\right)\equiv & {\widehat{\beta }}\left( x,t\right) =-\widehat{\mathcal {R}}_{12}, \nonumber \\= & \frac{1}{L}\left( \begin{array}{c} -\left( \frac{\cosh (\overline{\overline{\eta }}+\overline{\lambda })}{ \overline{\mu }-\overline{\zeta }}\right) e^{(-\eta +\lambda )}+\left( \frac{ \sinh (\eta -\overline{\lambda })}{\mu -\overline{\zeta }}\right) e^{( \overline{\eta }+\lambda )} \\ -\left( \frac{\cosh (\eta +\lambda )}{\mu -\zeta }\right) e^{(\overline{\eta }-\overline{\lambda })}-\left( \frac{\sinh (-\overline{\eta }+\lambda )}{ \overline{\mu }-\zeta }\right) e^{(-\eta -\overline{\lambda })} \end{array} \right) , \end{aligned}$$

(48)

where

$$\begin{aligned} L=\frac{\cosh (\eta +\lambda )\cosh (\overline{\eta }+\overline{\lambda })}{ (\mu -\zeta )(\overline{\mu }-\overline{\zeta })}-\frac{\sinh (\eta - \overline{\lambda })\sinh (-\overline{\eta }+\overline{\lambda })}{(\mu - \overline{\zeta })(\overline{\mu }-\zeta )}. \end{aligned}$$

Binary Darboux transformation solutions to Darboux transformation solutions

In order to transform BDT solutions to DT solutions we have to perform specific spectral parameter reduction. For this substitute $\overline{\mu }=\zeta$, $\mu =\overline{\zeta }$, we have

$$\begin{aligned} \alpha \left[ 1\right] \left( x,t\right)= & \left( \zeta +\overline{\zeta } \right) \sec \text {h}(\zeta +\overline{\zeta })\cosh (\zeta -\overline{\zeta }), \nonumber \\ \beta \left[ 1\right] \left( x,t\right)= & -\left( \zeta +\overline{\zeta } \right) \sec \text {h}(\zeta +\overline{\zeta })\cosh (\zeta -\overline{\zeta }). \end{aligned}$$

(49)

Now, further substituting $\zeta =\overline{\zeta }$, we deduce

$$\begin{aligned} \alpha [1]\left( x,t\right)= & \left( 2\zeta \right) \tanh (2\lambda ), \end{aligned}$$

(50)

$$\begin{aligned} \beta [1]\left( x,t\right)= & -\alpha [1]\left( -x,-t\right) {.} \end{aligned}$$

(51)

While we have computed breather and soliton solutions for $(\alpha (x,t)=\beta (x,t)=0)$ as a vanishing background seed solution which is the starting point for deriving exact solutions through DT and BDT. Whereas we may obtain other solution such as lump soliton for non-vanishing $(\alpha (x,t)=\beta (x,t)=3)$ background seed solution presented in sub figure (g, h) of Fig. 3.

Similarly we can calculate two-soliton solutions by using the two sets of distinct matrix solutions $S_{1}$ and $S_{2}$ having $\Xi _{1}=\left( \begin{array}{cc} \zeta _{1} & 0 \\ 0 & \overline{\zeta }_{1} \end{array} \right)$ and $\Xi _{2}=\left( \begin{array}{cc} \zeta _{2} & 0 \\ 0 & \overline{\zeta }_{2} \end{array} \right)$, which are presented in Fig. 4.

Results and discussion

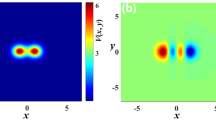
Figure 1, displays the contour and surface plots illustrating the dynamics of symmetry-breaking and symmetry-preserving interactions of breather with grammian across different $\zeta$ and $\mu$ values. In sub-figure (1a, b), for numerical values $\zeta$ = 0.055+0.96i, $\mu$ = 0.23+0.22i, represents the growing breather after the interaction with that of grammian for negative x and t values whereas plot (1c,1d) shows the spontaneously breaking of symmetry by breather before the interaction and after that breather maintains the symmetry. Further, Fig. (1e, f) explains the interaction of breather with grammain in which both tries to maintain the symmetry for numerical values $\zeta$ = 0.025+0.29i, $\mu$ = 0.32+0.12i. Here point to be noticeable that ${\widehat{\alpha }}(x,t)$ ${\widehat{\alpha }}(-x,-t)$ corresponds to the real-value potential.

Figure 2, demonstrates the dynamics of symmetry broken (decaying, growing) and symmetry preserved (stable) breather of the nonlocal CSP equation. In plot (2a, b), we presents the decay of unstable breather for numerical values $\zeta$ = 1.1+0.9i, whereas in Fig. (2c, d) we shows the spontaneously growing breather tries to achieve the symmetry for positive x and t values. Later on, Fig. (2e, f) clearly shows the contour and surface plot of symmetry preserving breather for $\zeta$ = 0.8+0.8i.

Figure 3, depicts the one-soliton solution in which we display the decaying and growing (symmetry non-preserving) soliton for $\zeta$ = 0.02+0.029i, for the negative and positive x and t values respectively. Also, the symmetry-preserving soliton for $\zeta$ = 0.09+0.59i is shown. Also we presented the lump solutions with non-vanishing background seed solution ($\alpha = \beta = 3$) for $\zeta = 0.08+0.32i$.

Finally, we construct and plot the profile of two-soliton solution (decaying, growing, before and after interaction) which is clearly explain through contour and surface plot in Fig. 4. It is to be noted that symmetry breaking solutions corresponding to non-Hermitian Hamiltonian which corresponds to the complex valued potential whereas symmetry preserving solutions belongs to Hermitian Hamiltonian systems having real valued potentials. The solutions presented here are the novel features of NL-CSP equation calculated by using BDT. Bright solitons are positive-amplitude and localized solutions of nonlinear wave equations that retain their shape throughout the propagation. They are often associated with focusing nonlinearity. Because of localized optical pulse that does not lose energy while traveling over a far off distances, bright solitons are used for high-speed communication systems. Whereas dark solitons have negative-amplitude and associated with defocusing nonlinearity. Due to defocusing nonlinearity, darks solitons are studied in optical fibers as pulse propagation. For controlling light pulses, dark solitons can be helpful as optical switching and soliton-based communication systems. Also, In optical fiber, breather solutions are particularly important to get understanding about the controlling light and pulse dynamics where the temporal evolution of light pulses may be controlled to attain desirable signal characteristics. The lump solitons enhance the analysis of nonlinear wave equations, particularly in exploring how the localized energy packets propagates in nonlinear media. These type of waves describes the localization of light pulses in optical fibers.

Fig. 1

Interaction of breather with grammian: (a, b) showing peak of breather at (− 18.6, − 8) for numerical values $\zeta = 0.055+0.96i, \mu = 0.23+0.22i$, whereas (c, d) showing peak of breather at (19.2, 8) for numerical values $\zeta = 0.055-0.96i, \mu = 0.23-0.22i$, (e, f) displays for $\zeta = 0.025+0.29i, \mu = 0.32+0.12i$.

Fig. 2

Dynamics of breather: (a, b) showing peak of breather at (1.8, 11.1) for numerical values $\zeta = 1.1+0.9i$, whereas (c, d) showing peak of breather at (− 1.4, − 12.3) for numerical values $\zeta = 1.1-0.9i$, (e, f) displays for $\zeta = 0.8+0.8i$.

Fig. 3

Dynamics of one soliton: (a, b) showing peak at (14, 0.3) for numerical values $\zeta = 0.02+0.029i$, whereas (c, d) showing peak at (− 14, − 0.3) for numerical values $\zeta = 0.02-0.029i$, (e, f) displays for $\zeta = 0.09+0.59i$, (g, h) shows lump solutions for $\zeta = 0.08+0.32i$.

Fig. 4

Dynamics of two soliton: (a, b) displays peaks at (10, 9), (2, 10) for numerical values $\zeta _{1}= 0.09+0.7i, \zeta _{2} = 0.05+0.5i$, whereas (c,d) showing peak at (− 2, − 10), (− 10, − 9) for numerical values $\zeta _{1}= 0.09+0.7i, \zeta _{2} = 0.05+0.5i$, (e, f) displays for $\zeta _{1}= 0.04+0.8i, \zeta _{2} = 0.08+0.5i$, (g, h) illustrates the interaction for $\zeta _{1}= 0.04-0.8i, \zeta _{2} = 0.08-0.5i$.

Concluding remarks

The aim of this paper was to propose a BDT for the NL-CSP equation. We present how under symmetry transformation NL-CSP equation transform to general complex CSP equation and also the Lax pair is defined. By calculating soliton solutions using DT, a systematic framework for BDT was constructed and applied to the NL-CSP equation, yielding explicit quasi-grammian solutions. The classical DT uses a single eigenfunction to generate new solutions whereas BDT uses a pair of eigenfunctions (direct and adjoint) to iteratively build solutions, preserving integrability and constructs a new potential solution by linking two solutions of the linear system. To the best of our knowledge, this is the first application of BDT to the NL-CSP equation, highlighting the adaptability of this method to nonlocal integrable systems. The resulting quasi-grammian solutions exhibit structurally stable and rich dynamics, extending the family of known solutions beyond what is accessible by using BDT. The dynamics of novel characteristics solutions symmetry-preserving and symmetry-breaking breathers, along with their interactions with grammian, one, two soliton and also lump solutions for vanishing and non-vanishing backgrounds were presented via BDT. Notably, the behavior of these solutions under nonlocal constraints differs significantly from their local counterparts, revealing novel features like shifted peak positions and symmetry breaking which is clearly verified by contour and surface plots.

BDT provided a precise method to obtain solutions where grammian and breather solutions enhanced the understanding of nonlinear wave phenomena. In particular, breather solutions played a crucial role in modeling the propagation of ultra-short pulses in optical fibers.Exploring the BDT to discrete NL-CSP multi-component system might lead more general solution classes, which would be compelling research direction. Investigating the Backlund transformation²⁷ and Dzyaloshinskii–Moriya interaction²⁸ for the bilinear SP could give significantly interesting dynamics. Future work may involve a detailed spectral stability analysis of these solutions, as well as their numerical evolution under perturbed initial conditions, to better understand their robustness and potential applications.