Evaluating climate shifts and drought regions in the central Indian river basins

Abstract

Climate change, characterized by erratic rainfall patterns and rising temperatures, is enhancing the severity and intensity of drought across India. Considering this impact, assessment of these changes is critical for developing effective adaptation and mitigation strategies. This study employs a stochastic entropy-based approach to compute the inter- and intra-annual rainfall variability for multiple temporal scales. Considering this assessment, we identified winter, pre-monsoon, and post-monsoon seasons as key contributors to annual rainfall variability. Furthermore, using the entropy approach, we prepared a water resource availability map. It presents that 53.88% of the Betwa’s water resources and 54.57% of the Kshipra’s resources fall under Classes B and C, highlighting significant vulnerability to drought conditions in both basins. Subsequently, meteorological and hydrological droughts were evaluated using SPI, SPEI, and SRI indices. It showed that the Southern and Central regions of the Kshipra and the Northern and Central regions of the Betwa are highly drought prone. The outcome of the present study provides vulnerable drought regions with prolonged duration and high severity and intensity regions across the basin. It will support policymakers in implementing timely and targeted interventions for water resource management, facilitating the development of effective drought action plans.

Introduction

The changing climatic conditions with rainfall variability and rising warming conditions enhance frequent and intense drought events across India. It impacts regional human health, crop production, and ecosystems^1,2,3. It is observed that India received more than 80% of its annual rainfall during the southwest monsoon between June and September⁴. However, India observed 9% of interannual variability in this period from its mean rainfall^5,6. This variability has an enormous impact on seasonal rainfall patterns⁷and socio-economic across India, specifically on the agriculture sector and its GDP (Gross Domestic Product)⁸. The Madhya Pradesh state in Central India, having more than 75% of the total population dependent on the agriculture sector and 12% of India’s forest cover, faces impacts of rising rainfall variability^9,10. The rising temperature and rainfall variability enhances the drought risk in the region for meeting the regional water demands¹¹. It is observed that drought arises with a prolonged duration of rainfall deficits along with the rise in regional temperature, which leads to meteorological drought¹². This further enhanced the conditions of hydrological drought with a decline in the regional surface and sub-surface water resources across the regional streams, rivers, and reservoirs^12,13. Based on a copula bivariate framework for the joint occurrences of the flash drought severity and duration, the study identified that Central India observed frequent and intense flash drought events, especially between spring and summer season¹⁴. Furthermore, a study identified that central parts of South Asia observe a significant decline in future water availability with an increase in temperature¹⁵. Considering these challenges, this study aims to explore how the stochastic entropy-based methodology can offer insights into regional rainfall variabilities and drought characteristics, with a broader focus on enhancing water resource management in the face of climate change using high spatial resolution regional datasets. Thus, the aim of this study to assess the variability in rainfall, water resources availability, and drought characteristics (Duration, Severity, and Intensity) for two major drought-prone and intermittent river basins, Kshipra and Betwa^16,17in Madhya Pradesh state, respectively. The study emphasizes identifying drought-prone regions that may be more susceptible to climate-induced water scarcity. In monitoring the drought events, we employed the Standardized Precipitation Index (SPI), Standardized Precipitation Evapotranspiration Index (SPEI), and Standardized Runoff Index (SRI) Indices. SPI and SPEI are both used to monitor the meteorological drought. However, in order to determine their predictive efficiency for meteorological drought across the river basins, we used both indices. The SPI considered the precipitation only, while SPEI was computed using potential evapotranspiration and precipitation¹⁸. Evapotranspiration is a critical component in the hydrological cycle, and regional water balance interconnects soil, vegetation, and water¹⁹. It generally accounts for more than 50% of regional precipitation¹⁹. Therefore, the rise in evapotranspiration induces soil moisture deficits and should be assessed in monitoring drought characteristics^20,21,22. The SRI indices are prominently used for assessing hydrological drought conditions based on runoff datasets^23,24. The hydrological drought significantly impacts the regional water demand²⁵energy production²⁶food and water security^27,28,29. The Kshipra River observed a significant rise in water demand, particularly due to its religious significance and annual gathering of more than 120 million people, estimated in Simhastha 2028^30,31. Therefore, the considered drought characteristics will enhance the efficient monitoring of drought events, as mentioned in recent studies^32,33,34,35. This integrated approach provides a conceptual framework to identify regions within the basin vulnerable to rainfall variability, assess water resource availability, and determine the proportion of resources in water-scarce zones. Considering this, drought indicators assist in identifying drought-prone regions within the basin. The novelty of this research lies in its dual approach: evaluating changes in rainfall patterns through a stochastic entropy-based method and identifying drought regions with their specific characteristics. On considering both meteorological and hydrological drought aspects, this research bridges the gap between theoretical frameworks and practical applications in water resource management. This integrated methodology provides a robust framework for assessing the impacts of climate change on regional water resources. It will help stakeholders in predicting declining streamflow and groundwater levels based on drought indicators and aid in identifying drought regions across the two river basins to support the development of an efficient hydrological drought early warning system³⁶. It will enhance urban climate change resilience, particularly in vulnerable regions, and improve water security for millions living across the Betwa and Kshipra River basins as an approach derived from run theory. This comprehensive framework will facilitate more informed decision-making and long-term planning to mitigate the adverse effects of climate change. Considering this, the present study outlines the following objectives for the Betwa and Kshipra River basin: (1) Intra- and Inter-annual spatiotemporal variability in rainfall amount and days, (2) Determine responsible months and seasons for annual rainfall variability, 3) Determine the shifting pattern under climate change, 4) Compilation of water resource availability maps that provide a visual interpretation of the distribution of water, and 5) Identifying the drought-prone regions using entropy-based approach derived from run theory.

Study area

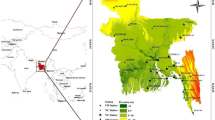
The study focused on the Kshipra and Betwa River basins, both of which are part of the Ganga River basin. The holy city of Ujjain is located across the Kshipra River. It originates through the Kakri-Tekdi hill (22°31’ N, 76° E) in the Vindhya range and flows in the north-western direction across the Malwa plateau to join the Chambal River near Kalu-Kher village (23°53’ N, 75°31’E). The river has a length of 195 km, a very sinuous course, and a catchment area of 5600 sq.km. The Kshipra River flows primarily through the Indore, Dewas, Ujjain, Dhar, and Ratlam districts of the state³⁷. The river basin observed annual rainfall of 984 mm in the southeast to 865 mm in the northwest, with more than 93% of rainfall occurring from June to September^17,38. The main tributaries of the Kshipra River include the Kahn River near Ujjain and the Gambhir River near Mahidpur. However, over the years, the Kshipra River has lost its perennial nature and now remains dry for five to six months annually. Since 2014, due to higher water demand across the Kshipra River, the water from the Narmada River has been lifted and discharged into the Kshipra River through the Narmada-Kshipra Simhastha Link Project³⁷.

The Betwa River basin is the tributary of the Yamuna River, with a southwest-to-northeast flow direction in the Bundelkand region of Central India. The Betwa River originates in the Dehgaon Bamori Forest Range (23°51′ N, 77°15′ E) in Raisen district at an elevation of 475 m and confluence with Yamuna River near Hamirpur (25°55′ N, 79°45′ E) Uttar Pradesh, with a total distance of 564 km¹⁶. The basin has a catchment area of 44,002 sq.km, of which 68.84% of its catchment is present in Madhya Pradesh and 32.16% in Uttar Pradesh, respectively³⁹. The basin is present in the sub-humid and semi-arid regions, with average annual rainfall ranging from 700 to 1200 mm¹⁶. The river basin has several tributaries like Kaliasot, Halali, and Sagar near its origin; mid-stream tributaries include Narain, Orr, and Jamni, while Dhasan and Birma are major downstream tributaries of the Betwa River⁴⁰. Betwa River basin comprises a drought-prone region of the Bundelkhand parts of Madhya Pradesh and Uttar Pradesh and is interlinked with the Ken River basin under the National River Linking Project^16,41,42,43. The location map of both river basins is shown in Fig. 1.

Results and discussion

In this section, we initially present the rainfall variability across the Kshipra and Betwa river basins. In association with this, we classified the regional water resources across these river basins and computed the drought characteristics like duration, severity, and intensity.

Fig. 1

Location map of the Betwa and Kshipra River basins⁴⁴.

Rainfall variability

In this section, we initially describe the inter-annual rainfall variability using marginal entropy at monthly, seasonal, and annual scales. Consequently, we present the intra-annual rainfall variability at monthly and seasonal scales using apportionment and intensity entropy for the Kshipra and Betwa river basins.

Inter-annual rainfall variability

The inter-annual rainfall variability was assessed using the standardized variability index of marginal entropy (SVI_ME) for annual, seasonal, and monthly temporal scales. The SVI_ME results were assessed from 1951 to 2022 for both Kshipra and Betwa river basins across the year, 4 seasons (Winter, Pre-monsoon, Monsoon, and Post-monsoon), and twelve months (January to December) as shown in Figs. 2, 3, and 4, respectively. Considering the inter-annual rainfall variability based on the annual SVI_ME values, we observed that both the Betwa and Kshipra River basins observed higher variability in their downstream sections. However, the Betwa River Basin observed 1.85 times higher variability in annual rainfall amounts in comparison to the Kshipra River basin, respectively. The maximum SVI_ME variability was observed for the Hamirpur (0.024) and Mahidpur (0.013) regions in the Betwa and Kshipra River basins, respectively. It indicates that both the river basins observe higher annual rainfall variability in their low rainfall region across their downstream sections, as shown in Fig. 2, respectively. However, certain upstream regions like Dewas of the Kshipra River basin observed significant variability.

Fig. 2

This spatial plot shows the annual intra-variability based on the Standardized Variable Index for Marginal Entropy (SVI_ME) across the Kshipra (left) and Betwa River (right) basins using a color gradient scale. The x-axis corresponds to longitude, while the y-axis corresponds to latitude. The color variations indicate higher values, as shown in red, and lower values in blue and purple, respectively⁴⁵.

Fig. 3

Red-colored highlight areas with high SVI_ME, while pink-colored show areas with low SVI_ME. The left-sided and right-sided spatial maps show monthly SVI_ME and seasonal variation of SVI_ME, respectively. This figure shows the responsible months (left) that caused seasonal (right) variability in rainfall amount for the Betwa River Basin⁴⁵.

Fig. 4

Red-colored highlight areas with high SVI_ME, while pink-colored show areas with low SVI_ME. The left-sided and right-sided spatial maps show monthly SVI_ME and seasonal variation of SVI_ME, respectively. This figure shows the responsible months (left) that caused seasonal (right) variability in rainfall amount for the Kshipra River basin⁴⁵.

It is significant to note here that the least inter-annual rainfall variability was observed for the Ashok Nagar (0.007) and Indore (0.009) regions across the Betwa and Kshipra River basins, respectively. It indicates that regions near the origin of the river basins indicate the least rainfall variability. However, near the origin of the river basins, we observed that the Kshipra River has relatively higher variability, which is enhanced significantly in the Dewas region. Overall consideration of the inter-annual rainfall variability indicates that it has a smaller value at a larger temporal scale. It is due to the larger rainfall amount at a larger scale, which observed the least variation^46,47,48. Therefore, in order to compute the reasons for this inter-annual variability, we have to assess the inter-variability of rainfall in the seasons and months, respectively. The seasonal inter-variability of SVI_ME for the Betwa and Kshipra River basins has been shown in Figs. 3 and 4, respectively. It is observed that the Betwa and Kshipra River basins have higher inter-annual rainfall variability due to higher seasonal variability in pre-monsoon and winter seasons, respectively.

In the pre-monsoon season, the Betwa River Basin observed SVI_ME values variation from 0.099 at Jhansi to 0.248 at Nivari. However, in the Kshipra River basin, SVI_ME values vary from 0.139 at Indore to 0.243 at Mahidpur, respectively. Subsequently, the monsoon season observed the least rainfall variability for the Kshipra River (0.010 to 0.013) basin and the Betwa River (0.007 to 0.026) basin, respectively. The minimal variability indicates consistent and predictable rainfall for both basins. However, the Betwa River has a 2 times higher maximum monsoon rainfall variability with a higher range compared to the Kshipra River basin, respectively. It indicates that drought-prone vulnerability is relatively high for the Betwa River basin due to higher uncertainty during the monsoon period.

The post-monsoon period has less predictable rainfall amounts with higher recorded SVI_ME values. The SVI_ME values vary from 0.120 at Raisen to 0.191 at Shivpuri across the Betwa River basin. However, in the Kshipra River basin, SVI_ME values vary from 0.122 at Sanwer to 0.184 at Mahidpur, respectively. Consequently, during winter, the SVI_ME values were relatively high compared to the post-monsoon period. The range of SVI_ME varied from 0.117 at Raisen to 0.221 at Tikamgarh, respectively. The seasonal variability in winter was more prominent in the upstream section for Betwa. Similarly, the range of SVI_ME varied from 0.177 at Ujjain to 0.248 at Indore for the Kshipra basin. This seasonal uncertainty in winter was more prominent in the upstream sections of both river basins. In order to assess the reasons for the seasonal rainfall variability, we assessed the monthly inter-variability.

In the period from January to May, there has been a gradual change observed across both the river basins in SVI_ME values from lower (light blue and green) to higher (yellow and red). This variability is observed at maximum in April before the monsoon months. The monsoon months from June to September indicate consistent rainfall with lesser variability due to low SVI_ME values. However, after September, a sharp change was observed, with a resurgence of variability since October. The Betwa and Kshipra River basins observed higher rainfall variability in November and December, respectively. It indicates higher unpredictable rainfall patterns in these months. Overall, April, November, and December showed more spatial variability, as indicated by higher SVI_ME values, indicating months of more erratic or unpredictable rainfall patterns. However, both the river basins observed the least SVI_ME values in July and August, followed by June and September, but still exhibited some variability. Furthermore, two transition shifts were observed, i.e., April to May (Pre-monsoon) and October to November (Post-monsoon). Transition shift means shifts between more stable conditions and unpredictable weather patterns observed, as lower or higher SVI_ME values are observed across the river basin. This phase likely corresponds to the buildup before and after the monsoon season.

Overall, the monthly inter-variability of SVI_ME for the Betwa and Kshipra River basins indicates higher pre-monsoon variability, which is attributed to the enhanced April month variability. However, during the post-monsoon period, the higher variability is prominent in the northern parts of the river basins due to higher monthly SVI_ME values in November and December, respectively. It indicates there is a transition from the stable monsoon period to more erratic weather patterns observed after October month. Subsequently, in the winter period, higher variability is observed due to significant variability in February in the downstream sections of the river basins, as shown in Figs. 3 and 4, respectively.

Intra-annual rainfall variability

The intra-annual rainfall variability was assessed using the standardized variability index of apportionment (SVI_AE) and intensity entropy (SVI_IE) at seasonal and monthly temporal scales. The SVI_AE and SVI_IE indicate variability in the rainfall amount and days, respectively, in the period 1951 to 2022. The results were assessed for both Kshipra and Betwa river basins across the 4 seasons (Winter, Pre-monsoon, Monsoon, and Post-monsoon) and twelve months (January to December), as shown in Figs. 5 and 6, respectively.

Monthly and seasonal intra-rainfall variability

It is observed that significant variation in the monthly rainfall amount was observed between 1980 and 2000 across the Kshipra and Betwa River basins, as shown in Figs. 5 (a) and (c), respectively. These colors represent a mid-range level of variability, indicating that rainfall amounts were more unpredictable at a monthly scale during this period. It is observed that both the Kshipra and Betwa River basins exhibit similar patterns, with mid-level variability in monthly rainfall that can be attributed to localized daily rainfall variability. The intra-rainfall variability is enhanced at larger temporal scales due to significant changes in rainfall across the different years. Considering this, we observed that the monthly variability is significantly higher in the recent period, 2000 to 2020, across the Betwa River basin, respectively.

These higher monthly variations were enhanced in the seasonal intra-rainfall amount variability. The seasonal variation is more pronounced between 2000 and 2020, where large red and orange areas dominate the seasonal SVI_AE plots, as shown in Fig. 5 (b) and (d), respectively, for both basins. These red zones indicate intense fluctuations in seasonal rainfall amounts, showing that the period from 2000 to 2020 experienced the highest seasonal variability. This period displays a trend for increasing variability, with rainfall amounts becoming more erratic across both basins. The 3D plots of SVI_AE illustrate that the highest variability in rainfall amounts on a seasonal scale between 2000 and 2020 for the regions like Indore, Shajapur, and Ujjain across the Kshipra River basin while Guna and Vidisha in the Betwa River basin, respectively.

Monthly and seasonal intra-rainy days variability

Significant monthly variations in the rainy days were observed between the years 1980–2000, as shown in Fig. 6 (a) and (c), respectively. It is indicated through higher patches of green and yellow during this period, showing a mid-range of variability across both the river basins. However, seasonal variability in the rainy days for both river basins is high throughout all the years, with the maximum in the recent period from 2000 to 2020. It is indicated by the higher prevalence of red and orange regions during these intervals, as depicted in Fig. 6 (b) and (d), respectively. Rainfall amounts follow a similar pattern. However, in most regions, the variation in total rainfall amounts is often more pronounced than in the number of rainy days, indicating that the magnitude of rainfall may remain relatively unstable. More significant variability in rainfall amounts, rather than the number of rainy days, often indicates shifts in the intensity and distribution of rainfall. It can lead to extreme events like floods during heavy downpours and droughts during dry spells, even if the overall number of rainy days remains constant. Such variability may affect water availability, agriculture, and ecosystems by creating unpredictable water cycles, making it harder to plan for and manage resources in the region.

Fig. 5

Three-dimensional (3D) plots of monthly and seasonal Standardized Variability Index for Apportionment Entropy (SVI_AE) showing variation in rainfall amounts across different grid points; Monthly and Seasonal SVI_AE for Kshipra River (a, b) and Betwa River (c, d) basins. The x-axis of the 3D plots represents grid stations or points, the y-axis represents the year, and the z-axis represents SVI_AE values. The range of SVI_AE values is shown by color scales, where red denotes high variability and purple denotes low variability in rainfall amounts⁴⁹.

Fig. 6

Three-dimensional (3D) plots of monthly and seasonal Standardized Variability Index for Intensity Entropy (SVI_IE) showing rainy days variations across different grid points; Monthly and Seasonal SVI_IE for Kshipra River (a, b) and Betwa River (c, d) basins. The x-axis of the 3D plots represents grid stations or points, the y-axis represents the year, and the z-axis represents SVI_IE values. The range of SVI_IE values is shown by color scales, where red denotes high variability and purple denotes low variability on rainy days⁴⁹.

Water resource availability

The water resources categorizations in four classes, i.e., Class A, B, C, and D, have been carried out based on mean annual rainfall (in mm/year) and daily SVI _AE. The visual representation of all these classes for the Betwa and Kshipra River basins is shown in Figs. 7 and 8, respectively. The Betwa and Kshipra River basins observed mean daily SVI_AE values of 0.373 and 0.401, respectively. The mean annual rainfall for the Betwa and Kshipra River basins was observed at 1001.9 mm and 957.5 mm, respectively.

Water resources categorization

Considering the water resources categorization, we observed that Class A observed the regional points with above-average rainfall and lower variability. It indicates higher rainfall consistency and abundant water resources throughout the year. While Class B indicates regions with low rainfall variability and below-average rainfall. It indicates regions with moderate yet consistent water availability. However, this class will require better water resource management to meet the regional water demand during the dry periods. Class C received below-average rainfall with higher variability, which indicates the rainfall will concentrate over fewer days and enhance the risk for drought events. Lastly, Class D received above-average rainfall with higher variability. It indicates the regions with higher rainfall clustered in fewer months or seasons, respectively.

Water resources availability map

Considering the assessment of the availability of water resources for the Betwa River basin, we group the percentage of two water resource classes. Class A and D, in combination, account for 46.12% of water resources in the Betwa River basin with higher regional rainfall. However, Class B and C combined account for 53.88% of water resources in the region. In the context of this study, we considered the Class B and C regions, which are collectively responsible for a larger share of water resources in the region with lower rainfall. It makes this region highly vulnerable and at a higher risk for drought events. Considering this, we observed that 53.88% of the Betwa River water resources, specifically across the downstream section of the basin, are highly vulnerable to drought events, as shown in Fig. 7.

Fig. 7

Classification of water resources based on mean annual rainfall (mm/year) and daily Standardized Variability Index for Apportionment Entropy (SVI_AE) for Betwa river basin. The left-sided scatter plot shows the four classes (A–D) of categorized water resources based on dashed lines, indicating threshold values of mean SVI_AE and mean Annual Rainfall for classification. The right-sided map shows the visual representation of these four classes across the study regions⁴⁵.

Considering the water resources availability assessment for the Kshipra River basin, we observed that Class A & D considered 45.13% of water resources with higher rainfall. However, Class B & C considered 54.57% of water resources across the Kshipra River basin with lower rainfall, as shown in Fig. 8. Considering this, we observed that 54.57% of the Kshipra River water resources are distributed across the basin, with higher concentrations in the downstream and mid-portion of the river basin. It makes the Ujjain and Mahidpur regions across the river basin highly vulnerable to drought-prone events. Therefore, based on this assessment, we identify the regions at risk of drought-prone events. Thus, we consider the assessment of the drought characteristics (Duration, Severity, and Intensity) in subsequent sections for multiple meteorological and hydrological drought indicators. It will be assessed in order to identify drought propagation at nine and twelve-month time scales.

Fig. 8

Classification of water resources based on mean annual rainfall (mm/year) and daily Standardized Variability Index for Apportionment Entropy (SVI_AE) for the Kshipra River basin. The left-sided scatter plot shows the four classes (A to D) of categorized water resources based on dashed lines, indicating threshold values of mean SVI_AE and mean Annual Rainfall for classification. The right-sided map shows the visual representation of these four classes across the study regions⁴⁵.

Drought characteristics assessment

In this section, we describe the changing patterns of the meteorological and hydrological drought characteristics, like mean duration, severity, and intensity between 1951 and 2022, for both the Betwa and Kshipra River basins. In this study, we used two meteorological drought indicators, i.e., SPI and SPEI, with the assessment of hydrological drought using the SRI. It will be assessed to identify the drought propagation between 9- and 12-month time scales across the river basins.

Betwa river basin

The drought duration assessment for the Betwa River Basin using three indices, SPI, SPEI, and SRI, at 9-month and 12-month time scales. Considering both the time scales, we observed more regions with higher drought events for the nine-month time scale. However, on a 12-month time scale, drought duration varies from 12 to 66 months for all three drought indicators in lesser regions. It was observed that the multiple regions (around latitude 25.5°N, longitude 79°E) in the northern and central areas exhibited extended durations of drought conditions, demonstrating persistence with a maximum of 66 months. However, southern areas were marked as better hydrological conditions as these regions exhibited shorter drought durations (12 to 18 months), as shown in Fig. 9.

Fig. 9

Spatial distribution of drought duration (in months) across Betwa river basin based on multiple drought indices at 9 and 12-months. Top row: Duration of drought events at 9-month timescale using (a) SPI-9, (b) SPEI-9, and (c) SRI-9. Bottom row: Duration of drought events at 12-month timescale using (d) SPI-12, (e) SPEI-12, and (f) SRI-12. Color scales indicate drought duration in months, with darker blue representing shorter durations and red representing longer durations⁴⁵.

Consequently, we assessed the drought severity for all three drought indicators at 9- and 12-month time scales. It provides us with an understanding of how severe drought propagates in the region. The northern (25.5°N to 26°N and 79.5°E to 80°E) and some parts of the central region (24.5°N to 25°N and 79°E to 79.5°E) of the Betwa basin experienced high drought severity as shown in Fig. 10. It indicates that the region is prone to longer-term dry periods due to the occurrence of less rainfall.

Fig. 10

Spatial distribution of severity of drought across Betwa river basin based on multiple drought indices at 9 and 12-months. Top row: severity of drought events at 9-month timescale using (a) SPI-9, (b) SPEI-9, and (c) SRI-9. Bottom row: severity of drought at 12-month timescale using (d) SPI-12, (e) SPEI-12, and (f) SRI-12. Color scales indicate the severity of drought, with darker blue representing shorter drought severity and red representing longer drought severity⁴⁵.

The range of drought severity varied between − 40 to -110. However, southern regions (23°N to 24°N and 77.5°E to 78.5°E) exhibited lower drought severity, suggesting that water conditions are more stable. Based on the assessment of drought duration and severity between 1951 and 2022, we compute the average drought intensity for all three drought indicators, as shown in Fig. 11. The SPI-9 indicates average drought intensity patterns over 9 months, with some regions in the northern part exhibiting higher average intensities. It possibly suggests drought conditions are dominant in the Northern region of the Betwa basin.

Fig. 11

Spatial distribution of average intensity of drought across Betwa river basin based on multiple drought indices at 9 and 12-months. Top row: severity of drought events at 9-month timescale using (a) SPI-9, (b) SPEI-9, and (c) SRI-9. Bottom row: average intensity of drought at 12-month timescale using (d) SPI-12, (e) SPEI-12, and (f) SRI-12. Color scales indicate the average intensity of drought, with darker blue representing shorter drought intensity and red representing longer drought intensity⁴⁵.

Moreover, SPEI-9 Indicates relatively less average intensity across all the grid points, while SRI-9 followed a similar pattern as SPEI-9 in terms of average drought intensity. The average drought intensity captured by SPI-12 was more prominent than other indices, such as SPEI-12 and SRI-12, in the northern areas of the Betwa basin, highlighting intense drought conditions. Overall, the drought characteristics assessment for the Betwa River basin revealed that the northern region across the Hamirpur in the downstream section observed prolonged drought duration with high severity and intensity. It is attributed to lower annual rainfall (729.4 to 839 mm), highlighting the need to adopt proper water resources conservation strategies. However, the mid-central part of the basin, having moderate drought duration and severity, enhances the average intensity of drought events. Lastly, the hydrological drought indicates prominent average intensity across the upstream and mid-section of the river basin in the SRI-12-month time scale. It will make water resources management more critical in the region. Therefore, proper watershed management practices need to be implemented across the basin.

Kshipra river basin

The drought duration assessment for the Kshipra River basin uses three indices, SPI, SPEI, and SRI, at 9-month and 12-month time scales, as shown in Fig. 12. Based on the assessment of the SPEI-9 and SPEI-12, we determined that both indicators display extended durations in the southern region of the basin. However, SPEI-12 shows longer durations over a broader area than SPEI-9. In addition, SPEI-12 shows more significant variability and extended durations than SPI-12, which may affect the overall flow regime of the river. Moreover, SPI-9 and SRI-9 maps show a relatively uniform distribution across the region with lower values. However, SPEI-9 shows a drought with a longer duration of 23 months in the southern region across Indore. It may be due to a deficit in rainfall and higher temperatures, which may result in a prolonged drought in this area. Moreover, the SRI-12 plot reveals much longer drought durations, with a maximum of 34 months. However, SPEI-12 has a relatively shorter duration (17 to 33 months) in the central region of the basin than SRI-12. Therefore, the higher duration of the meteorological and hydrological drought in the Central region of the basin makes the Ujjain region highly vulnerable to drought events.

Based on the assessment of drought duration and severity between 1951 and 2022, we compute the average drought intensity for all three drought indicators, as shown in Fig. 13. The average meteorological drought intensity for SPEI-12 is relatively higher than SPEI-9, with prolonged duration and severe drought extending further south to the north part of the Kshipra River basin. However, SPI-9 shows relatively low average intensities across the region, while drought intensity was more prominent in the central and Southern regions by SPEI-9 and SRI-9 of the Kshipra River basin. Furthermore, hydrological drought computation using SRI-12 showed a high intensity covering the larger area, while SPEI-12 showed similar pattern as 9-month scale. SPI-12 shows moderate intensity throughout the region except in the southern upstream region of Indore. In Fig. 13, areas with lower average intensity (SRI) are suggested regions where water availability may be less affected. However, more intense values suggest frequent impacts on water availability that may reduce river flow as it reflects the gradual response toward the hydrological network.

Fig. 12

Spatial distribution of drought duration (top row) and severity (bottom row) across the Kshipra River basin at different timescales using multiple drought indices. Top row: Duration of drought events (in months) at (a–c) 9-month and (d–f) 12-month time scales. Bottom row: Severity of drought events at (g–i) 9-month and (j–l) 12-month. Color scales indicate drought duration and severity at 9-month and 12-month, with darker blue representing lower values and red representing higher values⁴⁵.

Moreover, the intensity of drought or wet conditions directly influences water availability in the basin. When the intensity of dry periods is high, less water feeds into rivers and streams, leading to lower water levels. Overall, we conclude that both rainfall amount and rainy days have higher inter- and intra-annual variability for the Betwa River basin in comparison to the Kshipra River basin. It leads to higher rainfall distribution and deficit variability due to meteorological drought across the Betwa River basin. However, higher severity and intensity are observed for the hydrological drought across the Kshipra River basin. It can be attributed to a higher upstream meteorological rainfall deficit associated with higher water consumption for agricultural demands.

Fig. 13

Spatial distribution of average intensity of drought across the Kshipra River basin at different time scales using multiple drought indices. This plot shows the average intensity of drought in the left figure (a–c) and right figure (d–f). Color scales indicate drought duration and severity at 9-month and 12-month, with darker blue representing lower values and red representing higher values⁴⁵.

Discussions

The present study utilized drought indices, including SPEI, SPI, and SRI, to assess drought conditions. However, many other drought indices, such as the Effective Drought Index (EDI), Integrated Drought Index (IDI), Palmer Drought Severity Index (PDSI), Reclamation Drought Index (RDI), Surface Water Supply Index (SWSI), Vegetation Drought Response Index (VDRI), and many more are available in the literature to calculate drought, but this study basically connects the conceptual framework of Entropy coupled with drought. For instance, this study first assesses variability in the region and then estimates overall water resources using the concept of entropy to identify drought-prone regions in the Betwa and Kshipra River basins. This analysis revealed more than 50% of water resource classes fall under drought-prone areas concentrated in the downstream Betwa and mid-to-downstream Kshipra basins. Once drought-prone regions were identified, we employed the SPI (to assess precipitation-based drought variability), SPEI (to analyze drought considering both precipitation and temperature effects), and SRI (to assess hydrological drought impacts on water resources) to further analyze drought characteristics. The study revealed that February and April are crucial months for seasonal variability in both the Betwa and Kshipra basins. Furthermore, the drought analysis for the Kshipra River basin demonstrated a contrasting pattern compared to the Betwa basin, with the southern and central parts of the basin experiencing higher drought severity and intensity. The meteorological drought assessment using SPI-9 and SPI-12 revealed severe drought conditions concentrated primarily in the southern region, with SPI-12 displaying longer-lasting and more intense drought events compared to SPI-9. The findings indicate that the drought dynamics in the basins are largely governed by meteorological and hydrological drought^50,51,52 due to rainfall variability⁵³. The severity and intensity of drought conditions in the region have far-reaching implications for water availability, affecting irrigation demands, drinking water supply, and ecosystem sustainability. Therefore, the severity of drought affects the long-term water balance of the river basin^54,55. In association with this high, severe droughts can lead to prolonged periods of low water levels, affecting water supply for irrigation, drinking, and ecosystem services^53,56,57. However, it is observed that SPEI accounts for rainfall and evapotranspiration, offering a more precise picture of meteorological drought than SPI, as mentioned in recent studies^{58,59,60,61,62,63,64} for understanding the river basin dynamics. Therefore, integrated water resources management strategies, focusing on enhancing water storage, rainwater harvesting, and groundwater recharge, are essential for building drought resilience in these river basins. In addition, climate-adaptive measures such as promoting efficient irrigation practices and afforestation may further aid in mitigating drought impacts in these regions.

This study does not examine an in-depth assessment of the threshold for drought events because it does not fall within the scope of this study. Future research could focus on refining threshold criteria by incorporating diverse climatic datasets, machine learning approaches, and interdisciplinary methodologies to improve the accuracy and applicability of drought event classification. Additionally, integrating advanced machine learning modeling techniques will allow for more accurate and high-resolution predictions of regional drought event occurrences.

Conclusions

The primary objective of this study is to assess the rainfall variability-induced climatic shifts and identify the drought regions and their characteristics across the Betwa and Kshipra River basins using conceptual framework of Entropy and Drought indicators. This study quantified the inter- and intra-annual rainfall variability using a stochastic entropy approach. It is observed that pre-monsoon and winter seasons contribute significantly to variability in the Betwa and Kshipra River basins, respectively. The study identifies February and April as key months for winter and pre-monsoon seasonal variability in both basins. Rainfall variability is most pronounced in the downstream region of the Betwa basin and both upstream and downstream regions of the Kshipra basin. The changing rainfall patterns observed two transitional shifts from April to May (pre-monsoon) and October to November (post-monsoon). These shifts indicate a change from stable to unpredictable weather patterns, likely linked to climate change. It increases the risk of crop failure and reduced yields due to uncertainty in rainfall patterns. The water resource availability analysis assists in identifying 53.88% and 54.57% of water resources in the Betwa and Kshipra River basins present in drought-prone regions. These regions are concentrated more in the downstream section of the Betwa basin and across the mid and downstream regions of the Kshipra basin. Based on identified drought-prone regions, we assessed the drought characteristics using meteorological and hydrological indicators. Severe drought conditions were found in the southern and central Kshipra basin and the northern and central Betwa basin. The SPEI and SRI were found to be better indicators of drought than the SPI. The Kshipra River basin is observed to have higher hydrological drought severity, specifically in the Ujjain region. However, the Betwa River basin has a prolonged drought duration with high severity and intensity across the Hamirpur region in the downstream section of the basin. These combined conceptual frameworks of identifying climatic shifts and drought regions are more significant than traditional assessments and assist in providing efficient regional drought management and climate action plans. It will assist the concerned policymakers in better water resource allocation and provide preparedness strategies in these regions.

Datasets and methodology

In this section, we present all the data sets used for the assessment. Consequently, we present the entropy theory for the assessment of inter- and intra-annual rainfall variability across the Central India river basins. Further, we categorize regional water resources. Subsequently, we present the methods used for the assessment of meteorological and hydrological drought duration, intensity, and severity. The detailed methodology approach to determine climate shift based on various types of entropies and assessing the drought regions in the Central India river basins using the run theory at multiple time scales has been shown in Fig. 14. The study considered the India Meteorological Department (IMD) gridded daily rainfall datasets with a spatial resolution of 0.25^o x 0.25^o65,66. The rainfall datasets were used to compute the rainfall variability and meteorological drought across the study region. The study further considered the daily maximum and minimum temperature datasets with a spatial resolution of 1° x 1°⁶⁷. In recent years, numerous past studies employed the same dataset for various purposes, such as exploring the spatial diversity of precipitation teleconnections in India⁶⁸, analyzing spatiotemporal variability^47,69, downscaling of precipitation⁷⁰, and studying extreme precipitation events^71,72,73, and the widespread application of the IMD gridded and runoff datasets^3,74,75. These studies indicate its high accuracy and reliability across the country. The temperature datasets were used to compute the meteorological drought using SPEI. However, in order to compute the hydrological drought, we have determined SRI using the MERRA-2 runoff datasets with a spatial resolution of 0.5° x 0.625°⁷⁶. MEERA-2 dataset is recommended as a more realistic dataset to detect runoff variability and can signify better interactions between various physical processes and surface landscapes⁷⁷, and these datasets have been widely used in recent studies^3,74,75.

Entropy theory

Shannon, (1948) gave the idea of information entropy, or Shannon entropy, to quantify the degree of “surprise” in communication systems⁷⁸. In general, Shannon entropy quantifies uncertainty or disorder. Singh, (1997) explored how it can be used, its benefits, and its limitations, and suggested that it can be helpful in making decisions in hydrology and water resource fields⁷⁹. The mathematical expression for calculating Shannon entropy (H) for a random variable X with corresponding probability $\:{p(x}_{i})$ is given below in Eq. (1).

$$\:H\left(X\right)=-{\sum\:}_{i=0}^{N}p\left({x}_{i}\right){{log}}_{2}p\left({x}_{i}\right)$$

(1)

Marginal entropy (ME)

It is the inter-annual variability of rainfall amount at monthly, seasonal, and annual time scales⁴⁶ using Eq. (2) below. However, the seasons considered in this study as per IMD like Pre-Monsoon (March-May), Monsoon (June- September), Post-Monsoon (October- December), and Winter (January-February)^80,81.

$$\:H\left(X\right)=-{\sum\:}_{k=0}^{N}\left(\frac{{r}_{k}}{R}\right){{log}}_{2}\left(\frac{{r}_{k}}{R}\right)$$

(2)

$\:{r}_{k}$ = amount of rainfall for k^th year; R = Sum of rainfall from 1951 to 2022.

Fig. 14

Schematic flowchart outlining the complete workflow of the adopted approach, including data acquisition to the conceptual framework of Entropy to the implication of the Drought indicator of the study⁸².

Apportionment and intensity entropy

Maruyama et al. (2005) proposed the apportionment (AE) and intensity entropy (IE) that determines the intra-annual variability for rainfall amount and rainy days at monthly and seasonal time scales, respectively^83,84,85. The formulas AE and IE are shown below in Eqs. 3 and 4, respectively.

$$\:H\left(X\right)=-{\sum\:}_{k=0}^{N}\left(\frac{{r}_{k}}{TR}\right){{log}}_{2}\left(\frac{{r}_{k}}{TR}\right)$$

(3)

TR = Total rainfall for a given year; $\:{r}_{k}=$ rainfall amount for the k^th time scale of the respective year

$$\:H\left(X\right)=-{\sum\:}_{k=0}^{N}\left(\frac{{i}_{k}}{I}\right){{log}}_{2}\left(\frac{{i}_{k}}{I}\right)$$

(4)

I = rainy days for a given year; $\:{i}_{k}=$ rainy days for k^th time scale of the respective year.

Standardized variability index (SVI)

The study used the SVI to normalize the entropy value proposed by Guntu et al. (2020), to strengthen the indices value interpretation between zero (no variability) and one (high variability) at multiple scales^86,87. The mathematical expression of SVI is shown below in Eq. (5).

$$\:SVI=\left[\frac{{E}_{max}-E}{{E}_{max}}\right]$$

(5)

E_max = Maximum value of Entropy, E = Entropy value determined from particular time series.

Entropy-based approach to water resource availability maps

In order to classify the spatial regions based on the water resource availability, entropy-based measures were combined with the help of mean annual rainfall and daily SVI_AE as used in the recent studies^69,83,88. Therefore, based on the integration of two factors, we are able to categorize water resource availability across the two river basins, as shown in Fig. 15^83,86,89. The dashed lines indicate the average values of Mean annual rainfall and SVI_AE, splitting the scatter plot into four different classes. It is observed that Class B and C collectively may require relatively higher water resource management to meet demand during dry periods. However, Class A and D collectively may indicate the risk of flood conditions due to high variation in rainfall amount with high variability⁸⁶.

Run theory

In the present study, we employed run theory, proposed by Yevjevich (1967), to determine the drought Duration, Severity, and Intensity with a threshold ± 1 for SPEI, SPI, and SRI (-1 for drought and + 1 for wet conditions) as shown in Fig. 16⁹⁰. This threshold is adopted based on previous studies conducted by various researchers^91,92,93,94. The drought duration is computed based on the duration in which the drought events prevail. Subsequently, drought severity represents the cumulative value of drought at a specified threshold (-1). While drought intensity represents the total value of drought, it is divided by the total number of drought events at a specified threshold ( -1).

Fig. 15

Illustrating entropy-driven approach to categorize water resource classes based on SVI_AE and mean annual rainfall⁸².

Fig. 16

Identification of drought characteristics using run theory⁸².

The mathematical expression for drought duration, severity, and intensity is shown below in Eqs. (6), (7), and (8), respectively.

$$\:\begin{array}{cc}Drought&\:Duration\end{array}\left({D}_{d}\right)={T}_{de}-{T}_{di}$$

(6)

Where; T_de = Time when drought ends; T_di= Time when drought imitates

$$\:\begin{array}{cc}Drought&\:Severity\end{array}\left({S}_{d}\right)={\sum\:}_{n={T}_{di}}^{{T}_{de}}D{P}_{n}$$

(7)

DP = drought parameters for SPI/SPEI/SRI for the n^th time scale

$$\:\begin{array}{cc}Drought&\:Intensity\end{array}\left({I}_{d}\right)=\frac{{S}_{d}}{{D}_{d}}$$

(8)

Standardized precipitation index (SPI)

The methodology for the SPI was initially proposed by McKee et al. (1993)⁹⁵. This index has several advantages, such as a simple assessment with stability and the exclusion of spatiotemporal precipitation differences. It computes changes in climatic conditions for drought assessment by fitting regional time series precipitation datasets into the gamma distribution. It will convert to the normal distribution to compute the SPI index. The gamma function for the SPI assessment is shown in Eq. 9:

$$\:\varGamma\:\left(\alpha\:\right)={\int\:}_{0}^{x}{t}^{\alpha\:-1}\:{e}^{-t}\:dt\:\:for\:\xi\:\:>\:0$$

(9)

The best values for $\:\widehat{\alpha\:}$ and $\:\widehat{\beta\:}$ are computed using the maximum likelihood method based on the Eqs. (10) and (11).

$$\:\widehat{{\alpha \:}} = \:\frac{1}{{4D}}*\left( {1 + \sqrt {1 + \left( {\frac{{4D}}{3}} \right)} } \right.$$

(10)

$$\:\widehat{\beta\:}=\:\frac{\stackrel{-}{t}}{4D}$$

(11)

$$\:D=\:\text{ln}\stackrel{-}{t}-\:\frac{\sum\:\text{ln\:}(t)}{n}$$

(12)

Where n denotes the number of precipitation series, the cumulative probability for a specific month obtained through the Eq. (13)

$$\:p\left(x\right)=\frac{1}{{\beta\:}^{\alpha\:}\varGamma\:\left(\alpha\:\right)\:}{\int\:}_{0}^{t}{\int\:}_{0}^{x}{t}^{\alpha\:-1}\:{e}^{\frac{-t}{\beta\:}}\:dt$$

(13)

Based on this equation outcome, we compute the logarithmic distribution through the determination of its variance and mean of the time series precipitation datasets, as shown in Eq. (14).

$$\:SPI=\left(\pm\:1\right)*\left(q-\:\frac{{c}_{0}+\:{c}_{1}*g+{c}_{2}*{g}^{2}}{1+{d}_{1}*+\:{d}_{2}*g+{d}_{3}*{g}^{3}}\right)$$

(14)

$$\:q=\:\sqrt{\text{ln}\frac{1}{{p\left(x\right)}^{2}}}$$

(15)

Where t is the precipitation amount, and p(x) is Γ related to a precipitation probability distribution, and when p(x) > 0.5, + 1 is used in Eq. (15), and when p(x) < = 0.5, -1 is used in the Eq. (15). The values of coefficients in Eq. (15) are as follows: c₀ = 2.5155; c₁ = 0.8028; c₂ = 0.0103; d₁ = 1.4327; d₂ = 0.1892; d₃ = 0.0013. The SPI index assessment has wide-ranging applications in meteorological drought spatiotemporal duration⁹⁶severity⁹⁷intensity²¹and early forecasting^98,99,100 assessment.

Standardized runoff index (SRI)

Considering the meteorological drought, the study further assessed the hydrological drought across Central India’s River basins using the Standardized Runoff Index (SRI). Shukla & Wood (2008) initially defined the hydrological drought SRI index and is numerously used in various studies^2,23,56,101. It will assess the impacts of precipitation deficits and river interlinking across these river basins. The calculation procedure of SRI is the same as SPI by fitting the regional runoff datasets in appropriate statistical distributions. Subsequently, the fitted distribution transformed into a normal distribution to compute the SRI index.

Standardized precipitation evapotranspiration index (SPEI)

In order to assess the influence of the effects of evapotranspiration and appropriate predictors for metrological drought in the region, we considered the SPEI. It is a widely used and more reliable drought indicator^18,21,61. It will incorporate the influence of rising regional temperature⁵⁹ and moisture requirements in developing drought through a water balance approach. In the present study, the Hargraves method estimates the potential evapotranspiration (PET). In addition, the log-logistic probability distribution is applied to determine the final value of SPEI using the R package⁵⁹. The mathematical expression for the probability distribution function is shown below.

$$\:f\left(x\right)=\frac{\beta\:}{\alpha\:}\left(\frac{x-\gamma\:}{\alpha\:}\right){\left[1+\left(\frac{x-\gamma\:}{\alpha\:}\right)\right]}^{-2}$$

(16)

where, α = Size, β = Shape Y = Origin parameters.

Therefore, the probability distribution function can be written as a probability density function, and the following equation expresses it.

$$\:F\left(x\right)={\left[1+{\left(\frac{\alpha\:}{x-\gamma\:}\right)}^{\beta\:}\right]}^{-1}$$

(17)

Now, SPEI is calculated using the following equation:

$$\:SPEI={W}_{i}-\frac{{C}_{0}+{C}_{1}W+{C}_{2}{W}^{2}}{1+{d}_{1}W+{d}_{2}{W}^{2}+{d}_{3}{W}^{3}}$$

(18)

$\:{W}_{i}$ = probability weight amount

$$\:{W}_{i}=\left[\begin{array}{cc}\sqrt{-2{ln}(p)}&\:\begin{array}{cc}for&\:p\le\:0.5\end{array}\\\:\sqrt{-2{ln}(1-p)}&\:\begin{array}{cc}for&\:p>0.5\end{array}\end{array}\right]$$

(19)

Where, C₀ = 2.5155; C₁ = 0.8028; C₂ = 0.0203; d₁ = 1.4327; d₂ = 0.1892; d₃ = 0.001.