Study on the influence of blasting on the structural stability of newly-built and adjacent tunnels

Abstract

With the rapid development of urban underground spaces, newly constructed tunnels are being constructed increasingly closer to existing ones. In such cases, blasting may cause overbreak and underbreak, potentially compromising both the structural stability of the new tunnels and the operational safety of adjacent tunnels. In this study, we investigated the double-track tunnel project in Chongqing University Town; the blasting operation was classified into the blasting action period (from the beginning to load termination of blasting) and the overbreak period (from blasting termination to surrounding rock deformation stability). Overbreak and underbreak distribution data were acquired through self-developed blasthole detection devices and laser profile scanners. Using numerical models constructed with LS-DYNA and ANSYS, this study systematically analyzed the dynamic response characteristics of the blasting process of the newly-built tunnel and its effect on the structural stability of adjacent tunnels. Finite element simulation results using intelligent detection data matched the measured excavation contour with over 85% accuracy, revealing the correlation between the blasthole position offset and overbreak position and amount. During the formation period of overbreak in the newly-built tunnels, the section displacement attenuated gradually, and irregular contours increased the tensile stress concentration and rockfall risk. Moreover, uniform overbreak of the entire contour of the section decreased the stress concentration. During the blasting period of the adjacent tunnel, the overbreak and underbreak positions significantly affected the internal force on the lining of the adjacent tunnel. A prominent stress response of the vault and arch bottom was observed. The vibration velocity of the lining of the adjacent tunnel was positively correlated with the contour radius, and was regulated by the loading state at different positions. Therefore, blasting operations in new tunnels should take into account the void position of the adjacent tunnel base. During the formation period of overbreak of the adjacent tunnel, overbreak had a weak influence on the lining displacement, and excavation unloading dominated surrounding rock displacement. The peak stress was concentrated at the center and lower side of the arch foot, and the inner side of the arch bottom experienced tensile stress over a large area. Thus, the positions adjacent to the arch foot and arch bottom of the tunnel should be carefully considered in the construction of new tunnels.

Introduction

With the increasing scale of tunnel construction and intensive development of urban underground spaces, problems associated with constructing new tunnels adjacent to existing ones have become increasingly prominent. Drilling and blasting are widely used in underground engineering construction because of their simple processes and economic advantages^1,2. Although these methods are efficient and convenient, they affect the structural stability of both new and adjacent tunnels.

In recent years, extensive research has been conducted on the influence of blasting in newly-built tunnels on the structural stability of new and adjacent tunnels. The dynamic response characteristics of blasting are closely related to the blasting parameters and blasting technology. Xu et al.³ studied the damage characteristics of surrounding rocks due to hole blasting around the arch foot of a horseshoe tunnel in terms of the free surface shape, charge amount, and deflection angle of the hollow. Guo et al.⁴ analyzed the relationship between the surrounding rock damage and effective stress with different extrapolation angles of peripheral holes. They showed that overbreak increases with the extrapolation angle, and recommended an extrapolation angle of < 4 °. Yu et al.⁵ studied the crack propagation law under different hole spacings and hollow deviation angles and concluded that the optimal deviation angle was 15 ° when the hole spacing was ≤ 60 cm. Liu et al.⁶ analyzed the influence of the time delay between holes, charge, and surrounding rock lithology on the surrounding rock damage during millisecond-delay blasting of tunnel peripheral holes. Ling et al.⁷ showed that the maximum damage depth occurred in the middle of the floor, and was determined by the blasting of the adjacent excavation section. Peng et al.⁸ analyzed the conditions and distribution law of rock bursts in deep tunnel excavation. Zhao et al.⁹ proposed the “four charged holes, four uncharged holes, one throw hole (FCEO)” scheme, which optimized the blast hole design and improved the tunneling efficiency. Song¹⁰ studied and analyzed the influence of uncharged hole diameter and the distance between cut hole and uncharged hole on blasting effect, and provided recommended values for engineering projects.

During blasting of newly-built tunnels, the dynamic effect on the lining structure of adjacent tunnels directly affects the safety. Liang et al.¹¹ studied the influence of post-construction tunnel blasting excavation on adjacent tunnels and obtained the characteristics of blasting load propagation; distribution law of vibration velocity of adjacent tunnels; and relationship between the tunnel spacing, buried depth, surrounding rock grade, and vibration velocity of adjacent tunnels. Xue et al.¹² studied the influence of blasting excavation of new tunnels on the vibration of existing tunnel linings and obtained the vibration velocity and dynamic stress characteristics at different lining positions. Tran et al.¹³ studied the relationship between the burst pressure and surrounding rock displacement and stress and lining internal force in different projects. Liu et al.¹⁴ studied the influence of blasting of newly-built tunnels on adjacent existing tunnels and obtained a vibration response law and stress distribution characteristics. Song et al.¹⁵ proposed the “transition section + three-bench temporary invert” construction scheme, which can effectively control the stress concentration and deformation of surrounding rock.

The spatial relationship between the newly built and adjacent tunnels directly affects the vibration and stress propagation during blasting. Luo et al.¹⁶ concluded that the explosion phase is dangerous. Xu¹⁷ et al. found that the blasting vibration is significantly amplified in adjacent tunnels and peak vibration velocity decreases with increasing lateral distance between tunnels. These findings were related to the tunnel size, and a generalized formula for predicting the vibration velocity was established. Goel et al.¹⁸ studied the influence of shallow tunnels with different cross-sectional shapes on the surrounding soil, lining, and superstructure under the action of internal explosion. Xian et al.¹⁹ studied the effects of the blasting method, surrounding rock conditions, crossing angle, and clear distance, and quantified the influence of newly-built tunnel blasting on the dynamic response of existing tunnel structures with small crossing angle. Baofu²⁰ studied the influence of blasting vibration of a newly-built tunnel on an existing tunnel through field monitoring and numerical simulation and found that vibration had the highest influence on the vault, resulting in a secondary settlement that tended to stabilize with increasing distance.

In summary, domestic and foreign scholars have conducted relatively in-depth research on the optimization of blasting parameters, improvement of blasting techniques during tunnel construction, as well as the impact of the spatial position and cross-sectional shape of new tunnels on the dynamic response of adjacent tunnels. However, research data mostly rely on traditional measurement methods, resulting in insufficient sample size, limited measurement accuracy, and poor objectivity, making it difficult to fully capture the complex mechanical behaviors under different working conditions.

To address this issue, this study is based on the Chongqing University Town Double-line Tunnel project. By using blast hole spatial coordinates and cross-sectional profile data obtained through on-site measurements with independently developed intelligent detection equipment, it can effectively improve measurement accuracy and expand the database sample size. Based on the measured data, a stratum structure model using LS-DYNA and ANSYS is constructed, and a two-stage analysis framework is adopted to analyze the blasting action stage and the overbreak stage respectively. It focuses on revealing the impact of overbreak and underbreak positions on the structural stability of the new tunnel itself and the dynamic behavior of adjacent tunnels during the blasting construction of the new tunnel. The research results can provide theoretical support for the safety protection of adjacent tunnels and the optimization of blasting parameters, and are of great significance for improving the safety of coordinated construction of tunnel groups in complex environments.

Project overview

Project background

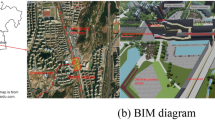
This study takes the University Town Double-Track Tunnel project in Chongqing, China as the engineering background, as shown in Fig. 1. The influence of new tunnel construction on adjacent existing railway lines and construction optimization control were studied. The double-track tunnel project of University Town starts from the Xiyong Xishan Interchange in Shapingba District in the west, connects with Hongcaofang Interchange in the east, and crosses Zhongliang Mountain. The designed mileage of the line is K0 + 900 ~ K5 + 560. The main project is a tunnel crossing the mountain, as shown in Fig. 1a. The total length of the double-track tunnel in University Town is approximately 4075 m, with a two-hole separate layout and six lanes in both directions. The tunnel is located in a narrow strip where the two surface water systems of the Yangtze and Jialing Rivers meet. Landform development is strictly controlled by the structure and lithology. The structural line is consistent with the ridge line and spreads in the NE-SW direction. The anticline forms a strip of low mountains and the syncline forms wide and gentle hills. The hard sandstone at the axis of the anticline comprises a cuesta or platform. The geomorphology along the line can be approximately classified into a tectonic denudation hilly area and low mountainous area.

The study section is located at mileage K5 + 076. 517 of the right line. The newly-built tunnel passes through the existing Bajiaogou Railway Tunnel of the Jingxi Line. The vertical clear distance between the two tunnels is only 4 m (0.4 times the tunnel span), as shown in Fig. 1b. The superposition effect of the existing tunnel operating load and the newly-built tunnel blasting dynamic load enhanced the stress redistribution in the surrounding rock caused by overbreak and underbreak; thus, mechanical excavation was conducted 100-m away from the crossing section.

Fig. 1

Spatial location map of the proposed tunnel: (a) Location plan of the proposed double-track tunnel in University Town, (b) 1-1 cross section.

Excavation process

The bench-cut method was used in this study. Considering the focus on tunnel excavation and forming without a support stage, the upper step was selected as the main analysis object to explore the engineering characteristics under specific conditions in detail. A refined controlled-blasting strategy was adopted to achieve precise excavation while ensuring operation safety. In the specific implementation, the short excavation cycle operation was adopted, and the footage of each cycle was strictly limited to 1.5 m. The charge used in a single blast was strictly controlled to reduce the instantaneous energy released, as shown in Fig. 2; Table 1.

In studying the effects of tunnel excavation without a support, the upper steps were analyzed for specific reasons. The upper step is the first part to be exposed after tunnel excavation, providing the earliest information helpful for timely assessment of rock formation stability and geological conditions. When the upper step is unsupported, potential safety hazards can be identified early and corresponding safety measures can be adopted. Moreover, analysis results of the upper step can provide important reference for subsequent support scheme formulation, aid in selecting suitable support measures, and improve the safety and efficiency of tunnel construction. Therefore, analyzing the upper steps can provide key information and guidance for tunnel construction.

Fig. 2

Schematic of the upper step hole layout.

Table 1 Charge distribution table of upper step Blasthole.

In this study, the cut holes and auxiliary holes were charged according to the continuous charge structure, and the peripheral holes were charged according to the interval charge structure. The charge structure is shown in Fig. 3. The charge structure characteristics presented in Fig. 3 served as important reference to establish an accurate finite element model for the blasting process.

Fig. 3

Schematic of the charge structure.

Field measurement

Intelligent detection equipment for blasthole parameters

The intelligent detection equipment for blasthole parameters mainly comprised five parts, as shown in Fig. 4. The working principle of its main functional components is as follows: the retractable connecting tube was adjusted according to the actual depth of the blasthole so that the end of the detection tube reached the actual depth of the blasthole. The laser ranging module integrated a high-precision gyroscope, accelerometer, and RM3100 geomagnetic field sensor. Moreover, it adopted a high-performance microprocessor, advanced dynamic calculation, and Kalman dynamic filter algorithm, which can quickly solve the real-time motion attitude of the module to accurately identify the elongation and spatial position of the detection device and obtain the actual depth and angle of the blasthole. The data processing terminal integrated a display, main circuit board, wireless receiver, battery module, and data storage and analysis module; it accepted and processed the blasthole parameters provided by the laser ranging module to obtain and display the actual depth and angle; the measurement accuracy of angle and length of the blasthole were ± 1 ° and ± 0.1 mm, respectively.

The laser ranging module also measured the relative position of the blasthole, recorded the three-dimensional (X, Y, Z) coordinates of each measurement point, and automatically outputted them to the acquired cloud system for position description. The measurement data were transmitted to an industrial flat panel in real time to complete the presentation of the blasthole position, which was compared and analyzed with the designed blasthole position. The measurement accuracy was ± 0. 1 mm.

Fig. 4

Intelligent detection equipment for blasthole parameters.

The eye parameter intelligent detection function module comprised five parts: the presentation, interface, application, service, and equipment layers. It measured blastholes with different size parameters to obtain the actual blasthole opening position, drilling angle, and charge, as shown in Fig. 5. Combined with the design section parameters, the position and angle of the blasthole were positioned and analyzed. The working principle of its main functional components is as follows. The representation layer adopted an industrial flat panel and PC terminal, which rapidly obtained the key blasthole parameters. The application layer realized the interaction of intelligent scanning equipment for the excavation contour and presented the data in the form of charts. The service layer used a 9-axis-inclination gyroscope data analysis engine to rapidly and accurately detect the measurement blasthole. The device layer integrated a laser infrared detector, communication equipment, and 9-axis tilt gyroscope.

Fig. 5

Composition of blasthole parameter intelligent detection function module.

Acquisition of measured blasthole parameters

The self-developed intelligent detection equipment of blasthole parameters was used to monitor the blasting Sect. 200-m before and after the intersection of the double-track tunnel in the University Town and Chengdu-Chongqing passenger dedicated line tunnels. The left and right lines were detected every five construction cycles, and the data of 12 excavation sections in six groups were collected. The actual spatial position, blasthole angle, and charge amount of 31 peripheral holes in 12 tunnel faces of the left and right holes were obtained. The blasthole location maps of five test sections are shown in Fig. 6.

Fig. 6

Location of blastholes in the experimental section: (a) Test Sect. 1, (b) Test Sect. 2, (c) Test Sect. 3, (d) Test Sect. 4, (e) Test Sect. 5.

Intelligent scanning equipment for the blasting excavation contour

The laser section instrument accurately scanned the actual contour line of the excavation section of the mountain tunnel after blasting. The radar scanner used was a hybrid solid-state LiDAR, which adopted modular transmitting and receiving technology. The data acquisition speed reached 430,000 points/second, range was 20 m, and upward angle was 120 ° horizontal. The contour line was automatically scanned after blasting in a fixed state, and a three-dimensional contour model was obtained. The equipment accurately obtained the overbreak and underbreak situations at each position of the excavation section and comprehensively evaluated the blasting effect of each excavation cycle. The laser equipment is shown in Fig. 7, and the composition of the functional modules is shown in Fig. 8.

The functional module of the intelligent scanning system comprised five parts: the presentation, interface, application, service, and equipment layers. It scanned the tunnel excavation section and located and analyzed the position and degree of overbreak according to the design section parameters. The working principle of its main functional components is as follows. The presentation layer used an industrial flat panel and PC terminal to intuitively display the scanned image of the section. The application layer realized the interaction of intelligent detection equipment for blasthole parameters and presented it in the form of a three-dimensional model. The service layer adopted an image synthesis and analysis engine to quickly and accurately complete the outline drawing of the excavation section. The device layer integrated LiDAR scanners, intelligent positioning devices, and communication devices.

Fig. 7

Laser section instrument.

Fig. 8

Functional module of the intelligent scanning system for blasting excavation profile.

The tunnel construction excavation face included the tunnel face area and exposed rock face area excavated around the tunnel, which was unsupported. Current Chinese tunnel engineering sets extremely high requirements for construction safety. Generally, it is required that side walls, arches, and other areas should be supported for each tunnel excavation cycle. Therefore, the distance between the initial support and tunnel face is generally within 10 m.

To analyze tunnel construction excavation face data, a three-dimensional laser scanner should be used to collect complete data. According to the characteristics of three-dimensional laser scanners, the collection distance is significantly higher than 10 m, and thus, only one measuring station can completely scan the area containing the complete tunnel face and exposed rock face excavated around the unsupported tunnel.

When there are joints and cracks in the tunnel rock mass, the excavation face area of tunnel construction is affected by drilling and blasting, and protruding structural planes are formed. When an excavator is used in the tunnel to discharge the ballast or tunnel face to remove dangers, the excavation face can become uneven, resulting in occlusions and making data collection extremely difficult. During data acquisition, the scanner position should be set such that complete tunnel excavation face data can be collected. When the three-dimensional laser scanning point cloud is specifically collected, two targets are set near the tunnel face to locate the three-dimensional laser data collected by scanning. The target design is shown in Fig. 9, where two targets are arranged near the tunnel face at different horizontal and vertical planes.

Fig. 9

Schematic of the three-dimensional laser scanning target layout: (a) Target, (b) Target setting position.

Data acquisition of excavation section profile

The self-developed over-and underbreak rapid detection equipment was used to collect cross-sectional measurement data from sections DK2 + 700. 600 to DK3 + 264. 559 of the double-track tunnel in University Town. According to the five selected working conditions, the excavation contours of five experimental sections after blasting were scanned by the experimental equipment, as shown in Fig. 10.

Fig. 10

Experimental section profile scanning diagram: (a) Experimental Sect. 1, (b) Experimental Sect. 2, (c) Experimental Sect. 3, (d) Experimental Sect. 4, (e) Experimental Sect. 5.

Numerical simulation of the dynamic response

LS-DYNA modeling

The nonlinear dynamic finite element software LS-DYNA was used to analyze the influence of blasting on the existing tunnel lining. The model dimensions were 115.620 m × 53.0 m × 2.5 m. The X axis denotes the horizontal direction perpendicular to the tunnel axis, Y axis denotes the horizontal direction perpendicular to the ground, and Z axis denotes the axis direction of the existing tunnel.

According to the spatial coordinates, angle, depth, and charge of the blasthole obtained by the blasthole detection equipment, five experimental sections were selected for modeling, as shown in Table 2. The structure of blast holes in the model is simplified using the method of concentrated coupled charging, replacing the eccentric uncoupled charging in actual construction. In the surrounding rock of limestone and dolomite, simulating the blasting of the new tunnel with concentrated coupled charging can not only improve the accuracy of the constitutive model and empirical formula²¹ but also reduce the computational load of the finite element model. The face of the new tunnel is 19 m away from the left boundary of the finite element model.

Table 2 Experimental protocol table.

In the modeling process, the cm-g-µs unit system was adopted, and element type 164 was used. The numerical model comprised 1,493,380 elements and 1,653,611 nodes. Explosions cause large deformation and blockage of the surrounding rock. Therefore, the arbitrary Lagrange-Euler algorithm was used for the air, explosives, blasthole blockage, and the Lagrange Algorithm was used for the surrounding rock and tunnel lining elements. According to the propagation law of stress waves and monitoring data of blasting vibration, the solution time of the numerical simulation was set as 16 ms. Results were obtained as output files every 100 µs, and Fig. 11 shows the finite element model.

Fig. 11

LS-DYNA finite element model.

The left, right, rear, and bottom boundaries of the model were assigned absorbing boundary conditions to simulate the propagation of blast-induced stress waves within an unbounded rock mass environment. The top surface and the tunnel face were set as free boundaries.

The explosive used in the construction of the new tunnel was 2 # rock emulsion explosive. In the numerical simulation, the material model MAT _ HIGH _ EXPLOSIVE _ BURN embedded in LS-DYNA was used to numerically simulate the detonation of explosives. The Jones-Wilkins-Lee equation of state was used to simulate the relationship between the specific volume and pressure in the explosion, and its expression is as follows:

$$\:p=A(1-\frac{\omega\:}{{R}_{1}V}){e}^{-{R}_{1}V}+B(1-\frac{\omega\:}{{R}_{2}V}){e}^{-{R}_{2}V}+\frac{\omega\:{E}_{0}}{V}$$

(1)

Here, $\:p$ is pressure; $\:A$, $\:B$, $\:{R}_{1}$, $\:{R}_{2},$ and $\:\omega\:$ are material constants; $\:V$ is the relative volume; and $\:{E}_{0}$ is the initial specific energy. The parameters of the explosives used in the calculation are shown in Table 3.

Table 3 Parameters of no.2 rock emulsion explosive.

According to the results of engineering geological survey combined with field and laboratory tests, the physical and mechanical parameters of the rock mass and tunnel lining were obtained. The surrounding rock in the study area was limestone. The constitutive model of the surrounding rock was the Drucker-Prager model, and the surrounding rock was modeled by the MAT _ PLASTIC _ KINEMATIC material model. The material model takes into account the elastic-plastic characteristics of the rock mass. The strengthening effect and strain rate change effect of the material can thus be described. Based on the Cowper-Symonds model, this model considers the strain rate effect by introducing a strain rate factor into the yield stress. The yield stress of the rock mass is expressed as:

$$\:{\sigma\:}_{y}=[1+(\frac{\dot{\epsilon\:}}{C}{)}^{\frac{1}{p}}\left]\right({\sigma\:}_{0}+\beta\:{E}_{p}{\epsilon\:}_{eff}^{p})$$

(2)

Here, $\:{\sigma\:}_{0}$ is the initial yield stress of rock mass material, $\:\dot{\epsilon\:}$ is the strain rate, $\:p\:$and $\:C$ are strain rate parameters, $\:\beta\:$ is the isotropic strengthening and follow-up strengthening parameter, $\:{E}_{p}$ is the plastic hardening modulus, and $\:{\epsilon\:}_{eff}^{p}$ is the equivalent plastic strain. Table 4 lists the mechanical parameters of the Class-IV surrounding rock adopted in this study.

Table 4 Parameters of surrounding rock materials.

For the constitutive model of the primary support and secondary lining structure adjacent to the existing tunnel, the material model MAT _ JOHNSON _ HOLMQUIST _ CONCRETE embedded in LS-DYNA was selected to numerically simulate the dynamic response of the lining adjacent to the existing tunnel during explosive detonation. The JHC constitutive strength model is described by the normalized equivalent stress, and its expression relationship is as follows:

$$\:{\sigma\:}^{\text{*}}=\left[A\right({1}_{1}-D)+B{P}^{\text{*}N}](1+C\text{l}\text{n}{\dot{\epsilon\:}}^{\text{*}})$$

(3)

Here, $\:{\sigma\:}^{*}$ is the normalized equivalent stress; $\:{P}^{*}$ is the normalized hydrostatic pressure; $\:D$ is the damage variable; $\:A$,$\:B$,$\:N,\:$and $\:C$ are intensity parameters; and $\:{\dot{\epsilon\:}}^{*}$is the normalized strain rates $\:{\dot{\epsilon\:}}^{*}=\dot{\epsilon\:}/{\dot{\epsilon\:}}_{0}$, where $\:\dot{\epsilon\:}$ and $\:{\dot{\epsilon\:}}_{0}$ are the actual and reference strain rates, respectively.

The parameters of C30 concrete HJC model were preliminarily determined, as shown in Table 5.

Table 5 C30 concrete HJC model parameters.

According to the above method, the parameters of the C40 concrete HJC model were recalibrated, as shown in Table 6.

Table 6 C40 concrete HJC model parameters.

Air is modeled using the NULL material model and described by the LINEAR_POLYNOMIAL equation of state. The linear polynomial equation of state is as follows:

$$\:P={C}_{0}+{C}_{1}\mu\:+{C}_{2}{\mu\:}^{2}+{C}_{3}{\mu\:}^{3}+({C}_{4}+{C}_{5}\mu\:+{C}_{6}{\mu\:}^{2})E$$

(4)

$$\:\mu\:=\frac{1}{V}-1$$

(5)

In the equation: $\:P$ is the detonation pressure; $\:E$ is the internal energy per unit volume; $\:V$ is the relative volume. For the air model, the parameters of the polynomial equation of state are: $\:{C}_{0}={C}_{1}={C}_{2}={C}_{3}={C}_{6}=0$, $\:{C}_{4}={C}_{5}=0.4$; the density of air is 1.225 kg/m³, and the initial relative volume $\:{V}_{0}$is 1.0.

ANSYS modeling

The modeling process adopted the cm-g-µs unit system, the lining adopted the SOLID65 unit type, and the surrounding rock adopted SOLID45 unit type. According to the excavation section profile data obtained by the laser section scanner, five experimental sections were selected for modeling, as shown in Table 7. The numerical model comprised 281,980 elements and 315,040 nodes. The size of the model was 115.620 m × 53.0 m × 2.5 m. The model is shown in Fig. 12. The dynamic response of the surrounding rock after excavation was simulated by the element birth and death method.

Fig. 12

ANSYS finite element model.

Table 7 Experimental protocol table.

Results and discussion

In this study, the construction process was deconstructed into two stages: blasting period (from the beginning of blasting to the end of blasting load) and overbreak period (from the end of blasting to the stability of surrounding rock deformation). In the blasting phase, the time scale is at the millisecond level, which is mainly characterized by the propagation of explosive stress waves and rock mass fragmentation, primarily causing dynamic damage to the lining of adjacent tunnels. In contrast, the overbreak phase has a longer time scale, usually ranging from several hours to several days, and is dominated by stress redistribution of surrounding rock and creep deformation, mainly manifested as diseases related to stress concentration. Considering this two-stage process, the dynamic response characteristics of the new tunnel structure and adjacent tunnels in different time periods are discussed.

Influence of blasting of the Newly-built tunnel on its structure

Influence of blasting period on the structure of the Newly-Built tunnel

(1) Finite Element Model Feasibility Verification.

Based on the blasthole position and charge parameters obtained by the intelligent blasthole parameter detection equipment, a numerical analysis model of the stress field of the tunnel face was constructed, and the distribution characteristics of the maximum principal stress in the tunnel face area were obtained by finite element calculation. The results are shown in Fig. 13.

Fig. 13

Stress nephograms of the tunnel face of the newly-built tunnel: (a) Stress cloud diagram of working condition 1, (b) Stress cloud diagram of working condition 2, (c) Stress cloud diagram of working condition 3, (d) Stress cloud diagram of working condition 4, (e) Stress cloud diagram of working condition 5,(f) Legend.

The excavation contour data generated by finite element simulation were compared and analyzed with the field-measured data collected by the intelligent scanning equipment, as shown in Fig. 14.

Fig. 14

Overbreak amount and coincidence degree of the finite element simulation and measured contour under different working conditions.

The analysis shows that the simulated overbreak amounts and their deviations from measured values under five working conditions are as follows (Fig. 14). Measured overbreak amounts in all conditions are larger than finite element simulation results, with deviations within 20%. This difference mainly stems from the finite element model not fully considering the surrounding rock crack distribution characteristics and cumulative effect of blasting residual stress.

Despite the above limitations, the finite element simulation excavation profile aligns well with the measured profile. As shown in Fig. 13, the coincidence degrees of simulated and measured excavation contours under conditions 1–5 are 98%, 85%, 89%, 90% and 87% respectively, all exceeding 80%. It indicates that the constructed model can simulate the cross-sectional contour of the tunnel after blasting according to the spatial positions of blast holes, which verifies the accuracy of the model. Meanwhile, we have also observed that blast hole position deviation is one of the important causes of overbreak.

(2) The correlation between the position deviation of blast holes and overbreak.

Fig. 15

Linear Fitting Relationship Between Blasthole Deviation and Overbreak Amount: (a) Vault area, (b) Arch shoulder area, (c) Sidewall area.

As can be seen from Fig. 15, in the tunnel excavation section, under the same geological conditions, the blasthole deviation and overbreak amount in the three characteristic regions (vault, arch shoulder, and sidewall) basically show a linear growth relationship. By fitting the relationship between blasthole deviation and overbreak amount using the least square method, the fitted functions of blasthole position deviation and overbreak amount in the three regions of the tunnel are all simplified to the form of y = kx + b, with specific expressions as follows:

Vault area:$\:y=1.11x+10.36$ (6)

Arch shoulder area:$\:y=1.43x+7.06$ (7)

Sidewall area:$\:y=0.91x+6.73$ (8)

In the equations, y represents the final overbreak amount in the region, unit: cm; x represents the blasthole deviation, unit: cm. The slope k ranges from 0.9 to 1.5, which characterizes the correlation between blasthole deviation and overbreak amount. When the blasthole is located in the sidewall area, the value of k is smaller; when it is in the arch shoulder area, the value of k is larger. b denotes the initial over-excavation amount caused by surrounding rock properties, construction errors in explosive charge quantity, and other factors, unit: cm.

The above formulas have been verified in the same engineering practice, with the verification results shown in Fig. 16a. As can be seen from Fig. 16b, although the residuals fluctuate to some extent, they do not show significant trend characteristics, indicating that the fitted formulas basically conform to the correlation law between blasthole deviation and overbreak amount. Figure 16c shows that the errors are mainly distributed in the range of 0–10 cm, and the right-tail characteristic is not significant, suggesting that most errors are within a controllable range.

To accelerate the on-site overbreak prediction speed, the correlation formulas between blasthole deviation and overbreak amount in this study only consider the same geological conditions. In actual engineering, k and b will be affected by surrounding rock grade, measurement errors, lithology, and joints. With the on-site promotion of this equipment, the obtained data samples will continue to expand, and the research on the correlation between blasthole position deviation and overbreak will become more accurate and refined.

Fig. 16

Error analysis between measured values and fitted values: (a) Comparison of Fitted and Measured Values. (b) Residual Plot: Measured vs. Fitted Values. (c) Distribution of Absolute Errors.

Influence of overbreak and underbreak formation period of the new tunnel on its own structure

(1) Distribution characteristics of displacement field in the newly-built tunnel.

Based on measured data of the tunnel face excavation profile from intelligent blasting excavation profile scanning equipment, a numerical analysis model was constructed in ANSYS using the life-and-death element method to study the displacement response of surrounding rock around the tunnel face (relevant displacement data in Fig. 17). Monitoring results show significant layering characteristics in tunnel section displacement: vault displacement is 9.5–10.1 mm, arch shoulder displacement 6–7 mm, and arch foot displacement controlled within 1.5 mm. Displacement decreases sequentially from vault top to arch bottom, forming obvious stepped layering, reflecting the attenuation of surrounding rock deformation from top to bottom due to excavation.

Fig. 17

Cloud map of surrounding rock displacement of the newly-built tunnel: (a) Cloud map of surrounding rock displacement in working condition 1, (b) Cloud map of surrounding rock displacement in working condition 2, (c) Cloud map of surrounding rock displacement in working condition 3, (d) Cloud map of surrounding rock displacement in working condition 4, (e) Cloud map of surrounding rock displacement in working condition 5,(f) Legend.

Blasting overbreak and underbreak significantly increases displacement in the tunnel vault range (Fig. 18), with the increase within 7%. The vault displacement in working condition 1 is 8.9 mm. Compared to this reference condition, vault displacement in working condition 2 is 9.1 mm (+ 2.25%), in condition 3 is 9.48 mm (+ 6.52%), in condition 4 is 9.45 mm (+ 6.18%), and in condition 5 is 9.5 mm (+ 6.74%). Data show overbreak has less influence on tunnel side-wall area displacement than on arch shoulder and vault; surrounding rock displacement caused by overbreak is dominated by the arch shoulder and vault, whose impact on surrounding rock displacement is 2.7–2.8 times that of the side-wall area.

Fig. 18

Characteristic position displacement of surrounding rock of the newly-built tunnel: (a) Schematic of feature position selection, (b) Displacement of the characteristic position of each working condition.

(2) Stress field distribution characteristics of the newly-built tunnel.

Based on the simulation, Fig. 19 shows the maximum principal stress data of the surrounding rock of the tunnel face after excavation. It is found that overbreak and underbreak causes significant distribution distortion of the first principal stress of the surrounding rock around the tunnel, and the distortion position appears in the position without overbreak. Nine points were selected for analysis, as shown in Fig. 20a, and the detailed data are shown in Fig. 20b.

Fig. 19

Stress cloud diagram of surrounding rock under various working conditions: (a) Stress cloud diagram of surrounding rock under working condition 1, (b) Stress cloud diagram of surrounding rock under working condition 2, (c) Stress cloud diagram of surrounding rock under working condition 3, (d) Stress cloud diagram of surrounding rock under working condition 4, (e) Stress cloud diagram of surrounding rock under working condition 5,(f) Legend.

Under different working conditions, the distribution of the first principal stress in surrounding rock and the variation amplitude compared with reference working condition 1 are as shown in Table 8.

Table 8 Comparison table of first principal stress in surrounding rock under different working conditions with reference working condition 1.

The data indicate that the tunnel excavation profile is significantly correlated with the distribution of the first principal stress in the surrounding rock: the variation of the principal stress is small in the case of uniform overbreak, while non-uniform overbreak tends to cause severe distortion of the principal stress.

The stress distortion area due to overbreak generally exhibits tensile stress concentration. Considering that the tensile strength of the surrounding rock is significantly lower than the compressive strength and the presence of widespread primary or blasting-induced cracks, this area is prone to rock block spalling, local collapse, and other disasters during the construction process. When there is overbreak in other areas, targeted excavation in areas with underbreak or regular excavation contours is recommended to effectively reduce the risk of structural instability by optimizing the regularity of the excavation contour.

Fig. 20

First principal stress at characteristic position of the newly-built tunnel: (a) Feature location selection map, (b) The first principal stress at the characteristic position of each working condition.

Influence of blasting operation of the new tunnel on adjacent tunnels

Influence of blasting period of the newly-built tunnel on adjacent tunnels

(1) Stress field distribution characteristics of adjacent tunnels.

The study location of the adjacent tunnel lining was determined. Four points were selected in this study, denoted as points A, B, C, and D in Fig. 21 which correspond to the positions of the vault, arch shoulder, arch foot, and arch bottom in the adjacent tunnel lining structure respectively. These locations are prone to stress concentration, and should be carefully considered.

Fig. 21

Node location selection diagram.

Based on the LS-DYAN numerical simulation, the blasting process was restored, and the Von Mises effective stress data at different positions adjacent to the tunnel lining structure during the blasting operation of the new tunnel were extracted, as shown in Fig. 22.This effective stress theory is suitable for analyzing the failure forms of general materials under plastic deformation under external force, and the related analysis methods are widely recognized ^22,23.

Fig. 22

Time-varying diagram of stress at different positions under different working conditions.

Through systematic observation of the time-varying stress curves at various positions under different working conditions, as shown in Fig. 21, and the coupling analysis combined with the overbreak data, this study clearly revealed the typical characteristics of the blasting stress distribution of adjacent tunnels and its spatial correlation with the overbreak area. The results are as follows.

The arch bottom and vault areas adjacent to the tunnel exhibit obvious high effective stress, dominating the stress distribution of the lining structure. Comparative analysis shows that the effective stress in the arch bottom area is 0.4–0.6 MPa, 2–3 times that of the arch foot (0.15–0.2 MPa); the effective stress in the upper arch bottom is 0.3–0.5 MPa, twice that of the arch foot, with a prominent stress concentration effect.

Over-excavation of the newly-built tunnel significantly increases the blasting stress of the adjacent tunnel’s vault and arch shoulder. The specific stress response data under different working conditions are shown in the Table 9.

Table 9 Comparison table of influences of Over-excavation of Newly-built tunnels on blasting peak stress of vault and arch shoulder of adjacent tunnels under different working Conditions.

This phenomenon is mainly attributed to the loss of lateral restraint of surrounding rock caused by over-excavation in the side-wall area of the newly-built tunnel, which changes the blasting energy transfer path and exacerbates the stress concentration at the arch shoulder.

Analysis of arch bottom stress response shows vault overbreak has no significant impact on the adjacent tunnel’s arch bottom stress. However, when overbreak occurs in side wall A or arch shoulder combined with the vault (comparing conditions 1, 2, 3), the arch bottom peak stress increases from 0.48 MPa to 0.62 MPa (29.17% rise). Numerical simulations indicate such overbreak combinations cause asymmetric deformation of the excavation profile, promoting directional expansion of the surrounding rock plastic zone toward the arch bottom (Fig. 23a). Notably, simultaneous overbreak of the side wall, arch shoulder, and vault forms a circumferential self-balancing space system despite increased total overbreak; hoop stress redistribution offsets local concentration, returning the arch bottom stress to the reference level (Fig. 23b).

Fig. 23

Dynamic response contour map: (a) Plastic strain contour, (b) Contour of maximum principal stress of the adjacent tunnel.

(2) Distribution characteristics of the vibration velocity field in adjacent tunnels.

Blast process reconstruction was carried out based on LS-DYNA numerical simulation, and the vibration velocity data at different positions of the lining structure of the adjacent tunnel during the blasting construction of the new tunnel are extracted as shown in Fig. 24. The of blasting vibration of the newly-built tunnel may cause fatigue damage to the lining of adjacent tunnels, and long-term accumulation weakens the strength of the lining and reduce its bearing capacity. Moreover, vibration changes the internal stress distribution of the lining structure, causes crack propagation or new cracks, and hampers the integrity and stability of the lining, as shown in Fig. 25.

Fig. 24

Time-varying diagram of the vibration velocity at different positions under different working conditions.

Fig. 25

Vibration velocity distribution diagram.

To study the vibration response characteristics of the adjacent tunnel lining structure caused by blasting of the newly-built tunnel, time history analysis was conducted with simulation data. Figure 24 shows that the vibration velocity of each monitoring point of the lining structure exhibits significant differences under different working conditions, and the vibration velocity follows a nonlinear distribution law along the geometric contour of the lining. The contour radius of the vault is 5.55 m, peak vibration velocity is 4.8–5.5 cm/s, contour radius of the arch shoulder is 5.55 m, and peak vibration velocity is 3.8 cm/s. The contour radius of the arch foot is 1.2 m, peak vibration velocity is 1.6 cm/s – 2.2 cm/s, contour radius of the arch bottom is 8.5 m, and peak vibration velocity is 4.8–5.2 cm/s. When the radius of the lining contour line is large, the vibration velocity is higher; when the radius of the lining contour line is small, the vibration velocity is lower. The stress state at different positions also affects the vibration velocity. Based on the side wall adjacent to the blasting side of the tunnel, the peak vibration velocity is 3.8 cm/s and contour radius is 5.55 m. Compared with the vault position with the same radius of 5.55 m, because of the thin-walled suspended structure, the vibration energy is mainly directly transmitted by elastic waves, and the vibration velocity increases by 26.32% – 44.74%. The contour radius of the bottom of the arch is 8.5 m, and the vibration velocity is equivalent to that of the top of the arch. Due to the support and restraint of the surrounding rock, the vibration velocity at this position is reduced by 34.7%. Because most adjacent tunnels are in the operation stage and there are structural diseases (e.g., lining cracks, water seepage, and rock mass weathering), it is necessary to prevent stress change to the tunnel arch bottom caused by basement voiding, which exacerbates the influence of blasting of new tunnels on adjacent tunnels.

Influence of overbreak and underbreak formation period of the new tunnel on adjacent tunnels

(1) Distribution characteristics of the displacement field in adjacent tunnels.

Based on the numerical simulation results of the displacement field of adjacent tunnels, the displacement of surrounding rock of adjacent tunnels caused by excavation of new tunnels shows significant displacement gradient characteristics, as shown in Fig. 26. The maximum displacement of the vault is 8.62 mm, minimum displacement of the arch bottom is 3.3 mm, and displacement of the vault is approximately 2.61 times that of the arch bottom. The displacement values are maintained at both positions under the five working conditions. The displacement of the side wall is slightly affected. The displacements of working conditions 2, 3, 4, and 5 at point C are 7.29 mm, 7.20 mm, 7.02 mm, and 6.91 mm respectively; compared with the reference working condition 1, the changes are 0.83%, 0.41%, 2.9%, and 4.4% respectively. It is worth noting that the additional displacement disturbance caused by overbreak and underbreak construction is only 0.4 mm, accounting for less than 5% of the total displacement and indicating that the main controlling factor of surrounding rock displacement is the unloading effect of new tunnel excavation rather than engineering deviation. Under a working condition with four times the tunnel diameter distance between the new tunnel and the adjacent tunnel, the similarity between the displacement field distribution and reference working condition 1 is 95%, which verifies that the displacement conduction caused by excavation unloading follows a stable spatial distribution law.

Fig. 26

Finite element calculation results of displacement of the adjacent tunnel structures: (a) structural displacement cloud diagram, (b) Characteristic position displacement diagram of each working condition.

(2) Stress field distribution characteristics of adjacent tunnels.

Based on the numerical simulation results of the stress field, as shown in Fig. 27, the lining structure of adjacent tunnels shows significant stress concentration. The stress distribution of the adjacent tunnel superstructure is relatively uniform: the first principal stress inside the vault is −0.006 MPa. The first principal stress on the inner side of the arch shoulder is −0.051 – −0.077 MPa, and the first principal stress on the inner side of the arch waist is − 0. 083 − 0. 09 MPa. However, the stress distribution of the substructure of the adjacent tunnel is concentrated: the center of the arch foot is the maximum compressive stress position, and the first principal stress is −0.846 – −1.47 MPa. The underside of the arch foot is the position with the maximum tensile stress, and the first principal stress is 2.26–2.38 MPa. The first principal stress on the inner side of the arch bottom is 1.78–1.82 MPa.

The center of the arch foot is significantly affected by the overbreak of the newly-built tunnel. The first principal stresses of the five working conditions 1–5 at this position are − 0.846, −1.46, −1.47, −1.47, and − 1.45 MPa, respectively. Compared with the reference working condition 1, the stresses of working conditions 2, 3, 4, and 5 are increased by 72.58%, 73.76%, 73.76%, and 71.39%, respectively. As the joint action position of the maximum tensile and compressive stresses, the stress state of the arch foot is complex. Therefore, targeted reinforcement measures should be adopted at the arch foot position during construction to improve the structural stability and avoid the risk of structural damage caused by stress concentration.

The tensile stress at the inner side of the arch bottom is 1.78–1.82 MPa. In view of the widespread micro-cracks in the concrete structure, this tensile stress can easily promote crack propagation and extension.

Fig. 27

Finite element calculation results of structural stress in the adjacent tunnel: (a) Structural stress cloud diagram, (b) Stress diagram of the characteristic position of each working condition.

Conclusion

Considering the double-track tunnel project in Chongqing University Town, this study systematically analyzed the influence law of blasting of newly-built tunnel on its own structure, lining, and surrounding rock of adjacent tunnels using self-developed equipment and numerical simulation in LS-DYNA and ANSYS. The main conclusions are as follows.

① Structural response of newly-built tunnel during blasting: A finite element simulation was conducted based on the intelligent detection data of blasthole parameters, and the coincidence degree was over 85% with the field measured excavation contour. The internal relationship between the blasthole layout parameters and overbreak and underbreak was clarified, and it was shown that the model can effectively predict the formation trend of overbreak and underbreak and provide an important theoretical basis for the optimal design of blasting parameters.

② Structural response of the newly-built tunnel during the formation period of overbreak and underbreak: The displacement of the tunnel section presents a stepped attenuation distribution of “vault → arch shoulder → arch foot”. Overbreak significantly increases the displacement of the vault and its influence range, and at the same time, leads to the distortion of the first principal stress distribution of the surrounding rock in the position without overbreak, which is mainly tensile stress. This increases the risk of rock block spalling and local collapse. However, uniform overbreak of the tunnel face can form a self-balancing system through stress redistribution and reduce the local stress concentration.

③ Dynamic response of the adjacent tunnel during blasting: The overbreak position has a significant influence on the internal force of the adjacent tunnel lining, among which the stress responses of the vault and arch bottom are the most prominent. Overbreak of the side wall increases the stress of the adjacent arch shoulder by 109%, and simultaneous overbreak of the side wall and arch shoulder increases the stress of the adjacent vault by 29.73%. Moreover, overbreak along circumferential directions restores the stress of the arch bottom to the reference value due to the stress self-balancing effect. The vibration velocity of the adjacent tunnel lining is positively correlated with the contour radius. It is adjusted by the stress state at different positions; the suspended state increases and the supporting state weakens. During the blasting operation on new tunnels, attention should be paid to the void position of the adjacent tunnel base.

④ Dynamic response of adjacent tunnels during the formation period of overbreak and underbreak: The influence of overbreak and underbreak on the lining displacement is weak, and the additional displacement disturbance is only 0.4 mm. Excavation unloading is the dominant factor causing surrounding rock displacement. The peak stress is mainly concentrated at the center of the arch foot and the side under the arch foot, and the center of the arch foot is significantly affected by overbreak and underbreak. The inner side of the arch bottom exhibits a large area of surface tension, and thus, the position of the adjacent tunnel arch foot and arch bottom should be carefully considered in the construction of new tunnels.