Introduction

According to the increasing need in sensing applications for high accuracy and processing speed, and at the same time compressing the structure to make the sensors portable and cost-effective, light and optical sensors have been presented as a suitable solution that uses the interaction of light and the material under investigation to realize the diagnosis1. On one hand, Photonic crystal fibers (PCF) possess characteristics such as compact size, excellent guiding, and design flexibility. In contrast, in comparison to traditional optical fibers, which necessitated a sample volume of 1 to 10 ml, only a small quantity ranging from tens to a few hundred microliters of the sample is required, making it highly advantageous for applications in detecting biological samples and hazardous compounds2. On the other hand, Surface plasmon resonance (SPR) is a highly sensitive detection method that does not require labeling and provides real-time monitoring3. The combination of these two techniques in SPR PCF sensors has attracted significant interest in recent years because of their low transmission loss, controllable dispersion and birefringence, high sensitivity, high resolution, label-free detection, fast response, real-time monitoring, and adjustable structural components4,5,6,7. These sensors have shown great promise for a range of uses such as detecting biomolecules, diagnosing medical conditions, analyzing blood groups, identifying viruses, ensuring food quality and safety, monitoring the environment, and other diverse applications. Food health and clinical diagnoses are one of the important fields of application of these sensors. Therefore, the detection and determination of some soluble substances will have an important impact in these areas8,9,10,11,12.

Sucrose (C12H22O11) is used as one of the important analytes in clinical diagnostics and the food industry. Sucrose is also known as table sugar and is very common in plants such as sugar cane and sugar beet, and is known as the most abundant low molecular-weight carbohydrate in nature13. In the medical field, sucrose is used as a marker in medical tests as a method to check the permeability of the intestine and duodenum. Since, under normal conditions, sucrose molecules are not absorbed in these parts or are absorbed in a small amount, with the increase of intestinal permeability or the creation of wounds in these areas, sucrose will be absorbed in larger amounts. By giving a certain amount of sucrose to the person and then measuring its level in the urine, the permeability of the digestive system can be checked. Since small changes in gastric permeability can cause problems such as leaky gut syndrome or intestinal inflammation, accurate measurement of sucrose levels with high sensitivity will be important in these tests14,15,16. Since many patients do not have symptoms and only realize when serious complications have occurred, current methods such as endoscopy and biopsy are not suitable for screening a large number of people and are invasive, SPR-PCF sensors can be used as a non-invasive and quick method used to check the amount of sucrose absorption and accurately measure the level of sucrose in blood or urine as an analyte under a high-sensitivity probe. In these sensors, a small amount of the transmitted light penetrates the cladding as an evanescent field. This interaction causes oscillation in the metal’s surface electrons, generating a surface plasmon wave (SPW) along the metal-dielectric interface17. When the wavelength of the SPW and the evanescent wave are equal in λSPR, a peak in the confinement loss (CL) spectrum is created18. This wavelength is highly dependent on the RI of its surrounding environment and has a unique value for each RI19. By changing the level of sucrose in the sample, its refractive index changes and When a small change occurs in the RI of the analyte under examination, it causes a shift in the resonance wavelength. By analyzing these shifts, changes in the analyte’s RI can be measured20. By examining these changes, the refractive index of the analyte and subsequently the level of sucrose can be measured. The detection capabilities of the sensor can be enhanced in determining the RI of the sample by adjusting the structure and utilizing various proportional plasmonic materials in these sensors21. Therefore, achieving the optimal detection parameters and considering manufacturing technological errors is a challenge in engineering and implementing these sensors1.

In recent years, numerical optimization has become essential in designing photonic sensors, especially when traditional modeling is difficult. The Nelder–Mead algorithm is simple and does not require derivatives. It has shown good results in different optical optimization tasks. For example, researchers have used it to design photonic crystal fiber grating sensors22, SPR-PCF biosensors23, nanoplasmonic couplers24, free-form optical couplers for photonic integrated circuits25, and metagrating-based optical devices26. This algorithm is practical for fine-tuning complex shapes without needing gradient information, making it useful for photonic simulations that are expensive in terms of computation.

In this research, the sensor presented is designed based on the vertical slit pupil of some animals’ eyes, taking inspiration from nature. The sensor is designed to concentrate the magnetic field for the core-guided mode in the central part of the eye and to control the leakage of the electromagnetic field to the plasmonic surface without using partial air holes. This is done to minimize manufacturing errors caused by inaccurate dimensions and placement of the holes. The Nelder-Mead optimization algorithm is utilized to optimize the sensor’s components to achieve an optimal structure. This algorithm has been employed to optimize the structural components for optimal diagnostic performance.

Sensor design

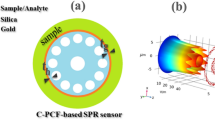
The sensor presented in this study is inspired by the vertical pupil structure that exists in some animals such as cats and crocodiles. This type of pupil shows the evolutionary adaptation according to the lifestyle and habitat of animals. This type of pupil is mainly seen in predatory animals and predators. This type of pupil can create the depth of the stigmatic field and since the binocular cortical neurons in the brain, which have the task of processing visual information, are more inclined to process vertical information, they can have better visual clarity in vertical direction than in horizontal direction. This adaptation helps these animals more accurately estimate the distance to their targets using stereoscopic vision and depth cues. Inspired by this, this type of design has been used to support single polarization (vertical polarization) in an application in the SPR PCF sensor. On the other hand, these narrow pupils allow animals that are active both at night and during the day to control incoming light well by changing their width and will bring light adaptation for animals so that for low light conditions, more photons will be absorbed by the retina and in bright light conditions, the quality of the image will be increased by reducing the spherical aberration and increasing the depth of field. Also, they have a larger range of aperture sizes than circular pupil eyes. This is beneficial in sensor design, as it increases the numerical aperture and reduces coupling losses from the light source to the sensor27. So, The design of this structure will have several key features. Firstly, due to the high occupied volume of the air holes placed on the sides, it will reduce the effective refractive index of the cladding and increase the numerical aperture. Due to the location of a wide core, this issue will increase the amount of light coupling from the source28. Second, by increasing the air-filling fraction, it will reduce the losses in the X-axis and focus the magnetic field in the center of the structure29. Thirdly, by creating birefringence, it limits the confinement loss in X polarization and supports Y polarization.

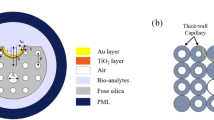
Figure 1 shows the two-dimensional cross-section of the proposed sensor. A layer with a thickness of Ts is placed around the structure to hold it and the plasmonic metal is deposited on this surface in front of the channels. Gold has been used due to its remarkable properties against oxidation and its high sensitivity.

The proposed sensor’s structure is defined by four key geometrical parameters: the thickness of the gold layer (Tg), the channel width (W), the core-to-channel radius (R), and the support layer thickness (Ts). These parameters were simultaneously optimized using the Nelder-Mead algorithm, aiming to maximize the amplitude sensitivity while minimizing the confinement loss. The optimal values obtained were Tg = 29 nm, W = 360 nm, R = 5.5 μm, and Ts = 850 nm. Since the optical core width is defined as 4 × W, and Tg and W significantly influence the coupling and confinement characteristics of the sensor, these two parameters were further analyzed independently.

The proposed experimental configuration of the sensor is illustrated in Fig. 1 In this conceptual setup, the electromagnetic wave is created by the laser source and transmitted to the sensor by the single-mode fiber after passing through the polarization controller. Analyte enters and exits the sensor by a programmable pump with suitable pressure. After the reaction between the analyte and the sensor, which causes a change in the effective RI of the plasmonic mode, any change in the RI of the analyte leads to a change in the signal wavelength. Then, the output light from the sensor is transferred to an optical spectrum analyzer by a single-mode fiber, and its information will be analyzed after being transferred to a computer.

Fabrication feasibility of the proposed sensor

This study is theoretical and relies on numerical simulations, but practical implementation of the sensor structure is also important. The proposed design features an uneven core with side air channels and a gold layer positioned at a specific point. While it may seem challenging to create, recent advancements in photonic crystal fibers and selective metal application suggest that this sensor can be successfully built with current technology.

3D printing has recently been used to create photonic crystal fibers with specific shapes, allowing for rapid prototyping30,31,32. Preform molding is another method that can produce shapes like biconvex cores33,34. After creating the fiber structure, the next step is to apply a gold layer. While traditional methods like chemical vapor deposition (CVD) provide uniform coatings, they struggle on curved surfaces. Electroless plating is a better option, allowing gold to be applied only where needed, like on the exposed core of the fiber, without electricity and minimal chemical preparation35. The plasma-enhanced layer deposition (PE-ALD) method allows for gold deposition at low, near-room temperatures, resulting in thin, uniform layers with strong adhesion. It is particularly effective on complex structures like photonic crystal fibers36.

Fig. 1
figure 1

(a) Proposed schematic diagram of the SPR-PCF sensor inspired by vertical pupil geometry and 2-dimensional illustration of the proposed sensor (b) vertical slit pupil in alligators (c) vertical slit pupil in cats (d) FEM-based mesh.

Full size image

Silica is used as the background material for this sensor. The performance of optical sensors is based on the RI of the material and surrounding environment. Therefore, the optical properties of the background environment will be a vital component in the design of the sensor. The description of the RI of silica as a background material is done by the Sellmeier equation37.

$$\:{n}_{\text{S}\text{i}\text{O}2}^{2}\left(\lambda\:\right)=1+\frac{{B}_{1}{\lambda\:}^{2}}{{\lambda\:}^{2}-{C}_{1}}+\frac{{B}_{2}{\lambda\:}^{2}}{{\lambda\:}^{2}-{C}_{2}}+\frac{{B}_{3}{\lambda\:}^{2}}{{\lambda\:}^{2}-{C}_{3}}$$
(1)

Which nSiO2 is the RI of fused silica, \(\:\lambda\:\) is the wavelength of the incident light in micrometer scale and B1, B2, B3, C1​, C2​, and C3 are equal to 0.69616300, 0.407942600, 0.897479400, 0.00467914826 µm2, 0.0135120631 µm2, 97.9340025 µm2 respectively.

$$\:{\varepsilon\:}_{Au}={\varepsilon\:}_{{\infty\:}}-\frac{{\omega\:}_{D}^{2}}{\omega\:\left(\omega\:+j{\gamma\:}_{D}\right)}-\frac{{{\Delta\:}}_{\varepsilon\:}\cdot\:{{\Omega\:}}_{L}^{2}}{\left({\omega\:}^{2}-{{\Omega\:}}_{L}^{2}\right)+j{{\Gamma\:}}_{L}\omega\:}$$
(2)

As mentioned earlier, the detection function of SPR PCF sensors is based on the reaction of light and metal surface electrons. Therefore, the characteristics of the plasmonic metal will be decisive in the detection performance. The permittivity characteristic of gold is expressed by the Drude-Lorentz approximation.

In this equation, \(\:{{\upepsilon\:}}_{\text{A}\text{u}}\) is the permittivity of gold and \(\:{\varepsilon\:}_{{\infty\:}}\) is the permittivity at high frequency and is equal to 5.9673. other constant parameters are obtained from37.

The performance analysis of the sensor is checked by examining and analyzing the CL spectrum, which is caused by the leakage of the electromagnetic field of the core. The amount of CL is obtained by the following equation38.

$$\:\alpha\:\left(\frac{dB}{cm}\right)=8.686\times\:\frac{2\pi\:}{\lambda\:}\times\:\text{I}\text{m}\left({n}_{eff}\right)\times\:{10}^{4}$$
(3)

Wich \(\:\text{Im}\left({\text{n}}_{\text{e}\text{f}\text{f}}\right)\) is the imaginary part of the effective RI and \(\:{\uplambda\:}\) is the incident light in micrometer scale.

The analysis of sensor sensitivity performance is performed by two methods of wavelength interrogation and amplitude interrogation. In the first method, the wavelength sensitivity can be determined by examining the changes in resonance wavelength that occur when the RI of the analyte is shifted, according to the following equation39.

$$\:{\text{S}}_{{\uplambda\:}}(\text{n}\text{m}/\text{R}\text{I}\text{U})={{\Delta\:}{\uplambda\:}}_{\text{p}\text{e}\text{a}\text{k}}/{\Delta\:}{\text{n}}_{\text{a}}$$
(4)

In this relation \(\:{{\Delta\:}{\uplambda\:}}_{\text{p}\text{e}\text{a}\text{k}}\) is the change of resonance wavelength in nanometer and \(\:{\Delta\:}{\text{n}}_{\text{a}}\) is the change of the analyte’s RI. In this method, the sharpness of the peak in the CL spectrum and the WS are used as two components to determine the suitability of the sensor according to the following equation40.

$$\:\text{F}\text{O}\text{M}\left({\text{R}\text{I}\text{U}}^{-1}\right)\:=\:{\text{S}}_{{\uplambda\:}}/\text{F}\text{W}\text{H}\text{M}$$
(5)

In this relationship, FWHM refers to the full width at half maximum, and it is expected to have low values.

Another method is AS, which is obtained using the amplitude interrogation method. Since this method does not require a spectrometer and does not involve spectral manipulation, it is a less expensive process compared to wavelength sensitivity41.

$$\:{\text{S}}_{\text{A}}\left({\text{R}\text{I}\text{U}}^{-1}\right)=-\frac{1}{{\upalpha\:}({\uplambda\:},{\text{n}}_{\text{a}})}\frac{\partial\:{\upalpha\:}({\uplambda\:},{\text{n}}_{\text{a}})}{\partial\:{\text{n}}_{\text{a}}}$$
(6)

In the studies that have been conducted, it has been challenging to achieve high diagnostic characteristics at the same time. Therefore, achieving this requires a compromise between the said components. In this study, the expected goal is to achieve a sensor that can display competitive characteristics in AS.

Optimization algorithm

The Nelder-Mead algorithm was first presented in 1965 as a direct search method for multidimensional and unconstrained minimization, which is very popular42. In order to provide solutions for unconstrained optimization problems, this algorithm works by providing an iteration strategy based on the concept of simplicity, which utilizes a simplex in n + 1 dimensions to optimize an n-dimensional problem. In this method, by analyzing and comparing the function values at the vertices, new vertices, and simplexes are created until convergence criteria are met43. The flowchart related to the Nelder-Mead algorithm to optimize the parameters is shown in Fig. 244. In this algorithm, the components of gold thickness and channel width have been optimized in order to achieve minimum CL and maximum AS. The reason for using these two components in optimization is their high impact on detection components compared to other parameters.

Fig. 2
figure 2

Flow chart of the Nelder-mead algorithm.

Full size image

Results and discussion

After receiving the optimized structural values ​​from the Nelder-Mead optimization algorithm, Fig. 3 represents the CL spectrum related to the RI of 1.41, which is plotted along with the lines related to the real part of the effective RI of the core mode and the surface plasmon mode. The basic working principle of SPR-PCF sensors is given in this figure. The structure of this type of sensor is designed in such a way that the light passing through the PCF is concentrated and confined in its core, which is called the core guided mode. The structure is also engineered so that some of the core’s electromagnetic field leaks to the metal surface, known as the evanescent field. This leakage causes the surface electrons of the metal to oscillate, activating the surface plasmon polariton (SPP). At a certain wavelength, the effective refractive index of the core mode and the SPP mode become equal, and coupling between these two modes occurs, creating a confinement loss peak in the confinement loss spectrum due to the maximum energy transfer between these two modes, and the governing condition is called the phase matching condition. Since the effective refractive index of the plasmon mode is highly dependent on the refractive index of the surrounding dielectric medium, changes in the refractive index of the analyte will cause a change in the resonance wavelength45.

Sensor response analysis

Figure 4 shows the CL spectrum related to the RI of 1.33 to 1.42,the AS associated with the RI of 1.33 to 1.41, and the WS for RI of 1.33 to 1.41. Other information related to these figures is shown in Table 1. As can be seen from the table, the highest WS of this sensor is equal to 12,000 nm/RIU and related to the RI of 1.41, and the highest AS is equal to −5430.24 RIU and related to the RI of 1.41. The increase in the wavelength sensitivity and amplitude sensitivity values ​​with increasing refractive index of the analyte, can be explained based on the enhancement of the interaction between the guided core mode and the surface plasmon mode. With the increase in the refractive index of the surrounding medium, the effective refractive index of the plasmon mode also increases and becomes closer to the effective refractive index of the core mode. This convergence improves the phase matching conditions between the two modes, and as a result, the coupling power and energy transfer between them increase. The improvement of the phase matching leads to stronger resonance and a more prominent optical response in the sensor. On the other hand, with the increase in the refractive index of the analyte, the penetration depth of the divergent field also increases, which causes more interaction between the guided light and the surrounding medium. This more interaction ultimately leads to an increase in the sensitivity of the sensor. Therefore, an increase in the refractive index of the analyte leads to a simultaneous improvement of the sensor performance indices, such as AS and WS. As shown in Eq. 5, with increasing WS and decreasing FWHM, we see an increase in the sensor’s FOM5,46.

Fig. 3
figure 3

(a) Illustration of phase matching condition and 3-dimensional mode field distribution of (b) SPR mode (c) SPP mode (d) core guided mode. λSPR = 0.8 μm, RI = 1.41.

Full size image
Fig. 4
figure 4

(a) CL spectrum for RIs from 1.33 to 1.42. (b) AS for RI of 1.33 to 1.41. (c) WS for RI of 1.33 to 1.41.

Full size image

Structural parameter analysis

As mentioned in the previous section, the sensor’s structure consists of four main components: Tg, W, Ts, and R. The optimal values for these components were obtained using the Nelder-Mead algorithm. In this section, we will examine the sensor’s performance at values that deviate by ±5% and ±10% from the optimal values with the RI = 1.33.

Fig. 5
figure 5

CL analysis under fabrication tolerances for key structural parameters of the proposed sensor at refractive index = 1.33. The variations are applied as ± 5% and ± 10% deviations to the parameters: (a) gold thickness (Tg), (b) channel width (W), (c) supporting layer thickness (Ts), and (d) core-to-channel radius (R).

Full size image

Figure 5(a) illustrates the sensor’s performance for different thickness values of gold. As shown in the figure, varying this parameter results in small changes in both confinement loss and resonance wavelength, with a tolerance of 10%. As can be seen, reducing the gold thickness from the optimal value reduces confinement losses as a result of weaker penetration of the electromagnetic field into the metal region and weaker excitation of the surface plasmon. Increasing the gold thickness above the optimal value reduces the penetration of the field as a result of the inherent damping property of the metal and less interaction of the field with free electrons and reduces confinement losses. Meanwhile, Fig. 5(b(highlights the effect of changing the optical channel width on sensor performance. Since the W serves as both the optical channel width and 4×W for the core width, it has the most significant effect on the sensor structure. As W increases, more of the optical field reaches the plasmonic surface, leading to an increase in confinement loss. By contrast, according to Fig. 5(c) and Fig. 5(d), alterations in R and Ts do not significantly impact the sensor’s performance.

Given that the gold and channel parameters exert the greatest influence, it is essential to investigate how these two parameters affect the sensor’s detection ability and sensitivity, and whether their impact compromises the sensor’s overall sensitivity.

Figure 6 shows the three-dimensional representation of the AS value under the influence of the simultaneous changes in the channel width and gold thickness. To form this diagram, 143 different values ​​of gold thickness and channel width were involved in order to have a detailed analysis of the changes in AS with the simultaneous change of these two components. As shown in the diagram, the highest AS is at the top of the figure and is equal to the value of −5430.24 RIU, and by moving towards values ​​larger or smaller than the two components ​​Tg = 29 nm and W = 360 nm, which are the optimized values obtained from thr Nelder-Mead algorithm the AS will decrease. This is due to the reduced electromagnetic field penetration ability caused by non-optimal values ​​of W and Tg, which was explained. As a result, it reduces the effective interaction between the plasmonic mode and the core optical mode, reducing the amplitude sensitivity. This trend strongly validates the correctness of the optimization results and confirms the dominant influence of Tg and W on the sensor’s performance. However, it can be seen that with the change in Tg and W values ​​due to manufacturing tolerances, this sensor still shows much higher values ​​than the sensors presented in Table 3. So that at a tolerance of 5%, the sensitivity is still above 4900 RIU−1 and at a tolerance of 10%, the sensitivity is above 4500 RIU−1.

Fig. 6
figure 6

3-dimensional illustration of AS related to simultaneous change of Tg and W.

Full size image
Table 1 Information related to sensor performance for RI of 1.33 to 1.42.
Full size table

Application analysis

Figure 7 shows the spectrum of CL associated with concentrations of 0% (water) to 50% of sucrose in steps of 5%, the AS associated with concentrations of 0–45% of sucrose in steps of 5%, and the WS associated with concentrations of 0–45% of sucrose in steps of 5%. The refractive indices corresponding to each concentration level of the sucrose solution are provided from2,16. The information related to the figure is given in Table 2. As can be seen from the table, the highest WS of this sensor is equal to 13,000 nm/RIU and related to the 45% of sucrose solution, and the highest AS is equal to −6202.62 RIU and related to the 45% of sucrose solution. The reason for the maximum sensitivity at 45% concentration can be explained by the better optical conditions for stronger interaction and stronger resonance between the core mode and the plasmonic mode at 50% concentration compared to 45% concentration, which causes a stronger loss peak. Since the AS of the sensor according to Eq. 6 is based on the difference in the loss amplitude of the CL at a certain wavelength, this has led to the achievement of maximum sensitivity at this concentration. This remarkable sensor boasts outstanding sensitivity when it comes to detecting sucrose, a crucial analyte. Its exceptional performance highlights its importance in various applications where sucrose measurement is vital. This indicates its capability to identify even the smallest changes in the concentration of sucrose.

Fig. 7
figure 7

(a) CL spectrum for concentrations of 0% to 50% of sucrose in steps of 5%. (b) AS for concentrations of 0% to 45% of sucrose in steps of 5%. (c) WS for concentrations of 0% to 45% of sucrose in steps of 5%.

Full size image

According to the investigations conducted in this study, a suitable adaptation of a natural element was implemented to address the design requirements of an SPR PCF sensor. The study focused on overcoming manufacturing challenges without utilizing partial air cavities. The proposed sensor structure exhibits several distinctive features that contribute to its outstanding sensing performance. First and foremost, the vertically pupil-shaped geometry, combined with an external thin gold coating, enhances the interaction between the core-guided light and the surface plasmon modes. The design incorporates side-positioned air holes with a high air-filling fraction, which significantly lowers the effective RI of the cladding and increases the numerical aperture. This modification facilitates greater light coupling from the source due to the presence of a wide core, thereby improving the energy transfer efficiency into the sensing region. Additionally, the increased air fraction in X-axis reduces propagation losses along it and concentrates the magnetic field at the structure’s center, enhancing field intensity at the metal–analyte interface for stronger plasmonic interaction. The design also introduces birefringence, which minimizes confinement loss for the X-polarized mode while supporting the Y-polarized mode, optimizing coupling conditions. By focusing on optimizing the structure based on the Nelder-Mead algorithm and achieving high AS, unlike conventional sensors that have high WS and poor performance in AS, this sensor demonstrated a significantly high amplitude sensitivity due to the optimization efforts aimed at achieving low loss and enhanced sensitivity. As a result of this optimized configuration, the proposed sensor achieved the highest amplitude sensitivity (5430.24 RIU⁻¹) among the reported structures, while also maintaining a competitive wavelength sensitivity of 12,000 nm/RIU. The figure of merit value of 315.9 RIU⁻¹ further reflects the excellent balance between sharp peak definition and high intensity variation. This combination demonstrates the superior performance of the proposed design when compared to previous studies36,37,38,39,40,41,42,47 listed in Table 3, and establishes it as a promising candidate for highly sensitive refractive index biosensing applications.

Table 2 Information related to sensor performance for detection of concentrations of 0–50% of sucrose in steps of 5%.
Full size table
Table 3 Performance comparison of the proposed sensor with other sensors.
Full size table

Conclusion

In this study, a surface plasmon resonance sensor with a structure inspired by a natural element that can be seen as a vertical pupil in some animals was used. The goal of this study was to achieve high amplitude sensitivity, which is achieved using the Nelder-Mead algorithm as an optimization algorithm. During the study, the accuracy of the algorithm performance was checked by examining the sensor performance in different structural values, and finally, the sensor performance was evaluated in the application of sucrose concentration detection as an important analyte in the food and clinical fields. As a refractive index sensor, a maximum WS of 12,000 nm/RIU, AS of −5430.24 RIU−1, and a maximum FOM of 315.9077 RIU−1 were obtained. Finally, for checking the ability of the sensor to be used in its application for determining the concentration of sucrose solution, it has shown the values ​​of 13,000 nm/RIU, −6202.62 RIU−1, and 356.9326 RIU−1 for WS, AS, and FOM respectively related to the concentration of 45%, which shows its excellent performance in sucrose solution detection applications.