Introduction

For efficient separation of water pollutants in liquid phase, membrane and adsorption are the common separation processes which offer superior properties and low energy demand. These separation processes can be considered as green processing as no chemical solvent is used for molecular separation and the processes possess higher separation yield compared to other conventional molecular separation processes. Among these processes, adsorption is one of the useful and common methods for removing water impurities in water treatment where the separation takes place in liquid phase between feed solution and solid phase. Highly porous materials are great choices for adsorption due to the large surface area which would enhance the separation efficiency. Also, nanosized solid materials can provide higher external surface which is favorable for adsorption1,2.

Recent development of advanced materials has progressed the application of nanomaterials for adsorption which is a robust process for molecular separation in liquid phase. The process of adsorption is suitable for molecular separation provided that the content of target molecules (pollutants) in the solution is low and then the separation method would be efficient. Some novel materials such as mesoporous silica have been synthesized for application in adsorptive molecular separation, and the separation efficiency is high due to the large pore volume of these materials which can accommodate more guest molecules in their structures3,4,5.

Despite the synthesis and development of novel materials, the mechanism of molecular separation through these materials is still ambiguous and novel computational techniques such as molecular modeling, computational fluid dynamics (CFD), and thermodynamics can be developed6,7,8,9. For adsorption, molecular modeling is useful to understand the intermolecular forces between the components in the solution and find the separation mechanisms. Molecular modeling can be integrated to other computational techniques like artificial intelligence (AI) and numerical simulation to obtain multi-scale modeling7. Also, the method of CFD has been utilized for description of adsorption by solution of differential equations and finding concentration distribution in the process10. Despite the predictive robustness of molecular modeling and CFD, these methods have been recognized as challenging and computationally expensive models for simulating adsorption and cannot be generalized for a wide range of adsorbents and solutes in water treatment11. Therefore, other facile computational strategies should be developed for analysis and optizmaition of adsorption process in water treatment.

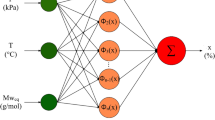
The method of AI has recently attracted much attention for modeling separation process. Under this category is Machine Learning (ML) which has become a versatile tool extensively applied across diverse domains for predictive modeling and aiding in decision-making processes. ML algorithms possess the capability to glean insights from data, extract valuable characteristics, and execute precise regression or categorization tasks12,13,14. To address the research gap in comprehensive modeling of adsorption process, we proposed a methodology utilizing Multi-layer Perceptron (MLP), Gaussian Process Regression (GPR), and Polynomial Regression (PR) as regression models, with gradient-based optimization utilized for finding the best hyper-parameters to predict concentration distribution of solute from CFD dataset. Recently, a number of ML-based algorithms have been linked to CFD concentration data for prediction of adsorption and concentration data15,16,17,18, however a larger number of algorithms need to be evaluated for better analysis of the water treatment.

GPR was utilized in this study as it is a flexible and probabilistic approach to regression modeling that allows for powerful and interpretable predictions. It has discovered utility in multiple domains, including machine learning, geostatistics, and Bayesian optimization, making it a valuable tool for data analysis and prediction tasks19. MLP Regression is a powerful and flexible ML method used for modeling complex relationships in regression tasks. Its capacity to handle nonlinear patterns makes it a valuable tool in various domains. Careful architecture design and training are critical for obtaining accurate and robust regression models using MLPs20. PR is a fundamental regression technique used in machine learning and statistics to model relationships between variables when the relationship is believed to be polynomial in nature21.

This paper presents substantial contributions to the field of adsorption by introducing innovative approaches and methodologies that advance our comprehension of intricate phenomena. Moreover, it enhances the scholarly dialogue by creating opportunities for investigation and examination within the field, thus facilitating future progress and revelations. The objective of this work is to develop data-driven models for accurately predicting solute concentration distributions within a spatially complex dataset generated from CFD model. Specifically, the work aims to assess the performance of three regression models (MLP, GPR, and PR), and to determine the most suitable approach for this type of prediction task. The novelty of this research is its integration of mass transfer insights, artificial intelligence techniques, and computational modeling tools, aligning them within the broader framework of separation science. This multidisciplinary approach aims to enhance prediction accuracy and modeling efficiency, offering a practical pathway to optimize separation processes.

Data of adsorption

The data set utilized in this study possesses a significant number of points, exceeding 19,000 in total. Consequently, it serves as a substantial resource that can be effectively employed for statistical analysis and machine learning endeavors to analyze adsorption process. The input parameters for this study consist of the coordinates (x and y), while the output variable of interest is the concentration (C) measured in units of mol/m³. Data is the concentration distribution of an organic compound adsorbed onto the surface of mesoporous silica. The adsorption was considered at the ambient pressure and temperature. CFD was carried out to find the concentration distribution (C), and then the obtained C versus x and y were used for ML fitting and optimization. The procedure was followed as reported in11,15,17,22 to build ML models.

In the pre-processing phase, an outlier detection and removal technique known as Local Outlier Factor (LOF) was employed, as detailed in the methodology section. The input parameters were normalized using the Min-Max scaler, and subsequently, the data was partitioned into test (20%) and train (80%) subsets. Figures 1 and 2 show the correlation heatmap, and variable boxplots as exploratory data analysis. Figure 2 presents the boxplots of the input and output variables, serving as a key part of the exploratory data analysis. This visualization highlights the central tendency, spread, and potential outliers in each variable, which is essential for understanding data distribution prior to ML modeling. Boxplots are especially useful when assessing the need for normalization or outlier treatment, and are commonly used when datasets may contain extreme values or imbalanced distributions22.

Fig. 1
figure 1

Correlation heatmap of the adsorption variables.

Full size image
Fig. 2
figure 2

Boxplot representation of adsorption variables.

Full size image

Methodology

Local outlier factor (LOF)

LOF is a robust and effective algorithm for identifying outliers within a dataset. It operates under the assumption that outliers are data points that significantly deviate from their local neighborhood. By using LOF, one can uncover and subsequently remove outliers from a dataset, enhancing the overall data quality. The local density of a data point \(\:{x}_{i}\) is defined by LOF in the following manner23:

$$\:LOF\left({x}_{i}\right)=\:\frac{{\sum\:}_{\forall\:{x}_{j}\in\:N\left({x}_{i}\right)}\frac{\text{density}\left({x}_{i}\right)}{\text{density}\left({x}_{j}\right)}}{\mid\:N\left({x}_{i}\right)\mid\:}$$

Here, \(\:N\left({x}_{i}\right)\) represents the neighborhood of data point \(\:{x}_{i}\), and \(\:\text{density}\left({x}_{i}\right)\) denotes the density of \(\:{x}_{i}\). The LOF for a data point quantifies how its density compares to the densities of its neighbors. A LOF value significantly greater than 1 suggests that the data point is an outlier24.

GPR (Gaussian process regression)

GPR stands as a resilient and adaptable non-parametric Bayesian technique employed in the realm of regression analysis. Unlike traditional parametric regression methods, GPR does not make explicit assumptions about the functional form of the underlying data distribution. Instead, it models the data as a distribution over functions, allowing for uncertainty quantification and robust predictions19.

The predictive distribution of GPR is derived through Bayesian inference. Given a set of observed data points (X, y), where X shows the input data and y stands for the corresponding output data, the goal is to make predictions for new input points \(\:{X}^{*}\), yielding predictions \(\:{y}^{*}\). The forecasted or estimated distribution for the variable \(\:{y}^{\text{*}}\) is expressed as follows25:

$$\:p\left({y}^{*}|X,y,{X}^{*}\right)=\mathcal{N}\left({{\upmu\:}}^{*},{{\upsigma\:}}^{*}\right)$$

where \(\:{{\upmu\:}}^{*}\) denotes the mean of the predictive distribution, and \(\:{{\upsigma\:}}^{*}\) stands for its standard deviation. These quantities can be computed as follows25:

$$\:{{\upmu\:}}^{*}={\upmu\:}\left({X}^{*}\right)+K\left({X}^{*},X\right){\left[K\left(X,X\right)+{{\upsigma\:}}_{n}^{2}I\right]}^{-1}\left(y-{\upmu\:}\left(X\right)\right)$$
$$\:{{\upsigma\:}}^{*}=K\left({X}^{*},{X}^{*}\right)-K\left({X}^{*},X\right){\left[K\left(X,X\right)+{{\upsigma\:}}_{n}^{2}I\right]}^{-1}K\left(X,{X}^{*}\right)$$

In the equations above, K(X, X) indicates the covariance matrix associated with the training inputs, K(X*, X) denotes the covariance between the test and training inputs, \(\:{\sigma\:}_{n}^{2}\) represents the variance of noise, and I stands as the identity matrix.

MLP regression (Multi-layer perceptron regression)

MLP Regression is a variant of artificial neural networks characterized by its multi-layered architecture, where nodes (neurons) are interconnected across these layers. It is a versatile and powerful regression technique capable of modeling complex, nonlinear relationships between inputs and outputs26.

The key equation for MLP Regression includes the forward propagation equation for a single neuron26:

$$\:{z}_{j}={\sum}_{i=1}^{n}{w}_{ij}{x}_{i}+{b}_{j}$$
$$\:{a}_{j}={\upsigma\:}\left({z}_{j}\right)$$

In this context, \(\:{z}_{j}\) signifies the weighted summation of inputs corresponding to neuron j, where \(\:{w}_{ij}\) represents the weight associated with the connection linking neuron i to neuron j.

PR (Polynomial regression)

PR is commonly employed in statistics and ML to model relationships between variables when a polynomial relationship is suspected. Unlike the assumption of linearity in Linear Regression, Polynomial Regression allows for the modeling of more complex, nonlinear relationships27. In PR, the correlation between the dependent variable (typically represented as y) and the independent variable (typically represented as x) is expressed as a polynomial function of a chosen degree, often denoted as n. The general form of a polynomial regression equation is as follows21:

$$\:y={{\upbeta\:}}_{0}+{{\upbeta\:}}_{1}x+{{\upbeta\:}}_{2}{x}^{2}+\dots\:+{{\upbeta\:}}_{n}{x}^{n}+\epsilon\:$$

In this context, y denotes the dependent variable, which serves as the target variable we seek to predict or elucidate, while x signifies the independent variable or predictor, representing the variable upon which y relies. Also, \(\:{\beta\:}_{0}\), \(\:{\beta\:}_{1}\), and so on are coefficients that need to be estimated from the data.

Gradient-based optimization

Gradient-based optimization is an effective method for fine-tuning regression model hyperparameters. It uses gradients to determine the direction and rate of the steepest decrease in the objective function. By calculating the gradients based on the hyperparameters, the optimization process can iteratively adjust the values of the hyperparameters to optimize the objective function and identify the most optimal set of hyperparameters28,29.

In the context of gradient-based optimization, the beginning step involves the establishment of an objective function that serves to quantify the performance of the predictive model in relation to the hyperparameters. In this work the objective function is the mean R2 score obtained by cross-validation. The objective is to minimize the previously mentioned function through the manipulation of the hyperparameters.

Next, the derivatives of the objective function based on the hyperparameters are computed using techniques such as automatic differentiation and backpropagation. The resulting gradients guide the adjustments needed to minimize the objective function.

Subsequently, an optimization algorithm (e.g. Adam or Gradient Descent) uses the calculated gradients to iteratively update the hyperparameters. This update process involves scaling the gradients by a learning rate, which controls the step size, and subtracting the scaled gradients from the current values of hyperparameters. The procedure mentioned above is executed iteratively until either convergence is attained or a stopping condition is satisfied30.

Results and discussion

All models described and optimized in this work have been fitted to the CFD data to compare their fitting accuracy and the results are listed in Table 1 where R2, RMSE, and error values have been measured and compared for all models. Machine learning and all models fitting and optimization were performed by using Python 3.8 package which is freely accessible from: https://www.python.org.

Table 1 List of models’ statistics.
Full size table

The R2 score assesses the degree of accuracy of fitness, with higher values indicating a better fit of the concentration dataset. The RMSE measures the model’s prediction accuracy, with lower values being preferable. Average Absolute Relative Deviation (AARD%) represents the average relative difference between fitted and expected points, with lower percentages indicating better accuracy. Finally, the Max Error indicates the largest discrepancy between fitted and expected points within the C dataset. Also, Figs. 3, 4 and 5 show the comparison of predicted and observed values using all three models. We can observe the visual deviation of predicated values by ML models from the CFD concentration values. At first glance, MLP (Fig. 4) shows the greatest performance as most data points accommodate close to the diagonal line. The results of MLP are promising and more accurate compared to the previous studies on ML modeling of adsorption15,16,17.

Fig. 3
figure 3

GPR model: Fitted vs. Expected points.

Full size image
Fig. 4
figure 4

MLP model: Fitted vs. Expected points.

Full size image
Fig. 5
figure 5

PR model: Fitted vs. Expected points.

Full size image

Also, we conducted 5-fold cross-validation to ensure robust performance evaluation for the model. The MLP model, which achieved an R² of 0.999 and RMSE of 0.583 on the test set, was validated using 5-fold cross-validation on the training data (80% of the 19,000 + point dataset). The cross-validation results yielded consistent performance, with R² values of 0.9974 ± 0.00192 (mean ± standard deviation) and RMSE values of 0.590 ± 0.01617 across the folds, indicating minimal variability and high reliability of this model in fitting the adsorption data. These metrics, alongside the test set performance, suggest that the MLP model generalizes well and is not significantly overfitted, supported by the use of gradient-based hyperparameter optimization and preprocessing techniques like LOF for outlier removal.

These results and figures showcase the superior performance of the MLP model in terms of R2 score and RMSE, highlighting its outstanding predictive accuracy in comparison to GPR and PR models. As a result, we can introduce the MLP as the best model for this research and base the rest of the analysis on it. Figures 6 depicts the influence of coordinate (x) on the resultant concentration output utilizing the present model, which turns out similar pattern with the results reported by Yang et al.17 for ML modeling C values in adsorption by mesoporous silica. Also, Fig. 7 represents the ultimate three-dimensional prediction surface depicted by MLP model22. The sensitivity analysis of the permutation-based feature importance using MLP model is illustrated in Fig. 8. The achieved ML outcomes for concentration variations as well as sensitivity evaluation show agreement and similarity with the reported results for adsorption of solute using porous materials15,16,17,18,22,31.

The variations of solute concentration revealed considerable changes in x direction due to the effects of solute diffusion from the bulk to the solid phase surface. In fact, the mass transfer driving force in this process is concentration gradient between the feed bulk and surface of adsorbent which causes concentration difference as evidenced in the results, and it has been captured by MLP model properly which proves that the model is physically valid15,17,18.

Our MLP model outperforms Yang et al.17 best model, ADA-SVR (CV R² = 0.966), with a higher CV R² and comparable error metrics for MLP optimized in this study. The MLP’s superior performance, validated through 5-fold cross-validation (R² = 0.998, RMSE = 0.590), likely stems from gradient-based hyperparameter optimization, enhancing its ability to capture complex spatial patterns in separation processes.

Fig. 6
figure 6

The constructed profile of solute concentration using MLP model.

Full size image
Fig. 7
figure 7

3D surface of the concentration as a function of coordinates, (MLP model). Created by Python 3.8 package which is freely accessible from: https://www.python.org.

Full size image
Fig. 8
figure 8

Permutation based importance of features using MLP model.

Full size image

Conclusion

This study evaluated three regression models for predicting solute concentrations generated from CFD simulation of adsorption process for water treatment. The results of this analysis, driven by gradient-based hyperparameter optimization, demonstrated that MLP model exhibited remarkable predictive capabilities, with an exceptionally high calculated R2 of 0.999 and the lowest Root Mean Square Error (RMSE) at 0.583. This superiority in predictive accuracy, along with the lowest Average Absolute Relative Deviation (AARD%) at 2.564%, highlights MLP’s potential for practical applications in fields such as environmental engineering and process optimization. While both GPR and PR showcased commendable performance, MLP’s outstanding results underscore its suitability for accurate chemical concentration predictions in adsorption process. Future research avenues may involve further fine-tuning of hyperparameters and exploration of advanced regression techniques to continue enhancing predictive precision in similar complex datasets.

Future work can evaluate the integration of ensemble learning methods or hybrid models to further enhance predictive performance. Additionally, applying the proposed models to time-dependent or multivariate concentration datasets could expand their utility in dynamic environmental systems. Investigating the interpretability of neural models and incorporating domain-specific physical constraints into machine learning frameworks may also provide more reliable and explainable predictions. Moreover, expanding the dataset to include more input features or real-time sensor data could help develop more robust and adaptive prediction systems.