Introduction

Accurate prediction of shale strength is essential for the safe and cost-effective design of structures interacting with shale formations, such as boreholes, tunnels, slopes, and foundations. Organic-rich shale is widely distributed across the globe and has become a major focus of recent research due to its complex behavior whereas the strength of shale is a critical parameter in the analysis and design of open-pit excavations1,2,3. The presence of variable organic matter content in such shales makes it a challenge to predict the behavior due to water interaction4,5,6,7,8 as the shale strength is closely related to the stability of well-bores9 and the design of support system for the excavations in soft shale strata10,11. Existing models often rely solely on conventional geo-mechanical and drilling parameters, overlooking critical shale-specific characteristics like fabric anisotropy and wettability, which significantly influence strength behavior. The purpose of this study is the development of an advanced ML- model that accurately predicts shale strength by incorporating shale-specific factors improving upon previous models through enhanced algorithmic design, large-scale validation, and detailed sensitivity analysis to support safer and more reliable and optimized foundation designs, and reduction in uncertainty in shale-dominated geotechnical environments.

Unconfined compressive strength (UCS) is widely adopted as the primary response for shale behavior for foundation systems, and in-situ stress evaluations12,13,14 as it directly influences the strength and stiffness of materials used beneath foundations of infrastructures15,16,17,18,19,20,21,22,23,24. Hence the ML-based prediction model of the UCS of shale presents a vital importance design of structures on shale strata. Incorporating geotechnical field and laboratory variables into ML models, enhances the predictive robustness and geotechnical reliability of UCS estimations for shale rocks especially non-destructive parameters like increase in UPV and dry density shows higher strength25,26 and the void ratio (VR), porosity and moisture content (MC) adversely affect the UCS of shale27,28,29. The higher clay content (CC), organic matter (OM), and plasticity index (PI) lower the shale strength30,31,32. Environmental and field-derived parameters such as rainfall duration (RFD), rainfall intensity (RFI), temperature (T), rock quality designation (RQD), recovery ratio (RR), and bedding angle (BA) also exert critical influence on the UCS of shale formations33,34,35,36,37,38,39,40. UCS of organic-rich shale is governed by a wide spectrum of variables which can be handled by ML methods as the recent advances in ML and AI offer powerful alternatives capable of modeling complex geo-mechanical behavior with high accuracy and generalizability41 using efficacy of ML models in predicting UCS using geotechnical and well-logging data42,43,44. A comparative analysis of recent literature, summarized in Table 1, highlights a range of ML-based UCS models employing input features such as drilling parameters (e.g., weight on bit, RPM, ROP), physical properties (e.g., porosity, density, shear wave velocity), and mineralogical indices. Prior models (Table 1) have limited predictor scope, ignoring shale-specific features like fabric anisotropy and wettability; whereas, the significant drilling parameters like RQD and recovery ratio are also missing in these studies.

Table 1 Key features of few existing ML-based predictive models for UCS of shales.
Full size table

The present research aimed to develop machine learning-based predictive models for estimating the unconfined compressive strength (UCS) of organic-rich clay shale, providing a scalable, data-driven alternative to conventional destructive testing. The methodology utilized a large, comprehensive dataset (1217 samples) integrating novel non-destructive indicators, specifically wettability potential and quantitative shale fabric metrics—alongside standard destructive and ultrasonic pulse velocity. Four supervised ML algorithms—Support Vector Machine (SVM), Decision Tree (DT), K-Nearest Neighbor (KNN), and Extreme Gradient Boosting (XGBoost) were employed using a dual-model strategy. The simple model utilizes core physical parameters, while the composite model incorporates the full suite of predictors. The composite XGBoost model achieved exceptional predictive accuracy (R2 = 0.981; RMSE = 0.02; MAE = 0.02) and demonstrated robust generalization on an external validation dataset (R2 = 0.91), supported by Taylor diagram and sensitivity analysis. The novelty lies in: (1) the first integration of wettability potential and fabric anisotropy as critical predictors for shale UCS; (2) the composite XGBoost model achieving unprecedented accuracy (R2 = 0.981) and exceptional generalization (R2 = 0.91); and (3) sensitivity analysis revealing the non-linear influence of these novel parameters, establishing a paradigm-shifting approach capable of replacing conventional UCS testing for rapid geo-mechanical characterization in geotechnical applications.

Methodology

The approach adopted to develop and validate the ML-based models and the conceptual framework are presented in Figs. 1 and 2, respectively. The methodology is based on input variables which plays a pivotal role in the development of AI-based predictive models. The selection was based on the physical and statistical significance regarding three different aspects like non-destructive test (i.e., UPV), index and field parameters. The high-quality sample preparation from cores is tedious task which is expensive and time consuming and the samples are likely to be disturbed due to stress-unloading effects due thinly bedded shale (Hu et al.49). The sampling in rock is preferably performed by drilling of core from the shale strata. The core samples are tested in the laboratory for different index tests and UCS correlations are developed which lack the field and environmental influencing factors; hence, generating the imprecise predictive models being used in the geotechnical field. 1217 datasets of significant and effective parameters i.e., Unconfined Compressive Strength (UCS) and Moisture Content, (MC) 50, Ultrasonic Pulse Velocity (UPV) 51, Void Ratio (VR) and Porosity (P) 52, Dry Density (DD) 53, Clay Content (CC)54, Plasticity Index (PI) 55, Rock Quality Designation (RQD) and Recovery Ratio (RR) 56, Bedding Angle (BA) and Regional Temperature, (T) 57 were performed in field and laboratory. These input parameters were used for the model development, encompassing the minimum and maximum range for different types of shale materials. The extensive datasets were arranged in categories of different ranges. A systematic comprehensive repository was meticulously assembled for the development of an AI-driven predictive model for the UCS response parameter. The important segments of input parameters are taken as non-destructive (i.e., UPV, wettability (MC, RFD, and RFI), fabric (VR, OM, DD, CC, PI, and P), and drilling parameters (RQD, RR, BA, and T) are the input parameters incorporated in the development of predictive model for the UCS.

Fig. 1
figure 1

Approach adopted to develop and validate the ML-based models.

Full size image
Fig. 2
figure 2

Conceptual framework of the study focusing on the determination of ultrasonic pulse velocity, rock wettability, rock fabric and drilling parameters to be used for model development and model comparison.

Full size image

Presented in the Table 2, a total of 1217 data points were obtained from an extensive experimental program carried out at the Rock Mechanics and Geotechnical Testing Laboratories, University of Engineering and Technology, Lahore, Pakistan. This dataset was compiled over several years as part of ongoing research activities on the characterization of organic-rich clay shale. The testing program was designed to capture a wide spectrum of shale properties through systematic laboratory measurements of unconfined compressive strength (UCS), ultrasonic wave velocities, mineral fabric, wettability, and drilling-related parameters. All tests were performed under standardized and controlled laboratory conditions to ensure consistency, accuracy, and repeatability. Data were carefully recorded, reviewed, and integrated into a centralized laboratory database. The large number of testing points was deliberately selected to reflect the inherent variability and anisotropy typical of shale formations. This robust, internally generated dataset serves as a strong foundation for the development and validation of the XGBoost model proposed in this study to predict UCS based on integrated geotechnical and geophysical parameters.

Table 2 Ranges of output and input variables used for model development.
Full size table

This study encompasses a comprehensive testing data which are critical for modeling the strength behavior of shale rock. UCS serves as a primary indicator of material strength, while UPV reflects material density and elasticity. VR and MC provide insights into natural structural void capacity and compaction characteristic. Likewise, DD and CC are critical for soil and rock stability regarding strength perspective. OM and PI capture the organic behavior and plasticity characteristics of the shale. All these factors describe the shale fabric characteristics which as a result affect the UCS response. The wettability of the shale is vulnerable to its strength and P and MC can describe the potential of void spaces along with water present in these voids whereas RFD and RFI demonstrate the parameters related to the wetting potential at site. The site drilling conditions and field parameters such as RQD and RR are used to assess the quality and integrity of rock cores. The inclusion of BAand T affect the surface moisture of the extracted core samples. Collectively, UPV, fabric characteristics, wettability factors and field drilling parameters enable robust modeling and precise prediction of mechanical properties in complex geological environments. An ML-based predictive model demonstrating the most efficient and favorable KPIs emerged in this study. The efficacy of the proposed model was validated by a comprehensive analysis regarding comparison of the tested models. A rigorous evaluation was conducted with existing models using a large independent dataset. The sensitivity and parametric analyses were conducted for assessment of the model’s behavior in different conditions. Simple and composite models are presented for the response and predictors.

Simple model UCS = f (UPV, VR, OMC, DD, CC, OM, PI).

Composite model UCS = f (UPV, VR, OMC, DD, CC, OM, PI, P, MC, RQD, RR, RFD, RFI, BA, T).

Data analysis

Normalization of variables

The lab and field values of the data obtained were normalized for model development as it is necessary for improving the performance and stability of machine learning models. It ensures that features with different ranges and units contribute equally to the model, preventing those with larger magnitudes from dominating. This is particularly important for algorithms like Support Vector Machines and k-nearest neighbors; where feature scale impacts model performance. Normalization also accelerates convergence in optimization processes, reduces bias, and allows for more balanced learning. Additionally, it enhances the interpretability of results by putting all features on the same scale, making it easier to compare their relative importance and ensure consistent distance calculations in distance-based algorithms.

Table 3 shows a single-factor ANOVA analysis conducted on 14 groups, each containing 1217 samples, to compare variations in key geotechnical parameters. The summary statistics for each group include the count, sum, average, and variance, with averages ranging between 0.47 and 0.52 and variances spanning from 0.077 to 0.089. The ANOVA results show a statistically significant difference between groups, with an F-value of 2.271 exceeding the critical F-value of 1.720 (p-value = 0.0055). The between-group sum of squares (SS) is 2.47, with a mean square (MS) of 0.190, while the within-group variability accounts for an SS of 1163.46 and an MS of 0.083. These findings highlight meaningful variability among the parameters, underscoring their importance in the study’s context.

Table 3 Analysis of variance of various groups used in this study.
Full size table

Density of the data

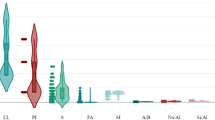
Figure 3 illustrates the density distributions of various geotechnical parameters. Each subplot combines a kernel density estimate (red line) and a histogram (blue area), offering a detailed visualization of the data’s spread and central tendencies. The red density curves highlight the underlying probability distributions, revealing the skewness, modality, and variance of each parameter. Most parameters exhibit unimodal distributions with slight variations in spread, indicating relatively consistent patterns within the dataset. Notably, UCS and a few other parameters show a wider spread, suggesting greater variability, which could influence their predictive capability in machine learning models. These plots provide insights into the statistical behavior and potential interrelationships of the input variables, serving as a foundational basis for model development and parameter optimization in geotechnical applications.

Fig. 3
figure 3

Density of the predictors and response providing foundational insights into the statistical behavior and interrelationships of input variables, supporting effective feature selection and model optimization in geotechnical machine learning applications.

Full size image

Pearson’s correlation matrix

Figure 4 represents the Pearson correlation matrix of various geotechnical parameters, emphasizing the response of UCS to other variables. UCS exhibits a strong positive correlation with Ultrasonic Pulse Velocity (UPV, r = 0.9939), Bulk Density (BA, r = 0.9598), and Void Ratio (VR, r = 0.9933), indicating that higher material density and reduced voids enhance compressive strength. Additionally, UCS is moderately positively correlated with Moisture Content (MC, r = 0.6627) and Optimum Moisture Content (OMC, r = 0.5653), suggesting that proper moisture levels during compaction improve material strength. Conversely, UCS demonstrates a negative correlation with Clay Content (CC, r =  − 0.6627) and Dry Density (DD, r =  − 0.6914), reflecting the weakening effects of clay’s deformability and inadequate compaction in drier conditions. A significant positive relationship between UCS and Tensile Strength (T, r = 0.9397) underscores the interplay between compressive and tensile properties in material behavior. These findings highlight UCS’s dependency on physical and compaction-related parameters, reinforcing its critical role in evaluating material performance in geotechnical applications.

Fig. 4
figure 4

Heatmap of Pearson’s correlation matrix underscoring the importance of Hybrid Destructive and Non-Destructive Inputs in influencing UCS and guiding predictive geotechnical modeling.

Full size image

Modelling framework

Following both physical and statistical significance, ten independent variables were meticulously examined as predictors for predicting UCS. This study focuses on predictive modelling as it lessens dependency on laborious and time-consuming testing procedures and gives predictions amidst the considerable variability inherent in established geotechnical data. The data was split into training data (80%) and testing data (20%) while separate independent data points were reserved for the validation of the models. Furthermore, the proposed model was validated alongside the existing models in the literature to demonstrate its effectiveness in predicting the UCS using Taylor’s diagram. Additionally, the parametric and sensitivity analysis was done to delineate the mechanism of modelling and emphasize the importance of geotechnical parameters (predictors) in the development of AI models for the prediction of UCS of shale rock.

Modelling techniques

  1. (a)

    Extreme Gradient Boosting (XGBoost)

XGBoost is a significant ensemble learning ML-algorithm. It comprises classification and regression trees along with analytical methods for boosting. The framework assessment is boosted by different tree construction in place of addressed tree. Then these trees are connected to establish a predictive algorithm. XGBoost’s objective function combines a loss function (measuring how well the model fits the training data) and a regularization term (to prevent overfitting). For a dataset with nnn examples, the objective function at iteration, t is shown in Eq. (1).

$${\text{Obj}}^{\left({\varvec{t}}\right)}={\sum }_{{\varvec{i}}=1}^{{\varvec{n}}}\mathbf{l}\left({{\varvec{y}}}_{{\varvec{i}}},\widehat{{{\varvec{y}}}_{{\varvec{i}}}^{\left({\varvec{t}}-1\right)}}+{{\varvec{f}}}_{{\varvec{t}}}\left({{\varvec{x}}}_{{\varvec{i}}}\right)\right)+{\varvec{\Omega}}\left({{\varvec{f}}}_{{\varvec{t}}}\right)$$
(1)

ℓ is the loss function (e.g., mean squared error), ft is the newly added tree at iteration t.

The regularization term Ω(ft)) controls the complexity of the model. For a tree ft​ with T leaves and weights w for each leaf, it’s defined as in Eq. (2)

$${\varvec{\Omega}}\left({{\varvec{f}}}_{{\varvec{t}}}\right)={\varvec{\upgamma}}{\varvec{T}}+\frac{1}{2}{\varvec{\uplambda}}{\sum }_{{\varvec{j}}=1}^{{\varvec{T}}}{{\varvec{w}}}_{{\varvec{j}}}^{2}$$
(2)

γ is the penalty for the number of leaves, λ controls the L2 regularization on leaf weights.

The predicted value at each iteration, t is updated as Eq. (3)

$$\widehat{{{\varvec{y}}}_{{\varvec{i}}}^{\left({\varvec{t}}\right)}}=\widehat{{{\varvec{y}}}_{{\varvec{i}}}^{\left({\varvec{t}}-1\right)}}+{{\varvec{f}}}_{{\varvec{t}}}\left({{\varvec{x}}}_{{\varvec{i}}}\right)$$
(3)

To optimize the objective function, XGBoost uses a second-order Taylor expansion of the loss function around the current predictions as presented in Eq. (4)

$${\sum }_{{\varvec{i}}=1}^{{\varvec{n}}}\mathbf{l}\left({{\varvec{y}}}_{{\varvec{i}}},\widehat{{{\varvec{y}}}_{{\varvec{i}}}^{\left({\varvec{t}}\right)}}\right)\approx {\sum }_{{\varvec{i}}=1}^{{\varvec{n}}}\left[\mathbf{l}\left({{\varvec{y}}}_{{\varvec{i}}},\widehat{{{\varvec{y}}}_{{\varvec{i}}}^{\left({\varvec{t}}-1\right)}}\right)+{{\varvec{g}}}_{{\varvec{i}}}{{\varvec{f}}}_{{\varvec{t}}}\left({{\varvec{x}}}_{{\varvec{i}}}\right)+\frac{1}{2}{{\varvec{h}}}_{{\varvec{i}}}{{\varvec{f}}}_{{\varvec{t}}}{\left({{\varvec{x}}}_{{\varvec{i}}}\right)}^{2}\right]$$
(4)

For a given leaf jjj, the optimal weight wjw_jwj​ that minimizes the objective function can be computed as in Eq. (5)

$${{\varvec{w}}}_{{\varvec{j}}}=-\frac{{\sum }_{{\varvec{i}}\in {{\varvec{I}}}_{{\varvec{j}}}}{{\varvec{g}}}_{{\varvec{i}}}}{{\sum }_{{\varvec{i}}\in {{\varvec{I}}}_{{\varvec{j}}}}{{\varvec{h}}}_{{\varvec{i}}}+{\varvec{\uplambda}}}$$
(5)

The optimal value of the objective function after adding a tree is given by Eq. (6)

$${\text{Obj}}_{\text{tree}}=-\frac{1}{2}{\sum }_{{\varvec{j}}=1}^{{\varvec{T}}}\frac{{\left({\sum }_{{\varvec{i}}\in {{\varvec{I}}}_{{\varvec{j}}}}{{\varvec{g}}}_{{\varvec{i}}}\right)}^{2}}{{\sum }_{{\varvec{i}}\in {{\varvec{I}}}_{{\varvec{j}}}}{{\varvec{h}}}_{{\varvec{i}}}+{\varvec{\uplambda}}}+{\varvec{\upgamma}}{\varvec{T}}$$
(6)

The final prediction boosting rounds is shown in Eq. (7)

$$\widehat{{{\varvec{y}}}_{{\varvec{i}}}}={\sum }_{{\varvec{t}}=1}^{{\varvec{T}}}{{\varvec{f}}}_{{\varvec{t}}}\left({{\varvec{x}}}_{{\varvec{i}}}\right)$$
(7)

where each ft is a tree added in iteration, t.

  1. (b)

    Support Vector Machine (SVM)

SVM makes use of machine learning to solve complex regression, classification and outlier detection problems by conducting optimal data changes that determine boundaries between data points based on predefined classes. Adopted in a wide range of disciplines; SVM has applications in healthcare, natural language processing and image recognition. The support Vector Machine model is chosen in this study because of its ability to perform complex and robust predictions. The limitations of this model include careful parameter tuning and the chances of overfitting. The goal of SVM is to maximize the margin between classes, which is equivalent to minimizing the norm of the weight vector was presented in Eqs. (viii and ix)

$$\underset{w,b}{\text{min}}=\frac{1}{2}|w{|}^{2}$$
(8)
$${y}_{i}\left(w\cdot {x}_{i}+b\right)\ge 1,\hspace{1em}\forall i$$
(9)

w is the weight vector, b is the bias term, yi are the class labels (+ 1 or -1), xi are the data points.

For non-linearly separable data, we introduce slack variables ξi\xi_iξi to allow some misclassifications as shown in Eqs. (x and xi):

$$\underset{w,b,\upxi }{\text{min}}=\frac{1}{2}|w{|}^{2}+C{\sum }_{i=1}^{n}{\upxi }_{i}$$
(10)
$${y}_{i}\left(w\cdot {x}_{i}+b\right)\ge 1-{\upxi }_{i},\hspace{1em}{\upxi }_{i}\ge 0,\hspace{1em}\forall i$$
(11)

where C is a penalty parameter controlling the trade-off between margin width and misclassification. To solve the optimization problem efficiently, SVM uses the dual formulation as presented in Eqs. (12 and 13)

$$\mathop {\max }\limits_{\alpha } \mathop \sum \limits_{i = 1}^{n} \alpha_{i} - \frac{1}{2}\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} \left( {x_{i} \cdot x_{j} } \right)$$
(12)
$$0\le {{\alpha }}_{i}\le C,\hspace{1em}{\sum }_{i=1}^{n}{{\alpha }}_{i}{y}_{i}=0$$
(13)

where αi\alpha_iαi are the Lagrange multipliers.

Once the optimal α\alphaα values are found, the decision function for a new point x is in Eq. (14)

$$f\left(x\right)={\text{sign}}\left({\sum }_{i=1}^{n}{{\alpha }}_{i}{y}_{i}\left({x}_{i}\cdot x\right)+b\right)$$
(14)

For non-linearly separable data, a kernel function K(xi,xj) is used in Eq. (15).

$$f\left(x\right)={\text{sign}}\left({\sum }_{i=1}^{n}{{\alpha }}_{i}{y}_{i}K\left({x}_{i},x\right)+b\right)$$
(15)

where K(xi,xj) = ϕ(xi)⋅ϕ(xj) maps data into a higher-dimensional space for linear separation.

  1. (c)

    Decision Tree

A decision tree algorithm works by partitioning input data recursively based on feature values, resulting in the prediction of a target variable. It starts with the entire dataset at the root node while selecting the best attribute to split the data into subsets for maximizing the information gain, and reducing impurity or variance as required. The process continues iteratively making a tree-like structure with internal nodes representing decision points. On the other hand, feature values and leaf nodes represent predicted outcomes. The Gini impurity for a node is calculated as in Eq. (16).

$$G=1-{\sum }_{k=1}^{K}{p}_{k}^{2}$$
(16)

where pk is the proportion of samples belonging to class k in the node.

The best split minimizes the impurity of child nodes as in Eq. (17).

$$\text{Split Criterion}=\underset{\text{split}}{\text{min}}\left(\frac{{N}_{\text{left}}}{N}{\text{Impurity}}_{\text{left}}+\frac{{N}_{\text{right}}}{N}{\text{Impurity}}_{\text{right}}\right)$$
(17)

where Impurityleft and Impurityright are the impurity measures (e.g., Gini or Entropy) of the left and right child nodes, respectively.

  1. (d)

    K-Nearest Neighbor

The k-nearest works by identifying the k-closest data points in the feature space to a given query instance; making predictions based on their labels or values. In classification, the predicted class is usually selected by a majority vote of the k-nearest neighbors, while in regression, the predicted value is frequently the average of the k-nearest neighbors’ values. The number of neighbors to consider (k) is an important hyperparameter that can have a significant influence on the algorithm’s performance. The kNN algorithm has applications in a variety of machine learning tasks due to its simplicity and effectiveness. The primary operation in KNN is finding the distance between a query point x\mathbf{x}x and each point xi in the dataset. The most commonly used distance metric is Euclidean distance, defined as in Eq. (18).

$$d\left(x,{x}_{i}\right)=\sqrt{{\sum }_{j=1}^{m}{\left({x}_{j}-{x}_{i,j}\right)}^{2}}$$
(18)

where: m is the number of features, xj and xi are the feature values of the query point and the i-th data point, respectively.

For classification, KNN assigns the class yyy based on the majority vote among the kkk nearest neighbors (Eq. 19)

$$\widehat{y}={\text{mode}}\left({y}_{{i}_{1}},{y}_{{i}_{2}},\dots ,{y}_{{i}_{k}}\right)$$
(19)

where yi1, yi2,…, yik are the classes of the k nearest neighbors.

For regression, KNN predicts the output by averaging the values of the k nearest neighbors as shown in (Eq. 20)

$$\widehat{y}=\frac{1}{k}{\sum }_{i=1}^{k}{y}_{i}$$
(20)

where yi are the target values of the k nearest neighbors.

Evaluation metrics

The proposed models were validated against existing models and independent datasets for predicting UCS of rock. The performance of the proposed model was validated based on various evaluation metrics. MAE (Mean Absolute Error) is the difference between the original and predicted values extracted by averaging the absolute difference over the data set (Eq.xxi)

$$\text{MAE}=\frac{1}{N}{\sum }_{i=1}^{N}\left|yi- y*\right|$$
(21)

MSE (Mean Squared Error) is the difference between the original and predicted values extracted by squared the average difference over the data set (Eq. 22)

$$\text{MSE}=\frac{1}{N}{\sum }_{i=1}^{N}{\left(yi- y*\right)}^{2}$$
(22)

RMSE (Root Mean Squared Error) is the error rate by the square root of MSE (Eq. 23)

$$\text{RMSE}=\sqrt{\frac{1}{N}{\sum }_{i=1}^{N}{\left(yi- y*\right)}^{2}}$$
(23)

R-squared (Coefficient of determination) represents the coefficient of how well the values fit compared to the original values (Eq. 24).

$${R}^{2}=1-\frac{\sum {\left(yi- y*\right)}^{2}}{\sum {\left(yi- y{^{\prime}}\right)}^{2}}$$
(24)

where y* is the predicted value of y and y’ is the mean value of y.

Parametric study and sensitivity analysis

Parametric analysis involved systematically varying the model parameters to evaluate their individual and combined effects on performance. Additionally, a sensitivity analysis was performed to determine the influence of each input parameter within the model framework, using a methodology aligned with the established approach. The following equations were utilized to compute the sensitivity of each input parameter (Eq. 25)

$${S}_{i}=\frac{{f}_{\text{max}}\left({x}_{i}\right)-{f}_{\text{min}}\left({x}_{i}\right)}{{\sum }_{j=1}^{N}{n}_{j}}\times 100$$
(25)

where fmax is the maximum and fmin is the minimum predicted value.

External validation

K-fold validation was used as Level-1 validation. Level-2 validation is done using independent data sets which were not used in the model development. The proposed model was further evaluated using a Taylor diagram analysis in comparison with existing models from the literature, leveraging an independent validation dataset as shown in Fig. 5.

Fig. 5
figure 5

Conceptual framework for model validation.

Full size image

Results and discussion

Figure 6 shows results showcase the performance of four machine learning models (Decision Tree, SVM, KNN, and XGBoost) in predicting UCS. Each figure compares the actual and predicted values for both training and testing datasets. The actual vs. predicted values show reasonable alignment but with noticeable scatter, particularly for the testing data.

Fig. 6
figure 6

Composite DT, SVM, KNN and XGBoost models.

Full size image

The model struggles with overfitting, as evident from higher variance in predictions for testing data compared to training data indicating limited generalization capability and lower reliability in real-world applications. Similarly, the SVM model shows a clear underestimation for higher values of UCS, resulting in deviations from the ideal diagonal line. The testing data demonstrates moderate alignment, but the model’s predictive capability diminishes for extreme values suggesting the model lacks robustness, especially for datasets with diverse environmental, mechanical, and drilling predictors. Furthermore, KNN exhibits improved alignment compared to DT and SVM but still suffers from moderate scatter in the testing data. Its performance is more consistent but does not achieve the level of accuracy seen in XGBoost as it delivers an almost perfect alignment between actual and predicted values, with minimal scatter for both training and testing datasets. The strong performance is evident from the model’s ability to predict across a wide range of UCS values, capturing complex relationships between predictors (mechanical, drilling, and environmental factors). The model’s superior performance, demonstrated through high R-squared values and low error metrics, highlights its robustness and adaptability. The composite strategy (using all predictor categories) enables XGBoost to outperform other models significantly by leveraging the comprehensive dataset effectively. Hence, the composite XGBoost model excels due to its superior predictive accuracy, robust validation, and practical utility, making it the optimal choice for modelling UCS in complex shale lithologies. Figure 7 shows the comparison of the actual versus predicted plots across the models—Decision Tree (DT), Support Vector Machine (SVM), K-Nearest Neighbor (KNN), and XGBoost—clearly illustrates the superior performance of XGBoost.

Fig. 7
figure 7

Simplified DT, SVM, KNN and XGBoost model.

Full size image

While all models demonstrate a general alignment along the ideal y = x line, simple XGBoost achieves the tightest clustering of points, indicating the highest accuracy and minimal error for both training and testing datasets. In contrast, the DT model shows significant scatter, particularly in the testing data, suggesting poor generalization and a tendency to overfit. SVM performs better than DT but struggles with extreme values, showing deviations from the ideal line. KNN produces more consistent results than DT and SVM, but its predictions exhibit a wider spread around the ideal line, especially for the testing data. In comparison, simple XGBoost demonstrates excellent generalization, with minimal scatter and high predictive precision, reinforcing its robustness and suitability.

Model comparison

Figure 8 shows the performance metrics that reveal the superior accuracy and robustness of the Composite Model compared to other machine learning models, including Decision Tree, Cubic SVM, K-Nearest Neighbors (KNN), and XGBoost, as well as a simpler XGBoost model.

Fig. 8
figure 8

Model performance comparison using average performance indicating the mean value of evaluation metrics (like R2, RMSE, MAE, etc.) calculated across multiple models and datasets.

Full size image

During training, the Composite Model achieves the lowest MSE (0.011), RMSE (0.011), and MAE (0.011), alongside the highest R-squared (0.991), demonstrating exceptional precision and its ability to explain nearly all variance in the training data. In testing, the Composite Model continues to outperform, achieving the best R-squared (0.981), while maintaining low MSE (0.011), RMSE (0.021), and MAE (0.021), reflecting its ability to generalize effectively to unseen data. When compared to the Simple Model, the Composite Model’s broader inclusion of predictors—integrating shale-water interaction, drilling, and fabric parameters—enables it to better capture complex relationships and dependencies, which the simpler model cannot fully address. This comprehensive approach results in superior performance metrics across all evaluation phases, making the composite models the most reliable and accurate tool for predicting UCS and ensuring its robustness for real-world applications.

Model validation

  1. (a)

    Level 1 Validation (K-Fold Cross Validation)

It is a widely used technique in machine learning to assess a model’s generalizability and prevent overfitting. The core idea is to split the data into K subsets and train the model on K-1 folds while testing it on the remaining fold. This process is repeated K times, with each fold serving as the test set exactly once. The results from each fold are then averaged to produce an overall performance metric. Unlike a simple train-test split, K-Fold ensures that each data point is used for both training and validation, reducing selection bias. Also, by averaging the performance across K iterations, K-Fold provides a more robust estimate of the model’s performance. The model development in this paper used K = 5.

  1. (b)

    Level 2 Validation (Using independent datasets for enhanced generalization)

Although the models demonstrated strong performance based on standard evaluation metrics, a comprehensive assessment of their effectiveness requires testing against data not used during the model development phase. To improve the generalizability of the proposed predictive models, validation with independent datasets from different geographic regions is crucial. While the current study shows high predictive accuracy within the primary study area, incorporating data from other parts of the country allows for a more robust evaluation of model stability and transferability. Validating against independent data helps assess the model’s performance under unfamiliar conditions, revealing any tendency toward overfitting to local patterns and supporting broader applicability58,59. Accordingly, to test the proposed models and assess their predictive capability, an independent dataset comprising 959 samples from a distinct region of the country was used for validation.

Figure 9 represents the performance of composite and simple XGBoost model showing distinctive trends. Both models show consistent trends across the sample population. The composite model showed even better prediction accuracy as the predictions generated by these models fall within an error margin of ± 1.51% as compared to a margin error of ± 1.86% for the Simple XGBoost model.

Fig. 9
figure 9

Validation of composite and simple models using independent datasets.

Full size image

Figure 10 compares the validation performance of the simple and composite XGBoost models highlights the superiority of the composite approach in achieving more reliable and robust predictions.

Fig. 10
figure 10

Performance evaluation of the models in validation.

Full size image

For the composite model, the training phase yielded a Mean Squared Error (MSE) of 0.16, Root Mean Squared Error (RMSE) of 0.01, Mean Absolute Error (MAE) of 0.01, and an R-squared value of 0.98, while the testing phase achieved an MSE of 0.14, RMSE of 0.02, MAE of 0.02, and R-squared of 0.92. In contrast, the simple model showed comparable performance during training, with an MSE of 0.03, RMSE of 0.03, MAE of 0.03, and R-squared of 0.98, but experienced a significant drop in testing accuracy, yielding an MSE of 0.16, RMSE of 0.06, MAE of 0.05, and R-squared of 0.67. The improved generalization of the composite model, as reflected in its higher R-squared and lower error metrics during testing, underscores its efficacy in capturing complex relationships within the dataset while mitigating overfitting. These findings emphasize the composite model’s suitability for real-world applications requiring both precision and reliability.

Sensitivity analysis

Figure 11 highlights the sensitivity (S%) of various predictors in the Simple XGBoost and Composite XGBoost models, showcasing the superior performance of the composite model across all parameters.

Fig. 11
figure 11

Sensitivity analysis of the predictors in proposed models measured in percentage (being a ratio having both numerator and denominator in the same unit).

Full size image

The blue bars, representing the Composite XGBoost, consistently achieve higher sensitivity values compared to the orange bars for the Simple XGBoost. Predictors such as UPV, VR, PI, BA, and T exhibit particularly high sensitivity in the composite model, often nearing or exceeding 90%, indicating their strong contribution to the model’s predictive accuracy. In contrast, the Simple XGBoost model shows lower sensitivity for many predictors, including OMC, MC, and PI, suggesting that it captures these relationships less effectively. The enhanced sensitivity of the composite model is attributed to its inclusion of a broader range of variables, which allows it to better account for the complex interactions between predictors. This demonstrates that the composite model not only utilizes the predictors more effectively but also offers a more reliable framework for capturing the nuances of geotechnical behavior. This sensitivity-driven comparison underscores the importance of comprehensive predictor inclusion in achieving high prediction accuracy. Figure 12 highlights the superior performance of the composite XGBoost model (A) in predicting Unconfined Compressive Strength (UCS) compared to other models, within an absolute error threshold of ± 5%. Model A demonstrates the closest alignment with experimental values across all data points, consistently maintaining minimal deviations and accurately tracking observed trends. Unlike other models, such as C and D, which exhibit noticeable fluctuations and deviations from experimental values, the composite XGBoost model provides stable and precise predictions. Furthermore, its predictions remain tightly bound within the error bars, signifying high reliability and precision. Even across significant variations in UCS, such as peaks and troughs observed around counts 5, 15, and 25, the composite model captures these trends effectively, outperforming its counterparts. These results confirm the robustness and accuracy of the composite XGBoost model, establishing it as the most reliable tool for UCS prediction in geotechnical applications.

Fig. 12
figure 12

Model comparison with the existing models. A: Composite XGBoost, B: Simple XGBoost, C: Davoodi et al.45, D: Kolawole et al.46, E: Mollaei et al.47.

Full size image

Figure 13 shows the Taylor diagram highlighting the superior performance of the composite XGBoost model (A) compared to other models (B, C, D, E) in predicting UCS. The composite XGBoost model achieves a correlation coefficient near 0.99, indicating an almost perfect linear relationship between the predicted and experimental values, surpassing the accuracy of all other models. Additionally, the composite model aligns closely with the reference standard deviation, reflecting its ability to replicate the variability of the experimental data accurately. Its proximity to the reference point further demonstrates that it has the lowest root mean square difference (RMSD), indicating minimal prediction error. Compared to the simple XGBoost model (B), the composite model benefits from a wider range of input variables, enabling more accurate and robust predictions. In contrast, models from previous studies (C, D, E) exhibit lower correlation coefficients, greater standard deviation mismatches, and higher prediction errors. Overall, the composite XGBoost model demonstrates superior accuracy, reliability, and consistency, making it the most effective tool for UCS prediction in geotechnical applications.

Fig. 13
figure 13

Model comparison with existing models in Taylor’s diagram illustrating the comparative performance of various models in predicting unconfined compressive strength (UCS). Model’s proximity to the reference point highlights its effectiveness in replicating both the strength and variability of experimental data. A: Composite XGBoost, B: Simple XGBoost, C: Davoodi et al.45, D: Kolawole et al.46, E: Mollaei et al.47.

Full size image

Field implications

The innovative methodology employed in this study holds significant importance. The systematic and comparative assessments of diverse ML-based based models and the proposed hybrid model offer a nuanced approach that enables end users to make informed decisions for accurately predicting UCS using a wide range of critical input factors. The proposed models demonstrate high utility due to their minimal errors, both in relative and statistical analyses. Traditional UCS tests, which rely on costly procedures such as rock drilling, sample preservation, core cutting, finishing, testing, analysis, and evaluation, often encounter laboratory errors and complexities, particularly with shale rock samples. Replacing these tedious and error-prone tests with an ML model that incorporates non-destructive UPV tests, shale index characteristics, and field drilling parameters would significantly enhance efficiency and reliability. Furthermore, conventional UCS values often fail to represent actual strata conditions, as weaker samples, typically in broken form, are excluded from strength tests, leaving only the strongest core samples. The proposed models address this limitation by offering a more comprehensive and practical alternative for UCS prediction.

Conclusions

The study highlights the critical importance of shale strength in geotechnical applications, particularly for shale gas drilling, fracturing, rock excavation, and tunneling projects in organic-rich strata. By leveraging a comprehensive dataset of 1217 entries, encompassing both non-destructive parameters such as ultrasonic pulse velocity and shale fabric characteristics, wettability parameters alongside destructive drilling parameters, the research successfully developed machine learning models for unconfined compressive strength prediction. The incorporation of a wide range of variables and ML algorithms such as SVM, DT, KNN, and XGBoost allowed for a robust evaluation of prediction accuracy having R2 values of 0.60, 0.61, 0.63 and 0.67 for the simplified models and 0.76, 0.81, 0.89 and 0.92 for the composite models respectively.

Among the machine learning models tested, the composite XGBoost model demonstrated the highest accuracy with an R-squared of 0.92, MAE of 0.02, and RMSE of 0.02, significantly outperforming simpler models and traditional approaches. Likewise, the validation through metrics such as R-squared, MAE, RMSE, and Taylor diagram analysis confirmed the accuracy and reliability of the model. Sensitivity analysis further revealed the complex interplay of predictors influencing UCS, underscoring the model’s robustness. It is anticipated that the ML-based framework presented in this study offers a rapid, cost-effective, and accurate tool for geotechnical planning and shale-related engineering projects, paving the way for improved wellbore efficiency and resource extraction strategies.