A network recovery strategy based on boundary nodes and tetrahedral approximation fermat points in three-dimensional wireless sensor networks

Abstract

Wireless Sensor Networks (WSNs) have emerged as a critical research frontier in the Internet of Things (IoT) domain, with widespread applications in three-dimensional environments. However, due to harsh environments (such as high temperature, high pressure, etc.), natural disasters (such as earthquakes, etc.), large-scale attacks (such as bombing), WSNs in a certain area is split into many isolated islands, and the regional network fails. In emergency scenarios, restoring network connectivity in a timely manner is essential for ensuring reliable data transmission. However, finding the minimum relay node to recover the network is an NP hard problem. To address this challenge, this paper proposes a novel connectivity recovery strategy for 3D wireless sensor networks by leveraging boundary nodes and tetrahedral approximate Fermat points. The proposed approach is evaluated through three distinct algorithms: (1) a variant of Prim’s algorithm (VPrim), which iteratively connects pairs of isolated segments until full network connectivity is restored, (2) a tetrahedral approximate Fermat point algorithm (TAFP), which simultaneously connects four isolated segments in each iteration until the network is fully recovered, and (3) Hybrid TAFP and VPrim Algorithm (HybridTV) to restore the entire network. Extensive simulation experiments demonstrate that our strategy significantly reduces the number of required relay nodes, enhances connectivity in the recovered network topology, and improves overall fault tolerance, offering a robust solution for network recovery in complex 3D environments.

Introduction

WSNs represent a class of large-scale, self-organizing networks characterized by dynamic topological changes, which demand exceptional reliability and robustness. The application scope of WSNs has expanded significantly from traditional two-dimensional configurations to encompass three-dimensional spaces, particularly in emerging domains such as underwater wireless sensor networks^{1,2,3,4,5,6,7,8,9}. These networks find extensive applications in three-dimensional environments, including but not limited to marine data acquisition, oceanographic sampling, environmental monitoring, coastal surveillance, search and recovery operations, network observation, marine climate recording, commercial marine operations, petroleum exploration, disaster prevention, navigation assistance, and meteorological management. However, the underwater deployment of sensor networks presents unique challenges: sensor nodes communicate through acoustic signals, which are subject to substantial propagation delays, elevated error rates, and multipath effects. Furthermore, underwater sensor nodes are particularly vulnerable to failures. Energy constraints may lead to node depletion, while harsh environmental conditions, including marine hazards such as jellyfish, sharks, anglerfish, boulders, and unpredictable weather patterns can cause node failures and network partitioning. Therefore, when the network is disconnected, timely recovery of network connectivity for real-time and effective data transmission is particularly important. The most critical issue when the network is severely damaged is how to deploy or move the minimum number of nodes to critical positions to restore network connectivity. Common methods in two-dimensional environments include the Steiner Minimal Tree (SMT) algorithm and the Minimal Spanning Tree (MST) algorithm^{10, 11}. Since this problem is NP-hard, approximate algorithms are mostly used.

Research on WSNs connectivity recovery is mostly conducted in two-dimensional planes^12,13,14. In three-dimensional environments, WSNs connectivity recovery is often limited to small-scale autonomous and directional recovery to enhance network reliability and coverage^15,16,17. However, there is limited research on the recovery of large-scale WSNs in three-dimensional environments after damage. Network recovery capability is one of the key indicators for evaluating network robustness. It is extremely important to design recovery strategies and contingency plans for WSNs to enhance network robustness in the face of large-scale damage. There is limited research on connectivity recovery in three-dimensional environments, with most researchers still using traditional active clustering recovery algorithms to restore network connectivity. They employ active recovery strategies for fault detection or vulnerability detection, followed by fault recovery^{3, 4}. This method is very effective for restoring network connectivity after damage to individual nodes or a small number of nodes. However, its efficiency will be significantly reduced for a large-scale damaged network that is divided into multiple network islands. Liu et al.¹⁸ proposed an effective connectivity recovery strategy for large-scale damaged networks. This strategy ensures network connectivity in the damaged network by constructing a constrained SMT and achieves good results by optimizing network connectivity through the selection of constrained Fermat approximate points. However, due to inaccuracies in the calculation of constrained Fermat points constrained by X and Y coordinates and the deployment of relay nodes, when connecting islands, selecting a head node within the island to represent the island, in practice, islands are often described as a collection of boundary nodes, which also affects the overall effectiveness of the recovery strategy.

This paper addresses the formation of information islands in three-dimensional WSNs under severe conditions of large-scale damage. It proposes a network recovery strategy that combines boundary nodes with tetrahedral approximate Fermat points to connect the isolated islands, aiming to enhance the reliability and robustness of the WSNs. A comparison is made with the ATCFS algorithm from reference¹⁸. The main contributions of this paper are summarized as follows:

• (1) We model the connectivity recovery of three-dimensional WSNs using a set of boundary nodes and abstract it as a graph connectivity problem.

• (2) We achieve network connectivity using unconstrained three-dimensional coordinates, derive a set of tetrahedral approximate Fermat points, and make good approximations of the tetrahedral Fermat points by adjusting parameters.

• (3) Based on the model constructed and formulas derived in this paper, three algorithms are proposed: a variant of the Prim algorithm, the tetrahedral approximate Fermat point algorithm, and hybrid TAFP and VPrim algorithm. Experimental results show that the three algorithms have achieved good performance in metrics such as the number of deployed nodes and average node degree.

The rest of this paper is organized as follows: In Sect. "Related works", we summarize related works of connectivity restoration in 2D and 3D WSNs. Section "Basic theory of algorithm" introduces the system model, defines the connectivity recovery problem and model, and establishes the mathematical basis for the tetrahedral approximate Fermat point set. Section "Combining boundary nodes with tetrahedral approximations of Fermat points for network connectivity recovery strategy" describes the details of the heuristic algorithm proposed in this paper. Section "Performance evaluation and analysis" presents the simulation results of the proposed algorithms. Finally, Sect. "Conclusion" concludes the paper and points out future research directions.

Related works

Connectivity recovery in 2D WSNs

In a two-dimensional environment, connectivity recovery in wireless self-organizing networks/sensor networks remains a hot topic of interest for many researchers, with many dedicating their efforts to research in this area. Recent studies^{15,16,17, 19,20,21,22,23,24,25} focus on connectivity recovery, with the majority still employing active, passive, or a combination of active/passive approaches for recovery. Most recovery methods still utilize clustering and controlled mobility to achieve network connectivity.

(1)Preprocessed active recovery.

Proactive recovery through preprocessing refers to all nodes in the network making pre-prepared decisions before a node failure occurs to minimize energy consumption and reduce the probability of node failures, enabling immediate recovery in case of node failure or network interruption. References^15,16,17 employ this method for fault tolerance recovery.

Reference¹⁵ proposes an adaptive fault-tolerant routing algorithm that utilizes particle swarm optimization to construct routes, considering inter-cluster and intra-cluster structures, as well as factors such as distance, energy, and traffic. Liu et al.¹⁶ introduce a multiple-path reliable transmission algorithm for fault-tolerant mechanisms in wireless sensor networks based on the Best Worst Ant System (BWAs) immune mechanism. S. Darwish et al.¹⁷ present an adaptive cellular automata approach (CA-based FT) for fault diagnosis and connectivity maintenance in wireless sensor networks.

(2) Passive recovery.

Passive recovery refers to the corresponding processing and restoration when a node fails. In passive recovery, some methods require preprocessing, such as evaluating area shapes in advance, training and learning several key parameters, while others do not store any information. Reference¹⁹ proposes a method to ensure persistent connectivity (DBCE) in severely damaged sensor network environments, primarily addressing secondary damage. Liu et al.²¹ introduce an industrial Internet of Things connectivity recovery strategy based on machine learning (CRrbf). To our knowledge, this is one of the few strategies that apply machine learning to connectivity recovery. Reference²³ presents a WSNs partition biconnected recovery algorithm based on Steiner trees and convex polygons.

(3) Active/passive hybrid recovery.

The active/passive hybrid recovery method includes some preprocessing, such as saving neighbor node information, as well as measures taken when a node fails. References²⁰ and²² employ this active/passive hybrid recovery method, with both strategies being K-connected recovery algorithms known for their high network robustness. References²⁴ and²⁵ review key technologies in WSNs, such as connectivity, coverage, and deployment, and highlight future research directions.

The aforementioned connectivity recovery methods all deal with connectivity restoration in 2D WSNs. While these methods are efficient in 2D WSNs, they may not necessarily be applicable to 3D WSNs.

Connectivity recovery in 3D WSNs

In 3D WSNs, real-time and effective data transmission is particularly important, making timely recovery of network connectivity crucial when network damage occurs. Currently, connectivity recovery methods mostly employ active recovery strategies for fault detection or use vulnerability detection for fault recovery, attracting significant research interest from many researchers recently.

In references^{1,2,3,4,5,6, 26,27,28,29}, they all explore active clustering methods for connectivity recovery in Underwater Sensor Networks (UWSNs). References¹ and² both propose coverage vulnerability repair algorithms based on clustering and sleep scheduling. Chaaf A et al.⁵ proposed a vulnerability prediction and repair method (RevoHPR) in UWSNs based on clustering and multiple Autonomous Underwater Vehicles (AUVs), combining clustering method and multiple AUVs. Reference³ introduced a cat group optimization-based autonomous recovery (CSO) for heterogeneous underwater wireless sensor networks. Reference⁶ proposed a hidden Poisson Markov model and applied it to node fault detection and recovery algorithms. Reference²⁶ also presented a fault prediction, detection, and recovery algorithm based on tree network topology, utilizing the Markov chain Monte Carlo (MCMC) process. References²⁸ and²⁹ are both cluster-based recovery algorithms, utilizing cluster head and candidate cluster head methods for recovery. Reference⁴ proposed an anomaly detection method for underwater sensor networks. This algorithm mainly represents the routing protocol using the detection algorithm and modifies the routing paths in underwater wireless sensor networks to reduce the number of damaged sensors. Lastly, Reference²⁷ introduced a node sinking algorithm for 3D coverage and connectivity of underwater sensor networks.

Reference⁷ proposed an innovative clustering routing model and a novel objective function to address the characteristics and requirements of UASN, accurately reflecting the specific characteristics and performance requirements of practical UASN. Zheng et al.⁸ proposed a periodic depth adjustment model for mobile nodes in UWSNs, leveraging stratified ocean current prediction. By layering regional currents based on error thresholds, the model balances prediction accuracy and computational efficiency. Using a CNN-Transformer model and kinematics, it predicts node trajectories at varying depths, then optimizes node depth via the Seagull Optimization Algorithm to enhance coverage and connectivity. Simulations confirm the system effectively mitigates ocean current impacts and improves network performance under diverse settings, offering a novel approach for node deployment and adjustment.

Reference⁹ proposed an obstacle-avoiding MWSN connectivity repair algorithm that minimizes energy consumption by transforming the problem into a minimum-energy solution model. The algorithm first determines the optimal deployment path based on node visibility and obstacle distribution, then identifies the best deployment position using a radius-based approach, and finally selects the optimal mobile node sequence considering movement distance. This ensures efficient network reconnection with minimal energy expenditure. Simulations confirm the algorithm effectively reduces energy consumption and extends network lifetime. Zear A et al.³⁰ reviewed the network partition detection and recovery techniques, emphasizing their limitations and the benefits of integrating UAVs in ground wireless networks. UAVs are emerging as crucial components in future wireless technologies, prompting an analysis of UAV-assisted networks, including technical challenges and deployment requirements. The study discusses existing UAV-assisted recovery methods and their application scenarios while highlighting key challenges in leveraging UAVs for network restoration.

All the aforementioned connectivity recovery methods address the issue of connectivity restoration in 3D wireless sensor networks. From the above references, it is evident that almost all the literature employs active clustering and mobility for recovery, involving two processes: fault detection and connectivity restoration. Some literature also combines sleep scheduling and power adjustment to achieve network connectivity. There are few methods that restore network connectivity by deploying new nodes, as it is challenging to redeploy new nodes in underwater environments. Most of them utilize underwater vehicle movement to collect data and restore network connectivity. To our knowledge, only Liu et al.¹⁸ proposed an effective connectivity recovery strategy when the network is severely damaged in UWSNs. However, their algorithm has some shortcomings, primarily because they only consider one node in the island as the representative node when building the model, and the X and Y coordinates are fixed when deploying relay nodes, making the solution suboptimal.

To our knowledge, there has been no prior proposal for a connectivity recovery strategy in 3D wireless sensor networks that combines boundary nodes with tetrahedral approximate Fermat points. This paper, for the first time, derives the calculation formula of three-dimensional coordinates of tetrahedral approximate Fermat points and accurately calculates the three-dimensional coordinates of the approximate Fermat point of the tetrahedral. We believe that the damaged network can be restored more quickly and data can be transmitted effectively in real-time using the method proposed in this paper.

Basic theory of algorithm

System model

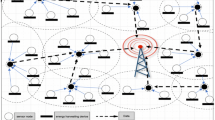
The WSNs studied in this paper is deployed in harsh 3D environments such as underwater, forest, mountainous, and mining areas to monitor designated regions. The sensor nodes are static, with fixed sensing and communication radii. As long as sensor nodes are within each other’s communication range, they can communicate with each other and transmit the collected data to a base station for further processing. Sensor nodes can obtain their own location information through relevant positioning algorithms, and the entire network adopts a hierarchical clustering topology. Typically, sensor nodes may fail due to energy depletion, but in most cases, only a few nodes fail. If the network connectivity is not affected, no action is taken; otherwise, only a small number of nodes need to be redeployed to restore network connectivity, identified through a detection algorithm. However, in the harsh 3D environment of interest in this paper, in addition to failures due to energy depletion, sensor nodes may experience large-scale failures due to external environmental factors (such as shark attacks, unpredictable weather, etc.). In such cases, the entire network will be disrupted, as illustrated in Fig. 1.

Fig. 1

3D severely damaged wireless sensor network.

When the sensor network is divided into multiple islands, sensor nodes can obtain information about other nodes within the same island through communication and obtain the boundary node set of each island using the boundary acquisition algorithm in reference^{31, 32}. This abstracts the network connectivity problem into a graph connectivity problem, i.e., finding a way to deploy a certain number of relay nodes to connect m islands with n boundary node sets.

To solve this problem, understanding the global information of the network is necessary. Therefore, information on the islands needs to be transmitted to the base station with the help of specific patrol devices, allowing the base station to restore network connectivity. In many practical applications, regular inspections are necessary and feasible, such as underwater inspections with underwater vehicles in underwater environments, regular personnel inspections in ecological environment monitoring, and regular drone reconnaissance on the battlefield.

For clarity of expression, detailed descriptions of all characters appearing in this article are listed in Table 1.

Table 1 Description of Character.

Problem definition

By constructing the above model, the connectivity recovery problem of 3D WSNs can be abstracted into a graph connectivity problem.

Definition 1: Island. An island is a region network within a partitioned network.

Definition 2: Boundary node set. The boundary node set is the set of boundary nodes for each island in the network, denoted by $U^{\prime}$. The boundary node set of all islands in the network is denoted by $U$, represented as $U = U_{1}^{\prime} U_{2}^{\prime} U_{3}^{\prime} \begin{array}{*{20}c} {...} & {(U_{i}^{\prime} (i = 1,2...n))} \\ \end{array}$, where n denotes the number of islands. Therefore, the ultimate goal of this problem is to connect the islands into a connected graph by constructing a minimum spanning tree and a tetrahedral Fermat approximate point Steiner tree.

In this model proposed in this paper, the network represented by G=(V, E), V includes some nodes in the boundary node set used in the process of constructing the tree and deployed relay nodes. E refers to the set of edges connecting the above two types of nodes, assuming that the length of each edge is represented by |v_iv_j|, Then the problem can be defined as follows:

$$\begin{gathered} {\text{minimize}}:\sum\limits_{{\text{E}}} {\left| {vivj} \right|} \hfill \\ {\text{subject to}}:{\text{ G is connected}} \hfill \\ \end{gathered}$$

Where E represents the set of edges in connected graph G, v_i and v_j are two nodes in set V. That is, v_i and v_j are either boundary nodes in islands or relay nodes.

Tetrahedral approximate Fermat point set

The tetrahedral Fermat point refers to a point in space where the sum of the distances from that point to the four vertices of a tetrahedron is minimized, known as the tetrahedral Fermat point. As shown in Fig. 2: The tetrahedral Fermat point does not exist outside the tetrahedron, as a point F outside the tetrahedron to the four vertices ABCD always has a shorter distance than a point F’’ on the edge.

Fig. 2

Illustration of Tetrahedral Fermat Point.

Fig. 3

Illustrates the calculation process of line segment point sets and plane point sets.

The general formula for the tetrahedral Fermat point was not directly obtained through mathematical reasoning and calculation in this paper. As an alternative approach, this paper exhaustively enumerated points within the tetrahedron based on mathematical reasoning and calculation at a certain density. The set of these points is referred to as the approximate point set of the tetrahedral Fermat point, representing the sample space connecting the tetrahedron. Ideally, if the density is infinitely large, the tetrahedral Fermat point would lie within this point set. The origin and mathematical theory of the sample space are as follows: Fig. 3 illustrates the calculation process of line segment point sets and plane point sets.

In a three-dimensional environment, any plane ABC is denoted as plane α. Given ${\text{A}}(x_{a} ,y_{a} ,z_{a} )$, $B(x_{b} ,y_{b} ,z_{b} )$, $C(x_{c} ,y_{c} ,z_{c} )$, It can be seen $\overrightarrow {{AB}} = (x_{b} - x_{a} ,y_{b} - y_{a} ,z_{b} - z_{a} )$, $\overrightarrow {{{\text{CB}}}} = (x_{b} - x_{c} ,y_{b} - y_{c} ,z_{b} - z_{c} )$, therefore, the normal vector of plane α is $\overrightarrow {{\text{n}}} = \overrightarrow {{{\text{AB}}}} \otimes \overrightarrow {{CB}} = (\left| {\begin{array}{*{20}c} {y_{b} - y_{a} } & {z_{b} - z_{a} } \\ {y_{b} - y_{c} } & {z_{b} - z_{c} } \\ \end{array} } \right|, - \left| {\begin{array}{*{20}c} {x_{b} - x_{a} } & {z_{b} - z_{a} } \\ {x_{b} - x_{c} } & {z_{b} - z_{c} } \\ \end{array} } \right|,\left| {\begin{array}{*{20}c} {x_{b} - x_{a} } & {y_{b} - y_{a} } \\ {x_{b} - x_{c} } & {y_{b} - y_{c} } \\ \end{array} } \right|)$, Denoted as formula (1) below:

$$\begin{gathered} \left| {\begin{array}{*{20}c} {y_{b} - y_{a} } & {z_{b} - z_{a} } \\ {y_{b} - y_{c} } & {z_{b} - z_{c} } \\ \end{array} } \right| = a, - \left| {\begin{array}{*{20}c} {x_{b} - x_{a} } & {z_{b} - z_{a} } \\ {x_{b} - x_{c} } & {z_{b} - z_{c} } \\ \end{array} } \right| = b, \hfill \\ \left| {\begin{array}{*{20}c} {x_{b} - x_{a} } & {y_{b} - y_{a} } \\ {x_{b} - x_{c} } & {y_{b} - y_{c} } \\ \end{array} } \right| = c \hfill \\ \end{gathered}$$

(1)

According to the point-normal form of the plane equation, substituting point A and the normal vector $\vec{n}$, the equation of plane α is given by formula (2) as follows:

$$a(x - x_{a} ) + b(y - y_{a} ) + c(z - z_{a} ) = 0$$

(2)

According to the two-point form of the line equation, by substituting the coordinates of points A, B, and C, the equations of line segments AB, AC, and BC are as follows: formulas (3), (4), and (5) are as follows:

$${\text{AB}}:\frac{{x - x_{a} }}{{x_{b} - x_{a} }} = \frac{{y - y_{a} }}{{y_{b} - y_{a} }} = \frac{{z - z_{a} }}{{z_{b} - z}}_{a} \begin{array}{*{20}c} {} & {} \\ \end{array} x \in \left[ {\min \left( {x_{a} ,x_{b} } \right),\max (x_{a} ,x_{b} )} \right]$$

(3)

$${\text{AC}}:\frac{{x - x_{a} }}{{x_{c} - x_{a} }} = \frac{{y - y_{a} }}{{y_{c} - y_{a} }} = \frac{{z - z_{a} }}{{z_{c} - z_{a} }}\begin{array}{*{20}c} {} & {} \\ \end{array} x \in \left[ {\min \left( {x_{a} ,x_{b} } \right),\max \left( {x_{a} ,x_{b} } \right)} \right]$$

(4)

$${\text{BC}}:\frac{{x - x_{b} }}{{x_{c} - x_{b} }} = \frac{{y - y_{b} }}{{y_{c} - y_{b} }} = \frac{{z - z_{b} }}{{z_{c} - z_{b} }}\begin{array}{*{20}c} {} & {} \\ \end{array} x \in \left[ {\min \left( {x_{a} ,x_{b} } \right),\max \left( {x_{a} ,x_{b} } \right)} \right]$$

(5)

Let plane β be defined by the plane equation in formula (6) as follows:

$$y = N,{\text{N}} \in \left[ {{\text{min}}(y_{a} ,y_{b} ,y_{c} ),\max (y_{a} ,y_{b} ,y_{c} )} \right]$$

(6)

The intersection of plane α and plane β is the line $l_{0}$. By simultaneously solving the equations of plane α and plane β, i.e., Eqs. (2) and (6), the equation of line $l_{0}$ can be obtained as Eq. (7), as follows:

$$l_{0} :\left\{ {\begin{array}{*{20}c} {a(x - x_{a} ) + b(y - y_{a} ) + c(z - z_{a} ) = 0} \\ {y = N} \\ \end{array} } \right.$$

(7)

Simplifying, the relationship between the coordinates z and x on line $l_{0}$ can be expressed as Eq. (8), as follows:

$$z = - \frac{a}{c}x + \frac{{ax_{a} - b(N - y_{a} ) + cz_{a} }}{c}$$

(8)

Therefore, knowing the specific x-axis or z-axis coordinate of line $l_{0}$ allows the determination of the specific point coordinates. Line $l_{0}$ intersects line segment AB and line segment BC at points E and F, respectively. Substituting ${\text{y}} = {\text{N}}$ into Eqs. (3) and (4), the coordinates of points E and F can be easily obtained. If the two-point form of the line equation is as follows: $l_{{\text{n}}} :\frac{{x - x_{1} }}{{x_{2} - x_{1} }} = \frac{{y - y_{1} }}{{y_{2} - y_{1} }} = \frac{{z - z_{1} }}{{z_{2} - z_{1} }}$, Points $(x_{1} ,y_{1} ,z_{1} )$ and $(x_{2} ,y_{2} ,z_{2} )$ are points on line $l_{n}$, and the general coordinates of point E or point F are as follows: $(\frac{{{\text{N}} - {\text{y}}_{1} }}{{{\text{y}}_{{\text{2}}} {\text{ - y}}_{{\text{1}}} }}(x_{2} - x_{1} ) + x_{1} ,N,\frac{{N - y_{1} }}{{y_{2} - y_{1} }}(z_{2} - z_{1} ) + z_{1} )$.

Assume the line segment point set $x \in \left[ {\min \left( {x_{E} ,x_{F} } \right),\max \left( {x_{E} ,x_{F} } \right)} \right]$lies on line $l_{0}$, from point E to point F, points are uniformly sampled at step length $\varepsilon = \frac{{{\text{Distance}}_{{{\text{EF}}}} }}{{{\text{200}}}}$, and this point set can be determined based on Eqs. (7) and (8). Assume the plane point set lies on plane α, with plane β as $y = N$, where N is $\left[ {\min \left( {y_{a} ,y_{b} ,y_{c} } \right),\max \left( {y_{a} ,y_{b} ,y_{c} } \right)} \right]$, and line segment EF is uniformly sampled at step length $\varepsilon = \frac{{{\text{Distance}}_{{{\text{y}}_{{{\text{min}}}} y_{{\max }} }} }}{{200}}$. Since the segment point set can be determined, the plane point set can be determined. Figure 4 illustrates the process from the plane point set to the spatial point set of the tetrahedron.

Fig. 4

Illustrates the process from the plane point set to the spatial point set of the tetrahedron.

In three-dimensional space, for any tetrahedron ABCD, for any plane α (plane ABC in Fig. 4), and for a point outside the plane (point D in Fig. 4), let the distance from this point to plane α be L. Move plane α uniformly outward from the plane by step length $\varepsilon = \frac{{\text{L}}}{{200}}$. Based on spatial relationships, dividing the distance L can be transformed into dividing the edges AD, BD, and CD. Dividing the edges successively affects the changes in the x-coordinate, y-coordinate, and z-coordinate for each step. According to the two-point form of the line equation, the x-coordinate, y-coordinate, and z-coordinate are interrelated. Therefore, dividing the edges is transformed into dividing $\left\| {x_{a} - x_{d} } \right\|$, $\left\| {x_{b} - x_{d} } \right\|$, and $\left\| {x_{c} - x_{d} } \right\|$. With each movement, through calculations in the x-axis direction, the specific plane is obtained, the plane point set is calculated, and the cumulative plane point set ultimately yields the spatial point set of tetrahedron ABCD.

Steiner tree problem

The Steiner tree, similar to the Minimum Spanning Tree (MST), is a type of shortest network, and even on an undirected graph, it is an NP-hard problem. The problem is defined as follows: Given an undirected weighted graph $G = (V,E)$, edge weight c: $E \to R \ge 0$, terminal nodes $R \subseteq V$, find a subgraph $T_{s} = (V_{s} ,E_{s} ) \subseteq G$, such that $T_{s}$ connect $R$ and the $c\left( {T_{s} } \right) \leftarrow \sum\nolimits_{{e \in E_{s} }} {c_{e} }$ is minimized. Nodes $S \leftarrow V\backslash R$ are referred to as potential Steiner nodes³³. As shown in Fig. 5, in which, black edges are the edges from the original graph, red edges are the constructed edges, A₁-A₄ are the nodes from the original graph, and S₁ and S₂ are the constructed Steiner points. The Steiner problem is to construct a graph after points have been added, or within a graph, to find a subgraph that minimizes the cost of the edges required to connect some nodes in the graph. If the Steiner point is one of the nodes to be connected in the graph, it is referred to as a degenerate Steiner tree, and the point is a degenerate point.

Fig. 5

Steiner Tree Problem schematic.

Ideal ATCFS recovery algorithm

The ATCFS algorithm is a typical three-dimensional underwater wireless sensor network recovery strategy¹⁸. This strategy uses cluster head nodes to represent isolated networks, first using a tree construction algorithm to connect the network, and then further reducing the number of relay nodes through Fermat point selection optimization based on the connectivity of cluster head nodes. Taking into account the practical issue of relay node deployment on ships in the actual environment, the algorithm specifies ship trajectories and fixed deployment points, resulting in relay nodes being positioned not in an ideal straight line layout, but with slight curvature, which increases the number of relay nodes deployed. The ideal ATCFS recovery algorithm in this paper refers to the ATCFS algorithm without considering the actual ship deployment, where the relay nodes are deployed in a straight line. The recovery strategy proposed in this paper is compared with it through experimental analysis.

Combining boundary nodes with tetrahedral approximations of Fermat points for network connectivity recovery strategy

The strategy proposed in this paper first detects isolated islands, identifies the boundary nodes and their positions for each island, and then transmits the information of each island and boundary node to the base station through patrol devices which have the ability to travel from the base station to the farthest boundary node, and has the ability to collect the basic information of the node, such as coordinates, working status, working information, etc. Finally, based on the collected position information of each boundary node of the isolated islands, the islands are connected using a variant of Prim’s algorithm or tetrahedral approximations of Fermat points algorithm to achieve connectivity of the entire network. The pseudocode and main idea of the algorithm are as follows.

Variant of Prim’s algorithm (VPrim)

The variant of Prim’s algorithm proposed in this paper is primarily based on the classical Prim’s algorithm as a reference, and has been improved by incorporating the model proposed in this paper. The variant of Prim’s algorithm consists of the following steps: as shown in Fig. 6 and the pseudocode of the variant of Prim’s algorithm, starting from any isolated island a, find the nearest island b to island a, record the path between island a and island b, merge island b into island a, continue to find the nearest island b to island a, record the path, and merge it into island a, until the entire network is connected.

The flowchart of the the variant of Prim’s algorithm is shown in Fig. 6, and the pseudocode is presented in Algorithm 1.

Time complexity analysis of the variant of Prim’s algorithm: Assuming there are n isolated islands in the environment, each island contains m boundary nodes. Line 1: Selecting the starting point is arbitrary, so the time complexity is $O(1)$. Line 3: Checking the existence of isolated islands, which takes n-1 iterations to eliminate all isolated islands, resulting in a time complexity of $O(n)$. Line 5: Traversing all isolated islands has a time complexity of $O(n^{2} )$. Line 9: Calculating the distance between isolated islands has a time complexity of $O(n^{2} \times m^{2} )$. Line 14: Merging isolated islands has a time complexity of $O(n^{2} \times m^{2} + 1)$. After analysis, the algorithm’s time complexity is determined by the highest order term, which is the highest complexity item, resulting in a time complexity of $O(n^{2} \times m^{2} )$.

Fig. 6

Flowchart of the variant of Prim’s algorithm.

Tetrahedral Approximation Fermat Point Algorithm (TAFP)

The core steps of the tetrahedral approximations of Fermat points algorithm proposed in this paper are divided into the following three steps:

Step 1: Partitioning, ensuring network connectivity by planning the form of connections between isolated islands and initially planning the positions of Steiner points. This paper adopts a greedy strategy starting from the island with the smallest label and using breadth-first search for selection.

Step 2: Node selection, selecting the corresponding isolated islands along the planned paths, and choosing optimal nodes within each isolated island as the calculation vertices for the tetrahedral approximations of Fermat points. This paper selects four boundary nodes from each isolated island, forming the shortest edge length of the tetrahedron.

Step 3: Computing the approximate Fermat points, deriving the point set based on the formula derivation steps in Section III.C, and selecting the optimal point as the approximate Fermat point based on the minimum number of required relay nodes from each point in the point set to the four boundary nodes.

The flowchart of the tetrahedral approximations of Fermat points algorithm is shown in Fig. 7, and the pseudocode is presented in Algorithm 2.

Time complexity analysis of the tetrahedral approximations of Fermat points algorithm: Assuming there are n isolated islands in the environment, each island contains m boundary nodes, and the total number of movements when calculating the point set is divided into l equal parts. Line 1: Initializing labels requires traversing the islands, hence the time complexity is O(n). Line 3: Checking if the island set contains labels has a time complexity of O(n). Line 5: Finding the nearest island has a time complexity of O(n+n). Line 7: Finding the tetrahedron with the shortest edge within the four islands has a time complexity of $O(n + n + m^{4} )$. Line 8: Calculating the point set of the tetrahedron has a time complexity of $O(n + n + m^{4} + l^{3} )$. Line 9: Traversing the set to find the approximate point has a time complexity of $O(n + n + m^{4} + l^{3} + l^{3} )$. Line 10: Recording the time complexity of this line as O(1), the analysis is complete. According to time complexity, the highest order term should be considered, which is the highest complexity item. Therefore, the time complexity of this algorithm is $O(2n + m^{4} + 2l^{3} )$.

Fig. 7

Flowchart of the tetrahedral approximations of Fermat points algorithm.

The specific implementation process of the tetrahedral approximations of Fermat points algorithm is illustrated in the sample Fig. 8.

Step 1 Selection: Plan approximate paths to connect the network, ensuring network connectivity. Start by connecting the isolated island 0 with the three closest regions, and enqueue these 3 regions. After planning isolated island 0, proceed to select isolated island 18, isolated island 6, isolated island 16, and so on, repeating this process until there are no labeled isolated islands left in the network.

Step 2 Point Selection: Process the planned approximate paths sequentially. Each time, select the optimal tetrahedron (with the shortest edge length) from four isolated islands to prepare for the next calculation step.

Step 3 Calculate Approximate Fermat Points: Calculate the tetrahedral approximations of Fermat points sequentially based on the derivation steps in Section III.C of this paper.

Fig. 8

Example of the tetrahedral approximations of Fermat points algorithm.

Hybrid TAFP and VPrim Algorithm(HybridTV)

The idea of the HybridTV algorithm is as the following steps:

Step 1: Divide the damaged network logic into restored networks and isolated networks to ensure the algorithm correctly and completely restores network connectivity.

Step 2: Define a divergence queue to constrain the direction selected for the isolated networks. The direction is determined by the first element in the queue. All elements in the divergence queue are isolated networks from the restored network, and the initial queue element is the isolated network with the smallest label.

Step 3: Each time, an island is taken from the divergent queue as a directional island(DI) for network pre-recovery. Firstly, the pre-recovery of the tetrahedral approximate Fermat point is performed to find the island of the three island networks closest to the directional island. If the distance from the three islands to the directional island is less than 3500 m, the recovery is performed. The three islands are added to the divergent queue and the recovery link is recorded. On the contrary, the approach is abandoned, and then the direct connection is used to select the nearest island in the island network to perform network recovery. The island is added to the divergent queue and the recovery link is recorded.

The flowchart of HybridTV algorithm is shown in Fig. 9, and the pseudocode is presented in Algorithm 3.

Fig. 9

Flowchart of HybridTV algorithm.

Time complexity analysis of the HybridTV algorithm: Assuming there are n isolated islands in the environment, each island contains m boundary nodes, and the total number of movements when calculating the point set is divided into l equal parts. The first line : select the island with the smallest label, need to traverse the island set, the time complexity of the line is O(n), the second line : the worst number of runs is n-1 times, and the time complexity of the line is O(n), the third line : select elements from the queue, the time complexity of the line is O(1), the fourth line : to find the nearest island, you need to traverse the island set, traverse the boundary node set, the time complexity of the line is O(nm), similarly line 6 : the time complexity of the line is O(nm), line 8 : calculates the approximate Fermat point, which has a time complexity of $O(2n + m^{4} + 2l^{3} )$, Line 9 : records the link, which has a time complexity of $O(1)$, according to the time complexity calculation rules, the time complexity of the algorithm is $O(n^{2} + nm^{4} + nl^{3} )$.

Performance evaluation and analysis

In this section, we will evaluate and analyze the proposed algorithms, namely the variant Prim algorithm (VPrim), the tetrahedron approximation Fermat point algorithm (TAFP), Hybrid TAFP and VPrim Algorithm (HybridTV), and compare with the ATCFS algorithm from reference¹⁸. The evaluation is based on the number of relay nodes and the average node degree to assess their performance. These algorithms are implemented in a simulated environment where the WSNs is generated from a random graph model.

In simulation, we mainly consider the following performance metrics and parameters:

(1)The number of islands: The more islands, the more work required for connectivity recovery, and more relay nodes required.

(2)Communication radius: The communication radius has a great impact on the performance of the algorithm proposed in this paper. The larger the communication radius, the fewer nodes are needed to connect each islands, and vice versa.

(3)The number of relay nodes: The relay node is deployed to achieve network connectivity. Obviously, under the condition of ensuring connectivity, the fewer relay nodes are used, the better of the algorithm.

(4)The average node degree: The average node degree refers to the average number of other nodes connected by each node. Obviously, the greater the average node degree, the better the robustness of the network.

Simulation environment construction

In the simulated three-dimensional wireless sensor network experimental environment, we assume a space size of 7000 m in length, 7000 m in width, and 7000 m in height. The three-dimensional space is divided into smaller spaces to represent gaps between islands. It is specified that if two sensors are in different islands and the distance between them is greater than or equal to the sensor’s sensing radius, the sensors cannot communicate; otherwise, they can communicate. If two sensors are in the same island, distance is not a consideration, and they can communicate through single or multiple hops. The spatial division is illustrated in Fig. 10: each island space is 1000 m x 1000 m x 1000 m, with a gap of 1000 m between island spaces. As shown in Fig. 10, the island spaces are highlighted in red, totaling 64 in number, sequentially numbered from 0 to 63.

Island initialization strategy: For each simulation experiment, the islands required are randomly selected from the divided island spaces. The selected island space randomly designates boundary nodes within it to form an island network, while the unselected island spaces are considered as voids in the network after damage.

Sensor initialization strategy: When sensors are randomly placed within an island, it is assumed that any two sensors within the island can communicate with each other. The degree of a sensor is the number of other sensors within its sensing radius. For boundary node sensors, the degree is 1, indicating connectivity to the island network.

Fig. 10

Selection of islands and designated islands.

Simulation result

For all the simulations, we repeat the experiment for 100 times and report the average values of the metric.

(1)The performance comparison on the number of relay nodes.

Figure 11 shows the impact of the number of islands to the number of relay nodes, when there are 20 boundary sensors in one island and the sensing radius is 500 m. As can be seen from Fig. 11, the ideal ATCFS, variant Prim algorithm, tetrahedron approximation Fermat point and HybridTV algorithm require an increasing number of relay nodes as the number of islands increases. The variant Prim algorithm shows better performance with the least number of required relay nodes, while the tetrahedron approximation Fermat point algorithm requires more relay nodes. This is because the tetrahedron approximation Fermat point algorithm utilizes local optimization and fails to achieve global optimality in achieving overall network connectivity, which is an area we aim to improve in the future. From Fig. 11, we can also observe that the ATCFS algorithm uses fewer relay nodes compared to the tetrahedron approximation Fermat point algorithm. This is because in our experimental setup, we assumed the optimal scenario of the ATCFS algorithm. Therefore, in a real-world environment, the ATCFS algorithm would require more relay nodes than in this idealized setting.

Fig. 11

The number of relay nodes of different islands.

Figure 12 shows the impact of the communication radius to the number of relay nodes, when there are 20 boundary sensors in one island and the number of islands is 25. The number of relay nodes of the ideal ATCFS, variant Prim algorithm, tetrahedron approximation Fermat point algorithm and HybridTV decreases with the increase of sensing radius, and remains stable after reaching 700. That because the size of the experimental environment remains unchanged, the spatial distribution remains unchanged, and the sensing radius increases, the number of relay nodes required for the connection between the islands will inevitably decrease. When the sensing radius is greater than 700 and less than 1000, the number of relay nodes remains stable because 2 to 3 sensors can connect 2 to 3 islands to each other relatively stably, and does not change with the change of sensing radius.

Fig. 12

The number of relay nodes of different communication radius.

(2)The performance comparison on the average node degree.

Figure 13 shows the impact of the number of islands to the average node degree, when there are 20 boundary sensors in one island and the sensing radius is 500 m. In the current environment, due to the wide range of simulation environment, the average node degree mainly depends on the original value of each island. The trend of Fig. 13 is consistent with Fig. 12. The smaller the number of relay nodes used, the greater the average node degree. Secondly, the average node degree is affected by multiple relay nodes with a relay node degree greater than 2. The more such nodes, the greater the average node degree. As shown in Fig. 13, the average node degree of the four algorithms is very close, and the overall performance is VPrim > HybridTV > ATCFS > TAFP.

Fig. 13

The average node degree of different islands.

Fig. 14

The average node degree of different communication radius.

Figure 14 shows the impact of the communication radius to the average node degree, when there are 20 boundary sensors in one island and the number of islands is 25. From Fig. 14, it can be observed that the ideal ATCFS, variant Prim algorithm, tetrahedron approximation Fermat point algorithm and HybridTV show a significant increase in the average node degree as the communication radius increases. However, comparing the data of the average node degree with a sensing radius of 500 m to Fig. 13, it is evident that the significant increase in the average node degree is mainly influenced by the increase in the sensing radius.When the sensing radius is 1000 m, almost all of them are connected to each other. The node degree of boundary nodes is extremely large, while the number of relay nodes is small. Therefore, the degree of average nodes is mainly determined by the degree of boundary nodes, so there is a sharp increase.

(3) Comparison of network connectivity graphs.

The comparison of network connection graphs is to observe the topology in the same environment. The coordinates of all boundary nodes are the same, and the specific parameters are shown in Table 2.

Table 2 Environmental parameter table.

As shown in Fig. 15, the graph represents the connectivity graph after restoring network connectivity using the variant Prim algorithm. It can be observed from the graph that the islands are fully connected, with a compact connectivity path and no significant cross-zone connections, indicating a relatively ideal connectivity approach. However, connectivity in certain areas can be further optimized.

Fig. 15

Recovery path using the variant Prim algorithm.

As shown in Fig. 16, the graph represents the connectivity graph after restoration using the tetrahedron approximation Fermat point algorithm. It can be observed from the graph that the islands are fully connected with a compact connectivity path, but there are noticeable cross-zone connections. The breadth-first greedy algorithm used in this paper did not fully consider the global zone allocation issue when ensuring proximity, leading to a few cross-zone connections and affecting the selection of approximation Fermat point, thus impacting the experimental results. There are complex local connections within a small range, which exhibit good robustness, but there is a single long chain in a large range, affecting robustness.

Fig. 16

Recovery path using the tetrahedron approximation Fermat point algorithm.

As shown in Fig. 17, the graph represents the connectivity graph after restoration using the ideal ATCFS algorithm. It can be observed from the graph that the islands are fully connected with a compact connectivity path, without significant cross-zone connection issues. However, due to representing the network with cluster head nodes, there are noticeable path selection optimizations that can be made in the space.

As shown in Fig. 18, the graph represents the connectivity graph after restoration using the HybridTV algorithm. The HybridTV algorithm improves the cross-regional link problem of the TAFP algorithm. Links are concentrated and compact.

Fig. 17

Recovery path using the ideal ATCFS algorithm.

Fig. 18

Recovery path using HybridTV algorithm.

Conclusion

In this paper, we have addressed the critical challenge of connectivity recovery in three-dimensional wireless sensor networks through three key contributions. First, we established a novel graph-theoretic model that formulates the 3D network recovery problem using boundary nodes, providing a mathematical foundation for connectivity restoration in fragmented networks. Second, we developed an optimization framework using unconstrained three-dimensional coordinates to derive tetrahedral approximate Fermat points (TAFP), demonstrating that parametric adjustments can yield highly accurate approximations for optimal relay placement. Third, building upon these theoretical advances, we proposed three practical recovery algorithms: a boundary-aware variant of Prim’s algorithm (VPrim), the TAFP algorithm for geometric optimization, and a hybrid approach combining their strengths.

Extensive experimental evaluations have validated the effectiveness of our approach, with all three algorithms showing significant improvements in two crucial performance metrics: (1) minimizing the number of required relay nodes for network restoration, and (2) maintaining optimal average node degree across various 3D deployment scenarios. These results confirm that our methods offer practical solutions for real-world applications where rapid network recovery is essential, such as in underwater sensor deployments or disaster response scenarios.

However, there are areas for optimization in the tetrahedron approximation Fermat point algorithm:

(1)Regarding island selection, identify islands that require cross-zone connectivity and establish direct connections, or allocate zones more reasonably to minimize instances of limited cross-zone connectivity.

(2)Directional zone selection: Experiment with local constraints in the three-dimensional environment to make the constructed tree closer to the ideal Steiner tree.

(3)Point set selection: Consider using machine learning techniques to expedite point selection convergence, reduce computation time, and avoid traversing all sample points.

(4)Real-world application: Simulate the algorithm in actual application environments.

(5)We will focus on extending this framework to incorporate dynamic network conditions and energy-aware optimization constraints, which could further enhance the practical applicability of our approach in time-sensitive operational environments.