Analysis of dramatic bedding landslide on dynamic instability and disaster factors

Abstract

In order to prevent the geological hazards of bedding landslides along the highway in mountainous areas, it is necessary to scientifically analyze the dynamic instability mechanism and the characteristics of the disaster-causing factors. On the basis of considering the effect of the retaining body, water pressure and compression deformation energy, a generalized chained regressive geomechanical model consisting of a slider, a lying soft rock and a retaining body was proposed, it also analyzed the four evolutionary stages of chained regressive phenomenon which included the initial stage of excavation, the middle stage of fracture development, the middle and late stage of system quasi-static deformation, and the stage of system instability before sliding. The stress field was derived by elastic theory. Based on the principle of energy conservation, the incremental balance equation of the generalized model was established, and the analytical formulas of the energy release curve and the energy dissipation curve, as well as the dynamic landslide starting slip force parameters were obtained. The method was applied to the landslide on national road 319 in Pengshui County, Chongqing city. Results illustrate: the generalized flexibility and generalized displacement are the control parameters for the dramatic instability of the slope. Energy accumulation, energy release curve and energy dissipation curve have two types: no intersection point and double intersection point. No intersection point corresponds to creeping slumping, and double intersection point corresponds to violent slumping. The contribution to the deformation energy accumulation is sorted from largest to smallest, followed by slider compression deformation energy, the function of the retaining body and the water pressure, among which the compression deformation energy of the slider cannot be ignored. The role of the retaining body has the dual effect of preventing sliding and increasing the deformation energy of the slider. The fissure water has a dual effect of hydrostatic pressure and erosion weakening effects. At the same time, the FLAC^3D finite difference method is used to verify the rationality of the theoretical model. The research results further explain the catastrophic law of the downhill chain regression model, reveal the disaster-causing efficiency of each influencing factor, it can provide a certain theoretical basis for the research and development of mountain road slope maintenance and disaster reduction technology.

Introduction

Mountainous hills in China account for more than two-thirds of the total land area. In recent years, human engineering disturbances superimposed on extreme weather have led to frequent landslide disasters in China^1,2. There are more classification schemes for landslides, and different landslide types correspond to different landslide destabilization mechanisms and corresponding stability analysis methods. There are more methods for landslide stability analysis, such as the theoretical analyses method^3,4,5,6, the numerical analyses method^7,8, the physical model test and the indoor specimen test^9,10. However, for some special rocky slopes, the traditional stability analysis methods have limitations.

Among them, dramatically dynamic landslides are characterized by suddenness, start-up elastic impulse, huge destructive force, uncertainty of disaster-causing factors, etc., and it is difficult to reflect their dynamic destructive attributes by using traditional research methods. As a result, some new theoretical approaches have been formed, such as analyzing the landslide initiation damage mechanism from the perspective of energy conservation and fracture mechanics^11,12; and introducing catastrophe theory into landslide research to analyze the suddenness of landslides, uncertainty of causative factors and other sudden and irreversible events occurring in nature^{13,14,15,16,17,18}. The first idea of the catastrophe theory is to establish the total potential energy function of the system, and then obtain an approximate catastrophe model through mathematical transformations, which is used to explain the phenomenon of system dynamics instability. The cusp catastrophe model^{16,17,18,19,20} and other types of catastrophe models^{17,21,22,23,24} are applied into the layered rock slopes and slopes containing weak structures. The second idea is to avoid applying a certain type of catastrophe model by carrying out complex approximate transformations based on establishing the total potential energy function. Instead, we should only analyze the total potential energy function itself¹⁶. Obviously, the starting point of the two ideas is the same, but the former is mainly based on the control variables of the catastrophe model to establish the landslide catastrophe destabilization criterion, which has strong engineering application value; while the latter can analyze the whole process of landslide deformation evolution, the accumulation and dissipation characteristics of the system energy, which focuses on the analysis of landslide destabilization mechanism and process, and the theoretical research has a certain degree of significance. However, the problem with this idea is that it is difficult to achieve energy equilibrium, especially since energy consumption is unclear and hard to quantify. Furthermore, the outcome of the second idea is hard to comprehend and explain, and only a few people familiar with the rock catastrophe theory can fully grasp it. Nevertheless, it is a valuable tool for scientists seeking to understand the entire rock failure process.

This paper mainly adopts the second idea, which is relatively lacking in research, to discuss the dynamic destabilization process of rocky landslides along the road graben from the energy point of view. Firstly, taking the hard and soft interlayer structure downslope chain recession model as the research object, from the mechanical point of view of comprehensive consideration of the fissure water pressure, the lower part of the slider stable rock body support force and other complex stress boundary conditions, it is proposed to establish a three-body mechanics model; and then, using elastic mechanics method to accurately calculate the complex stress state of the downslope within the slider; secondly, based on the energy balance theory to construct the total potential energy function, it is proposed to establish its dynamic instability. The analyzing method is proposed to establish its dynamic instability. The research results can explain the disaster law of downslope chain recession mode and reveal the disaster-causing efficiency of each influencing factor.

Geomechanical modeling of chain recession of bedding slope

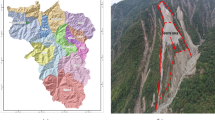
For the bedding rock cutting slopes in mountainous canyons with complex geological conditions, the free face formed by excavating the foot of the slope will greatly increase the sliding probability of the upper rock mass. Figure 1 shows the sliding traces of bedding slope sliders by the highway along river, whose potential sliders continuously slide down from bottom to top, presenting the chain recession phenomenon of bedding slope.

Fig. 1

Physical drawing of chain recession of the bedding slope by the highway along river.

The geological model is generalized from the physical map in Fig. 1, as shown in Fig. 2. The work site is located at a rock bedding slope with soft and hard interlayer structure. The chain recession phenomenon of the bedding slope generally undergoes three typical evolution stages: the early stage of free face excavation, the middle stage of fissure development, the late stage of deformation and instability:

(1) In the early stage of free face excavation. A new free surface AC is formed after the excavation of ABC rock mass, which is usually equipped with a retaining wall to prevent weathering and erosion of the slope surface;

(2) The middle stage of fissure development of the bedding slope. The excavation unloading of the lower part of the slope leads to the change of the stress state of the upper part of the rock mass, and the rock slides downward along the layer under the action of self-weight, and firstly, it forms the tensile fissure OD in the weak part of the joints or the rock, and develops into the single rock mass OACD, at this time, the higher rock mass is in a temporary stabilization state;

(3) The late stage of deformation and instability. The extension fissure, which is filled with water, is bored with water pressure acting on a single rock mass during the rainy season. The strength of the underlying soft rock is weakened by water infiltration, causing the slider to move downwards. Simultaneously, the underlying soft rock exerts an impediment to the slider’s downward movement, thereby providing an anti-shear force. A combination of factors, including fissure water pressure, the weakness of the underlying soft rock and its downward movement, results in the shear force reaching a certain threshold (shear strength). The deformation energy accumulated in the slider then exceeds the required dissipation energy, causing the rock block to suddenly collapse and slide. This results in the slope system exhibiting the phenomenon of dynamic instability.

Fig. 2

Geologic model map of slopes along the river highway²⁵.

According to the geological model shown in Fig. 2, the geomechanical model (Fig. 3) is obtained by mechanism analysis, and the rectangular coordinate system xOy is established with the end point O of the tensile fissure as the origin.

Fig. 3

Geomechanical modeling diagram Note: Fig. 3 was obtained with modifications based on literature²⁵.

The OECD in Fig. 3 is a slider, and the EAC is regarded as a retaining body, which plays a supporting role for the slider OECD, taking the intersection point C of the project slope and the environmental slope as a demarcation point, and forming a virtual interface CE by making a plumb line towards the layer level OA, which in turn divides the rock block OACD into two parts, i.e., the upper slider OECD and the lower retaining body EAC, with an interaction force P. The x-axial length of the extended x-axial length of the slider OECD is L and y-axis height is H. It is also subjected to self-weight G, fissure water pressure U, support force N of the underlying soft rock and shear force Q. The layer thickness of the underlying soft rock is h, and the inclination angle of the rock layer is α with respect to the slope inclination.

Load calculation and mechanical equations

The following assumptions are made according to Fig. 3:

(1) The rock mass above the tension fissure is stable that ensure no extrusion on the slider, and the fissure water pressure acts on the slider with a linear distribution;

(2) The slider has compression deformation along the sliding direction, and the compression deformation perpendicular to the sliding direction is not considered;

(3) The contact shear stress and positive stress between layers of soft and hard interbedded rock mass are uniformly distributed;

(4) The retaining body and slider formed by the cutting slope are both elastic uniform media, and the retaining body can be equated to a spring structure.

Although the aforementioned assumptions serve to simplify the slope system, it is important to note that there are deviations from the actual situation. The theoretical model’s output is intended to serve as a reference point, capable of depicting certain laws. For instance, the primary assumption is only capable of representing a stable state that exerts no influence on the slider. The secondary assumption is based on experience and neglects the secondary compression deformation along the y-axis. The third assumption is widely used in rock mass engineering for simplification. The fourth assumption regards the rock mass as an elastic uniform medium, which facilitates the calculation of the elastic energy. The spring structure is a novel concept for supporting the slider.

Figure 4a shows the system forces, labeled with the interaction forces between the structures; Fig. 4b shows the underlying soft rock isolation body, the level OE is subjected to normal load σ_y and tangential load τ₀ applied by the upper slider, which generates the corresponding internal resisting forces (support N and shear Q), and produces the shear deformation under the shear stress τ₀, with the direction of the displacement u along the x-axis in the positive direction; Fig. 4c shows the slider isolation body, self-weight is G, along the x-axis component is G_x, along the y-axis component is G_y, the tensile fissure OD is subjected to the normal linear distribution of fissure water pressure U, the level OE is subjected to the reaction force of the underlying soft rock (normal uniform positive stress σ_y and tangential uniform shear stress τ₀), and the lower part of it is subjected to the spring force P, and the displacement of the slider along the x-axis is marked as u₁; Fig. 4d is the retaining body, which is subjected to the spring reaction force P, and its displacement along the x-axis is marked as u₂.

Fig. 4

Mechanical model of the system and the associated parts.

Load calculation

The loads in Fig. 4 can be expressed in the following form:

$$U=\frac{1}{2}{\gamma _w}{H^2} \cdot \cos \alpha$$

(1)

$${G_x}=Mg \cdot \sin \alpha$$

(2)

$${G_y}=Mg \cdot \cos \alpha$$

(3)

$$P={k_2}{u_2}$$

(4)

where γ_w is the fissure water capacity (kN/m³); α is the rock inclination angle (°); M is the mass of the slide (kg); g is the acceleration of gravity (m/s²); and k₂ is the spring stiffness coefficient (kN/m). The rest of the symbols are the same as before.

Constitutive equation of underlying soft rock

The soft rock in Fig. 4b is subjected to the pressure σ_y along the y-axis by the upper slider, and according to Weibull’s assumption¹⁵, the shear force provided by the soft rock satisfies the following relationship with the displacement of the top of the soft rock layer:

$$Q\left( u \right)=\frac{{{G_0}L}}{h}u\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]=\lambda u\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]$$

(5)

$$Q'\left( u \right)=\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\lambda \exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]$$

(6)

$${\left( {\frac{1}{m}} \right)^{\frac{1}{m}}}{u_0}={u_c}$$

(7)

Where Q(u) is the shear resistance of underlying soft rock (kN); Q’(u) is the tangent slope of the constitutive curve of the underlying soft rock (kN/m); G₀ is the initial shear modulus (kN/m) of underlying soft rock; m is the curve family index; λ is the initial shear stiffness of underlying soft rock (kN/m); L is the length of underlying soft rock (m); h is the thickness of underlying soft rock (m); u_c is the peak displacement (m) of the shear constitutive curve of the underlying soft rock; u₀ is the conversion displacement (m) of the peak displacement u_c. The physical meaning of the parameters of the constitutive curve of the underlying soft rock is described in detail in Reference²⁵.

Block spring model

With the sliding deformation of the underlying soft rock, the slider exerts a thrust force on the block, which produces an elastic deformation that can be simplified to a spring model with a spring force of P. The elastic deformation of the block can be simplified to a spring model with a spring force of P:

$$P=qH$$

(8)

Where q is the uniformly distributed load acting along the height of the slider (kN/m); H is the average height of the slider (m).

Slider dramatic slump analysis

According to the theory of elastic mechanics, the stress field of the chain regression model of bedding rock cutting slope is solved (Sect. Slider stress field analysis), which is substituted into the corresponding energy integral expression (Sect. Subsystem energy solution). According to the principle of energy balance, the energy transfer and dissipation law of the system and the dynamic elastic impact and sliding mechanism of the active landslide are analyzed (Sect. System energy accumulation, transformation and release mechanism).

Slider stress field analysis

In Fig. 4c, since the slider is only acted by the self-weight component G_y along the y-axis direction, and σ_y is mainly caused by the self-weight component G_y and has no change along the direction, according to the semi-inverse solution method, it can be assumed that the stress component σ_y is unchanged along the direction and has the following functional form:

$$\sigma_{y}=f(y)$$

(9)

It is easy to find the form of the stress function φ:

$$\Phi =\frac{1}{2}{x^2}f\left( y \right)+x{f_1}\left( y \right)+{f_2}\left( y \right)$$

(10)

where f(y), f₁(y) and f₂(y) are functions to be determined with respect to y, and x and y are the coordinates of the position of the stress field in the Cartesian coordinate system.

According to the compatibility equation, the relationship between the stress and the stress function gives the stress field components as:

$$\left. {\begin{array}{*{20}{c}} {{\sigma _x}=\frac{{{x^2}}}{2}\left( {6{\lambda _1}y+2{\lambda _2}} \right)+x\left( {6{\lambda _5}y+2{\lambda _6}} \right) - 2{\lambda _1}{y^3} - 2{\lambda _2}{y^2}+6{\lambda _8}y+2{\lambda _9}} \\ {{\sigma _y}={\lambda _1}{y^3}+{\lambda _2}{y^2}+{\lambda _3}y+{\lambda _4}} \\ {{\tau _{xy}}= - x\left( {3{\lambda _1}{y^2}+2{\lambda _2}y+{\lambda _3}} \right) - 3\left( {{\lambda _5}{y^2}+2{\lambda _6}y+{\lambda _7}} \right)} \end{array}} \right\}$$

(11)

Where λ₁ to λ₉ are the undetermined coefficients.

The main boundaries are satisfied:

${\left( {{\sigma _y}} \right)_{y=0}}=\frac{{{G_y}}}{L}$, ${\left( {{\tau _{xy}}} \right)_{y=0}}={\tau _0}$, ${\left( {{\sigma _y}} \right)_{y=H}}=0$, ${\left( {{\tau _{xy}}} \right)_{y=H}}=0$

Secondary boundaries are met:

${\left( {{\sigma _x}} \right)_{x=0}}=\frac{1}{2}{\gamma _w}H\cos \left( \alpha \right)\left( {H - y} \right)$, $\int {\begin{array}{*{20}{c}} H \\ 0 \end{array}} {\left( {{\tau _{xy}}} \right)_{x=0}}dy=0$

$\int {\begin{array}{*{20}{c}} H \\ 0 \end{array}} {\left( {{\sigma _x}} \right)_{x=L}}dy=P$, $\int {\begin{array}{*{20}{c}} H \\ 0 \end{array}} {\left( {{\sigma _x}} \right)_{x=L}}ydy=0$, $\int {\begin{array}{*{20}{c}} H \\ 0 \end{array}} {\left( {{\tau _{xy}}} \right)_{x=L}}dy=0$

The coefficients to be determined from λ₁ to λ₉ can be obtained by substituting Eq. (11) into the above boundary conditions, and then the above coefficients can be obtained by substituting Eq:

$$\left. {\begin{array}{*{20}{c}} {{\sigma _x}=x\left( { - \frac{6}{{{H^2}}}y+\frac{4}{{3H}}} \right){\tau _0} - \frac{1}{2}{\gamma _w}H\cos \left( \alpha \right) \cdot y+\frac{1}{2}{\gamma _w}{H^2}\cos \left( \alpha \right)} \\ {{\sigma _y}=\frac{{{G_y}}}{L}} \\ {{\tau _{xy}}=\frac{{3{\tau _0}}}{{{H^2}}}{y^2} - \frac{{4{\tau _0}}}{H}y+{\tau _0}} \end{array}} \right\}$$

(12)

The derived stress field Eq. (12) contains positive and shear stresses along the axial direction, which is a complex stress state. It can be seen that the elastic potential energy accumulated in the deformation process of the slider includes compressive deformation energy and shear deformation energy.

Subsystem energy solution

(1)Slider shear deformation energy:

$$U_{1}^{s}=\int_{V}^{{}} {} \frac{{\tau _{{xy}}^{2}}}{{2G}}dV=\frac{{{Q^2}H}}{{15GL}}$$

(13)

$$\delta U_{1}^{s}=\frac{{2HQ}}{{15GL}} \cdot Q'\delta u$$

(14)

(2)Slider compression deformation energy

$$U_{1}^{c}=\int_{V} {\frac{{\sigma _{x}^{2}}}{{2E}}dV} =\frac{1}{{2E}}\left[ {\frac{{44L}}{{27H}}{Q^2}+\left( {\frac{2}{3} - \frac{5}{6}{{\cos }^2}\left( \alpha \right)} \right){\gamma _w}L{H^2}Q+\frac{1}{{12}}\gamma _{w}^{2}{H^5}L \cdot \cos \left( \alpha \right)} \right]$$

(15)

$$\delta U_{1}^{c}=\frac{1}{{2E}}\left[ {\frac{{88LQ}}{{27H}} \cdot Q'+\left( {\frac{2}{3} - \frac{5}{6}{{\cos }^2}\left( \alpha \right)} \right){\gamma _w}L{H^2}Q'} \right]\delta u$$

(16)

(3)Compressive deformation energy of the baffle body

$$\delta U_{2}^{c}=P \cdot \delta {u_2}=P \cdot \delta \frac{P}{{{k_2}}}=\frac{P}{{{k_2}}}\delta P$$

(17)

System energy accumulation, transformation and release mechanism

(1)Equivalent elastomer generalized sliding forces and relative values.

The retaining body and slider are two elastomers that are connected in series to synergistically accumulate deformation energy and provide shear dissipation of the underlying soft rock through deformation energy release. When there is a small displacement increment δu of the underlying soft rock, the energy change δU^e of the equivalent elastomer is the sum of Eqs. (14), (16) and (17):

$$\delta {U^e}=\delta U_{1}^{s}+\delta U_{1}^{c}+\delta U_{2}^{c}=\frac{{2HQ}}{{15GL}}Q'\delta u+\frac{1}{{2E}}\left[ {\frac{{88LQ}}{{27H}}Q'+\left( {\frac{2}{3} - \frac{5}{6}{{\cos }^2}\left( \alpha \right)} \right){\gamma _w}L{H^2}Q'} \right]\delta u+\frac{P}{{{k_2}}}\delta P$$

(18)

The derivation of Eq. (18) with respect to δu at both ends yields:

$$\frac{{\delta {U^e}}}{{\delta u}}=\frac{{2HQ}}{{15GL}}Q'+\frac{1}{{2E}}\left[ {\frac{{88LQ}}{{27H}}Q'+\left( {\frac{2}{3} - \frac{5}{6}{{\cos }^2}\left( \alpha \right)} \right){\gamma _w}L{H^2}Q'} \right]+\frac{P}{{{k_2}}}\frac{{\delta P}}{{\delta u}}$$

(19)

For Fig. 3, the static force balance equation in the x-direction yields:

$$P=U+{G_x} - Q$$

(20)

Considering U and G_x in Eq. (20) as constant values, there exists a negative linear relationship between P and Q whose increment satisfies:

$$\delta P= - \delta Q$$

(21)

Substituting Eqs. (5), (6), and (21) into Eq. (19) and organizing it gives:

$$\frac{{\delta {U^e}}}{{\delta u}}={\beta _1}{\lambda ^2}u\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\exp \left[ { - 2{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]+{\beta _2}\lambda \left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]$$

(22)

$${\beta _1}=\frac{{2H}}{{15GL}}+\frac{{44L}}{{27EH}}+\frac{1}{{{k_2}}}$$

(23)

$${\beta _2}=\frac{1}{{2E}}\left( {\frac{2}{3} - \frac{5}{6}{{\cos }^2}\left( \alpha \right)} \right){\gamma _w}L{H^2} - \frac{{U+{G_x}}}{{{k_2}}}$$

(24)

In Eq. (23), β₁ has a flexibility dimension (unit: m/kN), and the three items indicate the shear flexibility of the slider, the compression flexibility of the slider and the compression flexibility of the retaining body, which physically belongs to the generalized mechanical parameter, and we can define it as the “generalized flexibility” of the equivalent elastic body accordingly. In Eq. (24), β₂ has a displacement scale (unit: m), which contains the information of the elastic modulus of the slider E and the compressive stiffness of the retaining body k₂, which also belongs to the generalized mechanical parameter physically, and we can define it as the “generalized displacement” accordingly.

Equation (22) represents the energy release rate of the equivalent elastomer, and from the energy point of view, the physical nature is to drive the shear deformation of the underlying soft rock through the release of deformation energy of the equivalent elastomer, which has the same effect as the sliding force acting on the underlying soft rock. In addition, the left side of Eq. (22) indicates that the elastic deformation energy of the equivalent elastomer is derived from the displacement, and the concept of force is obtained; the right side of Eq. (22) is a function of the generalized flexibility β₁, generalized displacement β₂, the initial shear stiffness λ of the lying soft rock, the curvilinear homologous exponent m, the converted displacement u₀, and the relative displacement (u/u₀), and the relative displacement (u/u₀) of the soft rock is constant, and thus is the same as the downward force acting on the soft rock. For a certain geological system, except for the displacement u of the top of the underlying soft rock layer, which is a variable, the rest is a constant value, and thus is a function determined by the displacement u. Therefore, the left and right sides of Eq. (22) establish the functional relationship between force and displacement, forming the physical equations of the equivalent elastomer. For convenience of description, the force on the left side of Eq. (22) can be $(\delta {U^e}/\delta u)$named “generalized sliding force”.

Mathematically normalizing Eq. (22) by dividing both sides identically by λu₀, collapses to:

$$\frac{{\delta \mathop {{U^e}}\limits^{\_} }}{{\delta \mathop u\limits^{\_} }}=\frac{{\delta {U^e}}}{{\lambda {u_0}\delta u}}={\beta _1}\lambda \left( {\frac{u}{{{u_0}}}} \right)\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\exp \left[ { - 2{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]+\frac{{{\beta _2}}}{{{u_0}}}\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]$$

(25)

Equation (25) in which λu₀ is the product of the initial shear stiffness of the underlying soft rock and the converted displacement, has the magnitude of force and belongs to the shear force corresponding to the converted displacement of the underlying soft rock. And$(\delta {U^e}/\delta u)$ also has the magnitude of force, $(\delta {U^e}/(\lambda {u_0}\delta u))$it is the relative ratio of force to force, whose magnitude is 1, indicating the ratio of the equivalent elastomer generalized downward force to the shear force corresponding to the converted displacement of the underlying soft rock. For the convenience of description, it can be named as “relative value of generalized sliding force”.

• (2) Generalized shear resistance of underlying soft rock and relative values.

A small displacement δu occurs at the top of the under-lying soft rock, the energy to be expended by the underlying soft rock is:

$$\delta {U^P}=Q\left( u \right) \cdot \delta u$$

(26)

Substituting Eq. (5) into Eq. (26), the transformation gives the energy dissipation rate of the underlying soft rock as:

$$\frac{{\delta {U^P}}}{{\delta u}}=Q\left( u \right)=\lambda u\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]$$

(27)

Equation (27) represents the energy dissipation rate of the underlying soft rock, $\delta {U^p}$which is the energy that needs to be absorbed and dissipated for the deformation of the underlying soft rock to take place, i.e., the energy needed to be used to resist the deformation, and the effect is consistent with the shear resistance. In addition, the left side of Eq. (27) represents the derivation of the dissipated energy of shear deformation of the underlying soft rock on the displacement, which is obtained from the concept of force; the right side of Eq. (27) is a function on the initial shear stiffness λ of the underlying soft rock, the curvilinear homologous exponent m, the displacement u, and relative displacement (u/u₀), which is likewise a function decided by the displacement u. Therefore, the left and right sides of Eq. (27) establish the functional relationship between force and displacement, forming the physical equations of the underlying soft rock. For convenience of description, the force on the left side $(\delta {U^p}/\delta u)$ of Eq. (27) can be named “generalized anti-shear force”.

Mathematically normalizing Eq. (27) by dividing both sides identically by λu₀, we have:

$$\frac{{\delta \mathop {{U^P}}\limits^{\_} }}{{\delta \mathop u\limits^{\_} }}=\frac{{\delta {U^P}}}{{\lambda {u_0}\delta u}}=\left( {\frac{u}{{{u_0}}}} \right)\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]$$

(28)

The physical meaning of Eq. (28) is the same as that of Eq. (25), which indicates the ratio of the generalized shear resistance of the underlying soft rock to the shear resistance corresponding to the converted displacement of the underlying soft rock. In order to facilitate the description, it can be named as “relative value of generalized anti-shear force”.

• Balance equation for the incremental total potential energy function of the system.

According to the functional equilibrium relationship of the system there is

$$\delta {U^e}+\delta {U^P} - \delta W=0$$

(29)

Where, δU^e is the sum of three items: shear deformation energy of the slider, compression deformation energy of the slider and compression deformation energy of the retaining body; δU^p is the energy dissipation rate of the underlying soft rock; δW is the work done by the external force.

Literature¹⁷ points out that even if there is no external work δW, the system relies on its own energy accumulation and transfer, and the slope system can also undergo dramatic landslide damage. Therefore, let δW = 0 in Eq. (29), and divide λu₀δu on both sides of the equation:

$$\frac{{\delta {U^e}}}{{\lambda {u_0}\delta u}}+\frac{{\delta {U^P}}}{{\lambda {u_0}\delta u}}=0$$

(30)

Substituting Eq. (25) and Eq. (28) into Eq. (30) yields:

$$\frac{{\delta \mathop {{U^e}}\limits^{\_} }}{{\delta \mathop u\limits^{\_} }}+\frac{{\delta \mathop {{U^P}}\limits^{\_} }}{{\delta \mathop u\limits^{\_} }}={\beta _1}\lambda \left( {\frac{u}{{{u_0}}}} \right)\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\exp \left[ { - 2{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]+\frac{{{\beta _2}}}{{{u_0}}}\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]+\left( {\frac{u}{{{u_0}}}} \right)\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]=0$$

(31)

Equation (31) represents the limit equilibrium state of the generalized sliding force and generalized shear force obtained based on the energy incremental equilibrium equation, and the two generalized forces are equal and opposite, which are implicit equations about the relative displacements u/u₀, and they can characterize the features and interrelationships of the equivalent elastomer’s before sliding energy aggregation and deformation energy release curves (hereinafter referred to as the aggregation and energy release curves) and the energy dissipation curve of the underlying soft rock. When the deformation u of the underlying soft rock reaches the termination point u_s of the power slide point, the power slide of the underlying soft rock or the equivalent elastomer drastically slides, and the system breaks through the quasi-static state and destabilizes.

(4)Parameters of slider popping impulse power.

From the literature¹⁷, the slider elastic impulse dynamic parameters are shown in Eqs. (32) to (35). Where, the area of the shaded area enclosed by the energy release curve and the energy dissipation curve of the underlying soft rock is multiplied by ΔS with λu₀, which is the part of the elastomer release exceeding the dissipation of the underlying soft rock slide, i.e.

$$\Delta E=\lambda u_{0}^{2}\Delta S$$

(32)

The excess energy ΔE will be converted into kinetic energy T (unit: N·m), i.e.

$$T= - \Delta E= - \lambda u_{0}^{2}\Delta S$$

(33)

By the kinematics easy to know, the slider popping punch dramatization speed V_s (unit: m/s)

$${V_s}=\sqrt {\frac{{2T}}{M}}$$

(34)

Average bouncing acceleration of the slider a_s (unit: m/s²):

$${a_s}=\frac{T}{{M\left( {{u_s} - {u_j}} \right)}}$$

(35)

The above symbols have the same meaning as before.

Case study

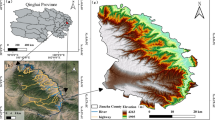
At about 8:00 a.m. on November 28, 2019, the impact of rainfall led to a mountain collapse of about 1,000 m³ at Jiaojiatan on National Highway 319 (K2 + 945) in Pengshui County, Chongqing Municipality, damaging and burying the roadbed pavement, which completely interrupted the road, and all the passing vehicles were bypassed, and the relevant departments made every effort to search and rescue and clear the obstacles to carry out emergency repair on the damaged roadway (Fig. 5).

Fig. 5

Aerial photo of the bedding slope landslide by the highway along river in Jiaojiatan, Pengshui County.

After field investigation, this landslide is a smooth rocky landslide under the condition of long drought and rain after the artificial excavation of the slope along the river highway, and the slope body is sandstone mudstone interlayer structure. The length of the slope is about L = 30 m, the height is about H = 5.4 m, the capacity of sandstone is γ = 25kN/m³, the weight of single width slope is Mg = 3.75 × 10³kN, the thickness of the underlying soft rock mudstone is h = 0.1 m, and the u_c =0.6 × 10⁻³m; the modulus of elasticity of the sandstone is E = 6.07GPa, Poisson’s ratio is µ = 0.25, and the shear modulus is G = 2.43GPa, considering the role of the blocking body P, the crack water pressure U, and the compression deformation of the slide block. The pressure U and slide compression deformation energy C and other three factors, using the theoretical model calculation in Sect. 3, set up eight working conditions to examine the influence characteristics of each factor respectively.

Analysis of the total potential energy function curve of the system

Based on the energy balance principle, the change law of the energy accumulation and the energy release could be discussed quantitatively and it’s convenient to analyze the contributions of different factors to energy changes.Therefore, according to the case data and Eq. (31), the MATLAB R2023a software is utilized to plot $\frac{{\delta {U^e}}}{{\lambda {u_0}\delta u}}\sim k$ and $\frac{{\delta {U^P}}}{{\lambda {u_0}\delta u}}\sim k$ curves. k is the relative displacement, which represents the ratio of the under-lying soft rock displacement u to the conversion displacement u₀. The relative value of the generalized sliding force corresponds to the energy accumulation stage of the equivalent elastomer before sliding and the deformation energy release stage, while the equivalent elastomer slide onset point k_j is the control point for the conversion of the above two stages. The relative value of the generalized shear force corresponds to the state of the energy dissipation of the under-lying soft rock.

The relative value of the generalized sliding force, the relative value of the generalized shear force and the relative displacement k are the values with a scale of 1, and thus the unit of the horizontal and vertical axes is “1”, as shown in Fig. 6. Among them, (P, U, C) indicates that three factors such as the action of the retaining body P, the fissure water pressure U and the compression deformation energy of the slide C are considered at the same time; when an influence factor is not taken into account, it is indicated by “0”, for example, Case II (0, U, C) indicates that the action of the retaining body is not taken into account, and the fissure water pressure and the compression deformation energy of the slider are only taken into account, and the rest is the same as that of the other factors. The rest is the same.

For the equivalent elastomer, there are two stages of energy accumulation and energy release. When the relative displacement k ≤ 1 (underlying soft rock displacement u ≤ u₀), the elastomer is in the stage of energy accumulation, which is located in the positive half-axis of the vertical axis in Fig. 6. When the relative displacement k>1 (underlying soft rock displacement u>u₀), the elastomer is in the energy release stage, which is located in the negative half-axis of the longitudinal axis in Fig. 6.

For the underlying soft rock, the shear force and displacement do negative work in the opposite direction, which belongs to the energy dissipation of the system and is located on the negative half-axis of the vertical axis in Fig. 6. When k > 1, the deformation energy released by the equivalent elastic body is used to provide the deformation dissipation of the underlying soft rock. The area ΔS enclosed represents the excess deformation energy after supplying the deformation dissipation energy. The intersection points k_j and k_s of the deformation energy release curve of the equivalent elastic body and the energy dissipation curve of the underlying soft rock are respectively the starting point and the end point of the dynamic rupture of the system. When the relative displacement k reaches the end point k_s, the ΔS deformation energy is instantaneously released and converted into the elastic impact kinetic energy of the system.

Fig. 6

The relation between the energy accumulation curve, energy release curve and energy dissipation curve.

1) Comparing Case I and Case II, the peak value of aggregated energy decreases by about 5 units and the stroke at the slide termination point decreases by about 0.39 units when the action of the blocking body P is not taken into account, which indicates that the blocking body blocks the deformation and damage of the slider and at the same time makes the deformation energy inside the slider to be accumulated more, i.e., it blocks the deformation and increases the deformation energy.

2) Comparing Case I and Case III, when the fissure water pressure U is not considered, the peak value of aggregated energy remains unchanged, but the stroke of slide termination point increases by about 0.81 units, which indicates that the contribution of fissure water pressure U to the deformation energy accumulated inside the slider is relatively small, but it reduces the critical relative displacement and accelerates the system destabilization process, and the system may be destabilized earlier under the same energy, which is the role of fissure water triggering.

3) Comparing Case I and Case IV, when the slider compression deformation energy C is not considered, the peak value of the aggregation energy is significantly reduced by about 31.2 units, and the stroke of slide termination point is reduced by about 1.59 units, because the less aggregation energy is the less release energy, and the equivalent elastomer release curve intersects with the energy dissipation curve of the underlying soft rock within the range of the smaller relative displacement, which makes the stroke of slide termination earlier, indicating that the contribution of the slider compression deformation energy C to the slider. This indicates that the contribution of deformation energy C of slide compression to deformation energy C of slide accumulation is very significant.

4) The energy accumulation and release curves and the energy dissipation curve of the underlying soft rock show the relative relationship between the energy accumulation, release and consumption of the system, and the two curves are characterized by no intersection and double intersection. The no-intersection point (Case VI and Case VIII) indicates that the deformation energy released by the equivalent elastomer is not enough to provide the consumption of further deformation of the lying soft rock, and the system only has creep phenomenon, corresponding to the creeping slide collapse type; the double-intersection point indicates that the deformation energy released by the slider not only provides the consumption of the further deformation of the lying soft rock, but also has excess deformation energy, and with the development of displacement of the lying soft rock to the termination point of the dynamic slide, the release curve and the energy consumption curve tend to coincide, indicating that the system is in the same state tending to coincide, that the system deformation energy instantaneous release, into kinetic energy and other forms, corresponding to the sudden change of the instability of the drastic type of slide collapse.

5) Case V, Case VI, Case VII and Case VIII are the dynamic instability characteristics of the system when only considering the action of the retaining body P, or the fissure water pressure U, or the deformation energy of slide compression C, or neither of them, and the system does not undergo dramatic slide collapse when only considering the fissure water pressure U (Case VI) or disregarding all the external factors (Case VIII); and the contribution values of the accumulated deformation energy are ranked in order from the largest to the smallest, which are, in order, as follows Slip compression deformation energy C, retaining body action P and fissure water pressure U.

Dynamic parameter analysis

Extracting the deformation energy release ΔS in Fig. 6 and combining with Eqs. (32) to (35), the energy curve T, the start-up velocity V_s and the start-up acceleration as during the sudden catastrophe damage of the slider can be plotted by Origin 2018 64Bit to show the trend of the changes in different modeled working conditions (Fig. 7). Since the working conditions VI and VIII do not have sudden catastrophe phenomenon, there is no power start-slip parameter, and thus there is no corresponding working condition data.

Fig. 7

The curve of logarithmic variation of each dynamic parameter under different working conditions.

Figure 7 shows the change rule of logarithmic value of each power parameter under different working conditions with the various force working conditions in the downslope chain recession model when the slope system is suddenly destabilized, and it can be seen that: (1) the trend of the three power parameter curves remains consistent, indicating that the larger the released energy, the larger the slider start velocity and acceleration; (2) according to working condition I and VII, it is calculated that the start velocity of the slider ranges between 4.27 m/s and 2.40 m/s, indicating that the dramatically moving landslide has a larger start velocity, which is basically in line with the actual situations, indicating that the dramatically moving slide has a large start-up speed, which is basically consistent with the actual situation.

Numerical simulation validation

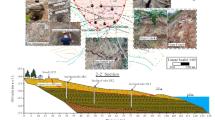
The FLAC^3D 6.0 software is used to establish the geological model of soft and hard interlayer bedding cutting slope to simulate the sliding process and the change law of shear stress during slide. Firstly, the solid model is established by the Rhinoceros 6.0 software, and the Griddle V2.0 plug-in (https://www.itascacg.com/software/Griddle) is used to mesh the solid model. The minimum grid length is 0.1 m, the maximum is 2.5 m, and the final grid file is formed and imported into the FLAC^3D 6.0 software, which generates a total of 8480 zone cells, and its computational model is shown in Fig. 8. Its physic-mechanical parameters and geometric parameters are the same as the case values in Sect. 4. Cyclic calculations are performed on the model, and the stress and displacement monitoring points are set at any point of the interface between the soft and hard rock layers.

Fig. 8

The finite difference numerical model of the soft and hard interlayered bedding cutting slope.

The measurement point in Fig. 8 is located at y = 0 in the local coordinate system, and the layer shear stress is equal to τ₀ by the 3rd sub-equation of Eq. (12). The theoretical value of the shear stress is also calculated according to Eq. (5) and the theoretical value of the shear stress is compared with the numerical simulation value, and the result is shown in Fig. 9.

Fig. 9

Comparison of theoretical and numerical simulation values of shear stress-displacement curves at monitoring points (Fig. 9a ~ Fig. 9d represents the changing process of the shear stress in different status, and Fig. 9e ~ Fig. 9h represents the changing process of the displacement in different status).

As can be seen from Fig. 9, the shear stress initially occurs in the interface between the block body and the soft rock and in the upper crack because of the cutting of the slope. The shear stress expands between the block body and the soft rock from Fig. 9b and d because of the increasing of the bedding cutting slope displacement. The displacement increases fast on the surface of the cutting slope because of the excavation unloading effect in the beginning and the displacement in the surface and lower part of the slope is larger than that in the upper part of the slope. However, the displacement will tend to the same value from the upper part of the slope to the lower part and finally collapse in a whole.

It can also been found that the soft and hard interface shear stress increases first and then decreases, and the peak shear stress is obtained when the slider displacement arrives at around 1.5 mm; when the slider displacement exceeds the threshold value of 1.5 mm, the slider displacement increases rapidly, and the sliding occurs finally, which leads to the shear stress falling. In a word, the theoretical value of the shear stress at the interface coincides well with the results of numerical simulation values.

With the slider downward movement, the underlying soft rock provides the anti-shear force in the process of deformation, and the anti-shear force does negative work on the slider, which belongs to the system dissipation energy. In the process of dissipation, the strength of the underlying soft rock is damaged, and the plastic zone develops and expands in the weak layer. The evolution process of slope sliding deformation and the change process of plastic zone are shown in Fig. 9a ~ 9 d, which correspond to the four status in Fig. 9, respectively. As can be seen from Fig. 9a which shows that the plastic zone first appears in the soft rock side and the foot of the slope in contact with the retaining body, and with the increase of the displacement of the slider, the plastic zone gradually expands below the retaining body (Fig. 9b and c), which indicates that the slider pushes out the retaining body and induces the retaining body to slip downward. When the pushing force exerted by the slider on the retaining body exceeded the bearing limit of the retaining body, the retaining body could not continue to provide support, and the deformation value of the underlying soft rock reaches the threshold value, which could not continue to consume the elastic deformation energy of the slider, the slider and the retaining body jointly appears to be damaged by slippage, and there is a large gap above the slider, and the plastic zone at the junction of the hard and soft layers is dominated by the shear state, and it is completely penetrated into the foot of the slope (Fig. 9d).

Figure 9 exhibits the plastic zone expansion, slide deformation and damage process of the soft and hard interlayer bedding cutting slope through numerical simulation, which is consistent with the evolution characteristics of the downslope chain recession geomechanical model proposed in this paper, indicating that the theoretical method of the mechanical model has a certain degree of reliability.

Discussion

(1) From Eqs. (23) to (24) and Fig. 6, it can be seen that the generalized flexibility β₁ and generalized displacement β₂ are functions about the internal factors (geometric dimensions, physico-mechanical indexes) and external environments (the action of the retaining body P, the fissure water pressure U, and the compression deformation energy of the slider C), which together determine the trend and value of the aggregation and energy release curves.

(2) When considering the slip resistance of the retaining body, the compression deformation energy of the slider is also increased. Once the system is destabilized by a sudden change, a larger kinetic energy will be released. However, whether to consider the slip-resisting effect of the retaining body needs to be evaluated according to the actual construction situation and the quality of the rock mass. If the retaining wall is applied in time after construction to effectively protect the rock bedding cutting slope and prevent the development of unloading fissure, the slip-resisting effect of the retaining body can be considered at this time, and the three-body mechanics model can be used for the analysis; if the retaining wall is not applied or used into a temporary slope after construction, the retaining body is subjected to the unloading effect and physical and chemical weathering processes, and the quality of the rock body is poor, so the slip-resisting effect of the retaining body will not be taken into account.

(3) Case VI is similar to Case VIII, which further shows that the fissure water pressure U contributes less to the deformation energy, and the retaining body effect P and the slide compression deformation energy C are the main parts of the accumulated deformation energy. In fact, when the slope inclination angle α is steeper, the fissure water pressure U is smaller, and under the condition of small deformation of the slide, the positive work done is relatively small. However, it does not mean that the effect of fissure water is small, because the fissure extension provides a channel for rainfall or groundwater infiltration into the underlying soft rock, and the hydrotropic weakening effect of fissure water on the underlying soft rock is the main reason for the stress drop of the underlying soft rock principal curve. Therefore, the fissure water has hydrostatic pressure and hydrotropic weakening effect, although some geometric boundary conditions have small hydrostatic pressure, but the contribution of its hydrotropic weakening cannot be ignored.

Conclusion

Highways along the river in mountainous areas are often faced with landslide geological hazards, and the destructive force of the down-stream dramatic landslides induced by manually excavated highway slopes is large, which may occur during construction or operation, and there is a large safety hazard. Therefore, theoretically analyzing the genesis mechanism and destabilization process of this type of landslides can contribute to reasonably deploying and scientifically mitigating the disaster. The main conclusions are as follows:

(1) The phenomenon of downslope chain recession is commonly found in bedding slopes that form a critical surface after excavation of highway, and the geological pattern of downslope chain recession is divided into three typical evolution stages, namely, the early stage of free face excavation, the middle stage of fissure development, the late stage of deformation and instability.

(2) The soft rock constitutive equation was introduced into the downslope chain recession geomechanical model. According to the elastic mechanics method, the generalized sliding force function of the equivalent elastic body, the relative generalized sliding force value function, the generalized anti-shear function and the relative generalized anti-shear value function of the underlying soft rock were obtained. Based on this, the incremental equilibrium equation of the total potential energy function of the system can be established.

(3) According to the incremental equilibrium equation of the total potential energy function established by the principle of energy conservation, the equivalent elastomer energy aggregation and release curve and the energy dissipation curve of the underlying soft rock can be obtained, which can be used for the analysis of the dynamic instability of downward slopes. The aggregation curve characterizes that the equivalent elastomer is in the elastic deformation stage, and continuously accumulates deformation energy; the release curve characterizes that the elastic energy released by the equivalent elastomer in the quasi-static stage is continuously transferred to the underlying soft rock; the energy dissipation curve characterizes that the soft underlying layer needs to consume energy due to the shear deformation in the elastic stage and the quasi-static stage, and when it is in the quasi-static stage, it continuously absorbs the deformation release energy from the equivalent elastomer, which will further occur the shear damage.

(4) According to the case study, it is concluded from the energy point of view that the compression deformation energy of the slider has a non-negligible contribution to the energy accumulation of the slope system, the role of the retaining body has the effect of blocking deformation and increasing deformation energy, the fissure water has both physical and chemical effects, and the fissure water pressure has a relatively small contribution to the accumulation of deformation energy in the slider, but it may lead to the system destabilization in advance; for the contribution to the accumulation of deformation energy, the contribution values were ranked according to the order from the largest to the smallest. For the contribution of accumulated deformation energy, in order of magnitude, they are sliding compression deformation energy, retaining body action and fissure water pressure; the energy accumulation and release curves and the energy dissipation curves of the underlying soft rock have two types of intersections: no intersection corresponds to the type of creeping sliding collapse, and the double intersection corresponds to the type of drastic sliding collapse. Using numerical simulation method, from the slide instability evolution process and soft and hard rock contact surface shear stress change rule, further verified that the geomechanical model proposed in this paper and its deformation damage process has rationality.

Deficiencies and prospects

• (1) This research was conducted by theoretical and numerical analyses. More indoor tests and field tests should be applied to certify the generalizability and reliability in the future.

• (2) Creep landslide generally undergoes a large deformation process before destruction, and this type of destruction mode belongs to the research scope of long-term stability analysis and prediction of slopes, which will be further discussed.