Introduction

In many fields, including physics, engineering, biology, and finance, nonlinear evolution equations (NLEEs) are essential tools for simulating complex systems1,2,3,4. Due to its ability to reveal the fundamental principles driving nonlinear occurrences, the analytical determination of their precise solutions continues to be an important and developing field of study.

Solitons have attracted significant attention due to the role of nonlinear wave phenomena in fields such as oceanography, plasma physics, and nonlinear optics5,6. These waves are distinguished by their particle-like characteristics and remarkable stability. In contrast to ordinary waves, solitons can propagate through a medium while maintaining their shape and structure. Several analytical techniques have been developed to investigate soliton solutions, including the inverse scattering transform7, Bäcklund transformations8, Darboux transformations (DTs)9, and the refined Hirota bilinear method10. Among these, the Hirota method stands out for its simplicity and directness, providing a practical tool for deriving exact solutions of NLEEs. The dynamics of soliton interactions are largely influenced by the interplay between dispersion and nonlinearity. When solitons with matched frequencies interact, they can undergo energy exchange, leading to soliton resonance, a phenomenon that generates complex patterns and underscores the nonlinear characteristics of the governing equations. In optical fiber communication, solitons are essential for long-distance data transmission with minimal distortion, often forming bound states through their interactions11,12,13.

In recent research, a variety of sophisticated analytical methods have been used to get precise solutions for NLEEs. These include the generalized Kudryashov approach14,15, the Sardar sub-equation method16,17, the Jacobi Elliptic function expansion method18, the Simple Equations approach using composite functions19, and the improved modified extended tanh-function method20,21. Additional techniques that have been successfully used to produce soliton, periodic, and rational solutions include the \(\phi ^6\)-model expansion22, modified extended direct algebraic method23, and Lie symmetry analysis24. In many different fields, these symbolic computational techniques are still essential for decomposing and resolving intricate nonlinear models. Wave propagation in optical fibers has been described by a variety of mathematical models, which have been improved upon to show intriguing phenomena fueled by the intricate interaction between nonlinearity and dispersion. These ideas have expanded the scope of study and technological innovation in a number of sectors, such as fluid dynamics, optical systems, and plasma physics25,26,27.

Recent development in the study of nonlinear evolution equations has made notable progress using symmetry-based approaches and solitonic structure analysis. Faridi et al.28 used the Lie point symmetry and Painlevé analysis to investigate exact solutions of the Kairat-II equation with an emphasis on integrability and soliton formation. In the same way, Asghar et al.29 studied the Lie algebra and Hamiltonian dynamics of a biofilm model, revealing new solitonic behavior. Tipu et al.30 further generalized these approaches to plasma dynamics, developing hyper-geometric soliton solutions to the Zhanbota-IIA equation. Faridi et al. also investigated fractional soliton structures in ion sound–Langmuir systems31, in addition to the Akbota equation, with a comparative visualization of generalized wave propagation32. Within financial mathematics, fractional soliton dynamics were used for the Ivancevic option pricing model, with wave profile behaviors and stability analysis33. Furthermore, Faridi et al.34 analyzed soliton structures in nonlinear telegraph systems with tunnel diode features using Lie symmetry analysis and chaos theory. Finally, in quantum field theory, exact invariant soliton solutions of the Landau-Ginzburg-Higgs model were constructed using the Khater method35, illustrating yet again the flexibility of analytical techniques for physical systems of diverse nature.

The modeling and analytical treatment of nonlinear evolution equations in higher dimensions, particularly those incorporating soliton dynamics and wave structures, has been greatly extended in the recent literature. Using analytical and approximative techniques pertinent to ocean engineering applications, Ntiamoah et al. examined the higher-order modified Korteweg–de Vries (KdV) equation and obtained a number of soliton and breather solutions36. Our knowledge of time-fractional wave models is expanded by Şenol et al.’s introduction of a novel conformable (3+1)-dimensional KdV equation and their analytical and numerical solutions37. In order to investigate Painlevé integrability and build multi-soliton solutions with physical significance in intricate random settings, Akpan et al. investigated stochastic extensions of the KdV equations38. Using a novel analytic framework, Kumar and Dhiman addressed the dynamics of a (4+1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili equation, presenting a variety of solitonic behaviors39. Their later work investigated multi-peakon solutions for a (3+1)-dimensional p-type equation, revealing intricate nonlinear interactions40. They also discovered lump-type, breather, and cone-shaped solutions to a linked breaking soliton system using the unified approaches and Lie symmetry41. They provide insight on wave development in oceanic contexts by deriving invariant solutions for a generalized Camassa-Holm–Kadomtsev–Petviashvili equation in shallow water wave models42. They also offered symmetry reductions and solitary wave dynamics for nonlinear wave propagation through their study of the extended Jimbo–Miwa equation43. In order to improve optical communication modeling, Niwas et al. also investigated a novel Schrödinger equation for optical fibers, building a range of soliton types using two efficient analytical techniques44.

Model of investigation

Integro-partial differential equations (IPDEs), which combine integral and differential elements, are crucial for simulating a variety of real-world occurrences where cumulative dynamics and memory effects are crucial45. These equations naturally occur in domains like population dynamics, where the growth rate may be dependent on historical population numbers, and viscoelasticity, where stress is dependent on the complete history of deformation. Integro-differential models are more accurate than solely differential equations in capturing charge buildup and current flow in electrical circuits with capacitive or inductive memory. They are also often employed to characterize systems affected by dispersed or delayed reactions in control theory, biological systems modeling, and finance. They are effective instruments for recording intricate temporal interactions in both continuous and discrete contexts because of their hybrid character.

Due to their importance, in this paper, a new structured (2+1)-dimensional nonlinear model, which is an IPDE, is investigated46,47. This equation can be written as:

$$\begin{aligned} \left( \Theta _t+6 \Theta \Theta _x+\Theta _{xxx}\right) _x+3 \Theta _{xx} \left( \int _{-\infty }^x \Theta _y \, dx\right) +6 \Theta _x \Theta _y+\Theta _{xxxy}+\delta \Theta _{xy}+3 \Theta \Theta _{xy}+\Theta _{yt}-\sigma \Theta _{yy}=0. \end{aligned}$$
(1)

where \(\Theta = \Theta (x, y, t)\) represents an analytic function to be determined, with \(\delta\) and \(\sigma\) being real constants different from zero. This equation is encountered in the problem of nonlinear wave propagation in dispersive media, where the interaction among nonlinearity, dispersion, and external driving leads to complex wave phenomena. It is especially applied to describe phenomena such as shallow water wave behavior, plasma drift waves, and wave packet evolution in nonlinear optics and fluid interfaces. Its structure allows it to address both unidirectional and bidirectional nonlinear interactions in multi-dimensional space and thus can be used to study integrable dynamics, soliton dynamics, and modulational instabilities in higher dimensions.

Novelty and motivation of the study

There is potential for this model to be used to describe how nonlinear waves evolve in oceanic environments. Numerous complex factors contribute to the generation and propagation of nonlinear waves. Among these, non-linearity and dispersion play a crucial role in defining how waves are disturbed and decay. Expanding initial models to incorporate more intricate aspects gains value as computer technology develops.

While existing approaches provide important findings, they frequently fail to produce a diverse range of solution types or handle higher-dimensional nonlinear systems in a coherent framework. Furthermore, the dynamics of singular and doubly periodic solutions in such systems are still poorly understood.

In this study, we create new soliton wave structures–bright, singular, dark (soliton), singular periodic, periodic, hyperbolic, Weierstrass elliptic doubly periodic, Jacobi Elliptic, and exponential solutions using the ME mapping approach that have never been documented before. In addition to studying the dynamical behavior of this system through the stability and bifurcation analysis.

The arrangement of the article is as follows: The suggested model and its theoretical underpinnings are summed up in Section 1. The main elements of the ME mapping technique are explained in Section 2, along with its justification and the advantages of using it with a variety of models. The mathematical justification and foundational formulas for the suggested model, with implementation of the ME mapping method, are presented in Section 3. In Section 4, the presentation of the reduction of the given model to a planar system is shown. The stability and bifurcation analysis are described in Section 5. Different dynamic wave patterns from different soliton solutions are graphically shown in Section 6 using 3-D, contour, and 2-D simulations. In Section 7, we present a collection of notes about the obtained results and their discussion to prove their novelties. The study’s findings are presented in Section 8, in addition to some future work recommendations.

Mathematical preliminaries of the proposed method

This section presents an overview of the ME mapping technique as introduced in48. We begin by considering the following nonlinear partial differential equation (NLPDE):

$$\begin{aligned} \mathfrak {H} \left( \mathcal {L},~ \mathcal {L}_t,~ \mathcal {L}_{x},~\mathcal {L}_{y},~ \mathcal {L}_{xx},~ \mathcal {L}_{yy},~\mathcal {L}_{xt}, \ldots \right) = 0. \end{aligned}$$
(2)

Suppose that the solution to the above equation is given in the following form:

$$\begin{aligned} \mathcal {L}~(x,~y,~t)=\mathcal {U}(\rho ), \qquad \qquad \qquad \rho =x+ y-\xi t. \end{aligned}$$
(3)

So, Eq. (2) can be redefined as the following nonlinear ordinary differential equation (NLODE):

$$\begin{aligned} \mathcal {Z} (\mathcal {U}, \mathcal {U}^\prime , \mathcal {U}^{\prime \prime }, \ldots ) = 0. \end{aligned}$$
(4)

Now, we can set the general solution to Eq. (4) as follows:

$$\begin{aligned} \mathcal {U}(\rho )=\sum _{i=0}^N \mathcal {A}_i \mathcal {W} ^i (\rho )+\sum _{i=-1}^{-N} \mathcal {B}_{-i} \mathcal {W} ^i(\rho )+\sum _{i=2}^N \mathcal {C}_i \mathcal {W} ^{i-2}(\rho )\mathcal {W} '(\rho )+\sum _{i=-1}^{-N} \mathcal {D}_{-i} \mathcal {W} ^i(\rho )\mathcal {W} '(\rho ), \end{aligned}$$
(5)

where \(\mathcal {W}(\rho )\) satisfies the subsequent auxiliary equation:

$$\begin{aligned} \mathcal {W}'(\rho )=\sqrt{\tau _0+\tau _1 \mathcal {W}(\rho )+\tau _2 \mathcal {W}^2(\rho )+\tau _3 \mathcal {W}^3(\rho )+\tau _4 \mathcal {W}^4(\rho )+\tau _6 \mathcal {W}^6(\rho )}. \end{aligned}$$
(6)

Equation (6) admits the following cases for its solutions:

Case 1: When \(\tau _0=~\tau _1=~\tau _3=\tau _6=0\), the following solutions are brought up:

$$\begin{aligned} & \mathcal {W}(\rho )=\sqrt{-\frac{\tau _2}{\tau _4}} \sec \left[ \rho \sqrt{-\tau _2} \right] ,\quad \tau _2<0,~ \tau _4>0, \\ & \mathcal {W}(\rho )=\sqrt{-\frac{\tau _2}{\tau _4}} \csc \left[ \rho \sqrt{-\tau _2} \right] ,\quad \tau _2<0,~ \tau _4>0. \\ & \mathcal {W}(\rho )=\sqrt{-\frac{\tau _2}{\tau _4}} \text {sech}\left[ \rho \sqrt{\tau _2}\right] , \quad \tau _2>0,~ \tau _4<0, \end{aligned}$$

Case 2: When \(\tau _1=\tau _3=\tau _6=0,\tau _0=\frac{\tau _2^2}{4 \tau _4}\), the following solutions emerge from the analysis:

$$\begin{aligned} & \mathcal {W}(\rho )=\sqrt{\frac{-\tau _2}{2 \tau _4}} \tanh \left[ \rho \sqrt{\frac{-\tau _2}{2}} \right] ,\quad \tau _2<0,~ \tau _4>0,\\ & \mathcal {W}(\rho )=\sqrt{\frac{\tau _2}{2 \tau _4}} \tan \left[ \rho \sqrt{\frac{\tau _2}{2}} \right] ,\quad ~~~~\tau _2>0, ~\tau _4>0. \end{aligned}$$

Case 3: When \(\tau _3=~\tau _4=~\tau _6=0\), the following solution is brought up:

$$\begin{aligned} \mathcal {W}(\rho )=-\frac{\tau _1}{2 \tau _2}+e^{\rho \sqrt{\tau _2} },~~~~~~~~\quad \tau _2>0,~ \tau _0=\frac{\tau _1^2}{4 \tau _2}. \end{aligned}$$

Case 4: When \(\tau _0=\tau _1=\tau _6=0\), the following solutions are brought up:

$$\begin{aligned} & \mathcal {W}(\rho )=- \frac{\tau _2}{\tau _3} \left( \tanh \left[ \frac{1}{2}\rho \sqrt{\tau _2} \right] +1\right) ,~~~~~~~~~~~~~~~~\quad \tau _2>0,~\tau _3=\pm 2 \sqrt{\tau _2 \tau _4}, \\ & \mathcal {W}(\rho )=- \frac{\tau _2}{\tau _3} \left( \coth \left[ \frac{1}{2}\rho \sqrt{\tau _2} \right] +1\right) ,~~~~~~~~~~~~~~~~\quad \tau _2>0,~\tau _3=\pm 2 \sqrt{\tau _2 \tau _4}, \\ & \mathcal {W}(\rho )=\frac{\tau _2 {{\,\textrm{sech}\,}}^2\left[ \frac{1}{2} \rho \sqrt{\tau _2} \right] }{2 \sqrt{\tau _2 \tau _4} \tanh \left[ \frac{1}{2}\rho \sqrt{\tau _2} \right] -\tau _3},~~~~~\quad \tau _2>0,~ \tau _4>0,~\tau _3\ne \pm 2 \sqrt{\tau _2 \tau _4}, \\ & \mathcal {W}(\rho )=\frac{\tau _2 \sec ^2\left[ \frac{1}{2} \rho \sqrt{-\tau _2} \right] }{2 \sqrt{-\tau _2 \tau _4} \tan \left[ \frac{1}{2}\rho \sqrt{-\tau _2} \right] +\tau _3},~~\quad \tau _2<0,~ \tau _4>0,~\tau _3\ne \pm 2 \sqrt{\tau _2 \tau _4}. \end{aligned}$$

Case 5: When \(\tau _1=\tau _3=0\), the following solutions are brought up:

$$\begin{aligned} & \mathcal {W}(\rho )=\sqrt{\frac{2 \tau _2~ \text {sech}^2\left( \rho \sqrt{\tau _2}\right) }{2 \sqrt{\tau _4^2-4 \tau _2 \tau _6}-\left( \sqrt{\tau _4^2-4 \tau _2 \tau _6}+\tau _4\right) \text {sech}^2\left( \rho \sqrt{\tau _2}\right) }},~~~~~~~~~~~\quad \tau _2>0, \\ & \mathcal {W}(\rho )=\sqrt{\frac{2 \tau _2 \sec ^2\left( \rho \sqrt{-\tau _2}\right) }{2 \sqrt{\tau _4^2-4 \tau _2 \tau _6}-\left( \sqrt{\tau _4^2-4 \tau _2 \tau _6}-\tau _4\right) \sec ^2\left( \rho \sqrt{-\tau _2}\right) }},~~~~~~~~~~~~~\tau _2<0. \end{aligned}$$

Case 6: When \(\tau _1=\tau _3=0 ~\text {and}~ 0\le \beta \le 1\), the following solutions are brought up:

No.

\(\tau _0\)

\(\tau _2\)

\(\tau _4\)

\(\mathcal {W}(\rho )\)

1

1

\(-1-\beta ^2\)

\(\beta ^2\)

\(\text{sn}(\rho ,\beta )\) or \(\text{cd}(\rho ,\beta )\)

2

\(\beta ^2-1\)

\(2-\beta ^2\)

\(-1\)

\(\text{dn}(\rho ,\beta )\)

3

\(-\beta ^2\)

\(2\beta ^2-1\)

\(1-\beta ^2\)

\(\text{nc}(\rho ,\beta )\)

4

-1

\(2-\beta ^2\)

\(\beta ^2-1\)

\(\text{nd}(\rho ,\beta )\)

5

\(\beta ^4-2 \beta ^3+\beta ^2\)

\(-\frac{4}{\beta }\)

\(-\beta ^2+6 \beta -1\)

\(\frac{\beta ~\text{cn}(\rho |\beta ) \text{dn}(\rho |\beta )}{c~ \text{sn}(\rho |\beta )^2+1}\)

To determine the integer N, the balance principle is applied between the highest-order nonlinear term and the highest-order derivative term in Eq. (4). Substituting Eqs. (5) and (6) into Eq. (4) yields a polynomial expression in \(\mathcal {W}(\rho )\). The coefficients of terms with the same powers are then set to zero to form a system of equations. This resulting system is solved using Mathematica software.

ME mapping approach implementation

Conversion to ordinary differential equation (ODE)

Let’s use the substitution \(\Theta =\mathcal {L}_x\) into Eq. (1), it will be converted to the following NLPDE

$$\begin{aligned} \left( \mathcal {L}_{xt}+6 \mathcal {L}_x \mathcal {L}_{xx}+\mathcal {L}_{xxxx}\right) _x-\sigma \mathcal {L}_{xyy}+\mathcal {L}_{xxxxy}+3 \mathcal {L}_y\mathcal {L}_{xxx} +6 \mathcal {L}_{xx}\mathcal {L}_{xy}+3 \mathcal {L}_x \mathcal {L}_{xxy}+\mathcal {L}_{xyt}+\delta \mathcal {L}_{xxy} =0. \end{aligned}$$
(7)

When applying the aforementioned transformation described in Eq. (3), Eq. (7) will be the following ODE:

$$\begin{aligned} 2 \mathcal {U}^{(5)}+12 \left( \mathcal {U}''\right) ^2+ \left( \delta -2 \xi -\sigma +12 \mathcal {U}'\right) \mathcal {U}^{(3)}=0. \end{aligned}$$
(8)

Integrating Eq. (8) twice with respect to \(\rho\) while neglecting the integral constants, then:

$$\begin{aligned} 2 \mathcal {U}^{(3)}+\mathcal {U}' \left( \delta -2 \xi -\sigma +6 \mathcal {U}'\right) =0. \end{aligned}$$
(9)

Assume \(\mathcal {U}'= \mathcal {H}\), then Eq. (9) will be

$$\begin{aligned} 2 \mathcal {H}''+6 \mathcal {H}^2+ (\delta -2 \xi -\sigma )\mathcal {H}=0. \end{aligned}$$
(10)

Derivation of the model solutions

This subsection introduces the implementation of MEMA. Firstly, applying the balance principle on Eq. (10) between \(\mathcal {H}^2\)  and  \(\mathcal {H}''\), then \(N=2.\)

Thus, we can write the solution of Eq. (10) as follows:

$$\begin{aligned} \mathcal {H}(\rho )=\mathcal {A}_0+\mathcal {A}_1\; \mathcal {W}(\rho )+\mathcal {A}_2 \;\mathcal {W}(\rho )^2+\frac{\mathcal {B}_1}{\mathcal {W}(\rho )}+\frac{\mathcal {B}_2}{\mathcal {W}(\rho )^2}+\mathcal {C}_2 \;\mathcal {W} '(\rho )+\mathcal {D}_1\frac{ \mathcal {W} '(\rho )}{\mathcal {W}(\rho )}+\mathcal {D}_2\frac{ \mathcal {W} '(\rho )}{\mathcal {W}(\rho )^2}. \end{aligned}$$
(11)

Here, \(\mathcal {A}_0, \mathcal {A}_1, \mathcal {A}_2, \mathcal {B}_1, \mathcal {B}_2, \mathcal {C}_2, \mathcal {D}_1,\) and \(\mathcal {D}_2\) are constants to be determined, with the condition that \(\mathcal {A}_2, \mathcal {B}_2, \mathcal {C}_2,\) and \(\mathcal {D}_2\) are all nonzero. Substituting Eq. (11) and Eq. (6) into Eq. (10), the coefficients of terms with the same powers are set to zero. The resulting system of equations is then solved using Mathematica software to find the values of these constants.

The following represent all possible scenarios for solving the algebraic system.

Case 1:   \(\tau _0=\tau _1=\tau _3=\tau _6=0\),

(1.1)  \(\mathcal {A}_0=0,~\mathcal {A}_1=0,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_1=0,~\mathcal {B}_2=0,~\mathcal {C}_2=0,~\mathcal {D}_1=0,~\mathcal {D}_2=0,~\sigma =\delta -2 \xi +8 \tau _2.\)

(1.2)  \(\mathcal {A}_0=-\frac{4\tau _2}{3} ,~\mathcal {A}_1=0,\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_1=0,~\mathcal {B}_2=0,~\mathcal {C}_2=0,~\mathcal {D}_1=0,~\mathcal {D}_2=0,~\sigma =\delta -2 \xi -8 \tau _2.\)

Based on the findings in Case (1.1), the solutions to Eq. (1) are divided into the following types:

(1.1.1) When \(\tau _2 > 0\) and \(\tau _4 < 0\), the system admits bright soliton solutions expressed as:

$$\begin{aligned} \Theta _{1.1.1}=2 \tau _2~ \text {sech}^2\left[ (x+y-\xi t)\sqrt{\tau _2}\right] . \end{aligned}$$
(12)

(1.1.2) Under the conditions \(\tau _2 < 0\) and \(\tau _4 > 0\), the solutions correspond to singular periodic waves, expressed as:

$$\begin{aligned} \Theta _{1.1.2.a}=2 \tau _2~ \text {sec}^2\left[ (x+y-\xi t)\sqrt{-\tau _2}\right] , \end{aligned}$$
(13)

or

$$\begin{aligned} \Theta _{1.1.2.b}=2 \tau _2~ \text {csc}^2\left[ (x+y-\xi t)\sqrt{-\tau _2}\right] . \end{aligned}$$
(14)

According to Case (1.2), the solutions of Eq. (1) are presented in the following categories:

(1.2.1) When \(\tau _2 > 0\) and \(\tau _4 < 0\), bright soliton solutions arise as indicated below:

$$\begin{aligned} \Theta _{1.2.1}=-\frac{4 \tau _2}{3} +2 \tau _2~ \text {sech}^2\left[ (x+y-\xi t)\sqrt{\tau _2}\right] . \end{aligned}$$
(15)

(1.2.2) If \(\tau _2<0~ \text {and}~\tau _4>0\),  solutions with singular periodic kind are provided as indicated:

$$\begin{aligned} \Theta _{1.2.2.a}=-\frac{4 \tau _2}{3} +2 \tau _2~ \text {sec}^2\left[ (x+y-\xi t)\sqrt{-\tau _2}\right] , \end{aligned}$$
(16)

or

$$\begin{aligned} \Theta _{1.2.2.b}=-\frac{4 \tau _2}{3} +2 \tau _2~ \text {csc}^2\left[ (x+y-\xi t)\sqrt{-\tau _2}\right] . \end{aligned}$$
(17)

Case 2:   \(\tau _1=\tau _3=\tau _6=0,~\tau _0=\frac{\tau _2^2}{4 \tau _4}\), we get \(\mathcal {A}_1=\mathcal {C}_2=\mathcal {D}_1= 0\) and

(2.1)  \(\mathcal {A}_0=-\tau _2,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_1=0,~\mathcal {B}_2=0,~\mathcal {D}_2=0,~\sigma =\delta -2 \xi -4 \tau _2.\)

(2.2)  \(\mathcal {A}_0=-\tau _2,~\mathcal {A}_2=0,~\mathcal {B}_1=0,~\mathcal {B}_2=-\frac{\tau _2^2}{2 \tau _4},~\mathcal {D}_2=0,~\sigma =\delta -2 \xi -4 \tau _2.\)

(2.3)  \(\mathcal {A}_0=-2\tau _2,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_1=0,~\mathcal {B}_2=-\frac{\tau _2^2}{2 \tau _4},~\mathcal {D}_2=0,~\sigma =\delta -2 \xi -16 \tau _2.\)

(2.4)  \(\mathcal {A}_0=-2\tau _2,~\mathcal {A}_2=0,~\mathcal {B}_1=0,~\mathcal {B}_2=-\frac{\tau _2^2}{2 \tau _4},~\mathcal {D}_2=-\frac{\tau _2}{2 \sqrt{\tau _4}},~\sigma =\delta -2 \xi -4 \tau _2.\)

Within the results of case (2.1), solutions of Eq.(1) shall be split into the subsequent:

(2.1.1) If  \(\tau _2<0~\text {and}~\tau _4>0\), a bright soliton-type solution is given as follows:

$$\begin{aligned} \Theta _{2.1.1}=-\tau _2~ \text {sech}^2\left[ \frac{\sqrt{-\tau _2} (x+y-\xi t)}{\sqrt{2}}\right] . \end{aligned}$$
(18)

(2.1.2) If \(\tau _2 > 0\) and \(\tau _4 > 0\), a singular periodic-type solution is provided as follows:

$$\begin{aligned} \Theta _{2.1.2}=-\tau _2~ \text {sec}^2\left[ \frac{\sqrt{\tau _2} (x+y-\xi t)}{\sqrt{2}}\right] . \end{aligned}$$
(19)

Within the results of Case (2.2), the solutions of Eq. (1) shall be split into the subsequent:

(2.2.1) If \(\tau _2 < 0 \text { and } \tau _4 > 0\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{2.2.1}=\tau _2~ \text {csch}^2\left[ \frac{\sqrt{-\tau _2} (x+y-\xi t)}{\sqrt{2}}\right] . \end{aligned}$$
(20)

(2.2.2) If \(\tau _2> 0 \text { and } \tau _4 > 0\), a singular periodic-type solution is provided as indicated:

$$\begin{aligned} \Theta _{2.2.2}=-\tau _2~ \text {csc}^2\left[ \frac{\sqrt{\tau _2} (x+y-\xi t)}{\sqrt{2}}\right] . \end{aligned}$$
(21)

Within the results of Case (2.3), the solutions of Eq. (1) can be categorized as follows:

(2.3.1) If \(\tau _2 < 0 \text { and } \tau _4 > 0\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{2.3.1}=4 \tau _2~ \text {csch}^2\left[ (x+y-\xi t)\sqrt{-2\tau _2}\right] . \end{aligned}$$
(22)

(2.3.2) If \(\tau _2> 0 \text { and } \tau _4 > 0\), a singular periodic-type solution is provided as indicated:

$$\begin{aligned} \Theta _{2.3.2}=-4 \tau _2~ \text {csc}^2\left[ (x+y-\xi t)\sqrt{2\tau _2}\right] . \end{aligned}$$
(23)

Within the results of Case (2.4), the solutions of Eq. (1) can be categorized as follows:

(2.4.1) If \(\tau _2 < 0 \text { and } \tau _4 > 0\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{2.4.1}=- \tau _2~\text {csch}^2\left[ \frac{(x+y-\xi t)\sqrt{-\tau _2}}{\sqrt{2}}\right] . \end{aligned}$$
(24)

(2.4.2) If \(\tau _2> 0 \text { and } \tau _4 > 0\), a singular periodic-type solution is provided as indicated:

$$\begin{aligned} \Theta _{2.4.2}=-4 \sqrt{2\tau _2}~\text {cot}^2\left[ \frac{(x+y-\xi t)\sqrt{\tau _2}}{\sqrt{2}}\right] . \end{aligned}$$
(25)

Case 3:   If \(\tau _3=\tau _4=\tau _6=0\), we get \(\mathcal {C}_2= \mathcal {D}_1= 0\) and

(3.1)  \(\mathcal {A}_0=0,~\mathcal {A}_1=0,~\mathcal {A}_2=0,~\mathcal {B}_1= -\frac{\tau _1}{2},~\mathcal {B}_2= -\tau _0,~\mathcal {B}_2=0,~\mathcal {D}_2=-\sqrt{\tau _0},~\sigma =\delta -2 \xi +2 \tau _2.\)

(3.2)  \(\mathcal {A}_0=-\frac{\tau _2}{3},~\mathcal {A}_1=0,~\mathcal {A}_2=0,~\mathcal {B}_1= -\frac{\tau _1}{2},~\mathcal {B}_2= -\tau _0,~\mathcal {B}_2=0,~\mathcal {D}_2=-\sqrt{\tau _0},~\sigma =\delta -2 \xi -2 \tau _2.\)

Within the results of case (3.1), solutions of Eq.(1) shall be split into the subsequent:

(3.1.1) If \(\tau _2> 0, \ \tau _0 > 0, \text { and } \tau _1 = 0\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{3.1.1}= -\frac{\tau _2}{2} \text {csch}^2\left[ \frac{1}{2} (x+y-\xi t)\sqrt{\tau _2}\right] . \end{aligned}$$
(26)

(3.1.2) If \(\tau _2 < 0, \ \tau _0 > 0, \text { and } \tau _1 = 0\), a periodic-type solution is provided as indicated:

$$\begin{aligned} \Theta _{3.1.2}=-\frac{\tau _2}{2}\tau _2 ~\text {csc}^2\left[ \frac{1}{2} (x+y-\xi t)\sqrt{-\tau _2}\right] . \end{aligned}$$
(27)

(3.1.3) If \(\tau _2 > 0 \text { and } \tau _0 = \frac{\tau _1^2}{4 \tau _2}\), an exponential solution is provided as indicated:

$$\begin{aligned} \Theta _{3.1.3}=-\frac{4 \tau _1 \tau _2^2 ~e^{ (x+y-\xi t)\sqrt{\tau _2}}}{\left( \tau _1-2 \tau _2 e^{ (x+y-\xi t)\sqrt{\tau _2}}\right) ^2}, \end{aligned}$$
(28)

where \(\left( \tau _1-2 \tau _2 e^{ (x+y-\xi t)\sqrt{\tau _2}}\right) ^2\ne 0\).

Within the results of case (3.2), solutions of Eq.(1) shall be split into the subsequent:

(3.2.1) If \(\tau _2> 0, \ \tau _0 > 0, \text { and } \tau _1 = 0\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{3.2.1}=-\frac{\tau _2}{6}\left( 2+3 \text {csch}^2\left[ \frac{1}{2} (x+y-\xi t)\sqrt{\tau _2}\right] \right) . \end{aligned}$$
(29)

(3.2.2) If \(\tau _2<0,~\tau _0>0~\text {and}~\tau _1=0\), a solution with singular periodic kind is provided as indicated:

$$\begin{aligned} \Theta _{3.2.2}=-\frac{\tau _2}{6}\left( 2+3 \text {csc}^2\left[ \frac{1}{2} (x+y-\xi t)\sqrt{-\tau _2}\right] \right) . \end{aligned}$$
(30)

(3.2.3) If \(\tau _2>0~\text {and}~\tau _0=\frac{\tau _1^2}{4 \tau _2}\), an exponential solution is provided as indicated:

$$\begin{aligned} \Theta _{3.2.3}=-\frac{1}{3}\left( \tau _2+\frac{12 \tau _1 \tau _2^2 ~e^{ (x+y-\xi t)\sqrt{\tau _2}}}{\left( \tau _1-2 \tau _2 e^{ (x+y-\xi t)\sqrt{\tau _2}}\right) ^2}\right) , \end{aligned}$$
(31)

where \(\left( \tau _1-2 \tau _2 e^{ (x+y-\xi t)\sqrt{\tau _2}}\right) ^2\ne 0\).

Case 4:   If \(\tau _0=\tau _1=\tau _6=0\), we get \(\mathcal {B}_1=\mathcal {B}_2=\mathcal {C}_2=\mathcal {D}_1= \mathcal {D}_2=0\) and

(4.1)  \(\mathcal {A}_0=0,~\mathcal {A}_1= 0,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_2=0,~\sigma =2 \xi +\sigma -8 \tau _2,~\tau _3= 0.\)

(4.2)  \(\mathcal {A}_0=-\frac{4 \tau _2}{3} ,~\mathcal {A}_1= 0,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_2=-\frac{\tau _2^2}{2 \tau _4},~\sigma =2 \xi +\sigma +8 \tau _2,~\tau _3= 0.\)

(4.3)  \(\mathcal {A}_0=0,~\mathcal {A}_1= 2 \sqrt{\tau _2\tau _4},~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_2=-\frac{\tau _2^2}{2 \tau _4},~\sigma =2 \xi +\sigma -2 \tau _2,~\tau _3= -2 \sqrt{\tau _2\tau _4}.\)

(4.4)  \(\mathcal {A}_0=-\frac{\tau _2}{3},~\mathcal {A}_1= 2 \sqrt{\tau _2\tau _4},~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_2=0,~\sigma =2 \xi +\sigma +2 \tau _2,~\tau _3= -2 \sqrt{\tau _2\tau _4}.\)

Within the results of case (4.1), solutions of Eq.(1) shall be split into the subsequent:

(4.1.1) If \(\tau _2> 0, \ \tau _4 > 0, \text { and } \tau _3^2 \ne 4 \tau _2 \tau _4\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{4.1.1}= -2\tau _2~\text {csch}^2\left[ (x+y-\xi t)\sqrt{\tau _2}\right] . \end{aligned}$$
(32)

(4.1.2) If \(\tau _2 < 0, \ \tau _4 > 0, \text { and } \tau _3^2 \ne 4 \tau _2 \tau _4\), a singular periodic-type solution is provided as indicated:

$$\begin{aligned} \Theta _{4.1.2}= -2\tau _2~\text {csc}^2\left[ (x+y-\xi t)\sqrt{-\tau _2}\right] . \end{aligned}$$
(33)

Within the results of case (4.2), solutions of Eq.(1) shall be split into the subsequent:

(4.2.1) If \(\tau _2> 0, \ \tau _4 > 0, \text { and } \tau _3^2 \ne 4 \tau _2 \tau _4\), a singular soliton-type solution is provided as indicated:

$$\begin{aligned} \Theta _{4.2.1}= - \tau _2\left( \frac{4}{3}+2\text {csch}^2\left[ (x+y-\xi t)\sqrt{\tau _2}\right] \right) . \end{aligned}$$
(34)

(4.2.2) If \(\tau _2 < 0, \ \tau _4 > 0, \text { and } \tau _3^2 \ne 4 \tau _2 \tau _4\), a singular periodic-type solution is provided as indicated:

$$\begin{aligned} \Theta _{4.2.2}= - \tau _2\left( \frac{4}{3}+2\csc ^2\left[ (x+y-\xi t)\sqrt{-\tau _2}\right] \right) . \end{aligned}$$
(35)

Within the results of case (4.3), solutions of Eq.(1) shall be split into the subsequent:

(4.3.1) If \(\tau _2>0~\text {and}~\tau _3^2=4 \tau _2 \tau _4\), solutions with bright and singular soliton kind are provided as indicated:

$$\begin{aligned} \Theta _{4.3.1.a}= \frac{1}{2}\tau _2~\text {sech}^2\left[ \frac{1}{2}(x+y-\xi t)\sqrt{\tau _2}\right] . \end{aligned}$$
(36)

or

$$\begin{aligned} \Theta _{4.3.1.b}= -\frac{1}{2}\tau _2~\text {csch}^2\left[ \frac{1}{2}(x+y-\xi t)\sqrt{\tau _2}\right] . \end{aligned}$$
(37)

Within the results of case (4.4), solutions of Eq.(1) shall be split into the subsequent:

(4.4.1) If \(\tau _2 > 0 \text { and } \tau _3^2 = 4 \tau _2 \tau _4\), solutions of dark and singular soliton types are provided as indicated:

$$\begin{aligned} \Theta _{4.4.1.a}= \frac{\tau _2}{6} \left( 1-3 \tanh ^2\left[ \frac{1}{2}(x+y-\xi t) \sqrt{\tau _2}\right] \right) . \end{aligned}$$
(38)

or

$$\begin{aligned} \Theta _{4.4.1.b}= \frac{\tau _2}{6} \left( 1-3 \coth ^2\left[ \frac{1}{2}(x+y-\xi t) \sqrt{\tau _2}\right] \right) . \end{aligned}$$
(39)

Case 5:   If \(\tau _0=\tau _1=\tau _3=\tau _6=0\), we get

$$\begin{aligned} \mathcal {A}_0=\frac{\sqrt{-\tau _1 \tau _3}}{2 \sqrt{3}},~\mathcal {A}_1=\mathcal {A}_2=\mathcal {C}_2=\mathcal {D}_1=0,~\mathcal {B}_1=-\frac{\tau _1}{2},~\mathcal {B}_2=-\tau _0,~\mathcal {D}_2=-\sqrt{\tau _0},~\sigma =\delta -2 \xi +2 \sqrt{-3 \tau _1 \tau _3}. \end{aligned}$$

If \(\tau _3>0\), solution with Weierstrass elliptic doubly periodic function is provided as indicated:

$$\begin{aligned} \Theta _{5}= \frac{1}{6} \left( \sqrt{-3\tau _1 \tau _3}-\frac{3 \left( 2 \tau _0+\tau _1~ \wp \left[ \frac{(x+y-\xi t) \sqrt{\tau _3}}{2};-\frac{4 \tau _1}{\tau _3},-\frac{4 \tau _0}{\tau _3}\right] +\sqrt{\tau _0\tau _3} ~ \wp '\left[ \frac{(x+y-\xi t) \sqrt{\tau _3}}{2};-\frac{4 \tau _1}{\tau _3},-\frac{4 \tau _0}{\tau _3}\right] \right) }{\wp \left[ \frac{(x+y-\xi t) \sqrt{\tau _3}}{2};-\frac{4 \tau _1}{\tau _3},-\frac{4 \tau _0}{\tau _3}\right] ^2}\right) . \end{aligned}$$
(40)

Case 6:   If \(\tau _1=\tau _3=0\), we get:

$$\begin{aligned} & \mathcal {A}_0=\frac{2}{3}\left( \sqrt{\tau _2^2-3 \tau _0 \tau _4}-\tau _2\right) ,~\mathcal {A}_1=\mathcal {A}_2=\mathcal {B}_1=\mathcal {C}_2=\mathcal {D}_1=0,~\mathcal {B}_2=-2 \tau _0,\\ & ~\mathcal {D}_2=-\sqrt{\tau _0},~\sigma =\delta -2 \xi +8 \sqrt{\tau _2^2-3 \tau _0 \tau _4}. \end{aligned}$$

If \(\tau _3>0\), solution with trigonometric function is provided as indicated:

$$\begin{aligned} \Theta _{6}=-\frac{2 \tau _2}{3}+ \frac{2}{3} \sqrt{\tau _2^2-3 \tau _0 \tau _4}-\frac{\tau _0 \left( \tau _4+\sqrt{\tau _4^2-4 \tau _2 \tau _6} \cos \left[ 2 (x+y-\xi t) \sqrt{-\tau _2}\right] \right) }{\tau _2}. \end{aligned}$$
(41)

Case 7:   If \(\tau _1=\tau _3=\tau _6=0\), we get \(\mathcal {A}_1=\mathcal {B}_1=\mathcal {C}_2=\mathcal {D}_1= 0\) and

(7.1)  \(\mathcal {A}_0=\frac{2}{3} \left( \sqrt{\tau _2^2-3 \tau _0 \tau _4}-\tau _2\right) ,~\mathcal {A}_2=0,~\mathcal {B}_2=-2 \tau _0,~\mathcal {D}_2=0,~\sigma =\delta -2 \xi +8 \sqrt{\tau _2^2-3 \tau _0 \tau _4}.\)

(7.2)  \(\mathcal {A}_0=\frac{2}{3} \left( \sqrt{\tau _2^2-3 \tau _0 \tau _4}-\tau _2\right) ,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_2=0,~\mathcal {D}_2=0,~\sigma =\delta -2 \xi +8 \sqrt{\tau _2^2-3 \tau _0 \tau _4}.\)

(7.3)  \(\mathcal {A}_0=\frac{2}{3} \left( \sqrt{\tau _2^2+12 \tau _0 \tau _4}-\tau _2\right) ,~\mathcal {A}_2=-2 \tau _4,~\mathcal {B}_2=-2 \tau _0,~\mathcal {D}_2=0,~\sigma =\delta -2 \xi +8 \sqrt{\tau _2^2+12 \tau _0 \tau _4}.\)

(7.4)  \(\mathcal {A}_0=\frac{1}{6} \left( \sqrt{\tau _2^2+12 \tau _0 \tau _4}-\tau _2\right) ,~\mathcal {A}_2=0,~\mathcal {B}_2=-\tau _0,~\mathcal {D}_2=\sqrt{\tau _0},~\sigma =\delta -2 \xi +2 \sqrt{\tau _2^2+12 \tau _0 \tau _4}.\)

Within the results of case (7.1), solutions of Eq.(1) shall be split into the subsequent:

(7.1.1) If \(\tau _0=1,\tau _2=-\beta ^2-1~\text {and}~\tau _4=\beta ^2\), solutions with Jacobi elliptic (JE) kind are provided as indicated:

$$\begin{aligned} \Theta _{7.1.1.1}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}-3\text {ns}^2[x+y-\xi t ]\right) , \end{aligned}$$
(42)

or

$$\begin{aligned} \Theta _{7.1.1.2} = \frac{2}{3} \left( 1 + \beta ^2 + \sqrt{1 - \beta ^2 + \beta ^4} - 3\, \textrm{dc}^2[x + y - \xi t]\right) , \end{aligned}$$
(43)

where \(0 \le \beta \le 1\).

When setting \(\beta = 1\) in Eq. (42), a singular soliton-type solution is obtained as follows:

$$\begin{aligned} \Theta _{7.1.1.1.a} = -2\, \textrm{csch}^2[x + y - \xi t]. \end{aligned}$$
(44)

When setting \(\beta = 0\) in Eqs. (42) and (43) respectively, singular periodic-type solutions are provided as follows:

$$\begin{aligned} \Theta _{7.1.1.1.b} = \frac{4}{3} - 2\, \textrm{csc}^2[x + y - \xi t], \end{aligned}$$
(45)

and

$$\begin{aligned} \Theta _{7.1.1.2.b} = \frac{4}{3} - 2\, \textrm{sec}^2[x + y - \xi t]. \end{aligned}$$
(46)

(7.1.2) If \(\tau _0 = \beta ^2 - 1, \ \tau _2 = 2 - \beta ^2, \text { and } \tau _4 = -1\), a solution of JE kind is provided as follows:

$$\begin{aligned} \Theta _{7.1.2} = \frac{2}{3} \left( 1 + \beta ^2 + \sqrt{1 - \beta ^2 + \beta ^4}\right) - 2\, \textrm{nd}^2[x + y - \xi t], \end{aligned}$$
(47)

where \(0 \le \beta < 1\).

When setting \(\beta = 1\) in Eq. (47), a hyperbolic soliton-type solution is obtained:

$$\begin{aligned} \Theta _{7.1.2.a} = -2\, \sinh ^2[x + y - \xi t]. \end{aligned}$$
(48)

(7.1.3) If \(\tau _0 = -\beta ^2, \ \tau _2 = -1 + 2\beta ^2, \text { and } \tau _4 = 1 - \beta ^2\), a solution of JE kind is given by:

$$\begin{aligned} \Theta _{7.1.3} = \frac{2}{3} \left( 1 + \beta ^2 + \sqrt{1 - \beta ^2 + \beta ^4}\right) - 2\, \textrm{cn}^2[x + y - \xi t], \end{aligned}$$
(49)

where \(0 < \beta \le 1\).

When setting \(\beta = 1\) in Eq. (49), a dark soliton-type solution is obtained:

$$\begin{aligned} \Theta _{7.1.3.a} = 2\, \tanh ^2[x + y - \xi t]. \end{aligned}$$
(50)

(7.1.4) If \(\tau _0 = -1, \ \tau _2 = 2 - \beta ^2, \text { and } \tau _4 = \beta ^2 - 1\), a solution of JE kind is given as:

$$\begin{aligned} \Theta _{7.1.4} = \frac{2}{3} \left( 1 + \beta ^2 + \sqrt{1 - \beta ^2 + \beta ^4}\right) - 2\, \textrm{dn}^2[x + y - \xi t], \end{aligned}$$
(51)

where \(0 \le \beta \le 1\).

(7.1.5) If  \(\tau _0=\frac{1}{4},\tau _2=\frac{1}{2}(\beta ^2-2)~\text {and}~\tau _4=\frac{\beta ^4}{4}\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.1.5}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}\right) -\frac{2 (1+\text {dn}[x+y-\xi t])^2}{\text {sn}^2[x+y-\xi t]}, \end{aligned}$$
(52)

where \(0\le \beta \le 1\).

When setting \(\beta =1\) in Eq.(52), a solution with singular soliton kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.1.5.a}=4 \text {coth}^2\left[ \frac{x+y-\xi t}{2}\right] . \end{aligned}$$
(53)

Within the results of case (7.2), solutions of Eq.(1) shall be split into the subsequent:

(7.2.1) If  \(\tau _0=1,\tau _2=-\beta ^2-1~\text {and}~\tau _4=\beta ^2\), solutions with JE kind are supplied as indicated:

$$\begin{aligned} \Theta _{7.2.1.1}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}-3\beta ^2\text {sn}^2[x+y-\xi t ]\right) , \end{aligned}$$
(54)

or

$$\begin{aligned} \Theta _{7.2.1.2}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}-3\beta ^2\text {cd}^2[x+y-\xi t ]\right) , \end{aligned}$$
(55)

where \(0\le \beta \le 1\).

When setting \(\beta =1\) in Eq.(54), a solution with bright soliton kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.2.1.1.a}=2\ \text {sech}^2[x+y-\xi t]. \end{aligned}$$
(56)

(7.2.2) If  \(\tau _0=\beta ^2-1,\tau _2=2-\beta ^2~\text {and}~\tau _4=-1\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.2.2}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}\right) -2\beta ^2\text {dn}^2[x+y-\xi t ], \end{aligned}$$
(57)

where \(0\le \beta < 1\).

(7.2.3) If  \(\tau _0=-\beta ^2,\tau _2=-1+2\beta ^2~\text {and}~\tau _4=1-\beta ^2\), a solution with JE kind is supplied as seen:

$$\begin{aligned} \Theta _{7.2.3}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}\right) -2\beta ^2 \text {nc}^2[x+y-\xi t ], \end{aligned}$$
(58)

where \(0< \beta \le 1\).

(7.2.4) If  \(\tau _0=-1,\tau _2=2-\beta ^2~\text {and}~\tau _4=\beta ^2-1\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.2.4}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}\right) -2\beta ^2\text {nd}^2[x+y-\xi t ], \end{aligned}$$
(59)

where \(0\le \beta \le 1\).

(7.2.5) If  \(\tau _0=\frac{1}{4},\tau _2=\frac{1}{2}(\beta ^2-2)~\text {and}~\tau _4=\frac{\beta ^4}{4}\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.2.5}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}\right) -2\beta ^2\frac{\text {sn}^2[x+y-\xi t]}{ (1+\text {dn}[x+y-\xi t])^2}, \end{aligned}$$
(60)

where \(0\le \beta \le 1\).

When setting \(\beta =1\) in Eq.(60), a solution with bright soliton kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.2.5.a}=2\ \text {sech}^2\left[ \frac{x+y-\xi t}{2}\right] . \end{aligned}$$
(61)

Within the results of case (7.3), solutions of Eq.(1) shall be split into the subsequent:

(7.3.1) If  \(\tau _0=1,\tau _2=-\beta ^2-1~\text {and}~\tau _4=\beta ^2\), solutions with JE kind are supplied as indicated:

$$\begin{aligned} \Theta _{7.3.1.1}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1+14\beta ^2+\beta ^4}-3\beta ^2\text {ns}^2[x+y-\xi t ]-3\beta ^2\text {sn}^2[x+y-\xi t ]\right) , \end{aligned}$$
(62)

or

$$\begin{aligned} \Theta _{7.3.1.2}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1+\beta ^4+14\beta ^2}-3\text {dc}^2[x+y-\xi t ]-3\beta ^2\text {cd}^2[x+y-\xi t ]\right) , \end{aligned}$$
(63)

where \(0\le \beta \le 1\).

When setting \(\beta =1\) in Eq.(62), a solution with singular soliton kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.3.1.1.a}=-8\ \text {csch}^2[2(x+y-\xi t)], \end{aligned}$$
(64)

and

$$\begin{aligned} \Theta _{7.3.1.2.b}=\frac{4}{3}-2 \csc ^2[x+y-\xi t]. \end{aligned}$$
(65)

(7.3.2) If  \(\tau _0=\beta ^2-1,\tau _2=2-\beta ^2~\text {and}~\tau _4=-1\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.3.2}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1+14\beta ^2+\beta ^4}\right) -2\text {nd}^2[x+y-\xi t ]-2\beta ^2\text {dn}^2[x+y-\xi t ], \end{aligned}$$
(66)

where \(0\le \beta < 1\).

(7.3.3) If  \(\tau _0=-\beta ^2,\tau _2=-1+2\beta ^2~\text {and}~\tau _4=1-\beta ^2\), a solution with JE kind is supplied as seen:

$$\begin{aligned} \Theta _{7.3.3}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1+14\beta ^2+\beta ^4}\right) -2\text {cn}^2[x+y-\xi t ]-2\beta ^2 \text {nc}^2[x+y-\xi t ], \end{aligned}$$
(67)

where \(0< \beta \le 1\).

When setting \(\beta =0\) in Eq.(67), a solution with periodic kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.3.3.a}=\frac{4}{3}-2 \text {cos}^2[x+y-\xi t]. \end{aligned}$$
(68)

(7.3.4) If  \(\tau _0=-1,\tau _2=2-\beta ^2~\text {and}~\tau _4=\beta ^2-1\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.3.4}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1+14\beta ^2+\beta ^4}\right) -2\text {dn}^2[x+y-\xi t ]-2\beta ^2\text {nd}^2[x+y-\xi t ], \end{aligned}$$
(69)

where \(0\le \beta \le 1\).

(7.3.5) If  \(\tau _0=\frac{1}{4},\tau _2=\frac{1}{2}(\beta ^2-2)~\text {and}~\tau _4=\frac{\beta ^4}{4}\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.3.5}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1-\beta ^2+\beta ^4}\right) -\frac{2 (1+\text {dn}[x+y-\xi t])^2}{\text {sn}^2[x+y-\xi t]}-2\beta ^2\frac{\text {sn}^2[x+y-\xi t]}{ (1+\text {dn}[x+y-\xi t])^2}, \end{aligned}$$
(70)

where \(0\le \beta \le 1\).

When setting \(\beta =1\) in Eq.(70), a solution with bright soliton kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.3.5.a}=2\ \text {sech}^2\left[ \frac{x+y-\xi t}{2}\right] . \end{aligned}$$
(71)

Within the results of case (7.4), solutions of Eq.(1) shall be split into the subsequent:

(7.4.1) If  \(\tau _0=1,\tau _2=-\beta ^2-1~\text {and}~\tau _4=\beta ^2\), solutions with JE kind are supplied as indicated:

$$\begin{aligned} \Theta _{7.4.1.1}=\frac{2}{3} \left( 1+\beta ^2+\sqrt{1+\beta ^4+14\beta ^2}+6 (\text {cn}[x+y-\xi t ]~ \text {dn}[x+y-\xi t ]-1)~\text {sn}[x+y-\xi t ]^2\right) , \end{aligned}$$
(72)

or

$$\begin{aligned} \Theta _{7.4.1.2}=\frac{1}{6} \left( 1+\beta ^2+\sqrt{1+\beta ^4+14\beta ^2}+6 (\text {cn}[x+y-\xi t ]~ \text {dn}[x+y-\xi t ]-1)~\text {dc}[x+y-\xi t ]^2\right) , \end{aligned}$$
(73)

where \(0\le \beta \le 1\).

(7.4.2) If  \(\tau _0=\beta ^2-1,\tau _2=2-\beta ^2~\text {and}~\tau _4=-1\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.4.2}=\frac{1}{6} \left( 1+\beta ^2+\sqrt{1+\beta ^4+14\beta ^2}+6 (1+\beta \text {cn}[x+y-\xi t ]~ \text {sn}[x+y-\xi t ])~\text {nd}[x+y-\xi t ]^2\right) , \end{aligned}$$
(74)

where \(0\le \beta < 1\).

(7.4.3) If  \(\tau _0=\frac{1}{4},\tau _2=\frac{1}{2}(\beta ^2-2)~\text {and}~\tau _4=\frac{\beta ^4}{4}\), a solution with JE kind is supplied as indicated:

$$\begin{aligned} \Theta _{7.4.3}=\frac{1}{12} \left( 2-\beta ^2+2 \sqrt{1-\beta ^2+\beta ^4}+3 (1+\text {dn}[\rho ]) (2 \text {cn}[\rho ]-\text {dn}[\rho ]-1)\text {ns}[\rho ]^2\right) , \end{aligned}$$
(75)

where \(0\le \beta \le 1\).

Reduction to a planar system

We begin with the second-order nonlinear differential equation:

$$\begin{aligned} 6 \mathcal {H}^2 + (\delta - 2\xi - \sigma )\mathcal {H} + 2\mathcal {H}'' = 0, \end{aligned}$$

where \(\delta , \xi , \sigma \in \mathbb {R}\) are constant parameters. Let us define

$$\begin{aligned} \tilde{\alpha } := \delta - 2\xi - \sigma . \end{aligned}$$

Then the equation becomes:

$$\begin{aligned} 6 \mathcal {H}^2 +\tilde{\alpha } \mathcal {H} + 2\mathcal {H}'' = 0. \end{aligned}$$
(76)

To convert this second-order scalar equation into a first-order system, we introduce the following change of variables:

$$\begin{aligned} x := \mathcal {H}, \quad y := \mathcal {H}'. \end{aligned}$$

Then:

$$\begin{aligned} x' = y, \quad y' = \mathcal {H}''. \end{aligned}$$

Substituting into equation (76), we obtain:

$$\begin{aligned} 6x^2 + \tilde{\alpha } x + 2y' = 0, \end{aligned}$$

which simplifies to:

$$\begin{aligned} y' = -3x^2 - \frac{\tilde{\alpha }}{2}x. \end{aligned}$$

Therefore, the equivalent first-order planar system is:

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = y, \\ y' = 3x^2 + \alpha x, \end{array}\right. } \quad \text {where } \alpha := -\frac{\tilde{\alpha }}{2}. \end{aligned}$$

This system will be the subject of our subsequent stability and bifurcation analysis.

Stability and bifurcation analysis

We consider the planar autonomous system:

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = y, \\ y' = 3x^2 + \alpha x, \end{array}\right. } \end{aligned}$$
(77)

where \(\alpha \in \mathbb {R}\) is treated as a bifurcation parameter.

Theorem 1

(Equilibrium Points) The system (77) has two equilibrium points:

$$\begin{aligned} E_1 = (0, 0), \quad E_2 = \left( -\frac{\alpha }{3}, 0\right) . \end{aligned}$$

Proof

Equilibrium points satisfy \(x' = 0\) and \(y' = 0\), which yields:

$$\begin{aligned} y = 0, \quad 3x^2 + \alpha x = 0 \quad \Rightarrow \quad x(3x + \alpha ) = 0. \end{aligned}$$

Hence, \(x = 0\) or \(x = -\frac{\alpha }{3}\). \(\square\)

Theorem 2

(Linearization and Jacobian Matrix) The Jacobian matrix of system (77) at a point \((x, y)\) is:

$$\begin{aligned} J(x, y) = \begin{bmatrix} 0 & 1 \\ 6x + \alpha & 0 \end{bmatrix}. \end{aligned}$$

Remark 1

(Stability at \(E_1 = (0, 0)\)) Evaluating the Jacobian at the origin:

$$\begin{aligned} J(0, 0) = \begin{bmatrix} 0 & 1 \\ \alpha & 0 \end{bmatrix}. \end{aligned}$$

The characteristic polynomial is:

$$\begin{aligned} \lambda ^2 - \alpha = 0 \quad \Rightarrow \quad \lambda = \pm \sqrt{\alpha }. \end{aligned}$$

The stability depends on the sign of \(\alpha\):

  • \(\alpha > 0\): eigenvalues real and of opposite sign \(\Rightarrow\) saddle point (unstable).

  • \(\alpha = 0\): eigenvalues zero \(\Rightarrow\) non-hyperbolic (degenerate).

  • \(\alpha < 0\): eigenvalues purely imaginary \(\Rightarrow\) linear center.

Remark 2

(Stability at \(E_2 = \left( -\frac{\alpha }{3}, 0\right)\)) At this point, we compute:

$$\begin{aligned} 6x + \alpha = 6\left( -\frac{\alpha }{3}\right) + \alpha = -2\alpha + \alpha = -\alpha , \end{aligned}$$

so:

$$\begin{aligned} J\left( -\frac{\alpha }{3}, 0\right) = \begin{bmatrix} 0 & 1 \\ -\alpha & 0 \end{bmatrix}. \end{aligned}$$

The characteristic polynomial is:

$$\begin{aligned} \lambda ^2 + \alpha = 0 \quad \Rightarrow \quad \lambda = \pm \sqrt{-\alpha }. \end{aligned}$$

Hence:

  • \(\alpha < 0\): eigenvalues real and of opposite sign \(\Rightarrow\) saddle point (unstable).

  • \(\alpha = 0\): eigenvalues zero \(\Rightarrow\) non-hyperbolic (degenerate).

  • \(\alpha > 0\): eigenvalues purely imaginary \(\Rightarrow\) linear center.

Theorem 3

(Bifurcation Behavior) The system (77) exhibits a saddle-center bifurcation at \(\alpha = 0\).

  • For \(\alpha < 0\): \(E_1 = (0, 0)\) is a center; \(E_2 = \left( -\frac{\alpha }{3}, 0\right)\) is a saddle.

  • For \(\alpha = 0\): both equilibria merge at the origin, forming a degenerate equilibrium.

  • For \(\alpha > 0\): \(E_1\) becomes a saddle; \(E_2\) becomes a center.

This is a classical example of a saddle-center bifurcation, in which a saddle and a center exchange roles via a degenerate equilibrium point as the parameter \(\alpha\) passes through zero. Figure 1 represents all three cases of stability.

Fig. 1
figure 1

Phase portraits for different values of the parameter \(\alpha\). (a) \(\alpha = 6\); (b) \(\alpha = -6\); (c) \(\alpha = 0\).

Full size image

Graphical depictions and physical interpretations of some solutions

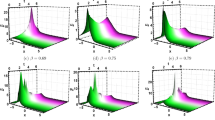
In this section, numerical simulations illustrating the physical representations of various solutions are presented in the form of 3D, contour, and 2D diagrams. Figure 2 offers a bright soliton solution associated with Eq. (12) when supposing \(\xi =0.7,~\tau _2=1.5,~y=0\) and \(x\) from \(-5\) to 7. This graphic demonstrates the energy-preserving behavior of bright solitons by showing the steady propagation of a confined wave with a prominent peak that holds its form over time. Figure 3 offers a singular periodic solution associated with Eq. (16) when supposing \(\xi =0.8,~\tau _2=-1.5,~y=0\) and \(x\) from \(-7\) to 7. The wave structure seen in this picture has many singular peaks, signifying abrupt changes and recurring singularities that might be related to physical processes such as wave collapse or resonance in nonlinear media. Figure 4 illustrates the singular soliton solution corresponding to Eq. (20) for the parameters \(\xi = 0.9\), \(\tau _2 = -1.6\), with \(y = 0\) and \(x\) ranging from \(-7\) to \(7\). This figure displays a single, strong spike with a non-smooth profile, which is indicative of a soliton with singular behavior that may be used to explain occurrences involving rapid energy concentration or discontinuities. Figure 5 offers the dark soliton solution associated with Eq. (50) when supposing \(\xi =0.6,~y=0\) and \(x\) from \(-7\) to 7. As is common with dark solitons, which are frequently encountered in optical fibers and Bose-Einstein condensates where phase shifts and intensity decreases are detected, this picture shows a localized dip in the wave amplitude against a continuous backdrop.

Fig. 2
figure 2

3D, contour and 2D diagrams of bright soliton solution associated with Eq. (12).

Full size image
Fig. 3
figure 3

3D, contour and 2D diagrams of singular periodic solution associated with Eq. (16).

Full size image
Fig. 4
figure 4

3D, contour and 2D diagrams of singular soliton solution associated with Eq. (20).

Full size image
Fig. 5
figure 5

3D, contour and 2D diagrams of dark soliton solution associated with Eq. (50).

Full size image

Results and discussion

In this study, we applied the ME mapping technique, well-adapted and methodically applied to a newly structured (2+1)-dimensional integro-partial differential equation. While the ME mapping technique itself is a well-known nonlinear science analytical tool, the novelty of this research stems from certain very important points:

First, this study represents the first application of the ME mapping technique to the above (2+1)-dimensional nonlinear integro-partial differential equation, a model that, to our best knowledge, has not yet been addressed by this method. This extension demonstrates the flexibility and adaptability of the ME mapping technique to solve complex nonlinear configurations, making it more applicable to more complex and higher-dimensional systems.

Second, our analysis effectively offers a rich and comprehensive set of precise analytical solutions, including bright soliton, dark soliton, singular soliton, and singular periodic, periodic, hyperbolic, exponential, Jacobi elliptic functions, and Weierstrass elliptic doubly periodic solutions. Strikingly, these kinds of solutions have not emerged in this particular equation before, which means that the results achieved are novel, enriching the solution space of such models. The findings of these new wave structures are insightful into the intrinsic physical phenomena encoded by this equation.

Third, the key contribution emphasized in this paper is the bifurcation and stability analysis of the reduced dynamical system from the reduced equation. This additional analytical method not only vindicates the solutions obtained but also sheds light on their nature of stability and the complex nonlinear dynamics of the system.

Overall, this multi-faceted approach enhances the analytical capability of the study and demonstrates that the proposed methodology is not a reworking of current techniques but a robust and new paradigm that can manage complex nonlinear models, revealing insights impossible with earlier proven techniques.

Conclusion and future recommendations

In this work, we used the ME mapping technique to investigate the solitonic and dynamical behaviors of a unique variant of the (2+1)-dimensional Kadomtsev–Petviashvili problem. This study was carried out for the first time on this particular formulation and produced a wide range of exact analytical solutions, such as periodic, singular periodic wave solutions, bright, dark, and singular solitons, exponential and hyperbolic function solutions, and Weierstrass elliptic doubly periodic solutions. These solutions not only show the complex dynamical aspects of the modeled nonlinear wave events, but they also exhibit the usefulness and flexibility of the approach used. To depict the dynamic features and physical interpretations of the derived solutions, a number of graphical visualizations were presented. This study adds to the existing body of knowledge by providing a more unified and flexible analytical framework for investigating (2+1)-dimensional nonlinear wave systems, with a focus on the results’ relevance to optical soliton propagation, oceanic wave patterns, and hydrodynamic models. In order to evaluate the resilience and adaptability of the ME mapping methodology, future studies might investigate its applicability to higher-dimensional and more complicated nonlinear models, especially those that contain variable coefficients or nonlocal components. Additionally, incorporating stochastic processes, such as noise perturbations or Wiener processes, would provide valuable insights into the influence of randomness on the system’s dynamics..