Introduction

The class E inverter and its practical derivatives play a pivotal role as the cornerstone of wireless power transfer (WPT) systems, enabling efficient energy conversion and transmission1,2,3,4,5,6. By leveraging its high-frequency switching capability and minimal power loss characteristics, it ensures optimal performance, making it indispensable for various applications such as wireless charging, biomedical devices, and industrial automation. Implantable devices like pacemakers, insulin pumps, and neural stimulators need a stable power source to function consistently and reliably7,8,9, Robots, automated machinery in factories, HTS devices, and HTS-based wireless power transfer frequently use WPT to remove the need for wires that could hinder their movement. A stable power supply is essential for these systems to ensure uninterrupted production. In general, achieving constant power in WPT systems is essential to ensure the protection of devices, accuracy in data collection and communication, battery life preservation, and support for sensitive applications10,11,12,13,14,15. This requires precise control and continuous feedback to adjust power according to the user’s needs. Various works based on controllers have been proposed to control the parameters of inverters and converters. In16 introduces a full-bridge inverter with a hybrid LCLC resonant tank, controlled by the optimum asymmetrical voltage cancellation (OAVC) approach, to achieve a constant output power for plasma applications. The design and realization of a PID controlled and DC/DC converter, which offers a flexible supply voltage to achieve specific output power for a radio frequency power amplifier has been presented in17. The PID method may require a certain amount of time to eliminate input errors, and occasionally it can exhibit sluggishness. The objective of the inverter introduced in18 is to ensure its resilience against changes in load and variations in component tolerances within the output resonant filter. The concept involves implementing frequency modulation control using the hill-climbing method for regulating the output voltage in a load-independent class-E inverter. A proposal has been made in19 for the design and control of a class E inverter capable of accommodating load variations. The suggested control scheme involves dynamically adjusting the input DC voltage, switching frequency, and duty ratio in response to changes in both load reactance and resistance. For application in a class-E2 dc–dc converter to manage the power flow, frequency and phase-shift control using the PI technique implemented on an FPGA has been discussed in20. In21 a class E power amplifier using perturbation and observation (P&O) method to maximize system efficiency has been presented. The control of the power amplifier using the P&O method is associated with delays and is characterized by a slower response. In order to prevent changes in the phase difference of the output of the class E inverter resulting from the transmitter–receiver displacement, multiple relays, and capacitors have been employed in22 to correct the resonant capacitor value of the output. Consequently, the circuit dimensions have increased, and the presence of relays in the circuit introduces the possibility of magnetic disturbances. In23, an approach to minimum input power operating point for a given output power in WPT systems has been introduced, which utilizes a maximum energy efficiency tracking (MEET) method. Notably, this method does not require any feedback from the receiver. Similar to the P&O method, the MEET method is also slow in controlling the WPT.

This paper presents the design, simulation, and fabrication of a load-independent class E inverter using two artificial neural networks (ANNs) to generate constant power independent of the load without feedback.

The structure of this article is as follows:

  • Load independent class E inverter with a compensation PID controller:

    In the initial phase, a class E inverter design is presented, incorporating a compensation PID controller to maintain a constant output power. Secondly, a buck converter is designed to generate the required input DC voltage for the inverter. Then, a system is developed that includes the inverter, converter, and PID controller to maintain constant output power, independent of the load. It is important to note that while a PID controller typically requires feedback from the system output, in practice, accurately measuring load resistance is often problematic.

  • ANN-based solution for PID feedback replacement:

    In the second section, a new methodology circuit is presented that replaces the PID controller with a primary ANN controller and substitutes the feedback system with a secondary ANN calculator. The secondary ANN takes the voltage and average input current of the inverter as inputs and solves the feedback from the output voltage and current. Its purpose is to calculate the appropriate load resistance, which is then provided as input to the primary ANN controller.

The designing of the proposed load-independent class E inverter

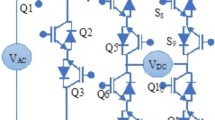
One of the key components influencing wireless power transfer systems in medical implants is the inverter used in the system, which is responsible for generating the required power for the proper operation of the device. Class E inverters have gained significant popularity in medical implants due to advantages such as easy construction, high power capability, and noise immunity. The main structure of a load-independent class E inverter is shown in Fig. 1a.

Fig. 1
figure 1

(a) The proposed load-independent class E inverter. (b) Wireless power transfer system in body.

Full size image

In the output block, as shown in Fig. 1b, the equivalent resistance between the transmitter and receiver coils in a wireless power transfer system which is established in and out of the body is represented as Rout. In different implants, achieving the desired power by modifying the fixed components used in the structure is a highly difficult and time-consuming task, requiring a complete redesign for each specific power requirement. To address this issue, an alternative solution must be proposed that enables the required power delivery to the load without altering the fixed components of the inverter structure. Therefore, the only adjustable element in the design as shown in Fig. 1a is the DC voltage of the inverter (VI). The relationship between VI, the current passing through the connected inductor in the DC block (Lin), and the output resistance (Rout) is given as follows. The transistor is off state in the range of 0 to π and on state in the range of π to 2π. Considering the output current as a pure sinusoidal waveform, the governing equations for the transistor voltage (Vs) in its off state, the capacitor current, and the current passing through the inductor Lin can be derived at node A based on KVL and KCL, which are expressed as:

$${{dV_{s} \left( \theta \right)} \mathord{\left/ {\vphantom {{dV_{s} \left( \theta \right)} {d\theta }}} \right. \kern-0pt} {d\theta }} = - \omega L_{in} \;{{d_{in}^{2} \left( \theta \right)} \mathord{\left/ {\vphantom {{d_{in}^{2} \left( \theta \right)} {d\theta }}} \right. \kern-0pt} {d\theta }}$$
(1)
$$i_{cex} \left( \theta \right) = \omega C_{ex} \;{{dV_{s} \left( \theta \right)} \mathord{\left/ {\vphantom {{dV_{s} \left( \theta \right)} {d\theta }}} \right. \kern-0pt} {d\theta }}$$
(2)
$${ }i_{in} \left( \theta \right) = \omega C_{ex} \;{{dV_{s} \left( \theta \right)} \mathord{\left/ {\vphantom {{dV_{s} \left( \theta \right)} {d\theta }}} \right. \kern-0pt} {d\theta }} + I_{m} \sin \left( {\theta + \varphi } \right)$$
(3)

where Vs is the switch voltage, ω represents the angular frequency calculated based on the equation ω = 2πf, iin is the current flowing through Lin, Cex is the external capacitor and Im is the amplitude of the output current. By combining the above-mentioned equations, a second-order differential equation based on the current passing through Lin is obtained, which can be solved as:

$$\begin{aligned} i_{in} \left( \theta \right) & = \left( {\frac{{{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times \sin \left( {\pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}} \right) \times I_{m} }}{{\left( {{1 \mathord{\left/ {\vphantom {1 {\omega L_{in} C_{ex} }}} \right. \kern-0pt} {\omega L_{in} C_{ex} }} - 1} \right)\left( {\cos \left( {\pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} - 1} \right)} \right)}}} \right. \\ & \quad \left. { + \frac{{\pi \times V_{I} }}{{2\omega L_{in} }}} \right)\cos \left( {\frac{1}{{\omega \sqrt {L_{in} C_{ex} } }}\theta } \right) + \left( { - \frac{{{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times I_{m} }}{{\left( {{1 \mathord{\left/ {\vphantom {1 {\omega L_{in} C_{ex} }}} \right. \kern-0pt} {\omega L_{in} C_{ex} }} - 1} \right)}}} \right. \\ & \quad \frac{{\pi \left( {\cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} + 1} \right)}}{{2\omega L_{in} \sin \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}}}\sin \frac{1}{{\omega \sqrt {L_{in} C_{ex} } }}\theta \\ & \quad + \frac{{\frac{1}{{\omega \sqrt {L_{in} C_{ex} } }}}}{{\frac{1}{{\omega^{2} L_{in} C_{ex} }} - 1}}I_{m} \sin \left( {\theta + \varphi } \right) \\ \end{aligned}$$
(4)

In the on-state of the transistor, the inductor current Lin is expressed as:

$$i_{in} \left( \theta \right) = \frac{{V_{I} }}{{\omega L_{in} }} \times \theta - \frac{{\pi V_{I} }}{{\omega L_{in} }} + i_{in} \left( \pi \right)$$
(5)

By applying boundary conditions to determine the exact current values at the transistor’s on and off transition times, specifically at θ = 0 and θ = π, and also enforcing the condition of no output voltage variation based on current, which forms the basis of load-independent conditions, the inductor current Lin can be calculated as a function of VI and is expressed as:

$$\begin{aligned} i_{in} \left( \theta \right) & = \frac{1}{\pi }\left[ {\theta \left( {1 - \cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}} \right)\left( {\frac{{{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times \sin \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times I_{m} }}{{\left( {{1 \mathord{\left/ {\vphantom {1 {\omega L_{in} C_{ex} }}} \right. \kern-0pt} {\omega L_{in} C_{ex} }} - 1} \right)\left( {\cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} - 1} \right)}} + \frac{{\pi \times V_{I} }}{{2\omega L_{in} }}} \right)} \right. \\ & \quad \left. - {\left( { - \frac{{{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times I_{m} }}{{\left( {{1 \mathord{\left/ {\vphantom {1 {\omega L_{in} C_{ex} }}} \right. \kern-0pt} {\omega L_{in} C_{ex} }} - 1} \right)}} - \frac{{\pi \left( {\cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} + 1} \right)}}{{2\omega L_{in} \;\sin \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}}}} \right)\theta \sin \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}} \right] \\ & \quad - 2\left[ {\left( {\frac{{{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times \sin \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times I_{m} }}{{\left( {{1 \mathord{\left/ {\vphantom {1 {\omega L_{in} C_{ex} }}} \right. \kern-0pt} {\omega L_{in} C_{ex} }} - 1} \right)\left( {\cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} - 1} \right)}} + \frac{{\pi \times V_{I} }}{{2\omega L_{in} }}} \right)} \right. \\ & \quad \times \left( {\frac{1}{2} - \cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}} \right) - \left( { - \frac{{{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} \times I_{m} }}{{\left( {{1 \mathord{\left/ {\vphantom {1 {\omega L_{in} C_{ex} }}} \right. \kern-0pt} {\omega L_{in} C_{ex} }} - 1} \right)}} - \frac{{\pi \left( {\cos \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }} + 1} \right)}}{{2\omega Lf\sin \pi \;{1 \mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}} \right. \kern-0pt} {\omega \sqrt {L_{in} C_{ex} } }}}}} \right) \\ & \quad \left. {\left( {\sin \pi {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\omega \sqrt {L_{in} C_{ex} } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega \sqrt {L_{in} C_{ex} } }$}}} \right)} \right] \\ \end{aligned}$$
(6)

The average input current (Iin_mean) is influenced by two factors: the load resistance (Rout), which is obtained based on the change of voltage (Vm) over current (Im), and the inverter’s input voltage (VI), as illustrated in Fig. 2. It is apparent that as the load resistance increases, the average input current of the inverter decreases. Conversely, as the inverter’s input voltage increases, the input current also rises. This demonstrates that the relationship between load resistance (Rout), input current (Iin), and input DC voltage (VI) is nonlinear. Therefore, to adjust the output power without changing the circuit components, the DC voltage of the load-independent inverter (VI) needs to be changed.

Fig. 2
figure 2

The average value of the input current of the inverter versus Rout and VI. Created using MATLAB version R2024a (https://www.mathworks.com).

Full size image

Design and development of the requisite converter and PID control system

To regulate the DC input voltage of the inverter (VI), a buck converter is required to provide a variable voltage range, allowing the output power to be adjusted to the desired level, as shown in Fig. 3. The output voltage range of the converter can be controlled by modifying the duty ratio of the transistor used in it. The design parameters, such as the inductor value (Lcon), can be determined using the following equation:

$$L_{con} = 1 \cdot 25 \times \frac{{\left( {1 - D} \right)}}{2 \times f} \times \frac{{V_{I} }}{{I_{in} }}$$
(7)
Fig. 3
figure 3

The proposed converter included in the load-independent class E inverter.

Full size image

In Eq. (7), the value of D represents the duty ratio, f represents the frequency of the pulses applied to the transistor, VI and Iin represent the output voltage and current of the converter, which are implied to the input of class E inverter. The value of Lcon is obtained as 5 µH under worst-case conditions for an operating frequency of 1 MHz. The value of the converter circuit’s capacitor (Ccon) is obtained from the following equation:

$$C_{con} = \frac{{\left( {1 - D} \right)}}{{8 \times L_{con} \times \left( {{{\Delta V_{I} } \mathord{\left/ {\vphantom {{\Delta V_{I} } {V_{I} }}} \right. \kern-0pt} {V_{I} }}} \right) \times f^{2} }}$$
(8)

In Eq. (8), the value of ΔVI represents the magnitude of the output voltage ripple of the converter. The value of Ccon is determined to be 100 µF.

To adjust the duty ratio of the designed converter for achieving a new set point output power, it is necessary to obtain feedback from the calculated output resistance (Rout) or (Vo and Io). Additionally, a PID controller must be designed to adjust the appropriate duty ratio of the converter based on the new set power of the load, ensuring the generation of a suitable DC voltage to supply the required new power. The circuit diagram of the proposed load-independent class E inverter, along with the control duty ratio of the converter circuit designed for regulating and stabilizing the output power level in the MATLAB Simulink environment, is illustrated in Fig. 3. Presented block diagram of the intended, system with PID controller for power stabilization of an inverter is shown in Fig. 4a. The parameter values used for presented load independent class E inverter in Fig. 4b are specified in Table 1.

Fig. 4
figure 4

(a) Presented block diagram of the intended system with PID controller for power stabilization of an inverter. (b) The proposed circuit with PID controller in MATLAB SIMULINK.

Full size image
Table 1 The values of the utilized components in the proposed circuit with the PID controller.
Full size table

The parameter values presented in Table 1 were carefully selected to meet the specific operational demands and limitations of medical implant applications. Such devices commonly operate within the MHz frequency range to facilitate efficient wireless power transfer through biological tissue while minimizing the physical footprint of the implanted system. The switching frequency of 1 MHz was chosen to align with medical implant standards and to reduce the size of passive components like Lr, Cr, and Cs. The resonant elements Lr = 55.2 µH and Cr = 460 pF were specifically designed to achieve load-independent zero-voltage switching (ZVS) operation of the class E inverter at 1 MHz by the design methodologies discussed in24,25. A load resistance of RL = 15 Ω was used to emulate typical conditions found in bio-implant systems, for the converter section, components such as Ccon = 100 µF and Vcon = 12 V were selected to ensure a stable, low-ripple DC supply to the inverter stage, crucial for the reliable performance of sensitive medical electronics. Overall, each parameter was chosen to balance efficiency, miniaturization, and safe operation within the strict biomedical constraints of implantable devices.

Figure 5 illustrates the drain-source voltage of the transistor (Vs), the inverter’s input current (iin), output current (io), and output voltage (Vo), as well as the inverter’s input DC voltage (VI) and output power (Po). It can be observed that to achieve an output power of 2 W with a load resistance of 15 Ω, the converter’s output voltage (or the inverter’s input voltage) needs to be 5.13 V. Additionally, the pulse frequency for both the converter and the inverter is 1 MHz.

Fig. 5
figure 5

Drain source voltage waveform of the transistor VS, input current of the inverter iin, output current of the inverter io, output voltage of the inverter VO, input DC voltage of the inverter VI, and output power Pout versus time.

Full size image

The voltage waveform generated by the converter, identified as the input voltage of the inverter, and the output power graph for varying load resistances of 15, 30, 45, and 15 Ω, respectively, are shown in Fig. 6. The PID controller parameters were calculated using the Ziegler–Nichols method. The proportional coefficient was set to 10, the integral coefficient to 0.002, and the derivative coefficient to 0.1. With the presented design of this PID controller, it is observed that with changes in output resistance or by changing the set point output power, the PID controller is able to efficiently stabilize the output power to a constant value of 2 W, following a few oscillations during each transition. Output power stabilization is accomplished by modifying the converter’s duty cycle, which in turn adjusts the inverter’s input voltage. One notable drawback of the PID controller is the relatively extended duration required to compensate for the output power. Another noteworthy factor is the significant reliance of the PID controller’s coefficients on the output resistance, the converter’s input DC voltage (Vcon), and the power set point (Psp). As a result, the PID controller’s coefficients must be continuously updated to maintain optimal controller performance and prevent system instability under the given parameters.

Fig. 6
figure 6

Vs, VI, and Pout of the presented circuit with PID controller for varying load resistances of 15, 30, 45, and 15 Ω.

Full size image

Development of a load-independent class E inverter using ANN controller with secondary ANN for output feedback substitution

In practical applications such as biomedical implants, accurately measuring load resistance is often insufficient and it may lead to the addition of extra components in the structure of the wireless transmission system, such as Bluetooth or Wi-Fi modules. Also, to achieve effective feedback, a processor with a high sampling frequency analog-to-digital converter is required to precisely calculate the maximum output current and voltage, ensuring accurate load resistance determination, which practically makes this impossible. The proposed solution, as shown in Fig. 7, employs a primary ANN to replace the traditional PID controller and a secondary ANN instead of the feedback system to resolve the identified challenges. Also, in Fig. 2, it was concluded that the output resistance of the inverter can be predicted based on the DC voltage value and the current flowing through the inductor in the DC blocking section. In the presented system, the primary ANN receives the output resistance value from the secondary ANN. Considering the desired power target (Psp) and the input DC voltage of the converter (Vcon), the primary ANN calculates the necessary duty ratio to generate an appropriate input voltage for the inverter.

Fig. 7
figure 7

Presented block diagram of the intended presented system with primary ANN controller and Secondary ANN for RL calculation.

Full size image

As illustrated, the Secondary ANN computes the necessary load resistance value for the primary ANN controller. In this instance, standard processors can effectively perform analog-to-digital conversion with sufficient accuracy. Taking into account all the aforementioned explanations, this paper employs two neural networks for Class E inverter control: one predicts the load, and the other stabilizes output power by adjusting the supply voltage through a converter. This approach uses feedback from the converter’s voltage and current instead of the inverter output, simplifying the control loop and improving stability. Despite its advantages, the ANN-based control depends heavily on training data quality, assumes a fixed switching frequency, and requires retraining for new conditions. Additionally, limited real-time learning reduces adaptability in dynamic environments. The desired secondary ANN for calculating the value of the load resistance consists of a hidden layer with 5 neurons and the hyperbolic tangent sigmoid function for this layer, and the Purlin function for the output layer. This neural network has been simulated using 112 MATLAB Simulink data. 80% of these data were used for training and 20% for testing. It has a suitable mean relative error (MRE) of less than 0.01 for the test data.

Figure 8 illustrates the overall structure of the load resistance calculator ANN, along with the primary controller ANN. As evident, the initial artificial neural network obtains the load resistance value based on the VI and Iin_mean and delivers it as input to the primary controller ANN. Psp represents the set point power, and Vcon represents the applied DC voltage to the converter. D represents the Duty ratio, which is the value of the applied signal to the gate transistor of the converter. The primary ANN is considered with 8 neurons in the first layer and 6 neurons in the second layer, as shown in Fig. 8. In the first step, an artificial neural network with a single-layer architecture was designed. The activation function chosen for this layer was the tangent sigmoid, which due to its nonlinear nature has a high capacity for modeling complex relationships between data. As the number of neurons in this layer increased, the MRE consistently decreased. After 8 neurons the test error began to increase. The second hidden layer was added to the network. The activation function for the first layer remained the tangent sigmoid, while the purlin function was used for the second layer. The reason for choosing purlin is its adaptability, which provides greater flexibility and allows the network to learn more complex patterns. The results showed that as the number of neurons in the second layer increased, the MRE indicated an improvement in model performance. Specifically, the configuration with 6 neurons in the second layer resulted in the lowest error. This two-layer structure with 8 neurons in the first layer and 6 in the second was identified as the optimal configuration. The obtained MRE for the test data is 0.0063. Furthermore, the dataset used for training and testing consists of 150 data points and is obtained from the simulation results of Simulink in MATLAB.

Fig. 8
figure 8

The overall structure of the load resistance calculator ANN, along with the main controller ANN.

Full size image

Figure 9a represents the regression plot of the primary ANN output. As can be observed, the predicted data by the neural network aligns well with the actual data, and the regression plot forms a linear graph. Figure 9b shows the plot of actual and predicted data based on their data numbers, and similar to the regression plot, the data points exhibit a high degree of similarity to each other.

Fig. 9
figure 9

(a) Regression plot of the presented ANN controller. (b) Predicted and actual output data versus data number.

Full size image

Figure 10 depicts the implemented system using two implemented ANNs in MATLAB SIMULINK. As observed, the input voltage of the inverter (VI) and the average input current of the inverter (Iin_mean) are sampled and fed into a neural network for detecting the load resistance value. The primary ANN, based on the load resistance, PSP power, and converter voltage, determines the appropriate value of the duty ratio.

Fig. 10
figure 10

The proposed circuit with ANN controller along with the load resistance calculator ANN in MATLAB SIMULINK.

Full size image

Figure 11 illustrates the voltage waveform of the inverter input, output power, and transistor voltage under varying load resistance conditions. Therefore, in this case, as previously mentioned, we can calculate the inverter load resistance without the need for output voltage and current sampling and provide it as input to the load resistance calculator ANN. In this scenario, there is no need for high-frequency sampling, and only the input DC voltage and current of the inverter are sampled.

Fig. 11
figure 11

The voltage waveform of the inverter input, output power, and transistor voltage under varying load resistance conditions for the proposed circuit with ANN controller along with the load resistance calculator ANN.

Full size image

The proposed load-independent Class E Inverter with the primary ANN controller along with the secondary ANN for RL calculation is fabricated as shown in Fig. 12. The switching frequency plays a critical role in determining the performance of Class E inverters, influencing efficiency, output power, and stress on circuit components. While higher frequencies allow for smaller passive elements and compact designs, they also increase switching losses and electromagnetic interference, potentially lowering efficiency. Class E inverters rely on precise zero-voltage switching (ZVS) conditions, which are sensitive to frequency changes; deviations can lead to higher power dissipation and stress. Recent studies confirm that optimal frequency selection is essential for maximizing performance and efficiency. In this paper, however, frequency variation is not addressed. The control circuit, based on an Artificial Neural Network (ANN), is designed assuming a fixed switching frequency of 1 MHz, generated reliably by an STM32F103C8 microcontroller. Although the ANN-based design targets medical implants, it can be adapted to support other frequencies with proper modifications.

Fig. 12
figure 12

The proposed class E inverter with ANN controller along with secondary ANN for RL calculation.

Full size image

The ANN architecture presented in this study is inherently adaptable and can be extended to accommodate a wide range of operating conditions. Although the current implementation is based on a fixed switching frequency and stable environmental parameters, the model can be retrained with new datasets to handle variations such as different switching frequencies, load profiles, and environmental disturbances (e.g., temperature fluctuations). This flexibility makes the proposed approach suitable for future applications in more complex and dynamic systems, where traditional feedback-based control methods may face limitations.

In the presented Class E Inverter, efficiency increases with higher load resistance and duty ratio. At lighter load resistances, conduction losses are reduced due to lower output current, and higher duty ratios lead to lower voltage stress and switching losses, resulting in improved efficiency. Figure 13 shows the variations of efficiency based on variations of duty ratio and output load resistance.

Fig. 13
figure 13

Efficiency variation of the proposed class E inverter based on changes in duty ratio and output resistance (RL).

Full size image

The experimental hardware presented in Fig. 12 has been designed to support different resistance values (15 Ω, 30 Ω, and 40 Ω), which were taken into account during both the design and fabrication phases. This flexibility was achieved by incorporating jumpers in the hardware layout, allowing easy selection between the three resistance values. As shown in Fig. 14, the hardware results corresponding to these three resistance values have been presented. These results demonstrate the practical implementation and performance of the proposed design under varying load conditions.

Fig. 14
figure 14

The waveform of switch voltage (Vs), output Voltage (Vout), and voltage applied to the transistor gate in the inverter.

Full size image

Figure 15 shows the results of the theory, simulation, and fabrication of the proposed system. As can be seen, the output power remains around 2 W in all three results with the change of resistive load.

Fig. 15
figure 15

PO versus RL variation for the presented system.

Full size image

Table 2 illustrates a comparison between the proposed work in this article and References. The proposed circuits in references12,13,14,15,16,17,18,19,20,21 have a control system. As revealed in Table 2 various methods have been presented for controlling voltage, power, and output efficiency in inverters. The duty ratio of the inverter transistor or the converter transistor providing the required DC voltage for the inverter can be adjusted, as well as the operating frequency of the inverter and the phase shift of the output voltage and current. In references12,13,14,15,16,17,18, the PID controller has been utilized to achieve the desired set point. Although the design of the PID controller is simple, it suffers from the issue of potential system instability due to changes in plant parameters such as load resistance and input DC voltage to the inverter. Therefore, the PID controller coefficients need to be updated continuously. Additionally, during startup and system changes, the desired variables such as output power and voltage exhibit significant overshoot, which can potentially damage the transistor. As previously mentioned, the proper functioning of PID controllers relies on receiving feedback from the system’s output. However, in high-frequency circuits, such as the one proposed in this study, real-time measurement of the output voltage and current not only requires high-speed operation but also necessitates the addition of extra sampling circuits at the output. This, in turn, results in additional circuitry and increased losses at the output. The Perturbation and Observation (P&O) method, which is a slow approach to reach the maximum available power at the inverter output, has been employed in19,20,21. Although this method can also be used to reach the set point of output current or voltage, each change requires a considerable amount of correction time. In this paper, Firstly, using a PID controller, the control capability for the output power value of this inverter was designed and presented by adjusting the duty ratio of the converter circuit providing the required DC voltage input to the inverter, based on the specifications provided in Table 2. It was observed that the system could become unstable during changes in the plant elements and variables in the PID controller mode. Furthermore, the time required for power correction was significant. Subsequently, a novel circuit was introduced that replaces the traditional PID controller with a primary ANN controller and the feedback system with a secondary ANN calculator. The secondary ANN uses the inverter’s voltage and average input current as inputs to determine the optimal load resistance. This calculated resistance is subsequently passed to the primary ANN controller for adjusting the duty ratio of the converter circuit to supply the necessary DC voltage input to the inverter. Therefore, the desired Class E inverter was successfully presented using two ANNs, effectively addressing the issues with the PID controller, based on the specifications provided in Table 2.

Table 2 Comparison between the proposed inverter and references.
Full size table

Limitations and future work

While the proposed ANN-based control strategy demonstrates reliable performance under fixed operating conditions, it is important to acknowledge certain limitations. The model currently operates at a fixed switching frequency, which may limit its adaptability to systems with variable conditions. Additionally, applying the ANN to new operating scenarios requires retraining with updated datasets, which may increase implementation complexity. However, in the context of biomedical applications particularly implantable devices fixed switching frequencies are often required due to safety, electromagnetic compatibility, and regulatory standards. Therefore, this design decision remains practical and justified for the intended use case. Future work will investigate the incorporation of adaptive or online learning mechanisms to enable real-time reconfiguration of the ANN, thereby improving robustness and extending applicability to more dynamic and uncertain environments.

Conclusion

In this paper, firstly a system for selecting the desired and constant output power, comprising the designed inverter, converter, and PID controller, was presented. It was observed that while the PID controller features a simple design, it faces challenges such as system instability and significant settling time. Additionally, accurate measurement of load resistance through feedback circuits is often difficult in practice especially in biomedical implants. As a result, the system replaces the PID controller with a primary ANN and utilizes a secondary ANN to determine the appropriate load resistance, instead of relying on feedback circuits. The secondary ANN takes the voltage and average input current of the inverter as inputs, with its primary function being to calculate the required load resistance, which is then provided as input to the primary neural network controller. The average input current to the inverter is influenced by both the load resistance and the input voltage. The desired load-independent Class E inverter delivers 2 W of output power at 1 MHz switching frequency. Theoretical, measurement, and simulation results show good agreement. This inverter is suitable for use in wireless chargers for mobile phones, smartwatches, and medical devices implanted in the body.