Real time wire rope detection method based on Rockchip RK3588

Abstract

In the era of fully mechanized and automated coal mine production, the need for autonomous fault detection and intelligent identification of wire ropes has become increasingly critical. Conventional model training and algorithmic computations rely on server-based systems, requiring significant computational resources. This study proposes a real-time wire rope detection system utilizing the Rockchip RK3588 platform. To enhance non-destructive wire rope inspection, a Mini-YOLO model was developed by integrating MobileNetV3, the Coordinate Attention (CA) mechanism, and a novel loss function, Inner-IoU, into the YOLOv8 framework. This paper’s innovation lies not in creating algorithmic components from scratch, but in their synergistic integration and targeted optimization to solve the specific challenges of real-time defect detection on resource-constrained edge devices. To optimize the Neural Network Processing Unit (NPU) for computational performance, a thread pool is implemented with the C++ programming language to partition and accelerate the output processing of the model. Additionally, a Docker container is employed for environment configuration, simplifying deployment. After testing, the raw data and test results are stored in real-time, with periodic uploads to the cloud for data backup. Experimental findings demonstrate that the Mini-YOLO algorithm achieves a computational speed 2 times faster than YOLOv8, with an accuracy improvement of 1.2%. After deployment, the inference time per image is approximately 18.5 ms per image, enabling efficient real-time detection.

Introduction

Wire ropes play an essential role in various applications, including ports, mines, elevators, and heavy-lifting operations. Failure to detect defective wire ropes can result in significant safety hazards during production¹. Common defects in wire ropes include broken wires, wear, and corrosion². The non-destructive testing technique(NDT) highlighted in this study focuses specifically on detecting broken wires. Among the existing non-destructive testing methods for wire ropes, optical analysis is often compromised by surface contaminants, while ultrasonic testing confronts challenges like instability. The most widely used method is electromagnetic testing^3,4,5, which identifies broken wire defects by detecting magnetic field leakage signals caused by localized damage in the wire ropes.

Among the means of detecting magnetic field leakage signals, time domain analysis is difficult to identify weak defects in a high noise environment; frequency domain analysis loses time information and is ineffective for non-stationary signals whose frequency changes with time. Therefore, in the field of non-destructive testing of wire ropes, two basic time-frequency analysis (TFA) methods - short-time Fourier transform (STFT) and wavelet transform (WT) - have been widely used⁶. By observing the spectrum or wavelet scale map, transient high-frequency events representing defects and periodic low-frequency components representing string waves can be distinguished. However, they also have inherent limitations. STFT uses a fixed-length window function to segment the signal, which cannot take into account both time resolution and frequency resolution. For leakage magnetic signals containing short-time defect pulses and specific frequency string components, any single fixed window size cannot achieve the best joint time-frequency resolution⁷. Wavelet transform provides a multi-resolution analysis framework through an extensible “mother wavelet” basis function, which is more suitable for analyzing leakage magnetic signals. However, the shape of the mother wavelet selected by wavelet transform must closely match the characteristics of the target signal to achieve optimal energy concentration and feature extraction. The selection of mother wavelets lacks universal theoretical guidance and usually requires a lot of prior knowledge and iterative experiments. These limitations of the TFA method have spawned other technical routes. For example, more adaptive TFA algorithms: synchrosqueezed transform (SST)^8,9,10 and empirical wavelet transform (EWT)¹¹, but these methods increase computational complexity and theoretical difficulty^12,13,14. A more disruptive path is to turn to a data-driven deep learning paradigm¹⁵. Specifically, convolutional neural networks (CNNs) can automatically learn the best feature representation directly from raw data, eliminating the complex process of manually designing and selecting analysis parameters.

Real-time object detection is a critical field in computer vision with diverse applications, including multi-object tracking, autonomous vehicles, and medical imaging analysis¹⁶. These tasks are commonly executed using computing devices such as mobile CPUs, GPUs, or specialized NPUs¹⁷. The AI terminal integrated into this system is designed with an NPU to enhance performance.

Most commercially available devices employing electromagnetic detection exhibit poor real-time performance, with inspection processes requiring 20 to 30 minutes after data collection¹⁸. Additionally, the majority of these systems depend on local or cloud-based GPU servers for model operation, resulting in high equipment costs. Practical deployment of such algorithms poses significant challenges, as the trained models exhibit sensitivity to environmental variations when transitioned from servers to edge devices¹⁹. To overcome these challenges, the Rockchip RK3588 platform was chosen due to its exceptional NPU capabilities (6 TOPS), energy-efficient design (5-13W), and broad compatibility with various operating systems. Compared to the Jetson Nano, RK3588 offers a higher computational density while remaining cost-effective, making it a suitable option for real-time wire rope detection. For a detailed comparison of hardware parameters, refer to Supplementary Table 1 in the Additional information.

The primary contributions of this paper are summarized as follows:

• 1. To improve the efficiency and accuracy of deep learning algorithms for edge computing devices, this study incorporates MobileNetV3²⁰, the Coordinate Attention (CA) mechanism²¹, which highlights spatial information, and an enhanced loss function, Inner-IoU²², into the YOLOv8 framework. These integrations led to the development of Mini-YOLO, a system specifically designed for non-destructive wire rope inspection. Compared to YOLOv8, Mini-YOLO exhibits superior speed and accuracy, enabling more effective and efficient inspection processes.

• 2. To further enhance edge computing performance, the final output is split to accelerate processing. Optimization is carried out using C++ programming alongside a thread pool, fully utilizing the NPU capabilities of the Rockchip RK3588 embedded platform. This approach significantly enhances detection speed on edge devices.

• 3. To simplify model deployment and effectively manage raw datasets and final testing results, a real-time non-destructive testing system for wire ropes has been developed. The system integrates critical functionalities, including model optimization, format conversion, acceleration, and data storage, facilitating the overall process.

The remainder of this paper is organized as follows: Section"Related work"presents an in-depth review of related research in the field of non-destructive wire rope testing. Section"Methodology"details the key components of the study, including MobileNetV3, the CA mechanism, the Inner-IoU loss function, model output splitting, and thread pool-based acceleration. Section"Experiment and results"highlights the experimental results and provides a thorough analysis. Finally, Section"Conclusion"summarizes the key findings of the study.

Related work

Nondestructive testing of wire ropes

Traditional methods directly apply techniques such as WT and STFT to electromagnetic signals, which usually require complex parameter adjustments and have insufficient generalization capabilities in different types of wire ropes and defect scenarios. To overcome these limitations, deep learning methods have emerged, which can be roughly divided into one-dimensional and two-dimensional paradigms. One-dimensional convolutional neural networks (1D-CNNs) have been used to directly classify defects from magnetic flux leakage (MFL) signals. For example, Liu and Chen et al. proposed a 1D-CNN-based method with a classification accuracy of over 98%. However, such methods usually focus only on classification and cannot accurately locate defects, and their inference time (e.g., 2.33 seconds per sample) is not suitable for real-time applications. Another popular paradigm is to convert the one-dimensional signal into a two-dimensional image for analysis using powerful vision-based models. This “imaging” of time series signals has been explored in various ways. Some researchers use STFT or CWT to convert the signal into a two-dimensional time-frequency representation (spectrogram or scalogram)^23,24, and then process it using 2D-CNN⁶. Wang et al.²⁵ converted the loss of metal area (LMA) signal into a two-dimensional grayscale image and applied a CNN-Transformer model for defect diagnosis, using techniques such as transfer learning to address the data scarcity problem. Although these image-based methods are flexible and can leverage mature computer vision architectures, their performance ceiling is often limited by the initial signal-to-image conversion. The choice of transformation parameters (e.g., window size in STFT or mother wavelet in CWT) still affects the input quality²⁶, which means that the model cannot completely get rid of the limitations of traditional TFA methods. Compared with these methods, our image-based Mini-YOLO method is able to directly obtain the features of defects and accurately obtain location information. In addition, the inference time per image after deployment is only 18.5 milliseconds, successfully achieving real-time detection capabilities that previous methods lack.

Huang et al.²⁷ proposed a method for detecting wire rope damage using a convolutional neural network (CNN), enabling the autonomous extraction of discriminative features by the trained model. Zhou et al.²⁸ developed an advanced deep convolutional neural network (DCNN) based on the LeNet-5 architecture for detecting surface damage in wire ropes. Furthermore, Zhou et al.²⁹ introduced an improved method based on YOLOv3³⁰ to enhance the accuracy of wire rope surface damage detection. Despite these advancements, these studies did not implement the models on edge devices, and the complexity of the models remained relatively high.

Several investigations have concentrated on modifying lightweight models to reduce the number of parameters and enhance detection speed. Chen et al.³¹ proposed a non-destructive detection algorithm for wire ropes based on an improved YOLOv7³², incorporating Ghost convolution modules to achieve a lightweight design and improve detection speed. However, lightweight models often sacrifice feature extraction capability and accuracy. In contrast, the proposed method enhances YOLOv8 effectively, utilizing the full computational power of NPUs during deployment. This ensures that the Mini-YOLO model achieves high accuracy and real-time performance on the RK3588 platform.

Model compression and acceleration

To facilitate the seamless deployment of deep learning (DL) algorithms on edge devices, a variety of optimization strategies have been developed, targeting both hardware and software aspects³³. For instance, Wei et al.³⁴ incorporated a fire module similar to SqueezeNet³⁵ into the YOLOv3 framework, successfully reducing the parameter count of the model. They also introduced dense connections within these fire modules to maintain the feature extraction capabilities of the model. Similarly, Wu et al.³⁶ applied sparse training and channel pruning techniques to eliminate less impactful channels, thus reducing the required parameter storage. This approach enables fast and accurate detection while meeting the constraints for deployment on embedded devices.

Methodology

Mini YOLO architecture

MobileNetV3 lightweight backbone

This study enhanced the YOLOv8 model by incorporating MobileNetV3, the Coordinate Attention (CA) mechanism, and the Inner-IoU loss function, resulting in the development of Mini-YOLO, specifically designed for non-destructive wire rope inspection. MobileNet models are optimized for efficient performance on mobile devices with constrained computing resources. Among them, MobileNetV3 stands out for its computational efficiency, resource optimization, and processing speed, making it a popular choice for edge devices with limited processing power. In the proposed approach, MobileNetV3 is incorporated into the YOLOv8 framework to enable real-time detection in wire rope inspection systems.

As shown in Fig. 1, the MobileNetV3 model introduces several improvements over its predecessor:

• 1. It replaces the traditional $3\times 3$ convolutional layers in the fusion block with $1\times 1$ convolutional layers. This modification simplifies the learning task of the block and prevents a significant increase in the number of parameters during scaling. For instance, doubling the input and output of a $3\times 3$ network would quadruple the input size and double the output, while a $1\times 1$ convolution layer maintains the same input and output dimensions.

• 2. MobileNetV3 strengthens the fusion of local and global features. The relationship between local and global features is enhanced, allowing for better feature extraction compared to the traditional approach that primarily focuses on the input and global features.

• 3. The model introduces residual connections from the ResNet architecture, which fuse input features to improve the performance of deeper networks.

• 4. The $3\times 3$ convolutional layer in the local representation block is replaced with a deeper convolutional layer, significantly reducing the number of model parameters while having minimal impact on recognition accuracy.

Fig. 1

Structure of the MobileNetV3 model.

Coordinate attention for localization

The CA mechanism offers an innovative and efficient approach to attention modules, as shown in Fig. 2. Based on the strengths of ECA³⁷ and CBAM³⁸, CA incorporates positional information into the channel attention calculation. This allows the network to focus on a wider range of features, improving the network accuracy without adding significant computational overhead. Additionally, the CA attention mechanism is simple and flexible, making it well-suited for integration into lightweight backbone networks like MobileNetV3 and EfficientNet³⁹.

Fig. 2

Structure of the coordinate attention module: “X Avg Pool” and “Y Avg Pool” denote one-dimensional global pooling operations in the horizontal and vertical directions, respectively.

The CA mechanism effectively captures information and long-range dependencies across different channels through a two-step process: coordinate information embedding and coordinate attention generation.

1) Coordinate Information Embedding: In conventional channel attention mechanisms, two-dimensional global pooling is commonly used to capture global information. While this method is computationally efficient, it results in the loss of positional information. This process can be mathematically expressed in the form below:

$$\begin{aligned} z_c = \frac{1}{H \times W} \sum _{i=1}^{H} \sum _{j=1}^{W} x_c(i, j) \end{aligned}$$

(1)

where $x_c$ represents the input from the convolutional layer, and $z_c$ is the result obtained by traversing the $c^{th}$ channel along the horizontal and vertical directions. The CA attention mechanism decomposes the two-dimensional global pooling from Equation 1 along two directions. The output $z_c$ in the vertical direction H is expressed as:

$$\begin{aligned} z_c^h(h) = \frac{1}{W} \sum _{0 \le i < W} x_c(h, i) \end{aligned}$$

(2)

The output $z_c$ in the horizontal direction W is:

$$\begin{aligned} z_c^w(w) = \frac{1}{H} \sum _{0 \le j < H} x_c(j, w) \end{aligned}$$

(3)

This approach allows for the capture of positional information in both the horizontal and vertical directions. At the same time, it preserves long-range dependencies, enabling the model to more accurately locate and identify the target areas.

2) Coordinate Attention Generation: To fully exploit the positional information generated in both the horizontal and vertical directions while simultaneously attending to long-distance dependencies, the coordinate attention generation process reprocesses the horizontal and vertical $x_c$ outputs obtained from Equations 2 and 3. First, the convolution transformation function $F_1$ is applied to process the horizontally and vertically connected $z^h$ and $z^w$ outputs along the spatial dimension. Then, the intermediate feature map f is derived through the activation function $\delta$:

$$\begin{aligned} f = \delta (F_1([z^h, z^w])) \end{aligned}$$

(4)

The intermediate feature map f incorporates spatial information from both directions during the encoding process. As a result, f is divided along these two directions as follows:

$$\begin{aligned} \begin{aligned} g^h&= \sigma (F_h(f^h)),&g^w&= \sigma (F_w(f^w)). \end{aligned} \end{aligned}$$

(5)

The intermediate feature map f is then processed into $f^h$ and $f^w$, which serve as convolution transformation functions, similar to Equation 4, with $\sigma$ representing the sigmoid activation function. The resultant output of the attention mechanism can be formulated as follows:

$$\begin{aligned} y_c(i,j) = x_c(i,j) \times g_c^h(i) \times g_c^w(j) \end{aligned}$$

(6)

By encoding spatial information along the horizontal and vertical directions, the model’s ability to accurately position and recognize targets is significantly enhanced.

Inner IoU bounding box regression

To resolve the challenges of poor generalization and slow convergence in existing IoU loss functions within detection tasks, this study introduces an innovative approach: using auxiliary bounding boxes for loss calculation. This modification can notably speed up the bounding box regression process. In the context of Inner-IoU, a scaling factor ratio is employed to resize the auxiliary box.

Figure 3 illustrates two distinct auxiliary boxes. The left box represents the reduced auxiliary box, while the right box represents the enlarged auxiliary box. In both boxes, $B^{gt}$ denotes the ground truth (GT) box, and B represents the anchor. The center points of both the GT box and the inner GT box coincide, denoted as $(x^{gt}_c, y^{gt}_c)$. Similarly, the center points of the anchor and the inner anchor align, marked as $(x_c, y_c)$. The width and height of all GT boxes within the two auxiliary boxes are denoted by $w^{gt}$ and $h^{gt}$, respectively, while those of the anchors are represented by w and h.

Fig. 3

Structure of the Inner-IoU model.

The scaling factor $r$, typically ranging from 0.5 to 1.5, adjusts the size of the auxiliary boxes. When $r> 1$, the auxiliary boxes are expanded, enabling non-zero gradients for low-overlap scenarios where standard IoU loss gradients would vanish. Conversely, when $r < 1$, the auxiliary boxes are contracted, amplifying gradients in high-overlap scenarios to facilitate faster fine-tuning.

The Inner-IoU loss is defined as:

$$\begin{aligned} L_{\text {inner}} = 1 - \text {IoU}^{\text {inner}} = 1 - \frac{|B'_p \cap B'_g|}{|B'_p \cup B'_g|} \end{aligned}$$

(7)

where $B'_p$ and $B'_g$ are auxiliary boxes derived from the predicted box $B_p$ and ground-truth box $B_g$, respectively, by scaling their widths and heights by $r$ while preserving their center points.

This approach adjusts the loss function’s sensitivity through the scaling factor $r$. When $r < 1$, it enhances precision by increasing gradient magnitudes in high IoU cases, accelerating convergence. When r > 1, it stabilizes the optimization process by expanding the non-zero gradient range in low IoU cases to prevent stagnation, thereby enhancing its ability to detect small objects that may be missed. These properties, detailed in the gradient analysis in the appendix, improve both convergence speed and generalization across diverse detection scenarios.

Three stage model enhancement

Figure 4 shows the network architecture of YOLOv8 (the detailed internal structure is shown in Supplementary Figure 1 in the Additional information). The improvements made to YOLOv8 are summarized as follows:

• 1) Step 1: Replace the backbone network of YOLOv8 with the structure of MobileNetV3-small. Due to the exceptional performance of the MobileNetV3 backbone, the MobileNetV3-small version is chosen for its ability to achieve rapid inference speed while being optimized for deployment on edge devices. Specifically, some of the original modules are replaced by the Inverted Residual modules in MobileNetV3. Following this modification, the model is referred to as YOLOv8_1.

• 2) Step 2: Replace all convolution modules in the neck of YOLOv8 with deep convolution modules to reduce computational complexity. Additionally, introduce a CA layer before the output of the neck. The CA attention mechanism is incorporated to enhance cross-channel communication, allowing the model to focus more effectively on location details within the image. After this modification, the model is referred to as YOLOv8_2.

• 3) Step 3: Replace the original IoU loss function with the novel Inner-IoU loss function to improve the model’s accuracy in detecting small objects. After this adjustment, the model is referred to as Mini-YOLO. Its network architecture is shown in Fig. 5(the detailed internal structure is shown in Supplementary Figure 2 in the Additional information).

Fig. 4

Architecture of the YOLOv8 model.

Fig. 5

Architecture of the Mini-YOLO model.

Model optimization and acceleration

1) Model Output Splitting: Output splitting refers to partitioning tensor outputs across NPU threads to avoid bottlenecks. The limitations of the original network: In the original YOLOv8 neural network, the decoding operation involves including the bounding box in the decode-encoding process. This results in significant computational overhead during the decoding and encoding of the image, which leads to inefficient utilization of the NPU during inference.

To resolve this, we innovatively split the model’s output head. As shown in Fig. 6: The merged output was split, and the original output was decomposed into six separate outputs, including three pairs of branches (category, box regression). This restructuring facilitates more efficient NPU utilization during inference, allowing for faster computation and improved performance.

Fig. 6

Structure of the output split model.

The original output of YOLOv8 is a tensor of size $1\times 7 \times 8400$, where 7 represents the coordinates of the detection box (x, y, w, h) and the 3 detection categories, and 8400 is the result of the output feature maps in three sizes: $80\times 80 + 40\times 40 + 20\times 20 = 8400$.

By implementing the modified model, significant performance improvements are achieved. The decoding and encoding operations of the image are now handled by the CPU, which frees up the NPU for more efficient processing. This modification increases the NPU utilization rate from 60% (with a single chip) to 90% (across three chips). As a result, the detection speed per image is improved by approximately 4.5 times.

2) Thread Pool Acceleration: The thread pool is a concurrency model primarily designed to manage and reuse threads to optimize hardware performance. A typical thread pool consists of several components, including the task queue, thread pool manager, and worker threads. Key parameters in thread pool management are the task queue size, task type, number of threads, and overall performance, ensuring system stability during operation. In this study, the hardware platform used is the RK3588 chip, which is equipped with three NPU cores that can operate in various combinations. By default, only a single thread is utilized during inference. To fully leverage the chip’s capabilities, the thread pool is employed for model acceleration. The number of threads in the thread pool is crucial. Too few threads may lead to an imbalance in resource distribution, resulting in suboptimal NPU utilization. On the other hand, too many threads may overload the NPU. Through testing, it was found that controlling the number of thread pools at around 12 allows the NPU to be fully utilized while maintaining optimal performance. This hardware-specific optimization is critical for achieving the real-time performance required by the application.

Real time detection system

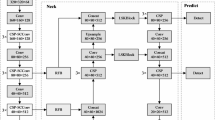
• 1) Model Conversion: One of the major challenges in model deployment is the variation in environments across different terminals, which requires resolving complex environment configuration issues before the algorithm can function properly. To overcome the issue of inconsistent environment setups, a deployment platform was designed to facilitate stable file format conversion. This platform utilizes two Docker images to efficiently handle the conversion process, ensuring seamless deployment across various environments. Additionally, the platform splits the model output to address the deficiencies in the original network before deploying it to the AI terminal. Ultimately, this approach enables the successful implementation of a real-time, non-destructive detection algorithm on the AI terminal.

• 2) Modify the Output of the Model: After training the YOLOv8 model, the resulting weight file typically has the.pt suffix. However, this file cannot be directly used for inference on the AI terminal, necessitating format conversion and model modifications.

• 1. In Docker1, use PyTorch’s model conversion tool to convert the.pt file into a.onnx format, and split the model output accordingly.

• 2. Then, place the.onnx file into Docker2, where RKNN’s model conversion tool is used to convert it into a.rknn weight file.

The.rknn file is compatible with running inference on the AI terminal in this study. Additionally, OpenCV’s function library is utilized to preprocess the input image data. By leveraging techniques such as thread pooling and quantization, the system can maximize the use of NPU computing resources for enhanced performance.

• 3) Data Storage and Management: During system operation, real-time files containing fault location information, such as fault type, broken wire location, and quantity, are collected. After the algorithm performs the necessary operations, both the raw data and corresponding fault diagnosis results are periodically uploaded to the server. Retaining the raw data is crucial for effective fault diagnosis.

The wire rope real-time detection system described in Section Methodology is shown in Fig. 7

Fig. 7

Structure of the Real-time wire rope detection system.

Experiment and results

Mini YOLO for non destructive testing of wire ropes

Dataset description

The dataset comprises 3,540 waveform images of electromagnetic signals from steel wire ropes, collected across multiple Chinese provinces (Anhui, Inner Mongolia, Shandong, Hunan, and Guangxi) and spanning the coal, port, and steel industries. Its diversity, derived from varied geographic regions and operational scenarios, enhances representativeness and ensures robust generalizability across different hardware configurations—a critical factor for practical applications. Data collection employed two types of electromagnetic detection probes (U-type and C-type) to ensure variation in detection equipment. The signals were recorded under diverse operational conditions, including varying load capacities (0-50 tons), multiple defect types (wire breakage, wear, and corrosion), environmental temperatures ranging from $-10^\circ$C to $40^\circ$C, and wire rope diameters between 10 mm and 50 mm. A data acquisition card (NI-9244, National Instruments, America) was used to capture electromagnetic signals at a 10 kHz sampling rate. The raw signals were normalized to a range of [−1,1] and filtered using a 5th-order Butterworth low-pass filter with a 500 Hz cutoff frequency to reduce high-frequency noise. The signals were then processed utilizing a sliding window approach to construct the dataset. Each image has a resolution of $2033\times 1196$, reflecting the actual resolution of the wire rope during data acquisition. Images were captured every ten meters in a distance-based mode. To increase dataset variability, random horizontal flipping ($\pm 15^\circ$ rotation) and contrast modification ($\pm 20\%$ gamma correction) were applied during the sliding window processing.

To prevent the broken wire from being exactly at the cutting position, the signal is processed with a margin during the sliding window segmentation, and an overlapping area is introduced at the cutting position. For instance, if the segmented image size is $640\times 640$ pixels, the overlap can be set to $640\times 0.2=128$ pixels. This overlapping area ensures that the data before and after the cutting position are retained, preventing the real broken wire signal from being overlooked. Additionally, this approach enriches the dataset by maintaining continuity across the segmented windows. Figure 8 illustrates the overlapping area processing.

Fig. 8

Illustration of overlapping area handling: (a) Results without configuring the overlapping area. (b) Results after configuring the overlapping area.

The dataset was split into training, testing, and validation sets in an 8:1:1 ratio. The training dataset consists of 2832 images, containing 4397 broken wire labels. The test dataset includes 354 images with 530 broken wire labels, while the validation dataset contains 354 images with 527 broken wire labels. LabelImg is used to annotate three types of targets: single broken wire, double broken wire, and triple broken wire. Several illustrative examples of these targets are shown in Fig. 9.

To thoroughly evaluate the robustness of Mini-YOLO, various noise types were incorporated into the test dataset, including Gaussian noise ($\sigma = 0.1$), impulsive noise (density = 0.05), Poisson noise, and a combination of Gaussian and impulsive noise. These noise levels were selected to simulate real-world challenges in electromagnetic wire rope detection, such as sensor disturbances and environmental interference. Performance metrics, including precision (P), recall (R), and mean average precision at 0.5 IoU (mAP@0.5), were computed for each noise scenario using a validation set of 354 images.

Fig. 9

Examples of three target types: (a)-(b) Single broken wire, (c)-(d) Single broken wire combined with double broken wires, and (e)-(f) Mixed single, double, and triple broken wires.

Experimental setup

The deep learning algorithm is executed on the CentOS 7.9 operating system with an Intel(R) Xeon(R) Gold 6346 CPU, eight NVIDIA RTX 3090 GPUs (24GB VRAM each), CUDA 11.8, Pytorch 1.12.1, and Python 3.8. Details of the training process are outlined in Table 1.

Table 1 Training parameter settings.

Discussion

Table 2 Mini-YOLO performance under various noise conditions.

The robustness evaluation of Mini-YOLO is presented in Table 2. The findings indicate that the model maintains a high precision rate (above 96.2%) and mAP@0.5 (exceeding 93.8%) across all noise conditions. While the recall rate experiences a slight decline in more demanding scenarios, such as mixed noise, the model continues to perform effectively against various types of noise. This resilience is particularly important for real-world applications, where wire rope signals are often influenced by multiple noise sources simultaneously. Among the tested conditions, mixed noise presents the greatest challenge compared to Gaussian and impulsive noise, yet Mini-YOLO’s strong performance underscores its reliability for practical deployments.

As discussed in Section Methodology, the scaling factor ratio used in this model is set to be greater than 1. Consequently, experiments were conducted across six groups, varying ratio from 1.00 to 1.25. The results indicate that adjustments to the ratio parameter influence the model’s mAP by approximately 0.5%. Based on the findings summarized in Table 3, the optimal ratio value for Inner-IoU in this study is determined to be 1.15.

Table 3 Comparison of different ratios in Inner-IoU.

To evaluate the effectiveness of the YOLOv8 improvements, the performance of YOLOv8, YOLOv8_1, YOLOv8_2, and Mini-YOLO was compared based on accuracy, recall, mAP@0.5, inference time, FLOPS, memory usage, and model size. The results are summarized in Table 4. Notably, the mAP of YOLOv8_1 outperformed YOLOv8 by 0.3%, indicating improved recognition performance. Additionally, the inference time reduced from 12.2 ms to 8.2 ms, while FLOPS decreased from 8.2B to 4.5B and memory usage from 2.1GB to 1.8GB, demonstrating that both accuracy and inference speed were significantly enhanced along with computational efficiency.

Table 4 Performance comparison of YOLOv8 and modified YOLO variants.

Compared to YOLOv8_1, the mean average precision (mAP) of YOLOv8_2 remained at 97.3%, while its inference speed improved, with the inference time reduced from 8.2 ms to 6.5 ms, FLOPS decreased from 4.5B to 1.8B, and memory usage dropped from 1.8GB to 0.9GB. In the experiment, replacing only the convolution module in the neck with a deep convolution module reduced the inference time to 3.5 ms, but the mAP decreased to 96.9%. To compensate for this accuracy loss, a lightweight CA module was introduced, which did not add to the inference time, resulting in the mAP being restored to 97.3%. These two steps together formed the comprehensive second-stage enhancement, allowing the network to focus more on channels with richer features, while significantly reducing computational complexity and memory requirements. The primary reason for this result is that the deep convolution module in the neck reduces computational complexity significantly, but this mismatch with the complexity of the backbone network slightly decreased accuracy and substantially improved speed. The CA module enhances accuracy by enabling cross-channel communication, which allows the network to prioritize channels that contain more informative features.

Compared to YOLOv8_2, Mini-YOLO showed a 1.0% improvement in mean average precision (mAP), with the inference time remaining unchanged. The improved accuracy may be attributed to the introduction of Inner-IoU, which did not impact model complexity, thus leaving the inference time, FLOPS, and memory usage unaffected. To further investigate the detection performance differences, the detection results of YOLOv8 and Mini-YOLO were compared on the dataset. Notably, Mini-YOLO demonstrated significantly better detection accuracy for multiple broken wires than YOLOv8. By examining the detection results of both models, two key advantages of Mini-YOLO in target identification emerged: it was more effective at detecting multiple broken wires and showcased superior precision in its results.

First, Mini-YOLO proves to be more accurate in identifying multiple broken wires, especially in cases where multiple single broken wires appear in close proximity or overlap. As illustrated in Fig. 9, single broken wires often appear densely, making them challenging to distinguish. However, Mini-YOLO shows a higher confidence level in detecting these tightly packed broken wires, allowing for more precise identification compared to YOLOv8.

Second, Mini-YOLO is more accurate in identifying small targets. Figure 10 highlights instances where certain broken wires occupy only a small portion of the entire waveform. Mini-YOLO demonstrates significantly higher accuracy in detecting these small targets. This improvement may be due to the fact that YOLOv8 has an overly large receptive field, which makes it difficult to extract the features of small broken wires after passing through multiple convolution layers. By introducing the Inner-IoU activation function, Mini-YOLO effectively amplifies the small target broken wires, addressing the issue of the large receptive field in YOLOv8 and significantly improving recognition accuracy.

Fig. 10

Detection results on the test set with a confidence threshold of 0.50. (a)-(b) Results from YOLOv8, (c)-(d) Results from Mini-YOLO.

Baseline methods

To comprehensively evaluate the performance of Mini-YOLO, we selected two categories of baseline methods for comparison: mainstream object detection algorithms (suitable for edge computing scenarios) and traditional nondestructive testing (NDT) methods for wire rope defects. Detailed information is as follows:

Object detection baselines

To comprehensively evaluate Mini-YOLO’s performance in edge computing environments, a detailed comparison was conducted between standard and edge-optimized models.The experimental parameter settings are shown in Table 1. As illustrated in Table 5, YOLOv7-tiny requires 3.9 milliseconds for inference, performs 3.5 billion floating point operations, and consumes 1.2GB of memory. However, its simplified CSPDarknet-tiny backbone and lack of an explicit attention mechanism limit feature richness and detection accuracy. In contrast, Mini-YOLO, with its 1.8 billion FLOPS and 0.9GB memory usage, employs MobileNetV3’s depthwise separable convolution and $1 \times 1$ fusion blocks to significantly reduce computational demands. Furthermore, while YOLOv7-tiny’s CIoU loss function struggles with low-overlap gradients, Mini-YOLO’s Inner-IoU with adaptive scaling (ratio=0.5–1.5) enhances gradient descent in high-overlap scenarios and extends gradient effectiveness in low-overlap cases, thereby improving detection accuracy. Although Mini-YOLO’s inference time of 6.5 ms is slightly longer than YOLOv7-tiny’s 3.9 ms, its computational efficiency and memory usage are comparable to those of EfficientNet-EdgeTPU, demonstrating an excellent balance between accuracy and efficiency. The EdgeTPU-optimized model⁴⁰ achieves computational efficiency similar to Mini-YOLO (1.8B FLOPS, 0.9GB memory). However, its accuracy remains relatively low (89.7% mAP@0.5), making it insufficient for precise defect detection. While EfficientDet offers relatively high accuracy (95.1%), its extended inference time (22.7 ms) makes it unsuitable for edge deployment. Additionally, several other single-stage detection algorithms were evaluated and analyzed for comparison. SSD and RetinaNet demonstrated significantly inferior performance in terms of accuracy, speed, and model size compared to the other algorithms. Among the top-performing algorithms, YOLOv8 stood out with a notably higher mean average precision (mAP) than both SSD and RetinaNet, along with a considerably shorter inference time. YOLOv10, which outperformed YOLOv8, reduced the inference time by 2.4 ms and had a model size that was 4.1 MB smaller than YOLOv8. While YOLOv11 built upon YOLOv8, it reduced the model size by 4.1MB, but the inference time increased by 2.4 ms. In contrast, In contrast, Mini-YOLO strikes an exceptional balance. Its architecture-combining the efficiency of MobileNetV3, the precision of the CA mechanism, and the convergence benefits of Inner-IoU-allows it to outperform all tested models. It outperformed all other algorithms in terms of accuracy, speed, computational efficiency (FLOPS), memory usage, and model size. With an average accuracy of 98.3%, an inference time of 6.5 ms, FLOPS of 1.8B, memory usage of 0.9GB, and a model size of 6.8 MB, Mini-YOLO demonstrates superior performance across all metrics.

Table 5 Comparison of varied object detection approaches.

Traditional NDT baselines

To evaluate the effectiveness of Mini-YOLO, we compared it with several established wire rope defect detection (NDT) methods. These methods use a 1D raw electromagnetic signal and segment it into 40 sample sequences around the detection peak. The parameter configuration of each baseline method is summarized in Supplementary Table 2, including 1D-CNN, multi-layer perceptron (MLP), random forest-based wavelet transform (Wavelet + RF), random forest-based short-time Fourier transform (STFT + RF), and support vector machine (SVM) combining time and frequency domain features.

• 1) Dataset:Experimental settings: The dataset is divided into training set (70%) and test set (30%), and stratified sampling is used to maintain class balance (the wire breaking rate is 54.05%). The performance indicators include accuracy, precision, recall, and F1 score, and the average of 10 runs is taken to ensure robustness (since the running time standards of various detection methods are difficult to unify, statistics are not performed here). The test results are calculated on a Windows 11 system using a CPU (AMD Ryzen 7 6800H).

• 2) Results and Analysis: The comparison results are shown in Table 6. The Mini-YOLO model achieved excellent performance on the test set, with an accuracy of 98.3%, a precision of 97.8%, and a recall of 87.5%. Among the baseline methods, STFT+RF performed best with an accuracy of 94.82%, effectively capturing the time-frequency features. Wavelet+RF ranked second with an accuracy of 92.86%, thanks to the robust feature extraction of wavelet coefficients. 1D-CNN achieved an accuracy of 88.00%, which may be due to the model’s insufficient ability to learn features. MLP performed the worst with an accuracy of only 87.86%, which may be due to its limited ability to model complex signal patterns without spatial or frequency transformations. It can be seen that Mini-YOLO has good recognition rate and accurate defect localization capabilities, which are lacking in 1D-CNN and MLP. Although STFT+RF and Wavelet+RF can also achieve fairly high accuracy, they require manual feature extraction and lack the end-to-end learning and localization capabilities of Mini-YOLO. The advantages of Mini-YOLO in recognition rate, defect localization, inference speed, and edge deployment feasibility highlight its applicability and specificity in real-time wire rope defect detection.

Table 6 Performance comparison of Mini-YOLO with baseline NDT methods.

Model acceleration on edge devices

• 1) Dataset: The validation set consists of 354 images, containing 527 broken wire labels. This dataset has been used to test the model on the embedded platform, with the training process being excluded from this section.

• 2)Experimental Environment: The embedded platform utilized in the experiment is based on the RK3588 chip, featuring a six-core CPU, an NPU with 6 TOPS of computing power, and 8GB of memory. The operating system for the embedded platform is Ubuntu 22.04.2 LTS. For the deep learning framework, PyTorch is employed. The model weight file conversion takes place within two Docker containers running on a virtual machine with Ubuntu 22.04.4 LTS. Specifically, Docker1 is operating on Ubuntu 20.04.4 LTS, while Docker2 runs Ubuntu 18.04.6 LTS.

To optimize the utilization of the three NPUs within the RK3588 and unlock their full potential, a detailed comparison was conducted during the deployment phase to evaluate the impact of varying the number of thread pools on overall model performance. As shown in Table 7, configuring thread pools as integer multiples of the number of NPUs (multiples of 3) results in better NPU performance. Specifically, using 12 or 15 thread pools yields the fastest detection speed. However, an excessively low or high number of thread pools does not maximize NPU performance. When the number of thread pools is below 12, the NPU’s performance is not fully utilized, leading to slower computation. Conversely, when the number of thread pools exceeds 12, the NPU enters an overloaded state, causing performance scheduling issues and a reduction in computation speed. Therefore, selecting 12 thread pools is optimal for achieving the best NPU performance.

Table 7 Comparison of different numbers of thread pools in NPU.

The quantized Mini-YOLO model was evaluated across three precision formats (FP32, FP16, and INT8) with the results detailed in Table 8. The FP32 model exhibited an inference time of 32.6 ms on the embedded platform, indicating room for optimization. Switching to FP16 led to a 15% increase in inference time (from 32.6 ms to 37.4 ms) while reducing accuracy by 3.2% (from 89.4% to 86.2%). In contrast, the INT8 model not only delivered a significant boost in inference speed but also maintained high accuracy, even surpassing the FP16 model. This enhancement is likely attributed to the regularization effect of INT8 quantization, which helps mitigate overfitting. Given its balance of efficiency and accuracy, the INT8 model was chosen for quantization. With an inference time of just 18.5 ms, it meets real-time processing requirements while demonstrating the strong computational performance of the RK3588 platform.

Table 8 Comparison of YOLOv8 network accuracy and performance before and after quantization.

Conclusion

This paper presents a wire rope real-time detection system based on the Rockchip RK3588 and the YOLOv8 algorithm. Its core contribution is not the innovation of algorithm, but the development of Mini-YOLO model based on the synergistic integration of existing components, and targeted optimization for challenging practical applications. The main achievements of the present research can be summarized as follows:

• 1. The Mini-YOLO model integrates the efficient MobileNetV3 backbone network, the position-aware coordinate attention mechanism, and the Inner-IoU loss function for accelerated convergence. Its detection speed is 2.0 times faster than YOLOv8 and its accuracy is 1.2%. This carefully designed combination is particularly suitable for identifying dense and small-sized targets in wire rope defects. Utilizing the C++ language further boosts the model’s performance on embedded platforms.

• 2. By optimizing model output splitting and using thread pools, the full computational power of the NPU is leveraged, and the model’s quantization enhances its computing speed post-deployment, enabling real-time detection.

• 3. The construction of the real-time wire rope detection system facilitates easier model format conversion and deployment, while also ensuring the preservation of raw input data and detection results.

Although this implementation is optimized specifically for the Rockchip RK3588 platform, it must be emphasized that the Mini-YOLO model itself does not depend on any specific hardware and can be deployed on other edge computing devices equipped with NPU or GPU by using standard model conversion tools (such as OpenVINO).