Investigation on the broadband active filtering characteristics of plasma composited frequency selective surface structure

Abstract

To address the demand for wideband, dynamically controllable filtering characteristics in radomes, a plasma composited frequency selective surface (PC-FSS) structure with broadband, active filtering properties is proposed and experimentally demonstrated. Initially, a broadband band-pass FSS was designed using a multilayer cascade method and integrated with inductively coupled plasma (ICP) to form the PC-FSS. The effects of various discharge conditions—including pressure, power, and ICP thickness—on the parameter distribution and filtering performance of the PC-FSS were investigated through experimental measurements. The results indicate that the filtering characteristics of the PC-FSS can be actively controlled across a wide frequency range by adjusting the discharge conditions. Furthermore, the PC-FSS exhibits strong polarization and angular stability. In its unexcited state, the PC-FSS functions as a broadband band-pass structure with a center frequency of 13.56 GHz and a -1 dB passband of 11.02 GHz (ranging from 8.05 to 19.07 GHz). When excited, the structure displays tunable band-pass and band-stop characteristics, which depend on the discharge conditions, thereby providing both switching and tuning functionalities. The active properties of the PC-FSS underscore its potential for applications in active stealth radome systems.

Introduction

The radome safeguards both the aerodynamic performance of the aircraft and the operational environment of the antenna¹. However, the radome’s property of permitting electromagnetic wave penetration results in the formation of a strong scattering region at the nose of the aircraft. At present, frequency selective surfaces (FSSs) are primarily employed to reduce the radar cross section (RCS) outside the antenna’s operational frequency band^2,3,4. Essentially, an FSS functions as a spatial filter exhibiting one or more band-pass or band-stop characteristics for the incident wave^5,6,7. However, conventional FSSs, typically fabricated from metallic materials in patch or slot configurations, lack adjustable filtering properties such as tunable center frequency and bandwidth.

To address above challenges in the practical application of traditional FSS, active frequency selective surfaces (AFSSs) have been developed by integrating controllable elements into conventional structures⁸. AFSSs enable dynamic control of filtering characteristics across various frequency bands by modifying these elements. Typical implementations of AFSSs involve incorporating active components such as PIN diodes and varactors, employing substrates composed of materials with tunable electromagnetic properties such as liquid crystals and ferrites, and integrating micro-electromechanical system (MEMS) switches^{8,9,10,11,12,13,14,15,16,17}. Additionally, the filtering properties of FSSs can be adjusted by varying the relative positions of their multilayer structures^18,19. Despite considerable progress in AFSS technology, several limitations remain. FSSs based on active devices exhibit high insertion loss and poor isolation. Furthermore, applying voltages becomes increasingly difficult as the FSS size increases, and the complexity of units utilizing variable electromagnetic materials or MEMS devices complicates their control. Moreover, current AFSS designs provide only a relatively narrow adjustable bandwidth, making it challenging to meet the requirements of increasingly complex electromagnetic environments.

Plasma stealth is an emerging active radar stealth technology that exploits the collisional attenuation and resonance absorption effects of plasma on electromagnetic waves^20,21. The dielectric constant of plasma is described by the Drude dispersion model.

$${\varepsilon _{\text{p}}}\left( \omega \right)={\varepsilon _0}\left( {1+\frac{{\omega _{{\text{p}}}^{2}}}{{\omega \left( {j{\nu _{\text{m}}} - \omega } \right)}}} \right)$$

(1)

where ω denotes the angular frequency and $\varepsilon _{0}$ is the permittivity of vacuum. The plasma frequency ω_p is given by

$$\omega _{p} = \sqrt {\frac{{N_{e} e^{2} }}{{m_{e} \varepsilon _{0} }}}$$

(2)

where e is the electron charge, m_e is the electron mass, and N_e is the electron density. The collision frequency ν_m is described as²²

$${\nu _{\text{m}}}=1.52 \times {10^7}P\sqrt {{T_{\text{e}}}}$$

(3)

where P is the pressure of the plasma and T_e is the electron temperature. Consequently, the attenuation effects of plasma on electromagnetic waves can be flexibly controlled by adjusting parameters such as ω_p and ν_m^23,24. Integrating FSS with plasma combines the filtering properties of the FSS with the dynamic attenuation capabilities of plasma, thereby enhancing the active stealth performance the radome.

Progressively, FSS integrated with plasma have been modeled to evaluate their scattering characteristics under various plasma parameter settings^25,26,27,28. These studies indicate that the filtering properties of the composite structure can be controlled by altering the plasma parameter distribution. However, in these simulations, plasma is typically simplified as a multilayer medium with assumed parameter distributions that do not sufficiently account for the inherent non-uniformity and complexity of physical plasma fields. This limitation restricts the accurate representation of the actual influence of plasma on the filter properties of the composite structure. To obtain a more precise understanding of the composite’s scattering characteristics, extensive experimental research has been conducted^29,30. Anderson et al.²⁹ introduced a approach by replacing the metallic elements of the FSS with plasma tubes, demonstrating, through experimental validation, that the transmission coefficient S₂₁ could be modulated by varying the N_e and ν_m within the plasma tube. Subsequently, Cross et al.³⁰ developed a thin-layer, large-area FSS integrated with plasma, and investigated the structure’s switchable characteristics and the variation of S₂₁ under different voltage conditions through experiments. Despite these innovations, challenges remain, including significant insertion loss, limited frequency tunability, and suboptimal switching performance caused by the characteristics of the plasma source.

To address these challenges, we propose a plasma composited frequency selective surface (PC-FSS) that employs an inductively coupled plasma (ICP) source as the medium, integrated with a wideband band-pass FSS as the structural unit. Nₑ of the ICP can reach 10¹¹ to 10¹³ cm⁻³, with a frequency response spanning the P ~ Ku bands, offering simplicity in device architecture and rapid response capabilities—crucial benefits for enhancing AFSS^31,32. By modifying the external discharge conditions (power, pressure, and thickness) of the ICP source, the distribution of parameters can be altered, thus actively controlling the electromagnetic wave’s attenuation amplitude and frequency band^33,34,35. In its unexcited state, the ICP allows electromagnetic waves to traverse the FSS passband with minimal loss. Conversely, exciting the ICP source enables adjustments in the band-pass and band-stop characteristics of the PC-FSS by altering the discharge conditions, thereby achieving switchable and tunable functionality.

To address these challenges, we propose a plasma composited frequency selective surface (PC-FSS) that utilizes an inductively coupled plasma (ICP) source as the medium, integrated with a wideband band-pass FSS as the structural unit. The Nₑ of the ICP can reach 10¹¹ to 10¹³ cm⁻³, providing a frequency response covering the P to Ku bands. This approach offers a simple device architecture and rapid response capabilities—key advantages for advancing AFSS technology^31,32. By adjusting the external discharge conditions (power, pressure, and thickness) of the ICP source, the distribution of plasma parameters can be modified, thereby enabling active control over the attenuation amplitude and frequency range of electromagnetic waves^33,34,35. In its unexcited state, the ICP allows electromagnetic waves to pass through the FSS passband with minimal loss. Conversely, when the ICP source is excited, the band-pass and band-stop characteristics of the PC-FSS can be tuned by altering the discharge conditions, thus achieving both switchable and tunable functionality.

The design of the broadband band-pass frequency selective surface

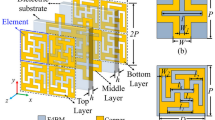
A broadband band-pass frequency selective surface (FSS) with a patch-slot-patch unit cell structure is designed, as shown in Fig. 1. The unit cell consists of three metal layers separated by two dielectric layers, each with a periodicity of p = 5.5 mm. In this structure, the yellow sheets represent the metal patches, while the blue slices denote the dielectric substrates, as illustrated in Fig. 1(a). The FSS is constructed by arranging these unit cells periodically along the x and y axes. The top and bottom layers are identical metal patches forming a cross-shaped gap structure with a gap width of w = 1.8 mm, as shown in Fig. 1(b). The middle layer comprises interlaced metal lines, each with a width of s = 0.15 mm, as shown in Fig. 1(c). Both dielectric layers are made of F4B, each with a thickness of h = 0.9 mm and a dielectric constant of ε_r = 2.65 + j*0.001.

Fig. 1

Geometry of the proposed FSS unit cell. (a) three dimensional view of the FSS unit cell. (b) top and bottom patch layer. (c) middle slot layer.

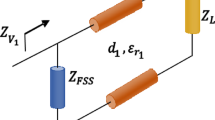
Using the equivalent circuit method, the FSS unit is modeled and simplified into a circuit consisting of lumped components to facilitate understanding of the FSS’s operating principle. The three metal layers of the FSS are symmetrically arranged around the middle layer, alternating between a cross-gap structure and a square metal ring. When a linearly polarized wave is incident perpendicularly, the cross-gap structure behaves as an equivalent capacitance, while the square ring acts as an equivalent inductance. According to transmission line theory, free space is represented by an equivalent impedance Z₀. Since the two dielectric substrate layers have identical properties and thickness, the characteristic impedance Zₛ introduced by the dielectric substrates is modeled as two parallel capacitors Cₛ and a series inductor Lₛ within the circuit. The equivalent circuit of the resonant unit, illustrating each structure’s equivalence to a capacitor, resistor, and inductor, is shown in Fig. 2(a). For simplicity, the equivalent capacitances at the same node are combined, and the final equivalent circuit is presented in Fig. 2(b), where $C^{\prime } \approx C_{s} \left\| C \right.$.

Fig. 2

Equivalent circuit model. (a) initial equivalent circuit model. (b) simplified equivalent circuit model.

The reflection coefficient S₁₁ and transmission coefficient S₂₁ of the FSS are obtained using the frequency domain solver in CST Microwave Studio. Boundary conditions are set as open in the z-direction and defined by the unit cell along the x and y directions. As shown in Fig. 3, the passband exhibits two reflection zeros at resonant frequencies of 10.30 GHz and 17.74 GHz. The interaction between these zeros broadens the passband, resulting in a maximum insertion loss of 0.52 dB due to ripple formation. The center frequency of the FSS passband is 13.25 GHz, with a -1 dB bandwidth of 11.2 GHz (8.02–19.22 GHz), corresponding to a relative bandwidth of 82.4%, and a -3 dB bandwidth of 13.5 GHz (6.6–20.1 GHz). Using Advanced Design System (ADS), the equivalent circuit model of the FSS is analyzed, as shown in Fig. 2. The resulting frequency response is presented in Fig. 3. The reflection zeros within the passband are located at 10.57 GHz and 17.82 GHz, with a center frequency of 13.97 GHz and a -1 dB bandwidth of 10.9 GHz (8.52–19.42 GHz). These values are in close agreement with the CST simulation results. A slight upward shift in the passband center frequency is observed, with the parameter values as follows: C = 0.0604 pF, Cₛ = 0.462 pF, L = 0.242 nH, and Lₛ = 1.301 nH.

Fig. 3

Response of the FSS at normal incidence.

Fig. 4

Response of FSS under oblique incidence with different polarization states. (a) TE. (b) TM.

Figure 4 presents the S₁₂ and S₁₁ of the FSS under oblique incidence for various linearly polarized waves. For TE-polarized waves, the FSS displays two reflection zeros at different incident angles. As the incident angle increases, the first reflection zero shifts slightly to higher frequencies, while the second reflection zero experiences a more pronounced shift toward higher frequencies. As a result, the transmission passband migrates to higher frequencies, and the in-band insertion loss increases as the separation between the reflection zeros widens. Specifically, at an incident angle of 45°, the second resonant frequency shifts from 17.74 GHz (at normal incidence) to 18.95 GHz. This increased separation introduces non-uniformity on the right side of the passband, leading to a maximum insertion loss of 1.46 dB. Additionally, the − 3 dB bandwidth of the passband narrows to 12.78 GHz (7.62–20.40 GHz).

For TM-polarized waves, the FSS also exhibits two reflection zeros at different incident angles; however, their behavior differs from that observed for TE waves. As the incident angle increases, the resonant frequency of the first reflection zero shifts markedly to higher frequencies, while the second reflection zero shifts slightly to lower frequencies. This results in the center frequency of the passband moving to higher frequencies. Furthermore, the reduced separation between the reflection zeros enhances the flatness of the passband. At an incident angle of 45°, the first reflection zero moves from 10.30 GHz to 11.82 GHz, while the maximum insertion loss in the passband decreases to 0.1 dB, with the passband bandwidth remaining unchanged. These results demonstrate the FSS’s excellent polarization stability and angle insensitivity, with the latter being more pronounced under TM polarization than under TE polarization.

The discharge system and parameter diagnosis of the plasma composited frequency selective surface

To further explore the influence of parameter distributions, such as plasma frequency ω_p and collision frequency v_m, on the filtering characteristics of the plasma composite frequency selective surface (PC-FSS), an inductively coupled plasma (ICP) discharge experimental system is established. The parameter distributions are measured under various discharge conditions, including variations in ICP thickness, pressure, and power.

The discharge system of the PC-FSS

The discharge system of the PC-FSS is shown in Fig. 5, including the PC-FSS, the vacuum system and the radio frequency (RF) power system.

Fig. 5

Schematic of the discharge system of the PC-FSS.

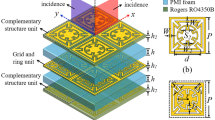
The PC-FSS consists of an ICP discharge chamber as the bottom layer and a band-pass FSS as the top layer, as illustrated in Fig. 6. The FSS is fabricated using printed circuit board technology based on the element design described in Section III. The overall dimensions of the FSS are 198 × 198 mm², comprising 36 × 36 basic elements, as shown in Fig. 6(a). The discharge chamber, constructed by integrally fusing high-permeability quartz, is depicted in Fig. 6(b). Owing to the absence of metallic materials and its high transmittance, the quartz chamber offers excellent impedance matching with free space, thereby avoiding additional reflections along the radar wave path. Additionally, the quartz material does not introduce impurities during discharge, thereby minimizing its impact on parameter diagnosis and scattering characteristics. These properties make quartz an ideal material for integration into radome systems, facilitating engineering applications.

Fig. 6

Sample of the PC-FSS. (a) the top layer. (b) the bottom layer.

The bottom surface of the chamber accommodates the planar coil, while the top surface supports the FSS, enabling electromagnetic wave transmission. The chamber adopts a square configuration with a wall thickness of 4 mm, ensuring both gas tightness and structural integrity. To investigate the effect of plasma thickness on the filtering characteristics of the FSS, two chamber geometries are used: 200 × 200 × 25 mm³ and 200 × 200 × 40 mm³. Additionally, the chamber incorporates two interfaces to allow connection with a vacuum pump and the working gas, respectively.

The vacuum system comprises a working gas, a pressure-reducing valve, a vacuum pump, a mass flowmeter, and a vacuum gauge. High-purity argon gas (Ar, 99.99%) is regulated by the pressure-reducing valve and introduced into the chamber via the mass flowmeter. The inlet flow rate and vacuum pump speed are adjusted using the mass flowmeter and vacuum gauge, enabling precise control of the ICP pressure from 1 Pa up to atmospheric pressure.

The RF power system consists of a radio frequency power source, an automatic matching network, an RF coil, and a water cooling system. The RF power source operates at 13.56 MHz with a maximum output power of 1000 W. An automatic matching network is positioned between the power source and the coil to optimize the transmission of forward and reflected power. The RF coil is constructed from a hollow copper tube with an outer diameter of 5 mm and an inner diameter of 2 mm, and is formed as a single turn with a diameter of 180 mm.

The influence of discharge conditions on the parameter distribution of the PC-FSS

Under different external discharge conditions, the N_e and T_e of the ICP source exhibit distinct distribution characteristics, which in turn influence the band-pass and band-stop behavior of the PC-FSS with respect to electromagnetic waves. This section investigates the distributions of electron density N_e and electron temperature T_e in the PC-FSS under varying discharge conditions, utilizing microwave transmission interferometry and emission spectroscopy for analysis.

The high aspect ratio of the thin-layer chamber renders the installation of a Langmuir probe interface impractical. Moreover, the reduced mean free path of particles within the thin-layer chamber significantly compromises the measurement accuracy of the probe. Consequently, the microwave interferometry method is employed in the experiment to diagnose the chord-averaged N_e. Compared to probe-based diagnostics, microwave interferometry offers higher accuracy and does not perturb the plasma. The transmission measurement system, as illustrated in Fig. 7, consists of a vector network analyzer, a transmitting antenna, and a receiving antenna. The electromagnetic wave signal from the vector network analyzer is divided into two channels: a measurement channel and a reference channel. By analyzing the phase difference between these signals, the chord-averaged N_e along the electromagnetic wave propagation path is determined.

Fig. 7

Schematic of the microwave transmission interference method.

When the pressure of the ICP source ranges from 1 to 50 Pa, the phase shift coefficient α of the plasma can be simplified as follows

$$\alpha =\frac{\omega }{c}{(1 - \frac{{{\omega _p}^{2}}}{{{\omega ^2}}})^{1/2}}$$

(4)

As the microwave emitted by the antenna passes through an ICP source with a thickness of H, the generated phase shift $\Delta \phi$ is

$$\Delta \phi =\int_{0}^{L} {({\alpha _0} - \alpha )dl} =\frac{\omega }{c}\int_{0}^{L} {\left[ {1 - {{(1 - \frac{{{\omega _p}^{2}}}{{{\omega ^2}}})}^{1/2}}} \right]dl}$$

(5)

The frequency of the interference waves is generally much higher than that of the plasma. Therefore, Eq. (5) can be expanded and solved to derive the following results.

$$\Delta \phi \approx \frac{\omega }{c}\int_{0}^{L} {\frac{{{\omega _p}^{2}}}{{2{\omega ^2}}}dl} =\frac{{{e^2}}}{{2{\varepsilon _0}{m_e}\omega c}}\int_{0}^{L} {{n_e}dl}$$

(6)

Consequently, by measuring the phase shift of the microwaves, the chord-averaged N_e along the detection path can be directly obtained. When this data is substituted into Eq. (3), the distribution of the ωₚ can be determined. Furthermore, uncertainties in microwave interferometry arise from phase measurement accuracy (± 5°), path-length calibration (± 0.5 mm), and plasma non-uniformity, resulting in a maximum error of ± 8% in ωₚ.

Fig. 8

The distribution of the ωp under various pressures and power (a) 40 mm. (b) 25 mm.

When the ICP thickness H is 40 mm, the distribution of ω_p under varying pressures and input powers is shown in Fig. 8(a). It can be observed that ω_p increases with increasing power, while the gradient distribution of N_e remains unchanged. This occurs because the energy of electrons in the skin layer rises with increasing power, resulting in more frequent collisional ionization within the heating field and, consequently, an effective enhancement of N_e. However, after leaving the heating field, low-energy electrons are primarily confined within the potential well in the high-density region. As a result, power variation has minimal impact on diffusion and transport, leading to a stable gradient distribution of ω_p. As the power increases from 200 W to 800 W, ω_p rises from 1.04 × 10¹⁰ m^-3 to 1.46 × 10¹⁰ m^-3 at 10 Pa. Additionally, ω_p increases significantly with rising pressure. This can be attributed to ohmic heating replacing stochastic heating as the dominant heating mechanism at higher pressures, thereby improving power coupling efficiency and substantially increasing ω_p. When the pressure is increased from 10 Pa to 50 Pa, ω_p increases from 1.46 × 10¹⁰ m^-3 to 2.12 × 10¹⁰ m^-3 at 800 W.

When the chamber thickness H is 25 mm, the distribution of ωₚ under varying pressures and input powers is shown in Fig. 8(b). Compared with H = 40 mm, ωₚ decreases as H is reduced under identical discharge conditions. This phenomenon can be attributed to two primary factors. First, increasing H extends the diffusion range of high-energy electrons. During this diffusion, collisions and ionizations between high-energy electrons and neutral particles produce additional low-energy electrons. However, as H increases, high-energy electrons located farther from the heating source experience greater energy loss, making it more difficult to couple radio frequency energy and thereby reducing the density of high-energy electrons. Second, a larger H reduces electron recombination, which in turn decreases the loss of low-energy electrons.

The electron temperature T_e can be diagnosed using emission line analysis from multiple spectral lines, as demonstrated in the literature³⁶. These results are substituted into Eq. (4) to obtain the distribution of νₘ. The measurement of Tₑ by emission spectroscopy carries an error of ± 10% due to line-ratio sensitivity. The distribution of νₘ under different discharge conditions is shown in Fig. 9. It is observed that both input power and chamber thickness have little effect on the distribution of νₘ, while increasing pressure significantly raises νₘ.

Fig. 9

The distribution of the νₘ under various pressures and power (a) 40 mm. (b) 25 mm.

The performance of the plasma composited frequency selective surface

The measurement system of the plasma composited frequency selective surface

The wideband time-domain measurement system used in the experiment is shown in Figs. 10 and 11. The system mainly includes a pulse generator, pulse head, transmitting antenna, receiving antenna, sampling unit, and digital sampling receiver.

In the experiment, the plasma composited frequency selective surface (PC-FSS) sample is vertically positioned on the test platform, perpendicular to both the transmitting and receiving antennas, with all components aligned at the same horizontal height. An ultra-short pulse with a half-width of 30 ps and a repetition frequency of 1 MHz serves as the signal source. Fast signal synchronization and time-window filtering of clutter are employed to minimize measurement errors caused by factors such as multipath effects, reactive field coupling, and signal leakage. This system achieves high-resolution time-domain response signals across a large dynamic range, from which the filtering characteristics of the PC-FSS are derived via Fourier transformation.

Fig. 10

The wideband time-domain measurement system.

Fig. 11

Photograph view of the experimental setup (a) the discharge of ICP. (b) the discharge of PC-FSS.

To eliminate interference from the coil and the experimental background, S₂₁ is first measured with the inductively coupled plasma (ICP) source unexcited, and the test background is normalized accordingly. Subsequently, the frequency selective surface (FSS) sample is placed on top of the ICP source to form the PC-FSS for further measurements. Simultaneously, an extremely narrow time gate is set to suppress multipath reflections as much as possible. The measurement uncertainty in S₂₁ is ± 1.2 dB, based on the signal-to-noise ratio (30 dB), system calibration repeatability, and antenna alignment tolerance.

Performance of plasma composited frequency selective surface in unexcited state

First, we experimentally investigate the filtering characteristics of the PC-FSS at various incidence angles and polarization states, with the ICP source in an unexcited state, as shown in Fig. 12.

The results indicate that, in the unexcited state, the PC-FSS exhibits a relatively flat passband with minimal insertion loss across different incidence angles and polarization states. The center frequency of the PC-FSS under vertical excitation by a TE-polarized wave is 13.56 GHz, with a -1 dB bandwidth of 11.02 GHz (8.05–19.07 GHz). For vertical excitation by a TM-polarized wave, the center frequency is 13.69 GHz, and the − 1 dB bandwidth is 11.10 GHz (8.14–19.24 GHz). Furthermore, the experimental results show a variation trend that closely aligns with the simulation results depicted in Fig. 3. However, the measured insertion loss is slightly higher than that observed in the simulations, and the operating frequency exhibits a marginal shift toward higher values. The primary causes of these discrepancies are: (1) errors introduced during the fabrication of the FSS samples, and (2) the influence of the coil antenna, quartz chamber, and environmental noise.

Fig. 12

Measured transmission coefficients at different polarizations when PC-FSS is unexcited. (a) vertical excitation. (b) oblique incidence.

Performance of plasma composited frequency selective surface in excited state

We then investigate the effect of various discharge conditions on the filtering characteristics of the excited PC-FSS when subjected to TE-polarized wave incidence. The cavity thicknesses are set to 25 mm and 40 mm, and Ar is employed as the discharge gas. The pressure was varied at 10 Pa, 20 Pa, and 50 Pa, while the discharge power was adjusted to 400 W, 600 W, and 800 W. To facilitate an intuitive comparison of the transmission characteristics before and after the excitation of the PC-FSS, the passband and stopband after excitation were defined within the frequency range of 8.05–19.07 GHz. This range corresponds to the − 1 dB passband bandwidth of the unexcited PC-FSS, as illustrated in Fig. 3.

Fig. 13

Variation in transmission coefficient of PC-FSS versus pressure and power at 25 mm (a) 10 Pa. (b) 20 Pa. (c) 50 Pa.

The variation of the transmission coefficient S₂₁ with power and pressure is presented in Fig. 13. When the chamber thickness is 25 mm and the pressure is 10 Pa, the collision frequency ν_m between electrons and neutral particles is low, resulting in weak plasma-induced attenuation of the incident electromagnetic wave. Consequently, the overall transmission coefficient remains above − 10 dB. When the frequency of the incident wave approaches the plasma frequency ωₚ, a resonance absorption effect produces an attenuation peak. At a discharge power of 400 W, a resonance point appears at 10.09 GHz, near the plasma cut-off frequency, reducing transmission within the FSS passband and generating an attenuation peak of 22.10 dB, as shown in Fig. 13(a). This attenuation peak results in a single stopband in the transmission curve, with a center frequency of 10.06 GHz and a -10 dB bandwidth of 2.15 GHz (8.98–11.13 GHz). Owing to the high-pass filter characteristics of the plasma, a narrow transmission passband appears in the frequency range above the plasma cut-off frequency. The passband has a center frequency of 15.53 GHz and a -3 dB bandwidth of 2.82 GHz (14.12–16.94 GHz). As the power increases to 600 W, the ωₚ increases, causing the resonance point due to resonance attenuation to shift to higher frequencies. This shift moves the stopband center frequency to 11.50 GHz, while the passband disappears. The − 10 dB bandwidth of the stopband widens to 2.26 GHz (10.37–12.63 GHz). Increasing the power further to 800 W shifts the stopband center frequency to 12.75 GHz, with the − 10 dB bandwidth further broadened to 2.87 GHz (11.31–14.18 GHz), and increases the attenuation peak to 24.1 dB.

As the pressure is up to 20 Pa, the S₂₁ curves under various input powers are shown in Fig. 13(b). The S₂₁ parameter exhibits multiple stopband characteristics. As the pressure increases, the v_m also rises, leading to a greater spatial gradient of ω_p and thereby enhancing the effects of multiple refraction, reflection, and absorption interactions between the transmitted wave and the plasma. This intensifies the fluctuations in the transmission curve, resulting in multiple attenuation peaks corresponding to different resonance points. Both N_e and ω_p increase instantaneously with rising power, which broadens the − 10 dB bandwidth of the stopband and enhances the peak attenuation values. At a power level of 400 W, the S₂₁ parameter displays two distinct stopbands. The center frequencies of these stopbands are 13.69 GHz and 16.05 GHz, with − 10 dB bandwidths of 1.68 GHz (12.85–14.53 GHz) and 0.92 GHz (15.64–16.56 GHz), respectively. The peak attenuation values at the resonance points are 24.2 dB and 13.7 dB, respectively.

As the power increases to 600 W, the stopband shifts to higher frequencies. The center frequencies are 13.69 GHz and 16.05 GHz, with − 10 dB bandwidths of 1.68 GHz (12.85–14.53 GHz) and 0.92 GHz (15.64–16.56 GHz), respectively. The peak S₂₁ attenuation values are 24.2 dB and 13.7 dB, respectively. When the power is further increased to 800 W, the attenuation peaks at the two resonance points are enhanced to 29.9 dB and 15.1 dB, leading to the stopband merging from two narrow bands into a single broadband. Consequently, the stopband working bandwidth is broadened to 4.41 GHz (14.66–19.07 GHz), and the center frequency shifts to 16.87 GHz.

To further broaden the working bandwidth of stopband, the pressure is adjusted to 50 Pa, and the corresponding S₂₁ curves under different power levels are shown in Fig. 13(c). Compared with the results at 20 Pa, the value of v_m increases by approximately half an order of magnitude, which further enhances the plasma’s collisional absorption. As a result, both the working bandwidth of stopband and the peak attenuation values are improved.

In addition, increased pressure intensifies the gradient of the ICP parameter distribution, resulting in greater fluctuations in the transmission curve and producing “ringing” phenomena due to multiple transmission zeros. At 400 W, attenuation peaks of 27.39 dB and 18.25 dB are observed at transmission zeros of 12.60 GHz and 16.08 GHz, respectively. These transmission zeros cause the PC-FSS to generate a broadband stopband, with a center frequency of 14.48 GHz and an operational bandwidth of 5.74 GHz (11.61–17.35 GHz). When the power increases to 600 W, the bandwidth of the stopband expands to 6.6 GHz (11.85–18.45 GHz), with the center frequency shifting to 15.15 GHz. At 800 W, the two attenuation peaks increase to 32.41 dB and 25.10 dB, respectively, while the operational bandwidth further expands to 6.99 GHz (12.27–19.07 GHz), and the center frequency shifts to 15.77 GHz. These results indicate that both the center frequency and operational bandwidth of the PC-FSS passband and stopband can be dynamically tuned across a wide frequency range by adjusting barometric pressure and input power, thereby enabling the PC-FSS to adaptively respond to incident electromagnetic waves.

To enhance the attenuation of electromagnetic waves by plasma and achieve frequency selective characteristics of the PC-FSS over a broader frequency range, the discharge chamber thickness was increased to 40 mm. At a pressure of 10 Pa, the S₂₁ parameter under various power levels is presented in Fig. 14(a). At 400 W, the transmission curve exhibits a single stopband and passband. The center frequency of the stopband is 13.86 GHz, with a -10 dB bandwidth of 2.80 GHz (12.46–15.26 GHz). The center frequency of the passband is 17.70 GHz, with a -3 dB bandwidth of 1.28 GHz (17.06–18.34 GHz). As the power increases, the passband vanishes. At 600 W and 800 W, the stopband center frequencies shift to 14.48 GHz and 15.79 GHz, respectively, with corresponding bandwidths of 3.80 GHz (12.97–15.99 GHz) at 600 W and 4.86 GHz (13.36–18.22 GHz) at 800 W.

Fig. 14

Variation in transmission coefficient of PC-FSS versus pressure and power at 4 cm. (a) 1 Pa. (b) 25 Pa. (c) 50 Pa.

When the pressure is increased to 20 Pa, the S₂₁ parameter under various power levels is shown in Fig. 14(b). The transmission curve displays multiple stopbands, similar to the behavior observed with a chamber thickness of 25 mm. Additionally, the ω_p increases with pressure, causing the frequency response of the PC-FSS to shift toward higher frequencies. At 50 Pa, the S₂₁ at different power levels is shown in Fig. 14(c). As pressure increases, the transmission curve develops multiple attenuation peaks, significantly broadening the stopband bandwidth. At power levels of 400 W and 600 W, the center frequencies of the stopband are 15.33 GHz and 15.29 GHz, with corresponding bandwidths of 7.48 GHz (11.59–19.07 GHz) and 7.56 GHz (11.51–19.07 GHz), respectively. When the power is increased to 800 W, the − 9.7 dB bandwidth of the stopband expands to 11.02 GHz (8.05–19.07 GHz). At this power level, the stopband overlaps with the passband observed in the unexcited PC-FSS. These results indicate that, under discharge conditions of 50 Pa and 800 W, the active switching function of the PC-FSS for signal transmission can be realized by controlling the excitation state of the ICP source.

Compared to the results obtained with a chamber thickness of 25 mm, the center frequencies of the stopband shift to higher values, the operational bandwidth increases, and the peak attenuation at the resonance point becomes greater. Additionally, the fluctuations in the transmission curve are more pronounced. These effects can be attributed to the following factors: (1) at the same power and pressure, both electron density N_e and electron temperature T_e increase with greater thickness, which in turn enhances the ωₚ and v_m in the main plasma region; and (2) the increased thickness expands the main plasma region, thereby enlarging the interaction space between the electromagnetic wave and the plasma.

Figure 15 presents the measured S₂₁ parameters of the PC-FSS under various incidence angles and polarization states. The chamber height is set to 25 mm, with an excitation power of 800 W and a pressure of 10 Pa. Due to limitations in the sample size, the maximum measured incident angle is 45°. It is observed that the PC-FSS exhibits enhanced stability with respect to both polarization state and incidence angle.

Fig. 15

Variation in transmission coefficient of PC-FSS versus incidence angles, polarization and excited states. (a) 0°.(b) 45°.

Conclusion

In summary, a broadband active frequency selective surface (FSS) has been comprehensively investigated. The proposed structure consists of a broadband band-pass FSS integrated with an inductively coupled plasma (ICP). By leveraging the tunable attenuation characteristics of ICP on electromagnetic waves, the plasma composited frequency selective surface (PC-FSS) achieves wideband, tunable, and switchable functionality. Experimental results demonstrate that adjusting external discharge parameters—such as power, pressure, and ICP thickness—can modulate the plasma properties, thereby enabling active control over the center frequency and bandwidth of both the passband and stopband.

When unexcited, the PC-FSS functions as a broadband passband FSS, with a center frequency of 13.56 GHz and a -1 dB passband of 11.02 GHz (8.05–19.07 GHz). Upon excitation, the discharge conditions modulate the band-pass and band-stop characteristics of the PC-FSS. Specifically, with increasing power, pressure, and ICP thickness, the − 1 dB passband bandwidth narrows and its center frequency shifts to higher values. Simultaneously, the center frequency of the stopband also shifts to higher frequencies, the − 10 dB bandwidth broadens, and the transmittance minimum deepens. Additionally, at low pressure, the − 10 dB stopband becomes narrower and is concentrated around the resonance frequency of the ICP. In contrast, at high pressure, collisional attenuation dominates electromagnetic wave attenuation, resulting in the formation of multiple stopbands. The capacity for active control of both passband and stopband characteristics in the PC-FSS significantly enhances the stealth performance of aviation radar antennas and demonstrates considerable potential for application in active radome stealth systems.

Although the distribution trends of key parameters such as plasma frequency ωₚ, and collision frequency v_m of the ICP source under various external conditions were obtained using the Drude model and chord-averaged parameters, the parameter distribution in thin-layer plasma exhibits pronounced non-uniformity. This non-uniformity poses challenges for diagnostic results to accurately capture the spatial characteristics of plasma parameter distributions and to analyze the interaction between plasma and electromagnetic waves at a fine scale. In future research, multiphysics numerical simulations of plasma parameter distributions will be performed at both temporal and spatial scales and combined with multi-probe diagnostic methods to address the problem of spatial gradients in plasma parameters.