Principle and calculation method of hydraulic fracturing technique for in-situ stress based on two arbitrary holes

Abstract

In order to precisely obtain the magnitude and orientation of in-situ stress in coal mine roadway, the principle and calculation method of hydraulic fracturing technique for in-situ stress with two arbitrary holes were established in this study. Deriving from the basic principle of the traditional hydraulic fracturing in-situ stress testing, this method, based on the basic data of in-situ stress measured from two arbitrary test holes, performed three stress equivalent transformations following the stress transformation formula in elasticity mechanics. The results suggest that all six stress values representing the stress state at a point were accurately obtained after mechanical and mathematical derivation. Furthermore, the practical application and in-situ stress calculation process of this method were introduced with the Nazuo Coal Mine in Fuyuan County, Yunnan Province of China as the engineering foundation, verifying that the testing results were relatively accurate. The proposed method has addressed the limitations of the traditional single-hole hydraulic fracturing method and mitigated the drawbacks of the three-hole hydraulic fracturing method, what is high requirements for drilling quality and is not practical. So it can be treated as a simple, accurate method for hydraulic fracturing in-situ stress testing.

Introduction

In-situ stress data are the basic reference for the support design of underground roadways and chambers in coal mines. They are also essential factors in the formulation of coal resource mining methods, advanced support design, gas seepage law research, and gas control scheme design. However, the accuracy of in-situ stress testing has long been unable to be guaranteed attributed to the complexity of the surrounding rock in underground projects, the limitation of in-situ stress testing technology and equipment, and numerous uncontrollable factors in the testing process^1,2. Therefore, it is of great theoretical research value and practical significance to investigate the principles and algorithms of in-situ stress testing technology and explore a simple, convenient, highly accurate, and strongly applicable in-situ stress testing method^3,4.

At present, in-situ stress testing methods can be roughly divided into two categories through borehole and core testing methods⁵, such as hydraulic fracturing method^6,7, hollow inclusion gauge method^8,9, non-elastic strain recovery method (ASR)^10,11, borehole collapse method^12,13, Kaiser effect method^14,15, acoustic emission method^{16]– [17}. In addition to these, there are many other methods for in-situ stress testing, each with its own advantages and disadvantages. Among different in-situ stress testing methods, the hydraulic fracturing method has the advantages of complete basic theory, simple testing operation, and no need to know the mechanical properties of rocks in advance^18,19. It has been widely applied in various fields and is one of the in-situ stress measurement methods recommended by the International Society for Rock Mechanics (ISRM)²⁰. Moreover, it is an irreplaceable in-situ stress testing technology^21,22. The early two-dimensional in-situ stress measurement by hydraulic fracturing assumed that the rock was a homogeneous, isotropic, impermeable elastic body and that one of the principal stress directions in the rock was parallel to the borehole axis^23,24. The three-hole orthogonal hydraulic fracturing in-situ stress testing method is broadly used at present^25,26. This method can provide accurate test results and determine the tensile strength of rock, the average specific weight of the overlying strata, and the Poisson’s ratio of rock. Nonetheless, this method requires that the three test points are in the same rock layer, the three test points are close to each other and far from faults, and the test boreholes are orthogonal, which is difficult to achieve in most coal mine tunnels with extremely limited construction space. This considerably restricts the engineering applicability of this method. Concurrently, the three-dimensional in-situ stress measurement by hydraulic fracturing in a single borehole has been realized. The single-borehole hydraulic fracturing in-situ stress testing method is a supplement and improvement to the three-hole orthogonal hydraulic fracturing in-situ stress testing method²⁷. While its requirements for test point selection are relatively low, it needs to obtain the elastic constants of the rock layer and the average specific weight of the overlying rock mass in advance during the calculation of the full stress, principal stress, and tectonic stress at the test point. Consequently, the links that may produce errors and the laboratory workload rise, and the accuracy of the test results cannot be guaranteed.

This paper starts with the basic principle of the hydraulic fracturing in-situ stress testing method. Then, the principle and calculation method of hydraulic fracturing in-situ stress testing are established based on two arbitrary holes, and the calculation formula for in-situ stress data is derived. This method does not require any geological parameters of the stratum and has no special requirements for the test boreholes such as orthogonal holes and vertical holes in conventional testing methods. It should only obtain in-situ stress data through stress equivalent conversion between two arbitrary holes. Moreover, it is an in-situ stress testing method with the advantages of fewer boreholes, a simple testing principle, and accurate calculation results.

Basic principle

Principle of hydraulic fracturing in-situ stress testing

• (1) Basic mechanical principle:.

The principle of hydraulic fracturing in-situ stress measurement follows the theory of Elasticity Mechanics and is premised on 2 assumptions:

• 1. The rock is homogeneous, linearly elastic, and isotropic;

• 2. The rock is intact and impermeable.

Under the above theoretical and hypothetical premises, the mechanical model of hydraulic fracturing in-situ stress measurement can be simplified to a plane model, as depicted in Fig. 1.

Fig. 1

The mechanical model of hydraulic fracturing in-situ stress measurement.

As revealed in Fig. 1, the normal stress and shear stress on the inclined plane corresponding to the angle φ can be solved as

$$\left\{ \begin{gathered} {\sigma _\varphi }=\left( {{\sigma _{\text{x}}}+{\sigma _z}} \right)/2+\left( {{\sigma _{\text{x}}} - {\sigma _z}} \right)\cos 2\varphi /2+{\tau _{{\text{x}}z}}\sin 2\varphi \hfill \\ {\tau _\varphi }= - \left( {{\sigma _{\text{x}}} - {\sigma _z}} \right)\sin 2\varphi /2+{\tau _{{\text{x}}z}}{\text{cos}}2\varphi \hfill \\ \end{gathered} \right.$$

(1)

where σ_φ denotes the normal stress on the inclined plane; τ_φ represents the shear stress on the inclined plane.

When τ_φ = 0, the corresponding fracture orientation angle γ indicates the angle between the maximum normal stress and the positive direction of the Z-axis, expressed as:

$$\tan 2\gamma =2{\tau _{{\text{x}}z}}/\left( {{\sigma _{\text{x}}} - {\sigma _z}} \right)$$

(2)

where γ denotes the fracture orientation angle.

Substituting φ = γ and φ = γ + 2π into Formula (1) yields the maximum and minimum plane stresses P_max and P_min corresponding to the fracturing pressure in Fig. 1

$$\left\{ \begin{gathered} {P_{\hbox{max} }}=\left( {{\sigma _{\text{x}}}+{\sigma _z}} \right)/2+\left( {{\sigma _{\text{x}}} - {\sigma _z}} \right)\cos 2\gamma /2+{\tau _{{\text{xz}}}}\sin 2\gamma \hfill \\ {P_{\hbox{min} }}=\left( {{\sigma _{\text{x}}}+{\sigma _z}} \right)/2 - \left( {{\sigma _{\text{x}}} - {\sigma _z}} \right)\cos 2\gamma /2 - {\tau _{{\text{xz}}}}\sin 2\gamma \hfill \\ \tan 2\gamma =2{\tau _{{\text{xz}}}}/\left( {{\sigma _{\text{x}}} - {\sigma _z}} \right) \hfill \\ \end{gathered} \right.$$

(3)

• (2) Test data acquisition.

Hydraulic fracturing stress testing involves injecting high-pressure water into a test hole. The rock at the location of the minimum compressive stress will be pulled apart when the water pressure overcomes the tensile strength of the rock and the minimum compressive stress at the hole edge induced by the in-situ stress, known as hydraulic fracturing pressure (P_b). After the fracturing of the test hole, the valve and hydraulic pump are closed, allowing the water pressure inside the test hole to naturally decline without external intervention. As the fractured crack is about to close, the water pressure in the test hole gradually stabilizes, and this pressure is called the closure pressure (P_s) of the crack. Subsequently, the depressurization valve is opened to release the water pressure, and the hole is re-pressurized to reopen the previously fractured crack. The pressure at which the crack reopens is called the reopening pressure (P_r). A time-pressure variation curve in Fig. 2 exhibits the relationship between pressure values and time during the entire pressurization and depressurization process, from which the above three key pressure values are obtained.

Fig. 2

The time-pressure variation curve of hydraulic fracturing.

As illustrated in Fig. 2, hydraulic fracturing in-situ stress testing typically requires two pressurization cycles. The first pressurization cycle completes the initial fracturing, yielding two key values: P_b and P_s. The second pressurization cycle completes the reopening of the fracture, yielding two key values: P_r and P_s. The P_s obtained from both fracturing cycles is consistent.

In accordance with the principle of hydraulic fracturing, P_s is equal to the minimum principal stress P_min in Eq. (3). Moreover, based on The Elasticity Theory²⁸, the relationship among P_max, P_min, P_r, and P_s is expressed as:

$$\left\{ \begin{gathered} {P_{\hbox{max} }} - 3{P_{\hbox{min} }}+{P_r}=0 \hfill \\ {P_{\hbox{min} }}={P_{\text{s}}} \hfill \\ \end{gathered} \right.$$

(4)

where P_r denotes the reopening pressure, and P_s represents the closure pressure.

Since the orientation angle of the fracture can be directly obtained during the testing process, the following results can be derived by combining Eqs. (3) and (4).

$$\left\{ \begin{gathered} {\sigma _X}={P_{\hbox{max} }}\left[ {1+\cos (2\gamma )} \right]/2+{P_{\hbox{min} }}\left[ {1 - \cos (2\gamma )} \right]/2 \hfill \\ {\sigma _Z}={P_{\hbox{max} }}\left[ {1 - \cos (2\gamma )} \right]/2+{P_{\hbox{min} }}\left[ {1+\cos (2\gamma )} \right]/2 \hfill \\ {\tau _{XZ}}=({P_{\hbox{max} }} - {P_{\hbox{min} }})\sin (2\gamma )/2 \hfill \\ \end{gathered} \right.$$

(5)

Thus, three out of the six stress components of a stress element (σ_X, σ_Z, and τ_XZ) can be determined by the hydraulic fracturing method in a single test hole.

Basic principle of in-situ stress measurement by hydraulic fracturing in two arbitrary holes

The overall idea of in-situ stress measurement by hydraulic fracturing in two arbitrary holes is described as follows. Only two spatially non-perpendicular and non-parallel in-situ stress test holes are set up at a test site, generally with a horizontal and vertical angle of about 15° between the two holes. The second test hole is utilized to obtain three out of the six stress values representing the stress state at a point (σ_x’, σ_z’, and τ_x’z’). The remaining three unknown stress values (σ_y’, τ_x’y’, and τ_y’z’) are determined by solving a system of equations established through three stress equivalent transformations upon the three stress values (σ_x, σ_z, and τ_xz) determined by the first test hole, as exhibited in Fig. 3. In this way, all six stress values representing the stress state of a stress element are determined by setting up only two test holes, contributing to the significantly curtailed drilling difficulty and workload compared to the conventional hydraulic fracturing method.

Fig. 3

Plastic zone I determined by stress constructing method.

As demonstrated in Fig. 3, two coordinate systems Oxyz and Ox’y’z’ can be established with the radial direction of the first test hole and the radial direction of the second test hole as the y-axis and the y′-axis, respectively (As the extremely small angles between the boreholes may result in a nearly singular transformation matrix, rendering the results unreliable, it is generally required that the horizontal and vertical angles between the two boreholes should not be less than 10°). Three element stress transformations are required to transform the Element ① represented by the coordinate system Ox’y’z’ to the Element ⑤ represented by the coordinate system Oxyz. After the three stress transformations, the element becomes the Element ④ represented by the coordinate system Ox⁰y⁰z⁰. Considering that the elements (④ and ⑤) represented by the coordinate systems Ox’y’z’ and Ox⁰y⁰z⁰ are completely identical, the stress values on each face of the two elements should be equal. Based on this relationship, three independent equations can be established for the remaining three unknown stress values (σ_y’, τ_x’y’, and τ_y’z’) of the second test hole by combining the three stress values already obtained from the first test hole. Consequently, all six stress values on Element ① are determined. Starting from this fundamental concept, the detailed process of stress equivalent transformation and solution is described below.

Stress equivalence transformation for in-situ stress measurement

Stress transformation process

Following the aforementioned basic principles, three stress components can be determined from the second test hole.

$$\left\{ \begin{gathered} {\sigma _{x^{\prime}}}={P_{\hbox{max} 2}}\left[ {1+\cos (2{\alpha _2})} \right]/2+{P_{\hbox{min} 2}}\left[ {1 - \cos (2{\alpha _2})} \right]/2 \hfill \\ {\sigma _{z^{\prime}}}={P_{\hbox{max} 2}}\left[ {1 - \cos (2{\alpha _2})} \right]/2+{P_{\hbox{min} 2}}\left[ {1+\cos (2{\alpha _2})} \right]/2 \hfill \\ {\tau _{x^{\prime}z^{\prime}}}=({P_{\hbox{max} 2}} - {P_{\hbox{min} 2}})\sin (2{\alpha _2})/2 \hfill \\ \end{gathered} \right.$$

(6)

where P_max2 represents the maximum normal stress in the x’z’ plane of the second test hole; P_min2 indicates the minimum normal stress in the x’z’ plane; α₂ designates the fracture orientation angle of the second test hole; σ_x’ denotes the normal stress in the x′ direction; σ_z’ embodies the normal stress in the z’ direction; τ_x’z’ refers to the shear stress acting on the plane perpendicular to the x′-axis and parallel to the z′-axis.

The remaining three stress components of the second test hole are solved by the equations determined by the three stress equivalent transformations in Fig. 3, namely the normal stress σ_y’ in the y′ direction, the shear stress τ_x’y’ acting on the plane perpendicular to the x′-axis and parallel to the y′-axis, and the shear stress τ_y’z’ acting on the plane perpendicular to the y′-axis and parallel to the z′-axis.

• (1) The first stress transformation: Element ① to Element ②

Rotation axis

The first stress transformation involves rotating Element ① around the x′-axis to form a new element representing the stress state. Before the rotation, the coordinate system representing the stress state of the element is Ox’y’z’. After the rotation, it becomes Ox’’y’’z’’. The angles between the corresponding axes of the two coordinate systems are: the angle between the x′-axis and the z-axis is θ₁, and the angle between the y′-axis and the z-axis is θ₂. Both θ₁ and θ₂ are known angles determined from the angular relationship between the two test holes.

Rotation angle criterion

The rotation of the element around the x′-axis terminates when the y′-axis lies in the horizontal plane of the first drill hole, that is, in the xOy coordinate plane. At this point, the y′-axis and the z′-axis transform into the y′′-axis and the z′′-axis, respectively. The element representing the stress state is Element ② presented in Fig. 3, and the corresponding spatial coordinate system is Ox’’y’’z’’, where the z-axis is perpendicular to the y′′-axis, as depicted in Fig. 4.

Rotation angle calculation

Before the element rotates around the x′-axis, an arbitrary point B on the y′-axis can be taken as a reference, corresponding to the line segment OB.

Fig. 4

Stress Transformation process diagram (rotation around the x′-axis).

After the element rotates around the x′-axis, the y′-axis rotates to the position of the y′′-axis, which lies in the xOy coordinate plane. Point A, point D, and point C denote the projection of point B on the y′′-axis, the xOy plane, and the z-axis, respectively. Therefore, quadrilateral ODBC forms a rectangle, with ∠COD = 90^∘. Since γ₂ is known, we have

$$\theta _{2} = \angle BOD = 90^{{\text{o}}} - \gamma _{2}$$

(7)

In the RTΔBOD, L_OB (where L_OB denotes the length of line segment OB, and similar notation is used below) represents an arbitrarily chosen length. Without loss of generality, it can be assumed to be the unit length 1. Thus,

$$\left\{ \begin{gathered} {L_{BD}}={L_{OB}}\sin {\theta _2} \hfill \\ {L_{OD}}={L_{OB}}\cos {\theta _2} \hfill \\ \end{gathered} \right.$$

(8)

where AE indicates the projection of AB in the zOy′′ coordinate plane, and AD denotes the projection of AB in the xOy coordinate plane. Since quadrilateral ADBE is a rectangle, the following relationships exist: ΔABE≌ΔBAD≌ΔOJC. In the RTΔBAD,

$$\left\{ \begin{gathered} {L_{AB}}={L_{BD}}/\cos \left( {{\gamma _1} - {{90}^{\text{O}}}} \right) \hfill \\ {L_{AD}}={L_{BD}}\tan \left( {{\gamma _1} - {{90}^{\text{O}}}} \right) \hfill \\ \end{gathered} \right.$$

(9)

Because the relationships L_BC=L_DO, L_DA=L_BE, and L_AO=L_EC hold, it follows that ΔBCE≌ΔDOA, and ∠DAO = ∠BEC = 90^∘. Equation (10) can be derived from the trigonometric relationships in the RTΔAOD,

$$\left\{ \begin{gathered} {\theta _4}=\angle AOD=\arcsin \left( {{L_{AD}}/{L_{OD}}} \right) \hfill \\ {L_{OA}}={L_{OD}}\cos {\theta _4} \hfill \\ \end{gathered} \right.$$

(10)

Similarly, the rotation angle for the first stress transformation can be determined based on the trigonometric relationships in the RTΔOAB, expressed as:

$${\theta _1}=\angle AOB=\arccos \left( {{L_{OA}}/{L_{OB}}} \right)$$

(11)

It should be noted that the meanings of the angles θ₁, θ₂, θ₃, θ₄, and β₂, among others, have been explained in the plot description of Fig. 4, and thus will not be repeated here.

Calculation of stress transformation

The first stress transformation involves the entire coordinate system rotating around the x′-axis by an angle θ₁. The transformation of the coordinate system is illustrated in Fig. 5.

Fig. 5

The first transformation rotation of coordinate axes.

Assume the stress components at a point in the known coordinate system Ox’y’z’ are

$${\sigma _{i^{\prime}j^{\prime}}}=\left( \begin{gathered} {\sigma _{x^{\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{x^{\prime}y^{\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{x^{\prime}z^{\prime}}} \hfill \\ {\tau _{y^{\prime}x^{\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\sigma _{y^{\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{y^{\prime}z^{\prime}}} \hfill \\ {\tau _{z^{\prime}x^{\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{z^{\prime}y^{\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\sigma _{z^{\prime}}} \hfill \\ \end{gathered} \right)$$

(12)

If the original coordinate system Ox’y’z’ is rotated as a whole around the x′-axis by an angle θ₁ to the new coordinate system Ox’’y’’z’’, the relationship between the two coordinate systems is:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}y^{\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}z^{\prime} \hfill \\ x^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{l_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{m_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{n_1} \hfill \\ y^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{l_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{m_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{n_2} \hfill \\ z^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{l_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{m_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{n_3} \hfill \\ \end{gathered}$$

(13)

where l_i, m_i, and n_i (i = 1,2,3) represent the direction cosines of the angles between the new coordinate axes Ox’’y’’z’’ and the original coordinate axes Ox’y’z’.

Following the relationship between the coordinate systems exhibited in Fig. 5, the angles between the coordinate axes can be obtained as:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}y^{\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}z^{\prime} \hfill \\ x^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{0^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}} \hfill \\ y^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\theta _1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}+{\theta _1} \hfill \\ z^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}} - {\theta _1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\theta _1} \hfill \\ \end{gathered}$$

(14)

Thus, the direction cosine matrix between the new coordinate axes Ox’’y’’z’’ and the original coordinate axes Ox’y’z’ is derived as:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}y^{\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}z^{\prime} \hfill \\ x^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}1\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}0\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}0 \hfill \\ y^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}0\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\cos {\theta _1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\cos ({90^{\text{o}}}+{\theta _1}) \hfill \\ z^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}0\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\cos ({90^{\text{o}}} - {\theta _1})\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\cos {\theta _1} \hfill \\ \end{gathered}$$

(15)

Substituting the stress vector component expressions into the above equations, the stress transformation formulas for the rotated axes can be obtained (Timoshenko and Goodier, 1951).

$$\left\{ \begin{gathered} {\sigma _{x^{\prime\prime}}}=l_{1}^{2}{\sigma _{x^{\prime}}}+m_{1}^{2}{\sigma _{y^{\prime}}}+n_{1}^{2}{\sigma _{z^{\prime}}}+2{l_1}{m_1}{\tau _{x^{\prime}y^{\prime}}}+2{m_1}{n_1}{\tau _{y^{\prime}z^{\prime}}}+2{n_1}{l_1}{\tau _{x^{\prime}z^{\prime}}} \hfill \\ {\sigma _{y^{\prime\prime}}}=l_{2}^{2}{\sigma _{x^{\prime}}}+m_{2}^{2}{\sigma _{y^{\prime}}}+n_{2}^{2}{\sigma _{z^{\prime}}}+2{l_2}{m_2}{\tau _{x^{\prime}y^{\prime}}}+2{m_2}{n_2}{\tau _{y^{\prime}z^{\prime}}}+2{n_2}{l_2}{\tau _{x^{\prime}z^{\prime}}} \hfill \\ {\sigma _{z^{\prime\prime}}}=l_{3}^{2}{\sigma _{x^{\prime}}}+m_{3}^{2}{\sigma _{y^{\prime}}}+n_{3}^{2}{\sigma _{z^{\prime}}}+2{l_3}{m_3}{\tau _{x^{\prime}y^{\prime}}}+2{m_3}{n_3}{\tau _{y^{\prime}z^{\prime}}}+2{n_3}{l_3}{\tau _{x^{\prime}z^{\prime}}} \hfill \\ {\tau _{x^{\prime\prime}y^{\prime\prime}}}={l_1}{l_2}{\sigma _{x^{\prime}}}+{m_1}{m_2}{\sigma _{y^{\prime}}}+{n_1}{n_2}{\sigma _{z^{\prime}}}+({l_1}{m_2}+{l_2}{m_1}){\tau _{x^{\prime}y^{\prime}}} \hfill \\ \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}({m_1}{n_2}+{m_2}{n_1}){\tau _{y^{\prime}z^{\prime}}}+({n_1}{l_2}+{n_2}{l_1}){\tau _{x^{\prime}z^{\prime}}} \hfill \\ {\tau _{y^{\prime\prime}z^{\prime\prime}}}={l_2}{l_3}{\sigma _{x^{\prime}}}+{m_2}{m_3}{\sigma _{y^{\prime}}}+{n_2}{n_3}{\sigma _{z^{\prime}}}+({l_2}{m_3}+{l_3}{m_2}){\tau _{x^{\prime}y^{\prime}}} \hfill \\ \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}({m_2}{n_3}+{m_3}{n_2}){\tau _{y^{\prime}z^{\prime}}}+({n_2}{l_3}+{n_3}{l_2}){\tau _{x^{\prime}z^{\prime}}} \hfill \\ {\tau _{x^{\prime\prime}z^{\prime\prime}}}={l_3}{l_1}{\sigma _{x^{\prime}}}+{m_3}{m_1}{\sigma _{y^{\prime}}}+{n_3}{n_1}{\sigma _{z^{\prime}}}+({l_3}{m_1}+{l_1}{m_3}){\tau _{x^{\prime}y^{\prime}}} \hfill \\ \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}({m_3}{n_1}+{m_1}{n_3}){\tau _{y^{\prime}z^{\prime}}}+({n_3}{l_1}+{n_1}{l_1}){\tau _{x^{\prime}z^{\prime}}} \hfill \\ \end{gathered} \right.$$

(16)

Substituting the direction cosine values from Eq. (15) into the above formula yields the stress values after the first stress transformation.

• (2) The second stress transformation: Element ② to Element ③

Rotation axis

The second stress transformation involves rotating the element around the y′′-axis to form a new Element ③ representing the stress state. Before the rotation, the coordinate system representing the stress state of Element ② is Ox’’y’’z’’. After the rotation, it becomes Ox’’’y’’’z’’’. The angle between the corresponding axes of the two coordinate systems is the angle between the x′-axis and the x′′-axis, γ₁-90^∘, which is a known angle determined from the angular relationship between the two test holes.

Rotation angle criterion

The rotation of the element around the y′′-axis terminates when the x′-axis lies in the horizontal plane of the first drill hole, that is, in the xOy coordinate plane. At this point, the x′′-axis and the z′′-axis transform into the x′′′-axis and the z′′′-axis, respectively. The element representing the stress state is Element ③ in Fig. 3, and the corresponding spatial coordinate system is Ox’’’y’’’z’’’. Moreover, the y′′-axis is perpendicular to both the x’’Oz’’ and x’’’Oz’’’ coordinate planes.

Rotation angle calculation

Before the element rotates around the y′′-axis, researchers draw a line BJ perpendicular to the z′′-axis through point B, and connect points A and B, as illustrated in Fig. 4, bringing about the formation of a rectangle OABJ. Since the rectangle lies in the coordinate plane y’Oz’, it is perpendicular to the x′′-axis.

After the element rotates around the y′′-axis, the z′′-axis rotates to the position of the z′′′-axis (z-axis) when the x′′-axis rotates to the position of the x′′′-axis, Simultaneously, the rectangle OABJ rotates around the y′′-axis to the coordinate plane y’’’Oz’’’. Notably, quadrilateral OAEC remains a rectangle.

The x′′-axis is perpendicular to the rectangle OABJ before rotation, and the x′′′-axis is perpendicular to the rectangle OAEC after rotation. Thus, the following equality relationships exist in Fig. 4.

$$\angle COJ=\angle EAB={\gamma _1} - {90^{\text{o}}}$$

(17)

Calculation of stress transformation

The second stress transformation involves the original coordinate axis rotating around the y′′-axis by an angle γ₁-90^∘. The transformation of the coordinate system is plotted in Fig. 6.

Fig. 6

The second transformation rotation of coordinate axes.

If the original coordinate system Ox’’y’’z’’ is rotated as a whole around the y′′-axis by an angle γ₁-90^∘ to the new coordinate system Ox’’’y’’’z’’’, the relationship between the two coordinate systems is:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}y^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}z^{\prime\prime} \hfill \\ x^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{u_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{v_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{w_1} \hfill \\ y^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{u_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{v_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{w_2} \hfill \\ z^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{u_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{v_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{w_3} \hfill \\ \end{gathered}$$

(18)

where u_i, v_i, and w_i (i = 1,2,3) represent the direction cosines of the angles between the new coordinate axes Ox’’’y’’’z’’’ and the original coordinate axes Ox’’y’’z’’.

Following the relationship between the coordinate systems illustrated in Fig. 6, the angles between the coordinate axes can be derived as:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}y^{\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}z^{\prime\prime} \hfill \\ x^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\gamma _1} - {90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{180^{\text{o}}} - {\gamma _1} \hfill \\ y^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{0^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}} \hfill \\ z^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\gamma _1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\gamma _1} - {90^{\text{o}}} \hfill \\ \end{gathered}$$

(19)

Then, the expressions for all the stress components after the second rotation can be obtained according to Eq. (16).

• (3) The third stress transformation: Element ③ to Element ④

Rotation axis

The third transformation involves rotating Element ③ around the z′′′-axis to form a new Element ④ representing the stress state. Before the rotation, the coordinate system representing the stress state of the element is Ox’’’y’’’z’’’. After the rotation, it becomes Ox⁰y⁰z⁰.

Rotation angle criterion

The rotation terminates when the x′′′-axis coincides with the x⁰-axis and the y′′′-axis coincides with the y⁰-axis. Concurrently, the element representing the stress state transforms from Element ③ to Element ④, as demonstrated in Fig. 3.

Rotation angle calculation

Figure 7 suggests that a crucial factor in this round of stress transformation is the calculation of ∠AOD’ between the y′′′-axis and the y⁰-axis. Since ∠AOD’=θ₃ + θ₄, and θ₄ is calculated, as expressed in Eq. (10). Specifically, θ₃, which is a known angle, denotes the horizontal azimuth angle between the two test holes.

Therefore, the rotation angle for the third stress transformation can be determined as

$${\theta _5}=\angle AOD^{\prime}={\theta _3}+{\theta _4}$$

(20)

Calculation of stress transformation

The third stress transformation involves the original coordinate axis rotating around the z’’’-axis by an angle θ₅. The transformation of the coordinate system is illustrated in Fig. 7.

Fig. 7

The third transformation rotation of coordinate axes.

If the original coordinate system Ox’’’y’’’z’’’ is rotated as a whole around the z’’’-axis by an angle θ₅ to the new coordinate system Ox⁰y⁰z⁰, the relationship between the two coordinate systems is:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}y^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}z^{\prime\prime\prime} \hfill \\ {x^0}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{r_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{s_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{t_1} \hfill \\ {y^0}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{r_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{s_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{t_2} \hfill \\ {z^0}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{r_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{s_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{t_3} \hfill \\ \end{gathered}$$

(21)

where r_i, s_i, and t_i (i = 1,2,3) represent the direction cosines of the angles between the new coordinate axes Ox⁰y⁰z⁰ and the original coordinate axes Ox’’’y’’’z’’’.

In accordance with the relationship between the coordinate systems presented in Fig. 7, the angles between the coordinate axes can be derived as:

$$\begin{gathered} \begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}x^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}y^{\prime\prime\prime}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}z^{\prime\prime\prime} \hfill \\ {x^0}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\theta _5}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}+{\theta _5}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}} \hfill \\ {y^0}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}} - {\theta _5}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{\theta _5}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}} \end{array}{90^{\text{o}}} \hfill \\ {z^0}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{90^{\text{o}}}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{0^{\text{o}}} \hfill \\ \end{gathered}$$

(22)

Then, the expressions for all the stress components after the third rotation can be obtained according to Eq. (16).

Thus, the stress transformation is completed in the Ox⁰y⁰z⁰ coordinate system, which is identical to the Oxyz coordinate system established based on the first test hole.

Establishing equations to determine stress

First, three stress values are determined by the results of the in-situ stress test from the first drill hole.

$$\left\{ \begin{gathered} {\sigma _x}={P_{\hbox{max} 1}}\left[ {1+\cos (2{\alpha _1})} \right]/2+{P_{\hbox{min} 1}}\left[ {1 - \cos (2{\alpha _1})} \right]/2 \hfill \\ {\sigma _z}={P_{\hbox{max} 1}}\left[ {1 - \cos (2{\alpha _1})} \right]/2+{P_{\hbox{min} 1}}\left[ {1+\cos (2{\alpha _1})} \right]/2 \hfill \\ {\tau _{xz}}=({P_{\hbox{max} 1}} - {P_{\hbox{min} 1}})\sin (2{\alpha _0})/2 \hfill \\ \end{gathered} \right.$$

(23)

Where P_max1 represents the maximum normal stress in the xz plane of the first test hole; P_min1 indicates the minimum normal stress in the xz plane; α₁ denotes the fracture orientation angle of the first test hole; σ_x embodies the normal stress in the x direction; σ_z refers to the normal stress in the z direction; τ_xz designates the shear stress acting on the plane perpendicular to the x-axis and parallel to the z-axis.

Second, Element ④ in Fig. 3 is in a completely equivalent relationship with Element ⑤, illustrated in Fig. 8.

Fig. 8

Equivalence relationship between Element ④ and Element ⑤.

Element ④ is the element obtained after three stress-equivalent transformations from Element ①. Particularly, there are only three unknown stresses in the resulting formula after the three stress equivalent transformations because Element ① is determined by the second test hole with the three stress values in Eq. (6). Element ⑤ can also be determined by the first test hole with the three stress values in Eq. (22) (σ_x, σ_z, and τ_xz). Since Elements ④ and ⑤ are equivalent, these three stress values must be equal to the corresponding stress $\left( {\sigma _{{x^{0} }} ,\,\sigma _{{z^{0} }} ,\,\tau _{{x^{0} z^{0} }} } \right)$ components derived from Element ① after three equivalent stress transformations. In other words, the following equations hold.

$$\left\{ {{\sigma _x}={\sigma _{{x^o}}};\begin{array}{*{20}{c}} {} \end{array}{\sigma _{\text{z}}}={\sigma _{{z^o}}};\begin{array}{*{20}{c}} {} \end{array}{\tau _{x{\text{z}}}}={\tau _{{x^o}{{\text{z}}^o}}}} \right.$$

(24)

The six stress values of the stress element in the second test hole can be calculated by establishing the system of equations from the above formulas. The specific method for obtaining the system of equations is described as follows.

If the coefficient matrices for the three stress transformations are denoted as A₁, A_2, and A₃, the matrix A₁ can be easily obtained by referring to the stress transformation formulas for the rotated axes:

$${A_1}=\left[ \begin{gathered} l_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}m_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}n_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{l_1}{m_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{m_1}{n_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{n_1}{l_1} \hfill \\ l_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}m_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}n_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{l_2}{m_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{m_2}{n_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{n_2}{l_2} \hfill \\ l_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}m_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}n_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{l_3}{m_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{m_3}{n_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{n_3}{l_3} \hfill \\ {l_1}{l_2}\begin{array}{*{20}{c}} {} \end{array}{m_1}{m_2}\begin{array}{*{20}{c}} {} \end{array}{n_1}{n_2}\begin{array}{*{20}{c}} {} \end{array}{l_1}{m_2}+{l_2}{m_1}\begin{array}{*{20}{c}} {} \end{array}{m_1}{n_2}+{m_2}{n_1}\begin{array}{*{20}{c}} {} \end{array}{n_1}{l_2}+{n_2}{l_1} \hfill \\ {l_2}{l_3}\begin{array}{*{20}{c}} {} \end{array}{m_2}{m_3}\begin{array}{*{20}{c}} {} \end{array}{n_2}{n_3}\begin{array}{*{20}{c}} {} \end{array}{l_2}{m_3}+{l_3}{m_2}\begin{array}{*{20}{c}} {} \end{array}{m_2}{n_3}+{m_3}{n_2}\begin{array}{*{20}{c}} {} \end{array}{n_2}{l_3}+{n_3}{l_2} \hfill \\ {l_3}{l_1}\begin{array}{*{20}{c}} {} \end{array}{m_3}{m_1}\begin{array}{*{20}{c}} {} \end{array}{n_3}{n_1}\begin{array}{*{20}{c}} {} \end{array}{l_3}{m_1}+{l_1}{m_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{m_3}{n_1}+{m_1}{n_3}\begin{array}{*{20}{c}} {} \end{array}{n_3}{l_1}+{n_1}{l_3} \hfill \\ \end{gathered} \right]$$

(25)

Similarly, the coefficient matrix A₂ for the second stress transformation can be derived by substituting parameters into Equations (l_i→u_i, m_i→v_i, and n_i→w_i, where i = 1, 2, and 3); the coefficient matrix A₃ for the third stress transformation can be obtained by substituting parameters into Equations (l_i→r_i, m_i→s_i, and n_i→t_i, where i = 1, 2, and 3). Therefore, A₂ and A₃ can be similarly obtained as follows.

$${A_2}=\left[ \begin{gathered} u_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}v_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}w_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{u_1}{v_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{v_1}{w_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{w_1}{u_1} \hfill \\ u_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}v_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}w_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{u_2}{v_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{v_2}{w_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{w_2}{u_2} \hfill \\ u_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}v_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}w_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{u_3}{v_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{v_3}{w_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{w_3}{u_3} \hfill \\ {u_1}{u_2}\begin{array}{*{20}{c}} {} \end{array}{v_1}{v_2}\begin{array}{*{20}{c}} {} \end{array}{w_1}{w_2}\begin{array}{*{20}{c}} {} \end{array}{u_1}{v_2}+{u_2}{v_1}\begin{array}{*{20}{c}} {} \end{array}{v_1}{w_2}+{v_2}{w_1}\begin{array}{*{20}{c}} {} \end{array}{w_1}{u_2}+{w_2}{u_1} \hfill \\ {u_2}{u_3}\begin{array}{*{20}{c}} {} \end{array}{v_2}{v_3}\begin{array}{*{20}{c}} {} \end{array}{w_2}{w_3}\begin{array}{*{20}{c}} {} \end{array}{u_2}{v_3}+{u_3}{v_2}\begin{array}{*{20}{c}} {} \end{array}{v_2}{w_3}+{v_3}{w_2}\begin{array}{*{20}{c}} {} \end{array}{w_2}{u_3}+{w_3}{u_2} \hfill \\ {u_3}{u_1}\begin{array}{*{20}{c}} {} \end{array}{v_3}{v_1}\begin{array}{*{20}{c}} {} \end{array}{w_3}{w_1}\begin{array}{*{20}{c}} {} \end{array}{u_3}{v_1}+{u_1}{v_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{v_3}{w_1}+{v_1}{w_3}\begin{array}{*{20}{c}} {} \end{array}{w_3}{u_1}+{w_1}{u_3} \hfill \\ \end{gathered} \right]$$

(26)

$${A_3}=\left[ \begin{gathered} r_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}s_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}t_{1}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{r_1}{s_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{s_1}{t_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{t_1}{r_1} \hfill \\ r_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}s_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}t_{2}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{r_2}{s_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{s_2}{t_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{t_2}{r_2} \hfill \\ r_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}s_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}t_{3}^{2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{r_3}{s_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{s_3}{t_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}2{t_3}{r_3} \hfill \\ {r_1}{r_2}\begin{array}{*{20}{c}} {} \end{array}{s_1}{s_2}\begin{array}{*{20}{c}} {} \end{array}{t_1}{t_2}\begin{array}{*{20}{c}} {} \end{array}{r_1}{s_2}+{r_2}{s_1}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{s_1}{t_2}+{s_2}{t_1}\begin{array}{*{20}{c}} {} \end{array}{t_1}{r_2}+{t_2}{r_1} \hfill \\ {r_2}{r_3}\begin{array}{*{20}{c}} {} \end{array}{s_2}{s_3}\begin{array}{*{20}{c}} {} \end{array}{t_2}{t_3}\begin{array}{*{20}{c}} {} \end{array}{r_2}{s_3}+{r_3}{s_2}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{s_2}{t_3}+{s_3}{t_2}\begin{array}{*{20}{c}} {} \end{array}{t_2}{r_3}+{t_3}{r_2} \hfill \\ {r_3}{r_1}\begin{array}{*{20}{c}} {} \end{array}{s_3}{s_1}\begin{array}{*{20}{c}} {} \end{array}{t_3}{t_1}\begin{array}{*{20}{c}} {} \end{array}{r_3}{s_1}+{r_1}{s_3}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}{s_3}{t_1}+{s_1}{t_3}\begin{array}{*{20}{c}} {} \end{array}{t_3}{r_1}+{t_1}{r_3} \hfill \\ \end{gathered} \right]$$

(27)

The stress component matrices for the three stress transformations are expressed as:

$$\left\{ \begin{gathered} B^{\prime}={\left[ {{\sigma _{x^{\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {{\sigma _{y^{\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\sigma _{z^{\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{x^{\prime}y^{\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{y^{\prime}z^{\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{x^{\prime}z^{\prime}}}} \end{array}} \right]^T} \hfill \\ B^{\prime\prime}={\left[ {{\sigma _{x^{\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {{\sigma _{y^{\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\sigma _{z^{\prime\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{x^{\prime\prime}y^{\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{y^{\prime\prime}z^{\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{x^{\prime\prime}z^{\prime\prime}}}\begin{array}{*{20}{c}} {} \end{array}} \end{array}} \right]^T} \hfill \\ B^{\prime\prime\prime}={\left[ {{\sigma _{x^{\prime\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {{\sigma _{y^{\prime\prime\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\sigma _{z^{\prime\prime\prime}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{x^{\prime\prime\prime}y^{\prime\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{y^{\prime\prime}z^{\prime\prime\prime}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{x^{\prime\prime\prime}z^{\prime\prime\prime}}}} \end{array}} \right]^T} \hfill \\ {B^0}={\left[ {{\sigma _{{x^0}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {{\sigma _{{y^0}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\sigma _{{z^0}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{{x^0}{y^0}}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{{y^0}{z^0}}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{{x^0}{z^0}}}} \end{array}} \right]^T} \hfill \\ B={\left[ {{\sigma _x}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {{\sigma _y}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\sigma _z}\begin{array}{*{20}{c}} {} \end{array}{\tau _{xy}}\begin{array}{*{20}{c}} {} \end{array}{\tau _{yz}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}{\tau _{xz}}} \end{array}} \right]^T} \hfill \\ \end{gathered} \right.$$

(28)

where B’, B’’, B’’’, B⁰ and B indicate the stress component matrices for Elements ①-⑤ in Fig. 3, respectively.

Then,

$$B=\left[ \begin{gathered} {\sigma _x} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} {\sigma _y} \hfill \\ {\sigma _z} \hfill \\ {\tau _{xy}} \hfill \\ {\tau _{yz}} \hfill \\ {\tau _{xz}} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered} \right]={A_3}B^{\prime\prime\prime}={A_3}{A_2}B^{\prime\prime}={A_3}{A_2}{A_1}B^{\prime}={A_3}{A_2}{A_1}\left[ \begin{gathered} {\sigma _{x^{\prime}}} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} {\sigma _{y^{\prime}}} \hfill \\ {\sigma _{z^{\prime}}} \hfill \\ {\tau _{x^{\prime}y^{\prime}}} \hfill \\ {\tau _{y^{\prime}z^{\prime}}} \hfill \\ {\tau _{x^{\prime}z^{\prime}}} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered} \right]$$

(29)

A system of three equations with three unknowns is directly determined. by performing the matrix calculations in Eq. (28). Solving this system of equations yields all six stress values for Element ① (the measurement point of the second test hole).

Field test analysis

Selection of measurement points and drill hole design

The coal mining layer in Nazuo Coal Mine, Fuyuan County, Yunnan Province, China is the 6# coal seam. Following the principle of ensuring that there are no fault fracture zones, goaf areas, or other tunnels (chambers) within a 50 m radius around the stress measurement point, the location near the No. 5 drilling site at Point 7 in the return airway of the 110,601 working face is selected through hydraulic fracturing stress testing method as the drilling site for the in-situ stress test, as exhibited in Fig. 9.

Fig. 9

In-situ stress test location.

Afterward, based on the rock strata of the tunnel roof and floor, the parameters for the two in-situ stress test holes are designed, as listed in Table 1, following the design principle that “the last 5 m of the two holes are in the same rock layer, and the horizontal and vertical angles between the two holes are 15^°”.

Table 1 Drilling design parameters.

Test results

• (1) Raw data

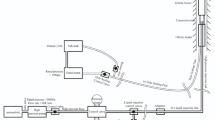
Through on-site testing, the relationship curve between the pressure gauge reading and time is obtained, as illustrated in Fig. 10.

Fig. 10

On-site test time-pressure curves.

The fracturing parameters are obtained from Fig. 10. In conjunction with the fracture surface angles measured on-site, the relevant parameters are listed in Table 2.

Table 2 Fracturing parameters.

• (2) Key angles determination

Upon the drilling parameters in Table 1, two rectangular coordinate systems are established with the hole mouth position as the origin O. The radial direction of the drill hole is the positive direction of the y (or y′) axis, the direction perpendicular to y (or y′) upward is the positive direction of the z (or z′) axis, and the direction perpendicular to the yOz (or $y^{{\prime }} Oz^{{\prime }}$ ) plane towards the tunnel is the positive direction of the x (or x′) axis. In this way, the rectangular coordinate systems for Elements ① and ⑤ in Fig. 3 are established.

During the process of in-situ stress calculation, four key angles, serving as known conditions, need to be determined in advance, including the vertical angle θ₂ between the y′-axis and the y-axis (the angle between the projections of the two test holes in the vertical direction), the horizontal angle θ₃ between the y′-axis and the y-axis (the angle between the projections of the two test holes in the horizontal direction), the angle γ₁ between the x′-axis and the z-axis, and the angle γ₂ between the y′-axis and the z-axis.

① Determination of θ₂: θ₂ represents the angle between the vertical projections of the two test holes, namely, the difference in the dip angles of the two test holes. Therefore, θ₂ = 30°-18°=12°, which can be determined by the dip angles of the boreholes measured by a geological compass.

② Determination of θ₃: θ₃ denotes the angle between the horizontal projections of the two test holes, that is, the difference in the azimuth angles of the two test holes. Thus, θ₃ = 26°-11°=15°, which can be determined by the azimuths of the boreholes measured by a geological compass.

③ Determination of γ₁: As revealed in Fig. 6, the angle between the x′ and z coordinates is

$$\gamma _{1} = 90^{^\circ } + \angle x^{\prime } Ox^{{\prime \prime \prime }} = 90^{^\circ } + \angle zOz^{\prime }$$

(30)

Since the angle ∠zOz’ is equal to the angle θ₂, θ₁ can be determined as

$$\gamma _{1} = 90^{^\circ } + \theta _{2} = 90^{^\circ } + \left( {13^{^\circ } - 18^{^\circ } } \right) = 102^{^\circ }$$

(31)

④ Determination of γ₂: According to Eq. (7), γ₂ = 90°-θ₂ = 78°.

Test results analysis

By employing the theoretical formulas in Sect. 2 and substituting the values of the key angles, computational programming yields 6 stress values representing the stress state at a point:

$$\left\{ {\begin{array}{*{20}c} {\sigma _{{x^{\prime } }} = 5.4572Mpa;\,\,\sigma _{{y^{\prime } }} = 4.9867Mpa;\,\,\sigma _{{z^{\prime } }} = 9.5128Mpa\,\,\,} \\ {\tau _{{x^{\prime } y^{\prime } }} = 0.7653Mpa;\,\,\tau _{{y^{\prime } z^{\prime } }} = 0.8123Mpa;\,\,\tau _{{x^{\prime } z^{\prime } \,}} = 0.8004Mpa} \\ \end{array} } \right.$$

(32)

The return airway of the 110,601 working face is 483 m in length, with an average length of 471.5 m and a dip width of 185 m (oblique distance), covering a planar area of 87,227.5 m². The upper limit elevation underground is + 1750 m, and the lower limit elevation is + 1702 m, with an average elevation of + 1726 m. The corresponding surface elevation of the working face ranges from an upper limit of + 2195 m to a lower limit of + 2027 m, with an average of + 2111 m. Additionally, the in-situ stress near the measurement point is approximately (2111 − 1726)×2.5 ÷ 100 = 9.625 MPa (about 2.5 MPa per 100 m of burial depth) according to empirical calculations, reflecting that the test results are reliable.

Following the stress state theory of elasticity mechanics, the three principal stresses at the measurement point are derived as:

$$\left\{ {\begin{array}{*{20}c} {\sigma _{1} = 9.8501Mpa} \\ {\sigma _{2} = 5.6926Mpa} \\ {\sigma _{3} = 4.4140Mpa} \\ \end{array} } \right.$$

(33)

Where σ₁, σ_2, and σ₃ are the first, second, and third principal stresses, respectively.

The angles between the three principal stresses at the measurement point and the coordinate axes of Ox’y’z’ are detailed in Table 3.

Table 3 Orientation parameters of the three principal stresses.

Accuracy validation of test results

To further validate the accuracy of the in-situ stress testing results mentioned above, the three-hole hydraulic fracturing method was used to conduct a second in-situ stress test near the aforementioned measurement point, and the results are shown in Fig. 11 below.

Fig. 11

On-site test time-pressure curves (the three-hole hydraulic fracturing method).

Similarly, the fracturing parameters of the three-hole hydraulic fracturing method are obtained from Fig. 11. In conjunction with the fracture surface angles measured on-site, the relevant parameters are listed in Table 4.

Table 4 Fracturing parameters (the three-hole hydraulic fracturing method).

According to relevant research literature, the stress tensor determined by the three-hole hydraulic fracturing in-situ stress testing method can be solved by the following formulas.

$$\left\{ \begin{gathered} {\sigma _x}=\frac{{{p_{\hbox{min} }}}}{2}\left[ {1 - \cos (2\zeta )} \right]+\frac{{{p_{\hbox{max} }}}}{2}\left[ {1+\cos (2\zeta )} \right]=\frac{{{{p^{\prime\prime}}_{\hbox{min} }}}}{2}\left[ {1 - \cos (2\zeta ^{\prime\prime})} \right]+\frac{{{{p^{\prime\prime}}_{\hbox{max} }}}}{2}\left[ {1+\cos (2\zeta ^{\prime\prime})} \right] \hfill \\ {\sigma _y}=\frac{{{{p^{\prime}}_{\hbox{min} }}}}{2}\left[ {1 - \cos (2\zeta ^{\prime})} \right]+\frac{{{{p^{\prime}}_{\hbox{max} }}}}{2}\left[ {1+\cos (2\zeta ^{\prime})} \right] \hfill \\ {\sigma _z}=\frac{{{p_{\hbox{min} }}}}{2}\left[ {1+\cos (2\zeta )} \right]+\frac{{{p_{\hbox{max} }}}}{2}\left[ {1 - \cos (2\zeta )} \right]=\frac{{{{p^{\prime}}_{\hbox{min} }}}}{2}\left[ {1+\cos (2\zeta ^{\prime})} \right]+\frac{{{{p^{\prime}}_{\hbox{max} }}}}{2}\left[ {1 - \cos (2\zeta ^{\prime})} \right] \hfill \\ {\tau _{xy}}=\left[ {\frac{{({{p^{\prime}}_{\hbox{max} }} - {{p^{\prime}}_{\hbox{min} }})}}{2}\sin (2\zeta ^{\prime}) - \frac{{({{p^{\prime\prime}}_{\hbox{max} }} - {{p^{\prime\prime}}_{\hbox{min} }})}}{2}\sin (2\zeta ^{\prime\prime})} \right] \hfill \\ {\tau _{yz}}=\frac{{({{p^{\prime}}_{\hbox{max} }} - {{p^{\prime}}_{\hbox{min} }})}}{2}\sin (2\zeta ^{\prime}) \hfill \\ {\tau _{xz}}=\frac{{({p_{\hbox{max} }} - {p_{\hbox{min} }})}}{2}\sin (2\zeta ) \hfill \\ \end{gathered} \right.$$

(34)

Where p_min, p’_min and p’’_min are the minimum principal stresses of the first, second, and third boreholes, respectively; while p_max, p’_max and p’’_max are the maximum principal stresses of the first, second, and third boreholes, respectively, all of which can be solved similarly by Eq. (3). ζ, ζ′ and ζ′′ are the fracture angles of the first, second, and third boreholes, respectively.

After substituting the test results of Table 4 into Eq. (3) for solution, and then back into Eq. (33), the stress tensor based on the three-hole hydraulic fracturing in-situ stress testing method can be obtained as

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {\sigma _{x} = 5.6495Mpa;{\mkern 1mu} {\mkern 1mu} \sigma _{y} = 5.2294Mpa;{\mkern 1mu} {\mkern 1mu} \sigma _{z} = 9.3619Mpa{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} } \\ {\tau _{{xy}} = 2.6265Mpa;{\mkern 1mu} {\mkern 1mu} \tau _{{yz}} = 0.4594Mpa;{\mkern 1mu} {\mkern 1mu} \tau _{{xz{\kern 1pt} }} = 0.6803Mpa} \\ \end{array} } \right. \hfill \\ \hfill \\ \end{gathered}$$

(35)

When comparing it with the in-situ stress tensor based on the arbitrary two-hole testing method, namely Eq. (29), it can be found that the two are basically consistent, which indicates that the hydraulic fracturing in-situ stress testing method based on arbitrary two holes proposed in this paper has good accuracy.

Discussion

In this paper, a two-arbitrary-holes method for in-situ stress testing and calculation is proposed based on the mechanical model of the classical hydraulic fracturing in-situ stress testing method. It has been applied in multiple coal mines in the southwestern region of Guizhou, proving its feasibility and reliability. The main input parameters of this method include the fracturing pressures and angles of the test holes, and the angles between the two test holes. During the in-situ stress calculation process, there will be no significant deviations in the results due to small perturbations in the borehole test results, e.i., “(the fracturing pressures and angles)”. While it is true that too small an angle between the two test holes may lead to matrix singularity in the in-situ stress calculation, which to some extent limits the applicability of this method. However, practical tests show that controlling the horizontal and vertical angles between the two test holes to be no less than 10 degrees can solve this problem. In other words, as long as the horizontal and vertical angles between the two test holes are no less than 10 degrees, the in-situ stress test data can be obtained using this method. Then combining an empirical burial depth stress estimation, the three-hole hydraulic fracturing in-situ stress testing method, or other in-situ stress testing method, the accuracy and reliability of the test results can be further assessed.

Conclusion

This study aimed to overcome the inaccuracies associated with the traditional single-hole hydraulic fracturing method and address the shortcomings of the three-hole hydraulic fracturing method, which requires high drilling quality and weak practicality. Thus, a simple, convenient, highly applicable, and high-precision geostress testing method was developed in this study. Starting from the basic principles of the hydraulic fracturing geostress testing method, this paper presents a principle of hydraulic fracturing geostress testing based on any two holes. Then, the geostress solution formula was derived through physical mechanics. Meanwhile, the practical application and geostress calculation process of this method were introduced with the Nazuo Coal Mine in Fuyuan County, Yunnan Province as an example. The results were relatively accurate. This method did not have special requirements for any geological parameters of the geological strata nor orthogonal holes, vertical holes, or other conventional testing methods in testing boreholes. It obtained geostress data only through equivalent stress conversion between any two holes. It demonstrated the advantages of small drilling volume, simple testing principle, and accurate calculation results, contributing to the improved applicability of the hydraulic fracturing geostress testing method. Furthermore, it can be applied to theoretical research and engineering fields in coal mine geological exploration.