Deep learning time-series modeling for assessing land subsidence under reduced groundwater use

Abstract

Intensive groundwater extraction and a severe 2021 drought have worsened land subsidence in Taiwan’s Choshui Delta, highlighting the need for effective predictive modeling to guide mitigation. In this study, we develop a machine learning framework for subsidence analysis using electricity consumption data from pumping wells as a proxy for groundwater extraction. A long short-term memory (LSTM) neural network is trained to reconstruct missing subsidence records and forecast subsidence trends, while an artificial neural network links well electricity usage to groundwater level fluctuations. Using these tools, we identify groundwater-level decline from pumping as a key driver of subsidence. The LSTM model achieves high accuracy in reproducing historical subsidence and provides reliable predictions of subsidence behavior. Scenario simulations indicate that reducing groundwater pumping, simulated by lowering well electricity use, allows groundwater levels to recover and significantly slows the rate of land subsidence. To assess the effectiveness of pumping reduction strategies, two artificial scenarios were simulated. The average subsidence rate at the Xiutan Elementary School multi-layer compression monitoring well (MLCW) decreased from 2.23 cm/year (observed) to 1.94 cm/year in first scenario and 1.34 cm/year in second scenario, demonstrating the potential of groundwater control in mitigating land subsidence. These findings underscore the importance of integrating groundwater-use indicators into subsidence models and demonstrate that curtailing groundwater extraction can effectively mitigate land subsidence in vulnerable deltaic regions.

Introduction

In recent years, Taiwan’s central and southern regions have faced severe droughts with increasing frequency due to climate change^1,2. As a result, excessive groundwater extraction has led to rapid land subsidence, with the Choshui delta experiencing a subsidence rate of up to 7.8 cm per year by 2021. The phenomenon of soil compression in the Choshui delta is a time-dependent geological process^3,4,5,6, where fluctuations in groundwater levels lead to soil consolidation, a gradual change in volume in response to pore water pressure variations^7,8. Accurate prediction of land subsidence is critical for mitigating geological hazards and forming effective adaptation strategies. The Choshui delta has been extensively studied with geodetic techniques, such as GPS and InSAR⁹, since 1991, and the introduction of multi-layer compression monitoring wells (MLCWs) in 2008 has provided valuable data for understanding subsidence trends^10,11,12,13.

Conventional physical models for subsidence analysis require complex hydrogeological parameters, which are challenging to acquire due to spatial variations in soil layers^14,15,16,17. With advancements in artificial intelligence, machine learning techniques, especially the long short-term memory (LSTM) model, have shown promise in predicting subsidence and groundwater fluctuations^18,19,20,21. LSTM’s success relies on extensive training data, making it an effective tool for time-series predictions^22,23. Specifically, a hybrid model integrating a convolutional-based autoencoder with LSTM to accurately perform multistep groundwater level forecasting across watersheds²⁴; the development of global and local LSTM frameworks for sequential groundwater forecasting that effectively capture both regional and temporal variability²⁵; the application of a hybrid deep learning framework for forecasting groundwater levels in Taiwan’s largest alluvial fan, demonstrating its utility in managing complex hydrological systems ²⁶; the employment of machine learning methods to analyze trends and seasonality in groundwater-induced subsidence²⁷; and the integration of a TCN-LSTM-attention network that enhances prediction accuracy of groundwater levels and enables detection of seismic-related anomalies²⁸.

The severe drought of 2021 in Taiwan resulted in a total annual rainfall of only 880 mm^29,30 led to a substantial decline in groundwater levels, contributing to severe land subsidence. Taiwan has increasingly reduced groundwater extraction and improve hydro-meteorological resilience. Measures like crop conversion and optimized irrigation have been proven to stabilize groundwater levels and reduce subsidence rates^31,32.

This study introduces a novel approach for analyzing and mitigating land subsidence by leveraging machine learning models and real-world indicators of groundwater use. An LSTM neural network is used to analyze time-series subsidence and groundwater data and to reconstruct missing subsidence data. We identify key factors influencing subsidence through statistical correlation analysis and incorporate these factors—particularly groundwater level fluctuations and well pumping intensity (inferred from electricity consumption)—into the model. A case study in the Choshui Delta demonstrates the model’s ability to capture subsidence dynamics and fill data gaps. Additionally, we evaluate a groundwater management scenario involving partial conversion of rice fields to less water-intensive crops, such as corn, as a means to reduce groundwater extraction. The integrated approach uses well electricity consumption as a proxy for pumping activity, linking human water-use behavior with land subsidence. Our findings provide insights into how reducing groundwater use can alleviate subsidence, offering guidance for sustainable management policies in subsidence-prone regions.

The Choshui delta and datasets

Land subsidence in Choshui delta

The Choshui delta, situated in central Taiwan, is one of the largest alluvial fans in the region, formed through the continuous deposition of sediments on the western side of a hilly terrain. Soil compression within the delta is a natural geological process, occurring due to the weight of accumulating sediments^4,5,6. However, human activities, particularly the extensive extraction of groundwater for agricultural and industrial use, have significantly exacerbated land subsidence in the area. The Choshui delta alone accounts for approximately 75% of Taiwan’s total land subsidence, covering an area of about 600 km² as of 2015. By the end of 2021, the region remained highly vulnerable to land subsidence, experiencing the highest rates in central Taiwan, with a maximum subsidence rate of 7.8 cm per year. This concerning trend highlights the urgent need for comprehensive monitoring and mitigation strategies to address the detrimental impacts on infrastructure, ecosystems, and local communities.

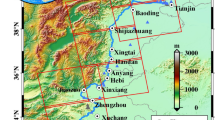
Figure 1 shows the location of the study area and the cumulative subsidence data from 2015 to 2023 (this figure was created with ArcGIS 10.8 software, obtained from https://www.arcgis.com/index.html), emphasizing the long-term effects of groundwater over-exploitation, which is a potential primary driver of subsidence in western Taiwan. Notably, the subsidence funnels have gradually shifted from coastal to inland areas, revealing the spatial and temporal evolution of subsidence patterns. This underscores the importance of effective groundwater management to mitigate further land instability. In addition, Fig. 1 is intended to provide context by showing the regions in Taiwan with severe land subsidence currently targeted for subsidence mitigation efforts and the locations of all MLCW stations within those regions as shown in the yellow diamonds in Fig. 1. The STES MLCW data were used in our study as a demonstration case. The purpose of including all MLCW locations in Fig. 1 is to highlight that STES is one of several stations in the critical subsidence areas, and to indicate that our methodology could be applied to other MLCW sites in these severely subsiding regions in the future.

Fig. 1

Study area overview: (top left) Location of the Choshui delta; (top right) Spatial distribution of MLCWs in the Choshui Delta; (bottom) Location of the STES (this figure was created with ArcGIS 10.8 software, obtained from https://www.arcgis.com/index.html).

Figure 2 presents thematic maps of the Choshui Delta, including: (a) accumulated subsidence from 2015 to 2023; (b) fine-grained soil content; (c) electric power consumption density distribution; (d) managed wells distribution. As illustrated in Fig. 2a, accumulated subsidence from 2015 to 2023 was assessed using leveling survey data collected (WRA, 2023). Accumulated subsidence was estimated using inverse distance weighting (IDW) interpolation within a GIS framework. Regarding spatial resolution, the IDW interpolation has a spatial resolution of 250 m × 250 m. Figure 2b presents the spatial distribution of fine-grained soil content, derived from comprehensive geological investigations that included 104 borehole logs. Each borehole was classified using the Unified Soil Classification System (USCS), where fine-grained soils are defined as materials with 50% or more passing through a No. 200 sieve, such as fine sand, silt, and clay. To generate a continuous surface from the point-based borehole data, the IDW interpolation method was employed within a GIS environment. This approach estimates values at unsampled locations by assigning greater influence to nearby data points, inversely related to their distance. The fine-grained soil percentage at each borehole was calculated by dividing the total thickness of fine-grained layers by the total drilling depth, resulting in a spatially continuous map of fine-grained soil distribution across the study area. Figure 2c and d show the spatial distribution of electric power consumption density and the locations of managed wells, respectively. Managed wells in this study refer to groundwater extraction wells that are officially registered under a government management system for simple agricultural wells. These wells differ from fully monitored or instrumented pumping wells, as they are manually operated by farmers and are not equipped with flow meters. Consequently, direct measurements of groundwater withdrawal volumes are unavailable. Instead, electricity consumption data, recorded via installed electricity meters, serve as a proxy for estimating groundwater use. The scale of agricultural groundwater extraction in the study area is substantial. Across the Choshui Delta, nearly 200,000 such managed wells have been registered. Specifically, within a 500-m radius of the Xiutan Elementary School MLCW (STES), a total of 141 officially registered wells are present, as illustrated in Fig. 4. All of these are simple agricultural wells primarily used for irrigation purposes. Electricity usage data from these wells are aggregated and analyzed to infer spatial and temporal patterns of groundwater abstraction in the region.

Fig. 2

Thematic maps of the Choshui delta: (a) Accumulated subsidence from 2015 to 2023; (b) Fine-grained soil content; (c) Electric power consumption density distribution; (d) Managed wells distribution (this figure was created with ArcGIS 10.8 software, obtained from https://www.arcgis.com/index.html).

Since 2008, 31 MLCWs have been established, particularly in areas like Yunlin County’s Tuku, Yuanchang, and Huwei Townships, which experience the most significant subsidence. The MLCW is a specialized monitoring instrument established by Taiwan’s Water Resources Agency to assess land subsidence, especially in areas vulnerable to excessive groundwater extraction. MLCWs are equipped with multiple sensors installed at various depths, which measure changes in the vertical distance between layers over time. These depth-specific observations allow for precise monitoring of soil compaction and deformation at different strata, providing invaluable data for evaluating the mechanisms of land subsidence.

The MLCW at Xiutan Elementary School (STES) in Tuku Township, located in one of the most subsided areas, has been selected for machine learning-based time-series analysis to predict land subsidence caused by groundwater depletion. At STES, the subsurface profile extends to a depth of 300 m and consists of predominantly coarse to medium sand and fine-grained clay, with interbedded layers. Figure 3 illustrates that the soil consists of up to 19 layers, with varying thicknesses of coarse and fine-grained materials, including significant clay intervals between 140–163 m and 218–255 m. The complex geological profile poses challenges for establishing a conventional hydrogeological model based on physical consolidation mechanisms for the area.

Fig. 3

Borehole logging data and observed subsidence data from the MLCWs at STES³⁸.

According to Fig. 3, the analysis of the stratigraphic column and the compression observations relative to the bottom of the MLCW at STES indicates the occurrence of compression behavior across the depth range of 0 to 300 m. Particularly, the highest compression rate is observed within the depth range of 9 m to 63 m in recent years. Based on the monitoring results, the primary compression layer of the MLCW at STES is located in the shallow soil layer (between 0 and 63 m). The soil distribution at this depth primarily consist of alternating layers of medium sand, fine sand and silt. The compression at STES is predominantly influenced by fluctuations in the groundwater level, and it demonstrates a continuous increase as the water level gradually decreases over time. Figure 3 also shows that significant subsidence is observed within a depth of 63 m in terms of compression rate.

Land subsidence is a direct result of excessive groundwater extraction, necessitating a thorough examination of groundwater utilization patterns. While data on groundwater usage specific to well discharge is unavailable, the electricity consumption by wells can serve as a major indicator for assessing groundwater usage. The land subsidence observed at an MLCW is affected by groundwater usage within a specific buffer radius. To determine the appropriate buffer radius, the correlation coefficient was calculated between well electricity consumption and cumulative subsidence for different buffer radii ranging from 100 to 2000 m, considering subsidence depths from 0 to 60 m. A buffer radius of 500 m yielded the highest correlation coefficient of 0.91. Therefore, a buffer radius of 500 m was selected for further analyses. Figure 4 depicts the map of land use, managed wells, and monitoring wells within a 500 m radius of the STES. Within a radius of 500 m from the MLCW at STES, there are a total of 141 managed wells. According to Fig. 4, it appears that the land use types within a 500 m radius of the STES, primarily dominated by agricultural land use. The location of multi-layer groundwater level monitoring well (MLGLW) with a depth of 134 m below the surface, is situated adjacent to the MLCW at STES.

Fig. 4

Map of land use, managed wells, and monitoring wells within a 500 m radius of the STES (this figure was created with ArcGIS 10.8 software, obtained from https://www.arcgis.com/index.html).

Figure 5 illustrates the relationship between drawdown and settlement at STES from 2017 to 2023. In this study, the drawdown and settlement values for 2017 are both set to zero to facilitate the comparison of changes in subsequent years. The results indicate that in 2021, following a severe drought, the drawdown reached its lowest recorded level in recent years. This substantial decline in groundwater levels led to an increase in settlement, resulting in significant and irreversible deformation. The results demonstrate the phenomenon of elastic–plastic deformation, which refers to the combined behavior of a material under stress.

Fig. 5

Relationship between drawdown and compression at STES.

The observed phenomenon—namely that settlement continues even after groundwater levels begin to recover—is primarily due to the time-lagged mechanical response of compressible soil layers³³. This means that settlement does not respond instantaneously to pore pressure changes, especially in fine-grained soil, which exhibit delayed consolidation. Moreover, the methodology used to construct.

Figure 5 draws on the concept of stress-compaction analysis, originally developed by³³ in their seminal work. In this framework, a correlation is established between cumulative drawdown and cumulative compaction (settlement). This figure helps to reveal whether the soil system undergoes elastic or inelastic (irreversible) deformation. In our case, the continued increase in settlement despite water level recovery suggests that irreversible compaction has occurred—an indication that permanent aquitard deformation has taken place. Therefore, even when groundwater levels rebound, the compacted soil layers do not recover their original thickness, and settlement continues due to prior stress history. Crucially, irreversible compaction occurs only when groundwater heads fall below the pre-consolidation level. Figure 5 is used to assess whether the subsurface system exhibits elastic or inelastic (permanent) deformation in response to groundwater level changes. The analysis indicates that groundwater heads have declined below the pre-consolidation threshold. Specifically, the data reveal that a drawdown exceeding approximately 6 m marks the onset of irreversible (inelastic) compression. This suggests that once groundwater levels fall below this threshold, permanent deformation of the soil strata is likely to occur.

Hydrogeologic characteristics of the STES

To evaluate the hydrogeologic characteristics of the monitoring well, we analyzed three borehole logs in the vicinity of the STES monitoring site, as shown in Fig. 6, and classified the subsurface stratigraphy based on grain size distribution. From this analysis, the aquifer system in the study area was delineated into four aquifers separated by three aquitards, as shown in Fig. 7. The groundwater level data used in the proposed machine learning model were collected from a monitoring well screened at a depth of 134 m, corresponding to Aquifer 2, which can be generally categorized as a leaky confined aquifer. However, based on site-specific in situ pumping tests and lithological analysis, we observed that the hydrogeological layering in this region is complex. The boundaries between aquifers and aquitards are not distinctly isolated, and fine-grained materials are interbedded within the aquifer zones.

Fig. 6

Location of three borehole logs in the vicinity of the STES monitoring site.

Fig. 7

Location of three borehole logs in the vicinity of the STES monitoring site.

To verify the hydraulic connectivity between aquifers, we conducted two controlled pumping tests. Under identical pumping conditions, the groundwater drawdown responses in Aquifers 1 and 2 yielded correlation coefficients of 0.86 and 0.94, respectively. These results, now presented in newly added Fig. 8 and Fig. 9, indicate strong vertical hydraulic connectivity between the upper and lower aquifers. This implies that although the water level data were obtained from a deeper well, they are influenced by near-surface pumping activity due to aquifer interconnection.

Fig. 8

Groundwater level response at STES during the first controlled pumping test.

Fig. 9

Groundwater level response at STES during the second controlled pumping test.

Datasets

In this study, multiple datasets were utilized, including accumulation of subsidence data, groundwater level fluctuations, electricity consumption of managed wells, and rainfall, as outlined in Table 1. The data availability, temporal resolution, and sources for each dataset are summarized in Table 1.

Table 1 Datasets in this study.

The data for the accumulation of subsidence, groundwater level, and electric power consumption are sourced from the Water Resources Agency (WRA), while precipitation data is obtained from the Central Weather Administration, Taiwan. It is worth mentioning that there is an absence of time series subsidence data for the period between 2012 and 2014 at STES.

Figure 10 illustrates the cumulative compression spanning from 2008 to 2023, utilizing data sourced from the WRA. Because subsidence data are missing from March 2012 to March 2014 at this site, the analyses in this study focus on the period with available data (2008–2023). We apply a data reconstruction technique to fill the 2012–2014 gap in the subsidence time series at STES. Figure 11 illustrates monthly variations in well electricity consumption and groundwater levels at STES. The well electricity use and groundwater level exhibit distinct seasonal patterns corresponding to the wet and dry seasons: higher electricity consumption, indicative of more pumping coincides with lower groundwater levels, and vice versa. Figure 12 shows monthly precipitation and groundwater level; groundwater levels tend to decline during the dry season and recover during the wet season, demonstrating the direct influence of rainfall on groundwater recharge. Detailed descriptions of these time series datasets are provided in the following sections.

Fig. 10

Monthly compression change and rebound, and cumulative compression at STES.

Fig. 11

Monthly electric power consumption and groundwater level at STES.

Fig. 12

Monthly precipitation and groundwater level at STES.

Monthly compression data

Compression at different soil depths is monitored using MLCW, which measure depth variations up to 340 m with 1 mm precision⁹. In this study, we use monthly compression changes from MLCWs installed at STES—the area with the highest subsidence—as input for the LSTM model. Figure 10 shows monthly compression, rebound, and cumulative compression at STES. Since subsidence data from 2012 to 2014 are missing, we apply LSTM to reconstruct this gap.

Monthly groundwater level data

Groundwater use may be driving subsidence in the study area^7,8. To investigate this, groundwater level data were collected. At STES, the MLGLW reaches a depth of 134 m. Figure 11 shows the relationship between monthly electricity use of managed wells and groundwater levels, highlighting clear seasonal fluctuations. Between 2008 and 2023, groundwater levels varied by up to 15 m within the aquifer at that depth.

Monthly electric power consumption data

Monthly electricity consumption data were collected for 141 managed wells within a 500 m radius of the MLCW at STES. These wells range in depth from 8 to 150 m, with an average depth of 27.5 m. On average, they consume 78 kWh per month. As shown in Fig. 11, electricity use shows seasonal variation, mirroring fluctuations in groundwater levels—higher consumption aligns with lower groundwater levels, and vice versa.

Monthly rainfall data

Precipitation data were sourced from the Central Weather Bureau. As shown in Fig. 12, both total monthly precipitation and groundwater levels follow a clear seasonal pattern, with about 80% of annual rainfall occurring from June to September. Increases in rainfall correspond to rising groundwater levels, while decreases lead to declines, highlighting the direct influence of precipitation on groundwater variation.

Methodology

This study employs a multi-factor machine learning approach to predict time-series land subsidence, centered on an LSTM model. First, a set of relevant variables is analyzed to identify the key factors influencing subsidence (via correlation analysis). These influential factors are then used as inputs to the LSTM, which is trained to capture the time-dependent subsidence patterns. Additionally, an artificial neural network (ANN) model is developed to relate well electricity consumption to groundwater level changes. By focusing the LSTM on the most important inputs and incorporating a proxy for groundwater extraction, the modeling approach improves prediction accuracy and efficiency. The overall research process is outlined in six steps below.

Figure 13 shows the research process flowchart. This study comprises several key steps: data collection, factor analysis, development of the land subsidence model, construction of the electricity–groundwater model, hyperparameter tuning, scenario design, and model prediction. Each of these steps is described in detail in the following sections.

• (1) Data collection Gather all relevant datasets as described in Sect. “Hydrogeologic characteristics of the STES” (subsidence measurements, groundwater levels, well electricity usage, precipitation records).

• (2) Factor analysis Examine the relationships among candidate factors and land subsidence. In this step, statistical analysis (correlation analysis) is used to identify critical factors influencing subsidence.

• (3) Land subsidence model development Employ an LSTM neural network to construct a predictive model of land subsidence, enabling the model to learn and forecast deformation patterns over time.

• (4) Electricity–groundwater model development Use an ANN to model the relationship between total monthly well electricity consumption and groundwater levels. This provides a tool for translating changes in electricity use (pumping activity) into changes in groundwater levels. The selection of ANN for modeling the relationship between pumping electricity and groundwater level was based on comparative model performance. Although LSTM networks are well-suited for time-series data, our experiments revealed that, in this specific one-to-one mapping context, ANN outperformed LSTM in terms of generalization accuracy on the testing dataset. The LSTM model achieved a high coefficient of determination (R² = 0.99) during training, but significantly underperformed during testing (R² = 0.69), indicating potential overfitting. In contrast, the ANN model yielded more balanced and reliable results with R² values of 0.75 and 0.77 for the training and testing sets, respectively. Therefore, ANN was chosen as the more robust and stable model for this specific task. The LSTM model was instead applied to the subsidence prediction task, where it demonstrated strong temporal learning capacity and superior performance.

• (5) Hyperparameter tuning The hyperparameters for both the LSTM and ANN models were determined through a systematic convergence-based tuning process. We conducted an extensive grid search across different parameter ranges—such as the number of hidden layers, number of neurons, learning rate, batch size, and activation functions—and evaluated model performance using the correlation coefficient (R) between predicted and observed values on both training and testing sets. A convergence criterion of R > 0.85 was adopted to ensure robust model generalization and stability. For the ANN model, a detailed summary of the selected parameters such as network architecture, activation function, and learning rate has been provided. The finalized optimal parameters obtained through the tuning process are presented in Table 5. Similarly, for the LSTM model, key parameters including the number of time steps and recurrent layers are fully reported to ensure transparency and reproducibility. The finalized optimal parameters for the LSTM model are summarized in Table 6.

• (6) Scenario setting Define and implement scenarios of reduced groundwater extraction through land-use change. In this study, two scenarios involving partial conversion of rice fields to corn (less water-intensive cultivation) are considered. Case 1 corresponds to an 8% reduction in monthly well electricity consumption (pumping), and Case 2 corresponds to a 17% reduction, representing strategies to decrease groundwater withdrawal.

• (7) Model prediction Finally, evaluate the impact of the two reduced-pumping scenarios on land subsidence. This involves using the trained models to predict how decreased groundwater extraction (via lower electricity usage) would affect groundwater levels and, consequently, subsidence. The outcomes provide insight into the potential effectiveness of different pumping-reduction strategies for mitigating land subsidence.

Fig. 13

Flowchart of this study. EC = monthly electricity consumption; GWL = monthly groundwater level; ECV = monthly electricity consumption variation; GWLV = monthly groundwater level variation; CV = monthly compression change. Subscripts 8 and 17 indicate scenarios with 8% and 17% reductions in monthly electricity consumption, respectively.

Analysis of influencing factors

To identify the main factors contributing to land subsidence, we considered eight candidate variables derived from the collected data (Table 2). These variables include both the monthly changes (variations) and the absolute monthly values (cumulative or total) of subsidence, groundwater levels, well electricity use, and precipitation. All data were normalized (standardized) over the period 2008–2023 at STES before analysis. We computed Pearson correlation coefficients among all variables to assess their interrelationships and their correlation with subsidence behavior.

Table 2 List of candidate variables considered for subsidence analysis.

Long short-term memory network

The LSTM network, a variant of recurrent neural network (RNN), is capable of automatically retaining and forgetting temporal information through specialized gating mechanisms. LSTM was introduced to overcome the vanishing gradient problem inherent in traditional RNN, particularly when learning long-term dependencies in sequential data³⁴. In standard RNNs, gradients tend to diminish exponentially as they are backpropagated through many time steps, making it difficult to effectively update earlier weights and thus impeding the model’s ability to capture long-range dependencies. LSTM addresses this limitation by introducing a unique memory cell structure governed by three gating mechanisms: the forget gate, input gate, and output gate. These gates regulate the flow of information, enabling the model to retain or discard information over time. This architecture allows gradients to flow more steadily through the network without vanishing or exploding, thereby enhancing its capacity to model complex temporal patterns. Given these strengths, LSTM is particularly well suited for tasks requiring long-term dependency learning, such as speech recognition, language modeling, and time-series forecasting—contexts in which traditional RNNs often fall short.

In this study, we use an LSTM model to capture time-dependent features in the subsidence time series. The LSTM network architecture typically involves layers of LSTM cells; the specific configuration is determined by the data characteristics and the prediction task. For time-series prediction of subsidence, the LSTM learns patterns and dependencies from sequential data through its gated cell state structure.

The input gate has a crucial role in determining the information from the current input stored in the memory cell. It accomplishes this by computing a candidate activation vector through a sigmoid function. On the other hand, the forget gate plays a role in regulating the information from the previous state to the current state. It receives inputs from both the previous hidden step and the current input, and utilizes a sigmoid function to decide the information be disregarded. Similarly, the output gate controls the transmission of information from the memory cell to the output of the LSTM. It combines the current input with the previous hidden step using a sigmoid function, and multiplies it with the state to produce the final output of the LSTM^35,36. During training, the LSTM model learns to adjust the parameters of its gates and cell state based on the input data and the desired output. This is done through backpropagation and gradient descent optimization.

A comprehensive LSTM network consists of an input gate, forget gate, and output gate. At each time step, the forget gate (f_t), input gate (i_t), and output gate (o_t) perform specific operations to regulate the flow of information and update the cell state. The forget gate calculates the amount of information to discard from the previous cell state based on the current input and the previous hidden stage.

$${\mathbf{f}}_{t} = \sigma ({\mathbf{W}}_{xf} {\mathbf{x}}_{t} + {\mathbf{W}}_{hf} {\mathbf{h}}_{t - 1} + {\mathbf{b}}_{f} )$$

(1)

where ${\mathbf{f}}_{t}$ denotes the forget gate, $\sigma$ is the sigmoid function, ${\mathbf{W}}_{xf}$ denotes matrix of weight between ${\mathbf{x}}_{t}$ and the forget gate unit, ${\mathbf{x}}_{t}$ denotes the input at time step t, ${\mathbf{W}}_{hf}$ denotes weight matrix between ${\mathbf{h}}_{t - 1}$ and the forget gate unit, ${\mathbf{h}}_{t - 1}$ denotes the output at time step $t - 1$, and ${\mathbf{b}}_{f}$ denotes the bias vectors of the forget gate at time t. The input gate determines the amount of new information to be added to the cell state by considering the current input and the previous hidden stage.

$${\mathbf{i}}_{t} = \sigma ({\mathbf{W}}_{xi} {\mathbf{x}}_{t} + {\mathbf{W}}_{hi} {\mathbf{h}}_{t - 1} + {\mathbf{b}}_{i} )$$

(2)

where ${\mathbf{i}}_{t}$ denotes the nonlinear input gate function at time t, ${\mathbf{W}}_{xi}$ denotes weight matrix between ${\mathbf{x}}_{t}$ and the input gate unit, ${\mathbf{W}}_{hi}$ denotes weight matrix between ${\mathbf{h}}_{t - 1}$ and the input gate unit, and ${\mathbf{b}}_{i}$ denotes the bias vectors of the input gate at time t. The output gate computes the output activation based on the current input and the updated cell state as follows.

$${\mathbf{o}}_{t} = \sigma ({\mathbf{W}}_{xo} {\mathbf{x}}_{t} + {\mathbf{W}}_{ho} {\mathbf{h}}_{t - 1} + {\mathbf{b}}_{o} )$$

(3)

where ${\mathbf{o}}_{t}$ denotes the nonlinear output gate function at time t, ${\mathbf{W}}_{xo}$ denotes matrix of weight between ${\mathbf{W}}_{xo}$ and the output gate unit, ${\mathbf{W}}_{ho}$ denotes matrix of weight between ${\mathbf{h}}_{t - 1}$ and the output gate unit, and ${\mathbf{b}}_{o}$ denotes the bias at time t. The ultimate output of an LSTM network is governed by the nonlinear output gate function and the current state of information as follows

$${\mathbf{h}}_{t} = {\mathbf{o}}_{t} \times \tanh ({\mathbf{C}}_{t} )$$

(4)

$${\mathbf{C}}_{t} = {\mathbf{C}}_{t - 1} \times {\mathbf{f}}_{t} + {\mathbf{i}}_{t} \times {\tilde{\mathbf{C}}}_{t}$$

(5)

$${\tilde{\mathbf{C}}}_{t} = \tanh ({\mathbf{W}}_{xg} {\mathbf{x}}_{i} + {\mathbf{W}}_{hg} {\mathbf{h}}_{t - 1} + {\mathbf{b}}_{g} )$$

(6)

where ${\mathbf{h}}_{t}$ denotes the current output value, ${\mathbf{C}}_{t}$ denotes the current state of information from the previous moments to the current moment, ${\mathbf{f}}_{t}$ denotes the nonlinear forget gate function at time t, tanh denotes the hyperbolic tangent function, ${\tilde{\mathbf{C}}}_{t}$ denotes the temporary memory cell state at time t, ${\mathbf{W}}_{xg}$ denotes weight matrix between ${\mathbf{x}}_{t}$ and the input squashing unit, ${\mathbf{W}}_{hg}$ denotes weight matrix between ${\mathbf{h}}_{t - 1}$ and the input squashing unit at time step $t - 1$, and ${\mathbf{b}}_{g}$ denotes the bias of the memory cell. By utilizing these gates, the LSTM network can effectively capture and retain relevant information while selectively discarding irrelevant information.

Results and discussion

Investigation of the influencing factors

This study uses PCA to identify key factors influencing land subsidence, based on normalized data from the MLCW at the STES site (2008–2023, Table 1). As shown in Table 2, several factors were included in the PCA. Using the approach described in Sect. “Analysis of influencing factors”, we identified key factors influencing land subsidence at STES. Table 2 lists the eight candidate variables representing various aspects of subsidence, groundwater, pumping, and rainfall. We calculated the correlation coefficients to quantify the relationships between subsidence (monthly compression change) and each of these variables. The correlation analysis highlights the importance of groundwater and pumping variables: as noted, the subsidence rate (compression change) correlates strongly with groundwater level variation and electricity use.

Figure 14 presents the correlation matrix for all variable pairs. Monthly subsidence change (Factor 1) shows notable positive correlations with monthly groundwater level variation (Factor 2), monthly electricity consumption variation (Factor 3), total monthly groundwater level (Factor 6), and total monthly electricity consumption (Factor 7). Among these, the correlation between subsidence change and groundwater level variation is the highest (R = 0.74). This confirms that drops in groundwater level (i.e., drawdown) due to intensive pumping are closely associated with increased land subsidence. Other related factors, such as total groundwater level (overall aquifer head) and electricity usage (as a proxy for pumping volume), also exhibit significant correlations with subsidence behavior. In contrast, precipitation factors (Factors 4 and 8) and cumulative compression (Factor 5) have relatively lower direct correlation with the short-term subsidence changes, suggesting that short-term rainfall variability is less directly linked to immediate subsidence rates, or its effect is mediated through groundwater level changes. These results indicate that fluctuations in groundwater level and pumping intensity are key drivers of land subsidence in this area. Based on the correlation analysis, we selected Factors 2, 3, 6, and 7 (groundwater level variation, electricity consumption variation, total groundwater level, and total electricity consumption) as the most influential inputs for the LSTM subsidence model.

Fig. 14

Correlation coefficient matrix.

Reconstruction of missing land subsidence data

Having validated the relationships among factors, we next applied the LSTM model to reconstruct the missing segment of subsidence data at STES (March 2012–March 2014) and to evaluate the model’s performance. The workflow of the LSTM network for data reconstruction is illustrated in Fig. 15. The chosen input features (the key factors identified in Sect. ”Investigation of the influencing factors”) were used to train the LSTM to reproduce the observed subsidence time series and fill in gaps.

Fig. 15

Flowcharts of LSTM network for reconstructing the subsidence data.

By performing this validation, we can evaluate the performance and robustness of the LSTM model in recovering missing data. We initiated an examination to determine the optimal number of hidden layers for the LSTM model. The relationship between the root mean square error and the number of hidden layers is investigated. From the convergence analysis results for the LSTM model, it is found that promising performance within the range of 100 to 400 hidden layers. Therefore, for the following example, we employ an optimal number of 350 hidden layers. Table 3 lists the model parameters in the LSTM network for reconstructing the missing data.

Table 3 Optimization of LSTM model parameters.

The findings from Sect. “Investigation of the influencing factors” indicate that factor 2 (monthly groundwater level variation), factor 3 (monthly electricity consumption variation), factor 6 (total monthly groundwater level), and factor 7 (total monthly electricity consumption) are key factors influencing land subsidence. Therefore, these factors have been selected as inputs for the subsequent LSTM analysis.

The training dataset comprises two time periods: February 2008 to February 2012 and March 2014 to December 2020, yielding a total of 130 records. The testing dataset includes two intervals as well—March 2012 to April 2014 and January 2021 to June 2023—containing 16 records in total. The termination condition of the model is defined such that training concludes only when the cumulative predicted compression falls within a ± 1 cm range of the observed cumulative compression, ensuring a high level of predictive accuracy. The accuracy of the proposed LSTM in reconstructing monthly compression changes is then evaluated (Table 4). The coefficient of determination (R²) and root mean square error (RMSE) values reported in Table 4 for the testing dataset were calculated based on the observed data available for the full year of 2021 and the period from March to June 2023, during which actual subsidence measurements were recorded. These observed values were then compared against the model predictions to derive the reported performance metrics. The model demonstrated strong performance during the training phase, achieving a RMSE of 6.88 × 10^–3 and a R² of 0.99. In the testing phase, the model maintained reasonable predictive capability, with a RMSE of 5.36 × 10^–1 and R² of 0.69.

Table 4 Accuracy of the LSTM model for data reconstruction.

Following this, the recovered monthly compression changes obtained using the LSTM model are presented in Fig. 16. Utilizing these reconstructed results, the cumulative compression data is derived and visualized in Fig. 17. This cumulative representation highlights the effectiveness of the LSTM model in reconstructing missing subsidence data while preserving essential characteristics of the subsidence dataset. Furthermore, the results highlight the proposed LSTM’s ability to capture long-term subsidence patterns.

Fig. 16

Results of the recovered monthly compression variation.

Fig. 17

Results of the reconstruction of the cumulative compression.

Impact of reducing groundwater extraction on land subsidence

An important aim of this study is to assess how reducing groundwater extraction could alleviate land subsidence. Using the developed models, we explored the effects of decreased pumping through a crop-conversion scenario. Based on WRA land-use data indicating rice paddies as the dominant water consumers in the area, we consider shifting a portion of rice cultivation to corn (a less water-intensive crop) as a sustainable groundwater management strategy.

We examined three scenarios: the current condition (baseline with existing land use and pumping rates) and two reduced-extraction scenarios (Case 1 and Case 2 as defined in Step 5 of the methodology). In Case 1, 10% of the rice cultivation area is converted to corn, leading to an approximate 8% reduction in irrigation water demand and thus an 8% decrease in well electricity consumption (pumping) in that area. In Case 2, 20% of rice area is converted to corn, yielding roughly a 17% reduction in water use and electricity consumption. These land-use changes are expected to significantly reduce groundwater pumping. We used our ANN and LSTM models in tandem to evaluate the impact of these scenarios on groundwater levels and subsequent land subsidence.

In the absence of direct measurements of groundwater pumping volumes, we rely on well electricity consumption as a reliable proxy for pumping intensity. Previous studies in the region^6,37 have demonstrated a strong correlation between pumping rates and electricity use, which validates the use of electricity data to estimate groundwater extraction. Thus, for each scenario, we first translate the reduced electricity consumption into changes in groundwater level using the ANN model. Then, we input the modified groundwater level time series (along with corresponding changes in electricity use and other factors) into the LSTM subsidence model to predict how subsidence would evolve under the reduced pumping conditions.

We assume that the reduction in pumping occurs uniformly throughout the year in the affected percentage of fields (reflecting a consistent land-use change). The ANN model relating electricity consumption to groundwater level was trained on historical data (2008–2023) from the STES area. Of the 186 monthly groundwater level records available, 130 samples (~ 70%) were randomly selected for ANN training, and 28 samples each (~ 15% each) for testing and validation. The network (a feed-forward ANN) was trained with randomized batching to ensure robust performance across multiple runs. The reason for adopting a random sampling approach rather than a temporal split in training the ANN model is that this study incorporates time-based dummy variables (temporal indicators) into the input layer of the ANN. These temporal features effectively capture seasonal patterns and hydrologic memory effects within the dataset. As a result, the random selection of training samples does not compromise the model’s ability to learn and represent time-dependent behaviors such as seasonality or groundwater persistence.

Table 5 presents the optimized parameters of the ANN model determined through hyperparameter tuning. The final ANN achieved a training RMSE of 5.54 × 10^–3 and a R² of 0.75; on the testing set, RMSE = 7.41 × 10^–2, with a R² value of 0.74; and on the validation set, RMSE = 4.30 × 10^–2 with R² = 0.69 (Table 6). These accuracy levels indicate the ANN model can reasonably predict groundwater level changes based on electricity consumption data. To further evaluate its predictive capability, we fed the entire sequence of observed electricity consumption (including data not used in training) through the trained ANN (“independent prediction”). The ANN’s overall prediction for groundwater levels yielded RMSE = 5.47 × 10^–1 and R² = 0.73, confirming its applicability for scenario analysis.

Table 5 Optimization of ANN model parameters.

Table 6 Accuracy of the ANN model relating electricity consumption to groundwater level.

Using the ANN, we adjusted the groundwater level time series for STES under the two pumping-reduction cases. Figure 18 illustrates the ANN-predicted groundwater levels versus electricity consumption data ³⁸. As expected, both reduced-pumping scenarios result in higher groundwater levels compared to the baseline, since less water is withdrawn from the aquifer.

Fig. 18

ANN model for relationship between monthly well electricity consumption and groundwater level.

With these adjusted groundwater level projections, we then employed the LSTM subsidence model to simulate subsidence under each scenario. By inputting the scenario-specific time series (modified groundwater levels and electricity usage, along with unchanged precipitation series), the model predicts how monthly subsidence (compression) would respond.

The results show a clear effect of reduced pumping on subsidence. Figures 19 and 20 summarize the immediate impacts of the scenarios on electricity use and groundwater levels, respectively. Under both Case 1 and Case 2, electricity consumption is lower than the current situation throughout the time series (Fig. 19), by design of the scenarios. Correspondingly, Fig. 20 shows that groundwater levels in Case 1 and Case 2 are consistently higher than the baseline after the implementation of pumping reductions. In essence, cutting back on irrigation pumping allows the aquifer to maintain higher water levels, particularly during the dry seasons.

Fig. 19

Projected monthly electric power consumption under reduced pumping scenarios (Case 1: 8% reduction, Case 2: 17% reduction) compared to the current scenario.

Fig. 20

Predicted groundwater level under the reduced pumping scenarios, compared to the current scenario.

We next examine how these changes translate to land subsidence. Figures 21 and 22 present the predicted subsidence outcomes under the scenarios, in terms of monthly compression change and cumulative compression, respectively. In both figures, the subsidence under reduced pumping is compared with the baseline subsidence. The results demonstrate that reducing groundwater withdrawal has a tangible mitigating effect on land subsidence. In Case 1 (8% pumping reduction), the magnitude of monthly compression is generally lower than in the baseline, and the growth of cumulative subsidence slows down. Case 2 (17% reduction) shows an even more pronounced effect: subsidence rates are further reduced, and the cumulative subsidence curve flattens noticeably relative to the baseline over the simulation period.

Fig. 21

Predicted monthly compression change under the reduced pumping scenarios, compared to the current scenario.

Fig. 22

Predicted cumulative compression (total subsidence) under the reduced pumping scenarios, compared to the current scenario.

These findings confirm that decreasing groundwater extraction can significantly alleviate subsidence. The degree of subsidence mitigation is directly related to the extent of pumping reduction: a greater reduction in groundwater use yields a greater reduction in subsidence. This highlights the pivotal role of groundwater management in controlling land subsidence. Implementing crop conversion or similar water-saving measures over a larger area (as in Case 2) produces more substantial benefits in terms of subsidence reduction.

Overall, the scenario analysis underscores that proactive groundwater-use reduction strategies can enhance the resilience of the Choshui Delta’s aquifer systems and ground stability. By integrating well electricity consumption data into our models, we capture the human influence on hydrological processes and can quantitatively evaluate the benefits of management interventions. The results encourage the integration of such groundwater conservation practices into regional planning as a means to slow or prevent further land subsidence.

Discussion

In this study, we proposed a machine learning-based approach for analyzing and mitigating land subsidence over time, utilizing an LSTM model in conjunction with correlation analysis of multiple influencing factors. The main findings are summarized in the following conclusion section. However, the study has several limitations that should be acknowledged:

• 1. A key limitation of this study lies in the complexity and uncertainty surrounding the hydrogeologic setting of the monitored well. Although additional borehole data were incorporated in Sect. “Hydrogeologic characteristics of the STES” to delineate the aquifer system into four aquifers and three aquitards, the aquifer boundaries in the study area are not sharply defined. Fine-grained materials are interbedded with coarser deposits, and site-specific pumping tests indicate strong vertical hydraulic connectivity between aquifers, particularly between Aquifers 1 and 2. The groundwater level data used in this study were obtained from a monitoring well screened at a depth of 134 m, generally corresponding to a leaky confined aquifer. However, due to the interconnected nature of the aquifers, the observed groundwater fluctuations may reflect both confined and unconfined system responses. This complexity introduces uncertainty in establishing a direct causal link between water level changes and inelastic compaction typically associated with confined aquifers. As a result, caution is warranted when interpreting subsidence responses based solely on water level changes from a single well. Future studies should consider incorporating pore pressure monitoring within aquitards and using multiple nested piezometers at different depths to better differentiate between confined and unconfined behaviors. A more refined hydrogeologic characterization would improve the reliability of subsidence prediction models in areas with heterogeneous stratigraphy.

• 2. The development of reliable deep learning time-series models for land subsidence prediction necessitates the availability of long-term, high-resolution datasets, particularly continuous records of groundwater levels and stratified soil compression. These datasets are critical for capturing the temporal evolution of subsidence and for ensuring the generalizability of model performance. The predictive accuracy of such models is highly dependent on the quality and intercorrelation of input and output variables. Robust associations, such as those between groundwater drawdown and deformation behavior, are essential to support effective model training and validation. In contrast to conventional physical models that incorporate detailed hydrogeological parameters, machine learning approaches are data-driven and inherently empirical. Therefore, the selection of representative variables and the interpretation of model outputs must be grounded in domain-specific expertise to maintain scientific rigor and practical relevance.

Conclusions

In this study, we presented a machine learning approach for analyzing and mitigating land subsidence over time, using an LSTM model alongside correlation analysis of multiple factors. The key findings are summarized as follows:

• 1. LSTM-based subsidence modeling with multi-factor inputs The LSTM model effectively captures long-term dependencies in the subsidence time series, making it well-suited for this analysis. By considering multiple input variables, the model identifies and utilizes essential features from a range of factors. Specifically, we examined monthly variations and cumulative values of groundwater levels, well electricity consumption, and precipitation to assess their contributions to subsidence. The results show a strong correlation between land subsidence and fluctuations in groundwater levels. Monthly subsidence (compression) changes are notably influenced by variations in groundwater levels and pumping intensity (indicated by electricity consumption of wells).

• 2. Reconstruction of missing subsidence data The LSTM model successfully reconstructed missing land subsidence data, demonstrating its effectiveness in handling incomplete datasets. The model achieved a very high accuracy in training (RMSE = 6.88 × 10^–3, R² = 0.99) and maintained good performance in testing (RMSE = 5.36 × 10⁻¹, R² = 0.69). These results highlight the LSTM model’s ability to preserve the essential characteristics of the subsidence record, indicating robustness and reliability in modeling subsidence even with gaps in the observations.

• 3. Effects of reduced groundwater extraction We investigated the impact of groundwater pumping reduction on land subsidence through scenario analysis. By converting a portion of rice paddies to corn (a less water-demanding crop), we simulated an 8% (Case 1) and 17% (Case 2) reduction in groundwater use. At the STES, the average subsidence rate over the period from 2008 to 2023 was 2.23 cm/year. Under moderate reduction (Case 1), the average rate dropped to 1.94 cm/year, while a more aggressive reduction (Case 2) further decreased the rate to 1.34 cm/year. Year-by-year comparisons consistently supported this trend. For example, in 2021, the observed subsidence rate was 4.85 cm/year, whereas Case 1 and Case 2 showed reduced rates of 2.50 cm/year and 1.80 cm/year, respectively. Our findings underscore the critical role of reducing groundwater extraction in mitigating land subsidence. The scenarios show that lowering pumping rates leads to higher groundwater levels and a clear reduction in subsidence rates and cumulative subsidence over time. The magnitude of subsidence mitigation is proportional to the reduction in pumping, emphasizing that aggressive groundwater conservation can be an effective strategy for subsidence control. These insights demonstrate the value of integrating groundwater management strategies (such as crop rotation or improved irrigation practices) into broader land subsidence mitigation efforts to enhance the long-term resilience of subsiding regions.