Introduction

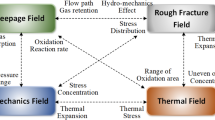
Gas energy extraction from low-permeability coal seams is often restricted by the coal seam’s permeability, leading to poor extraction efficiency1,2,3. To ensure the gas energy extraction efficiency from low-permeability coal seams, methods such as hydraulic fracturing, slotting, and perforation have gradually become commonly used in mines4,5. However, the use of hydraulic measures can cause clay minerals in the coal seam to swell due to water, blocking the seepage channels and resulting in water lock effects. To overcome the water lock effect, acid fracturing technology has gradually become a hot topic6,7,8. Studies have shown that CO2 foam fracturing, as a type of acid fracturing technology, under high-pressure conditions, CO2 foam transforms into saturated carbonic acid. Through chemical reactions, it dissolves minerals in the coal’s pore structure, optimizes the pore and fracture structure, promotes gas flow, enhances coal seam permeability, and further effectively improves the gas energy extraction efficiency of low-permeability coal seams9,10. However, during the CO2 foam fracturing process, the coal rock is subjected to the combined effects of acid corrosion and stress, which not only causes the internal pores of the coal to expand and fractures to connect, but also alters the mechanical properties of the coal, leading to further damage and degradation of the coal’s mechanical characteristics.

Numerous studies have been conducted on coal damage under acid erosion using laboratory testing methods and field measurements. From a laboratory perspective, Huang11 employed scanning electron microscopy and other techniques to investigate the changes in coal’s pore structure before and after acid treatment. He concluded that fracturing fluid enters and adheres to the coal pores, thereby altering the coal’s pore structure. Li12 and colleagues found that fracturing fluid not only modifies the micropore structure of coal but also enhances its mechanical sensitivity, leading to a reduction in its mechanical strength. Zhang13 used surface tensiometry and other methods to demonstrate that acidic fracturing fluid has varying effects on the mechanical properties of different coal types. Regarding the impact of acid treatment on coal seam adsorption-desorption performance, Zhao B14 conducted methane diffusion experiments before and after acidification and found that the desorption amount after acidification was consistently higher than that of raw coal. Haoran Dou15 employed X-ray diffraction and low-temperature nitrogen adsorption methods to confirm that acid treatment increases the desorption amount and shortens the desorption time. From a field application perspective, addressing the unclear mechanisms related to acid concentration and acidification time, Fan C16 proposed a thermo-hydro-mechanical-chemical coupling model. To address the issue of short acid-etched fractures and low fracture conductivity, Murtada17 and Mateus18 proposed novel fracturing fluid injection methods based on the instantaneous total filtrate loss of the entire fracture, including multi-stage alternating injection and three-stage alternating injection. However, there is currently limited research on the constitutive relationship of coal damage under acid corrosion. As a result, issues such as the unclear range of acid-induced fracture propagation and limitations in fracturing borehole arrangements arise due to the undefined constitutive relationship of acidified coal. Therefore, determining the constitutive relationship of coal damage under CO2 foam fracturing fluid erosion is crucial for understanding the stress-deformation behavior of acidified coal. This will enhance fracturing borehole arrangements, optimize fracture stimulation effects, improve coal seam permeability, and significantly improve the efficiency of gas energy extraction from low-permeability coal seams.

This study conducts field sampling using mine-grade CO2 foam fracturing fluid. A self-designed physical experimental platform for CO2 foam acidizing and fracturing in low-permeability coal seams was employed to perform fracturing fluid erosion tests on raw coal samples. Parameters such as peak stress, elastic modulus, failure modes, and fracture development characteristics were measured. The acid corrosion process of the coal body was analyzed, and the enhancement of permeability was evaluated. A damage constitutive model for acidified coal under fracturing was established, and a novel fracturing borehole arrangement was proposed.

Theory

(1) Acid fracturing.

Coal seam acid fracturing is an enhanced production technique specifically designed for coal seams. It involves injecting acid into the coal seam, where the acid reacts with the minerals in the coal, dissolving materials that block the flow paths, while also inducing fractures in the coal under high pressure. These fractures enhance the permeability of the coal seam, allowing gas to flow more freely. The primary objective of this technique is to improve coal seam permeability, thereby significantly enhancing the efficiency of gas energy extraction from low-permeability coal seams. The implementation of this technique requires strict control over parameters such as acid type, concentration, and injection pressure to ensure the safe and efficient achievement of production enhancement goals.

(2) Constitutive Relationship.

A constitutive relation is a mathematical expression used to describe the regularity of material deformation under external forces, such as compression, shear, and other loading conditions. It represents the relationship between stress (or other physical quantities) and strain (or other state variables), reflecting the material’s mechanical behavior. Through the constitutive relation, we can predict the material’s response under various loading conditions.

(3) Damage Factor.

The damage factor is a parameter used to describe the extent of material damage. It reflects the degradation of the internal structure of the material under external loading. The damage factor is typically defined based on changes in the material’s mechanical properties, such as the ratio of the elastic modulus before and after damage or the degree of strength reduction. It can also be determined from the perspective of the material’s microstructure, considering factors such as the number, size, and distribution of internal defects like microcracks and micropores. The value of the damage factor ranges from 0 to 1, where 0 represents an undamaged state and 1 indicates complete damage. Its magnitude is crucial for assessing the material’s reliability and service life.

Experiments

In order to construct the Weibull statistical damage constitutive model for acidized coal under fracturing, this study conducts field sampling using mine-grade CO2 foam fracturing fluid. A self-designed physical experimental platform for CO2 foam acidizing and fracturing in low-permeability coal seams is employed, with stringent control over experimental conditions, including pH and time. Acid fracturing permeability enhancement tests are performed on raw coal samples using this platform.

Materials

(1) Research background.

The coal-bearing strata of the XIASHIJIE Coalfield belong to the Jurassic Yan’an Formation (Middle Jurassic). The mine operates a single coal seam, primarily mining the 4 − 2# coal seam, with localized extraction of the 4 − 1# seam. The 4 − 2# seam thickness ranges from 0 to 34.28 m, with an average thickness of 10.51 m. The seam is relatively stable, with a gentle dip angle of 15° to 20° in the shallow section and 5° to 10° in the deeper section. The geological structure is simple, consisting of a northwestward-dipping monocline. The mine has been identified as a high-gas mine, with gas geological data indicating that the 226mining face is located within a high-gas zone. Based on borehole gas content measurements, the gas content of the 226 mining face ranges from 0.58 to 1.0 ml/g. Gas emission during tunneling is predicted to range from 1 to 2.8 m3/min, and during mining, from 9 to 16 m3/min. The actual gas emission may vary due to multiple influencing factors.

(2) Material preparation.

The coal samples were collected from the 226 comprehensive mining face of the XIASHIJIE Coal Mine in Shaanxi Province. The geological strength index (GSI) of the coal is greater than 65, with 2–3 sets of fractures and a fracture spacing ranging from 0.3 to 1 m. XRF analysis revealed that the coal contains mineral components such as 14.50% Ca, 2.3% Si, and 1.2% Mg. To prevent sample deterioration, the coal samples were sealed and transported to the laboratory. Standard cylindrical specimens with Φ50 × 100 mm dimensions were prepared in accordance with ISRM standards19.

Non-metallic ultrasonic testing equipment was used to screen coal samples with an average wave velocity ranging from 1.195 to 2.220 km/s. After vacuum drying at 30 °C for 24 h, the density parameters were determined using the mass-volume method. Samples with abnormal physical property parameters were excluded, and a final selection of 25 representative coal samples (XF-1 to XF-25) was made for further experimentation. The coal sample screening process is shown in Fig. 1.

Fig. 1
figure 1

Coal sample selection.

Full size image

Methodologies

(1) Modeling principles.

Using Lemaitre’s equivalence principle, the damage strain in the coal body during the acid fracturing process is equivalent to the strain caused by coal damage under the effect of effective acid fracturing20,21. From this, the stress-strain relationship in the damaged state can be derived as follows:

$$\sigma =\sigma '\left( {1 - D} \right)=E\varepsilon \left( {1 - D} \right)$$
(1)

where: σ represents the nominal stress during the acid fracturing process, in MPa; σ′ represents the effective stress during the acid fracturing process, in MPa; E denotes the elastic modulus of the coal body, in GPa; ε represents the strain in the coal body; D is the damage variable, dimensionless.

The damage model is defined based on the elastic modulus of the coal samples22,23, leading to the damage variable Da under acid erosion:

$${D_a}=1 - \frac{{{E_a}}}{{{E_0}}}$$
(2)

where: Da represents the damage variable under acid erosion, dimensionless; Ea represents the elastic modulus of the coal body under acid erosion, in GPa; E0 represents the initial elastic modulus of the coal body, in GPa.

The variation of the damage variable with acid exposure time can be reflected through the change in the elastic modulus over time. By applying Lemaitre’s equivalence transformation to Eq. (1), the stress-strain relationship at different acid exposure times can be derived as follows:

$$\sigma ={E_0}\varepsilon \left( {1 - D} \right)$$
(3)

Under the combined action of acid erosion and stress, the damage variable associated with the acid-chemical interaction in the coal body can be obtained using the equivalent strain principle to derive the generalized damage variable D24,25, where:

$$D={D_a}+{D_s} - \lambda {D_a}{D_s}$$
(4)

where: Ds represents the damage variable under stress, dimensionless; λ is the proportionality coefficient under the combined action of acid erosion and stress. According to the research by Bian et al.26,27, λ is taken as 1 in this study. In this case, D represents the damage variable under the combined effect of acid erosion and stress, and Da represents the damage variable under acid erosion, dimensionless.

(2) Experimental equipment.

The experimental platform used in this test primarily consists of a reactor acidizing system (independently developed) and a quasi-static loading test system.

① Reactor acidizing system.

To simulate the damage conditions of coal rock under high pressure and acid erosion, the experiment utilized the self-developed reactor acidizing system, which includes key components such as the reactor, high-pressure gas cylinder, sensors, data acquisition device, and computer. The reactor acidizing system is shown in Fig. 2.

Fig. 2
figure 2

Reactor acidizing system.

Full size image

② Quasi-static loading test system.

The axial pressure is provided by a DDL600 electronic universal testing machine, which has an axial pressure adjustment range of 0 to 600kN. This equipment is capable of performing triaxial compression tests on standard cylindrical specimens (Φ50 × 100 mm). The quasi-static loading rate required for the experiment can be pre-set through the axial pressure control system, which enables an automatic loading process during operation. The quasi-static loading test system required for this experiment is shown in Fig. 3.

Fig. 3
figure 3

Quasi-static loading test system.

Full size image

(3) Experimental procedure.

The experimental process can be divided into the following key steps:

① First, the reactor acidizing system was used to conduct fracturing fluid erosion tests on coal samples. Based on the references28,29, a CO2 foam fracturing fluid was prepared using NA/K-12 (6:4 compound) foaming agent as the base fluid. After placing the coal samples into the reactor, the fracturing fluid was injected, and a CO2 atmosphere was introduced to adjust the system to pH = 4.3 and a pressure of 2 MPa30,31,32, thereby creating an acidic erosion environment. The evolution of the acid fluid saturation was monitored dynamically by tracking changes in the coal sample’s mass (Fig. 4.). As shown in Fig. 4. after 2.5 days, the saturation stabilized at 1.0, indicating that the coal sample reached complete saturation in the fracturing fluid after 3 days of exposure under this formulation.

Fig. 4
figure 4

Variation curve of coal sample saturation with acid exposure time.

Full size image

This fracturing fluid system is suitable for high-gas, low-permeability coal seams with a GSI greater than 65, developed with 2–3 sets of fractures (spacing 0.3–1 m), and rich in Ca/Si mineral components. The CO2 foam fracturing fluid exhibits excellent foaming performance (half-life of 10.5 h), high temperature and shear resistance, and superior rheological properties, making it highly effective in the stimulation of low-permeability coal seams. The fracturing fluid must be freshly prepared and used immediately to maintain CO2 phase stability. The erosion duration should be controlled between 0.3 and 6 days33, which not only accelerates mineral dissolution (with significant hydration and swelling of clay minerals in the first 8 h) but also inhibits the formation of secondary minerals (such as calcite).

② To investigate the quasi-static damage characteristics of coal under the erosion of acid-based CO2 foam fracturing fluid, the samples were divided into five groups, with five coal samples in each group corresponding to erosion times of 1 to 5 days, labeled XF-1 to XF-25, for a total of 25 samples. The coal samples were then collected from the reactor for SEM analysis and quasi-static triaxial compression tests to analyze the damage characteristics.

③ SEM was employed to observe the microstructure of coal samples eroded by fracturing fluid. By examining the pore and fracture structures, including their size, shape, distribution, and fracture density, after acid treatment, further insight can be gained into the types, genesis, and filling conditions of the pores and fractures in the acid-eroded coal. This allows for a better understanding of the coal’s permeability and flow capacity, as well as the extent of structural modification induced by acid fracturing.

④ To investigate the quasi-static damage characteristics of coal rock, triaxial compression tests were conducted using a DDL600 electronic universal testing machine, with a displacement rate of 0.1 mm/min applied until the specimen failed. The data acquisition system continuously recorded the compressive strength, axial/radial strain, and stress-strain curves in real-time, focusing on analyzing the evolution of the mechanical properties during each stage of loading.

Results and discussions

The acidified coal body is a composite medium subjected to both physical and chemical actions. In this study, a mine-grade acid-based CO2 foam fracturing fluid was used in conjunction with a self-designed physical experimental platform for CO2 foam acidizing and fracturing in low-permeability coal seams to conduct acid fracturing permeability enhancement tests on raw coal samples. Based on the stress-strain relationship of the coal body, the effect of acidification on the constitutive parameters was analyzed, and the permeability enhancement effect was evaluated. A Weibull statistical damage constitutive model for acidized fracturing coal was established, and a novel borehole arrangement method for fracturing was proposed based on this model.

Stress-strain relationship of acidified coal body

Based on the experimental data, the triaxial compression stress-strain curves of samples with partial erosion under quasi-static loading rates were plotted, as shown in Fig. 5. From Fig. 5, it can be observed that under different erosion times and varying confining pressures with quasi-static loading rates of CO2 foam fracturing fluid, the compression process of the specimens exhibits four distinct phases: (I) Compaction phase (OA), (II) Linear elastic phase (AB), (III) Yield phase (BC), and (IV) Failure phase (post-peak strength, C-point and subsequent curve segment).

Fig. 5
figure 5

Axial stress-strain curves of coal rock under different erosion times.

Full size image

Figure 6 shows that the native pore fractures of the coal body are filled with minerals, resulting in poor connectivity. After the acid infiltrates, it preferentially dissolves the minerals in the larger fractures, forming expanded channels that then penetrate into deeper pores and fractures. This process involves the generation of soluble salts through reactions with minerals such as carbonates, quartz, and kaolinite, ultimately leading to the modification of the pore network. The acid-mineral reactions are shown in Fig. 6.

Fig. 6
figure 6

Acid-mineral reactions.

Full size image

The acid’s erosive effect on the minerals within the pores and fractures has led to a series of impacts:

① Effect on coal porosity: Increasing the erosion time of the fracturing fluid leads to the reorganization of the coal body’s physical structure, which promotes the expansion of the polymer’s free volume, thereby driving a sequential transformation of the coal pores (micro-pores → small pores → medium pores → large pores), progressively enhancing pore connectivity and, ultimately, improving the compressibility of the coal sample. The tests indicate that under the same confining pressure, an increase in erosion time results in a simultaneous increase in the concave length, amplitude, and compaction point strain during the compaction phase (OA), with a significant pore expansion effect. This process accelerates after reaching saturation at 2.5 d (Fig. 4).

② Impact on the coal body during the II. Linear Elastic Phase (AB) and IV. Failure Phase: The coal body, as a vitreous macromolecular system, exhibits brittleness due to intermolecular forces being higher than thermal energy, which limits molecular movement. During the II. Elastic Phase (AB), pore compaction stores energy. After erosion, brittleness increases, significantly shortening the duration of the II phase. Following the peak strength at point C, the coal body undergoes abrupt instability, with rapid energy release, showing complete brittle failure characteristics, this transition is accelerated in saturated samples (t ≥ 3 d, Fig. 4). Under the same confining pressure, the post-failure curve exhibits a steeper decline, further emphasizing the brittleness.

③ Under the same erosion time, an increase in confining pressure significantly enhances the compressive strength of the coal rock. Although the fracturing fluid promotes the expansion of pores and fractures, the newly formed and pre-existing fractures are compacted under the confining pressure. This process improves the coal sample’s density and homogeneity, thereby strengthening its mechanical properties.

The effect of acidification on the constitutive parameters of the coal surrounding the borehole

The following experimental results further confirm that the corrosive fracturing effect of the acid-based CO2 foam fracturing fluid on the coal body is a physico-chemical process. Scanning electron microscope (SEM) analysis reveals that as the erosion time of the fracturing fluid increases, the minerals and colloidal fillers in the coal sample’s pores and fractures gradually dissolve, leading to increased clarity of pore contours, enhanced connectivity, and a significant rise in porosity. Clay minerals expand and soften when in contact with water, exacerbating fracture propagation and resulting in the formation of white precipitates. Eroded coal samples become more prone to disintegration, and both compressive strength and elastic modulus decrease more rapidly with increasing erosion time. Corresponding to the saturation threshold at 2.5 days (Fig. 4), the deterioration of mechanical properties in the fully saturated state (t ≥ 3 d) is significantly higher than in the unsaturated state (t ≤ 2 d). The test results of coal samples under different erosion times of fracturing fluid are shown in Table 1.

Table 1 Test results of coal samples under different erosion times of fracturing fluid.
Full size table

This study uses peak strength (compressive strength) and elastic modulus as representative parameters to reveal the mechanical response behavior of coal rock during the erosion process by acid-based CO2 foam fracturing fluid. To quantitatively characterize the influence mechanism of erosion time on the mechanical behavior of coal rock, the variation range of the above parameters is defined, as expressed by the following formula:

$$\Delta {S_\varepsilon }=\left( {1 - {\raise0.7ex\hbox{${{S_\varepsilon }}$} \!\mathord{\left/ {\vphantom {{{S_\varepsilon }} {{S_0}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{S_0}}$}}} \right) \times 100\%$$
(5)
$$\Delta {E_\varepsilon }=\left( {1 - {\raise0.7ex\hbox{${{E_\varepsilon }}$} \!\mathord{\left/ {\vphantom {{{E_\varepsilon }} {{E_0}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{E_0}}$}}} \right) \times 100\%$$
(6)

where: ∆Sε and ∆Eε represent the changes in compressive strength and elastic modulus due to variations in erosion time, respectively. Sε and Eε are the values of compressive strength and elastic modulus at a specific erosion time, while So and Eo represent the baseline parameters of the un-eroded sample.

Based on the experimental test results and Eq. (5) and Eq. (6), the relationship between the mechanical properties of the coal rock specimens and the erosion time of the fracturing fluid was plotted, as shown in Figs. 7, 8, 9, 10, 11, and 12.

Figures 7, 8, and 9 show that the compressive strength of coal rock is influenced by variations in erosion time and confining pressure.

Fig. 7
figure 7

Compressive strength test results of coal rock specimens under triaxial compression. (a) Compressive strength 3D bar chart. (b) Compressive strength stacked bar chart.

Full size image
Fig. 8
figure 8

Contour plot of the variation in compressive strength

Full size image
Fig. 9
figure 9

Radar chart of the variation in compressive strength.

Full size image

Under triaxial compression conditions, an increase in confining pressure enhances the frictional and interlocking forces between particles within the coal sample, suppressing lateral deformation and thereby increasing its compressive strength. However, the erosion effect of the fracturing fluid leads to the degradation of the coal rock’s mechanical properties. As erosion time increases, the chemical and physical interactions between the fracturing fluid and the coal rock promote the degradation of cementitious materials and the expansion of microfractures, resulting in a time-dependent reduction in compressive strength. This reduction follows a nonlinear increasing relationship with erosion time. Notably, saturated coal samples experience an intensified erosion damage mechanism due to the pore filling effect. The liquid medium enhances the synergistic destructive effects of mineral dissolution, hydration expansion, and fracture propagation, leading to a significantly higher degradation in strength compared to unsaturated coal samples.

Figures 10, 11, and 12 show that the elastic modulus of coal rock is influenced by variations in erosion time.

Fig. 10
figure 10

Elastic modulus test results of coal rock specimens under triaxial compression. (a) 3D bar chart of elastic modulus. (b) Stacked bar chart of elastic modulus.

Full size image
Fig. 11
figure 11

Contour plot of the variation in elastic modulus.

Full size image
Fig. 12
figure 12

Radar chart of the variation in elastic modulus.

Full size image

Under a constant fracturing fluid erosion time, an increase in confining pressure enhances the lateral confinement effect, suppressing the development of lateral strain in the coal sample. This leads to an increase in the slope of the II elastic phase in the stress-strain curve, which macroscopically manifests as an apparent increase in the measured elastic modulus, without altering the intrinsic elastic modulus of the coal rock.

However, under constant confining pressure, the erosion effect of the fracturing fluid disrupts the internal cementitious structure of the coal rock through chemical dissolution and physical softening mechanisms, promoting the expansion of microfractures and causing a significant reduction in the actual elastic modulus of the coal rock. Saturated coal samples, due to the pore-filling effect, intensify the interaction between the fracturing fluid and mineral components, resulting in a higher degree of damage compared to unsaturated coal samples, with a more pronounced elastic modulus reduction.

Thus, the corrosive fracturing effect of acid-based CO2 foam fracturing fluid on the coal body is a physico-chemical process. The H⁺ ions in the fracturing fluid penetrate the coal rock through pores and fractures, initially adsorbing and reacting on the surface. The acid fluid generates a lubrication effect within the pores, reducing the friction coefficient between particles and flushing the cementitious material, while simultaneously dissolving clay minerals to soften the coal structure. Furthermore, H⁺ ions chemically alter the mineral composition. As the surface reactions approach saturation, the erosion effect diffuses into the interior of the coal rock, triggering secondary mineral dissolution and lattice reconstruction, among other deep chemical reactions. These processes ultimately compromise the structural integrity of the coal rock, as illustrated in Fig. 13.

Fig. 13
figure 13

Interaction between minerals and acid in the coal seam.

Full size image

Improvement and validation of the constitutive model for acidified coal

The strength of coal rock is influenced by various complex factors, including particle gradation, defect distribution, mineral composition, and environmental loads, exhibiting characteristics of random variables. Acidification, through a chemical dissolution-pore reconstruction mechanism, induces heterogeneous modification of the coal rock, forming a new composite medium with secondary mineral phases and a damage network. This process intensifies the interactive effects of cement weakening, fracture propagation, and compositional heterogeneity, causing the strength characteristics of acidified coal rock to follow a more pronounced random field distribution pattern. Therefore, in this study, it is assumed that the strength of the coal rock under acid-based CO2 foam fracturing fluid erosion follows a Weibull distribution.

(1) Improvement and validation of the constitutive model for acidified coal.

In this study, the strength of the coal rock under acid-based CO2 foam fracturing fluid erosion follows a Weibull distribution34, with its probability density function given by:

$$p(\varepsilon )=\frac{m}{F}{\left( {\frac{\varepsilon }{F}} \right)^{m - 1}}\exp \left[ { - {{\left( {\frac{\varepsilon }{F}} \right)}^m}} \right]$$
(7)

where: m represents the coal rock’s response characteristics to external loading; F is the parameter characterizing the Weibull distribution, primarily dependent on the mechanical properties of the coal; ε denotes the distribution variable of the random distribution of microelement strength. Since the strain strength theory is applied here, ε refers to the strain of the coal body.

When the coal body is subjected to load, some micro-elements will gradually fail. In order to reflect this gradual process, statistical damage variables are used. The statistical damage variable of coal under a certain load can be expressed as:

$${D_s}={\raise0.7ex\hbox{$c$} \!\mathord{\left/ {\vphantom {c N}}\right.\kern-0pt}\!\lower0.7ex\hbox{$N$}}$$
(8)

where: Ds represents the dimensionless damage variable under stress; c represents the number of damaged micro-elements of coal under a specific load; N represents the total number of micro-elements of coal in undamaged state.

In any interval [ε, ε + dε], the number of micro-units destroyed by coal is NP(x)dx. When the load reaches a certain level ε, there are35:

$$c(\varepsilon )=\int_{0}^{\varepsilon } {NP(x)} dx=N\left\{ {1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{F}} \right)}^m}} \right]} \right\}$$
(9)

By substituting Eq. (8) into Ds = c / N, we obtain :

$${D_s}=1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{F}} \right)}^m}} \right]$$
(10)

Equation (10) represents the evolution equation of statistical damage in coal under stress.

In Eq. (1), the damage is such that it cannot transmit stress. However, during the actual compression process, the micro-element body, even after being damaged, can still transmit a portion of the shear stress and compressive stress. Since the effective area of the transfer stress is the same, the damage variables in all directions of the coal body are D. Therefore, the damage correction coefficient δ (the value range is [0,1]) is introduced.

According to the generalized Hooke ‘s law, Eq. (3) becomes:

$${\sigma _m}={E_0}\varepsilon \left( {1 - \delta D} \right)+v({\sigma _1}+{\sigma _2})$$
(11)

where: v represents the Poisson’s ratio; σm represents the maximum principal stress, σm > σ1 = σ2.

Substituting Eq. (4) into Eq. (11), we obtain:

$${\sigma _m}=(1 - \delta ){E_0}\varepsilon +{E_0}\varepsilon \delta \left( {1 - {D_a}} \right)\left( {1 - {D_s}} \right)+v({\sigma _1}+{\sigma _2})$$
(12)

By substituting Eq. (2) and Eq. (10) into Eq. (12), we obtain a triaxial coal damage statistical constitutive model using the Weibull distribution.

$${\sigma _m}=\left( {1 - \delta } \right){E_0}\varepsilon +\delta {E_a}\varepsilon \exp \left[ { - {{\left( {\frac{\varepsilon }{F}} \right)}^m}} \right]+v({\sigma _1}+{\sigma _2})$$
(13)

The slope of the peak strength C (εc, σc) under triaxial compression is 0, thus we can obtain:

$$\frac{{d{\sigma _m}}}{{d\varepsilon }}\left| {_{{\varepsilon ={\varepsilon _c}}}} \right.=(1 - \delta ){E_0}+\delta {E_a}\left[ {1 - m{{\left( {\frac{{{\varepsilon _c}}}{F}} \right)}^m}} \right] \cdot \exp \left[ { - {{\left( {\frac{{{\varepsilon _c}}}{F}} \right)}^m}} \right]=0$$
(14)

The relationship is satisfied at the peak strength C (εc, σc):

$${\sigma _c}=\left( {1 - \delta } \right){E_0}{\varepsilon _c}+\delta {E_a}{\varepsilon _c}\exp \left[ { - {{\left( {\frac{{{\varepsilon _c}}}{F}} \right)}^m}} \right]+v({\sigma _1}+{\sigma _2})$$
(15)

Transforming Eq. (15), we obtain:

$$\frac{{{\sigma _c}+\left( {\delta - 1} \right){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}{{\delta {E_a}{\varepsilon _c}}}=\exp \left[ { - {{\left( {\frac{{{\varepsilon _c}}}{F}} \right)}^m}} \right]$$
(16)
$$In\frac{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}{{\delta {E_a}{\varepsilon _c}}}= - {\left( {\frac{{{\varepsilon _c}}}{F}} \right)^m}$$
(17)

The Eq. (16) and Eq. (17) are simultaneously substituted into Eq. (12) to obtain:

$$(1 - \delta ){E_0}+\left[ {1+mIn\frac{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}{{\delta {E_a}{\varepsilon _c}}}} \right] \cdot \left[ {\frac{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}{{{\varepsilon _c}}}} \right]=0$$
(18)

From Eq. (18), we derive:

$$\begin{gathered} m= - \frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{[{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})] \cdot In\left[ {\frac{1}{\delta }\left( {\frac{{{\sigma _c}}}{{{E_a}{\varepsilon _c}}}+\delta - 1} \right) - \frac{{v({\sigma _1}+{\sigma _2})}}{{\delta {E_a}{\varepsilon _c}}}} \right]}} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{E_0}{\varepsilon _c}}}+\delta - 1>0,\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{E_0}{\varepsilon _c}}} - 1<0} \right) \hfill \\ \end{gathered}$$
(19)

From Eq. (17), we derive:

$$F= - {\varepsilon _c}{\left[ {In\frac{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}{{\delta {E_a}{\varepsilon _c}}}} \right]^{ - \frac{1}{m}}}$$
(20)

By rearranging Eq. (19), we obtain:

$$- In\left[ {\frac{1}{\delta }\left( {\frac{{{\sigma _c}}}{{{E_a}{\varepsilon _c}}}+\delta - 1} \right) - \frac{{v({\sigma _1}+{\sigma _2})}}{{\delta {E_a}{\varepsilon _c}}}} \right]=\frac{1}{m}\left[ {\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}} \right]$$
(21)

Substituting Eq. (21) into Eq. (20), we obtain:

$$F={\varepsilon _c}{\left[ {\frac{1}{m} \cdot \frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}} \right]^{ - \frac{1}{m}}}$$
(22)

Substituting Eq. (22) into Eq. (13), we obtain:

$$\begin{gathered} {\sigma _m}=(1 - \delta ){E_0}\varepsilon +\delta {E_a}\varepsilon \exp \left\{ { - {{\left\{ {\frac{\varepsilon }{{{\varepsilon _c}}}{{\left[ {\frac{1}{m} \cdot \frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}} \right]}^{\frac{1}{m}}}} \right\}}^m}} \right\}+v({\sigma _1}+{\sigma _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} \left( {\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{E_0}{\varepsilon _c}}}+\delta - 1>0,\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{E_0}{\varepsilon _c}}} - 1<0} \right) \hfill \\ \end{gathered}$$
(23)

Due to the defects of the statistical damage constitutive model using the Weibull distribution in describing the compaction stage of the coal body during the initial loading phase, a piecewise function is employed to depict the damage caused by acid fracturing of the coal body. Therefore, Eq. (24) is utilized to describe the stress-strain relationship in the compaction stage.

$$\sigma =A{\varepsilon ^2}+B\varepsilon$$
(24)

where: A and B are the respective fitting coefficients of the compaction stage function.

In this paper, defining the stress at the end of the compaction stage as σe yields the Weibull statistical damage constitutive model for acidified coal bodies.

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _m}=A{\varepsilon ^2}+B\varepsilon {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma \leqslant {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\sigma _{e{\kern 1pt} }}{\kern 1pt} } \\ \begin{gathered} {\sigma _m}=\left( {1 - \delta } \right){E_0}\varepsilon +\delta {E_a}\varepsilon \exp \left\{ { - {{\left\{ {\frac{\varepsilon }{{{\varepsilon _c}}}{{\left[ {\frac{1}{m} \cdot \frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{\sigma _c}+(\delta - 1){E_0}{\varepsilon _c} - v({\sigma _1}+{\sigma _2})}}} \right]}^{\frac{1}{m}}}} \right\}}^m}} \right\}+v({\sigma _1}+{\sigma _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma >{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\sigma _{e{\kern 1pt} }}{\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{E_0}{\varepsilon _c}}}+\delta - 1>0,\frac{{{\sigma _c} - v({\sigma _1}+{\sigma _2})}}{{{E_0}{\varepsilon _c}}} - 1<0} \right) \hfill \\ \end{gathered} \end{array}} \right.$$
(25)

Using sample group XF-2 as an example, based on initial parameters (σc = 45.36 MPa, εc = 2.328 × 10−3, Eo = 26.4227 GPa, σ1 = σ2 = 5 MPa, ν = 0.2, δ = 0.97), the values m = 2.868 and F = 3.316 × 10−3 were calculated. Referring to parameters from similar experiments in literature, including (σc, εc, Eo, σ1 = σ2, ν), m and F values were recalibrated to reconstruct the constitutive model. The theoretical peak strain εc was computed by substituting σc = 45.36 MPa into each model and compared with experimental values to assess model applicability. The inversion results of relevant model parameters are presented in Table 2.

Table 2 Inverse results of relevant model parameters.
Full size table

Comparison and analysis of the constitutive models using multi-lithology samples (three types of coal, one type of sandstone, and one type of granite) revealed that under the same stress levels, the calculated strain values ε from different models are relatively close. This validates the applicability of the model proposed in this paper (Eq. 25). Comparison with experimental curves shows that the calculated ε values from Eq. (25) have the smallest deviation from measured values.

Moreover, its equation form and computational process significantly simplify existing models, demonstrating combined advantages in computational accuracy and efficiency. The existing models listed in Table 2 are primarily developed for specific lithologies or damage mechanisms and do not account for acid-chemical erosion. In contrast, the proposed model in this study: (1) Explicitly incorporates acid-induced damage (Da) through elastic modulus degradation (Eq. 2), capturing the physico-chemical weakening due to mineral dissolution. (2) Addresses the initial nonlinear compaction behavior of acid-softened coal using a segmented function (Eq. 24), a limitation of classical Weibull models. These improvements enable accurate characterization of acidified coal under triaxial stress conditions, as evidenced in Fig. 14.

(2) Validation of improved constitutive model of acidified coal.

Based on triaxial compression tests, the compressive strength σc, peak strain εc, and elastic modulus Eo of coal rock were obtained. By setting δ = 0.97 and substituting into Eqs. (19) and (22), mechanical parameters F and m were calculated, and subsequently, a Weibull statistical damage constitutive model for coal rock was constructed. Experimental stress-strain curves were compared with theoretical curves to verify the accuracy of the constitutive equations in characterizing the deformation and failure behavior of coal rock. The comparison curves are shown in Fig. 14.

Fig. 14
figure 14

Comparison curves between damage constitutive model and experimental results. (a) XF-1 and its fitting curve. (b) XF-7 and its fitting curve. (c) XF-13 and its fitting curve. (d) XF-19 and its fitting curve. (e) XF-25 and its fitting curve.

Full size image

From Fig. 14, it can be observed that if the abrupt stress drop behavior after the peak is ignored, the theoretical curve of the established Weibull statistical damage constitutive model aligns well with the experimental results curve. To address the shortcomings of the Weibull model in describing the compaction stage of acidified coal, this study proposes a segmented damage function. In order to express the influence of acid erosion-stress conditions on the coal rock failure process during acid fracturing, acid erosion damage variable Da and stress damage variable Ds are introduced. The constitutive model can be established by determining an appropriate proportion coefficient δ. Subsequent computational studies have shown that the proposed modeling approach is equally applicable to other brittle rocks, demonstrating its universal engineering application value.

Application of improved constitutive model in determining fracture radius

In acid-based CO2 foam fracturing engineering, the parameters of hole layout significantly control the development pattern of coal fractures. As indicated by Eq. (26)41,42, during coal fracturing, the extension pressure and final extension length of fractures are closely related not only to the principal stress borne by the coal body but also to its mechanical characteristic parameters.

$$R=\frac{{\pi E\xi }}{{2{{(P - {\sigma _0})}^2}(1 - {v^2})}}$$
(26)

where: P represents the initiation pressure; R denotes the fracture radius; σ0 is the minimum principal stress of coal rock; E stands for the elastic modulus of coal rock; ξ represents the specific surface energy; and v denotes Poisson’s ratio.

According to Eq. (25), the stress σ and elastic modulus E of coal under acid-based CO2 foam fracturing can be determined. Since the crack initiation stress level of coal is mainly distributed between 44.1% and 51.67%43,44,45,46, this paper assumes the crack initiation stress to be 50% of the peak stress of coal. By combining Eq. (25) with Eq. (26), we can derive:

$${R_1}=1.3{R_0}$$
(27)

where: R1 represents the fracture radius of coal under the erosion of fracturing fluid; R0 represents the fracture radius of coal without being eroded by fracturing fluid.

According to Eq. (27), due to the use of acid-based CO2 foam fracturing technology, the fracturing range of coal bodies expands. To enhance the efficiency of gas energy extraction, it is necessary to optimize the traditional hole arrangement method.

At present, the 226 fully-mechanized coal mining face adopts a single-row horizontal dense high-low hole layout method, with two holes per group, a hole spacing of 4.0 m, and a group spacing of 6.0 m. To reduce blind areas in fracturing and avoid collapse holes, it is recommended to reduce the number of holes required for the same effective area and to optimize the arrangement of drilling holes. A schematic diagram of the optimized hole arrangement method is shown in Fig. 15.

Fig. 15
figure 15

Schematic diagram of hole arrangement optimization.

Full size image

According to Eq. (27), the spacing between boreholes can be increased to 5.2 m. The optimized ‘three-flower borehole’ layout consists of three non-overlapping circles, with boreholes arranged in an equilateral triangle configuration, with a base angle of 30° and a top angle of 120°. The spacing between boreholes is 5.2 m, and the spacing between groups is 9.0 m. The optimized borehole layout for the 226 fully mechanized coal mining face is shown in Fig. 16.

Fig. 16
figure 16

The optimized borehole layout for the 226 fully mechanized coal mining face.

Full size image

According to calculations, the optimized borehole layout method can increase the effective fracturing range of the 226 fully mechanized mining face in the mine by 1.69 times and reduce the fracturing blind area by 36.71%. Furthermore, the 36.71% reduction in the fracturing blind area and the 1.69 times increase in effective range significantly improve operational efficiency. Crucially, for achieving the same effective fracturing coverage, the optimized “triple-flower hole” arrangement requires approximately 33% fewer boreholes compared to the original dense drilling pattern needed to mitigate blind zones. Field data from the 226 face indicates an average drilling cost of ¥8,500 per borehole (including labor, materials, and equipment). Implementing the optimized layout for a typical 300 m long panel is projected to reduce the required number of boreholes by ~ 50 (based on eliminating redundant drilling for blind zone compensation), translating to a direct cost saving of approximately ¥425,000. These results validate the damage process law of acid-invaded coal bodies and confirm the significant impact of acid-based CO2 foam fracturing fluid on the mechanical properties of coal. This optimization enhances the effectiveness of fracture reformation, thereby improving coal seam permeability and enhancing the efficiency of gas energy extraction. It provides technical support for gas prevention and control in low-permeability coal seams.

Conclusions

  1. (1)

    Under triaxial stress conditions, the stress-strain curve of acid-invaded coal delineates its deformation and failure processes. Driven by the vitreous nature of coal, acid erosion initiates a physical restructuring of its composition, promoting expansion of polymer free volume. As erosion time increases under constant confining pressure, the compaction phase extends, exacerbating brittle failure. Higher confining pressures enhance coal density and homogeneity, leading to a significant rise in peak stress. Experimental findings confirm that the duration of acid erosion, coupled with confining pressure, predominantly influences the path of coal damage evolution.

  2. (2)

    The acid erosion-stress condition is the primary factor influencing the fracturing process of coal bodies. Acidic media diffuse into the pores of coal rock, initiating adsorption and corrosion reactions on the coal surface, which then propagate inward, leading to chemical reactions within the coal rock. Under identical confining pressure conditions, with increasing erosion time, the intensity of chemical reactions intensifies, enhancing the connectivity of pore fractures. White precipitates gradually accumulate on the surface of the coal rock, and the reductions in compressive strength and elastic modulus become more pronounced in saturated coal samples compared to unsaturated ones. This demonstrates significant brittle damage in the coal body.

  3. (3)

    The established constitutive relationship effectively delineates the fundamental stress-deformation behaviors of low-permeability coal seams subjected to acid fracturing. Employing the Lemaitre equivalence principle and the Weibull distribution law for coal strength, and integrating acid erosion damage factor Da and stress damage factor Ds, this Weibull statistical damage model accurately captures the stress-deformation characteristics during acid fracturing of low-permeability coal seams. This model not only ensures computational precision but also enhances efficiency. Subsequent computational analyses confirm the broad applicability of this modeling method to various brittle rocks, underscoring its universal value in engineering applications.

  4. (4)

    The proposed optimization of the “triple-flower hole” drilling layout effectively reduces the fracture initiation blind zone and extends the coal fracture range. By applying this constitutive model and considering the specific conditions of the 226 fully mechanized caving face at the XIASHIJIE mine, a refined method is introduced for optimizing the “triple-flower hole” drilling layout (three non-overlapping circles connected to form an isosceles triangle with a base angle of 30° and a top angle of 120°). This approach significantly minimizes the fracture initiation blind zone, enhances the coal fracture range, and improves drilling stability. These research findings provide theoretical calculations to determine the acid fracturing radius of coal bodies, offering pivotal guidance for optimizing fracturing drilling layouts in practical applications.