Enhanced secure storage and data privacy management system for big data based on multilayer model

Abstract

As big data systems expand in scale and complexity, managing and securing sensitive data—especially personnel records—has become a critical challenge in cloud environments. This paper proposes a novel Multi-Layer Secure Cloud Storage Model (MLSCSM) tailored for large-scale personnel data. The model integrates fast and secure ChaCha20 encryption, Dual Stage Data Partitioning (DSDP) to maintain statistical reliability across blocks, k-anonymization to ensure privacy, SHA-512 hashing for data integrity, and Cauchy matrix-based dispersion for fault-tolerant distributed storage. A key novelty lies in combining cryptographic and statistical methods to enable privacy-preserving partitioned storage, optimized for distributed Cloud Computing Environments (CCE). Data blocks are securely encoded, masked, and stored in discrete locations across several cloud platforms, based on factors such as latency, bandwidth, cost, and security. They are later retrieved with integrity verification. The model also includes audit logs, load balancing, and real-time resource evaluation. To validate the system, experiments were tested using the MIMIC-III dataset on a 20-node Hadoop cluster. Compared to baseline models such as RDFA, SDPMC, and P&XE, the proposed model achieved a reduction in encoding time to 250 ms (block size 75), a CPU usage of 23% for 256 MB of data, a latency as low as 14 ms, and a throughput of up to 139 ms. These results confirm that the model offers superior security, efficiency, and scalability for cloud-based big data storage applications.

Introduction

In the 21st century, Cloud Computing Environment (CCE) and Big Data (BD) technologies have emerged as groundbreaking paradigms that are transforming the landscape of computing and data management¹. They are involved in redefining the future of computer information construction, effectively modernizing and automating information systems. CCE provides a dynamic, efficient, scalable, and cost-effective solution for storing, processing, and analyzing vast amounts of data. With CCE, organizations can change their heavy computational loads to remote servers with specialized hardware and software capabilities. This offloading significantly reduces the problem on local resources, allowing organizations to dedicate more focus and resources to their core competencies.

BD methodologies provide a comprehensive model for analyzing and interpreting data that is too large, complex, or rapidly changing for traditional data processing techniques². These technologies provide a range of tools for collecting, storing, analyzing, and interpreting large and complex datasets, including sophisticated algorithms and Machine Learning (ML) models. When combined, cloud computing and BD create a powerful, agile, and robust set-up well-equipped to meet the real-world diverse and extensive computational demands, such as real-time data analytics, ML, Artificial Intelligence (AI)- driven simulations, and many more³.

In personnel information management, robust, secure, and efficient data storage and processing solutions are increasingly critical⁴. Every day, organizations generate a vast amount of data, including, but not limited to, employee records, work histories, performance evaluations, and sensitive Human Resource (HR) documents⁵. This data is extensive and highly sensitive, frequently subject to rigorous legal and regulatory requirements in different countries. Unauthorized access or breaches of this sensitive data can lead to severe consequences, such as serious employee privacy violations and, hypothetically, steep legal penalties for the organizations involved⁶.

To address these challenges, several security models have been proposed to ensure secure storage and access to BD in CCE:

• (a) Encrypted Data Storage: One crucial method involves encrypting data using robust cryptographic algorithms such as Advanced Encryption Standard (AES) and ChaCha20 before it’s uploaded to the cloud. This ensures that even if the data is intercepted or accessed without authorization, it remains unreadable⁷.

• (b) Multi-Factor Authentication (MFA): MFA introduces an additional layer of security by requiring users to provide two or more forms of identity verification—a password, a biometric scan, a smart card, or a secure token—before gaining access to the data⁸.

• (c) Virtual Private Cloud (VPC): A VPC provides an isolated, private section of the cloud where organizations can launch resources within a network they define. This methodology proposes more granular control over data access, sharing, and transfer, thereby enhancing security measures⁹.

As organizations continue to collect BD, the requirement for storage solutions that are not just secure but also efficient, scalable, and fault-tolerant becomes increasingly urgent. In this context, partitioned and distributed storage in CCE becomes increasingly important¹⁰. Organizations can achieve high scalability, efficiency, and fault tolerance by dividing data into smaller, more manageable blocks and distributing these across multiple nodes or servers in a cloud environment¹¹.

While existing solutions provide partial measures—such as encryption, remote anonymization, or virtual network isolation—most lack an integrated, scalable network that addresses privacy, fault tolerance, data integrity, and performance optimization in a single cloud-native architecture. Specifically, there is a requirement for a system that combines recent encryption, privacy-preserving partitioning, secure distribution, and real-time system monitoring, all while maintaining compatibility with high-volume BD environments.

This proposed model addresses these issues using a multi-layered security and efficiency architecture. It begins by encrypting extensive, large datasets using the ChaCha20 algorithm, renowned for its speed and security. After encryption, the data is divided into smaller, manageable blocks via a sophisticated Dual Stage Data Partitioning (DSDP) technique. These blocks are further secured by applying a masking layer using k-anonymization, enhancing privacy protections. The fragmented and masked data blocks are then intelligently distributed across multiple cloud storage locations, selected based on a range of criteria, including latency, bandwidth, data security, and cost-effectiveness. During this distribution phase, Secure Hash Algorithm 512 (SHA-512) hashing is employed to ensure the consistent and secure placement of data blocks across different cloud locations.

Additionally, our model includes real-time load monitoring and balancing provisions, periodic integrity checks of the stored data, and efficient data retrieval procedures based on performance metrics. All these actions are meticulously recorded in an audit log to ensure compliance with relevant regulations and to provide a traceable history for future auditing and compliance checks. The proposed model was experimentally evaluated using the Medical Information Mart for Intensive Care III (MIMIC-III) dataset against other models for several metrics and was found to be more efficient compared to the other models.

The main contributions of this work are as follows:

• a. Integration of the ChaCha20 encryption algorithm, which is lightweight, fast, and secure, is ideal for high-throughput data environments.

• b. Development of a DSDP that ensures random-sample statistical consistency across blocks, improving distributed processing.

• c. Application of k-anonymization at the block level, safeguarding quasi-identifiers while maintaining data utility.

• d. Implementation of Cauchy matrix-based dispersion with SHA-512 hashing, ensuring data availability and integrity in multi-cloud storage.

• e. Design of a dynamic distribution algorithm, which considers cloud-specific metrics (latency, bandwidth, cost, security) and supports load balancing and auditing.

The paper is organized as follows: Sect. 2 presents the literature survey, Sect. 3 provides the methods used in this work, Sect. 4 presents the proposed model, Sect. 5 provides the Threat model and security analysis, Sect. 6 illustrates the experimental result analysis, Sect. 7 provides discussion and future work, and Sect. 8 concludes the work.

Literature survey

An et al.¹² investigated the challenges of proactively identifying attacks in CCE. The enduring potential advantages of Cloud computing encompass cost reduction and enhanced business outcomes. To enhance the prominence of Cloud computing, users must contend with numerous security threats. This survey encompassed a comprehensive examination of the CCE.

Halabi & Bellaiche¹³ addressed security concerns within the Software as a Service (SaaS) realm. Seth et al.¹⁴ introduced a model that integrates dual encryption and data fragmentation methods, ensuring the secure dissemination of data within a multi-cloud setting. The study addressed several problems in this domain, including integrity, security, confidentiality, and authentication challenges.

Prabhu et al.¹⁵ introduced a security model featuring access control, encryption, and digital signature methods. It includes a new key-generation algorithm using Elliptic Curve Cryptography (ECC), an Identity-based Elliptic Curve Access Control (Id-EAC) scheme, a Two-Phase encryption/decryption scheme, and a lightweight digital signature algorithm for data integrity.

Bhansali et al.¹⁶ presented a cloud-based Health Care System (HCS). The system enhances traditional ciphertext-policy attribute-based encryption by incorporating hashing and digital signatures. It ensures secure, authenticated, and confidential exchange of medical data between HCS through the cloud.

Ramachandra et al.¹⁷ suggest using the Triple Data Encryption Standard (TDES) to secure big data in cloud settings. This improved method expands the key dimensions of the fundamental Data Encryption Standard (DES) to enhance defense against attacks and enhance data privacy measurEl-Booz et al.¹⁸ introduce a storage system to secure organizational data from cloud providers, third-party auditors, and, hypothetically, rogue users with outdated accounts. The system elevates authentication security through two mechanisms: Time-based One-Time Passwords (TOTP) for verifying users accessing the cloud and an Automatic Blocker Protocol (ABP) to prevent unauthorized third-party audits.

Zhao and Wang¹⁹ introduce a secure and efficient data partitioning method to accelerate data distribution and enhance data privacy. The method utilizes a data compression algorithm for increased efficiency and employs Intelligent Document Analysis (IDA) for data splitting. Data retrieval relies on proactive secret sharing, an extension of Shamir’s techniques, to reconstruct data without requiring access to all cloud storage locations.

The emphasis has shifted towards advancing data partitioning and distributed storage technologies to overcome the challenge of extensive dataset sizes in cloud storage. Sindhe et al.²⁰ introduced an early partition-based data storage model for the CCE. The model outlines data fragmentation and features three algorithms: one for data partitioning and storage, another for data querying and linkage, and a third for fragment updates and re-partitioning. Experimental findings suggest the model is versatile enough for use with multiple cloud storage services and large datasets or files.

Levitin et al.²¹ propose an efficient, secure alternative to traditional encryption for securing BD in the CCE. Their method divides data into sequences and distributes it across multiple Cloud providers, focusing on securing the mapping between data elements and providers through a trapdoor function. Analysis shows that this method effectively protects Cloud-based BD.

Shao et al.²² developed a method for secure cloud storage utilizing logical Pk-Anonymization and MapReduce. This method efficiently clusters cloud data and verifies user connection security. It leverages MapReduce to handle large datasets, employing a parallel processing model that accommodates data updates. The anonymization methods ensure both security and data utility, thereby minimizing data loss and update time.

Cheng et al.²³ introduce innovative methods, specifically a probabilistic co-residence coverage model and an optimal data partitioning approach to reduce the impact of co-resident attacks. The efficacy of these methods is validated through demonstrative examples. Using cloud services requires tenants to upload data to the provider’s databases, posing challenges in balancing privacy and security against snooping or leaks by DBAs and maintaining good application performance.

To address this problem, Hasan and Chuprat²⁴ propose a cloud data fragmentation mechanism that optimizes privacy using a Bond Energy Algorithm and tenant-specified privacy constraints.

Zhang et al.²⁵ address the significant challenge of data privacy in cloud-based BD storage by introducing an efficient, secure system featuring a leakage-resilient encryption scheme. Their formal security analysis shows that the scheme can maintain data privacy even if a partial key is compromised, and it outperforms other methods in terms of leakage resilience.

Tian et al.²⁶ present a data partitioning and encryption backup (P&XE) method to counter user data leaks and co-resident attacks in CCE. The technique divides data into blocks, backs them up using XOR operations, and then encrypts the backup with a random string. In contrast to currently available solutions, the P&XE scheme balances data security and survivability while minimizing the storage cost. The paper employs existing probabilistic models to evaluate and compare the performance of P&XE with traditional methods in terms of security, survivability, and storage costs.

es. Experimental outcomes confirm its efficacy in securing large-scale HCS data in the cloud.

Table 1 Comparative summary of related cloud storage security and privacy Models.

Table 1 presents a comparative summary of recent cloud storage security and privacy models. It outlines key features, including encryption methodology, data partitioning approaches, anonymization techniques, integrity verification mechanisms, support for distributed cloud storage, and whether the models were empirically evaluated. As the table highlights, while prior studies have made significant progress in remote dimensions—such as access control¹⁵, encryption¹⁷, or partitioning^20,25—most fall short of integrating these mechanisms into a unified, multi-layered network. Furthermore, few models^{27,28,29,30,31,32,33,34,35,36} incorporate modern encryption standards (e.g., ChaCha20), k-anonymization, or hash-based integrity checks (e.g., SHA-512), and even fewer evaluate their performance under real-world workloads. The proposed model addresses these gaps through a holistic design that ensures data security, privacy, integrity, and performance efficiency in distributed BD environments.

Methods

Chacha20 encryption algorithm

The ChaCha20 encryption algorithm builds on the ideas introduced by its predecessor, the Salsa20 algorithm, designed by Daniel J. Bernstein. The basis of ChaCha20 is establishing an initial state matrix (Figure 1), denoted as $\:{I}_{M}$, which plays a critical role throughout the encryption process. This matrix includes four key components³⁷:

• a) 256-bit Key (K): This secret key is used to encrypt the data. It ensures that the encryption process is secure, as only those with the key can decrypt the data.

• b) 96-bit Nonce (N): The nonce, short for “number used once,” ensures that each encryption is unique and distinct. This prevents attackers from using patterns in the ciphertext to infer details about the plaintext.

• c) 32-bit Counter (C): The counter is used to generate new matrix states for each block of plaintext, ensuring that the encryption of each block is unique and distinct.

• d) Plaintext (PT): This is the data to be encrypted, which can vary in length.

The initial state matrix $\:{I}_{M}$ is configured as a $\:4\times\:4$ grid, where each cell contains a 32-bit unsigned integer, totaling 512 bits. The structure of $\:{I}_{M}$ takes on a little-endian format, meaning the least significant byte is stored first. Algorithm 1 details the ChaCha20 encryption.

Fig. 1

ChaCha20 illustration state Matrix.

The encryption starts with the initialization of $\:{I}_{M}$ using the key, nonce, and counter. Once initialized, ChaCha20 processes the plaintext in 512-bit blocks. For each block of plaintext (PT):

• The matrix $\:{I}_{M}$ is duplicated into an operational matrix $\:{O}_{M}$.

• The algorithm performs ten “double-rounds” of mixing on $\:{O}_{M}$. Each double-round consists of a series of “quarter-round” operations, which are specific transformations that shuffle and mix the bits of $\:{O}_{M}$ to obscure the original data. These operations are crucial for the security of the encryption, as they prevent attackers from reversing the encryption without the key.

• After completing the rounds, $\:{O}_{M}$ is combined with $\:{I}_{M}$, and this result is serialized into a sequence of bits.

• The serialized bits are then XOR-ed (exclusive OR operation) with the plaintext block to produce the ciphertext block. The XOR operation ensures that similar plaintext blocks produce different ciphertext when encrypted under other parts of the key or nonce.

• The counter in $\:{I}_{M}$ is incremented to modify the state for the next plaintext block, ensuring that subsequent blocks are encrypted differently even if the plaintext repeats.

This process is repeated for each PT block until all the data is encrypted. The final output is the ciphertext $\:CT$, which is the encrypted form of the plaintext $\:PT.$

Algorithm 1

ChaCha20 Encryption Process.

Proposed secured partitioned BD storage in CCE

This section provides a comprehensive overview of the proposed BD storage model. It starts with clear diagrams and explanations for each method involved in encoding the BD, then describes the proposed distribution model, and finally explains the retrieval and decoding of the BD. The detailed process of the model is illustrated in Fig. 2.

Fig. 2

Illustration of the proposed model.

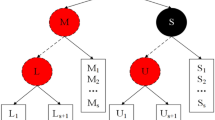
The proposed secure BD storage framework, as shown in Fig. 3, operates through a multi-stage pipeline ensuring confidentiality, integrity, privacy, and availability in a CCE. Initially, raw big data $\:B=$ $\:\left\{{z}_{1},{z}_{2},\dots\:,{z}_{N}\right\}$ is encrypted using the ChaCha20 algorithm with a 256-bit key, 96-bit nonce, and 32-bit counter to produce $\:EB$. This encrypted data is then partitioned using Dual-Stage Data Partitioning (DSDP), ensuring statistical representativeness via Random Sample Partitioning (RSP)³⁸. The resulting blocks are encoded using Cauchy matrix dispersion, which generates redundant slices to enhance fault tolerance. Each slice is subsequently masked through k-anonymization, where quasi-identifiers are generalized or suppressed to preserve privacy, generating $\:{S}^{\text{mask\:}}$. To guarantee data integrity, each slice is hashed using SHA-512, producing secure pairs $\:{f}_{i}\Vert\:{f}_{i}^{{\prime\:}}$. Finally, these secured and anonymized slices are distributed across cloud storage locations using SHA-512-based consistent hashing, enabling efficient, redundant, and tamper-detectable storage. This unified network ensures end-to-end security, statistical soundness, and scalability across heterogeneous multi-cloud setups.

The multi-layered network (Fig. 3) outlines a secure and structured method for BD storage in CCE, starting with raw data input and culminating in distributed storage across multiple cloud locations. Initially, raw big data was represented as $\:B=\left\{{z}_{1},{z}_{2},\dots\:,{z}_{N}\right\}$, is input into the system. This data undergoes encryption via the ChaCha20 algorithm, employing a 256-bit key $\:k$, a 32-bit counter $\:C$, and a 96-bit nonce $\:N$, resulting in an encrypted data set $\:EB$. Once encrypted, $\:EB$ is dealt with through the DSDP, which splits the encrypted data into multiple blocks, $\:P=\left\{{b}_{1},{b}_{2},\dots\:,{b}_{L}\right\}$. The partitioning ensures that each block $\:{b}_{l}$ is statistically consistent with the whole, helping individual statistical analysis while being suitably formatted for storage in a distributed file system like HDFS.

The DSDP blocks then undergo K-Anonymization, where quasi-identifiers within the data are masked. This stage anonymizes sensitive attributes, replacing precise identifiers with more general categories to ensure privacy and compliance with data security standards. The blocks are now represented as $\:{P}^{\text{mask\:}}=\left\{{b}_{1}^{\text{mask\:}},{b}_{2}^{\text{mask\:}},\dots\:,{b}_{L}^{\text{mask\:}}\right\}$. Following anonymization, Cauchy Matrix Dispersion is applied to distribute and encode the data across multiple cloud storage locations. This ensures data resiliency, supporting fault tolerance and recovery. The data, now dispersed and anonymized, is stored across numerous cloud locations in a manner that supports efficient retrieval and high availability.

As the final step in the encoding process, each data block is hashed using the SHA-512 algorithm. This cryptographic hash function adds a layer of security, verifying the integrity of the data at rest and during retrieval. The network leverages a network of cloud storage locations, where the data is redundantly stored to provide resilience against individual node failures. The data is distributed to maximize fault tolerance while minimizing latency and preserving the efficiency of retrieval operations. Upon retrieval, the data is decoded by reversing the anonymization and dispersion processes. The data is first unmasked and then collected from its dispersed state using the reverse operations of the Cauchy matrix. Finally, it is decrypted using the ChaCha2O algorithm, returning it to its original form for use.

The choice of ChaCha20 and SHA-512 in the proposed model is driven by their balance of security and efficiency for cloud-scale systems. ChaCha20 was selected over block ciphers such as AES due to its superior performance on general-purpose CPUs, constant-time execution, and resistance to timing attacks, making it ideal for distributed environments without hardware acceleration. SHA-512, while computationally more intensive than SHA-256, offers stronger collision resistance and is applied only once per encrypted block after partitioning. This limited use ensures that integrity verification is robust without introducing performance bottlenecks.

• A. Dual-Stage Data Partition (DSDP).

The partitioning scheme revolves around the RSP concept³⁹, which segments a large input file into multiple blocks, each functioning as a random sample. The DSDP is introduced to implement this. This method can break down a large file into random sample blocks⁴⁰. When applied to BD files stored in HDFS format, DSDP transforms them into RSP blocks. This strategy ensures that each data block retains features reliable with the overarching dataset, making them apt for individual statistical analysis.

The core principles of DSDP are summarized in two key definitions:

Definition 1

Data Partitioning Framework Suppose $\:\mathcal{B}=\left\{{\text{z}}_{1},{\text{z}}_{2},\cdots\:,{\text{z}}_{N}\right\}$ represents a dataset comprising M entities. A partitioning function P divides D into a collection of disjoint subsets, denoted as $\:\text{P}=\left\{{\text{b}}_{1},{\text{b}}_{2},\cdots\:,{\text{b}}_{L}\right\}$.

The function P is deemed a data partitioning framework for $\:\mathcal{B}$ if:

$$\:{\bigcup\:}_{l=1}^{L}\:{\text{b}}_{l}=\mathcal{B}$$

(1)

$$\:{\text{b}}_{i}\cap\:{\text{b}}_{j}={\varnothing} , when \:i,j\in\:\{\text{1,2},\cdots\:,L\} and \:i\ne\:j$$

(2)

In a typical HDFS environment, a large file is sectioned into smaller data blocks, essentially constituting$\:\:\left\{{\text{b}}_{1},{\text{b}}_{2},\cdots\:,{\text{b}}_{L}\right\}$, albeit without ensuring that these blocks retain the statistical properties of $\:\mathcal{B}$.

Fig. 3

Proposed Secured Partition-based Storage for BD in CCE.

Definition 2

Random Sample Partition (RSP) Given a dataset $\:\mathcal{B}$, considered as a random sample from a broader population, let $\:\mathcal{G}\left(z\right)$ signify its Sample Distribution Function (SDF). When P partitions $\:\mathcal{B}$ into $\:\text{P}=\left\{{\text{b}}_{1},{\text{b}}_{2},\cdots\:,{\text{b}}_{L}\right\}$ is referred to as a Random Sample Partition (RSP) If:

$$\:E\left[{\stackrel{\prime }{\mathcal{G}}}_{l}\left(z\right)\right]=\mathcal{G}\left(z\right)\:\text{\:For\:Each\:}\:l=\text{1,2},\cdots\:,L$$

(3)

where $\:{\stackrel{\prime }{\mathcal{G}}}_{l}\left(z\right)$indicates the SDF of $\:{\text{b}}_{l}$ and $\:E\left[{\stackrel{\prime }{\mathcal{G}}}_{l}\left(z\right)\right]$ is its predictable value. Subsequently, each $\:{\text{b}}_{l}$ is termed an RDP block of $\:\mathcal{B}$, and P is called an RSP operation on $\:\mathcal{B}$. By employing DSDP with RSP, we aim to ensure that individual data blocks are not only disjoint subsets but also statistically consistent with the overarching dataset, facilitating more reliable analytics on big data⁴¹.

To convert a big dataset $\:\mathcal{B}$ with ‘n’ records into L-RSP blocks, the DSDP, as illustrated in Algorithm 2, is used. The algorithm is primarily divided into “Data Chunking” and “Data Randomization” stages, as outlined below:

• (i) Data Chunking: The original dataset $\:\mathcal{B}\mathcal{\:}$ is initially segmented into P original data blocks. These blocks are not inherently randomized but represent contiguous slices of the original dataset. Modern BD frameworks readily support this type of operation.

• (ii) Data Randomization: A subset of $\:\phi\:\:$records is selected at random, without replacement, from each of the P original data blocks. The process commences with the local randomization of each original block. Each randomized block is then further divided into L sub-blocks, each containing $\:\phi\:$ records. A new RSP block is formulated by selectively amalgamating one sub-block from each randomized original block. This procedure is reiterated L times to generate the requisite ‘L’ RSP blocks. Each resultant RSP block thus comprises n$\:=\phi\:L$ records.

The parameter $\:\phi\:$ is adaptable and can be computed based on L and n, allowing for an equitable distribution of records across blocks (e.g., $\:\phi\:=n/L$)). The selection of L (the number of RSP blocks) and ‘n’ (the number of records in an RSP block) is determined by balancing available computational resources and specific analytical objectives⁴². This ensures that a single RSP block can be processed optimally on an individual computational node or core.

Algorithm 2

Dual Stage Data Partitioning (DSDP).

• B. Masking Using k-Anonymization.

After generating a collection of RSP blocks $\:=\{{b}_{1},\:{b}_{2},\dots\:,\:{b}_{l}\:\}$, through the DSDP, the RSP blocks $\:{b}_{l}$ are masked using k-anonymization. The focus is on attributes identified as quasi-identifiers, represented as Q, like age or ZIP code, which have the potential to compromise individual privacy⁴³. The process involves clustering records within each $\:{b}_{l}$​ based on these quasi-identifiers, aiming to form clusters $\:{\varvec{C}}_{\varvec{l}}$​ with a minimum of k records to achieve the k-anonymity principle. Attribute generalization is then applied to these clusters. For instance, if “age” is a quasi-identifier, specific ages in a cluster $\:{\varvec{C}}_{\varvec{l}}$​ ​ would be replaced by an age range, such as converting ‘35’ to ‘30–40’. Upon generalization, each block $\:{b}_{l}$​ becomes its k-anonymized version, denoted $\:{\varvec{b}}_{\varvec{l}}^{\varvec{m}\varvec{a}\varvec{s}\varvec{k}}$​.

The result is a set of k-anonymized RSP blocks, collectively represented as:

$$\:{P}^{mask}=\{{b}_{1}^{mask},\:{b}_{2}^{mask},\dots\:,\:{b}_{l}^{mask}\:\}$$

(4)

This separate k-anonymization module ensures that the statistical properties of each RSP block are retained while conforming to stringent data privacy regulations.

• C. De-Masking.

To revert the k-anonymized RSP blocks, denoted as $\:{P}^{mask}$, back to their original form $\:P$, a series of steps are followed⁴⁴:

• 1. Attribute Specialization: Each $\:{\varvec{b}}_{\varvec{l}}^{\varvec{m}\varvec{a}\varvec{s}\varvec{k}}$​ is examined to specialize the generalized attributes back to their more specific forms. For example, an age range like ‘30–40’ could be converted to a more specific age range, such as ‘30–39’ or ‘30–40’.

• 2. Cluster Disintegration: If possible, clusters $\:{\varvec{C}}_{\varvec{l}}$​ are disintegrated, breaking the k records back into individual records based on the quasi-identifiers Q.

• 3. Reassembly into Original Blocks: Records are then reassembled into their original RSP blocks $\:{b}_{l}$​, using the original block metadata if available.

The system is designed to provide a balanced trade-off between data privacy and analytic flexibility by applying attribute specialization methods. This enables compliant storage and data analytics, while providing a route to revert to a less generalized dataset when required, subject to certain limitations and assumptions.

• D. Encoding Process.

The encoding process proceeds first by encrypting the Big Dataset $\:\mathcal{B}=\left\{{\text{z}}_{1},{\text{z}}_{2},\cdots\:,{\text{z}}_{N}\right\}$ using the ChaCha20 explained in Sect. 3 by employing the 256-bit encryption key ‘k’, a randomly generated, 32-bit block_counter (C), and 96-bit nonce (N). The ChaCha20 encrypts the input data $\:\mathcal{B}$ to $\:E\mathcal{B}$.

$$\:E\mathcal{B}=\mathcal{E}\left(\mathcal{B},k\right)$$

(5)

The $\:E\mathcal{B}$ is fragmented into ‘P’ disjointed slices using the proposed DSDP model. It is understood that at least some value m of these ‘P’ number of slices will be used for reconstructing the encrypted data file ED. Assume $\:E\mathcal{B}=\left({\text{z}}_{1}^{{\prime\:}},{\text{z}}_{2}^{{\prime\:}},\dots\:{\text{z}}_{l}^{{\prime\:}}\right)\:$be the file size of l. The symbols $\:{z}_{i}^{{\prime\:}}$ is inferred as a component in some finite field B. Thus, encrypted big data $\:E\mathcal{B}$ will be split into ‘m’ blocks. Then,

$$\:E\mathcal{B}=\left({\text{z}}_{1}^{{\prime\:}},\dots\:{\text{z}}_{m}^{{\prime\:}}\right),\:\left({\text{z}}_{m+1}^{{\prime\:}},\dots\:{\text{z}}_{2m}^{{\prime\:}}\right),\dots\:,\left({\text{z}}_{l-(m+1)}^{{\prime\:}},\dots\:{\text{z}}_{l}^{{\prime\:}}\right)$$

(6)

The file EB is represented as an m×w matrix, whereas w is the size of every data slice:

$$\:\Omega \:_{{\omega \times \:{\text{m}}\:}} = \:\left( {\begin{array}{*{20}l} {{\text{Y}}_{1} } \hfill & {{\text{Y}}_{{{\text{m}} + 1}} } \hfill & \cdots \hfill & {{\text{Y}}_{{\left( {\omega - 1} \right).{\text{m}} + 1}} } \hfill \\ {{\text{Y}}_{2} } \hfill & {{\text{Y}}_{{{\text{m}} + 2}} } \hfill & \cdots \hfill & {{\text{Y}}_{{\left( {\omega - 1} \right).{\text{m}} + 2}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {Y_{m} } \hfill & {Y_{{2m}} } \hfill & \cdots \hfill & {Y_{{\omega - m}} } \hfill \\ \end{array} } \right)\omega \: = \left( {\frac{l}{m}} \right)$$

(7)

Hence, $\:{z}_{i}^{{\prime\:}}=\:{z}_{\left(i-1\right)m+1,}^{{\prime\:}}{z}_{\left(i-1\right)m+2,\dots\:{z}_{im,}^{{\prime\:}}}^{{\prime\:}}$specifies the i^th m number of blocks.

Let us consider that G will be an n×m Cauchy matrix stated for transforming novel matrix W into ‘n’ slices:

$${\text{G}}_{{\:{\text{n}} \times \:{\text{m}}\:}} = \:\left( {\begin{array}{*{20}l} {a_{{11}} } \hfill & {a_{{12}} } \hfill & \cdots \hfill & {a_{{1{\text{m}}}} } \hfill \\ {a_{{21}} } \hfill & {a_{{22}} } \hfill & \cdots \hfill & {a_{{2{\text{m}}}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {a_{{n1}} } \hfill & {a_{{n2}} } \hfill & \cdots \hfill & {a_{{nm}} } \hfill \\ \end{array} } \right)$$

(8)

The subset of ‘m’ rows is the linearly autonomous vector. For diffusing, it multiplies the G and $\:{\Omega\:}$ values that generate an n×m matrix ‘d’:

$${\text{G}}_{.} \Omega = \left( {\begin{array}{*{20}l} {a_{{11}} } \hfill & {a_{{12}} } \hfill & \cdots \hfill & {a_{{1{\text{m}}}} } \hfill \\ {a_{{21}} } \hfill & {a_{{22}} } \hfill & \cdots \hfill & {a_{{2{\text{m}}}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {a_{{n1}} } \hfill & {a_{{n2}} } \hfill & \cdots \hfill & {a_{{nm}} } \hfill \\ \end{array} } \right).\left( {\begin{array}{*{20}l} {{\text{Y}}_{1} } \hfill & {{\text{Y}}_{{{\text{m}} + 1}} } \hfill & \cdots \hfill & {{\text{Y}}_{{\left( {\omega - 1} \right).{\text{m}} + 1}} } \hfill \\ {{\text{Y}}_{2} } \hfill & {{\text{Y}}_{{{\text{m}} + 2}} } \hfill & \cdots \hfill & {{\text{Y}}_{{\left( {\omega - 1} \right).{\text{m}} + 2}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {Y_{m} } \hfill & {Y_{{2m}} } \hfill & \cdots \hfill & {Y_{{\omega - m}} } \hfill \\ \end{array} } \right)$$

(9)

$$= \left( {\begin{array}{*{20}l} {f_{{11}} } \hfill & {f_{{12}} } \hfill & \cdots \hfill & {f_{{1\omega }} } \hfill \\ {f_{{21}} } \hfill & {f_{{22}} } \hfill & \cdots \hfill & {f_{{2\omega }} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {f_{{n1}} } \hfill & {f_{{n2}} } \hfill & \cdots \hfill & {f_{{n\omega }} } \hfill \\ \end{array} } \right)$$

.

where,$\:{f}_{ij}=\sum\:_{k=1}^{m}{a}_{ik}.{Y}_{\left(j-1\right)m+k};1\le\:i\le\:n\:;1\le\:j\le\:\:\omega\:$

Given W, the dispersal algorithm will generate a matrix ‘d’ encompassing n×m (rows and columns). Every row has its ‘d’ corresponding value to the exact file slice: $\:{f}_{i}\:=\:(\:{f}_{i1},{\:f}_{i2},\:\dots\:,{\:f}_{iw})$. Then, masking each slice using k-anonymization to EB produces $\:{S}^{mask}$ contains ‘n’ slices. Where any value ‘m’ out of ‘n’ will be represented for reconstruction:

$$\:{S}^{mask}=\left({f}_{11},\:\dots\:,{f}_{1\omega\:}\right),\:\dots\:,\:\left({f}_{i1},\dots\:,\:{f}_{i\omega\:}\right),\:\dots\:,\:\left({f}_{n1},\:\dots\:,\:{f}_{nw}\right)$$

(10)

Finally, it computes the hash value of every slice $\:{f}_{i}$ by using SHA-512, and it adds the corresponding hashing value $\:{f}_{i}$ for producing $\:\left(\:{f}_{i}\:{f}_{i}^{{\prime\:}}\right)$. This results in

$$\:{ES}^{mask}=\:{f}_{1}\left|\left|{f}_{1}^{{\prime\:}},{f}_{2}\right|\right|{f}_{2}^{{\prime\:}},\:\dots\:,\:{f}_{n}\left|\right|{f}_{n}^{{\prime\:}}$$

(11)

The scattered data slices will be stored in multiple locations in a CSP. So that files can be retrieved from other locations even if one location in a CSP is compromised or one server goes offline⁴⁵. The Encoding Algorithm is displayed in Algorithm 3 below.

Algorithm 3

For the Encoding Process.

• E. Data Distribution Model.

In the data distribution model as described in Algorithm 4, the initial phase of data storage incorporates a multi-criteria evaluation function⁴⁶ $\:\text{Feval}\left(L,B,S,C\right)\to\:{Cloc}_{\text{Weighted\:}}$ to measure the cloud location “C_loc” of a Cloud Service Provider (CSP). The function considers latency $\:L$, bandwidth $\:B$, security features $\:S$, and cost $\:C$ to produce a weighted ranking of C_loc denoted as $\:{\text{C}\text{l}\text{o}\text{c}}_{\text{Weighted\:}}$. This ranking serves as a guide for the initial data block assignment, applying the function $\:{\text{D}}_{\text{Init\:}}\left(E{S}^{\text{Mask\:}},{\text{C}\text{l}\text{o}\text{c}}_{\text{Weighted\:}},R\right)\to\:{\text{C}\text{l}\text{o}\text{c}}_{\text{Mapping.}}\:$This function distributes blocks from $\:E{S}^{\text{mask\:}}$ to Cloud locations based on their weighted scores while creating $\:R$ replicas for each block according to $\:{\text{D}}_{\text{replicate\:}}\left({B}_{i},R\right)\to\:R\times\:{B}_{i}$. The model leverages Consistent Hashing, represented by $\:H\left(x\right)$, which provides a uniform data distribution across multiple locations across a Cloud Service Provider while minimizing reorganization costs. The hash function $\:H\left(x\right)$ maps each data block $\:{B}_{i}$ and the C_loc identifier to a point on a circular hash ring. Therefore, each data block $\:{B}_{i}$ from the encoded set $\:E{S}^{\text{mask\:}}$ is positioned on the hash ring through $\:H\left({B}_{i}\right)$. The assignment of blocks to Cloud locations relies on locating the closest clockwise point that represents a C_loc on the hash ring, denoted mathematically by $\:A\left({B}_{i}\right)$. In a typical setting, multiple replicas $\:R$ of each data block are generated to ensure high availability and fault tolerance. The replicas for each $\:{B}_{i}$ are stored in the $\:R$ closest unique C_loc in the clockwise direction on the hash ring, represented by the function $\:R\left({B}_{i},R\right)$.

A mapping matrix M is generated and updated in real-time to keep track of the data block locations. The mapping matrix $\:M$, which serves as a real-time record of Cloud locations for each block $\:{B}_{i}$, is updated accordingly. The matrix $\:M$ now has entries that are sets of ‘C_loc’s represented by:

$$M = \left[ {\begin{array}{*{20}c} {{\text{Cloc}}_{{{\text{1,1}}}} } & {{\text{Cloc}}_{{{\text{1,2}}}} } & \ldots & {{\text{Cloc}}_{{1,R}} } \\ {{\text{Cloc}}_{{{\text{2,1}}}} } & {{\text{Cloc}}_{{{\text{2,2}}}} } & \ldots & {{\text{Cloc}}_{{2,R}} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\text{Cloc}}_{{N,1}} } & {{\text{Cloc}}_{{N,2}} } & \ldots & {{\text{Cloc}}_{{N,R}} } \\ \end{array} } \right]$$

(12)

In this simplified matrix, $\:N$ is the sum of data blocks, $\:R$ is the number of replicas for each data block, and $\:{\text{C}\text{l}\text{o}\text{c}}_{i,j}$ indicates the identifier for the j^th C_loc where the i^th data block is stored. Each row ‘i’ contains $\:R$- C_loc identifiers representing the C_loc’s where the $\:R$ replicas of the i^th data block $\:{B}_{i}$ are stored.

For resource management, the model employs a threshold-based load-balancing $\:{\text{L}\text{B}}_{\text{threshold\:}}\left({\text{C}\text{l}\text{o}\text{c}}_{\text{util\:}}\right)\to\:{Cloc}_{\text{redist.\:\:}}$If the deployment metric $\:{\text{C}\text{l}\text{o}\text{c}}_{\text{util\:}}$, when it crosses a predefined threshold, the algorithm triggers a redistribution of blocks, thereby mitigating the risk of resource exhaustion. Security measures include periodic integrity verification through a checksum function $\:\chi\:\left({B}_{i}\right)$. If differences are found, indicated by $\:\chi\:\left({B}_{i}\right)\ne\:{\chi\:}_{\text{stored}}\left({B}_{i}\right)$, the corrupted blocks are regenerated and redistributed according to the encryption algorithm $\:E(B,k,m)$.

Lastly, to ensure compliance and transparency, all data distribution and retrieval activities are logged using the Λ (Activity) function⁴⁷. These logs serve as an audit trail and a basis for future optimization and compliance verification. With this comprehensive method, the model achieves high efficiency, security, and robustness, effectively managing data across multiple CSPs.

Algorithm 4

For the Distribution Algorithm.

• F. Data Retrieval and Decoding Process.

During data retrieval, an optimal C_loc is selected through a real-time performance evaluation function $\:{\text{P}}_{\text{eval\:}}\left({\text{C}\text{l}\text{o}\text{c}}_{\text{Mapping}}\text{m}\text{e}\text{t}\text{r}\text{i}\text{c}\text{s}\:)\to\:{\text{C}\text{l}\text{o}\text{c}}_{\text{O}\text{p}\text{t}\text{i}\text{m}\text{a}\text{l}}\right.$, considering several metrics, such as latency and bandwidth. Data blocks are fetched from $\:{\text{C}\text{l}\text{o}\text{c}}_{\text{Optimal\:}}$ and are then subjected to integrity checks and decoded. In the decoding process, an empty set, $\:{\varvec{D}}^{\varvec{m}\varvec{a}\varvec{s}\varvec{k}}$, is first initialized to hold the eventual decrypted data⁴⁸. The algorithm then proceeds by extracting and verifying each hashed slice, $\:{\varvec{f}}_{\varvec{i}}^{\varvec{{\prime\:}}}$, against its corresponding original data slice, $\:{\varvec{f}}_{\varvec{i}}$, in the encoded set $\:{\varvec{E}\varvec{S}}^{\varvec{m}\varvec{a}\varvec{s}\varvec{k}}$. Upon successful verification, the slices are unmasked to construct the original n×w matrix, ‘d’. Applying the inverse of the Cauchy matrix, $\:{G}^{-1}$, this matrix is multiplied by ‘d’ to reconstruct the original m×w matrix, Ω. The data slices represented in Ω are then reassembled to form the original encrypted file $\:EB$. Finally, the ChaCha20 algorithm decrypts $\:EB$ back into the original big dataset B using the original 256-bit key ‘k’, 32-bit block_counter (C), and a 96-bit nonce (N). Thus, as illustrated in Algorithm 5, the decoding algorithm effectively reverses each step of the encoding process⁴⁹, providing a robust method for securely retrieving the original data.

Algorithm 5

For Decoding.

Threat model and security analysis

The security of multi-cloud big data storage systems hinges on a well-defined threat model and comprehensive security analysis to ensure resilience against diverse attack vectors. This section presents a formal security network for the proposed model by defining adversarial roles, classifying probable threats, and analyzing the system’s defense mechanisms. The analysis provides a structured basis for understanding how the model upholds key security properties—confidentiality, integrity, privacy, and availability—under realistic cloud deployment scenarios.

Adversarial model and threat categories

Cloud-based personnel information systems are vulnerable to a standard range of sophisticated adversaries with variable access privileges, computational capabilities, and attack motivations⁵⁰. A complex security model must characterize these actors and predict their strategies to design effective countermeasures. This section defines four primary adversary types and outlines the core security assumptions that guide our formal analysis⁵¹.

Adversarial model

The cloud storage environment is inherently distributed and multi-tenant, introducing complex trust limits and system exposure points. The adversarial model captures realistic threat scenarios involving internal and external actors⁵².

• Semi-Honest Cloud Service Provider (CSP): These providers execute protocols as expected but attempt to extract sensitive information from encrypted data, access logs, or metadata. Although they preserve service functionality, their passive curiosity poses a credible threat to confidentiality.

• Malicious External Adversary: These are unauthorized attackers who operate outside the system infrastructure, targeting data in transit or at rest through network sniffing, server breaches, or brute-force cryptographic attacks. While lacking insider privileges, they may possess substantial computational resources.

• Curious Insider Adversary: Internal actors such as IT staff or HR personnel with legitimate access may attempt to escalate privileges or retrieve unauthorized records. Their position within the system makes them especially dangerous if least-privilege enforcement is lax.

• Colluding Multi-Party Adversary: This represents the strongest adversary class, involving coordinated efforts between insiders, external attackers, or compromised cloud providers to reconstruct sensitive data fragments that are independently non-informative.

• A. Security Assumptions:

To ensure meaningful analysis, the following assumptions are made⁵³:

• (A1) ChaCha20 offers IND-CPA security, and SHA-512 maintains collision resistance.

• (A2) Key generation and distribution processes are cryptographically secure and authenticated.

• (A3) Fewer than m out of n storage nodes are compromised simultaneously.

• (A4) Communication channels between system components are encrypted and authenticated (e.g., via TLS or VPN tunneling).

Threat types

The threat model for cloud-hosted personnel data is multifaceted, with each class of attack targeting a different security dimension⁵⁴. This work classifies the threats as follows to support structured analysis and countermeasure design:

• T1 – Data Confidentiality Threats: These attacks aim to reveal PT data or infer patterns from CT scans. Common vectors include brute-force attacks, cryptanalytic exploits, and side-channel leakage during encryption or transmission.

• T2 – Privacy Violation Threats: Adversaries use auxiliary datasets to re-identify individuals by correlating quasi-identifiers (e.g., ZIP code, age) across anonymized partitions. Linkage and background knowledge attacks pose significant risks in sensitive HR datasets.

• T3 – Data Integrity Threats: These involve unauthorized modification, insertion, or replay of records. Attackers may attempt to substitute blocks, generate valid-looking but fraudulent hashes, or roll back data to outdated states to cause confusion and disruption.

• T4 – System Availability Threats: Adversaries may target the system’s operational continuity using Distributed Denial of Service (DDoS) attacks, coordinated corruption of redundant fragments, or resource exhaustion to trigger performance degradation or Denial-of-Service (DoS).

• T5 – Statistical Inference Threats: Even anonymized data may leak insights through frequency analysis, attribute correlation, or temporal access trends. These attacks attempt to infer sensitive data without directly accessing individual records.

• T6 – Information Leakage Threats: These involve indirect channels of exposure, such as the timing of operations, access pattern profiling, or analysis of distribution metadata, which may reveal sensitive correlations or usage patterns.

Security analysis

Formal security analysis establishes the mathematical basis for evaluating the guarantees offered by cryptographic and distributed storage systems. This section presents a rigorous theoretical examination of the proposed multi-layer security architecture by defining a set of formal theorems and proofs. The integrated use of ChaCha20 encryption, DSDP, k-anonymization, and Cauchy matrix dispersion is shown to propose strong, provable guarantees against confidentiality attacks, privacy violations, integrity compromises, and availability disruptions⁵⁵.

Confidentiality analysis

Confidentiality hinges on the strength of encryption and the entropy of the data dispersal scheme.

The following theorems establish bounds on the probability that adversaries can gain meaningful insights from encrypted data under the defined adversarial model.

Theorem 1

B. (Data Confidentiality): Assuming the IND-CPA security of ChaCha20 and assuming fewer than $\:\text{t}<\text{m}$ storage locations are compromised, the probability that a polynomially bounded adversary can distinguish encrypted personnel data from random noise is negligible in the security parameter $\:{\uplambda\:}$.

Proof

• Assume an adversary $\:A$ attempts to distinguish the ciphertext $\:{E}_{B}$ of big data $\:B$ from random strings. Under the IND-CPA guarantee of ChaCha20, $\:{E}_{B}$ is computationally fuzzy from a uniform distribution. DSDP ensures that each partition $\:{b}_{l}$ is independently formed using random sampling, thereby disregarding structural redundancy. The application of Cauchy matrix dispersion results in a linear system $\:G$. $\:{\Omega\:}=D$, where $\:G$ is an $\:n\times\:m$ Cauchy matrix. For $\:t<m$ compromised locations, the adversary obtains at most $\:t$ linear equations. Since any $\:m\times\:m$ submatrix of $\:G$ is invertible, fewer than $\:m$ equations yield $\:{2}^{(m-t)\cdot\:{\text{l}\text{o}\text{g}}_{2}\left|\mathbb{F}\right|}$ possible solutions. Hence, the system remains information-theoretically secure against underdetermined reconstruction.

Theorem 2

D. (Encryption Semantic Security): ChaCha20 satisfies IND-CPA security such that the adversary’s advantage is bounded by $\:{\text{A}\text{d}\text{v}}_{\text{ChaCha20\:},A}^{\text{IND-CPA\:}}\left(\lambda\:\right)\le\:\text{n}\text{e}\text{g}\text{l}\left(\lambda\:\right)$ for any PPT adversary $\:A$.

Proof

ChaCha20’s security stems from the pseudorandom nature of its ARX-based quarter-round function and the 20-round structure, which provides diffusion and avalanche effects. This ensures that CT appears pseudorandom, satisfying semantic security under the IND-CPA definition.

Privacy analysis

The system preserves anonymity through k-anonymization, which is applied independently to each DSDP block.

Theorem 3

B. (K-Anonymity Preservation): Each masked block $\:{b}_{l}^{\text{mask\:}}$ satisfies ( $\:k,Q$ )-anonymity, ensuring that each quasi-identifier tuple appears in at least $\:k$ records.

Proof

The anonymization process clusters quasi-identifiers into similarity classes $\:{E}_{i}$, each substantial $\:\left|{E}_{i}\right|\ge\:k$ This guarantees that the probability of correctly identifying any individual is upper-bounded by $\:1/k$ per block. As DSDP creates disjoint blocks, this guarantee holds independently across all blocks.

Theorem 4

D. (Cross-Partition Privacy): Given L DSDP partitions with independently applied $\:k$-anonymization, the probability of cross-partition reidentification is bounded above by:$\:1-(1/k{)}^{L}$

Proof

Randomized partitioning and block-local anonymization prevent adversaries from consistently tracking the same record across multiple blocks. As the number of partitions increases, the probability of successful linkage drops exponentially.

Integrity analysis

Integrity is maintained via SHA-512 hashes appended to each stored data block.

Theorem 5

(Integrity Verification): The probability that unauthorized tampering goes undetected is upper-bounded by $\:{2}^{-256}$.

Proof

SHA-512 produces 512-bit digests and offers 256-bit collision resistance. For any altered block $\:{f}_{i}^{{\prime\:}}\ne\:{f}_{i}$, the probability that SHA-512 $\:\left({f}_{i}^{{\prime\:}}\right)=\text{S}\text{H}\text{A}-512\left({f}_{i}\right)$ is negligible.

Theorem 6

(Tamper Detection): Assumed that hashes are recomputed during retrieval, any modification is detected with overwhelming probability $1 - \varepsilon$, where $\:\varepsilon \le\:{2}^{-256}$.

Proof

For every block $\:{f}_{i}$, its stored hash $\:{h}_{i}$ is compared with the recomputed $\:{h}_{i}^{{\prime\:}}$. Any discrepancy signals tampering, except in the negligible case of a collision.

Availability and fault tolerance analysis

The use of Cauchy matrix dispersion guarantees resilience against partial system failures.

Theorem 7

(Fault Tolerance Guarantee): The original data matrix is recoverable with probability 1 when at least $\:m$ out of $\:n$ slices are available.

Proof

Since the Cauchy matrix $\:G$ possesses the MDS result, any $\:m\times\:m$ submatrix is invertible. Hence, recovery follows from solving $\:{D}^{{\prime\:}}={G}^{{\prime\:}}\cdot\:{\Omega\:}$, with $\:{\Omega\:}={\left({G}^{{\prime\:}}\right)}^{-1}\cdot\:{D}^{{\prime\:}}$.

Theorem 8

(Optimal Storage Overhead): The ( $\:n,m$ )-threshold scheme achieves minimal storage overhead of $\:n/m$, while tolerating up to $\:n-m$ failures.

Proof

This follows from coding theory bounds for MDS codes. Redundancy is minimized when exactly $\:m$ fragments are required for reconstruction.

Computational security bounds

The overall system security is determined by the lower of the cryptographic and dispersal scheme bounds.

Theorem 9

(Computational Security): The system achieves a minimum of $\:\lambda\:=\text{m}\text{i}\text{n}\left(256,{\text{l}\text{o}\text{g}}_{2}\left|\mathbb{F}\right|\cdot\:(m-t)\right)$-bit security against adversaries compromising fewer than $\:m$ nodes.

Proof

ChaCha20 provides 256-bit security. The dispersal scheme adds an entropy contribution of $\:{\text{l}\text{o}\text{g}}_{2}\left|\mathbb{F}\right|\cdot\:(m-$ $\:t$ ). The minimum of the two represents the effective system-wide security level.

Corollary 1

For $\:\left|\mathbb{F}\right|={2}^{32},m=10$, and $\:t<5$, the dispersal layer alone offers at least 160 bits of security, with ChaCha20 remaining the limiting factor at 256 bits.

Experimental analysis

The distributed storage set-up is built on a Hadoop 3.3x model deployed over a high-performance computing cluster of 20 nodes. Each node runs the Windows 11 operating system and is outfitted with an AMD Ryzen 9 5950X processor. The system memory for each node includes 64 GB of high-speed DDR4 RAM clocked at 3200 MHz. Each node features a 2 TB NVMe M.2 SSD for storage, presenting read/write speeds of up to 5000/4400 MB/s. The proposed work is employed for the dataset.

The Medical Information Mart for Intensive Care (MIMIC)-III dataset comprises 53,423 hospital admissions involving adults aged 16 or above. These admissions occurred in intensive care units between 2001 and 2012. Additionally, the dataset includes data on 7,870 new admissions that occurred between 2001 and 2008. The dataset details 38,597 distinct adult patients and 49,785 individual hospital admissions. Every entry in the data set is represented by ICD-9 codes that specify analyses and trials carried out. These codes are further divided into subcodes, which frequently provide additional details on the circumstances. The dataset contains 112,000 clinical reports, an average length of 709.3 tokens, and features 1159 primary ICD-9 codes. On average, each report is linked to approximately 7.6 codes. The data encompasses a range of information, including vital signs, prescribed medications, lab test results, care provider notes and observations, fluid balance records, codes for procedures and diagnoses, imaging reports, duration of hospital stays, survival statistics, and additional relevant data.

The recommended method is evaluated using specific metrics, such as (i) CPU time, (ii) Network Utilization, and (iii) CPU Usage. Several security measures designed to enhance the cloud computing environment are discussed. The proposed model was compared against other models such as (i) Relevancy Cluster based Data Fragmentation Algorithm [RDFA]²², (ii) storage and sharing scheme for cloud tenant [SSCT]²³, (iii) SDPMC²⁴, (iv) Leakage Resilience based Cloud Secured Storage (LRCSS)²⁵, and (v) P&XE²⁶.

Comparative analysis

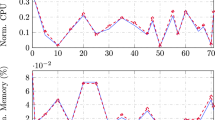
In a comparative analysis against existing secured cloud storage models such as RDFA, SSCT, SDPMC, LRCSS, and P&XE, the proposed model consistently exhibits superior performance across multiple performance vectors—execution time, network utilization, and CPU usage—making it especially suitable for BD storage in a CCE. Beginning with CPU execution time (Fig. 3a), the model is markedly more efficient across variable data sizes, requiring only 20 min for 256 MB and scaling efficiently to 54 min for 4 GB, underscoring its robust scalability. Regarding network utilization (Fig. 3b), although initially consuming slightly more bandwidth at 256 MB (0.25 GB), the system optimizes its network use at higher data sizes, essentially matching SDPMC’s performance for 512 MB and 4096 MB, and only slightly exceeding P&XE’s utilization. This indicates that the model’s network performance is both competitive and scalable. Finally, in terms of CPU usage (Fig. 3c), the proposed model consistently requires less CPU resources than its contemporaries, utilizing only 23% of CPU at smaller data sizes like 256 and 512 MB and continuing this efficiency at larger scales, with a modest 32% CPU utilization for 4096 MB. In summary, the proposed methodology is a holistically optimized solution, excelling in execution time, network performance, and CPU resource efficiency, making it a highly compelling choice for secured and efficient cloud storage applications.

The comparison is selectively restricted to RDFA, SDPMC, and P&XE, as these are partition-based secured cloud storage models, thus ensuring an equitable and targeted evaluation. Regarding encoding time (Fig. 4a), the proposed model consistently outperforms its counterparts, requiring only 250 ms for a block size of 75 and maintaining superior efficiency with a time of 396 ms at a block size of 525. In the context of the decoding time (Fig. 4b), the proposed algorithm exhibits sustained efficiency, requiring only 468 and 594 ms for block sizes of 75 and 525, which is faster than RDFA, SDPMC, and P&XE. Regarding execution time (Fig. 4c), the proposed model proves marked efficacy, necessitating only 733 ms for a block size of 75 and 894 ms for a block size of 525, thereby surpassing RDFA and SDPMC while marginally exceeding P&XE. In summary, the proposed algorithm consistently delivers superior performance metrics across encoding, decoding, and runtime evaluations for different block sizes, substantiating its suitability as an optimized solution for partition-based secure cloud storage applications.

Starting with latency, the proposed model demonstrates (Fig. 5a), with a latency of just 14 ms for a block size of 75, in stark contrast to RDFA’s 86 ms, SDPMC’s 72 ms, and P&XE’s 55 ms. As the block size scales up to 525, the model sustains this advantage with 82 ms, comfortably beating RDFA’s 153 ms and standing competitive against SDPMC’s 154 ms and P&XE’s 117 ms. The proposed methodology outperforms its competitors at all block sizes tested in terms of throughput (Fig. 5b). At the smallest block size of 75, the model achieves a throughput of 107 ms, significantly better than RDFA’s 18 ms, SDPMC’s 48 ms, and P&XE’s 78 ms. When we reach a block size of 525, the model still dominates with 139 ms, almost double RDFA’s 70 ms and notably higher than SDPMC’s 79 ms and P&XE’s 123 ms. Lastly, the proposed model consistently outperforms the baseline in evaluating the Packet Delivery Ratio (PDR) (Fig. 5c). At the 75-block size, its PDR is 77 ms, marginally better than RDFA’s 75 ms, SDPMC’s 74 ms, and P&XE’s 76 ms. As we scale up to 525 blocks, the model maintains this superiority by registering 103 ms, besting RDFA’s 96 ms, outdoing SDPMC’s 100 ms, and matching P&XE’s 100 ms (Fig. 6).

Fig. 4

Performance comparison between different models.

Fig. 5

Performance comparison using different block counts for (a) Encoding Time, (b) Decoding Time, and (c) Execution Time.

Fig. 6

Performance comparison using different block counts for (a) Latency, (b) Throughput, and (c) PDR.

These results indicate that the proposed model excels in low-latency operations, high throughput, and reliable PDR, making it an exceptionally balanced and effective solution for cloud storage applications.

Discussion

The increasing reliance on cloud-based setups to store, manage, and process sensitive personnel data requires a shift toward more comprehensive and resilient data security models. This study addresses that requirement through a unified model that integrates encryption, data partitioning, anonymization, dispersion, and verification into a multi-layered secure storage model. The results attained from empirical validation using the MIMIC-III dataset confirm the practical viability of the model, and it is probable to advance the state of cloud security research.

Implications for research

This work contributes to the increasing body of literature on secure BD storage by presenting an integrated, modular framework capable of operating across multi-cloud environments. It bridges gaps between cryptographic efficiency, privacy preservation, and data integrity assurance, areas that are often treated separately in existing models. The DSDP, when combined with block-level anonymization and Cauchy matrix dispersion, introduces a statistically sound and operationally scalable method of data fragmentation and distribution. These innovations provide a robust basis for further research into adaptive partitioning, context-aware anonymization, and Artificial Intelligence (AI)-driven cloud orchestration in secure data environments.

Implications for practice

From an implementation perspective, the proposed model applies to sectors such as healthcare, financial services, and human resources, where privacy regulations and data sensitivity are of paramount importance. The use of ChaCha20 encryption ensures computational speed, while SHA-512 hashing and block replication increase system resilience and integrity assurance. Moreover, the load-aware distribution approach can be leveraged by CSP to optimize resource allocation while maintaining compliance with data security regulations (e.g., GDPR, HIPAA). The model’s modularity also makes it suitable for integration into existing CCEs and distributed file systems, such as Hadoop and HDFS.

Limitations and assumptions

While the proposed model demonstrates promising results, several limitations and assumptions should be acknowledged:

• Trust in Initial Key Management: Like most symmetric encryption-based systems, the model assumes a trusted mechanism for key distribution and nonce generation. Without secure key management protocols (e.g., via PKI or TPM), the encryption layer may be compromised.

• Fixed K in k-Anonymization: The current implementation uses a static k-value across all blocks, which may not provide optimal privacy in datasets with highly heterogeneous distributions. Dynamic k-tuning may improve anonymization precision.

• Cloud Homogeneity Assumption: The distribution algorithm assumes relatively consistent behavior across cloud providers in terms of latency, bandwidth, and fault response. In real-world multi-cloud deployments, heterogeneity and Application Programming Interface (API) discrepancies may impact performance or reliability.

• Resource Overhead for Auditing: While the audit logging system improves compliance and traceability, it introduces additional Input/Output (I/O) and storage overhead, which may become significant in large-scale deployments.

Future directions

Future research will explore several promising directions to enhance the applicability and robustness of the proposed model. One path involves incorporating dynamic trust negotiation and federated key distribution mechanisms to strengthen encryption key management, especially in decentralized or multi-tenant environments. Additionally, developing adaptive anonymization techniques that adjust according to the context and sensitivity of the data will enhance privacy preservation without compromising data utility. The model may also be extended to support edge–cloud hybrid deployments, allowing for secure and efficient BD management in distributed Internet of Things (IoT) ecosystems. Finally, the automation of audit and compliance monitoring will be investigated using blockchain-based integrity verification or AI-driven anomaly detection, thereby improving transparency and regulatory alignment in high-stakes environments.

Conclusion

The summary development of BD related to personnel information presents opportunities and hurdles. While the proliferation of this data supports organizational research and individualized employee management, it also triggers problems about security, privacy, and operational efficiency. A specialized, Partition-Based, Distributed Big Data Storage Model tailored for personnel information is introduced for cloud storage. This model fuses multiple security layers to mitigate these problems. The model incorporates ChaCha20 encryption, DSDP, and k-anonymization to ensure data confidentiality and privacy. The decision to distribute data across multiple cloud locations, combined with the implementation of SHA-512 hashing, significantly enhances both security and performance. Empirical tests demonstrate that this model surpasses existing ones in security, efficiency, and fault tolerance. While the Secured Partition-Based Distributed Big Data Storage Model enhances cloud security and data management, its real-world application may encounter challenges. Complex integration, potential performance overheads, and variable scalability across CCE are significant considerations. Additionally, adherence to diverse international data security regulations and associated costs necessitates strategic planning to ensure both practical and regulatory compliance.

Future studies will focus on implementing the model in real-time and mitigating the associated challenges.