Introduction

Graph theory is a fascinating branch of mathematics that specializes in the study of graphs, which are structures consisting of vertices (or nodes) and edges (or links). These graphs are used to represent pairwise relationships between items, making them a crucial tool for understanding connections and interactions in diverse systems. The vertices constitute entities, whilst the rims define the relationships or interactions among these entities1. Graphs can take many forms, inclusive of directed or undirected, weighted or unweighted, and easy or complex, depending on how the edges and vertices are described. The versatility of the graph concept has led to its use in several fields. In computer technological know-how, it is used to model networks, optimize algorithms, and layout statistical systems. In biology, it helps researchers recognize molecular systems and ecological systems. In social sciences, it offers insights into relationships within social networks. Graph theory’s summary yet practical nature makes it a powerful device for solving issues and studying systems in an extensive range of disciplines2.

Network localization refers to the process of locating a node precisely within a network. The precise location of a node is a fundamental concept in networks. Localization helps locate the closest printer, a malfunctioning node, an intrusion into the network, a damaged device, unauthorized connections, and the location of a moving robot when a computer sends a printing command inside a building. The process of network localization is highly complex, costly, and time-consuming3,4.

The position of the appropriate node is identified by its specific representation with the selected nodes, allowing for the precise placement to be determined in this way, many nodes are chosen. To make this procedure efficient in terms of both time and energy, we must choose the fewest possible nodes. The nodes selected form the locating set (metric basis), and the locating number (also known as the cardinality of the smallest set of those nodes or metric dimension) is used to describe it. It is still unclear how to solve the NP-hard problem of determining a graph’s location number; see5,6.

According to Slater7, the concept of a resolving set has the lowest cardinality of any resolving set for a graph locating number. He used sonar and Loran stations to demonstrate how important this idea is. As GPS was widely available for commercial use, Loran stations were viewed as being outdated. Later, Harary and Melter conducted a study on this subject as well, albeit they used the term metric dimension8 rather than location number to describe it. According to Chartrand et al.9, this concept was referred to as the metric basis, and the resolving set was the smallest set of the metric basis. Blumenthal provided an early characterization of the resolving set and the metric dimension in his monograph, exploring these concepts in the broader context of metric space and the applications of distance geometry10.

In a network or graph, a metric base is the smallest set of selected reference vertices such that the distance from any vertex in the graph to these reference points uniquely determines its location in the network. The metric dimension of a graph is the number of such reference points required to uniquely determine the position of every vertex in the graph. If (\(W^\prime\) /w) for all w \(\in W^\prime\) is also a resolving set of G, then, technically speaking, a resolving set \(W^\prime\) of any graph G is a fault-tolerant resolving set (FTRS). The symbol \(\beta ^\prime (G)\) denotes the fault-tolerant metric dimension (FTMD), which is the FTRS’s minimum cardinality. In other words, for all s,t \(\in\) V(G), \(AD((s,t)|W^\prime\)) has at least two components in the l vector that are not zero. A fault-tolerant resolving set is a robust version of a resolving set. It ensures that even if one of the reference vertices becomes unavailable (due to failure, removal, or attack), the remaining vertices still form a resolving set and can uniquely determine the position of every vertex in the graph. Fault-tolerant metric dimension is the minimum cardinality of a fault-tolerant resolving set11.

Many authors have examined the intriguing idea of FTMD. For instance, Hernando et al. demonstrated that \(P_{n}\) on \(n\ge 2\) for the path graph \({n}>2\) vertices by computing the FTRS resolution set for tree graphs in11. Edge partition dimension and exchange property for nanotube discussed in12. Voronov in13 estimated the king’s graph’s FTMD. Homogeneous caterpillar graphs with FT partition size studied in14, fault-tolerance of the lattices of boron nanotubes embedded in15,16 discuss certain types of line graphs’ FT resolvability. FTMD of graphs discussed in11,17 discusses chemical graphs, FT partition resolvability, and extremal structures, and FT resolvability of graphs is studied in18, FTMD and FTEMD of hollow coronoid discussed in19, some families of ladder networks FTRSs are studied in20. Over the last four decades, extensive research has been conducted on the metric dimension of diverse graph types. For example,21 delved into the metric dimension of honeycomb networks, while the mixed metric dimension of the hexagonal network was discussed in22. The metric dimension of convex polytopes graphs was discussed in the work of23, and the edge metric dimension was addressed in24. The concept of metric dimension has proven valuable in solving challenging problems across various domains, and its application has extended to resolving parameters for different chemical structures, as discussed in works such as25,26.

The metric dimension, with its diverse applications, has become a subject of extensive research and holds practical significance in various aspects of daily life. Notably, researchers draw inspiration from its utility in determining similar patterns among various medications27. Metric dimensions find applications in diverse fields such as combinatorial optimization28,29, robot navigation30, pharmaceutical chemistry9, computer networks31, canonical graph labeling32, sonar, location problems, coast guard Loran7, the use of metric dimension in the development of a city33, image processing facilities, weighing problems34, and the coding and decoding of the Mastermind game35.

To gain further insights into the physical and chemical properties of octagonal grids, additional references are available in36,37,38. The definitions of distance, resolving set, and metric dimension given below are basic mathematical terms that are necessary to understand the ideas covered in this article. This paper makes use of a few basic theorems. The metric dimension of a graph G is one if and only if it is \(G=P_{n},\) denoted \(dim(P_{n})=1\) as demonstrated in39. \(dim(C_{n})=2\) for \(n\ge 3\) is proven in40, where \(C_{n}\) is a cycle graph. The path graph likewise has one mixed metric dimension.

Theorem 1.1

The path and cycle graphs of order n have line graphs with FTMD of 2 and 3, respectively.

Theorem 1.2

Assuming that dim(G) and \(dim_f(G)\), respectively, are the graph G’s metric and FTMD, we find that \(dim_{f}(G) \ge dim(G) +1\)41.

Lemma 1.1

Let be any graph; then, \(\beta (G) < \beta ^\prime (G)\)

Lemma 1.2

For all G \(\beta ^\prime (G)\) \(\ge\) 3 if \(G \ne P_{n}\)42

Definition 1.1

Let \(G = (V, E)\) be a connected simple graph, where \(V\) is the vertex set and \(E\) is the edge set. For any two vertices \(u, v \in V\), let \(d(u, v)\) denote the length of the shortest path between \(u\) and \(v\). Let \(W \subseteq V\) be an ordered subset of vertices. For each vertex \(v \in V\), define its representation with respect to \(W = \{w_1, w_2, \dots , w_k\}\) as \(r(v|W) = \left( d(v, w_1), d(v, w_2), \dots , d(v, w_k) \right)\) The set \(W\) is called a resolving set (or metric generator) if for every pair of distinct vertices \(u, v \in V\), we have \(r(u|W) \ne r(v|W)\) A metric base of \(G\) is a resolving set of minimum cardinality. The metric dimension of \(G\), denoted by \(\dim (G)\), is defined as \(\dim (G) = \min \{ |W| : W \text { is a resolving set of } G \}\)7

Definition 1.2

Let \(G = (V, E)\) be a connected simple graph, and let \(W \subseteq V\) be a resolving set of \(G\). The set \(W\) is called a fault-tolerant resolving set if, for every vertex \(w \in W\), the set \(W \setminus \{w\}\) is still a resolving set of \(G\). In other words, the resolving capability of \(W\) remains intact even if any one of its elements fails or is removed. The minimum cardinality of such a set is called the fault-tolerant metric dimension of \(G\), denoted by \(\dim _{f}(G)\) and \(\dim _{f}(G) = \min \{ |W| : W \text { is a fault-tolerant resolving set of } G \}\)11.

Construction of hexagonal nanosheet

In Fig. 1, edges are color-coded for clarity: red edges represent edges with degree two and 3 end nodes, edges with degree two end nodes are blue, and edges with degree 3 end nodes are black. Nodes with degree two are shown in green, and vertices with degree 3 are shown in black. Nodes that are part of the parsed cluster are represented by two colors. Specifically, \({a_{1,1}}, {a_{2h+1,1}}, {a_{1,v+1}}\) and \({a_{2h+1,v+1}}\) is shown in green and red due to its degree two, indicating its membership in the parsing process. Number 6 where \({h},{v}\ge 1, {v},{h}\in \mathbb {Z^+}\). The count of vertices with degree two is \(2{h}+{v}+3\), and the number of vertices with degree 3 is \(5{h}+4{v}-3-(2{h}+{v})\). The total number of vertices of \(H N S_{{h},{v}}\) is \(\vert V( H N S_{{h},{v}})\vert =(2{h}+1)(v+1)\), and the number of edges \(\vert E(H N S_{{h},{v}})\vert = (2{h}+ 1)(v+1)+1\). h and v are two parameters are used and two index s, t are used for drawing, where \(1\le {s}\le {h}\) and t vary twice with v. Figure 1 shows the log on vertex and edge clusters from our main results.

Fig. 1
figure 1

Generalize nanosheet derived from Hexagonal network.

Full size image

The edge and vertex sets of the nanosheet are

Edge and vertex set

$$\begin{aligned} E\left( {HNS} \right) = & \left\{ {a_{{s,t}} a_{{s,t + 1}} ,a_{{s,ts + 1t}} ;1 \le s \le v,\;1 \le t \le 2h + 1} \right\} \\ V(HNS) = & \left\{ {a_{{s,t}} ;1 \le s \le v,\;1 \le t \le 2h + 1} \right\} \\ \end{aligned}$$

Main results

In this section, we determine the fault-tolerant metric dimension (FTMD) of hexagonal nanosheet graphs, which model the structure of advanced nanomaterials. We provide an exact FTMD value for hexagonal nanosheets and construct minimal fault-tolerant resolving sets. Our results demonstrate that these nanosheets maintain unique vertex identification even under single-node failures, ensuring robustness in nanoscale applications such as drug delivery systems, nanonetworks, and sensor-based monitoring.

Theorem 2.1

If \(HNS_{{h},{v}}\) is a hexagonal nanosheet for \({v},{h} \ge 1,\) then fault-tolerant metric dimension is 4,  which is represented by the expression \(dim_{f}(H N S_{{h},{v}})=4.\)

Proof

This assertion will be supported by evidence demonstrating the FT metric dimension of 4 for a hexagonal nanosheet. We use the FTRS specification for the FTMD. The distinct representation of each vertex in \(H N S_{{h},{v}}\) for \({h}, {v} \ge 1.\) is provided below.

Fig. 2
figure 2

Hexagon for R as FTRS.

Full size image

The representation of Fig. 2 for \({h}=1={v}\) in Table 1

\(R=\{ a_{11}, a_{31},a_{12},a_{32}\}\)

Table 1 Vertices representation of Fig. 2.
Full size table

Table 1 shows the unique representation of the vertices of the hexagonal nanosheet. So R is resolving set of cardinality 4.

Now we want to show the representation for \(h=2=v\)

Fig. 3
figure 3

Hexagonal structure for \({h}=2={v}\).

Full size image

The representation of Fig. 3 for \({h} = 2= {v}\) in Table 2

The revolving set is \(R=\{{a}_{11}, {a}_{51},a_{13},a_{53}\}\)

Table 2 Vertices representation of Fig. 3.
Full size table

Table 2 shows the unique node representation of the hexagonal nanosheet. So R is a resolving set of cardinality 4. Now we want to make generalized formulas of distances that are unique.

Generalize Formulas of Distances of All Vertices of \(\varvec{HNS}\) to \(\varvec{R}\)

Since each distance is unique, the generalized equations for each vertex’s distance in the hexagonal nanosheet demonstrate that the FTRS has cardinality 4. Let \({{d}}(a_{s,t}, a_{1,1 }) =w_{1},{{d}}(a_{s,t} , a_{2h+1,1}) =w_{2},{{d}}(a_{s,t}, a_{1,v+1}) =w_{3},{{d}}(a_{s,t} , a_{2h+1,v+1}) =w_{4} ,\) and \(r({a}_{{s},{t}}\mid R)=({w}_{1},{w}_{2},{w}_{3},{w}_{4})\)

$$\begin{aligned} w_{1} = & \left\{ {\begin{array}{*{20}l} {s + t - 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{2} = & \left\{ {\begin{array}{*{20}l} {2h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{3} = & \left\{ {\begin{array}{*{20}l} {h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{4} = & \left\{ {\begin{array}{*{20}l} {3h - s - t + 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v.} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

\(r({a}_{{s},{t}}\mid R)=({s}+{t}-2, \ 2{h}+{s}-{t},\ {h}+{s}-{t}, \ 3{h}-{s}-{t}+2)\) for \(\ 1\le {s}\le {h}, \ \hbox {and} \ 1\le {t}\le {v}.\)

Let \({\zeta }\) and \({\xi }\) be any random vertices on the nanosheet \(NS_{{h},{v}} .\) Let \(R=\{ {a_{1,1}},{a_{2h+1,1}},{a_{1,v+1}},{a_{2h+1,v+1}}\}\)

Case I: When \({\zeta }=a_{s,t}\) and \({\xi }=a_{s^{\prime },t^{\prime }}\) then further three cases arise.

Case 1: If \(s=s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can say that \(t < t^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+q\) where \(q=t^{\prime }-t\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 2: If \(s\ne s^{\prime },\) \(t=t^{\prime }\) then without loss of generality we can say that \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+p\) where \(p=2(s^{\prime } -s)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 3: If \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can say that \(t < t^{\prime },\) \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },R) \ne {{d}}({\xi },R),\) because \({{d}} ({\zeta },R) ={{d}} ({\xi },R)+(p+q)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

When \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) the location of \({\zeta }\) and \({\xi }\) where \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\)then \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1}).\)

One can see from Fig. 1 when \({{d}} ({\zeta },a_{1,1})={{d}}({\xi },a_{1,1})\) this would implies that \({{d}}({\xi },a_{2h+1,1}) \ne {{d}}({\zeta },a_{2h+1,1})\) also \({{d}}({\xi },a_{2h+1,1}) ={{d}} x,a_{2h+1,1})\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}).\)

we discuss all cases where \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1})\) while \({{d}} ({\zeta },a_{2h+1,v+1})={{d}} ({\xi },a_{2h+1,v+1})\)

or \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\) \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1}).\) Since it is impossible for the two representations in any of the aforementioned scenarios to be identical, the FTMD is four. We now aim to demonstrate that every subset of cardinality 3 also serves as a RS for the nanosheet.

Unique Representation of \(\varvec{R}_{{\textbf {1}}}\) for Resolving Set

Here we want to show that the subset \(R_{1}\) of R of cardinality one less than R also has a unique representation.

Fig. 4
figure 4

Hexagon for \(R_{1}\) as RS.

Full size image

The double-color vertices are the points of the RS. \({a_{1,1}},\) \({a_{2h+1,1}}\), and \({a_{1,v+1}}\) are green and red colors as a result of degree two, and these points are the members of RS.

The representation of Fig. 4 for \({h}=1={v}\) in Table 3

\(R=\{ a_{11}, a_{31},a_{12}\}\)

Table 3 Vertices representation of Fig. 4.
Full size table

Table 3 shows the unique representation of the vertices of the hexagonal nanosheet. So R is resolving set of cardinality 3.

Generalize Formulas of Distances of All Vertices of \(\varvec{HNS}\) to \(\varvec{R}_{{\textbf {1}}}\)

Since each distance is unique, the generalized equations for each vertex’s distance in the hexagonal nanosheet demonstrate that \(R_{1}\) is a resolving set of cardinality 3. Let \({{d}} (a_{s,t}, a_{1,1 }) =w_{1},{{d}}(a_{s,t} , a_{2h+1,1}) =w_{2},{{d}}(a_{s,t}, a_{1,v+1}) =w_{3},\) and \(r({a}_{{s},{t}}\mid R)=({w}_{1},{w}_{2},{w}_{3})\)

$$\begin{aligned} w_{1} = & \left\{ {\begin{array}{*{20}l} {s + t - 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{2} = & \left\{ {\begin{array}{*{20}l} {2h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{3} = & \left\{ {\begin{array}{*{20}l} {h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

\(r({a}_{{s},{t}}\mid R)=({s}+{t}-2,\ 2{h}+{s}-{t},\ {h}+{s}-{t})\) for \(1\le {s}\le {h}, \ \hbox {and} \ 1\le {t}\le {v}.\)

Let \({\zeta }\) and \({\xi }\) be any random vertices on the nanosheet \(NS_{{h},{v}} .\) The distance is represented by d. Let \(R=\{ {a_{1,1}},{a_{2h+1,1}},{a_{1,v+1}}\}\)

Case I: When \({\zeta }=a_{s,t}\) and \({\xi }=a_{s^{\prime },t^{\prime }}\) then further three cases arise.

Case 1: If \(s=s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can \(t < t^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+q\) where \(q=t^{\prime }-t\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 2: If \(s\ne s^{\prime },\) \(t=t^{\prime }\) then without loss of generality we can say that \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+p\) where \(p=2(s^{\prime } -s)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 3: If \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can say that \(t < t^{\prime },\) \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },R) \ne {{d}}({\xi },R),\) because \({{d}} ({\zeta },R) ={{d}} ({\xi },R)+(p+q)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

When \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) the location of \({\zeta }\) and \({\xi }\) where \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\)then \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1}).\)

One can see from Fig. 1 when \({{d}} ({\zeta },a_{1,1})={{d}}({\xi },a_{1,1})\) this would implies that \({{d}}({\xi },a_{2h+1,1}) \ne {{d}},a_{2h+1,1})\) also \({{d}}({\xi },a_{2h+1,1}) ={{d}} x,a_{2h+1,1})\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}).\)

we discuss all cases where \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1})\) while \({{d}} ({\zeta },a_{2h+1,1})={{d}} ({\xi },a_{2h+1,1})\)

or \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\) \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1})\) The two representations can’t be the same in any of the aforementioned scenarios, so \(R_{1}\) is a resolving set of cardinality 3.

Unique Representation of \(\varvec{R}_{{\textbf {2}}}\) for Resolving Set

Here we want to show that the subset \(R_{2}\) of R of cardinality one less then R is also have representation of resolving set of cardinality 3.

Fig. 5
figure 5

Hexagon for \(R_{2}\) as RS.

Full size image

The representation of Fig. 5 for \({h}=1={v}\) in Table 4

\(R=\{ a_{11}, a_{31},a_{12}\}\)

Table 4 Unique representation of the vertices of Fig. 5.
Full size table

Table 4 shows the unique representation of the edges of the hexagonal nanosheet. So R is resolving set of cardinality 3.

Generalize Formulas of Distances of All Vertices of \(\varvec{HNS}\) to \(\varvec{R}_{{\textbf {2}}}\)

Since each distance is unique, the generalized equations for each vertex’s distance in the hexagonal nanosheet demonstrate that the RS has cardinality 3. Let \({{d}}(a_{s,t}, a_{1,1 }) =w_{1},{{d}}(a_{s,t} , a_{2h+1,1}) =w_{2},{{d}}(a_{s,t} , a_{2h+1,v+1}) =w_{4} ,\) and \(r({a}_{{s},{t}}\mid R)=({w}_{1},{w}_{2},{w}_{4})\)

$$\begin{aligned} w_{1} = & \left\{ {\begin{array}{*{20}l} {s + t - 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{2} = & \left\{ {\begin{array}{*{20}l} {2h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{4} = & \left\{ {\begin{array}{*{20}l} {3h - s - t + 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v.} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

\(r({a}_{{s},{t}}\mid R)=({s}+{t}-2, \ 2{h}+{s}-{t}, \ 3{h}-{s}-{t}+2)\) for \(\ 1\le {s}\le {h}, \ \hbox {and} \ 1\le {t}\le {v}.\)

Let \({\zeta }\) and \({\xi }\) be any random vertices on the nanosheet \(NS_{{h},{v}} .\) The distance is represented by d. Let \(R=\{ {a_{1,1}},{a_{1,v+1}},{a_{2h+1,v+1}}\}\)

Case I: When \({\zeta }=a_{s,t}\) and \({\xi }=a_{s^{\prime },t^{\prime }}\) then further three cases arise.

Case 1: If \(s=s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can \(t < t^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+q\) where \(q=t^{\prime }-t\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 2: If \(s\ne s^{\prime },\) \(t=t^{\prime }\) then without loss of generality we can say that \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+p\) where \(p=2(s^{\prime } -s)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 3: If \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can say that \(t < t^{\prime },\) \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },R) \ne {{d}}({\xi },R),\) because \({{d}} ({\zeta },R) ={{d}} ({\xi },R)+(p+q)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

When \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) the location of \({\zeta }\) and \({\xi }\) where \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\)then \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1}).\)

One can see from Fig. 1 when \({{d}} ({\zeta },a_{1,1})={{d}}({\xi },a_{1,1})\) this would implies that \({{d}}({\xi },a_{2h+1,1}) \ne {{d}},a_{2h+1,1})\) also \({{d}}({\xi },a_{2h+1,1}) ={{d}} x,a_{2h+1,1})\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}).\)

we discuss all cases where \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1})\) while \({{d}} ({\zeta },a_{2h+1,1})={{d}} ({\xi },a_{2h+1,1})\)

or \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\) \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1})\) The two representations can’t be the same in any of the aforementioned scenarios, so \(R_{2}\) is a resolving set of cardinality 3.

Unique Representation of \(\varvec{R}_{{\textbf {3}}}\) for Resolving Set

Here we want to show that the subset \(R_{3}\) of R of cardinality one less then R is also have representation of resolving set of cardinality 3.

Fig. 6
figure 6

Hexagon for \(R_{3}\) as RS.

Full size image

Construction of Hexagonal Nanosheet for \(R_{3}\): The double-color vertices are the points of the RS. \({a_{1,1}},\) \({a_{1,v+1}}\), and \({a_{2h+1,v+1}}\) are green and red colors as a result of degree two, and these points are the members of RS.

The representation of Fig. 6 for \({h}=1={v}\) in Table 5

\(R=\{ a_{11}, a_{31},a_{12}\}\)

Table 5 Unique representations of the vertices of Fig. 6.
Full size table

Table 5 shows the unique representation of the edges of the hexagonal nanosheet. So R is resolving set of cardinality 3.

Generalize Formulas of Distances of All Vertices of \(\varvec{HNS}\) to \(\varvec{R}_{{\textbf {3}}}\)

Since each distance is unique, the generalized equations for each vertex’s distance in the hexagonal nanosheet demonstrate that the RS has cardinality 3. Let d represent the distance. Let \({{d}}(a_{s,t}, a_{1,1 }) =w_{1},{{d}}(a_{s,t},{{d}}(a_{s,t}, a_{1,v+1}) =w_{3},{{d}}(a_{s,t} , a_{2h+1,v+1}) =w_{4} ,\) and \(r({a}_{{s},{t}}\mid R)=({w}_{1},{w}_{3},{w}_{4})\)

$$\begin{aligned} w_{1} = & \left\{ {\begin{array}{*{20}l} {s + t - 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{3} = & \left\{ {\begin{array}{*{20}l} {h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{4} = & \left\{ {\begin{array}{*{20}l} {3h - s - t + 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v.} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

\(r({a}_{{s},{t}}\mid R)=({s}+{t}-2,\ {h}+{s}-{t}, \ 3{h}-{s}-{t}+2)\) for \(\ 1\le {s}\le {h}, \ \hbox {and} \ 1\le {t}\le {v}.\)

Let \({\zeta }\) and \({\xi }\) be any random vertices on the nanosheet \(NS_{{h},{v}} .\) The distance is represented by d. Let \(R_{3}=\{ {a_{1,1}},{a_{2h+1,1}},{a_{2h+1,v+1}}\}\)

Case I: When \({\zeta }=a_{s,t}\) and \({\xi }=a_{s^{\prime },t^{\prime }}\) then further three cases arise.

Case 1: If \(s=s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can \(t < t^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+q\) where \(q=t^{\prime }-t\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 2: If \(s\ne s^{\prime },\) \(t=t^{\prime }\) then without loss of generality we can say that \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}),\) because \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1})+p\) where \(p=2(s^{\prime } -s)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 3: If \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can say that \(t < t^{\prime },\) \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },R) \ne {{d}}({\xi },R),\) because \({{d}} ({\zeta },R) ={{d}} ({\xi },R)+(p+q)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

When \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) the location of \({\zeta }\) and \({\xi }\) where \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\)then \({{d}} ({\zeta },a_{1,2h+}) \ne {{d}} ({\xi },a_{2h+1,1}).\)

One can see from Fig. 1 when \({{d}} ({\zeta },a_{1,1})={{d}}({\xi },a_{1,1})\) this would implies that \({{d}}({\xi },a_{2h+1,1}) \ne {{d}},a_{2h+1,1})\) also \({{d}}({\xi },a_{2h+1,1}) ={{d}} x,a_{2h+1,1})\) this would implies that \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1}).\)

we discuss all cases where \({{d}} ({\zeta },a_{1,1}) \ne {{d}} ({\xi },a_{1,1})\) while \({{d}} ({\zeta },a_{2h+1,v+1})={{d}} ({\xi },a_{2h+1,v+1})\)

or \({{d}} ({\zeta },a_{1,1}) ={{d}}({\xi },a_{1,1}),\) \({{d}} ({\zeta },a_{2h+1,v+1}) \ne {{d}} ({\xi },a_{2h+1,v+1})\) The two representations can’t be the same in any of the aforementioned scenarios, so \(R_{3}\) is a resolving set of cardinality 3.

Unique Representation of \(\varvec{R}_{{\textbf {4}}}\) for Resolving Set

Here we want to show that the subset \(R_{4}\) of R of cardinality one less then R is also have representation of resolving set of cardinality 3.

Fig. 7
figure 7

Hexagon for \(R_{4}\) as RS.

Full size image

The representation of Fig. 7 for \({h}=1={v}\) in Table 6

\(R=\{ a_{11}, a_{31},a_{12}\}\)

Table 6 Unique representations of the vertices given in the Fig. 7.
Full size table

Table 6 shows the unique representation of the edges of the hexagonal nanosheet. So R is resolving set of cardinality 3.

Generalize Formulas of Distances of All Vertices of \(\varvec{HNS}\) to \(\varvec{R}_{{\textbf {4}}}\)

Since each distance is unique, the generalized equations for each vertex’s distance in the hexagonal nanosheet demonstrate that the RS has cardinality 3. Let \({{d}} (a_{s,t} , a_{2h+1,1}) =w_{2},{{d}}(a_{s,t}, a_{1,v+1}) =w_{3},{{d}}(a_{s,t} , a_{2h+1,v+1}) =w_{4},\) and \(r({a}_{{s},{t}}\mid R)=({w}_{2},{w}_{3},{w}_{4})\)

$$\begin{aligned} w_{2} = & \left\{ {\begin{array}{*{20}l} {2h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{3} = & \left\{ {\begin{array}{*{20}l} {h + s - t} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v,} \hfill \\ \end{array} } \right. \\ w_{4} = & \left\{ {\begin{array}{*{20}l} {3h - s - t + 2} \hfill & {{\text{for}}\;1 \le s \le h,\;{\text{and}}\;1 \le t \le v.} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

\(r({a}_{{s},{t}}\mid R)=(2{h}+{s}-{t},\ {h}+{s}-{t}, \ 3{h}-{s}-{t}+2)\) for \(\ 1\le {s}\le {h}, \ \hbox {and} \ 1\le {t}\le {v}.\)

Let \({\zeta }\) and \({\xi }\) be any random vertices on the nanosheet \(NS_{{h},{v}}.\) The distance is represented by d. Let \(R_{4}=\{{a_{2h+1,1}},{a_{v+1,1}},{a_{2h+1,v+1}}\}\)

Case I: When \({\zeta }=a_{s,t}\) and \({\xi }=a_{s^{\prime },t^{\prime }}\) then further three cases arise.

Case 1: If \(s=s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can \(t < t^{\prime }\) this would implies that \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1}),\) because \({{d}} ({\zeta },a_{2h+1,1}) ={{d}}({\xi },a_{2h+1,1})+q\) where \(q=t^{\prime }-t\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 2: If \(s\ne s^{\prime },\) \(t=t^{\prime }\) then without loss of generality we can say that \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1}),\) because \({{d}} ({\zeta },a_{2h+1,1}) ={{d}}({\xi },a_{2h+1,1})+p\) where \(p=2(s^{\prime } -s)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

Case 3: If \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) then without loss of generality we can say that \(t < t^{\prime },\) \(s < s^{\prime }\) this would implies that \({{d}} ({\zeta },R) \ne {{d}}({\xi },R),\) because \({{d}} ({\zeta },R) ={{d}} ({\xi },R)+(p+q)\) so \(r({\zeta }\mid R) \ne r({\xi }\mid R).\)

When \(s\ne s^{\prime },\) \(t\ne t^{\prime }\) the location of \({\zeta }\) and \({\xi }\) where \({{d}} ({\zeta },a_{2h+1,1}) ={{d}}({\xi },a_{2h+1,1}),\)then \({{d}} ({\zeta },a_{2h+1,v+1}) \ne {{d}} ({\xi },a_{2h+1,v+1}).\)

One can see from Fig. 1 when \({{d}} ({\zeta },a_{2h+1,1})={{d}}({\xi },a_{2h+1,1})\) this would implies that \({{d}}({\xi },a_{2h+1,v+1}) \ne {{d}},a_{2h+1,v+1})\) also \({{d}}({\xi },a_{2h+1,1}) ={{d}} x,a_{2h+1,1})\) this would implies that \({{d}} ({\zeta },a_{1,v+1}) \ne {{d}} ({\xi },a_{1,v+1}).\)

we discuss all cases where \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1})\) while \({{d}} ({\zeta },a_{2h+1,v+1})={{d}} ({\xi },a_{2h+1,v+1})\)

or \({{d}} ({\zeta },a_{1,v+1}) ={{d}}({\xi },a_{1,v+1}),\) \({{d}} ({\zeta },a_{2h+1,1}) \ne {{d}} ({\xi },a_{2h+1,1})\) The two representations can’t be the same in any of the aforementioned scenarios, so \(R_{4}\) is a resolving set of cardinality 3.

All possible subsets of cardinality 3 of R are also RSs so R is FTRS of cardinality 4.

Converse case

Now we want to show that the FTRS is not less than four. And the \(dim_{f}(G)\le 4.\) It means the converse case for FTRS is \(1, \ 2\) and 3. FTMD 1 is not possible for any graph, and FTRS two is for a path graph. Now, for FTMD, it 3 is not possible to have some cases.

Case 1: Suppose \(R^{\prime }\subseteq \{{{a}_{{s},{t}},{a}_{{s},{t}+1}},{a}_{{s},{t}+2}:1\le {s}\le {v} \ ,1\le {t}\le 2{h}+1\}\) of 3-cardinality, then some subsets of \(R^{\prime }\) of cardinality two are not RS. Let \(R^{\prime \prime }=\{{{a}_{{s},{t}},{a}_{{s},{t}+1}}:1\le {s}\le {v} \ ,1\le {t}\le 2h+1\}\)

be the subsets of cardinality one less the \(R^{\prime }\)

Case 2: Suppose \(R^{\prime }\subseteq \{{a}_{{s},{t}},{a}_{{s+1},{t},{a}_{{s+2},{t}}}:1\le {s}\le {v} \ ,1\le {t}\le 2h+1\}\) of 3-cardinality,then some subsets of \(R^{\prime }\) of cardinality two are not RS. Let \(R^{\prime \prime }=\{{{a}_{{s},{t}},{a}_{{s+1},{t}}}:1\le {s}\le {v} \ ,1\le {t}\le 2h+1\}\)

be the subsets of cardinality one less the \(R^{\prime }\)

Case 3: Suppose \(R^{\prime }\subseteq \{{a}_{{s},{t}},{a}_{{s}+1,{t+1},{a}_{{s}+2,{}}}:1\le {s}\le {v} \ ,1\le {t}\le 2h+1\}\) of 3-cardinality,then some subsets of \(R^{\prime }\) of cardinality two are not RS. Let \(R^{\prime \prime }=\{{{a}_{{s},{t}},{a}_{{s+2},{}}}:1\le {s}\le {v} \ ,1\le {t}\le 2h+1\}\)

be the subsets of cardinality one less the \(R^{\prime }\)

Case 4: suppose \(R^{\prime }\subseteq \{{a}_{{1},{1}},{a}_{{2h}+1,{1},{a}_{{2h}+1,{v+1}}}:1\le {s}\le {v} \ ,1\le {t}\le 4{h}\}\) of 3-cardinality,then some subsets of \(R^{\prime }\) of cardinality two are not RS. Let \(R^{\prime \prime }=\{{a}_{{1},{1}},{a}_{{2h}+1,{v+1}}:1\le {s}\le {v} \ ,1\le {t}\le {2h}+1\}\)

be the subsets of cardinality one less the \(R^{\prime }\)

Case 5: suppose \(R^{\prime }\subseteq \{{a}_{{1},{1}},{a}_{1},{v+1}{a}_{{2h}+1,{1}}:1\le {s}\le {v} \ ,1\le {t}\le 4{h}\}\) having 3-cardinality,then some subsets of \(R^{\prime }\) of cardinality two are not RS. Let \(R^{\prime \prime }=\{{a}_{{1},{2}},{a}_{{2h}+1,{1}}:1\le {s}\le {v} \ ,1\le {t}\le {2h}+1\}\)

$$\begin{aligned} ^\vert {} ^{v}{}^\vert G_3 =\frac{\vert {v} \vert !}{3!( \vert {v} \vert -3 )!} = \frac{(5{h}+3{v}) !}{3!(5{h}+3{v}-3)!} \end{aligned}$$

of vertex set of \(HNS_{{h},{v}}.\) This demonstrates that not all subset RSs are present when finding or solving set of 3-cardinality. Hence; \(dim_{f}(HNS_{{h},{v}})\ge 4.\) therefore

$$\begin{aligned} dim_{f}(HNS_{{h},{v}})=4. \end{aligned}$$

\(\square\)

Application of fault-tolerant metric dimension for emergency response and services in a city

Context: In a city, homes represent the vertices, and the roads connecting them represent the edges in a graph. The goal is to provide emergency services, medical supplies, or utility services efficiently throughout the city. The fault-tolerant metric dimension concept can be used to identify key locations (from the resolving set) where resources can be placed. These locations must be selected such that even if some of these locations fail (due to an emergency, power outage, or another issue), the city can still be effectively serviced without any ambiguity.

Application: Graph Representation:

  • The vertices in the graph represent homes (or other essential locations like hospitals, schools, etc.).

  • The edges are the roads connecting the homes.

  • The faces could represent different districts or zones of the city (though this may be an optional structure depending on the city’s layout).

Fault-Tolerant Metric Dimension: A fault-tolerant metric dimension (FTMD) provides a set of locations (vertices in the graph) from which the distance to all other locations is unique. The goal of the fault-tolerant metric dimension is to ensure that if a few of these locations fail (e.g., due to power outages, road blockages, or damage during a disaster), the remaining locations can still ensure unique identification of every other location. The FTMD ensures that even with some failure of service points, the city’s emergency or utility systems will still operate without confusion.

Fault-Tolerant Emergency Service Provision:

  • The resolving set in this case represents the key locations (e.g., hospitals, fire stations, police stations) from which services can be provided.

  • By selecting a minimal fault-tolerant resolving set, the number of emergency service stations can be minimized, but the coverage will still be reliable even in the case of failure or disruption.

  • If some key stations fail, the remaining stations can still maintain the capability to resolve the unique identification of locations for efficient dispatching of resources like ambulances, fire trucks, or police.

Benefits of Fault-Tolerant Metric Dimension: Resilience: The system remains effective even if some locations fail or become unreachable due to emergencies. Cost-Effective: Minimizes the number of locations required to ensure full coverage, reducing the need for redundant service points. Efficient Dispatching: Ensures that services like ambulance dispatch, fire response, or utilities can still identify their locations, even under failure scenarios, ensuring faster response times and fewer errors. Example: Consider a small neighborhood represented by a graph where:

Homes are the vertices, and roads are the edges. A hospital, police station, and fire station are placed at certain homes (vertices). A fault-tolerant resolving set ensures that the failure of one station (due to road blockage or damage) does not affect the identification of other homes that need service. The FTMD guarantees that even with a failure of one or two stations, the rest can still uniquely resolve the distances to homes for emergency services.

Summary of this application:

Using the fault-tolerant metric dimension in this urban scenario optimizes the placement of essential services in a city, ensuring that services remain effective even when some service points fail. This method provides resilience and efficiency, ensuring that cities are better prepared for emergencies while minimizing resource requirements.

Problem:

  • An organization embarking on the development of an emergency response network in a city intends to determine where and at least how many rescue service centers (fire, medical, disaster response) should be established.

  • Emergency services assign unique codes to each construction in a city based on proximity to response units (e.g., fire stations, hospitals).

  • These codes reflect the shortest distance to the nearest emergency hub, enabling quick navigation and efficient dispatching.

  • Even if one emergency center becomes non-operational (due to overload or damage), the system retains accuracy through fault-tolerant coding, ensuring no area is left untraceable.

  • This approach improves response time, route planning, and resource allocation during critical situations like fires, medical emergencies, or natural disasters.

Fig. 8
figure 8

Structure of a city.

Full size image

Solution:

  • The organization contacts a mathematician to solve the problem.

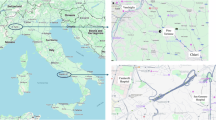
  • The mathematician converts the map of the city as presented in Fig. 8 into a mathematical graph like in Fig. 9, where vertices represent houses or buildings and edges denote roads.

  • He applies the definition of a fault-tolerant resolving set to this graph.

  • According to this definition, he takes a subset R of the vertices of the graph.

  • R of minimum rescue service centers (e.g., fire, medical, and disaster response units) and calculates the shortest distances from all houses to these centers.

  • The set R provides a unique code for every building based on its distances to the selected rescue centers.

  • Then, he examines subsets of R with cardinality one less then R.

  • These subsets also yield unique representations for all constructions.

  • As a result, he concludes that the organization can establish a minimum number of rescue service centers equal to the cardinality of R.

  • These selected positions fulfill the organization’s requirements: unique coding of houses and shortest distance access, even if one rescue center is relocated or unavailable.

  • If a citizen faces an emergency, they can open an app provided by the organization, enter their house’s code, and the system will immediately guide them to the nearest rescue service center.

Fig. 9
figure 9

graph representation of a city structure.

Full size image

Now we discussed an example of this hexagonal structure. In this work, we find four corners as emergency units and calculate the distances based on codes for each construction through these units. Suppose multiple emergency vehicle like Fig. 10 are present at different units and a citizen calls for emergency, the organization track the codes of this person and decides from where we respond.

Fig. 10
figure 10

Emergency vehicle.

Full size image

Let a person be present at house \({a}_{26}\) and another person be at \({a}_{42}\), both call for the emergency. The system check the codes of both person according to their position. The code of \({a}_{26}\) is (6, 2, 8, 4) and \({a}_{42}\) is (4, 8, 2, 6). The person that is present at point \({a}_{26}\) is very near to second emergency unit so the system send the information to emergency vehicle like Fig. 10 present at second emergency unit and other one is present at \({a}_{42}\) and is near to third unit so \({a}_{26}\) is response by emergency unit that is present at \({a}_{17}\) but \({a}_{42}\) is helped by unit \({a}_{51}.\) Both codes are unique, and like this, all codes of the graph are unique. If any unit is closed, then the codes are regenerated with cardinality one less than. suppose the unit at \({a}_{17}\) is closed then the codes of these two houses are (6, 8, 4) and (4, 2, 6). Now the person present at \({a}_{26}\) is near to unit at \({a}_{57}\), so it is helped by this one and \({a}_{42}\) is response by same unit because it again close to this one.

Conclusion In this work, we have efficaciously proven the relevance of the fault-tolerant metric dimension (FTMD) of hexagonal nanosheets in optimizing emergency reaction and concrete provider structures. By leveraging the strong structural properties of hexagonal nanosheets, we evolved a framework that enhances the precision and reliability of locating service points, which include emergency reaction units and essential metropolis infrastructure, even under disruptive situations. The FTMDs ability to account for fault tolerance guarantees resilience in actual global eventualities, wherein disruptions can compromise response performance. This adaptability makes the methodology an effective tool for urban planners and policymakers striving to create sustainable, responsive towns. The integration of FTMD into urban systems not handiest optimizes resource allocation but also strengthens the general network’s capability to respond correctly to crises, minimizing delays and improving public safety. Our findings underscore the potential of graph-theoretical ideas, such as FTMD,  in addressing real-life demanding situations. This work sets the stage for destiny studies into advanced applications of graph theory, bridging the gap between abstract mathematical fashions and tangible societal benefits. By applying FTMD to urban emergency systems, we take an extensive step toward constructing smarter, safer, and more resilient cities. The FTMD of hexagonal sheet is 4.