Bearing fault diagnosis method based on SAGAN and improved ResNet

Abstract

Traditional rolling bearing fault diagnosis methods struggle to adaptively extract features under complex industrial environments, and obtaining large and rich fault data under real operating conditions is difficult and expensive. Aiming at these issues, a bearing fault diagnosis method based on Self-Attention Generative Adversarial Networks (SAGAN) and Improved Deep Residual Networks (IResNet) was proposed (SAGAN_IResNet). Firstly, the original vibration signals are transformed into two-dimensional time–frequency images using continuous wavelet transform, providing both time domain and frequency domain information. Secondly, SAGAN is used to generate new samples similar to the original sample distribution, thereby expanding the data. Furthermore, a bearing fault diagnosis model is constructed using an improved residual network that incorporates the Multi-head Self-Attention (MHA) to adaptively obtain the global feature information, alleviate the problem of gradient dispersion and network degradation, and enhance the model’s diagnostic performance in the presence of strong noise and variable load conditions. Experimental verification is conducted using bearing datasets from Case Western Reserve University, Southeast University and Jiangnan University. The results show that the method proposed in this paper has strong bearing fault diagnosis performance under the condition of few samples, strong noise and variable load.

Introduction

With the continuous advancement of industrial manufacturing, mechanical equipment is undergoing a transformation towards higher precision, high efficiency, automation, and complexity. Bearings, as vital components in aerospace, high-end machine tools, and advanced medical equipment, play a crucial role in the overall operation of these systems^1,2. Research indicates that nearly 30% of faults in rotating machinery are related to rolling bearings³. Consequently, the development of a bearing fault diagnosis method with high accuracy and strong robustness holds profound significance in enhancing industrial production efficiency, operational costs, and eliminating safety hazards^4,5.

Currently, fault diagnosis methods for rotating machinery can be broadly categorized into three types: those based on analytical models⁶, knowledge-based approaches⁷, and data-driven methods⁸. Diagnosing faults in complex mechanical systems through the establishment of high-precision analytical models or extensive empirical knowledge bases can be challenging and expensive, Additionally, there are also some practical limitations in practical industrial applications. With the rapid development of intelligent manufacturing, a substantial volume of equipment condition monitoring data has been collected and stored for further analysis. As a result, data-driven fault diagnosis algorithms have become a research hotspot in mechanical fault diagnosis research⁹. Among these, the support vector machine¹⁰, K-nearest neighbor¹¹, BP neural network and extreme learning machine¹² gained widespread use. Although these methods have achieved certain results, their shallow network structures and insufficient feature extraction capabilities restrict further improvements in the accuracy of bearing fault diagnosis.

In recent years, deep learning has gained significant attention from researchers due to its powerful ability to automatically extract features. This technique has achieved impressive results across various domains including speech recognition, natural language processing, and computer vision. It has also been extensively applied in the field of fault diagnosis^13,14,15. For instance, Hoang et al.¹⁶ converted original vibration signals into two-dimensional images using the fast Fourier transform and then employed convolutional neural networks to extract features and diagnose faults. Similarly, Xu et al.¹⁷ combined one-dimensional convolutional neural networks with autoencoders to enhance fault diagnosis accuracy and reduce diagnostic delays. Furthermore, Siddique et al.¹⁸ proposed a novel method for bearing fault diagnosis. This method extracts fault features through convolutional layers and pooling layers, optimizes the model weights using the FOX optimizer, and achieves a high classification accuracy. Zaman et al.²⁰ proposed a centrifugal pump fault detection method that integrates a hybrid feature pool with deep learning, aiming to enhance fault identification accuracy and generalization capability under complex operating conditions. Zaman et al.²⁰ developed a hybrid deep learning model that integrates the strengths of deep learning in feature extraction and classification with the capabilities of wavelet coherence analysis in time–frequency feature extraction, effectively enhancing the accuracy of fault diagnosis in centrifugal pumps.

Despite the achievements of various bearing fault diagnosis methods, several challenges and difficulties persist in achieving effective and high-precision fault diagnosis in real-world industrial scenarios. The two most significant challenges are as follows:

• (1) Insufficient samples: data is an important factor affecting the performance of the model, but it is difficult to collect fault samples in the actual industrial environment. It is time-consuming and expensive to obtain a large amount of balanced fault data²¹.

• (2) Difficulty in feature extraction: The presence of environmental noise and load variations in industrial production complicates the extraction of meaningful features from vibration signals. This complexity and instability hinder the effective extraction of features for accurate mechanical fault diagnosis²².

To enhance the accuracy of fault diagnosis in insufficient datasets, researchers have employed various techniques. Taylor et al.²³ utilized data augmentation methods such as flipping, rotating, color jitter, and polar coordinate transformation to process images. Meanwhile, Udmale et al.²⁴ employed the transfer learning method to tackle the challenges of fault diagnosis under various operating conditions. It effectively addresses the issue of insufficient fault samples and achieves good diagnostic performance. Generative Adversarial Networks (GANs) offer a promising new approach to address the issue of insufficient samples. Initially used for image generation, GANs have demonstrated effectiveness and have been extended to the field of mechanical fault diagnosis²⁵. For example, Xie et al.²⁶ proposed a Deep Convolution GAN (DCGAN) model to simulate the original distribution of a few classes and generate new data to expand the bearing fault data set. Liang et al.²⁷ combined GANs with wavelet transform and Convolutional Neural Networks (CNN) to propose a new intelligent fault detection method for rotating machinery.

To address the challenge of extracting bearing fault features in complex environments, there has been a trend towards enhancing fault diagnosis models. Huang et al.²⁸ combined convolutional neural networks with the channel attention mechanism. This approach adaptively scores and assigns weights to learned features, improving the learning capability of convolutional layer features. Guo et al.²⁹ proposed a fault diagnosis method based on attention CNN with BiLSTM network, leveraging the attention mechanism to emphasize critical features. Moreover, Wang et al.³⁰ explored the application of attention mechanisms in fault diagnosis networks by designing an attention module that fully considers the characteristics of rolling bearing faults, enhancing fault-related features while ignoring irrelevant ones.

Although these above methods have improved the accuracy of bearing fault diagnosis, it is difficult to achieve a balance between handling insufficient samples and extracting fault features. Therefore, this paper proposes a new approach to rolling bearing fault diagnosis based on a Self-Attention Generative Adversarial Networks (SAGAN) and improved residual network. The main contributions of this paper can be summarized as follows:

• (1) Proposal of an intelligent fault diagnosis method for rolling bearings based on the Self-Attention generative adversarial network and improved residual network. The method demonstrates robust fault diagnosis performance even under challenging conditions such as insufficient samples, strong noise, and variable loads.

• (2) Utilization of SAGAN to generate high-quality synthetic bearing fault data, SAGAN’s ability to learn global and long-distance dependencies improves the accuracy of data generation, effectively addressing the problem of insufficient data volume.

• (3) A bearing fault diagnosis model based on an improved residual network is proposed. The Multi-head Self-Attention is combined with the residual neural network to alleviate the problems of gradient dispersion and network degradation, and the global feature information is adaptively obtained, which improves fault diagnosis performance of the model under strong noise and variable loads.

The rest framework of the article is as follows: The second section briefly introduces some theoretical background knowledge. In the third section, we provide a detailed description of the proposed basic settings and the implementation process of the model. The fourth section validates the effectiveness of the proposed method through experimental results and compares it with other common bearing fault diagnosis methods. Lastly, the fifth section provides a discussion and summary of the research methods utilized in this paper, highlighting key findings and implications for future research.

Theoretical background

Continuous wavelet transform

The Continuous Wavelet Transform (CWT) is a multi-scale time–frequency analysis method with strong time–frequency analysis ability. CWT can collect both high and low-frequency components to ensure the integrity of feature information³¹. In general, assuming that the input signal is $x(t)$ and $x(t){ = }L^{{2}} (R)$, and the basic wavelet function is $\psi (t) \in L^{2} (R)$, where $L^{2} (R)$ the space of square-integrable real-number functions. The CWT of $x(t)$ can be expressed as:

$$CWT_{x} (a,b) = \frac{1}{\sqrt a }\int_{ - \infty }^{ + \infty } {x(t)\psi^{*} } \left( {\frac{t - b}{a}} \right)dt = < x(t),\psi_{a,b} (t) >$$

(1)

$$\psi_{a,b} (t) = \frac{1}{\sqrt a }\psi \left( {\frac{t - b}{a}} \right)$$

(2)

where a and b represent the scale and displacement parameters in wavelet transform respectively. $\psi^{*} (x)$ denotes the complex conjugate value of $\psi (x)$ , $CWT_{x} (a,b)$ denotes the inner product of signal and wavelet $\psi_{a,b} (t)$. By performing continuous wavelet transform to the original vibration signal, the original vibration signals are converted into two-dimensional time–frequency images, and the time–frequency mixed representation of the signal is extracted to facilitate subsequent data generation and feature extraction.

Generative adversarial networks

Generative adversarial networks (GANs) consist of two main components: the generator (G) and the discriminator (D)²⁵. The generator is trained to learn the distribution of real sample data and generates more realistic synthetic data, while the discriminator is trained to distinguish between real and generated data. During the training process, the generator aims to produce increasingly realistic data to deceive the discriminator, while the discriminator strives to correctly classify the authenticity of the data. Through multiple iterations of this adversarial process, the generator and discriminator reach a Nash equilibrium. The structure of GANs is illustrated in Fig. 1.

Fig. 1

The structure of GAN.

The objective function of GANs can be defined as:

$$\mathop {\min }\limits_{G} \mathop {\max }\limits_{D} V(D,G) = E_{{x\sim P_{data} (x)}} [\log D(x)] + E_{z\sim p(z)} [\log (1 - D(G(z)))]$$

(3)

where $z$ represents the random noise, which is input into the generator D to generate pseudo-sample data.$x$ denotes the real sample input whose distribution is $P_{data} (x)$, and $D(x)$ is the output of discriminator D. If $D(x) > 0.5$, the input x is considered to be a real sample; if $D(x) < 0.5$, the input $x$ is considered to be a pseudo sample³².The generator and the discriminator are essentially two independent networks, thus, their training is performed independently. During training, the parameters of one network are fixed and those of the other are updated. Firstly, the generator G is optimized (the parameters of the discriminator D are fixed), and the loss function of the generator is as follows:

$$\mathop {\min }\limits_{G} = E_{z\sim p(x)} [\log (1 - D(G(Z)))]$$

(4)

Secondly, the discriminator D is optimized (the parameters of the generator G are fixed, and the loss function of the discriminator is as follows:

$$\mathop {\max }\limits_{D} V(D,G) = E_{{x\sim p_{data} (x)}} [\log (D(x))] + E_{z\sim p(z)} [\log (1 - D(G(Z)))]$$

(5)

Through adversarial learning, the generator and discriminator collaborate to produce data that closely imitate genuine data, which can compensate for the deficiency of insufficient samples.

Convolutional neural networks

The convolutional neural network originated from the study of the cerebral cortex vision capabilities and has been used in image recognition since the 1980s. At present, convolutional neural networks have achieved superhuman performance in some complex visual tasks^33,34,35,36.The main structures of convolutional neural networks are convolutional layers, pooling layers, and fully connected layers.

Convolution layers. The function of convolution layers is to extract image features. These layers are composed of several convolution units, and the parameters in the convolution unit are optimized by the backpropagation propagation algorithm. The convolution operation formula is as follows:

$$X_{j}^{l} = \int {\left( {\sum\nolimits_{{i \in M_{j} }} {X_{i}^{l - 1} \cdot w_{ij}^{l} } + b_{j}^{l} } \right)}$$

(6)

In the formula,$X_{j}^{l}$ represents the $j$th element of the $l$th layer, $M_{j}$ represents the $j$th convolution,$X_{i}^{l - 1}$ represents the element,$w_{il}^{l}$ represents the weight matrix,$b_{j}^{l}$ represents the bias and $f(x)$ represents the activation function. The commonly used activation function for convolution operation is ReLU, whose formula can be expressed as follows:

$$RELU(x) = \max (0,x)$$

(7)

The ReLU activation function introduces a nonlinear factor into the neural network so that the neural network can fit any nonlinear relationship.

Pooling layers. Pooling layers reduce the load and parameter amount by secondary sampling of the feature map. The pooling operation is mainly divided into maximum pooling and average pooling. Maximum pooling obtains local information to retain texture features, while average pooling retains overall features. The maximum pooling operation formula is as follows:

$$P_{k}^{(i,j)} = \mathop {\max }\limits_{(j - 1)w + 1 < t < jw} \{ q_{k}^{(i,t)} \} ,j = 1,2,...,m$$

(8)

where $P_{k}^{(i,j)}$ represents the result of the pooling of the $j$th output map in the $k$th layer, $q_{k}^{(i,j)}$ represents the local input feature of the pooling of the $k$ th layer.

Fully-connected (FC) layers: Fully-connected layers are usually set after the last convolution and pooling, which act as a classifier within the network. The commonly used activation function for full connection is Softmax. The full connection operation formula is as follows:

$$y^{k} = \sigma (w^{k} x^{k - 1} + b^{k} )$$

(9)

where $k$ represents the network layer number, $y^{k}$ represents the output of the fully connected layer,$\sigma$ represents the Softmax activation function, $w^{k}$ represents the weight coefficient, denotes one-dimensional vector input, and $b^{k}$ represents bias.

Residual neural network (ResNet)

In order to address the problems of gradient dispersion and network degradation caused by deep convolution neural networks, He et al.³⁷ proposed Residual Neural Networks (ResNet). ResNet breaks the convention that the output of the n-1 layer of the neural network can only give the n layer as input. Instead, it enables the output of a certain layer to skip several layers and directly serve as the input of a later layer. The residual module is depicted in Fig. 2.

Fig. 2

The structure of ResNet.

The residual network operation formula is as follows:

$$H(x){ = }F(x) + x$$

(10)

where $x$ represents identity mapping, $F(x)$ denotes the represents mapping and $H(x)$ represents the unknown mapping.

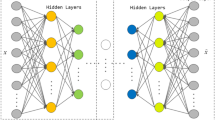
Self-attention mechanism

The Self-Attention mechanism enhances the sensitivity of a network model to important features. In normal circumstances, only certain parts of the input data are significant to impact the network’s performance. The mechanism assigns weights to various parts of the data, giving more attention to the key parts, thereby improving the overall performance of the model. The principle of this mechanism is illustrated in Fig. 3. The calculation formula of the Self-Attention mechanism is as follows:

$$\begin{gathered} Q = XW^{q} \hfill \\ K = XW^{k} \hfill \\ V = XW^{v} \hfill \\ \end{gathered}$$

(11)

$$Self - Attention(Q,K,V) = Soft\max (\frac{{QT^{T} }}{{\sqrt {d_{k} } }})V$$

(12)

Fig. 3

Schematic diagram of the Self-attentive mechanism.

In the formula: $X$ represents the input data, $Q$ is the query vector, $K$ is the key vector, and $V$ is the value vector. $Q$, $K$ and $V$ are derived from linear transformations of the input data, and the obtained matrix is input into the Self-Attention mechanism. Firstly, the query vector $Q$ and the key vector $K$ are subjected to a matrix dot product, the result of which is divided by the scaling factor $\sqrt {d_{k} }$ to prevent overly large values. Secondly, the Softmax function normalizes the correlation to obtain the attention weights. Finally, these weights and the value vector $V$ are weighted and summed to produce the Self-Attention representation of the input data.

The Self-Attention mechanism is effective in enhancing the model’s ability to extract global features. However, a single-head attention mechanism has limited feature capacity for learning complex features. In contrast, the Multi-head Self-Attention captures feature information from multiple subspaces of the input data. This enhancement allows the model to better grasp global features and long-range dependencies. Consequently, thus more effectively uncovering the underlying relationships between variables. The formula for calculating the Multi-head Self-Attention mechanism is as follows:

$$MultiHead(Q,K,V) = concat(H_{1} ,H_{2} ,...,H_{n} )W$$

(13)

$$H_{i} { = }Self - Attention(Q_{i} ,K_{i} ,V_{i} ),i = 1,2,...,h$$

(14)

In the formula: $h$ represents the number of heads in the Multi-head Self-Attention mechanism,$H_{i}$ represents the output of the $i$ attention mechanism. The operation “concat” refers to the concatenation of matrices, which splices the outputs from each single-head attention mechanism, and then fuses through a linear mapping with the weight matrix $W$, producing the output of the Multi-head Self-Attention mechanism.

Framework of the proposed method

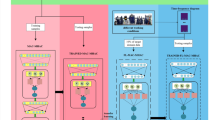
To address the challenges of bearing fault feature extraction and the insufficient samples in complex environment, this paper proposes a bearing fault diagnosis method based on SAGAN_IResNet. The method begins with preprocessing the original vibration signals, converting the one-dimensional vibration data into two-dimensional time–frequency images. Subsequently, SAGAN is used to generate high-quality samples to solve the issue of insufficient bearing fault sample data. An improved residual network model for bearing fault diagnosis is then established and trained. The trained model is used to perform the bearing fault diagnosis task. The flow chart of the proposed method is shown in Fig. 4. The detailed fault detection steps are as follows:

Fig. 4

The framework of the proposed method to realize the bearing fault diagnosi.

Step 1: Signal Acquisition and Processing. Obtain bearing vibration signals in various health states and segment the signals by overlapping sampling. In addition, the vibration signals are converted into time–frequency images via CWT, and the images are divided into training, validation and test.

Step 2: Data augmentation based on SAGAN. A Self-Attention Generative Adversarial network (SAGAN) is built. Training set samples are used as input to train the SAGAN until the network converges. This training produces a new set of samples that closely resemble the original sample distribution, which is used to enrich the original data set and solve the problem of insufficient samples.

Step 3: Fault diagnosis based on IResNet. To improve the accuracy of bearing fault diagnosis under conditions of strong noise and variable load, a bearing fault diagnosis model based on an improved residual network (IResNet) has been developed. Both the original sample and the generated samples in Step 2 are combined as input to train the diagnostic model. At the same time, the accuracy of the model is verified by the validation set, and the model parameters are fine-tuned until the network converges.

Step 4: Diagnosis result analysis and visualization. The test data set obtained in Step 1 is input into the trained bearing fault diagnosis model to realize the bearing fault diagnosis task, and the diagnosis results are analyzed and discussed.

CWT for time–frequency imaging

In complex industrial production, the obtained bearing vibration signals contain a large number of non-stationary signals, which makes it difficult for generating and diagnostic models to extract effective features for sample generation and fault diagnosis. As a commonly used time–frequency analysis method, CWT converts one-dimensional time-domain vibration signals from into two-dimensional time–frequency images. This transformation integrates the frequency characteristics of fault signals from both time-domain and frequency-domain to effectively process non-stationary signals. For example, Tran et al.³⁸ proposed a motor fault detection model based on continuous wavelet transform and convolutional attention neural network. Liang et al.²⁷ proposed a rotating machinery fault detection method based on wavelet transform (WT), generative adversarial networks (GANs) and convolutional neural networks (CNN), which addressed the issue of insufficient samples.

Data augmentation based on SAGAN

Most GAN-based data generation models are constructed by convolutional neural networks. The convolution operation is used to process information within local neighborhood, so it is inefficient to use the convolution layer alone to model the long-distance relationships within images. In order to solve this problem, Zhang et al. proposed the Self-Attention generative adversarial networks (SAGANs)³⁹, which allow attention-driven long-term dependence modeling for image generation tasks. The Self-Attention mechanism shows a better balance between long-term dependent modeling capabilities and computational efficiency. By incorporating the Self-Attention mechanism, the generator can draw an image, where the fine details of each position are carefully coordinated with the fine details of the distant part of the image. In addition, the discriminator can also impose complex geometric constraints on the global image structure:

$$L_{D} = - E_{{(x,y)\sim P_{data} }} [\min (0, - 1 + D(x,y))] - E_{{z\sim p_{z} ,y\sim p_{data} }} [\min (0, - 1 - D(G(z),y))]$$

(15)

$$L_{G} = - E_{{z\sim p_{data} ,y\sim p_{data} }} D(D(z),y)$$

(16)

In addition to Self-Attention, SAGAN introduces spectrum normalization to stabilize the training of the model and avoid abnormal gradients. Compared with other normalization techniques, spectrum normalization does not require additional hyper parameter adjustment, and has a relatively low computational cost.

Leveraging the strengths of SAGAN in image generation, we use SAGAN as the data augmentation method to solve the problem of insufficient fault samples. The schematic diagram of the generator and discriminator structure is shown in Figs. 5 and 6, respectively. The generator G starts with a uniform distribution noise variable Z, which is projected and reshaped into a convolutional feature map representation. Then, time–frequency image samples of size (63, 64, 3) are generated through a five-layer transposed convolution operation. Each layer of the transposed convolution has a kernel size of 4 and a stride of 2, with channel counts of 512, 256, 128, 64, and 3 respectively. The first four layers of transposed convolution are processed by using spectrum normalization and the ReLU activation function. From the 3rd to the 4th layers of convolution, the attention mechanism is used to obtain the global dependencies. The activation function of the fifth layer is the Tanh function. In the discriminator D, there are five convolution layers with a convolution kernel size of 4, a stride of 2, and channel counts of 64, 128, 256, 512, and 1, respectively. After each convolution, spectrum normalization and the LeakyReLU activation function are applied. During the SAGAN training, model parameters are updated iteratively based on the aforementioned loss function. The batch size is set at 16. The RMSprop optimizer is used with a learning rate of 0.0005 for both the generator and discriminator, which are alternately trained until convergence.

Fig. 5

The architecture of the generator.

Fig. 6

The architecture of the discriminator.

Fault diagnosis based on IResNet

Convolutional neural networks can effectively capture local information of images through convolutional operations, but visual tasks require establishing long-distance dependencies. In order to globally aggregate the responses from locally captured filters, the network structure needs to be stacked with multiple layers. However, increasing the number of layers can lead to issues such as gradient dispersion or explosion, and network degradation, which seriously impacts the accuracy of the model. In order to solve the above problems, we improve the residual network by integrating the Multi-head Self-Attention mechanism (with 4 heads) into the residual network structure. The residual network deepens the network layers through residual learning, enabling it to obtain deep features, and alleviate the problem of network degradation caused by high network layers in convolutional neural networks. The Multi-head Self-Attention mechanism facilitates the capture of long-distance dependency relationships and global features of images by processing and aggregating feature information captured through convolution. This hybrid design is beneficial for improving the ability of key feature extraction in the model, thus achieving network control of global information, improving the accuracy of bearing fault diagnosis under conditions of strong noise and variable loads.

As illustrated in Fig. 7, the Multi-head Self-Attention mechanism (MHA) replaces the traditional convolution (3 × 3) operation within the residual network to achieve global Self-Attention on the 2D feature map. By improving the residual network module, the long-distance dependence and global feature information are obtained, and the problems of gradient dispersion and network degradation are also solved.

Fig. 7

The structure of IResNet.

The improved residual formula is as follows:

$$H(x)^{*} { = }MultiHead(Q_{i}^{*} ,K_{i}^{*} ,V_{i}^{*} ) + x,i = 1,2,3,...,h$$

(17)

In the formula: $x$ is the input data, $x^{*}$ is the output of the input data after convolution, $h$ is the number of heads of the Self-Attention mechanism,$Q_{i}^{*}$,$K_{i}^{*}$,$V_{i}^{*}$ are the matrices obtained by linear transformation of the data $x^{*}$.The obtained matrix is input into the Multi-head Self-Attention mechanism function to obtain the Self-Attention representation of the input data. Finally, the input and output are added element by element through the jump connection.

The bearing fault diagnosis model based on IResNet is mainly composed of convolution layers, pooling layers, improved residual block A, block B, and fully-connected layers. The network structure is shown in Fig. 8. Firstly, after two stages of convolution and maximum pooling operations, the convolution operation can effectively learn abstract and low-resolution features from the image, while maximum pooling retains the main features of the data and removes redundant information. Subsequently, the improved residual modules block A and block B deepen the number of network layers. Additionally, the Multi-head Self-Attention mechanism is introduced into the residual network, which not only avoids issues such as gradient dispersion, gradient explosion, and network degradation caused by the increased depth of network layers, but also enables the network to acquire global features and long-range dependencies efficiently. Finally, dropout is also incorporated between the two fully-connected to enhance the generalization ability and prevent overfitting, and the Softmax layer is used as a classifier to facilitate fault diagnosis. The fault diagnosis model is trained using a batch size of 32 and over 30 epochs. Cross-entropy loss is utilized as the error loss function, with Adam as the optimizer. The learning rate is set at 0.001. The learning rate attenuation mechanism is employed to fine-tune the learning rate, optimize training effectiveness, and minimize training costs. The model parameter settings are shown in Table 1.

Fig. 8

The structure of bearing fault diagnosis model based on IResNet.

Table 1 Model parameter settings of IResNet.

Experimental verification

To verify the effectiveness and superiority of the method proposed in this paper, experimental verification has been carried out for two bearing datasets: the bearing dataset of Case Western Reserve University⁴⁰, the bearing dataset of Southeast University⁴¹ and the bearing dataset of Jiangnan University⁴².

Case 1: CWRU bearing dataset

Experiment setup and data preprocess

The experimental dataset was sourced from the Case Western Reserve University (CWRU) Bearing Data Center. The experimental equipment is shown in Fig. 9, and the test bench is composed of a motor, rolling bearings, a torque transducer, and a dynamometer⁴⁰. The test bearing model are SKF6205 motor bearings. Faults in the bearing, including the inner ring (IR), outer ring (OR), and ball (BD), have been machined through Electrical Discharge Machining (EDM). The fault diameters are 0.1778 mm, 0.3556 mm, and 0.5334 mm for each kind of fault bearing, respectively. During the experiments, the motor was subjected to various load conditions: 0HP, 1HP, 2HP and 3HP, the sampling frequency was set at 12 kHz.

Fig. 9

CWRU rolling bearing experimental platform by⁴⁰.

The signal is intercepted by overlapping sampling. The overlapping sampling operation formula is as follows:

$$N = \frac{{L - L_{1} }}{d} + 1$$

(18)

where $N$ is the total number of one-class samples, $L$ is the total length of the one-dimensional signal, $L_{1}$ is the length of each signal segment, and $d$ is the step length determining the degree of overlap between consecutive segments. The statistics of the dataset are described in Table 2. The dataset contains 10 fault categories, and the number of data samples for each fault category is 1000, including 800 training samples, 100 validation samples, and 100 test samples. Additionally, the number of data points for each data sample is 1024.

Table 2 The experiment dataset.

The original vibration signal is converted into a two-dimensional time–frequency diagram by CWT, and the results are shown in Fig. 10. After CWT, the time–frequency domain characteristics of the signal are fully obtained, which is conducive to subsequent data expansion and fault diagnosis processes.

Fig. 10

1D vibration signals are converted into 2D time–frequency images.

Experimental environment and training parameter configuration

The experiments were conducted on a Windows 10 operating system with a Tesla T4 GPU, utilizing the PyTorch deep learning framework. During training, the input image resolution was set to 64 × 64, with a batch size of 32 and 30 training epochs. The initial learning rate was 0.001, and the cross-entropy loss function was employed as the optimization objective. The Adam optimizer was adopted, coupled with StepLR scheduler to dynamically adjust the learning rate: the learning rate was halved every 10 epochs.

Data generation experiment based on SAGAN

In this experiment, the data generation method based on SAGAN is combined with a traditional CNN fault diagnosis model to explore the impact of synthetic sample generation on the accuracy of bearing fault diagnosis.

Figure 11 displays the sample images generated by SAGAN of different fault types at the training epochs of 50, 100, and 300. Initially, at 50 epochs, image backgrounds were blurry and clarity was inconsistent. By 100 epochs, some features of the time–frequency image were roughly represented, though the background clarity still required improvement. At 300 epochs, the image clarity is high, and the generated samples and the original samples have similar feature distributions, but there are still slight differences because the generated samples are obtained by the model learning and training from real samples, not merely simple image replication. Based on these observations, the training epoch count for SAGAN is set at 300 for optimal image quality.

Fig. 11

Generated images of different training epochs.

The generated images by various Generative Adversarial Networks (GANs) are shown in Fig. 12. From the figure, it can be observed that the basic outline of the original samples can be learned by GAN, but the generated samples exhibit significant differences from the real samples. With DCGAN, the similarity between the generated samples and the real samples improves compared to GAN, but the images appear blurry, indicating insufficient learning of fault features. In contrast, SAGAN generates images that are more similar to the original ones, capturing most of the original sample’s features. This improvement demonstrates that incorporating the Self-Attention mechanism significantly enhances the model’s capability to learn global feature information.

Fig. 12

Comparison of generated images of different models.

In the sample generation task, Pearson correlation coefficient is often used to detect the quality of sample generation. This coefficient measures the linear relationship between two variables; a coefficient close to 1 indicates a strong linear relationship. The Pearson correlation coefficient is used to analyze the correlation between the generated sample and the original sample. The analysis results are shown in Fig. 13. The analysis illustrates that SAGAN’s sample generation capabilities are substantially superior to those of both standard GAN and DCGAN, highlighting its effectiveness in producing high-quality, realistic samples.

Fig. 13

Comparison of image correlation coefficients.

In order to verify the influence of the number of generated images on the accuracy of bearing fault diagnosis, the experiment is divided into three categories: the first category does not perform data expansion, and only uses the original data for model training (experiment 1); the second category only uses the generated data for training (experiment 2–7); the third category uses data expansion to combine the original data with the generated data to jointly train the model (experiment 8–13). The experimental results are shown in Table 3. It can be seen from the table that when the original data and the generated data are combined, the diagnostic accuracy is significantly improved. Notably, there is a clear trend showing that accuracy increases as more generated images are added to the training dataset. Specifically, when 6000 generated images are added to 8000 original samples, the accuracy rate reaches 100%. Based on these findings, subsequent experiments were conducted based on the original sample size of 8000 and the generated sample size of 6000 to further validate the benefits of this approach.

Table 3 Accuracy of diagnosis comparison under different datasets.

The generated data and the original data are used as the input of the CNN fault diagnosis model to train the network. The training process is shown in Fig. 14. It can be seen from the figure that after data expansion, the convergence speed of model training is obviously accelerated and the convergence is more stable. Therefore, using data generation technology to train the model by combining real data with generated data can significantly improve the stability of model training and the accuracy of bearing fault diagnosis.

Fig. 14

The influence of data expansion on model accuracy and loss.

The influence of network depth on diagnostic accuracy

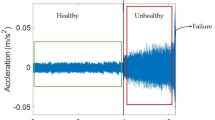
In actual industrial production, bearing environments are typically intricate, and signals collected are often compromised by different types of noise. Therefore, varying degrees of Gaussian white noise are added to the original signal to simulate noise pollution in the industrial environment. The signal-to-noise ratio (SNR) serves as a benchmark for assessing noise intensity, which is defined as follows:

$$SNR_{dB} = 10\log_{10} \left( {\frac{{P_{signal} }}{{P_{noise} }}} \right)$$

(19)

where $P_{signal}$ and $P_{noise}$ are the power of the signal and the noise, respectively. The more noise contained in the signal, the smaller the SNR value. At 0 dB SNR, signal and noise energy are equal.

While theoretically, deeper network layers can lead to higher model accuracy, they also increase the complexity and training time of the model. To find a balance between fault diagnosis accuracy, network complexity, and model training time, this paper proposes four different depths of improved residual network structures combined with traditional CNN, referred to as CNN, CNNI, CNNII, CNNIII, and CNNIV when the number of IResNet modules is 0, 1, 2, 3 and 4, respectively. To minimize the influence of random factors on experimental results, the final accuracy of each model is the average of 5 repeated experimental runs, as shown in Fig. 15. It can be seen that CNNI, with one IResNet module, significantly improves the performance of bearing fault diagnosis in noisy environments compared to the basic CNN. However, as the network depth increases further, the gains in diagnostic accuracy diminish progressively, suggesting a diminishing return on deeper configurations. This pattern underscores the importance of striking an optimal balance when designing network architectures for practical applications, particularly in settings characterized by significant noise interference.

Fig. 15

Recognition accuracy of different depth networks in noisy environment.

To provide a clearer understanding of how network depth affects fault diagnosis accuracy and training time, Fig. 16 shows the experimental results and average training time of these four different depth models across various noise environments (SNR levels of – 8, – 6, and – 4). As the network depth increases, the model training time increases, but the bearing fault diagnosis performance reaches its peak with CNNIII when the number of IResNet modules stacked on the model is 3. On the basis of the comprehensive analysis of model accuracy and training time, it is determined to use an improved residual network stacked with three IResNet modules for effective bearing fault diagnosis.

Fig. 16

Comparison of model accuracy and training time.

The influence of the number of heads on diagnostic accuracy

In order to verify the influence of the number of heads of the Multi-head Self-Attention on the performance of the model, this section adds the verification experiment of the number of heads, and sets the number of heads of the Multi-head Self-Attention to 1, 2, 3, 4, 8 respectively. The experimental results are shown in Fig. 17. From the graph, as the number of heads increases from 1 to 4, the diagnostic performance of the model under different signal-to-noise ratios is systematically improved. However, when the number of heads is increased to 8, the performance of the model decreases, and the noise robustness of the model is optimal when the number of heads is 4. Based on this, this paper finally chooses 4-head attention mechanism as the core module of SAGAN_IResNet.

Fig. 17

Recognition accuracy of different heads in noisy environment.

The training and validation curves of the proposed method are illustrated in Fig. 18. As depicted, the diagnostic accuracy exhibits rapid growth during the initial training phase. When the epoch reaches 5–15, minor fluctuations emerge in the training accuracy, likely attributed to the model’s exploration of optimal feature representations. Beyond 15 epochs, both training and validation accuracies stabilize, indicating effective convergence and sufficient model training.

Fig. 18

The model training and validation curves of SAGAN_IResNet.

Performance comparison under noise environment

This section aims to evaluate the robustness of the proposed method in noisy environments. To simulate bearing vibration signals acquired in noisy environments, Gaussian white noise with signal-to-noise ratios (SNRs) ranging from – 8 dB to 6 dB is added to the original vibration signals. The proposed method is compared with SVM, MLP, DRL_ResNet⁴³, SECNN²², DFCNN⁴⁴, Improved ResNet⁴⁵, CNN-LSTM-Attention⁴⁶, CNN, and SAGAN_CNN. Among them, CNN is a bearing fault diagnosis model based on convolutional neural networks. SAGAN_CNN first uses SAGAN to generate sample data, increase the number of samples, and then uses the CNN model to achieve fault diagnosis. In order to reduce the influence of random factors, the final result of each method is the average of five repeated experimental results, as shown in Fig. 19. As the noise intensity increases, the average recognition accuracy of all diagnostic algorithms decreases, but there are significant differences in the magnitude of the decrease among different algorithms. The average accuracy of the proposed method in a strong noise environment reaches 97.13%, which improved by 11.7%, 14.86%, 3.32%, 0.97%, 0.51%, 1.56%, 0.73%, 4.45%, and 4.21% compared to the other methods, respectively. By improving the residual network and introducing the Multi-head Self-Attention mechanism, the model can learn sample features to the maximum extent, reduce noise interference, enhance network robustness, and improve the accuracy of bearing fault diagnosis.

Fig. 19

The average accuracy of different models in noisy environment.

To ensure that the proposed method does not excessively favor the identification of a single fault type, the confusion matrix is used to analyze the classification results of the test set. According to Fig. 20a, at an SNR of 6, the accuracy of the test set reaches 99.9%. There is only one instance where a sample labeled B021 is misdiagnosed as B007. Although the specific fault scale identification is incorrect, the misdiagnosed sample still falls within the category of rolling element fault. It can be seen from Fig. 20b that in the high noise environment with an SNR of – 8, the overall diagnostic accuracy of this method is higher at over 86%, indicating strong robustness.

Fig. 20

Confusion matrix of diagnostic results in different noise environments.

Furthermore, t-SNE technology is used to reduce the dimensionality of high-dimensional features and realize the visualization of feature vectors⁴⁷. Figure 21a is the visualization result of the convolutional feature t-SNE at the second layer. The data overlap and mix with each other indicate a poor clustering effect at this stage of the model. In contrast, Fig. 21b is the result of feature visualization of the last layer of IResNet module. All samples have been basically divided into ten distinct categories. The clear aggregation effect of each sample group demonstrates that the improved residual neural network, with the integration of Multi-head Self-Attention, can maximize the learning of sample features and significantly enhance the fault diagnosis performance of the model. These visualizations effectively illustrate how the model evolves to better discriminate between different fault types as it processes through its layers, culminating in a highly effective fault classification by the final layer.

Fig. 21

Visualization of feature vectors at different positions.

Performance comparison across different load domains

In actual industrial environments, the load conditions of bearings are variable, which requires fault diagnosis methods to have high generalization performance. To assess the generalization capabilities of the proposed method, it was compared against several established models: SVM, MLP, SECNN, DRL_ResNet, DFCNN, Improved ResNet, CNN-LSTM-Attention, CNN and SAGAN_CNN. The fault diagnosis results of each method under variable load conditions are shown in Fig. 22. The analysis reveals that SVM and MLP exhibit lower accuracy in bearing fault diagnosis under variable load conditions, which points to their poor generalization capabilities. In contrast, the proposed method in this paper achieves an average accuracy of 93.69%. This represents performance improvements of 2.73%, 1.22%, 4.16%, 2.84%, 3.54%, 2.88% and 1.9% over SECNN, DRL_ResNet, DFCNN, Improved ResNet, CNN-LSTM-Attention, CNN, and SAGAN_CNN respectively. The proposed method exhibits the strong generalization capability and is suitable for bearing fault diagnosis in environments with variable loads.

Fig. 22

The average accuracy of different models in the variable load domain.

Case 2: Southeast university gearbox dataset

Experiment setup and data preprocessing

The gear data set of Southeast University comes from the open source data of Southeast University. The test bench is composed of a variable speed motor, motor controller, planetary gearbox, parallel shaft gearbox, brake, and brake controller⁴¹. The vibration signal is measured by a driveline dynamic simulator (DDS). The fault types are divided into five types: normal, ball fault, comb fault, inner ring fault and outer ring fault. These fault types are artificially set in the laboratory and can simulate the basic faults in the machinery. Regarding the operational parameters of the equipment, the speed-load settings vary between 20 Hz at 0 V and 30 Hz at 2 V.

The data is processed using overlapping sampling, with each fault category represented by 1,000 single-class samples, each with a signal segment length of 1,024. The dataset is organized into training, validation, and test sets with a distribution ratio of 8:1:1. This allocation is detailed in Table 4, which provides a statistical description of the dataset. The vibration signal is converted into a time–frequency image using CWT, and the results are shown in Fig. 23.

Table 4 The experiment dataset of Southeast University.

Fig. 23

Time–frequency images of ten fault categories.

Experimental results and performance comparison

The 8000 original training samples and 6000 pseudo-samples are used to train the classification model. To mitigate the effects of anomalies and ensure the robustness of the results, each experiment was conducted five times. The average accuracy from these trials was computed and compared with that achieved by the improved method. The findings are presented in Fig. 24, which clearly shows that the SAGAN_IResNet method yields the highest accuracy among the tested approaches. By improving the fault classification model, the residual network is combined with the Multi-head Self-Attention mechanism to learn the sample features to the greatest extent, and the model performance is optimized as much as possible.

Fig. 24

Classification accuracy of the five trials in testing samples.

The detailed performance comparison of different diagnostic methods in a noisy environment is shown in Fig. 25. As can be seen from the figure, the method proposed in this paper demonstrates excellent robustness and anti-interference performance. When the signal-to-noise ratio (SNR) is 2, the fault diagnosis accuracy of this method reaches as high as 97.2%. Compared with other methods, there is a significant improvement in accuracy, which fully demonstrates its outstanding advantages and application value in a noisy environment.

Fig. 25

The average accuracy of different models in noisy environment.

Displayed in Fig. 26 is the comprehensive confusion matrix for the SAGAN_IResNet model under SNR conditions of 0 and 6. Notably, at an SNR of 0, this method yields an impressive average fault diagnosis rate of 95%. Similarly, under an SNR of 6, the model’s fault accuracy reaches 98.42%, showcasing its ability to adeptly learn fault features and accurately identify health statuses.

Fig. 26

Confusion matrix of diagnostic results in different noise environments.

The fault feature learning results of the proposed method are shown in Fig. 27, which showcases the effects of increasing network depth on the classification of fault features. Initially, after CNN layer feature extraction, the results are visualized in Fig. 27a, the samples have a tendency to aggregate, but the clustering effect remains suboptimal, indicating some overlap and unclear boundaries between different fault categories. By superimposing the IResNet module, the number of network layers is gradually deepened, as shown in Fig. 27b, which significantly expands the distribution distance of fault features among different health conditions and makes the feature classification boundary clear and distinguishable.

Fig. 27

Visualization of feature vectors at different positions.

Case 3: Jiangnan university bearing dataset

Experiment setup and data preprocessing

To verify the universality of the method proposed in this paper, the bearing dataset of Jiangnan University is used for verification⁴². This data was collected under the conditions of a sampling frequency of 50 kHz and rotation speeds of 600 r/min, 800 r/min, and 1000 r/min. The bearing dataset with a frequency of 50 kHz and a rotation speed of 800 r/min is adopted as the experimental data. According to the fault location, the bearing data is divided into four states: normal (N), inner ring (IR), outer ring (OR), and rolling element (TB). The signals are intercepted by means of overlapping sampling. The number of samples of a single class is 1000, and the signal length is 1024. The ratio of the training set, verification set, and test set is 8:1:1. The parameters of the experimental dataset are shown in Table 5. The image of each type of fault signal after continuous wavelet transform is shown in Fig. 28.

Table 5 The experiment dataset of Jiangnan University.

Fig. 28

Time–frequency images of four fault categories.

Experimental results and performance comparison

To verify the effectiveness of the proposed method, a comparative experiment was conducted between SAGAN_IResNet and the method before the improvement. The experimental results are shown in Fig. 29. It can be seen from the figure that the traditional convolutional neural network (CNN) performs poorly in terms of fault diagnosis performance. However, after the introduction of the sample generation technology, the bearing fault diagnosis performance has significantly improved. It is worth noting that the method proposed in this paper performs the best in terms of fault diagnosis performance, fully demonstrating its remarkable advantages in improving the accuracy and reliability of fault diagnosis.

Fig. 29

Classification accuracy of the five trials in testing samples.

The model proposed in this paper was respectively compared with SVM, MLP, DRL_ResNe, SECNN, DFCNN, Improved ResNet, CNN-LSTM-Attention, CNN, and SAGAN_CNN in comparative tests under noise conditions, and the results are shown in the Fig. 30. It can be seen from the figure that the method proposed in this paper has stronger noise resistance and practicality compared with other models.

Fig. 30

The average accuracy of different models in noisy environment.

According to the speed, the data is divided into three loads of 0, 1 and 2 to carry out the model variable load comparison experiment. The proposed method is compared with SVM, MLP, DRL_ResNet, SECNN, DFCNN, Improved ResNet, CNN-LSTM-Attention, CNN, and SAGAN_CNN, respectively. The experimental results are shown in the Fig. 31. It can be seen from the figure that the method proposed in this paper has high accuracy of bearing fault diagnosis under variable load and good generalization performance of the model.

Fig. 31

The average accuracy of different models in noisy environment.

Conclusion

In this paper, an intelligent bearing fault diagnosis method named SAGAN_IResNet is proposed to overcome challenges in feature extraction and insufficient bearing fault data in complex industrial environments. The main conclusions of this study are as follows:

• (1) SAGAN is utilized to generate high-quality bearing fault data, effectively addressing the issue of insufficient fault diagnosis datasets. The proposed data enhancement method demonstrates notable applicability, leading to a significant improvement in the accuracy of bearing diagnosis after data enhancement.

• (2) An improved residual network (IResNet) is used to construct the bearing fault diagnosis model, combining a Multi-head Self-Attention mechanism with the residual network to solve the problems related to gradient dispersion and network degradation. The method enables adaptive acquisition of long-distance correlation and global feature information, resulting in an average fault diagnosis accuracy of 97.13% in strong noise environments. This performance marks a 4.21% increase compared to SAGAN_CNN, showing strong robustness.

• (3) The experimental results under variable load conditions have underscored the efficacy of the proposed bearing fault diagnosis method, which achieves an accuracy rate of 94.14%. This performance not only demonstrates the method’s robustness but also its superior generalization capabilities when compared to other fault diagnosis models.

In summary, the proposed method stands out due to its ability to generate high-quality bearing fault data, effectively address the challenge of insufficient samples, and maintain robust performance under conditions of strong noise and variable loads. These attributes make it highly suitable for practical applications in bearing fault diagnosis. By integrating advanced data generation techniques and leveraging a sophisticated model architecture that includes improved residual networks and Multi-head Self-Attention, the method enhances the accuracy and reliability of fault detection in real-world industrial settings. Although the research in this paper has achieved certain results, in order to further promote its implementation in industrial scenarios, the authors will further explore the adaptability of the model proposed in this paper in online learning scenarios to cope with new fault modes or load conditions that may arise in bearing fault diagnosis; at the same time, we will further study the embedded deployment of this model in real-time monitoring systems to achieve faster and more accurate fault detection and early warning.