Introduction

MT sounding is widely applied in geophysical exploration–including crustal imaging, geothermal exploration, and oil-gas prospecting–due to its low cost, deep penetration, and strong structural reflectivity1,2,3,4. At the core of MT data interpretation lies forward modeling, which simulates electromagnetic responses of geoelectric models–a process fundamental to iterative inversion algorithms that refine subsurface structures to match observed data.

In the field of MT forward modeling, traditional numerical methods such as the finite difference method (FDM), finite element method (FEM), and integral equation method (IEM) have long played a dominant role. Among them, the application of FDM in geophysics dates back to the 1960s5, and it is mainly used to calculate the resistivity of geoelectric models6,7,8. The IEM, on the other hand, is more suitable for forward modeling in complex media scenarios9. In contrast, the FEM stands out as a widely applied and technically mature approach in current MT sounding. Since its introduction into electromagnetic forward modeling in the 1970s, researchers have improved the FEM based on general grid meshing, enhancing computational accuracy, speed, and the method’s applicability10. Later studies further explored its forward response characteristics by performing numerical simulations of 2D topography using rectangular element triangulation based on FEM11.

Recent research has focused on enhancing the accuracy and efficiency of MT forward simulation. Approaches include leveraging advanced hardware12,13 and developing novel algorithms14,15,16. For instance, a multilevel downsampling FDM algorithm has been introduced to accelerate forward simulation of electric fields17, while hybrid solvers combining FEM and IEM have been developed to speed up forward modeling computations18. These innovations have enhanced the efficiency of forward modeling to varying degrees.

Notwithstanding their capability to compute precise theoretical field values, traditional numerical methods remain constrained by the number of discrete grid elements in the model, resulting in relatively low computational efficiency. In recent years, the geophysical data processing community has made significant progress in addressing numerical simulation challenges through big data and artificial intelligence. Deep learning (DL)-based approaches have emerged as a prominent solution, employing data driven strategies to derive simulation solutions. Specifically, these methods train multi dimensional networks of weights and biases using input data and corresponding labels (outputs) to minimize loss functions.

In recent years, dl neural networks have been increasingly applied to geophysical inversion tasks. For example, dl neural networks have been used to achieve 2D resistivity inversion for direct current methods19. A back propagation neural network model optimized by a genetic algorithm has been developed for 2D inversion of MT data20. Convolutional neural networks (CNNs) have been employed to perform 2D inversion of electromagnetic data transmitted by vertical magnetic dipole sources in wells and received at the surface21. Dl techniques have also been applied to 1D inversion of marine frequency-domain controlled-source electromagnetic data, as well as 1D inversion of frequency-domain airborne electromagnetic data using CNNs22.

In contrast, the application of neural networks in geophysical forward modeling remains relatively limited. Early studies utilized artificial neural networks (ANNs) for MT forward modeling, followed by iterative inversion using a traditional covariance matrix adaptive evolution strategy to optimize results from the neural network. This approach demonstrated that MT forward modeling results computed by neural networks can be used for geoelectric model inversion, effectively addressing the problem of anomaly location mismatch in MT forward simulation. CNN-based methods have surpassed traditional statistical models in computer vision tasks, particularly in segmentation23,24. The Transformer model, quickly gained popularity in the domain of natural language processing (NLP) due to its ability to capture the entire sequence of arrays without losing valuable information, unlike recurrent neural networks (RNNs). In recent years, Transformer architectures have expanded to computer vision, achieving notable results in object detection, image classification, and segmentation25,26. Combining Transformer’s global dependency modeling with other methods often yields more robust and efficient outcomes.

While CNNs excel at capturing local features in image analysis, they may struggle with global context. Transformers, though powerful for global dependency modeling in NLP, require substantial computational resources and face convergence challenges with small datasets. To address these limitations and leverage complementary strengths, researchers have integrated CNN and Transformer architectures. This hybrid approach has proven effective in various segmentation tasks by combining local and global features to enhance performance27.

Inspired by this framework, we propose enhancing the classic U-Net segmentation network28 with Transformer layers to create an end-to-end image semantic segmentation network. Following the methodology outlined, we incorporate Transformer layers to directly process input data and decode outputs. Specifically, our T-Unet network concatenates feature maps from Transformer and CNN branches in the decoder, enabling effective capture of both local and global information. Experimental results demonstrate that the T-Unet framework significantly improves the accuracy and efficiency of MT forward modeling. This validates the effectiveness of our proposed approach.

Method

T-Unet model

Before introducing the implementation of MT forward response using T-Unet, a brief introduction to the traditional FEM forward modeling is provided here, taking transverse magnetic (TM) polarization as an example:

$$\begin{aligned} & {\frac{\partial }{{\partial y}}\left( {\rho \frac{{\partial {H_x}}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\rho \frac{{\partial {H_x}}}{{\partial z}}} \right) = - i\omega \mu {H_x}} \end{aligned}$$
(1)

In this context, \(\rho\) denotes the subsurface resistivity, \(H_x\) represents the magnetic field component in the \(x\)-direction, \(\omega\) is the angular frequency, and \(\mu\) signifies magnetic permeability. By employing the FEM and a specific type of boundary conditions, these equations can be converted into a problem of solving a large complex sparse matrix:

$$\begin{aligned} & {{H_x}{|_{z = 0}} = 1} \end{aligned}$$
(2)
$$\begin{aligned} & \mathbf {A{H_x} = b} \end{aligned}$$
(3)

Here, \(\textbf{A}\) represents a large-scale complex sparse matrix, \(\mathbf {H_x}\) denotes the horizontal magnetic field vector to be solved, and \(\textbf{b}\) is the right-hand side term.

Through solving Eq. (3) and leveraging its relationship with the electric field, the apparent resistivity \(\rho _a^{\text {TM}}\) and phase \(\phi ^{\text {TM}}\) at any frequency for a measurement point can be obtained as:

$$\begin{aligned} {\rho _a^{TM} = \frac{1}{{\omega \mu }}{\left| {\frac{{{E_y}}}{{{H_x}}}} \right| ^2}} \end{aligned}$$
(4)
$$\begin{aligned} {\phi _{}^{TM} = \arctan \left( {\frac{{{\mathop {\textrm{Im}}\nolimits } ({E_y}/{H_x})}}{{Re({E_y}/{H_x})}}} \right) } \end{aligned}$$
(5)

Where \(E_y\) represents the electric field component in the \(y\)-direction.

$$\begin{aligned} {E_y} = \rho \frac{{{H_{{x_z}}} - {H_{{x_{z - 1}}}}}}{{\Delta z}} \end{aligned}$$
(6)
Fig. 1
figure 1

The architecture of the proposed forward modeling based on multitask T-Unet.

Full size image

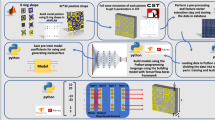
In summary, the apparent resistivity dataset and phase dataset are generated using FEM based on Eqs. (4) and (5), and then subjected to multitask training with T-Unet29. The architectural diagram of the T-Unet multitask framework is shown in Fig. 1. During the training phase, two distinct loss functions are employed to optimize the loss of the magnetotelluric forward neural network model. Specifically, for the model mismatch term, a multitask loss function is adopted, denoted as \(\ell _{\text {mt}}\).

The loss function for apparent resistivity, denoted as \(\ell _{\rho _a}\), can be expressed by the following formula:

$$\begin{aligned} \ell _{\rho _a} = \frac{1}{T \cdot H \cdot L} \sum _{t=1}^{T} \sum _{i=1}^{H} \sum _{j=1}^{L} \left( \hat{\rho }_a^{(t,i,j)} - \rho _a^{(t,i,j)} \right) ^2 \end{aligned}$$

Where \(T\) represents the number of training samples; \(H\) and \(L\) denote the two-dimensional size of the resistivity model matrix; \(\rho _a\) is the apparent resistivity; \(\hat{\rho }_a\) signifies the predicted apparent resistivity data; and \(\rho _a\) represents the labeled apparent resistivity data.

The loss function for phase, denoted as \(\ell _{\varphi }\), is formulated as:

$$\begin{aligned} \ell _{\varphi } = \frac{1}{T \cdot H \cdot L} \sum _{t=1}^{T} \sum _{i=1}^{H} \sum _{j=1}^{L} \left( \hat{\varphi }^{(t,i,j)} - \varphi ^{(t,i,j)} \right) ^2 \end{aligned}$$

Where \(\hat{\varphi }\) is the predicted phase, \(\varphi\) is the labeled phase data, and the other parameters are consistent with those defined above.

The multitask loss function is given by:

$$\begin{aligned} \ell _{\text {mt}} =\alpha \cdot \ell _{\rho _a} + \beta \cdot \ell _{\varphi } \end{aligned}$$

Here, the weights for both the apparent resistivity loss function (\(\alpha\)) and the phase loss function (\(\beta\)) are set to 0.5.

These two quantified loss functions measure the discrepancy between the predicted forward responses (apparent resistivity and phase) and the true forward responses (observed resistivity and phase). By minimizing these losses, the network is forced to closely match the predicted forward response data with the labeled data, thereby enhancing the network’s capability to learn characteristic features.

Fig. 2
figure 2

Example of the generated composite resistivity model and its corresponding TM-mode apparent resistivity and phase.

Full size image
Fig. 3
figure 3

MSE loss function curves of Unet and T-Unet.

Full size image

Experiments and results

Dataset preparation

Before engaging in multitask network learning, the creation of sample datasets represents a critical step in generating neural network models. Considering the volume effect, the gradual variation of subsurface resistivity structures is a primary characteristic attribute. The designed models are no longer simple anomaly bodies or horizontal high-low resistivity models; instead, resistivity model sets are generated through cubic spline interpolation, where resistivity values in the dataset evolve gradually within randomly composite resistivity models. The objective is to establish a training dataset that closely aligns with actual subsurface models, ensuring its effective applicability in real-world measurement environments. Meanwhile, to demonstrate the practical utility of the forward simulation neural network model, random noise ranging from 0% to 5% is added to the resistivity model data.

In the synthetic model designed in this paper, the resistivity model was sized at 5 km \(\times\) 3 km, with \(H\) set to 32 (representing the number of frequencies) in the range of 0.05 to 320 Hz, and \(L\) also set to 32 (representing the number of observation points) , the resistivity value range is 0.1-100000 \({\Omega }\). m. For different tasks, new dataset creation can be achieved simply by adjusting the model size and parameters \(H\) and \(L\). A total of 20,000 sample data points were created in this study, with 80% allocated for training, 10% for validation, and the remaining 10% reserved for testing. Figure 2 shows the designed resistivity models and corresponding examples of apparent resistivity and phase.

Normalization in neural networks is crucial for stabilizing the training process, as it helps maintain the stability of input distributions, particularly in deep neural networks. This stability accelerates the convergence of the network by mitigating the problems of gradient vanishing and explosion, while enhancing the stability of weight adjustments. Additionally, normalization helps limit the input range, preventing gradient explosion and improving the generalization ability of the neural network, enabling it to perform better on data with different scales and distributions. Furthermore, normalization can reduce the sensitivity to the selection of initial weights and learning rates, and adjust the inputs to activation functions to ensure they operate within sensitive regions. Therefore, when processing geoelectric model data and apparent resistivity data, we first take the base-10 logarithm of these data. Since the range of impedance phase data is relatively small, the impedance phase data remain unchanged. Subsequently, we calculate the maximum and minimum values of the inputs and outputs in the dataset. The actual values are mapped to the range [0,1] using Eq. (7), i.e., the value of . For impedance phase, the \({\log }_{10}\) in Eq. (7) is removed, as shown in Eq. (8).

$$\begin{aligned} & Y = \frac{{{{\log }_{10}}X - \min }}{{\max - \min }} \end{aligned}$$
(7)
$$\begin{aligned} & Y = \frac{{X - \min }}{{\max - \min }} \end{aligned}$$
(8)

For the output of the neural network predicting the forward response, the forward response values need to be inverse-mapped. The inverse mapping formula for apparent resistivity is as follows:

$$\begin{aligned} x' = {10^{(\max - \min ) \times y' + \min }} \end{aligned}$$
(9)

where \(\mathrm{{x'}}\) is the predicted value of the true apparent resistivity, and \(\mathrm{{y'}}\) is the predicted value of the neural network. The inverse mapping formula for impedance phase is as follows:

$$\begin{aligned} x' = (\max - \min )y' + \min \end{aligned}$$
(10)

where \(\mathrm{{x'}}\) is the predicted value of the true impedance phase, and \(\mathrm{{y'}}\) is the predicted value of the neural network for impedance phase.

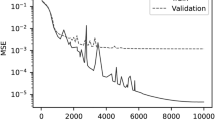
During training, the sigmoid function was used as the activation function30, MSE loss served as the loss function31 and the Adam optimizer was employed to optimize the parameters of the T-Unet model32. The learning rate was set to 0.001, the batch size to 10, and the number of training epochs to 100. The loss function curve is shown in Fig. 3.

$$\begin{aligned} {MSE = \frac{{{{\sum \limits _{i = 1}^H {\sum \limits _{j = 1}^L {|{T_{i,j}} - {P_{i,j}}|} } }^2}}}{{H \times L}}} \end{aligned}$$
(11)

where H and L represent the length and width of the input data dimension, respectively, and T and P represent the calculation results at (i, j) and the prediction results of the neural network model respectively.

Noise free model experiment

Fig. 4
figure 4

Comparison of apparent resistivity of different methods without noise. The first column is the designed resistivity model, the second column is the apparent resistivity calculated by FEM, the third column is the apparent resistivity simulated by T-Unet, and the fourth column is the apparent resistivity simulated by T-Unet. The fifth column shows the relative error distribution of apparent resistivity between FEM and Unet method, which is recorded as RE Unet. The sixth column shows the relative error distribution of apparent resistivity between FEM and T-Unet method, which is recorded as RE T-Unet.

Full size image
Fig. 5
figure 5

Comparison of phase of different methods without noise. The first column is the designed resistivity model, the second column is the phase calculated by FEM, the third column is the phase simulated by T-Unet, and the fourth column is the phase simulated by T-Unet. The fifth column shows the relative error distribution of phase between FEM and Unet method, which is recorded as RE Unet. The sixth column shows the relative error distribution of phase between FEM and T-Unet method, which is recorded as RE T-Unet.

Full size image
Table 1 Quantitative evaluation metrics for the forward prediction methods of Unet and T-Unet under without noise.
Full size table
Fig. 6
figure 6

Comparison of apparent resistivity of different methods with noise. The first column is the designed resistivity model, the second column is the apparent resistivity calculated by FEM, and the third column is the apparent resistivity simulated by T-Unet. The fourth column shows the relative error distribution of apparent resistivity between FEM and T-Unet method.

Full size image
Fig. 7
figure 7

Comparison of phase of different methods with noise. The first column is the designed resistivity model, the second column is the phase calculated by FEM, the third column is the phase simulated by T-Unet, and the fourth column is the phase simulated by T-Unet. The fifth column shows the relative error distribution of phase between FEM and Unet method, which is recorded as RE Unet. The sixth column shows the relative error distribution of phase between FEM and T-Unet method, which is recorded as RE T-Unet.

Full size image

To verify the effectiveness of multitask magnetotelluric forward modeling, the simulation results are compared with the finite element simulation results and the prediction results of the multitask Unet. Figure 4 shows the apparent resistivity simulation results of the test model, including the following components: the model, FEM calculated apparent resistivity, apparent resistivity simulated by Unet, apparent resistivity simulated by T-Unet, and the relative errors of apparent resistivity between both Unet simulated and T-Unet simulated results versus the FEM-calculated apparent resistivity. As shown in Fig. 4, when Unet and T-Unet perform forward modeling on without noise geoelectric models, they can reconstruct the apparent resistivity corresponding to the measured random models and reveal the distribution characteristics and variation trends of the corresponding apparent resistivity. Among the four models, the apparent resistivity results simulated by Unet and T-Unet are highly consistent with those calculated by FEM in terms of the range, boundary, and morphology of the anomaly zones, indicating that T-Unet can achieve apparent resistivity calculations comparable to FEM. However, although the apparent resistivity predicted by Unet is similar to that calculated by FEM in the four models, there are still differences in details. For example, in Model 4, the high resistivity area is smaller than the FEM calculated value, and the resistivity morphology in the lower right corner also differs. Overall, the error of the apparent resistivity predicted by Unet is relatively larger, which is confirmed by the relative errors shown in the figure.

Table 2 Quantitative evaluation metrics for the forward prediction methods of Unet and T-Unet under with noise.
Full size table

Figure 5 displays the phase simulation results of the test models, which also consist of the following components: the model itself, FEM calculated phase, phase simulated by Unet, phase simulated by T-Unet, and the relative errors of phase between both Unet simulated and T-Unet simulated results versus the FEM calculated phase. As illustrated in the figure, in Examples 1, 2, and 3, the phase predicted by Unet is morphologically similar to the FEM calculated phase, but there are significant differences in numerical values. In Example 4, however, morphological discrepancies can be observed. In contrast, the phase obtained by T-Unet is generally highly consistent with the FEM-calculated phase, as evidenced by the phase errors shown in the last two columns. To accurately evaluate the differences in forward responses simulated by T-Unet, this study uses average peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) as metrics to assess the similarity of inversion results. A higher PSNR indicates closer agreement between the two methods, while a higher SSIM signifies greater similarity in results. The specific quantitative indicators of apparent resistivity and phase are shown in Table 1.

By analyzing the data in Table 1, it can be seen that under different test examples, T-Unet demonstrates superior performance compared to Unet in terms of the two evaluation metrics, namely the PSNR and SSIM. In terms of the PSNR metric, T-Unet performs better in most examples, whether for the prediction of apparent resistivity or phase. Taking Example 2 as an instance, the PSNR value of Unet for apparent resistivity prediction is 21.9360, while that of T-Unet reaches 26.0297. This clearly indicates that T-Unet’s prediction results for apparent resistivity are closer to the true values. In terms of phase prediction, as in Example 4, the PSNR value of Unet is 20.6474, and that of T-Unet is 26.1076, fully demonstrating the advantage of T-Unet in phase prediction. Regarding the SSIM metric, T-Unet also stands out. For the prediction of apparent resistivity, in Example 1, the SSIM value of Unet is 0.9268, and that of T-Unet is 0.9293, indicating that T-Unet has a slight edge in the structural similarity of the predicted apparent resistivity. In phase prediction, for example, in Example 3, the SSIM value of Unet is 0.9477, and that of T-Unet is 0.9522, further confirming that the phase predicted by T-Unet has a higher structural similarity to the true phase.

$$\begin{aligned} {PSNR = 10 \cdot {\log _{10}}\left( {\frac{{MAX_I^2}}{{MSE}}} \right) = 20 \cdot {\log _{10}}(\frac{{MA{X_I}}}{{\sqrt{MSE} }})} \end{aligned}$$
(12)

where MSE is shown in Eq. (6), and \({MA{X_I}}\) represents the maximum value among the apparent resisitivity or phase values.

$$\begin{aligned} {SSIM\left( {x,y} \right) = \frac{{(2{\mu _x}{\mu _y} + {c_1})(2{\sigma _{xy}} + {c_2})}}{{\left( {\mu _x^2 + \mu _y^2 + {c_1}} \right) \left( {\sigma _x^2 + \sigma _y^2 + {c_2}} \right) }}} \end{aligned}$$
(13)

where \({{\mu _x}}\) is the mean of x, \({{\mu _y}}\) is the mean of y, \({\sigma _x^2}\) is the variance of x, \({\sigma _y^2}\) is the variance of y, \({{\sigma _{xy}}}\) is the covariance of x and y, x and y are the pixel values of the predicted and target values, \({c_1} = {({K_1}L)^2}\) and \({c_2} = {({K_2}L)^2}\) are constants used to maintain stability, L is the dynamic range of pixel values, \({K_1}\) = 0.01 and \({K_2}\) = 0.03.

Noisy model experiment

Fig. 8
figure 8

Flowchart of T-Unet_LBFGS inversion technology. (a) shows the traditional LBFGS inversion, and (b) demonstrates the use of a multitask T-UNet network to predict forward responses.

Full size image
Fig. 9
figure 9

MT line distribution.

Full size image
Fig. 10
figure 10

Observed data.

Full size image
Fig. 11
figure 11

RMS curve of actual data inversion.

Full size image
Fig. 12
figure 12

Comparison of final inversion results. From left to right, the first to two columns are LBFGS and T-Unet_LBFGS.

Full size image
Fig. 13
figure 13

Comparison of forward response corresponding to inversion results. From left to right, the first to two columns correspond to the apparent resistivity and impedance phase of LBFGS and T-Unet_LBFGS. The rightmost two columns are the relative error distribution of LBFGS forward response and observation data, and the relative error distribution of T-Unet_LBFGS forward response and observation data.

Full size image

To evaluate the model robustness of the proposed T-Unet multitask forward simulation method under noisy conditions, we synthesized Gaussian distributed random relative noise with noise levels ranging from 3% to 5% in the test resistivity model dataset. The simulation results of apparent resistivity are shown in Fig. 6, which include: the noisy model, the apparent resistivity of the noisy model calculated by the FEM, the apparent resistivity simulated by Unet, the apparent resistivity simulated by T-Unet, and the relative error results between the apparent resistivity of Unet and T-Unet and that of FEM.

The apparent resistivity results of Unet and T-Unet preserve the range, boundary, and morphology of the anomaly area. The boundaries are smoother, and compared with the apparent resistivity obtained by FEM, they are less disturbed by noise. Although the errors indicate that the relative differences of the apparent resistivity values of T-Unet in Example 1 and Example 3 are relatively large, the differences between them are still relatively small. In contrast, Unet shows larger errors, and in Example 4, the errors are relatively significantly larger than those of T-Unet. Therefore, although T-Unet is adversely affected by noise, it can still capture the overall apparent resistivity distribution and variation trends compared with the calculation results of FEM.

The phase simulation results are shown in Fig. 7, which include: the noisy model, the phase of the noisy model calculated by FEM, the phase simulated by Unet, the phase simulated by T-Unet, the relative phase error between the FEM noisy data and the Unet result, and the relative phase error between the FEM noisy data and the T-Unet result.

Similar to the apparent resistivity results in Fig. 6, both Unet and T-Unet reflect the overall phase distribution and trend consistent with those of FEM. It is worth noting that the relative error plots and noisy points indicate that compared with the FEM forward simulation, T-Unet can also reconstruct the phase very well, demonstrating its excellent robustness. In contrast, Unet has relatively larger errors, especially in Example 1 and Example 4. Table 2 shows the specific quantitative evaluation metrics of PSNR and SSIM for Unet and T-Unet under noisy conditions.

As shown in Table 2, T-Unet can still stably predict apparent resistivity and phase under noisy conditions. The metrics of apparent resistivity and phase predicted by T-Unet and FEM exhibit specific patterns: for apparent resistivity, the PSNR and SSIM values under noisy conditions are significantly lower than those under noise free conditions, indicating a certain discrepancy between the two. As observed in Fig. 6, the values obtained by FEM show streaking under noisy conditions, while T-Unet predictions are smoother, which explains the lower PSNR and SSIM values. However, the PSNR and SSIM values for phase remain stable and relatively high, suggesting minimal discrepancy between the two methods. This indirectly demonstrates that T-Unet can effectively process MT data under noisy conditions.

As shown in Table 2, in each example, the PSNR values of T-Unet are higher than those of Unet. The SSIM values of T - Unet are generally higher than those of Unet across all examples. T-Unet can still stably predict the apparent resistivity and phase under noisy conditions. The resistivity and phase indicators predicted by T-Unet and FEM exhibit specific patterns: for apparent resistivity, the PSNR and SSIM values under noisy conditions are significantly lower than those under without noise conditions, indicating a certain difference. As shown in Fig. 6, the values of FEM under noisy conditions display stripes, while the predictions of Unet and T-Unet are smoother, which explains the lower PSNR and SSIM. However, the PSNR and SSIM values of the phase remain stable and relatively high, indicating a small difference between the two methods. This indirectly proves that the deep learning network can handle MT data under noisy conditions. Since T-Unet can obtain higher quality forward responses compared to Unet, in the discussion section, only T-Unet is used for testing in the inversion.

Discussion

This section further explores the applicability and practicality of integrating the proposed T-Unet multitask forward prediction method into the LBFGS method to replace its forward prediction in field MT exploration scenarios (T-Unet_LBFGS).

In MT inversion, the objective function is usually given by:

$$\begin{aligned} \varphi = {({\mathbf{{d}}^{obs}} - F(\mathbf{{m}}))^T} \mathbf{{C}}_\mathbf{{d}}^{ - \mathbf{{1}}}({\mathbf{{d}}^{\mathbf{{obs}}}} - F(\mathbf{{m}})) + \mathbf{{\lambda }}{(\mathbf{{m}} - {\mathbf{{m}}_\mathbf{{0}}})^\mathbf{{T}}} \mathbf{{C}}_\mathbf{{m}}^{ - \mathbf{{1}}}(\mathbf{{m}} - {\mathbf{{m}}_\mathbf{{0}}}) \end{aligned}$$
(14)

where \({\textbf{d}^{obs}}\) is the observation data (apparent resistivity and phase), F is the forward operator (FEM or T-Unet network model), \({\lambda }\) is the regularization parameter. \(\textbf{m}\) and \({\mathbf{m_0}}\) are the model parameters and a priori modes, respectively, and \(\mathbf{C_d}\) and \(\mathbf{C_m}\) are the covariance matrix of the data and model, respectively. The flow chart of T-Unet_LBFGS is shown in Fig. 8.

We use the observed data from the Guane’egou area, Gansu Province, China a planned development zone–as shown in Fig. 9. The survey line of the measured data in the study area is 5 kilometers, including 64 observation points and 32 frequencies. The observed data are shown in Fig. 10. Based on previous geological surveys, we further incorporate geological survey information into our training dataset, Notably, part of the training dataset is derived from forward responses generated by traditional inversion algorithms under an initial model with a resistivity of 100 \({\Omega }\). m. For the tests in this area, we selected the following relevant inversion parameters: the initial model resistivity is 1000 \({\Omega }\)· m, the error level is 0.2, \({\lambda }\) is 0.1, the RMS threshold is 1.05, and the iteration count is 50. To compare the inversion effects of different inversion methods, traditional LBFGS inversion was compared with inversion using T-Unet_LBFGS, with both using the same parameters. The RMS curves of data inversion are shown in Fig. 11, and the final inversion results are shown in Fig. 12. In Fig. 12, we plotted the fault lines F1 and F2 based on geological surveys. From left to right, Fig. 12 shows the results of underground resistivity structure inversion by LBFGS and T-Unet_LBFGS. Clearly, both inversion methods can well invert the abnormal areas. Specifically, the low-resistance water channel area at a depth of 1.5 km is well inverted by both methods.

Figure 13 illustrates the differences in forward responses between the two methods at different iterations. In each subplot of Fig. 13, from left to right, the apparent resistivity and impedance phase corresponding to the inversion results of LBFGS and T-Unet_LBFGS are shown, along with the corresponding relative error distributions of the apparent resistivity and impedance phase. Specifically, it can be seen from each subplot that the forward responses of the two methods are very similar, and the relative errors are relatively small. This also demonstrates the stability and effectiveness of the T-Unet forward prediction method. The specific quantitative evaluation indexes of the average PSNR and SSIM of the two forward response calculation methods of the measured data are shown in Table 3.

Table 3 The evaluation parameters of the results of two forward calculation methods for measured data.
Full size table

As shown in Table 3, for the forward responses corresponding to LBFGS inversion, both in terms of apparent resistivity and phase, their PSNR values are lower than those of the forward responses predicted by T-Unet_LBFGS inversion. This indicates that the forward responses predicted by T-Unet exhibit less distortion and smaller MSE compared to the observed data. In terms of SSIM, although the forward responses corresponding to LBFGS show slightly better performance, the SSIM values for T-Unet still exceed 80%. This demonstrates that the forward responses predicted by T-Unet are visually comparable to the observed data in terms of structural similarity.

In this experiment, we used the same computer equipment. The CPU was an i5-8250U, the memory was 16 GB, and the GPU was an NVIDIA GeForce MX150. Both T-Unet_LBFGS and the traditional LBFGS inversion iterated 36 times. The traditional LBFGS inversion took approximately 266.5547 seconds, while the T-Unet_LBFGS inversion took about 141.5625 seconds. Specifically, the reduction in inversion time achieved by T-Unet_LBFGS accounted for 46.89% of the total time consumed by the traditional LBFGS inversion.

Conclusion

To rapidly compute the forward response of resistivity models, we propose a multitask T-Unet forward simulation method. By constructing a dataset that matches subsurface resistivity scenarios, we successfully trained a multitask T-Unet model for forward responses. Under noise-free and noisy conditions, relative error distributions of apparent resistivity and phase between T-Unet and traditional FEM were visualized, and comparative analyses were conducted using PSNR and SSIM metrics. Results show that T-Unet can approximate FEM simulation values. Notably, when integrated into the traditional LBFGS inversion to replace forward response calculations during iteration, the method yields inversion results well-fitted to traditional LBFGS, with apparent resistivity and forward responses showing close similarity, confirming its effectiveness.

Additionally, this method offers a novel solution for accelerating inversion processes. We argue that integrating deep learning-based forward modeling with traditional optimization-based inversion represents a promising research avenue in the field of geophysical inversion, thereby establishing a foundation for subsequent investigations.