Introduction

Autism is a neurodevelopmental condition associated with developmental delay and clusters of symptoms in social communication and interaction, restricted repetitive patterns of behaviors and interests, and sensory processing1. Early alterations in social initiation and response to social cues impact experience-dependent experience-expectant learning within early interactions2,3, and may result in developmental milestone acquisition delay4,5. Autism intervention has been shown to be effective in narrowing developmental gaps and promoting adaptive changes, with current gold-standards for intervention including early start, individualization, and monitoring6. Since response variability remains consistently high7, a continuing challenge is better understanding active ingredients and mechanisms of change, particularly in Naturalistic Developmental Behavioral Interventions (NDBIs), a set of play-based models of intervention for autistic children integrating behavioral techniques within a developmental framework8. Core aspects of autism intervention involve scaffolding adaptive interactions to promote experiential learning mediated by interpersonal contexts and experiences, as seen in typical development9.

Challenges in monitoring interventions largely arise from the centrality of observational methods in clinical research. While these methods are non-invasive and ecologically valid, they suffer from limited quantification and objectivity. More importantly, they are also highly time-consuming and labor-intensive, preventing the systematic collection of large amounts of data and their translation to everyday clinical practice. Computational methods may represent a pivotal strategy to improve clinical measures and develop automated systems for data collection10. This is particularly true in developmental clinical contexts like in autism intervention, which happens in naturalistic settings and requires direct and extensive behavioral observation to be successfully monitored.

Interpersonal synchrony depicts the dynamic and reciprocal adaptation of the temporal structure of behaviors and states, reflecting multimodal interpersonal coordination11. It can indicate the presence or perception of simultaneous behaviors and biological rhythms. Biological rhythms involve some sort of coordination of complex behavioral cycles that may exhibit a variety of temporal and structural properties, flexible interdependence, and mutual co-regulation12. Mathematically, it refers to the degree to which the interaction is non-random, patterned, or synchronized in time and form, setting off behavioral cycles of engagement and disengagement that can involve different modalities and assume different structures and organizations13. Synchrony is pivotal for child development, starting from infant-caregiver emotional communication14. It has also been studied in contexts such as psychopathology and autism15,16,17. However, the complex interplay between synchrony and developmental dimensions resists straightforward or linear “more is better” explanations18.

In the context of psychotherapy and psychological interventions, synchrony has been investigated as a marker of therapeutic alliance19,20 and biological mechanism for change21. In the acoustic domain, some studies have focused on patient-clinician interpersonal exchanges using manual annotations and linear approaches22,23. This is also the case in autism research, where some works investigated the relationship between child-clinician therapeutic relationship and outcomes24, including changes over time in children’s vocalization25. However, research focused solely on speech quantity, excluding prosody and non-linguistic elements like emotional expression and interaction dynamics. In general, the role of emotional synchrony in terms of repeated exposure to the co-ordination between affective states and interactive behaviors within each partner and between them which promote the development of self- and co-regulatory capacities11 as an active ingredient of autism intervention remains largely under-investigated, especially from a quantitative perspective. Existing research in the acoustic domain has mainly focused on child-caregiver interaction prosody outside therapeutic settings26.

Aim

Focusing on acoustic synchrony27, this study aimed to employ a fully automatic analytic pipeline based on Artificial Intelligence (AI) to: (i) perform acoustic data segmentation in terms of voice detection and speaker diarization, i.e., automatically figuring out “who spoke when” in an audio recording by separating the audio into segments based on different speakers; (ii) extract non-linear complex relationships to model the child-clinician interaction synchrony; and (iii) develop predictive models to evaluate the longitudinal impact of interpersonal synchrony on clinical outcome. Developmental interventions such as NDBIs8 with autistic children happen during free interactions scaffolded by the therapist while following the child’s initiative, intentionality, and lead. A key computational challenge is to adapt to such a flexible context28. To overcome this hurdle, we developed and validated a Deep Learning (DL) system to automatically segment child-clinician speech in naturalistic clinical contexts. This system fully automates data annotation and allows for the extraction of high quantities of data, including entire therapy sessions. The annotation system was designed to encompass all forms of vocalizations, both linguistic and non-linguistic, including onomatopoeic sounds, laughter, crying, and other naturalistic vocal expressions. Importantly, the system was specifically trained to distinguish child from adult voices independently of the linguistic content, thus allowing for a comprehensive prosodic analysis. The training dataset incorporated a broad and representative range of linguistic and non-linguistic vocalizations derived from our clinical material to ensure robustness and reliability29. Here, we modeled the child-clinician interaction dynamics in the acoustic modality based on affective computing over a longitudinal sample of preschool autistic children (N = 25 children; N = 50 therapy sessions) undergoing NDBI for one year, and predicted outcome by means of a rigorous computational pipeline. Specifically, we aimed at examining whether changes in synchrony dynamics during the first few months of intervention were predictive of longer term outcomes in terms of developmental recovery. To capture the complex dynamics of coordination that constitute interpersonal synchrony, we used an information-based approach able to model both linear and non-linear dependencies, mutual influence, and temporal flexibility.

Materials and methods

Participants and procedure

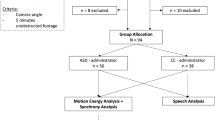
Twenty-five European/Italian preschool autistic children (22 males, lower- to upper-middle socioeconomic status) underwent NDBI (mean age = 37.72 months, SD = 10.06 range=[23, 56]; mean developmental age = 26.08 months, SD = 7.23 range=[14, 45], and were monitored for about one year (mean = 15.2 months, SD = 4.9) at the Laboratory of Observation, Diagnosis, and Education (ODFLab), a clinical and research center of the Department of Psychology of the University of Trento, Italy. At first, participants underwent a complete clinical assessment with gold-standard procedures for the diagnosis of neurodevelopmental conditions. Afterwards, they started a personalized intervention (2–4 h per week). After about one year, they underwent a second clinical evaluation to monitor their progress, including developmental profile and symptom severity. The diagnosis of Autism Spectrum Disorder was confirmed by following the DSM-5 criteria and through the administration of the Autism Diagnostic Observation Schedule-2 (ADOS-2) by trained clinicians different from the therapists30. Seventeen European/Italian therapists participated in this study (14 females) with the same training, regular supervision, and following the same intervention protocols tailored to the individual patients’ profile. The inclusion criteria were: (i) having a DSM-5 diagnosis of Autism Spectrum Disorder before 5 years of age; (ii) having two complete clinical assessments, before and after about one year of intervention; (iii) having undergone the NDBI without significant interruptions between the two assessments; and (iv) the presence of vocalizations, either linguistic or non-linguistic. The procedures of this study followed the last version of the Declaration of Helsinki31 and were approved by the Research Ethics Board of the University of Trento (protocol number: 2020-042). All participants gave informed consent to participate in this study. Data were collected between 2015 and 2021.

For each patient, therapy sessions were video-recorded by bird’s eye cameras. Audio signals were acquired through environmental microphones. We extracted a first session (T0) right after the clinical evaluation and a second session after 3–4 months (T1), for a total of 50 videos. Sessions were processed through the automated data analysis pipeline described hereafter. The system analyzed the entire therapy session, which usually lasts one hour.

Naturalistic developmental behavioral intervention

The intervention at ODFLab follows the NDBI framework, in line with guidelines from the Italian National Health Institute. Therapists are licensed developmental clinical psychologists formally trained in NDBI programs such as ESDM, JASPER, and PACT. Individualized intervention plans are developed based on functional assessments and include personalized goals, interaction methods, developmental targets, and caregiver involvement. Some children may also receive complementary therapies like speech or music therapy tailored on individual needs.

This study focuses on one-on-one NDBI sessions involving direct therapist-child interaction. The intervention integrates behavioral, developmental, and relationship-based strategies to promote intentionality, reciprocity, and emotional communication. Therapists use children’s spontaneous interests to build routines based on turn-taking and intersubjective engagement, and assign communicative value to behaviors by following the child’s lead. Cognitive, social, emotional, and symbolic aspects are targeted through the scaffolding of play-based activities characterized by shared rhythms and mutual attunement. Goals are regularly monitored and adjusted using structured observational tools, and updated to match the child’s developmental progress.

Clinical measure of outcome

Developmental progress was assessed using Developmental Learning Rates (LRs)32, calculated as the change in developmental age equivalents divided by the number of months between two clinical assessments. These values were derived from the Griffiths Mental Development Scales-Edition Revised (GMDS-ER)33, a semi-structured instrument that provides standardized developmental Z-quotients and age equivalents across five domains: locomotion, personal-social, language, eye-hand coordination, and performance (mean = 100; SD = 15). LRs offer a time-sensitive and interpretable measure of developmental change, with an LR of 1 indicating typical progress, values below 1 reflecting a widening developmental delay, and values above 1 suggesting accelerated gains during intervention. By incorporating the time dimension, LRs effectively capture the pace of development, allowing the identification of children who are responding to treatment versus those who are not. Consistent with prior research on treatment response heterogeneity in autism7, a Gaussian Mixture Model (GMM) was applied to the LR distribution, revealing that a two-cluster solution provided a significantly better fit than a single-cluster model (likelihood ratio test = 8.39, p = 0.015), distinguishing responders (LR > 1) from non-responders (LR < 1) (Figure. S1 and S2, see Supplementary Material).

Voice segmentation and speaker diarization

A deep learning system for double-layer classification, trained on naturalistic clinical data, performed the automated segmentation of clinical session audio signals. Validated in29, it consists of two siamese neural networks designed and trained to perform the second-by-second similarity-based classification over mel-frequency cepstral coefficients spectrogram features. The first layer detects human voice presence, while the second handles speaker diarization. Trained on noisy clinical interactions between autistic preschool children and clinicians, the system also processes and recognizes non-linguistic vocalizations which are typical of this population and a cornerstone for prosody and affective analyses. The system was validated through a robust cross-validation procedure and showed optimal performance in voice activity detection under diverse conditions (average balanced accuracy = 0.92 (0.04), F1 = 0.95 (0.01), sensitivity = 0.94 (0.02), specificity = 0.90 (0.08), precision = 0.97 (0.02), AUC = 0.98 (0.01)). Speaker diarization also performed well (average balanced accuracy = 0.80 (0.04), F1 = 0.80 (0.06), sensitivity = 0.76 (0.10), specificity = 0.84 (0.08), precision = 0.85 (0.08), AUC = 0.90 (0.04)). For this study, we assessed reliability by extracting a random speaker- and session-balanced sample of N = 300 1-second vocalization segments (automatically detected and diarized by the DL system) which were then human-annotated. The annotator was masked to outcome labels. The evaluation showed good classification performance (balanced accuracy = 0.89; F1-score = 0.89; sensitivity = 0.89; specificity = 0.88; precision = 0.88; MCC = 0.78, AUCROC = 0.89; AUCPR = 0.84). No noise segments were detected in the diarization evaluation. Cohen’s k indicated good inter-rater reliability accounting for chance agreement (k = 0.77).

Pipeline for synchrony extraction

Once the signal was segmented, we extracted acoustic features using the OpenSMILE eGeMAPSv02 set of 25 low-level features34. We included features related to pitch, harmonic and formant structure, spectral energy distribution, signal periodicity, and voice stability. Features were extracted for both child and clinician signals, with vocalizations detected by the deep learning system. Non-vocal segments were initialized to a placeholder based on features from a silent second to exclude environmental noise. Features were computed over 1-second segments, consistently with the deep learning system segmentation, and aggregated at 500ms. Features were standardized at the signal level with a robust scaler based on median and interquartile range to compensate for possible numerical instability during acoustic feature extraction. A binary signal reflecting turn-taking behaviors was included, marking vocalization moments. The signal was processed with overlapping windows, excluding silent ones to avoid modeling non-interactive moments. For each window, we computed a non-linear, non-parametric synchrony metric using Mutual Information (MI) regression, an entropy-based measure complex enough to reflect synchrony computed through k-nearest neighbors35. MI quantifies shared information between variables, assessing how much one can predict the other non-linearly, without constraining the temporal dynamics. To select the window size, we performed a sensitivity analysis, testing combinations from 10 to 60 s with an overlap of 40%. The range was based on two criteria: (i) Clinically, we needed a minimum window to capture interaction and attunement in the acoustic domain without being too large for a single ‘unit of interaction’; (ii) Numerically, the window had to be large enough to compute MI scores. We chose the parameter combinations maximizing variability, resulting in a 25s window size with a 15s hop size. For each window, we computed MI scores over two signals (child and therapist) using 50 acoustic feature samples.

From the dyadic synchrony signal we extracted functionals with increasing complexity to model synchrony dynamics, including descriptive and trend statistics, Shannon entropy, and Recurrence Quantification Analysis (RQA) to analyze signal properties in terms of complex dynamical systems36,37. The multidimensional set of functionals captures the temporal and structural richness of the synchrony signal, encompassing its stability (mean, median, 90th percentile), variability (standard deviation, interquartile range), temporal trends (moving average mean and standard deviation), non-linear information content (entropy), and recurrence properties (RQA metrics). The RQA-derived metrics provide insights into the dynamic structure of the signal, capturing patterns of repetition, complexity, and temporal organization. This approach aligns with the developmental conceptualization of interpersonal synchrony as a dynamic process characterized by phases of attunement, sustained states, transitions, misalignments, ruptures, and reparations, reflecting the nuanced nature of the dyadic dance14. From the MI variance distribution across acoustic features we set a fixed radius neighborhood threshold of 0.05 (standard deviation) for RQA to identify synchrony scores representing the same underlying system state. Our final candidate feature set consisted of 285 features, i.e., (14 acoustic features + the binary signal) times 19 functionals. Detailed information about features, functionals, and RQA are reported in the Supplementary Material.

Feature selection

Given the small sample size and large number of candidate predictors with no aprioristic hypotheses, we employed a rigorous feature selection and model development procedure using nested cross-validation38, integrating a statistically robust machine learning approach. Feature selection was based on Random Forest (RF) feature importance using Gini’s impurity, with tree depth limited to 5. The Boruta algorithm iteratively creates permuted versions of original predictors, refitting the RF model with “shadow attributes” to derive p-values for feature importance, testing the null hypothesis that importance is due to random factors. P-values are controlled for multiple comparisons at each step. The algorithm stops once all candidate predictors are tested39.

Predictive modeling

First, we computed the relative rate of change of each functional to form the set of candidate independent variables. We employed regularized logistic regression to predict responders (LR > 1), and non-responders (LR < 1), as regularization reduces multicollinearity and overfitting40. To reduce bias, a two-step procedure for model development was performed. The first step involved nested Leave-One-Out Cross-Validation (LOOCV), suitable for small datasets. The outer loop performed feature selection, while the inner one tuned regularization parameters using grid search. The final model included features selected at least 80% of times and the most common hyperparameters configuration. The second step involved final evaluation through another LOOCV to test model performance through balanced accuracy, sensitivity, specificity, precision, F1-score, Matthews Correlation Coefficient, Area Under the Receiver Operating Characteristic curve (AUCROC), and Area Under the Precision-Recall curve (AUCPR). Model coefficients were tested against the null hypothesis that their true mean value is 0. Multicollinearity was assessed using Variance Inflation Factor (VIF).

As complementary validation, we tested the final model on an augmented dataset. Data augmentation was performed by standardizing features and adding randomly extracted gaussian noise (SD = 0.2). Classes were balanced during data augmentation, and data were back-transformed. The dataset was augmented by a factor of five (N = 156) and evaluated using Leave-One-Group-Out Cross-Validation (LOGOCV). During cross-validation, data were independently standardized based on training data only to avoid data leakage. We also performed a post-hoc correlational analysis between selected independent and clinical variables. The computational pipeline ran in Python with the libraries: pyRQA, BorutaPy, scikit-learn, and sci-py, and is schematized in Fig. 1.

Fig. 1
figure 1

Diagram of the automated pipeline for the longitudinal analysis of child-clinician acoustic synchrony. (A) The clinical settings of NDB Intervention with timeline, sample characteristics and outcome measure description (LR). (B) The architecture of the deep learning system for the automated segmentation of the acoustic signal and the ongoing reliability testing. (C) Feature extraction procedure. (D) Model development and evaluation procedure.

Full size image

Results

Sample characteristics and pre-treatment group differences

Sample clinical characteristics are reported in Table 1 for the whole sample and for responders (N = 12; mean LR = 1.40; SD = 0.33) and non-responders (N = 13; mean LR = 0.56; SD = 0.18). Clinical scores differed significantly between the groups in eye-hand coordination and performance, and for the restricted repetitive patterns of behaviors and interests score of the ADOS-2.

Table 1 Sample characteristics and pre-treatment between-group differences.
Full size table

Feature selection and hyperparameters tuning

The nested CV for feature selection selected 3 features, L2-regularized with C = 0.1. Two features are functionals of the F3 bandwidth signal, i.e., entropy, and moving average SD. F3 bandwidth represents the frequency range of the third formant. Formants are the concentration of acoustic energy around a particular frequency in the speech wave. They reflect the resonance modes of the vocal tract, differentiate vocal and consonant sounds, and represent key features in speech analysis and affective computing. The third feature is the determinism/recurrence rate ratio of the acoustic Alpha ratio. The Alpha ratio is defined as the ratio between the summed energy of lower (50–1000 Hz) and higher (1–5 kHz) frequencies in the spectrum. It estimates the spectral tilt of the glottal source by measuring the distribution of speech energy (sound pressure level) over the frequency bandwidth34. The determinism / recurrence rate ratio describes the proportion of recurrent states in the signal that actually form deterministic patterns36,37. Table 2 reports descriptive statistics of the selected predictors based on response trajectory.

Table 2 Between-group differences longitudinal rates of change for the selected features.
Full size table

Predictive modeling of treatment response

Using the three selected features, the logistic regression accurately predicted patients who improved (LR > 1) from those who did not (LR < 1) (balanced accuracy = 0.96; F1-score = 0.96; sensitivity = 1; specificity = 0.92; precision = 0.92; MCC = 0.92; AUCROC = 0.99; AUCPR = 0.99). Model performance is shown in Fig. S3 (Supplementary Material).

All model coefficients were significantly different from zero: F3 bandwidth moving average SD (mean = 0.39; SD = 0.01; odds ratio = 1.48 (0.02); t = 163.02; p < 0.001; VIF = 1.35), F3 bandwidth signal entropy (mean = -0.37; SD = 0.01; odds ratio = 0.69 (0.01); t = 112.97; p < 0.001; VIF = 1.32), and alpha ratio determinism/recurrence rate (mean = 0.39; SD = 0.02; odds ratio = 1.48 (0.02); t = -126.78; p < 0.001; VIF = 1.62) (Fig. 4, see Supplementary Material). The VIF indicated low multicollinearity.

Finally, complementary evaluation by data augmentation yielded similar prediction performance (balanced accuracy = 0.92; F1-score = 0.92; sensitivity = 0.95; specificity = 0.90; precision = 0.90; MCC = 0.85; AUCROC = 0.98; AUCPR = 0.98) (Fig. S5, Supplementary Material), indicating that the model’s predictive performance was preserved even when trained on synthetic data generated from a perturbed input space.

Post-hoc correlational analysis

The correlational analysis showed significant associations between LR and chronological age (r = -0.55; p = 0.004), and the selected independent variables: F3 bandwidth moving average standard deviation (r = 0.63; p < 0.001), F3 bandwidth entropy (r = -0.45; p = 0.02), and alpha ratio determinism/recurrence rate (r = 0.74; p < 0.001). No significant correlations emerged between independent variables and pretreatment general developmental quotient: F3 bandwidth moving average standard deviation (r = 0.36; p = 0.08), F3 bandwidth entropy (r = -0.17; p = 0.40), alpha ratio determinism/recurrence rate (r = 0.40; p = 0.05). Similarly, no significant associations were found between independent variables and baseline symptom severity (ADOS-2 total score): F3 bandwidth moving average standard deviation (r = -0.20; p = 0.32), F3 bandwidth entropy (r = 0.13; p = 0.53), alpha ratio determinism/recurrence rate (r=-0.21; p = 0.32). Variations in synchrony metrics were not associated with chronological age at intake: F3 bandwidth moving average standard deviation (r = -0.10; p = 0.62), F3 bandwidth entropy (r = 0.28; p = 0.17), alpha ratio determinism/recurrence rate (r = -0.27; p = 0.19). F3 features were not significantly correlated (r = -0.30; p = 0.15). Conversely, alpha ratio determinism/recurrence showed significant correlations with both F3 bandwidth moving average SD (r = 0.51; p = 0.01) and entropy (r = -0.49; p = 0.01). The correlational analysis is shown in Figs. S6–S12 in Supplementary Material.

Discussion

This work explored the longitudinal predictive relationship between child-clinician acoustic synchrony and autism intervention outcome. We hypothesized that changes in child-clinician interaction dynamics during the first months of intervention were particularly predictive of response at one year41. To test this, we developed a fully automatic pipeline for data segmentation, modeling child-clinician synchrony, and predicting longitudinal therapy outcomes.

The results suggest that responders are predicted by changes in synchrony patterns characterized by: (i) increased variability in average trends of the F3 bandwidth synchrony signal, i.e., greater fluctuations over time in the synchrony signal trends for the third formant frequency range; (ii) decreased entropy of the same F3 bandwidth synchrony signal, i.e., an increase in the synchrony signal predictability and internal organization with respect to the third formant frequency range; and (iii) increased determinism/recurrence rate ratio for alpha ratio synchrony signal. An increase in the determinism-to-recurrence rate ratio indicates that the synchrony signal for the alpha ratio acoustic feature evolves towards more predictable, and organized recurrent patterns relative to overall recurrence. The alpha ratio reflects the balance between higher and lower frequency energy in the speech signal.

The acoustic features from our analysis involve speech formant frequency range and speech energy distribution across the frequency spectrum. Particularly, the first two formants are known to convey linguistic meaning and are related to speech quality. On the contrary, higher formants like F3 have been linked to nonlinguistic aspects like emotional content42. Therefore, results suggest a role of acoustic synchrony in emotional vocal expression. A better response is marked by increased trend variability in synchrony patterns and decreased entropy. Entropy quantifies randomness and unpredictability, and decreased entropy reflects a signal becoming less chaotic and more predictable.

Additionally, the alpha ratio has been studied in relation to voice quality43 and fatigue44. Voice quality refers to the characteristic acoustic properties of the voice, including aspects such as pitch, timbre, breathiness, and roughness, which convey emotional and physiological states during interpersonal interactions. Additionally, vocal fatigue refers to a state of vocal tiredness characterized by altered acoustic measures often accompanied by subjective sensations of effort and discomfort in the voice. More importantly, the alpha ratio was shown to be sensitive to changes in response to emotional expression training45. In our results, a better response at one year was predicted by increased determinism/recurrence rate ratio of the alpha ratio synchrony signal within the first months of intervention. Determinism quantifies the proportion of recurrence points forming diagonal lines in the recurrence plot. Diagonal lines indicate similar state evolutions over time, suggesting the presence of deterministic structures and predictable patterns. Further, the recurrence rate measures the degree to which a signal returns in similar states over time. When their ratio increases, the system becomes more predictable with respect to its recurrent states36,37. That is, recurrences in the signal do not simply represent random reappearances, but form structured and deterministic patterns while evolving during the session. In contrast, non-responders show synchrony patterns that become less variable, less predictable, less deterministic, and more chaotic, exhibiting the opposite trend.

Results from the complementary analysis suggest that the model is robust to meaningful distortions in the input space, preserving predictive accuracy even when trained on synthetically augmented data, which supports its potential for generalization to slightly altered or noisy real-world conditions.

Together, these trends indicate that successful interventions involve increasing variability in synchrony over time while becoming more structured in acoustic features related to emotional content. Clinically, our results emphasize the importance of child-clinician prosodic and affective synchronization in effective intervention. Specifically, successful interventions are characterized by prosodic alignment patterns that grow in complexity while becoming more predictable and internally organized. This likely reflects a therapeutic process in which clinicians first attune to the child’s spontaneous vocalizations and prosodic style, establishing a shared acoustic rhythm, and then gradually support the development and consolidation of richer, more varied, and more structured prosodic patterns. These early dynamics may be crucial for building relationships and mutual engagement46.

Overall, our results align with developmental evidence on the role of emotional communication and the importance of communicative cycles involving mutual attunement, periods of synchrony, as well as ruptures and reparations47. In fact, our analysis suggests that the response to intervention is more closely linked to complex, fine-grained aspects of child-therapist prosodic synchrony such as the evolving balance between internal variability and consistency and its recurrence properties, rather than to overall synchrony levels. It also supports our hypothesis that the child-clinician interpersonal synchrony in affective dimensions may represent a key mechanism in the therapeutic process, as well as the importance of the first period of intervention.

Our findings have several implications. First, they emphasize the need for clinicians to match children’s rhythm when designing and delivering interventions. Psychotherapy research is familiar with the fact that patients’ individual characteristics influence therapists’ abilities to engage effectively and vice versa48,49. Second, the fact that the evolution of the child-therapist synchrony dynamics in the first phase of intervention was able to predict longer-term developmental response unrelatedly to baseline child variables highlights the contribution of emotional participation via prosodic synchrony to the therapeutic process, in line with developmental evidence, e.g., the importance of prosody modulation and parentese in early child-caregiver social interaction26,50. These affective synchrony aspects are central to developmental models of intervention in autism46,51,52. Third, the first few months of intervention may be crucial for therapy outcome, representing a critical window to allocate resources for expert supervision and early treatment monitoring in order to maximize efficacy6.

The current study also has limitations, the most important being the sample size and an unbalanced sample with respect to biological sex (the majority of children being male and the majority of therapists being females). Despite a rigorous procedure and complementary data augmentation analysis, the small sample size limits generalizability and power. Therefore, our results should be cautiously interpreted in terms of generalization and require replication on larger samples. Second, there were significant pre-intervention differences between responders and non-responders, the latter showing lower performance and eye-hand coordination, and more severe restricted repetitive patterns of behaviors and interests. However, their general development was comparable (particularly locomotion, personal-social, and language subdomains), as well as their overall symptom severity, especially in the social affect area. These aspects more closely impact psychotherapy dynamics. Although no correlations emerged between the evolution of synchrony profiles and baseline variables, further investigation should evaluate the potential contribution of fine motor and coordination aspects related to restricted repetitive behaviors and eye-hand coordination on interpersonal synchrony patterns, since they could influence the child-therapist interaction dynamics in specific ways. Third, we could not investigate the role of therapists’ and children’s individual characteristics on synchrony patterns. In fact, we could not systematically account for therapist effects. Future studies using a one therapist-many children design will be needed to examine potential therapist-specific influences on synchrony and intervention outcomes. Children were not systematically assigned to therapists in order to study the effect of the clinician over interaction features. As well, some children were followed by more than one therapist from the beginning, for training or clinical purposes. Although we ensured that child-clinician synchrony was calculated only on sessions where the dyad was single and stable, this naturalistic clinical design prevented us from investigating broader therapist-related effects. Future studies should also focus on investigating the contribution of therapist’s variables (e.g., expertise, personality traits, interaction style with different children), as well as children’s characteristics in terms of externalizing behaviors, self-regulation, and negative affect. Fourth, while MI is a powerful metric, it lacks interpretability compared to linear techniques and does not provide information about directionality. Future research should address this. However, we employed a linear predictive technique which yields clinically interpretable relationships. Additionally, RQA could benefit from data-driven parameter estimation53. Finally, despite the multimodal nature of synchrony, this study focused only on the acoustic modality.

In conclusion, our computational pipeline may enable automated, large-scale, quantitative methods to monitor interventions in naturalistic clinical contexts with minimal need of human effort while remaining completely non-invasive54. This methodology opens the door for future process research, such as fine-grained interaction dynamic modeling to disclose “synchrony blocks” and distinguishing effective interactions. It may also enable the nearly real-time automated therapeutic feedback, advancing precision approaches55 and supporting relational clinical frameworks based on interpersonal synchronization and affective exchanges.