Multi-objective optimization design approach for prefabricated buildings to minimize cost, duration and carbon emissions using ant colony algorithm

Abstract

A multi-objective optimization design approach for prefabricated components such as columns, beams, slabs, walls and stairs in prefabricated buildings using ant colony algorithm is proposed to minimize cost, duration and carbon emissions in this paper. The proposed approach takes cost, duration, and carbon emissions as objective functions, the construction technologies of cast-in-place and prefabricated components as variables, prefabrication rate as constraints, and the ant colony algorithm as a solution tool, to minimize the cost, duration, and carbon emissions of prefabricated buildings. The validity of the proposed approach was verified by applying it to the multi-objective optimization design of a three-story frame structure. The results showed that:(1) Compared to all cast-in-place buildings, the prefabricated building under the baseline scenario achieves a reduction of 0.42% in cost, 19.05% in duration, and 13.49% in carbon emissions. (2) The main factor influencing the optimal combination of prefabricated building components is the incremental benefit of cost, duration, and carbon emissions resulting from changes in sub-target weight and prefabrication rate. The weight coefficients of each sub-objective determine “how” the construction technologies of the components is selected, while the prefabrication rate determines “how much” of the construction technologies is chosen. (3) Under four scenarios with different weighting coefficients, the optimized solution for prefabricated buildings compared to cast-in-place construction shows maximum reductions of 1.26% in cost, 27.89% in duration, and 18.4% in carbon emissions. The proposed approach provides an effective pathway for the transformation from cast-in-place construction to prefabricated construction and promotes sustainable development in the building industry.

Introduction

With the rapid pace of urbanization and increasing market demand, the scale of construction projects continues to grow. During the 13th Five-Year Plan period, the national construction industry witnessed an average annual growth rate of 5.1% in added value, accounting for over 6.9% of GDP. This has reinforced the construction industry’s role as a key pillar of the national economy, contributing significantly to China’s economic growth¹. Despite these achievements, the construction industry still faces challenges related to low development quality and efficiency. Issues such as inadequate project management and insufficient coordination among stakeholders often lead to cost overruns and project delays^2,3. Simultaneously, the rapid growth of the construction industry has posed significant threats and challenges to ecological resources, making it a major contributor to carbon emissions⁴. The construction industry currently consumes approximately 40% of the world’s energy annually and generates around 33% of global greenhouse gas emissions⁵. It accounts for one-third of the world’s total energy consumption and, if left unchecked, is projected to increase energy demand by nearly 50% by 2050⁶. This also reflects the significant potential for emissions reduction within the construction industry. According to research, the construction sector has the capacity to effectively reduce approximately 29% of carbon emissions⁷. The need to achieve transformation, upgrade, and sustainable development within the construction industry is therefore urgent.

Prefabricated building is a modern construction method characterized by standardized design, component prefabrication, and mechanized assembly construction. It integrates the entire industrial chain of building industrialization to achieve energy efficiency, high quality, and maximize the lifecycle value of products⁸. In the 14th Five-Year Construction Industry Plan, it is proposed that by 2025, the proportion of prefabricated buildings in new construction projects in China should exceed 30%. Prefabricated buildings have garnered widespread attention and strong support both domestically and internationally due to their ability to significantly improve the construction working environment, enhance productivity, and shorten construction periods⁹. Sustainability encompasses not only environmental and economic dimensions but also social aspects. The impact of construction projects on communities, the quality of life for residents, social equity, and the social acceptability of building projects are all important indicators for assessing their sustainability¹⁰. For example, during the construction process, a building project may affect the surrounding community in terms of traffic, noise, and air quality, which in turn can influence residents’ quality of life. The social acceptability of a construction project also affects its sustainability, including residents’ satisfaction with the project and their recognition of its functions and design¹¹.Given the current focus on sustainable development and energy conservation in the industry, prefabricated buildings have emerged as a crucial solution to mitigate environmental pollution and reduce carbon emissions. They achieve high resource utilization efficiency, reduce energy consumption, and minimize environmental impact¹². Currently, the development of prefabricated buildings is considered the only pathway for building transformation, upgrade, and sustainable development.

Prefabricated buildings are constructed using prefabricated components. In the early stages, these components mainly consisted of prefabricated concrete structures, steel structures, prefabricated partition walls, flues, etc. However, more complex and comprehensive components such as prefabricated decoration projects, integrated kitchens, and integrated toilets have been gradually introduced. As the scale of prefabricated buildings continues to increase and the prefabrication rate improves, there is a growing number of different types of prefabricated components involved, along with the collaboration of multiple participants in the construction process^13,14. This significantly increases the complexity of construction management and directly contributes to rising project costs. It becomes challenging to control factors such as project quality, duration, and even safety according to the planned schedule¹⁵. The factory production of prefabricated buildings leads to higher production costs compared to cast-in-place buildings, resulting in a substantial increase in construction costs. This cost factor becomes a primary constraint on the widespread adoption of prefabricated buildings¹². In the realm of prefabricated buildings, the selection of the optimal combination of prefabricated components plays a critical role in determining the overall benefits of the building. Different types of prefabricated components can have varying impacts on the overall project cost. Additionally, the duration associated with different types of prefabricated components can also differ¹⁶. Therefore, the careful selection of the prefabricated component combination is of utmost importance in order to achieve higher comprehensive benefits upon the completion of the building.

However, incorporating environmental considerations adds an additional layer of complexity to the selection of prefabricated component combinations in prefabricated buildings. A significant portion of carbon emissions during the construction phase are embedded within building materials^17,18, with traditional construction methods accounting for approximately 85% of these emissions¹⁹. In prefabricated technology, a majority of building materials are processed into prefabricated components. As a result, the carbon emissions of prefabricated buildings are largely attributed to the prefabricated components made from new composite materials. Therefore, measuring and controlling the carbon emissions associated with prefabricated components becomes an essential task in implementing a low-carbon building approach. On the other hand, carbon trading has gained significant attention as a policy for effectively controlling greenhouse gas emissions and promoting sustainable development in recent years. The fundamental concept behind carbon trading is to guide enterprises in reducing their carbon emissions through market mechanisms, incentivizing technological innovation, and improving energy efficiency²⁰. In a carbon trading market, enterprises have the ability to buy or sell carbon emission allowances based on their emission levels, enabling flexible adjustment of emission reduction costs²¹. By implementing carbon trading policies, carbon emissions become an integral part of business activities for enterprises, transforming the external environmental cost of carbon emissions into internal costs. As a result, the overall life cycle cost of buildings is influenced by carbon emissions²². Consequently, considering the factors that impact carbon emissions becomes particularly important when making informed decisions about the selection of an appropriate prefabricated component combination.

The conceptual design phase has the greatest impact on the overall project, and the decisions made during this phase are crucial in determining the environmental impact and cost-effectiveness of the building’s entire life cycle²³. The choice of conceptual design scheme is closely related to whether a prefabricated building can achieve better social, economic, and environmental benefits upon completion. However, since it is not possible to evaluate all configurations during the conceptual design phase, this phase is often considered the most"ill-defined“and”fuzzy"²⁴. To ensure that stakeholders do not make decisions without a clear understanding of how those decisions will impact future project performance and benefits, the decision-making process in the engineering field often relies on the intuition and experience of engineers²⁵. Engineers utilize rapid and high-quality decision methods and tools to improve the rationality and optimality of their choices. While the use of building information modeling technology²⁶ and building virtual simulation technology²⁷ can effectively address issues in traditional cast-in-place buildings, the more complex nature of prefabricated buildings still poses challenges in this regard.

In the conceptual design stage, if the selection of components can be based on the project requirements and specific scenarios, prefabricated buildings can achieve maximum cost and duration savings while meeting the prefabrication rate requirements, and also minimize carbon emissions. This approach will significantly reduce the haphazard selection of prefabricated building components and stimulate the development of prefabricated buildings. Therefore, the optimization research of prefabricated buildings is crucial. However, the cost, duration, and carbon emission targets of a building are interrelated and mutually constrained. This means that when selecting

a combination of prefabricated components, it is not possible to consider one factor in isolation. Instead, a comprehensive consideration of the balance and mutual influence between these factors is necessary. Dealing with multiple and conflicting objectives also presents significant challenges in selecting the optimal combination of prefabricated components.

To address the issue of selecting prefabricated component combinations in the conceptual design stage, we propose a structural design approach that utilizes an ant colony algorithm for multi-objective optimization of prefabricated component combinations in prefabricated buildings. This approach takes into account the factors of cost, duration, and carbon emissions. The objective of this approach is to maximize cost and duration savings while adhering to prefabrication rate constraints, and to minimize the carbon emissions of the building. Cost minimization involves reducing the financial expenditures associated with the construction of prefabricated buildings, including direct costs, management fees, profit margins, and taxes. Duration minimization refers to shortening the total duration of a construction project from initiation to completion. Carbon emission minimization aims to reduce the environmental impact by lowering the carbon dioxide emissions associated with the construction process, which includes emissions generated during material production, transportation, and on-site construction activities. By considering cost, duration, and carbon emissions as objective functions, and the cast-in-place and prefabricated processes as variables, the ant colony algorithm is employed to solve the multi-objective optimization model. This allows us to obtain the optimal Pareto solution for the prefabricated component combination. An empirical study was conducted on the design of a three-storey frame structure in Shenzhen, Guangdong Province, China. Additionally, a scenario analysis is conducted on the weighting coefficients and prefabrication rates. The proposed approach can assist stakeholders in choosing the most suitable prefabricated component combinations based on their specific circumstances and construction needs.

Literature review

Building optimization

In traditional engineering project management, the optimization research of buildings has primarily focused on cost and duration constraints. In 1959, Kelly et al. assumed a linear relationship between duration and cost and used a heuristic algorithm to address the construction-cost balance problem²⁸. Kapur discussed the optimization of duration and cost, suggesting that the relationship between the two is a nonlinear quadratic function, and proposed a label algorithm to optimize it²⁹. In 1984, Adel et al. successfully solved general nonlinear problems within the acceptable relative error range of duration³⁰. Considering the uncertainties inherent in project implementation, scholars have introduced factors such as resource constraints and network planning to the optimization field. In 2010, Klerides et al. introduced uncertainty into the discrete cost-time optimization problem³¹. By analyzing the distribution and diversity of Pareto solution sets, Ghoseiri et al. concluded that the ant colony algorithm performs well and exhibits high efficiency in solving the shortest path problem of cost-duration³². Hazir et al. investigated the multi-model discrete problem of duration-cost and effectively mitigated the impact of uncertainty on the project by evaluating previous activity data. As engineering project optimization research advances, scholars have begun to consider other indicators as well. EI-Rayes et al. quantified project quality using specific measurement indicators and developed a discretized multi-objective optimization model for duration-cost-quality, which was solved using genetic algorithms³³. Asadi et al. focused on the multi-objective optimization of building renovation strategies, aiming to minimize energy use in a cost-effective manner while meeting the needs and requirements of occupants³⁴. Penna et al. investigated the relationship between the initial characteristics of residential buildings and the definition of optimal retrofit strategies, such as achieving maximum economic benefits or minimizing energy consumption to achieve the lowest thermal comfort in nearly zero-energy buildings³⁵. Milat et al. considered the complexity of construction projects and used stability as an objective in multi-objective optimization to manage the effects of uncertainty³⁶.

Building carbon emissions optimization

In recent years, the significance of sustainable development in buildings has reached unprecedented levels due to increasing environmental pollution and energy consumption. Energy conservation and emission reduction in buildings have become crucial issues both internationally and domestically³⁷. Chen et al. conducted a comprehensive study on the multi-objective optimization of building performance throughout the entire life cycle to explore optimal building schemes³⁸. With the aim of minimizing carbon emissions from buildings and activity systems, Chen et al. developed a co-simulation model for active and passive solar heating systems³⁹. Tabrizikahou and Nowotarski reduced energy consumption and carbon emissions in building structures by implementing lean construction methods to optimize construction processes⁴⁰. Zhou et al. conducted a comparative analysis on carbon emissions between prefabricated buildings and cast-in-place buildings throughout five construction stages⁴¹. Zhu et al. studied the design method of building maintenance structures based on intersection experimental design (OED) to minimize carbon emissions from energy consumption during building operation⁴². Combining carbon emission factors with the emergy analysis method, Zhao et al. developed an Em-CEF accounting model to compare and analyze carbon emissions during the physical and chemical stages of traditional, prefabricated, and green materials buildings⁴³.

Prefabricated component research

The selection of a prefabricated component combination scheme has a significant impact on the overall benefits of prefabricated buildings. Prefabricated components, as a crucial aspect of prefabricated buildings, have garnered attention from researchers. Zhang et al. developed a model for the dynamic transportation planning problem based on the just-in-time (JIT) strategy and utilized particle swarm optimization (PSO) to address the dynamic challenges of urban transportation planning in the prefabricated component supply chain⁴⁴. Building upon the multi-agent theory, Du et al. studied the decision-making process within the prefabricated component supply chain and proposed a decision support framework for supply chain management¹⁶. Taking into account demand fluctuations, Du et al. proposed a dynamic process shop scheduling model based on prefabricated component production, resulting in potential cost savings of up to 43.2%⁴⁵. Tao et al. implemented a waste recycling strategy for the byproducts generated during the production of prefabricated components, converting them into fuel. This approach contributes to the conservation of natural resources and environmental protection⁴⁶. Du et al. utilized RFID technology to efficiently track the supply chain of prefabricated components, enabling the calculation and analysis of costs and benefits at each stage⁴⁷. Liu et al. analyzed the quality liability of prefabricated components using evolutionary game theory and found that prefabricated component quality liability insurance can reduce governance costs and yield significant social benefits⁴⁸. Xu et al. employed slice point cloud technology to conduct geometric modeling and surface quality inspections of precast concrete components, addressing challenges such as the loss of local details, interference from noise points, and manual processing in the inspection process of prefabricated buildings⁴⁹.

Intelligent algorithm

Since the 1990 s, intelligent algorithms have been utilized by foreign scholars to address design optimization problems in numerous large projects, as they demonstrate strong performance in solving complex problems⁵⁰. Intelligent algorithms can analyze the cost, duration, and carbon emissions of prefabricated buildings during the selection of prefabricated component combinations in the conceptual design stage. This analysis aids senior engineers in making informed decisions by rapidly considering multiple complex factors and a wide range of component types. The main types of intelligent algorithms used include genetic algorithms (GA), particle swarm optimization (PSO), simulated annealing algorithms (SA), and ant colony algorithms (ACO). Genetic algorithms are primarily employed to solve multi-objective optimization problems when the process is fixed. Notable achievements have been made in the field of component production resource allocation, site optimization layout, and production scheduling in the engineering field. However, the fitness function in genetic algorithms is often subjectively determined based on experience, potentially leading to local optimization that deviates from the actual project scenario⁵¹. Particle swarm optimization (PSO) is similar to genetic algorithms but simpler in implementation. It is straightforward and easy to implement, but it may be susceptible to local optima⁵². The simulated annealing algorithm is well-suited for large-scale combinatorial optimization problems, exhibiting high operating efficiency and requiring fewer initial conditions. However, its convergence rate is slow and random, and the parameter settings greatly influence the results⁵³.

In comparison, the Ant Colony Optimization (ACO) algorithm demonstrates a high degree of adaptability when addressing the multi-objective optimization problem of prefabricated component combinations in prefabricated building. Specifically, ACO simulates the foraging behavior of ants and utilizes a pheromone mechanism for path selection, effectively avoiding local optima and identifying global optima. In the optimization of prefabricated component combinations for modular buildings, there are various construction process choices and complex constraints. The global optimization capability of ACO enables it to find optimal solutions from numerous possible combinations, ensuring a comprehensive optimization of cost, duration, and carbon emissions³⁸. Additionally, ACO inherently features parallelism, allowing it to process multiple solutions simultaneously. This characteristic enables the algorithm to quickly explore the solution space during the computation process, thereby enhancing optimization efficiency. In the context of prefabricated component combination optimization, a large variety of component types and multiple construction processes must be considered. The parallel computing nature of ACO allows it to efficiently handle these complexities and rapidly identify optimal solutions⁵⁴. Moreover, ACO exhibits strong adaptability to the scale and complexity of the problem. In prefabricated building, as the prefabrication rate increases, the variety and quantity of prefabricated components significantly rise, complicating the construction process. ACO can flexibly adapt to this complexity by adjusting parameters and the pheromone mechanism, effectively addressing problems of varying scales and complexities. Finally, ACO employs a dynamic pheromone updating mechanism that allows it to adjust the search direction based on feedback information during the optimization process. In the optimization of prefabricated component combinations, the weights among various objectives may change according to actual requirements. ACO can quickly respond to these changes and dynamically adjust optimization strategies, ensuring that the optimization results consistently meet real-world needs⁵⁵. In summary, due to its global optimization capabilities, parallel computing characteristics, strong adaptability, and dynamic adjustment abilities, the ACO algorithm is an ideal choice for solving such problems. This study applies the ACO algorithm to optimize the combinations of prefabricated components.

ACO algorithm

Since its inception in 1992, ant colony algorithms have achieved significant breakthroughs in numerous engineering design optimization problems⁵⁶. Ant colony algorithms simulate the foraging mechanism of ants, which can efficiently find the shortest path from their nest to food sources in nature⁵⁷. Since its proposal, ant colony algorithms have been widely applied to various cutting-edge optimization fields, including distribution

network optimization⁵⁸ and optimal power scheduling⁵⁹ in the electric power sector, robot collaboration and path planning in the field of artificial intelligence⁶⁰, and environmental optimization in the water resources domain⁶¹. Moreover, ant colony algorithms have found extensive applications in the engineering field due to their suitability for solving complex multi-objective optimization problems encountered in engineering projects. Zhang et al. developed a multi-objective optimization model for time and duration using the ant colony algorithm with Visual Basic for Application (TM). This model provides an effective tool for planners and managers to make informed decisions regarding time and cost⁶². Li et al. utilized an improved ant colony algorithm to optimize multiple objectives, including quality, schedule, cost, and safety, in construction engineering projects. This approach enhanced the overall efficiency of project management⁶³. Chen et al. established a model aimed at minimizing the variance of production capacity utilization rates for prefabricated components within the production cycle. They employed the ant colony algorithm to solve the optimization problem of production line sequencing⁶⁴. Du et al. optimized the production plan and scheduling of prefabricated components to reduce costs, enhance engineering efficiency, and improve the capacity of prefabricated component manufacturers to handle uncertain events⁶⁵.

Research gaps

The literature review reveals an increasing focus on the multi-objective optimization and model solving of prefabricated buildings among scholars. These studies highlight the optimization objectives of engineering projects, explore the related research on prefabricated components, and compare and apply intelligent algorithms. Although these existing studies offer valuable insights, there are still research gaps that need to be addressed:

• (1) Research objectives: Currently, optimization research objectives for construction projects primarily revolve around cost and duration in traditional fields. However, with the growing urgency of climate issues, carbon emissions have become a significant factor to consider in the development of prefabricated buildings. Nevertheless, existing research on carbon emission optimization in prefabricated buildings often focuses on single-target carbon emissions, neglecting the interrelationships among different influencing factors of prefabricated buildings. Addressing only single-target problems may result in suboptimal overall building performance.

• (2) Research objects: The current focus of optimization studies in prefabricated buildings primarily revolves around the entire building project, with limited research on the optimization of prefabricated components. Existing research on prefabricated components mainly centers around construction quality, supply chain management, and cost. However, there is a lack of studies on the selection of prefabricated component combination schemes during the conceptual design stage. Blindly choosing high-assembly rate schemes or low-cost prefabricated components may not be conducive to the sustainable development of prefabricated buildings.

• (3) Research content: In prefabricated buildings, the determination of different requirements and prefabrication rates during construction significantly impacts the overall benefits of the building. However, current research has not thoroughly analyzed the influence of weight coefficients and precast rate ranges on the composition of prefabricated components. A comprehensive analysis of these factors is necessary to optimize the selection of prefabricated component combinations.

The objective of this study is to propose a multi-objective optimization approach for the structural design of prefabricated building components, taking into account cost, duration, and carbon emissions. Firstly, quantify the cost, duration, carbon emissions, and prefabrication rate of prefabricated building components. And establish a multi-objective optimization model for selecting the combination of prefabricated components. Secondly, utilize the ant colony algorithm to solve the multi-objective optimization model and obtain the Pareto solution set that satisfies the constraints. Finally, conducting scenario analysis on weight coefficients and prefabrication rate ranges allows for a comprehensive evaluation of the impact of these factors on the selection of prefabricated component combinations. The innovations of this study include:

• (1) We propose a multi-objective optimization model that considers the prefabricated component combination from the perspective of cost, duration, and carbon emissions. This model efficiently accounts for a wide range of component types, enabling stakeholders to select an appropriate prefabricated component combination scheme based on their specific conditions and construction requirements. The aim is to minimize costs, shorten durations, and reduce carbon emissions in prefabricated buildings.

• (2) A precise mathematical expression was formulated to quantitatively assess the cost, duration, carbon emissions, and prefabrication rate of the prefabricated component combination during the materialization stages. This expression fully considers the direct influence of duration and carbon emission targets on the cost, as well as the variations that arise from different types of components in the production, transportation, and construction stages.

• (3) By considering different construction demands, conducting scenario analysis on weight coefficients and prefabrication rate ranges can provide a comprehensive assessment of the impact of weight coefficients and prefabrication rates on the selection of prefabricated component combinations. This analysis helps decision-makers understand the trade-offs and advantages of different component combinations under various construction demands, enabling them to make optimal decisions.

The remaining sections are organized as follows: the third section introduces the methodology and the establishment of multi-objective optimization model, the methodology mainly includes the solution of multi-objective optimization problem and ant colony algorithm, and the establishment of multi-objective

optimization model is mainly developed from the cost, duration and carbon emission optimization objectives and prefabrication rate constraints. The fourth section presents the solution results, including the Pareto chart, the selection results of component processes and the analysis of optimization effects. The fifth section is the discussion section, primarily focusing on the impact of reduced construction duration, reduced carbon emissions, and carbon trading prices on the overall cost of prefabricated buildings. It also addresses the limitations of the study. The research summary is presented in the sixth section.

Methodology

Multi-objective optimization problem

The objective of a multi-objective optimization problem is to efficiently allocate resources in order to minimize the consumption of production materials while maintaining a constant output⁶⁶. This theory has been applied in various fields, including economics, systems engineering, construction projects, and production scheduling. In the context of construction projects, multi-objective optimization primarily involves the comprehensive optimization of indicators such as project duration, cost, safety, and carbon emissions. By utilizing relevant theories and methods of multi-objective optimization, the optimization problems in construction projects can be effectively addressed⁶⁷. The multi-objective optimization problem is typically formulated as a mathematical model, represented by equation (1).

$$\left\{ \begin{gathered} \min Y = \left( {f^{\prime}\left( x \right),f^{\prime\prime}\left( x \right), \cdots } \right),x \in T^{m} \hfill \\ s.t.g^{\prime}\left( x \right) \le 0,h^{\prime}(x) \ge 0 \hfill \\ \end{gathered} \right.$$

(1)

where Y is the value of the objective function,$f^{\prime}\left( x \right),f^{\prime\prime}\left( x \right), \cdots$ are the expressions of the mathematical functions of each sub-objective, $T^{m}$ are the solution sets of feasible solutions, and $g^{\prime}\left( x \right),h^{\prime}(x)$ are the constraints of the objective function.

When conducting multi-objective optimization, it is crucial to consider the requirements of each sub-objective comprehensively. However, in practical situations, these sub-objectives often have mutual restrictions and contradictions, making it challenging to achieve optimal results simultaneously. Therefore, it is necessary to consider the proportion of sub-objectives in the overall objective and the optimization scenarios of each sub-objective to achieve overall optimization⁶⁸. Traditional optimization methods are unable to directly solve multi-objective optimization problems. Typically, these problems are transformed into single-objective optimization problems by constructing a comprehensive objective function. Various methods are employed for this purpose, including objective programming⁶⁹, constraint methods⁷⁰, hierarchical sequence methods⁷¹, efficiency coefficient methods⁷², and aggregation functions⁷³. Among these methods, the aggregation function method is widely used and has a solid theoretical basis. Therefore, this paper adopts the aggregation function method to address the multi-objective optimization problem. The aggregation function method combines multiple sub-goals into a single objective optimization problem by assigning weights to each sub-goal. If there are n sub-objectives, v_i represents the weight of the i-th sub-objective, and the weights satisfy the condition: ${\sum }_{i=1}^{n}{v}_{i}=1$.

Ant colony algorithm

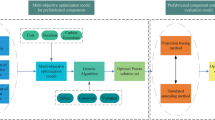
Once the multi-objective optimization problem is formulated and transformed into a solvable model, it is crucial to select an appropriate algorithm for solving it. The ant colony algorithm, known for its high level of integration and parallelism, is chosen in this study to solve the multi-objective optimization model. Figure. 1. illustrates the optimization process of the ant colony algorithm for the selection of prefabricated component combinations.

Fig. 1

Ant colony algorithm component combination optimization.

Figure. 1. illustrates the process of using the ant colony algorithm to optimize the component combination. The input variables include the project’s control objectives, such as contract price, target duration, carbon emission limit, and prefabrication rate requirements. It also includes basic information about the cast-in-place and prefabricated components involved in the project, as well as the weights assigned to each sub-objective.

Once the input variables are provided, the ant colony algorithm is employed to select the components from a multi-objective optimization perspective. The output variables obtained from the algorithm include the optimal set of prefabricated component combinations, along with the corresponding total cost, total duration, total carbon emissions, and prefabrication rate of the project. Figure. 2. presents the specific steps involved in solving the multi-objective optimization model of prefabricated component combination using the ant colony algorithm. The steps include:

Fig. 2

Flow chart of ant colony optimization.

Pseudocode

• Initialize the parameters;

• Input parameter;

• NC=1;

• Randomly generate a set of initial solutions;

• Calculate the values of the time, cost and carbon emission sub-objective functions, respectively.

• Calculation of weights;

• Calculate the target composite value.

• NC=2;

While (NC≤NC_max)

• Updating pheromones.

• Calculate the visibility of each side path and the probability of ants choosing each construction process for the next step;

• Selecting paths for each ant (generating a set of solutions);

• Calculation of time, cost and carbon emission sub-objective function values;

• Calculation of weights;

• Calculate the target composite value;

• NC=NC+1;

End while

Finding the Pareto solution.

End

• (1) Variable definition: The ant colony algorithm relies on several key parameters that govern its iterative process. These parameters include the number of cycles (N), the number of ants (m), the significance of pheromone (α), the significance of heuristic factors (β), the intensity of pheromone (Q), and the volatility of pheromone (p).

• (2) Variable initialization: Prior to executing the algorithm, all parameters are initialized. Each ant is assigned a random path from the starting point to the end point, representing a construction process that is randomly selected for each component experienced by the ant. This initialization process effectively simulates the construction process and represents a feasible solution for the project.

• (3) Calculation of project metrics: The algorithm calculates various metrics for the engineering project, including cost, duration, carbon emission, and prefabrication rate. These metrics are determined using a weighted formula, as shown in equation (2), where the weights assigned to each subitem determine their relative importance in the final evaluation of the project.

  $$\begin{gathered} rt = a;{\text{ rc = b;}}re = c; \, \hfill \\ r = rt + rc + re;w_{t} = rt/r;w_{c} = rc/r; \, w_{e} = re/r \hfill \\ \end{gathered}$$

  (2)

In the equation, rt, rc, and re represent the weights of the sub-objectives for duration, cost, and carbon emissions, respectively. a, b, and c denote the weighted values for duration, cost, and carbon emissions sub-objectives. r is the sum of the weighted values for duration, cost, and carbon emissions sub-objectives, while $w_{t}$, $w_{c}$ and $w_{e}$ indicate the proportions of the weights of the duration, cost, and carbon emissions sub-objectives relative to the total sum.

Based on this, the total project production time, cost, carbon emissions, and prefabrication rate of each ant along the path were calculated, representing the objective function value of each sub-item.

• (4) Assign weights and calculate the value of the composite objective function. Assign weights to each sub-objective of cost, project duration, and carbon emissions. This paper will perform sensitivity analysis on the results of multi-objective optimization based on different weights. Therefore, a fixed weight method is used to assign target weights. The multi-objective optimization problem is transformed into a single-objective optimization problem using the aggregation function method after the weights are assigned. When solving the multi-objective optimal solution, the optimal solution is required to:

• ① The smaller the value of the composite objective function, the better the corresponding optimal solution.

• ② Each relaxation goal is dimensionless and the concept of deviation degree is introduced, where the deviation of each optimization goal from the ideal solution affects the overall objective.

Therefore, the composite objective function is as follows:

$$f\left( x \right) = v_{t} \frac{{Z_{t} - Z_{t}^{\min } + r}}{{Z_{t}^{\max } - Z_{t}^{\min } + r}} + v_{c} \frac{{Z_{c} - Z_{c}^{\min } + r}}{{Z_{c}^{\max } - Z_{c}^{\min } + r}} + v_{e} \frac{{Z_{e} - Z_{e}^{\min } + r}}{{Z_{e}^{\max } - Z_{e}^{\min } + r}}$$

(3)

In the equation, $f\left( x \right)$ represents the comprehensive objective function value, while Z_t, Z_c, and Z_e denote the total duration, total cost, and total carbon emissions, respectively, after the ant completes its path. $Z_{t}^{\min }$, $Z_{c}^{\min }$, and $Z_{e}^{\min }$ represent the minimum values of total duration, total cost, and total carbon emissions after the ant completes its path, while $Z_{t}^{\max }$, $Z_{c}^{\max }$, and $Z_{e}^{\max }$ denote the maximum values of total duration, total cost, and total carbon emissions, respectively. The variable r is a random number uniformly distributed between (0, 1). The introduction of the random number r is intended to prevent the occurrence of invalid or zero values in the comprehensive objective function.

• (5) Pheromone update. The calculation of the pheromone concentration left by ants on each path is based on the pheromone intensity of ants and the corresponding composite objective value. The calculation formula is as follows:

  $$f(x) = \left\{ \begin{gathered} \frac{Q}{f\left( k \right)},{\text{If the ith ant passes through path (i, j)}} \hfill \\ 0 \, ,{\text{ Others}} \hfill \\ \end{gathered} \right.$$

  (4)

In the equation, Q is a constant that represents the total amount of pheromone released by an ant after completing one cycle. $f\left( k \right)$ denotes the comprehensive values of duration, cost, and carbon emissions for the k-th ant.

• (6) Calculation of ant path selection probability. The main factors influencing the ant’s path selection are the pheromone concentration and path visibility. Among them, the pheromone concentration of the path is given by:

  $$\tau_{ij} \left( {nc} \right) = \rho \times \tau_{ij} \left( {nc - 1} \right) + \vartriangle \tau_{ij}$$

  (5)

where (i, j) represents the current component adopting construction technology i and the next component adopting construction technology j. And $\tau_{ij} \left( {nc} \right)$ and $\tau_{ij} \left( {nc - 1} \right)$ represent the pheromone concentration on the path after the NC cycle and the NC-1 cycle. ρ is the retention coefficient of pheromone on the path, which is a constant between 0 and 1. ∆τ_ij represents the increment of pheromone on the path after one cycle, which can be calculated using the following formula:

$$\vartriangle \tau_{ij} { = }\sum\nolimits_{k = 1}^{m} {\vartriangle \tau_{ij}^{k} }$$

(6)

where m denotes the total number of ants; $\vartriangle \tau_{ij}^{k}$ denotes the pheromone left on the (i,j) route after the k-th ant completes a cycle.

Path visibility:

$$\lambda_{ij} = v_{t} \frac{{t_{j}^{\max } - t_{j} + r}}{{t_{j}^{\max } - t_{j}^{\min } + r}} + v_{c} \frac{{c_{j}^{\max } - c_{j} + r}}{{c_{j}^{\max } - c_{j}^{\min } + r}} + v_{e} \frac{{e_{j}^{\max } - e_{j} + r}}{{e_{j}^{\max } - e_{j}^{\min } + r}}$$

(7)

where $\lambda_{ij}$ is the path visibility, $t_{j}^{\max }$ and $t_{j}^{\min }$ are the maximum and minimum values, respectively, for the project duration required for the next component under different construction technologies, $c_{j}^{\max }$ and $c_{j}^{\min }$ are the maximum and minimum costs, respectively, for the next component in different construction technologies; $e_{j}^{\max }$ and $e_{j}^{\min }$ are the maximum and minimum carbon emission values, respectively, for the next component in different construction technologies.

Therefore, by considering the pheromone concentration of the path and the path visibility, the selection probability of ants for each path can be calculated as follows:

$$P_{ij}^{k} = \left\{ \begin{gathered} \frac{{\left[ {\tau_{ij} } \right]^{\alpha } \left[ {\lambda_{ij} } \right]^{\beta } }}{{\sum\nolimits_{{k \in allowed_{k} }} {\left[ {\tau_{ij} } \right]^{\alpha } \left[ {\lambda_{ij} } \right]^{\beta } } }},j \in allowed_{k} \hfill \\ 0{\text{ ,Others}} \hfill \\ \end{gathered} \right.$$

(8)

where $P_{ij}^{k}$ denotes the probability that the k-th ant chooses route (i,j), α represents the relative importance of pheromones and β represents the relative importance of path visibility.

• (7) Path selection for ants. The formula for each ant to select its path is as follows:

  $$j = \left\{ \begin{gathered} \arg \max_{{k \in allowed_{k} }} \left[ {\tau_{ij} } \right]^{\alpha } \left[ {\lambda_{ij} } \right]^{\beta } ,{\text{if }}q \prec q_{0} \hfill \\ \, U,{\text{others}} \hfill \\ \end{gathered} \right.$$

  (9)

  where q is a random number uniformly distributed between 0 and 1; q₀ is a given parameter between 0 and 1; U is selected according to the formula (8).

• (8) Repeat the process multiple times until the end of the cycle. If the loop reaches the pre-set maximum number of iterations, the loop stops. Otherwise, the program continues to run and proceeds to the next iteration until the maximum number of iterations is reached. After the end of the loop, the Pareto solution set is found, and the Pareto solution set that satisfies the constraints is selected by setting constraints.

Definition of the research scope

The entire life cycle of a building can be categorized into five stages: building material production, building material transportation, building construction, building operation, and building demolition. Among these stages, the building operation phase accounts for the majority of energy consumption, approximately 80%^74,75, while the materialization phases only consume about 20% of the energy^76,77. Current research on carbon emissions primarily focuses on reducing energy consumption and carbon emissions during the building’s operation phase. Numerous studies suggest that promoting energy-saving technologies can effectively reduce energy consumption during the operation phase of buildings^78,79. However, it should be noted that energy-efficient buildings often require more advanced technologies compared to traditional buildings, which can potentially increase energy consumption during their construction phase^19,76. Moreover, it is important to recognize that the implementation of energy-saving technologies can lead to an increase in implied carbon emissions, particularly during the materialization phase^80,81,82. Meanwhile, carbon emissions during the operational phase of a building are mainly associated with building materials, heating and cooling systems, lighting, domestic hot water systems, and other factors. When the building energy systems are the same, different types of buildings have similar carbon emissions during the operational phase. The optimization study proposed in this research primarily focuses on the impact of different types of component choices, whether cast-in-place or prefabricated construction techniques on cost, construction duration, and carbon emissions. It does not differentiate between the operational phases of cast-in-place and prefabricated buildings, including their building energy systems. Therefore, from the perspective of the building’s life cycle, the carbon emissions studied in this paper are mainly determined by the materialization stages of the building. Consequently, the scope of the cost, duration, and carbon emissions estimation for prefabricated components is limited to the materialization stages of the building, including the production and transportation of building materials and the construction process, as shown in Figure. 3.

Fig. 3

Boundary Measurement.

The definition of the research scope plays a crucial role in measuring the sub-objectives. By clearly defining the measurement scope, we can determine the specific scope to be studied and establish a basis for setting and measuring the sub-objectives. In this paper, the cost of prefabricated components is a comprehensive cost that takes into account the impact of duration and carbon emissions on cost. This includes the construction cost, duration cost, and carbon emission cost. The duration refers to the total number of calendar days from the start to the completion of the project⁸³. In actual projects, the prefabricated components should be in place before the construction of the project. Therefore, the duration of prefabricated components mainly refers to the time from when the components enter the construction site to the completion of their installation. This primarily includes assembly processes such as lifting and installation of components. The time consumed in the production and transportation of the prefabricated components is not included in the calculation of the duration of the prefabricated components. The carbon emissions of prefabricated components are mainly calculated in accordance with the"Building Carbon Emissions Calculation Standard"(GB/T 51366-2019). This calculation includes the implied carbon emissions of building materials in the production of prefabricated components, as well as the carbon emissions generated by direct energy consumption during transportation and construction⁸⁴.

Construction of the cost target model

The cost objective function proposed in this paper is a comprehensive cost that considers the duration and carbon emission factors. It includes the construction and installation cost, duration cost, and carbon emission cost. The construction and installation cost refers to the expenses incurred for materials, labor, equipment, and other aspects required in the construction project. The duration cost primarily takes into account the impact of the project’s completion time on the overall cost. The carbon emission cost represents the additional expenses associated with carbon emissions generated during the construction process. By calculating the comprehensive cost of prefabricated components, a better assessment can be made regarding their economy and rationality in the context of building energy conservation. Selecting components based on comprehensive cost considerations ensures not only economic cost efficiency and duration efficiency but also environmental sustainability by addressing carbon emissions. This enables more informed and sustainable decision-making processes.

The construction and installation costs of components can be divided into four main parts: direct costs (including labor costs, material costs, and machinery costs), management fees, profits, and taxes. The proportion of management fees, profits, and taxes is determined by referring to the Comprehensive Quota of Housing Construction and Decoration Engineering in Guangdong Province (2018). Taking the first floor frame column as an example, through the use of Quanta BIM civil construction measurement platform GTJ2021 (Version number: 1.0.29.2) (https://www.glodon.com/product/145.html) can directly calculate the cost of the first floor frame column, the direct cost of the calculation of the content of the following Table 1. Therefore, the construction and installation cost of a component can be calculated as shown in equations (10) and (11).

$$C_{J} = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {C_{ij} X_{ij} } }$$

(10)

$$C_{ij} = \sum\nolimits_{k \in K} {m_{ij}^{k} c_{ij}^{k} + M_{ij} + O_{ij} + T}_{ij}$$

(11)

where C_J represents the construction and installation cost; n represents the component type; m_i represents the i-th component with the construction technology m_i; C_ij represents the cost of the i-th component under the j-th construction technologies; X_ij represents whether the construction technology j is applied to the component type i; $r_{ij}^{k}$ represents the manpower and machinery consumption for No. k under the construction technology.

Table 1 Direct cost components of first floor frame columns.

m_i and the construction technologies j of the i-th component; $c_{ij}^{k}$ represents the unit cost of manpower and machinery for No. k under the construction technology mi and the construction technologies j of the i-th component; M_ij, O_ij, and T_ij respectively represent the management fee, profit, and tax under the construction technologies j of the i-th component.

The adherence of a project’s schedule to the planned timeline can have a direct impact on costs. An extension of the project duration typically leads to increased costs, while a reduction in the project duration can lower costs. The most significant direct impacts arise from measures project costs and the incentives for early completion or penalties for delays in completion.

• (1) The cost of measures refers to the expenses incurred to meet the requirements of the project construction process. Its purpose is to ensure environmental protection and safety during the construction process and provide necessary temporary facilities and measures. The cost of measures can be influenced by the project duration. Each day ahead of schedule can reduce the cost of measures by one day, while each day of delay can increase the cost of measures by one day. Examples of measures include scaffolding engineering and vertical transportation engineering.

• (2) If the actual duration exceeds the target duration due to uncertainties and changes during the project implementation, the defaulting party is liable for breach of contract. According to the Civil Code of the People’s Republic of China, the parties involved can agree that the breaching party should pay liquidated damages to the other party based on the circumstances of the breach. They can also agree on the method of calculating the amount of compensation for the losses caused by the breach. Additionally, when the construction party completes the project ahead of schedule through effective construction organization and management, the construction unit may reward the construction party based on the number of days the project is completed in advance.

Therefore, the impact of the duration on cost can be defined as follows:

$$C_{T} { = }\eta \Delta {\text{T = }}\left( {\eta_{A} + \eta_{P} } \right)\Delta {\text{T}}$$

(12)

where C_T represents the duration cost; $\eta$ represents the cost of delayed or early completion per unit duration, which includes the cost of measures and incentives or penalties; $\eta_{A}$ represents the cost of measures per unit period; $\eta_{P}$ represents the cost of incentives or penalties per unit period; $\Delta {\text{T}}$ represents the number of days the project is delayed or completed ahead of schedule.

The cost of carbon emissions refers to the social, environmental, or economic cost associated with the production of greenhouse gas emissions. Carbon trading is an economic tool and policy measure developed to address climate change and reduce greenhouse gas emissions. It involves the trading and exchange of carbon emission rights through market mechanisms. The fundamental principle of carbon trading is to limit the carbon emissions of enterprises or organizations by establishing carbon emission quotas, also known as carbon emission permits or carbon credits. In Shenzhen, the Interim Measures for the Management of Carbon Emission Rights Trading of Buildings are implemented. The building carbon quotas in Shenzhen are established using the“baseline system”method. This mechanism aims to control carbon emission intensity by implementing energy consumption quota management for buildings based on the energy consumption intensity quota value specified in the energy consumption quota standard of Shenzhen. Buildings that fall below the energy consumption limit line can sell their excess quota amount, while buildings that exceed the energy consumption limit can purchase additional quota amounts from the market or face penalties. The mechanism is illustrated in Figure. 4. below:

Fig. 4

Carbon trading mechanism diagram.

The cost of carbon emissions under carbon trading is calculated as the actual emissions multiplied by the unit cost of carbon emissions. Currently, the unit carbon emission cost includes the carbon trading market price, carbon tax price, and marginal cost of carbon emission reduction. However, it is important to note that China has not yet implemented a carbon tax, so there is no official data available to directly reference for carbon tax prices. Additionally, different countries have different tax subjects, tax methods, and tax rates for carbon taxes, so directly referring to prices from other countries may not be entirely applicable to the Chinese context. Determining the marginal cost of carbon emission reduction is complex, as it involves various factors. The exact cost is difficult to determine due to inconsistent calculation methods and data sources, leading to different results in different studies. This makes it challenging to compare and reference. In the case of carbon trading market prices, China has established a national unified carbon emission trading market in 2021. The Chinese government has been actively promoting the development of the carbon market and has introduced several policy measures to support carbon trading. Therefore, this paper selects the carbon trading market price as the unit carbon emission cost, which provides a more realistic estimate of the carbon emission cost.

Therefore, the cost of carbon emissions can be defined as follows:

$$C_{E} { = }\varphi \Delta E$$

(13)

where C_E represents the cost of carbon emissions; $\varphi$ represents the cost per unit of carbon emissions, which is the carbon trading market price; $\Delta E$ represents the amount of allowances required or in excess for carbon emissions.

In summary, the comprehensive cost of the project can be calculated as follows:

$$C{ = }C_{J} + C_{T} + C_{E}$$

(14)

where C represents the total cost of the project; C_J is the cost of construction and installation; C_T represents the duration cost; C_E represents the cost of carbon emissions.

Construction of the duration target model

The construction quota of an enterprise refers to the standardized quantity of labor, machinery, material consumption, and management expenses required by a construction enterprise to complete qualified products based on its construction technology and management level⁸⁵. In this paper, the duration of the processes involved in the construction of the component is calculated based on the enterprise time quota in Shenzhen. This allows us to estimate the duration required for each component, which can be calculated as shown in equations (15) and (16).

$$T = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {T_{ij} X_{ij} } }$$

(15)

$$T_{{{\text{ij}}}} = \sum\nolimits_{l \in L} {\frac{{n_{ij}^{l} t_{ij}^{l} }}{{a_{ij}^{l} b_{ij}^{l} }}}$$

(16)

where T represents the total project duration; n represents the component type; m_i represents the i-th component with the m_i construction technology; T_ij represents the duration of the i-th component under the j-th construction technology; X_ij indicates whether the construction technology j is applied to the component type i; $n_{ij}^{l}$ represents the consumption required by the l-th process of the j-th construction technology for the construction process of the i-th component; $t_{ij}^{l}$ represents the time quota for the l-th construction process under the j-th construction technology of the i-th component; $a_{ij}^{l}$ and $b_{ij}^{l}$ represent the number of stage shifts arranged for the l-th construction process and the number of each stage shift under the j-th construction technology of the i-th component.

Construction of the carbon emission target model

In this paper, the carbon emissions of prefabricated components are primarily calculated based on the"Building Carbon Emission Calculation Standard"(GB/T 51366-2019). The basic equation for carbon calculation is as follows: Carbon emissions of the building = Energy and material consumption × Carbon emission factor. The carbon emissions of the component should be calculated for different stages, and the carbon emissions for the entire life cycle can be obtained by accumulating the calculation results for each segment. The materialization stage of construction is primarily divided into three stages: production of building materials, transportation of building materials, and construction of buildings. Therefore, the calculation of carbon emissions for components can be expressed using equations (17) to (21):

$$E = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {E_{ij} X_{ij} } }$$

(17)

$$E_{ij} { = }E_{scij} + E_{ysij} + E_{jzij}$$

(18)

$$E_{{{\text{scij}}}} { = }\sum\nolimits_{k = 1}^{n} {M_{ijk} F_{ijk} }$$

(19)

$$E_{{{\text{ysij}}}} { = }\sum\nolimits_{k = 1}^{n} {M_{ijk} D_{ijk} T_{ijk} }$$

(20)

$$E_{{{\text{jzij}}}} { = }\sum\nolimits_{k = 1}^{n} {N_{ijk} NF_{ijk} }$$

(21)

where E represents the total carbon emissions of the project; n represents the component type; E_ij represents the carbon emissions of the i-th component under the j-th construction process. X_ij indicates whether the construction technology j is applied to the component type i; E_sij represents the carbon emissions during the production of building materials stage for the i-th component and the j-th construction process. E_ysij represents the carbon emissions during the transportation of building materials stage for the i-th component and the j-th construction process. E_jzij represents the carbon emissions during the construction process of the i-th component under the j-th construction technology. M_ijk represents the consumption of the i-th component, the j-th construction process, and the k-th main building materials; F_ijk represents the carbon emission factor of the i-th component, the j-th construction process, and the k-th main building materials. D_ijk represents the average transport distance for the first component, the first construction technology, and the first main building materials. T_ijk represents the carbon emission factor per unit weight of transportation distance under the transportation mode for the i-th component, the j-th construction process, and the k-th building materials; N_ijk represents the total consumption of energy k for the j-th construction process of the i-th component; NF_ijk represents the carbon emission factor of the i-th component, the j-th construction process, and the k-th energy source.

Constraints

The prefabrication rate is a significant factor in evaluating prefabricated buildings. Various provinces and cities in China have issued local evaluation standards based on their development scenarios and regional characteristics⁸⁶. In this paper, the case study is located in Shenzhen, Guangdong Province, so the calculation of the prefabrication rate primarily follows the local standards of Shenzhen. The calculation method for the prefabrication rate and assembly rate, as specified in the Rules for Calculating the Prefabrication Rate and Assembly Rate of Shenzhen Residential Industrialization Projects issued by the Shenzhen Municipality, is shown in Equation (22).

$${\text{V}}_{{\text{Prefabrication rate}}} { = }\frac{{{\text{V}}_{{\text{Standard floor precast concrete components}}} }}{{{\text{V}}_{{\text{Standard layer full volume}}} }} \times 100{\text{\% }}$$

(22)

From the above formula for calculating the prefabrication rate, it can be observed that the overall prefabrication rate is the sum of the prefabrication rates of each component. Therefore, the prefabrication rate of each component is determined by the ratio of the volume of that component to the total volume of all components. Thus, the calculation of the engineering prefabrication rate can be expressed as equations (23) and (24):

$$A = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {A_{ij} X_{ij} } }$$

(23)

$$A_{{{\text{ij}}}} { = }\frac{{V_{{\text{Prefabricated components}}} }}{{V_{{\text{Total volume}}} }}$$

(24)

where A represents the total prefabrication rate of the project; n represents the component type; A_ij represents the prefabrication rate of the i-th component under the j-th construction technology. X_ij indicates whether the construction technology j is applied to the component type i; V_{Prefabricated} components represents the volume of the i-th component when the prefabrication process is used; V_total volume represents the total volume of all components.

Construction model

The multi-objective optimization model is established based on the following hypotheses:

• 1. Establishing a multi-objective optimization model is approached from the contractor’s perspective, within the framework of compliance with construction regulations, safety standards, and a sufficient market context. During the conceptual design phase, the model facilitates the selection of prefabricated components in a scientific and rational manner, thereby assisting the contractor in reducing costs, duration, and carbon emissions during the materialization phase, ultimately leading to better overall benefits for the construction project.

• 2. The benchmark scenario for comparison is selected as all-cast-in-place buildings. The optimization level of cost, duration, and carbon emissions for the prefabricated scheme needs to be compared and evaluated against the all-cast-in-place scenario. Therefore, special consideration is given to the comparison with the all-cast-in-place architecture during the model formulation.

• 3. The main focus of the research is on the optimization of the combination of selected components such as columns, beams, and slabs. Therefore, the total construction cost is the sum of the costs of the selected components, and the costs of other non-selected components such as doors and windows are not included in the total cost. The same applies to the duration and carbon emissions.

• 4. The objective of this paper is to explore the multi-objective optimization study of the selection between cast-in-place or assembly construction technologies for components, assuming that the building structure has already been determined. It does not consider the changes in structural stress caused by the cast-in-place or prefabrication of components and their impact on other component structures.

Based on the construction of sub-objective models for cost, duration, carbon emissions, and prefabrication rate constraints, the multi-objective optimization model is formulated as follows.

Objective function:

$$\left\{ \begin{gathered} \min C = C_{J} + C_{T} + C_{E} { = }\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {C_{ij} X_{ij} + \left( {\eta_{A} + \eta_{P} } \right)\Delta {\text{T}} + \varphi \Delta E} } \hfill \\ \min T{ = }\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {T_{ij} X_{ij} } } { = }\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {\left( {\left( {\sum\nolimits_{l \in L} {\frac{{n_{ij}^{l} t_{ij}^{l} }}{{a_{ij}^{l} b_{ij}^{l} }}} } \right)X_{ij} } \right)} } \hfill \\ \min E = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {E_{ij} X_{ij} } } = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {\left( {E_{scij} + E_{ysij} + E_{jzij} } \right)X_{ij} } } \hfill \\ \end{gathered} \right.$$

(25)

Constraints:

$$f\left( x \right) = \left\{ \begin{gathered} X_{ij} = 1,{\text{The ith member selects the jth construction process}} \hfill \\ X_{ij} = 0,{\text{The ith member does not choose the jth construction process}} \hfill \\ \end{gathered} \right.$$

(26)

$\sum\nolimits_{j = 1}^{{m_{i} }} {X_{ij} = 1}$ The i-th component can only choose one construction process (27)

$$A_{\min } \le A = \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {A_{ij} X_{ij} } } { = }\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{{m_{i} }} {\left( {\frac{{V_{{\text{Prefabricated components}}} }}{{V_{{\text{Total volume}}} }}} \right)X_{ij} } } \le A_{\max }$$

(28)

$$C \le C^{*} ,T \le T^{*} ,E \le E^{*} ,\eta_{P} \le \eta_{P}^{*}$$

(29)

In the formula, $\Delta {\text{T = T - T}}{\prime} ,\Delta E{\text{ = E - E}}{\prime}$, T represents the duration of the prefabricated component scheme, T’ represents the construction period of the all-cast-in-place building, E represents the carbon emission of the prefabricated scheme, E’ represents the carbon emission of the all-cast-in-place building, A_max represents the maximum prefabrication rate of the building, A_min represents the minimum prefabrication rate of the building, C* represents the contract price, T* represents the target duration, C* represents carbon emission allowances, $\eta_{P}$ represents the cost of incentives or penalties per unit duration, and $\eta_{P}^{*}$ represents the upper limit of the duration reward or penalty.

Results

Case background

The project is situated in Shenzhen, Guangdong Province, and it features a frame structure with a construction area of 1054.86 m². The building has three floors above ground. The prefabricated construction technology for frame structures is relatively mature, making it relatively easier to achieve a high prefabrication rate. The types of prefabricated components selected for this study mainly include frame columns, frame beams, composite floor slabs, walls, and staircases. The selection of these components is primarily based on the following considerations: Firstly, these components serve as the main load-bearing and enclosing elements of the frame structure. Secondly, the prefabrication technology for these components is well-established in the Shenzhen area, with a high degree of standardization, meeting the requirements of the"Technical Standards for Prefabricated Concrete Structures"(GB/T 51231-2016). Furthermore, these components have a significant impact on the building’s cost, duration, and carbon emissions. To model the building, both cast-in-place components and prefabricated components were created using the BIM civil measurement platform GTJ2021 (Version number: 1.0.29.2) (https://www.glodon.com/product/145.html) by Guanglida and PKPM-PC 2023 R 2.4 structural calculation and analysis software (https://product.pkpm.cn/downloadlist). The project scenario is depicted in Figure. 5. below.

Fig. 5

Three-dimensional view and the layer plan of the building project.

In Figure. 5, (a) represents the three-dimensional model created using GTJ2021, (b) represents the three-dimensional building model created using PKPM-PC, and (c) represents the floor plan of the building. By establishing both cast-in-place and prefabricated models of the building, the quantities of the selected components can be summarized and calculated. Based on this, formulas (10) to (24) were utilized to calculate the cost, duration, carbon emissions, and prefabricated rate of the components under different construction technologies. The results of these calculations are summarized in Table 2.

Table 2 Summary table of parameters.

Based on the analysis of Table 2, it is evident that cast-in-place components have a lower cost compared to prefabricated components, while prefabricated components have shorter durations and lower carbon emissions compared to cast-in-place components. This highlights the inherent trade-offs and conflicts among different objectives. Therefore, it is crucial to select component combinations in a rational manner to achieve overall optimization. To facilitate the calculation of the program, each component’s construction process is assigned a number based on its construction sequence. These numbers are indicated in Table 2. By aggregating the cost, duration, and carbon emissions of components under different construction technologies, the variables $C_{ij} ,T_{ij} ,E_{ij}$ can be defined in the multi-objective optimization model.

Referring to the"Guangdong Province Housing Construction and Decoration Engineering Comprehensive Quota (2018)", the daily cost of using comprehensive scaffolding for an external wall area of 844.2 m² is calculated to be 266.02 yuan. Similarly, the daily cost of vertical transportation within the building, within a range of 20 m, is calculated to be 1285.16 yuan. Therefore, the total cost for this case $\eta_{A}$ is calculated to be 1551.18 yuan per day. According to the"Specification for the Valuation of the Bill of Quantities of Construction Projects"(GB50500-2018), the maximum limit for compensation due to delays is set at 5% of the contract price. Additionally, the"Interim Provisions on the Implementation of Early Completion Awards for Construction Projects"propose that the proportion of bonuses and penalties should be equal. The amount of the award (or penalty) for each day of early completion (or delay) can be calculated based on the ease of construction of the project, ranging from 0.02% to 0.04% of the project budget. Furthermore, in case of cost claim disputes caused by delays in the construction period, the contractor is required to pay liquidated damages to the owner. According to the Shenzhen Housing and Construction Bureau, the amount of liquidated damages is set at four thousandths of the contract price per day. For this case, the unit cost for rewards or penalties is set at 0.04% of the contract price. With a contract price of 9.53 × 10⁵ yuan, the cost of reward or penalty per unit period $\eta_{P}$ is calculated to be 381.2 yuan per day, and the value of variable $\eta_{P}^{*}$ is 47,650 yuan.

The Shenzhen Carbon Emission Exchange (SZEE) is a carbon emission trading market established by the Shenzhen Municipal Government in 2013. It is the first city-based carbon emission exchange in China. The SZEE facilitates the trading of carbon emission allowances and aims to promote the reduction of carbon emissions. According to the trading data released by the SZEE, the average price of carbon emission trading over the past five months is illustrated in Figure. 6.

Fig. 6

Average carbon emission price of shenzhen carbon exchange.

Since the project is located in Shenzhen, Guangdong Province, this paper considers the carbon emission price based on the prices of the Shenzhen Carbon Emission Exchange. To capture the long-term trend and market equilibrium, and to provide a comprehensive reflection of the market price level while avoiding the influence of a single point in time, this paper selects the average carbon emission price from the Shenzhen Carbon Emission Exchange over the past five months, which is 62.76 yuan/ton.

This study determined the algorithm parameter settings through systematic sensitivity analysis and multiple experiments. Firstly, based on the initial ranges suggested in the literature, the method of controlling variables was employed to test the effects of different parameter combinations on optimization results. Through numerous comparative experiments, it was found that when the number of iterations N = 200 and the number of ants m = 35, the algorithm achieves the best balance between computational efficiency and solution quality. Further testing indicated that the combination of α = 1.1 and β = 0.6 yields optimal convergence characteristics, while the settings of Q = 15 and p = 0.15 effectively maintain the positive feedback mechanism of pheromone. Therefore, the determined parameters are as follows: cycle number (N) = 200, ant number (m) = 35, pheromone importance (α) = 1.1, heuristic factor importance (β) = 0.6, pheromone intensity (Q) = 15, pheromone evaporation rate (p) = 0.15.

Scenario setting

The optimization of the prefabricated component combination using the ant colony algorithm is influenced by the weights assigned to each sub-objective and the range of the prefabrication rate. The weight coefficients reflect the different importance and trade-offs among the sub-objectives, indicating the requirements or urgency of each sub-objective in the engineering project. The level of prefabrication rate represents the degree of industrialization of the building, and various provinces and cities have specific requirements for the prefabrication rate of prefabricated buildings. To explore the impact of the range of weight coefficients and prefabrication rates on the selection of prefabricated component combinations, this paper conducts a multi-level sensitivity analysis. The specific scenarios for the analysis are depicted in Figure. 7.

Fig. 7

Scenario simulation settings.

In Figure 7, the prefabrication rate is divided into four ranges: 0-20%, 20%−40%, 40%−60%, and above 60%. Scenarios 1, 5, 9, and 13 represent the baseline scenarios within the respective prefabrication rate ranges of 0-20%, 20%−40%, 40%−60%, and above 60%. Scenarios 2, 6, 10, and 14 indicate cost-conscious scenarios within the four prefabrication rate ranges. Scenarios 3, 7, 11, and 15 represent time- conscious scenarios, while scenarios 4, 8, 12, and 16 illustrate carbon emission- conscious scenarios. In total, there are 16 different defined scenarios. Horizontally, within each prefabrication rate range, the difference between scenarios mainly lies in the variation of the weight coefficients of the sub-objectives. Vertically, within each weight coefficient setting, the difference between scenarios primarily lies in the variation of the prefabrication rate range. By comparing scenarios with different weight coefficients within the same prefabrication rate range and scenarios with the same weight coefficients within different prefabrication rate ranges, we can observe the influence of variables at different levels on the selection results. This enables more accurate and reliable decision-making processes.

Algorithm convergence test

To verify the suitability and feasibility of the ant colony algorithm for component combination selection, as well as its ability to quickly and efficiently find optimal solutions, it is necessary to assess the convergence of the algorithm⁸⁷. In this paper, the weight coefficients for cost, duration, and carbon emissions are set to be the same, i.e., rc=rt=re=1 in equation (2). The ant colony algorithm is then executed, and its convergence curve is plotted, as shown in Figure. 8.

Fig. 8

Convergence graph of optimization curve.

In Figures 8 (a), (b), and (c) represent the relationship graphs of the total duration, total cost, and total carbon emissions, respectively, against the number of iterations. These graphs illustrate the corresponding average values of the total duration, total cost, and total carbon emissions for each iteration of the ant colony algorithm. It can be observed from the figure that the convergence curve exhibits a clear convergence trend and is relatively smooth. This indicates that the ant colony algorithm is suitable for solving the multi-objective optimization problem of selecting prefabricated building component combinations. The algorithm demonstrates high operational efficiency and good convergence properties. To quantitatively assess the performance of the algorithm, this study employs two statistical methods: the spacing metric and the one-sample t-test for in-depth analysis. The spacing metric serves as an important measure of the uniformity of the solution set distribution, where smaller values indicate a more uniform distribution of solutions⁸⁸. The results show that the spacing metric values for the three objectives—duration, cost, and carbon emissions—are 4.42, 3702.52, and 6190.46, respectively. This indicates that the use of the Ant Colony Optimization (ACO) algorithm in the multi-objective optimization process can generate a relatively uniform solution set, particularly excelling in terms of duration. For stability validation, we employed the one-sample t-test to evaluate the reliability of the optimization results. The test results indicate that the p-values for the three objectives—duration, cost, and carbon emissions—are 0.995, 0.999, and 0.999, respectively, all of which are well above the significance level of 0.05. This outcome demonstrates that there are no statistically significant differences in the optimization results, indicating that the algorithm exhibits excellent convergence stability. In summary, through the dual validation of the spacing metric and the one-sample t-test, we have not only confirmed the algorithm’s advantages in the uniformity of solution set distribution but also statistically validated its good convergence performance. These quantitative results clearly illustrate that the Ant Colony Optimization algorithm possesses a high degree of stability and adaptability when addressing such multi-objective optimization problems.

Reliability and scalability testing

To validate the applicability of the proposed multi-objective optimization model based on the Ant Colony Optimization (ACO) algorithm in large-scale prefabricated construction projects, this study selected the Harmony Garden project in Shenzhen, Guangdong Province for scalability testing. This project features an 11-story frame structure, as illustrated in Figure 9. Compared to the original three-story frame structure case, the complexity of the number of components and combination schemes has significantly increased, allowing for a more comprehensive assessment of the algorithm’s optimization capabilities in large-scale engineering. The project’s costs, durations, carbon emissions, and prefabrication rates under different construction processes are presented in Table 3.

Fig. 9

Basic building conditions.

Table 3 Summary table of parameters.

This study uses a baseline scenario with equal weight coefficients for cost, duration, and carbon emissions for reliability and scalability testing, specifically setting rc=rt=re= 1 in Equation (2). The Ant Colony Optimization (ACO) algorithm was executed, and its convergence curve is depicted in Figure 10.

Fig. 10

Reliability and scalability test optimization convergence plot.

The ACO algorithm was employed to perform multi-objective optimization on this project case, and the algorithm’s performance was evaluated through the convergence curve and quantitative metrics. Figures 10(a), (b), and (c) illustrate the relationships between the average total duration, total cost, and total carbon emissions with respect to the number of iterations. The trends in total cost, total duration, and total carbon emissions indicate that after approximately 150 iterations, the values of the objective functions stabilize, confirming that the algorithm exhibits good convergence performance. To quantitatively assess the algorithm’s performance, this study employed the spacing metric and one-sample t-test for statistical analysis. In terms of the spacing metric, the values for duration, cost, and carbon emissions were 22.24, 49307.31, and 47879.77, respectively. These results indicate that the ACO algorithm can generate a relatively uniform solution set when addressing large-scale problems, particularly excelling in terms of duration. Furthermore, a t-test was conducted to statistically evaluate the stability of the optimization results. The p-values for duration, cost, and carbon emissions were 0.982, 0.999, and 0.999, respectively, all significantly higher than the critical value of 0.05, confirming the statistical stability of the optimization results. In summary, through quantitative analysis using the spacing metric and one-sample t-test, this study not only validates the superiority of the ACO algorithm in terms of solution set uniformity but also confirms its good convergence when dealing with large-scale projects from a statistical perspective. This indicates that the algorithm possesses high reliability and scalability for complex large-scale projects, providing reliable optimization solutions for practical engineering problems.

Analysis of pareto diagram results

The result of multi-objective optimization is typically not a single optimal solution, but a set of optimal solutions. To better explore the influence of different weights and prefabrication rates on the selection of component combinations, the Pareto diagram of the optimal component combinations is analyzed. In this paper, the ant colony algorithm is employed to obtain the optimal prefabricated component combinations under different scenarios, and Pareto diagrams are drawn for analysis.

(1) Pareto set graph

Using the Matlab.R2019b platform (https://ww2.mathworks.cn/products/matlab.html), the optimal prefabricated component combinations are obtained for different scenarios. The number of optimal solutions may vary depending on the range of prefabrication rates and weights. Figure. 11. illustrates the number of pareto solution sets obtained under different scenarios.

Fig. 11

Number of pareto solution sets under different scenarios.

As shown in Figure. 11, the number of optimal solutions varies depending on the scenario. In the cost-conscious scenario, the number of optimal solutions decreases as the prefabrication rate increases. This is because the cost-conscious scenario tends to select cast-in-place components, and in the low prefabrication rate range, the selection range for cast-in-place components is larger. On the other hand, in the duration and carbon emission-conscious scenarios, the number of optimal solutions increases as the prefabrication rate increases. This is because these scenarios prioritize prefabricated components, and in the high prefabrication rate range, the selection range for prefabricated components is larger. Therefore, the number of Pareto solution sets varies with different weights and prefabrication rate ranges.

(2) Pareto frontier diagram

To gain a better understanding of the impact of different scenarios on the selection of prefabricated component combinations, as well as the associated costs, durations, and carbon emissions, this paper presents the pareto frontier diagram of the optimized component combinations. The result is illustrated in Figure. 12.

Fig. 12

Pareto frontier plots for different scenarios.

In Figures 12(a), (b), and (c), and (d) represent the Pareto frontier charts for the baseline scenario, cost-conscious scenario, duration-conscious scenario, and carbon emission-conscious scenario, respectively. The different colors in the chart represent the range of prefabrication rates. The analysis of the Pareto frontier graph under different scenarios is as follows:

• (1) The influence of weight coefficients on the Pareto frontier graph can be analyzed by observing the position of scatter points on the graph. In the baseline scenario where the weight coefficients of each sub-objective are the same, the selection of the optimal solution is relatively balanced, considering costs, duration, and carbon emissions. The optimal solutions in the baseline scenario aim to minimize the overall objective value by reducing each sub-objective. Therefore, the optimal solutions in the Pareto solution set are evenly distributed, mainly concentrated in the middle part of the three-dimensional graph. In the cost-conscious scenario, where the weight coefficient of cost is higher, changes in unit cost have a greater impact on the objective value compared to changes in unit duration and carbon emissions. In the cost-conscious scenario, the

• selection of cast-in-place components is preferred to achieve a lower overall objective value by directly reducing costs. Therefore, the Pareto solution set is concentrated in the upper right corner of the three-dimensional graph, indicating lower costs. Under the duration-conscious scenario, where the weight of the duration is higher, the variation in the unit duration has a greater impact on the target value compared to the unit cost and carbon emissions. In this scenario, the primary focus is on reducing the duration to achieve the minimum comprehensive target value, leading to the selection of prefabricated components. As a result, the Pareto solution set primarily concentrates on the parts of the 3D graph with lower carbon emissions and shorter construction periods. In the carbon emissions- conscious scenario, due to the relatively small difference in carbon emissions between cast-in-place and prefabricated components compared to cost and duration, the primary approach to minimizing the comprehensive target value is by selecting prefabricated components that reduce carbon emissions or cast-in-place components that have a greater cost reduction than the increment in carbon emissions. Consequently, the Pareto solution set is divided between the parts of the 3D graph with lower carbon emissions and higher costs, and the parts with higher carbon emissions but lower costs.

• (2) The influence of the prefabrication rate range on the Pareto frontier graph can be analyzed by observing the color of the scatter points on the graph. When the prefabrication rate is low, the number of prefabricated components is lower than that of cast-in-place components. Although the duration and carbon emissions are higher, which adds additional costs to the project, the overall construction and installation cost is low. Therefore, the Pareto solution set is mainly located in the upper right part of the graph, representing higher costs, longer durations, and higher carbon emissions. As the prefabrication rate increases, the number of selected prefabricated components also increases. This leads to an increase in the construction and installation cost of the component combinations, but a reduction in carbon emissions and duration. When the assembly rate is high, the number of prefabricated components is higher than that of cast-in-place components. As a result, the optimal solutions in the Pareto solution set are concentrated in the part of the graph with higher costs, lower durations, and lower carbon emissions.

In conclusion, through analyzing the Pareto solution sets under different scenarios, we can conclude that the quantity of prefabricated component combinations and the construction technology of prefabricated buildings are influenced by the prefabrication rate, cost, duration, and carbon emission target weight. The weight assigned to each sub-objective will impact the cost, duration, and carbon emissions of the project by influencing the selection of the construction technologies for the components, which determines how the construction technologies of the components is chosen. The prefabrication rate will affect the number of selected components under the construction technologies, thereby impacting the cost, duration, and carbon emissions of the project, which determines the extent to which the component construction technology is selected.

Analysis of component technology selection results

In order to further explore the influence of weight coefficients and the range of prefabrication rates on the specific selection of construction technologies for components, this study analyzes the results of the construction technologies selection for component combinations. Considering that there may be multiple optimal prefabricated component combinations obtained using the ant colony algorithm when the weight coefficients and prefabrication rate range are determined, this study selects the component combination with the lowest comprehensive target value for analysis, using formula (3) in the optimal solution. This approach aims to provide a clearer and more accurate understanding of the influence of weight coefficients and prefabrication rate range on the selection results. The component combination is illustrated in Figure. 13.

Fig. 13

Component process selection chart under different scenarios.

In Figures 13 (B), (C), and (D), and (C)’ represent the baseline scenario, cost-conscious scenario, duration-conscious scenario, and carbon emission- conscious scenario, respectively. Within each scenario, a, b, c, and d represent the ranges of prefabrication rates: 0-20%, 20-40%, 40-60%, and 60% above, respectively. Different construction technologies for components are represented by different colors, and the numbers indicate the selection results of the construction technologies for each component. The detailed numbering can be found in Table 2. For example, taking B-a as an example, it represents the selection of construction technologies for components with a prefabrication rate of 0-20% in the baseline scenario. The selection results are as follows: (Selection results for the first-floor components) (3) Prefabricated Column [Cost: 5.67×104 yuan, Duration: 5 days, Carbon Emission: 7.42 t] —— (5) Prefabricated Beam [Cost: 7.93×104 yuan, Duration: 4 days, Carbon Emission: 11.93 t] —— (6) Cast-in-Place Slab [Cost: 5.52×104 yuan, Duration: 9 days, Carbon Emission: 18.87 t] —— (8) Cast-in-Place Wall [Cost: 3.98×104 yuan, Duration: 10 days, Carbon Emission: 18.47 t] —— (10) Cast-in-Place Staircase [Cost: 0.49×104 yuan, Duration: 6 days, Carbon Emission: 2.29 t] —— (Selection results for the second-floor components) (12) Cast-in-Place Column - (15) Prefabricated Beam - (17) Prefabricated Slab - (18) Cast-in-Place Wall - (20) Cast-in-Place Staircase - (Selection results for the third-floor components) (22) Cast-in-Place Column -(24) Cast-in-Place Beam - (27) Prefabricated Slab - (28) Cast-in-Place Wall. The same analysis applies to other scenarios. The construction technologies selection diagram is analyzed as follows:

• (1) The influence of weight coefficients on the selection of construction technologies for components can be analyzed by observing B, C, D, C’-a, B, C, D, C’-b, B, C, D, C’-c, and B, C, D, C’-d, where the prefabrication rate range remains constant while the weight coefficients differ. In the cost-conscious scenario, the selection of prefabricated components is mainly based on the extent of cost variation caused by the unit target value of the components, i.e., the cost increment. This scenario prioritizes components with smaller cost increments, such as prefabricated slabs, while using fewer components with larger cost increments. In the duration-conscious scenario, the selection is based on the extent of duration variation caused by the unit target value of the components, i.e., the duration saving rate. This scenario chooses prefabricated components with higher duration saving rates, such as prefabricated beam components and prefabricated staircase components, which greatly reduce the project’s duration. In the carbon emission-conscious scenario, the selection is based on the magnitude of carbon emission reduction achieved by the prefabricated components, such as prefabricated column components.

• (2) The influence of the prefabrication rate range on the selection of construction technologies for components can be analyzed by observing B-a, b, c, d, C-a, b, c, d, D-a, b, c, d, and C’-a, b, c, d, where the weight coefficients remain constant while the prefabrication rate range differs. In terms of the prefabrication rate, the selection is primarily based on the magnitude of the prefabrication rate for the components. In the low prefabrication rate scenario, there is a tendency to select components with lower prefabrication rates, such as columns, slabs, and staircase components. In the high prefabrication rate scenario, there is a tendency to select components with higher prefabrication rates, such as wall and beam components.

From this, it can be concluded that changes in the weight coefficients of cost, duration, and carbon emission target and the range of prefabrication rates have an impact on the optimization results of the construction technologies combinations for prefabricated components in prefabricated buildings. The degree of cost, duration, and carbon emission increment benefits resulting from the selection of cast-in-place or prefabricated construction technologies is the main

influencing factor in optimizing the selection of prefabricated component combinations in prefabricated buildings. This also leads to a clear bias in the selection of prefabricated component types based on different weight coefficients and prefabrication rate ranges.

Analysis of optimization effect

As prefabricated components serve as the fundamental elements of prefabricated buildings, multi-objective optimization of component combinations aims to optimize the overall cost, duration, and carbon emissions of prefabricated buildings by selecting appropriate component combinations. To analyze the optimization effect of component combinations, this study selects cast-in-place construction as the reference and compares the degree of optimization in component selection under different scenarios with cast-in-place construction. The comparative analysis is depicted in Figure. 14.

Fig. 14

Comparative analysis chart of different scenarios.

In Figures 14 (a), (b), and (c) represent the comparative analysis of cost, duration, and carbon emissions, respectively. The figure is divided into four regions from left to right, representing the prefabrication rate ranges of 0-20%, 20-40%, 40-60%, and 60% above. For example, 1-5 represents the Pareto optimal solutions for the prefabrication rate range of 0-20%, while 6-10 represents the Pareto optimal solutions for the prefabrication rate range of 20-40%, and so on. Different colors represent different weight coefficient scenarios. The bar chart represents the degree of optimization of the component combination compared to cast-in-place construction, where a higher bar indicates a better degree of optimization. The analysis of the figure is as follows:

• (1) The influence of the prefabrication rate range on the optimization effect can be analyzed through the trends observed in the line graph and bar chart. As the prefabrication rate increases, the number of prefabricated components exceeds the number of cast-in-place components. This results in higher construction and installation costs for the entire project, but lower duration and carbon emissions. Although the lower duration and carbon emissions can reduce the costs associated with duration and carbon emissions, the decrease in these costs is much lower compared to the increase in construction and installation costs. Therefore, as the prefabrication rate increases, the optimization effect of the component combination on cost gradually decreases, while the optimization effect on duration and carbon emissions gradually increases.

• (2) The influence of weight coefficients on the optimization effect can be analyzed by observing the relative positions of the line graphs in different colors. Taking the cost optimization effect in Figure (a) as an example, in the cost-conscious scenario, the variation in unit cost has a greater impact on the objective value compared to the variations in unit duration and carbon emissions. This leads to a preference for selecting cast-in-place components to directly reduce costs and achieve the minimum comprehensive objective value. Therefore, the cost optimization effect is more significant in the cost-conscious scenario compared to other scenarios, resulting in a lower cost optimization curve. The same analysis applies to other scenarios, where the duration-conscious scenario shows a more significant optimization effect on duration, and the carbon emission-conscious scenario shows a more significant optimization effect on carbon emissions.

In conclusion, as the prefabrication rate increases, the optimization effect of the component combination on cost gradually decreases, while the optimization effect on duration and carbon emissions gradually increases. In terms of weight coefficients, as the weights increase, the optimization effect of sub-objectives with higher weights becomes more pronounced.

The ant colony optimization algorithm generates multiple optimized solutions across various scenarios with different weight coefficients and prefabrication rate ranges. This study selects the optimal solution for each scenario based on the comprehensive objective values calculated using Equation (3). By employing the optimization rate, a more intuitive analysis of the optimal combinations of prefabricated components under different scenarios is conducted. The optimal prefabricated component combinations and their optimization effects are presented in Table 4.

Table 4 Optimization effect analysis.

Table 4 presents the selection results of prefabricated components for the optimal scheme under different scenarios, as well as the corresponding cost, duration, and carbon emissions of the projects. Taking the baseline scenario as an example, where the weight coefficients for cost, duration, and carbon emissions are 1:1:1, the construction technologies of the optimal scheme is as follows: (First floor) prefabricated column - cast-in-place beam - prefabricated slab - prefabricated wall - prefabricated staircase (Second floor) cast-in-place column - prefabricated beam - prefabricated slab - cast-in-place wall - cast-in-place staircase (Third floor) cast-in-place column - cast-in-place beam - cast-in-place slab - cast-in-place wall. The prefabrication rate is 25.259%, the cost is 7.11×10⁵ yuan, the duration is 119 days, and the carbon emissions are 263 tons. Similar patterns can be observed for other scenarios. From the table, we can analyze that:

• (1) The optimal scheme under the baseline scenario reduces costs by 0.42%, duration by 19.05%, and carbon emissions by 13.49% compared to an all-cast-in-place building. This indicates that the prefabricated component combination obtained using the method in this study has been optimized in terms of cost, duration, and carbon emissions. It can effectively save project costs and duration while minimizing the carbon emissions of the building.

• (2) The weight coefficients reflect the preferences of stakeholders towards different objectives, and the degree of optimization for each objective primarily depends on its weight in multi-objective optimization. With different weight coefficients, the cost, duration, and carbon emissions of prefabricated buildings are reduced by 1.26%, 27.89%, and 18.4% respectively, compared to all-cast-in-place buildings. This demonstrates the adaptability of the method used in this study to different project types and scales. For instance, in emergency projects, more attention can be given to the project duration, and additional costs and resources can be allocated accordingly.

• (3) The prefabrication rate range of the optimal combination of prefabricated components is mainly concentrated in the range of 20% to 60%. This suggests that in prefabricated buildings, it is important not to blindly pursue a high prefabrication rate. Instead, the optimal prefabrication rate should be determined based on the specific needs and requirements of the project. A suitable prefabrication rate range can achieve the best balance in terms of cost, duration, and carbon emissions, resulting in optimal outcomes.

Discussion

The impact of reduced duration and carbon emissions on the comprehensive cost of prefabricated buildings.

The comprehensive cost of prefabricated buildings is composed of construction and installation costs, duration costs, and carbon emissions costs. Compared to cast-in-place construction, prefabricated buildings have reduced duration and carbon emissions. The following explores the impact of reduced duration and carbon emissions of prefabricated buildings on comprehensive costs in four scenarios, as shown in Figure. 15.

Fig. 15

Impact of reduced duration and carbon emissions on the comprehensive cost of prefabricated buildings.

In Figure. 15, the horizontal axis represents cast-in-place construction and prefabricated buildings in four different scenarios. The left vertical axis represents costs, while the right vertical axis represents the proportion of cost reduction components to the sum of project duration and carbon emissions cost reduction. Construction and installation costs, as well as comprehensive costs, are positive values. The negative values on the left vertical axis indicate the reduction in project duration costs and carbon emissions costs for prefabricated buildings compared to cast-in-place construction.

In Figure. 15, the construction and installation cost for cast-in-place construction is 7.14×10⁵ yuan. For the four scenarios of prefabricated buildings, the construction and installation costs are 7.68×10⁵, 7.73×10⁵, 7.94×10⁵, and 7.86×10⁵ yuan, respectively. The sum of duration costs and carbon emissions costs reduction compared to cast-in-place construction is 56680, 68462, 82491, and 76945 yuan, respectively. The comprehensive costs are 7.11×10⁵, 7.05×10⁵, 7.12×10⁵, and 7.09×10⁵ yuan, respectively. Compared to cast-in-place construction, the comprehensive costs are reduced by 0.42%, 1.26%, 0.28%, and 0.7%, respectively. Compared to cast-in-place construction, in the four scenarios of prefabricated buildings, the reduction in vertical transportation costs is 35984, 43695, 52692, and 48836 yuan, respectively. The reduction in integrated scaffolding costs is 7449, 9045, 10907, and 10109 yuan, respectively. The reduction in duration incentive costs is 10674, 12961, 15629, and 14486 yuan, respectively. The reduction in carbon emissions costs is 2573, 2761, 3264, and 3515 yuan, respectively. Among them, the vertical transportation costs are reduced by an average of 63.66%. The integrated scaffolding costs are reduced by an average of 13.18%. The project duration incentive costs are reduced by an average of 18.88%. The carbon emissions costs are reduced by an average of 4.28%. It can be observed that for the four scenarios of prefabricated buildings, the construction and installation costs are higher than those of cast-in-place construction. However, the duration costs and carbon emissions costs are reduced compared to cast-in-place construction, resulting in lower comprehensive costs for prefabricated buildings. Among the factors influencing the impact of reduced duration and carbon emissions on comprehensive costs of prefabricated buildings, the vertical transportation costs have the greatest impact, followed by duration incentive costs, while the influence of integrated scaffolding costs and carbon emissions costs is relatively smaller.

The impact of carbon trading prices on the overall cost of prefabricated buildings

Currently, the carbon trading market is still in its early exploration stage. The average carbon emissions price in the Shenzhen Emissions Trading Scheme over the past five months has been 62.76 yuan per ton. However, as the carbon trading market continues to develop, carbon trading prices in China are expected to gradually increase. According to the"Research Report on China’s Carbon Neutrality by 2060"(GEIDCO, 2021), the marginal cost of carbon emission reduction for the entire society is approximately 260 yuan per ton. The following explores the impact of carbon trading prices on the comprehensive costs of prefabricated buildings. Taking the baseline scenario as an example, the effect of varying carbon trading prices between 62.76 yuan/ton and 260 yuan/ton on the comprehensive costs of prefabricated buildings is shown in Figure. 16.

Fig. 16

Impact of carbon trading prices on the overall cost of prefabricated buildings.

In Figure. 16, the horizontal axis represents carbon trading prices, the left vertical axis represents costs, and the right vertical axis represents the proportion of carbon emissions cost reduction to the sum of project duration and carbon emissions cost reduction. Construction and installation costs, as well as comprehensive costs, are positive values, while duration costs and carbon emissions costs are negative values indicating reductions compared to cast-in-place construction. Compared to cast-in-place construction, the optimized result in the baseline scenario shows a reduction of 28 days in duration and a reduction of 41 tons in carbon emissions. The construction and installation cost is 7.68×10⁵ yuan, and the comprehensive cost of prefabricated buildings is 7.11×10⁵ yuan. The reduction in duration leads to cost reductions in duration incentives, integrated scaffolding costs, and vertical transportation costs, amounting to 10674 yuan, 7449 yuan, and 35984 yuan, respectively. When the carbon trading price is 62.76 yuan/ton, the reduction in carbon emissions costs is 2573 yuan. From Figure. 16, it can be observed that when the carbon trading prices are 62.76, 100, 150, 200, 250, and 260 yuan/ton, the reduction in carbon emission costs is 2573, 4100, 6150, 8200, 10250, 10660 yuan, respectively. The overall cost of prefabricated construction is 7.11×10⁵, 7.09×10⁵, 7.07×10⁵, 7.05×10⁵, 7.03×10⁵, 7.02×10⁵ yuan, respectively. The proportion of carbon emission costs to the total costs of duration and carbon emission reduction is 5.3%, 6.9%, 10%, 12.9%, 15.6%, and 16.9%, respectively. It can be observed that compared to cast-in-place construction, as the carbon trading price increases, the reduction in carbon emissions costs gradually increases, resulting in a gradual decrease in the comprehensive costs of prefabricated buildings. The optimized result shows a reduction of 1.68% in comprehensive costs. As the carbon trading market continues to improve, the reduction in comprehensive costs of prefabricated buildings will become more significant, which is of great importance for cost management in construction projects.

Building sustainability pathways

During the construction process, buildings often encounter issues such as high costs, extended durations, and environmental pollution. The structural design scheme in the conceptual design stage plays a crucial role in the economy, duration, and environmental impact of buildings. However, there is a lack of comprehensive studies that consider factors such as cost, duration, and carbon emissions in the structural design scheme of buildings.

The proposed multi-objective optimization design approach for prefabricated building structures has resulted in prefabricated component combinations that reduce costs, duration, and carbon emissions compared to cast-in-place construction. This promotes sustainable development in the construction industry and provides an effective approach for transitioning from cast-in-place construction to prefabricated construction and achieving sustainable development in buildings.

Recommendations and implications for practitioners

The multi-objective optimization design method for prefabricated buildings based on the Ant Colony Optimization (ACO) algorithm proposed in this study provides practitioners in the construction industry with a scientific and efficient decision support tool. This method can significantly improve the cost, duration, and carbon emissions of prefabricated building projects. The specific recommendations or implications are as follows:

• (1) Optimized decision support for rational selection of prefabricated component combinations. Traditional methods for selecting prefabricated components often rely on the experience and intuition of engineers, which can be influenced by subjective factors, leading to suboptimal choices. This study presents a systematic and scientific decision-making approach through the multi-objective optimization model and ACO algorithm, allowing practitioners to comprehensively consider multiple objectives such as cost, duration, and carbon emissions, thus avoiding the one-sidedness of single-objective optimization. Practitioners can refer to the case studies presented in this research, aligning them with the characteristics of their own projects to conduct practical operations and comparative analyses, gradually accumulating experience to make more scientific and rational decisions during the project design phase.

• (2) Achieving a balance between cost and benefit. The construction costs of prefabricated buildings are typically higher than those of cast-in-place buildings. However, by optimizing the combinations of prefabricated components, it is possible to significantly reduce the overall project costs without sacrificing duration or carbon emissions. In the early stages of a project, practitioners should conduct a detailed analysis of the cost composition of prefabricated components, including production, transportation, and installation phases, and adjust the project budget based on the optimization results to ensure that costs remain within a reasonable range. Additionally, by optimizing the production schedules and transportation arrangements of prefabricated components, unnecessary cost expenditures can be minimized. Furthermore, practitioners should flexibly adjust the prefabrication rate according to specific project requirements rather than pursuing a high prefabrication rate indiscriminately.

• (3) Optimizing project management to enhance duration and resource management efficiency. Optimizing the combinations of prefabricated components can not only reduce the overall project duration but also improve the efficiency of resource utilization on the construction site, thereby lowering uncertainties and risks during the construction process. Practitioners can develop detailed construction plans based on the optimized combinations of prefabricated components, rationally scheduling the construction time and resource allocation for each phase. Additionally, establishing close collaborative relationships with prefabricated component suppliers is essential to ensure that components are delivered on time and to the required quality, thus avoiding delays due to supply issues. Furthermore, utilizing digital tools such as Building Information Modeling (BIM) allows for real-time monitoring and management of the construction process, enabling the timely identification and resolution of potential issues, thereby enhancing project management.

• (4) Commitment to sustainable development. As global attention to environmental protection and sustainable development continues to grow, the construction industry faces increasingly stringent carbon emission requirements. This study aids practitioners in controlling carbon emissions to the lowest levels during the project design phase by optimizing the combinations of prefabricated components, thus better addressing the demands of environmental protection policies and carbon trading markets. Practitioners can establish carbon emission monitoring systems to regularly record and analyze carbon emission data for the project, ensuring that the implementation of the optimization meets expectations. Additionally, by leveraging the mechanisms of the carbon trading market, optimized carbon emission allowances can be traded to generate additional economic benefits. Moreover, during the production and construction processes of prefabricated components, it is essential to actively promote low-carbon technologies, such as using renewable energy and optimizing production processes, to further reduce carbon emissions.

Limitations of the proposed methodology

The proposed approach is only an exploratory attempt to optimize prefabricated component combinations considering cost, duration, and carbon emissions under the constraint of prefabrication rate. It has certain limitations, as described below:

• 1. When calculating the construction and installation cost of prefabricated components in prefabricated buildings, we mainly consider the transaction prices in the construction market, without taking into account the impact of formwork amortization costs during the component production stage on costs. In actual engineering projects, the amortization cost of formwork during the production stage of prefabricated components refers to the allocation of the formwork cost over a certain period or number of uses. This means that the usage quantity of the same prefabricated component during the construction stage will have an impact on the production cost of the prefabricated component. Additionally, considering the efficiency of repeated use of the same component can help optimize the design and construction plans of prefabricated buildings, improve the reusability of components, and reduce waste and costs. Therefore, when performing cost accounting for prefabricated components in prefabricated building, amortization costs are an important consideration. Future research should further explore how to incorporate template amortization expenses into the cost accounting model while also considering the efficiency of component reuse to more comprehensively reflect the actual costs of prefabricated components. Additionally, studies could investigate how to optimize template design and management to further reduce the impact of template amortization costs on overall expenses.

• 2. The proposed approach is a detailed design of component construction technologies selection based on the preliminary determination of the building structure. It assumes that choosing between cast-in-place or prefabricated construction technologies will not affect the structural behavior of the building. However, in actual construction, the choice between cast-in-place or prefabricated construction technologies can have an impact on the structural stiffness, load transfer, component joints, and structural deformations. Therefore, future research should involve necessary structural calculations and analyses to ensure that the.

• selected construction processes for the components do not adversely affect the building’s structure. Specifically, more accurate structural analysis models can be established to consider the impact of different construction processes on structural performance. Additionally, tools such as finite element analysis can be employed to conduct detailed structural validation of the optimized combinations of prefabricated components. Furthermore, studies could explore how to enhance the overall structural performance of modular buildings by optimizing the design of component connections.

• 3. Considering the differences in construction needs among different types of projects, different scenario modes have been set based on different weight coefficients. For example, commercial projects may prioritize cost, emergency projects may prioritize duration, and environmental projects may focus more on reducing carbon emissions. This helps decision-makers understand the trade-offs and advantages/disadvantages of component combination choices under different construction needs and make optimal decisions. The proposed method aims to explore comparative studies of prefabricated component solutions under different scenarios, so the setting of weight coefficients is subjective. Future research should explore how to scientifically and rationally quantify weight coefficients to adequately reflect the actual construction needs of a project. For example, expert systems and big data analysis can be utilized in conjunction with real project data to dynamically adjust the weight coefficients. Additionally, research could investigate the development of adaptive weight adjustment mechanisms based on different project types and objectives to enhance the scientific rigor and flexibility of decision-making.

Conclusions

A structural design approach for multi-objective optimization of prefabricated component combinations such as columns, beams, slabs, walls, staircases of prefabricated buildings by using ant colony algorithm with consideration of cost-duration-carbon emission is proposed, which is applied to the design of three-storey framed structure, and the following conclusions are drawn:

• 1. The optimal scheme under the baseline scenario reduces costs by 0.42%, duration by 19.05%, and carbon emissions by 13.49% compared to an all-cast-in-place building. This indicates that the prefabricated component combination obtained using the method in this study has been optimized in terms of cost, duration, and carbon emissions. It can effectively save project costs and construction time while minimizing the carbon emissions of the building.

• 2. The weight coefficient reflects the preferences of stakeholders towards different objectives, and the degree of optimization for each objective primarily depends on its weight in multi-objective optimization. In the case of different weight coefficients, the cost, duration, and carbon emissions of prefabricated buildings are reduced by 1.26%, 27.89%, and 18.4%, respectively. This also demonstrates the adaptability of the approach to different project types and sizes.

• 3. The optimization effect of the component combination on cost gradually decreases with the increase of the assembly rate, while the optimization effect on duration and carbon emissions gradually increases. The prefabrication rate range of the optimal combination of prefabricated components is mainly concentrated in the range of 20% to 60%. It is important to determine the appropriate prefabrication rate range that achieves the best balance in terms of cost, duration, and carbon emissions, rather than blindly pursuing a high prefabrication rate. This approach enables optimal outcomes for the building project.

• 4. Changes in cost, duration, carbon emission target weight, and prefabrication rate have an impact on the optimization results of the construction process combination for prefabricated building components. The degree of incremental benefit in cost, duration, and carbon emissions resulting from the selection of cast-in-place or prefabricated construction technology is the main influencing factor for the optimal combination of prefabricated construction components. The weight coefficients determine“how”the construction technology of the component is chosen, while the prefabrication rate determines“how much”of the construction technology is used. Additionally, different weight coefficients and prefabrication rate ranges exhibit a clear bias towards the selection of prefabricated component types.

• 5. Applying the ant colony algorithm to solve the multi-objective optimization problem of prefabricated building component combinations is feasible, as the algorithm demonstrates high operational efficiency and good convergence.