Assessing the impact of air pollution on lung function in South Korea using Bayesian kernel machine regression

Abstract

This study investigates the relationship between air pollution and lung function in the South Korean adult population using Bayesian Kernel Machine Regression (BKMR). By integrating 2017 Korea National Health and Nutrition Examination Survey (KNHANES) data with air pollution data, the study examines the individual and joint effects of key air pollutants—$\hbox {PM}_{10}$, $\hbox {PM}_{2.5}$, $\hbox {SO}_2$, $\hbox {NO}_2$, $\hbox {O}_3$, and CO—on lung function indicators, including COPD (binary) and $\hbox {FEV}_1/$FVC (continuous). The findings reveal that $\hbox {PM}_{10}$ and $\hbox {O}_3$ have negative effects on lung function, both individually and interactively. As the concentrations of these pollutants increase, the probability of developing COPD and the decline in $\hbox {FEV}_1/$FVC become more pronounced. This study highlights the compounded risks posed by pollutant mixtures, providing critical insights for public health interventions and air quality policy improvements in South Korea. Future research directions include addressing time-lagged effects and regional variations to enhance the understanding of these relationships.

Introduction

Environmental exposure factors, particularly air pollutants, play a critical role in public health, considerably impacting respiratory function and increasing the risk of chronic respiratory diseases. Over the decades, the adverse health effects of air pollutants such as particulate matter ($\hbox {PM}_{10}$ and $\hbox {PM}_{2.5}$), nitrogen dioxide ($\hbox {NO}_2$), sulfur dioxide ($\hbox {SO}_2$), ozone ($\hbox {O}_3$), and carbon monoxide (CO) have been extensively studied. These pollutants are known to exacerbate chronic obstructive pulmonary disease (COPD), asthma, and other respiratory conditions^1,2.

Research into the relationship between air pollution and lung function has employed a variety of statistical and epidemiological methodologies. Earlier studies primarily relied on linear regression models, which provided valuable insights into the individual effects of specific pollutants^3,4. However, such approaches were limited in capturing the complex, nonlinear relationships and interactive effects among multiple pollutants –conditions more reflective of real-world exposure scenarios. To address these limitations, more advanced techniques, including generalized estimating equations⁵, distributed lag non-linear models⁶, and quantile regression⁷, have been increasingly adopted.

More recently, Bayesian Kernel Machine Regression (BKMR) has emerged as a powerful methodological advancement. BKMR allows for the simultaneous modeling of high-dimensional pollutant mixtures and their nonlinear, interactive effects on health outcomes^8,9. This represents a significant innovation in the field, as it enables researchers to move beyond isolated pollutant effect models and more accurately approximate the complex nature of environmental exposures.

Despite these methodological advancements, research focused on pollutant mixtures remains limited. Most existing studies have examined pollutants individually or in simple additive models, often neglecting the synergistic or antagonistic interactions among them. Moreover, the application of BKMR has been largely concentrated in North America and Europe, with relatively few studies incorporating this approach into national health datasets in South Korea.

Globally, the adverse impact of air pollution on lung health has been widely documented. In China, $\hbox {PM}_{2.5}$ exposure has been shown to reduce forced expiratory volume in one second ($\hbox {FEV}_1$) and forced vital capacity (FVC), particularly among youth^6,10. European studies such as the LifeLines Cohort Study have explored occupational exposures using linear mixed-effects models¹¹, while U.S. research has investigated heavy metal exposure using quantile regression and BKMR⁷.

In South Korea, where air quality remains a pressing concern, a growing body of work has examined the long-term effects of individual pollutants on respiratory health. For instance, a cohort study linked $\hbox {PM}_{10}$ and $\hbox {NO}_2$ exposure to reduced FVC and increased emphysema index, using advanced imaging techniques¹². Another national cohort study found associations between chronic particulate matter exposure and increased mortality risk¹³. However, these studies primarily focus on single pollutants or linear effects, offering limited insights into the health impacts of pollutant mixtures.

In addition, individuals are not typically exposed to single pollutants in isolation. Rather, they are concurrently exposed to complex mixtures of air pollutants in real-world settings. These real-life exposure scenarios are influenced by various environmental, behavioral, and temporal factors that lead to simultaneous inhalation of multiple substances. Therefore, to more accurately assess the impact of air pollution on respiratory health, it is essential to incorporate environmentally realistic conditions into the analysis–conditions under which these pollutants may interact with each other, either synergistically or antagonistically, thereby modifying their combined health effects. A comprehensive understanding of such interactive mechanisms is crucial for more accurate risk assessment and the development of effective public health interventions.

To address these gaps, this study investigates the joint and individual effects of multiple air pollutants on lung function among South Korean adults by integrating environmental monitoring data with the Korea National Health and Nutrition Examination Survey (KNHANES). Specifically, we employed Bayesian Kernel Machine Regression (BKMR), a flexible semi-parametric modeling framework that captures both non-linear and non-additive associations, including interactions, among pollutants. This approach is particularly advantageous for evaluating high-dimensional environmental mixtures without the need to pre-specify interaction terms or functional forms. Using BKMR, we assessed the health effects of a key set of ambient pollutants–$\hbox {PM}_{10}$, $\hbox {PM}_{2.5}$, $\hbox {NO}_2$, $\hbox {SO}_2$, $\hbox {O}_3$, and CO–on critical respiratory outcomes, including the presence of chronic obstructive pulmonary disease (COPD) and reductions in $\hbox {FEV}_1$/FVC ratios. This modeling strategy enables a more realistic and nuanced evaluation of air pollution impacts that aligns closely with real-world exposure patterns in environmental epidemiology.

This study contributes to the literature in three key ways. First, it advances methodological rigor by utilizing BKMR to model complex pollutant interactions. Second, it provides empirical evidence on the health impacts of air pollution mixtures in a South Korean population, where such research remains scarce. Finally, it aims to inform national policy by identifying key pollutant combinations most detrimental to lung health, thereby supporting targeted interventions in air quality management and public health strategy.

Data

In this study, we use two datasets: raw data from the 2017 Korean National Health and Nutrition Survey(KNHANES) and air pollution data converted to latitude and longitude coordinates based on subject addresses and examination dates. The KNHANES dataset, accessible through its official portal (available at knhanes.kdca.go.kr/knhanes/rawDataDwnld), provides comprehensive information on health behaviors, the prevalence of chronic diseases, and nutritional intake among Korean citizens. It also includes demographic and behavioral variables such as age, sex, education level, income level, smoking status, alcohol consumption, and lung function indicators. In addition, air pollution data (available at knhanes.kdca.go.kr/rlatmtial/wsiAirPolut.do) contain individual-level estimates of exposure to major pollutants, including PM10, PM2.5, $\hbox {SO}_2$, $\hbox {NO}_2$, $\hbox {O}_3$, and CO. Note that the two datasets can be merged by a common variable, ”id”, which represents the unique identifier of the subject. Also, air pollution exposure is the daily average of the KNHANES subjects on the examination date.

Response variables

The primary indicators of lung function used in this study were FVC, $\hbox {FEV}_{1}$, and the ratio of these two measurements, $\hbox {FEV}_{1}$/FVC. FVC represents the maximum volume of air exhaled after a deep inhalation, while $\hbox {FEV}_{1}$ measures the volume of air expelled in the first second of exhalation. The $\hbox {FEV}_{1}$/FVC ratio serves as a diagnostic marker, with values below 0.7 indicating COPD. For this study, $\hbox {FEV}_{1}$/FVC was treated as a continuous variable to assess lung function. Additionally, a binary variable was created to distinguish between normal lung function (coded as 0) and COPD (coded as 1) based on the 0.7 threshold.

Exposure factors

Exposure to air pollution was quantified using data on six major pollutants: $\hbox {PM}_{10}$, $\hbox {PM}_{2.5}$, $\hbox {SO}_2$, $\hbox {NO}_2$, $\hbox {O}_3$, and CO. Concentrations of $\hbox {PM}_{10}$ and $\hbox {PM}_{2.5}$ were expressed in micrograms per cubic meter ($\upmu\,\mathrm{g}/\mathrm{m}^3$), while $\hbox {SO}_2$, $\hbox {NO}_2$, $\hbox {O}_3$, and CO were measured in parts per million (ppm). Numerous studies have established substantial associations between these air pollutants and adverse respiratory health outcomes, including reduced lung function and increased risks of COPD^{1,2,5,6,14,15}.

With regard to air pollution exposure estimation, the satellite-based air pollution data were derived through a multi-step process involving CMAQ modeling, data assimilation, and regression-based downscaling using satellite-derived aerosol optical depth (AOD). Based on previous validation studies^16,17, the performance of these models–evaluated using metrics such as R, $R^2$, index of agreement (IOA), and RMSE–demonstrated sufficient accuracy. Notably, the $R^2$ values for $\hbox {PM}_{10}$ and $\hbox {PM}_{2.5}$ exceeded 0.7, indicating that the satellite-based estimates used in this analysis are considered reliable.

Covariates

To control for potential confounding factors, a range of demographic and lifestyle variables were included as covariates in the analysis. These variables encompassed age, sex, body mass index (BMI), income level, smoking status, education level, and alcohol consumption. The inclusion of these factors aligns with best practices in studies examining the health impacts of air pollution and ensures a robust assessment of the pollutants’ effects on lung function^18,19,20,21.

Data preprocessing

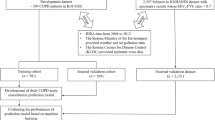
KNHNES data and air pollution data were merged based on the “id” variable, and the number of unique values was compared with the number of data to confirm that the numbers matched. A complete dataset was constructed through preprocessing, including removing missing rows for $\hbox {FEV}_1/$FVC to be used as continuous response variables and checking missing values for air pollutants and covariates. Due to computational time costs issues when building the BKMR model, the model was constructed by randomly sampling 500 out of 3453 samples from the complete dataset. In a similar way, the binary variable COPD was created by recategorizing using the “HE_COPD” variable with 4 categories (1: normal, 2: restrictive lung disease, 3: obstructive lung disease, 9: indistinguishable). Specifically, because we don’t know if we have COPD with a 9, that data was excluded, and if HE_COPD had a value of 1 or 2, it was coded as 0 (normal), and if HE_COPD had a value of 3, it was coded as 1 (COPD). Likewise, a model was built by randomly sampling 500 samples from the final dataset. Figure 1 shows data preprocessing process.

Two datasets were merged using a unique identifier variable (”id”). Of the initial 8,127 observations, 4,529 cases with missing values in the response variables were excluded. An additional 145 observations were removed due to missing information on smoking status and drinking status, which were key covariates of interest. After these exclusions, a total of 3,453 complete cases remained. After creating the binary variable COPD, 500 of 3,453 were randomly sampled. Meanwhile, the dataset comprising 3,453 observations spanned all 17 metropolitan cities and provinces in South Korea. Based on a random subsample of 500 cases, we assessed the spatial distribution of the two groups and found them to be spatially similar.

Note that the generated variable COPD was determined to be an outlier by checking whether it matched the value classified by setting the continuous variable $\hbox {FEV}_1/$FVC to 1 if it was small based on 0.7 and 0 otherwise.

Fig. 1

Flowchart of data preprocessing: In the integrated dataset with the “id” variable, 4,529 missing values and 145 cases with unknown “smoking status” and “drinking status” information were excluded to construct 3,453 datasets. After creating the COPD binary variable, an analysis was conducted on a dataset with 500 randomly sampled samples due to computing cost issues.

Methods

Considering covariates, we would like to know not only the linear relationship but also the non-linear relationship between lung function and air pollutants. One of the models used to understand how air pollutants have a complex effect on lung function is a Bayesian kernel machine regression (BKMR) model⁸. In this methodology, Kernel function is used to capture nonlinearity and takes uncertainty into account through a Bayesian statistical approach. This allows us to fit the model flexibly while taking into account uncertainty in the data. BKMR is used in a variety of fields, including environmental and health sciences^9,22,23,24.

For each subject $i=1,\ldots , n,$

$$\begin{aligned} Y_i = h(\varvec{z}_i) + \varvec{X}_i^\top \varvec{\beta } + \varepsilon _i \end{aligned}$$

(1)

where $Y_i$ is response variable (e.g $\hbox {FEV}_{1}$/FVC, COPD), $\varvec{z}_i = \left( z_{i1}, \ldots , z_{iM}\right) ^\top$ is a vector of M exposure variables (e.g $\hbox {PM}_{10}$, $\hbox {SO}_{2}$), $\varvec{X}_i$ is a vector of J covariates (e.g age, sex) and $\varepsilon _i \sim N(0, \sigma ^2)$. Also, exposure-response function h is a high-dimensional exposure-response function that can catch nonlinearity and/or interation among the mixture components in the context of environment. In the BKMR model, h can be represent as

$$h(z) = \sum _{i=1}^{n} \alpha _i K(z; z_i) \quad \text{ for } \quad z \in \mathbb {R}^{n \times M}$$

where $\alpha = \left( \alpha _1, \ldots , \alpha _n \right) \in \mathbb {R}^n$ is a parameter vector and K is positive definite kernel function. Using the kernel representation of h, it has been shown that the basic model (1) is equivalent to the hierarchical model²⁵.

$$\begin{aligned} Y_i \sim N(h_i + X_i^\top \beta , \sigma ^2) \end{aligned}$$

$$\begin{aligned} \varvec{h} = (h_i, \ldots , h_n) \sim N_n(\varvec{0}, \sigma ^2\tau ^2 \varvec{K}), \end{aligned}$$

where $\varvec{K}$ is an $n \times n$ matrix with $K_{ij} = K(z_i; z_j)$ for $i,j = 1, \ldots , n$. As a kernel function, a Gaussian kernel is chosen because it can flexibly capture a wide range of underlying function forms⁸. A Gaussian kernel is defined as follows:

$$K_{ij} = \exp \left\{ -\sum _{m=1}^{M}\rho _m\left( z_{im}-z_{jm}\right) ^2\right\}$$

where $\rho _m$ is an auxiliary variable corresponding to the m-th exposure factor. Finally, the goal of these model is to estimate the function h based on the observed data.

In R, BKMR can be implemented in the bkmrhat packages^26,27. From bkmrhat package, multiple parallel chains can be implemented. In this study, the bkmrhat package was used. Note that R program version is 4.3.0.

On the other hand, if the response variable is binary, we can consider the probit model from model (1) as follows:

$$\begin{aligned} \Phi ^{-1}(\mu _i) = h(z_{i1}, \ldots , z_{iM}) + \varvec{X}_i^\top \varvec{\beta } \end{aligned}$$

(2)

Herein, $\Phi$ is the cumulative distribution function (CDF) for the standard normal distribution ($\Phi ^{-1}$ is the probit link function) and $\mu _i = P(Y_i = 1)$ is the probability of an event. Also, $Y_i$ is a binary variable (0 or 1). Then the probit model can be expressed using a latent normal random variable ($Y_i^*$) formaulation.

$$\begin{aligned} Y_i^* = h(z_{i1}, \ldots , z_{iM}) + \varvec{X}_i^\top \varvec{\beta } + \varepsilon _i \end{aligned}$$

(3)

where $Y_i = I(Y_i^* > 0)$ is equal to 1 if $Y_i^* > 0$ and is equal to zero otherwise.

h estimated by applying the MCMC algorithm can be interpreted as the relationship between exposure and the underlying continuous latent variable ($Y^*$). For example, if Y is whether a person has COPD, then $Y^*$ can be interpreted as the potential to have COPD.

Results

Considering the covariates age, sex, BMI, income level, education level, smoking level, and drinking level, we examined how air pollutants affect the probability of developing COPD and decrease $\hbox {FEV}_1/$FVC through BKMR. BKMR results can display univariate effect, joint/interaction effect, overall effect, single effect through plots. Note that we fit the BKMR to know impact for $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD, $\text {PM}_{2.5}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD, $\text {PM}_{10}, \text {SO}_2, \text {NO}_2$, and CO on $\hbox {FEV}_1/$FVC, and $\text {PM}_{2.5}, \text {SO}_2, \text {NO}_2$, and CO on $\hbox {FEV}_1/$FVC.

In addition, the posterior estimates of covariates for each model are shown in Table S1–Table S4. The results present the posterior estimates for covariates including sex, age, education level, income level, BMI, smoking level, and drinking level. For each covariate, the posterior mean, posterior standard deviation, and the 95% credible interval (lower and upper bounds) are reported.

Tables S1–S2 present the estimated effects of covariates on COPD incidence, with gender, age, and BMI all showing statistically significant effects at the 5% significance level. The signs of the estimated coefficients for these variables were consistent between the two tables.

Meanwhile, Tables S3–S4, which present the results of the estimated $\hbox {FEV}_1/$FVC ratio, show that in addition to gender, age, and BMI, smoking level was also a statistically significant covariate at the 5% significance level. The signs of the estimated coefficients for all variables were consistent between the two tables, except for one case.

Summarizing the results from Tables S1–S4, the signs of the posterior mean estimates for the same covariates were opposite in Tables S1–S2 and Tables S3–S4. This is expected because for COPD incidence, a negative coefficient indicates a decreased risk and a positive coefficient indicates an increased risk, whereas for the $\hbox {FEV}_1/$FVC ratio, a negative coefficient indicates a decreased lung function. Therefore, this difference in signs suggests a consistent interpretation of the decreased lung function.

The result of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD

Fig. 2

The plots of the univariate effect of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. The x-axis is the standardized value for each exposure factor, and the y-axis is the corresponding exposure-response function (h) estimate. As the values of $\text {PM}_{10}$ and $\text {O}_3$ increase, the probability of contracting COPD increases.

Figure 2 shows the univariate effects of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. As the standardized value of $\text {PM}_{10}$ increases, the risk of developing COPD increases linearly. In contrast, as the standardized value of $\text {O}_3$ increases, the risk of developing COPD exhibits a non-linear upward trend. For $\text {PM}_{10}$, the estimated effect becomes positive at values greater than approximately 0 (actual average: 49.73 $\upmu\,\mathrm{g}/\mathrm{m}^3$). Similarly, for $\text {O}_3$, the estimated effect becomes positive at values exceeding about 1 (actual average: 0.0470 ppm, corresponding to a standardized value of 1). These findings suggest that the probability of developing COPD becomes higher than the probability of not developing the condition under these circumstances. For $\text {NO}_2$ and CO, the estimated curves remain flat near 0, indicating no substantial influence in either direction. However, these pollutants may contribute slightly to reduced lung function.

Fig. 3

The plots of the joint/interaction effect of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. The x-axis represents the standardized value for the first exposure factor, and the y-axis represents the exposure-response function estimate for the first exposure factor according to the quantile of the second exposure factor when the values of the remaining exposure factors are fixed.

Figure 3 shows the plots of the joint/interaction effect of $\text {PM}_{10}, \text {SO}_2$, $\text {NO}_2$, $\text {O}_3$, and CO on COPD. When $\text {SO}_2, \text {NO}_2$, $\hbox {O}_3$ and CO are fixed at their median, the estimated exposure-response function value increases as the standardized $\text {PM}_{10}$ value increases as it can seen in the 4th column. Here, when having the same $\text {PM}_{10}$ value, the exposure-response function value was estimated to be larger as the quantile of $\text {O}_3$ increased as it can seem in the 3rd row and 4th column. This suggests that when $\text {PM}_{10}$ and $\text {O}_3$ are considered together, the potential for developing COPD increases as these values increase.

Fig. 4

The plots of the overall effect of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. When all exposure factors are fixed at the 50th percentile (median), these are the relative exposure-factor estimates as they change to the 25th, 30th, $\ldots$, 70th, and 75th percentiles.

Figure 4 shows the overall effect on COPD for $\text {PM}_{10}$, including $\text {SO}_2$, $\text {NO}_2$, $\text {O}_3$, and CO. We examined each of the five exposure factors by simultaneously changing them from the 25th percentile to the 75th percentile. As a result, Fig. 4 shows that as the values of exposure factors increase, the potential for developing COPD increases.

Fig. 5

Plot of the single effects of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. This plot shows the effect of a single exposure to estimate the contribution of each exposure to the total exposure, with all but one of the exposure factors of interest fixed at the 25th, 50th, and 75th quantiles.

Figure 5 shows the single exposure effect to estimate the contribution of each exposure to the total exposure. The y-axis represents a single exposure factor of interest, and the x-axis represents the difference between the exposure-response function estimates at the 75th and 25th quantiles of the single exposure factor of interest, with all but one of the factors of interest fixed at the 25th(red, bottom-line), 50th(green, mid-line), and 75th(blue, top-line) quantiles, respectively. For example, when the remaining exposure factors $\text {SO}_2, \text {NO}_2, \text {O}_3$, and CO excluding $\text {PM}_{10}$ are fixed at the 25th, 50th, and 75th percentiles, the difference between 75th percentile and 25th percentile of $\text {PM}_{10}$ in exposure-response function values is greater than 0. Therefore, it can be said that the potential to develop COPD is greater when $\text {PM}_{10}$ is at the 75th percentile compared to when $\text {PM}_{10}$ is at the 25th percentile. Meanwhile, the larger the $\text {SO}_2, \text {NO}_2, \text {O}_3$, and CO values, the greater the difference in the estimated exposure-response function when the $\text {PM}_{10}$ value is large, thus it can be interpreted that the potential for developing COPD is greater. In addition, when $\text {PM}_{10}, \text {SO}_2, \text {NO}_2$ and CO are fixed at the 25th, 50th, and 75th percentile, the potential for developing COPD is greater when $\text {O}_3$ has a value at the 75th percentile compared to when $\text {O}_3$ is also at the 25th percentile.

The result of $\text {PM}_{2.5}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD

Figure S1 shows the plots of the univariate effect of $\text {PM}_{2.5}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. As the standardized value of $\hbox {PM}_{2.5}$ increases, the potential for COPD increases linearly, and as the standardized value of $\hbox {O}_3$ increases, the potential for COPD tends to increase non-linearly. $\hbox {PM}_{2.5}$ was estimated to be positive if it had a value greater than about 0, and $\hbox {O}_{3}$ was estimated to be positive if it had a value greater than about 1, thus the probability of developing COPD can be considered to be greater than the probability of not suffering from COPD. Regarding $\hbox {NO}_{2}$ and CO, the estimated curves remain straight near 0, thus it can be said that these two air pollutants have affect on reducing lung function.

Figure S2 shows the plots of the joint/interaction effect of $\text {PM}_{2.5}, \text {SO}_2, \text {NO}_2, \text {O}_3$, and CO on COPD. When $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, $\hbox {O}_{3}$, and CO are fixed at their median, the estimated exposure-response function estimate increases as the standardized $\hbox {PM}_{2.5}$ value increases as it can seen in the 4th column. Here, when having the same $\hbox {PM}_{2.5}$ value, the exposure-response function value was estimated to be larger as the quantile of $\hbox {O}_{3}$ increased as it can seen in the 3rd row and 4th column. This suggests that when $\hbox {PM}_{2.5}$ and $\hbox {O}_{3}$ are considered together, the potential for developing COPD increases as these values increase.

Figure S3 shows the overall effect on COPD for $\hbox {PM}_{2.5}$, including $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, $\hbox {O}_{3}$, and CO. We examined each of the five exposure factors by simultaneously changing them from the 25th percentile to the 75th percentile. As a result, Fig. S3 shows that as the values of exposure factors increase, the potential for developing COPD increases.

Figure S4 shows the single exposure effect to estimate the contribution of each exposure to the total exposure. For example, when the remaining exposure factors $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, $\hbox {O}_{3}$, and CO excluding $\hbox {PM}_{2.5}$ are fixed at the 25th, 50th, and 75th percentiles, the difference between 75th percentile and 25th percentile of $\hbox {PM}_{2.5}$ in exposure-response function values is greater than 0. Therefore, it can be said that the potential to develop COPD is greater when $\hbox {PM}_{2.5}$ is at the 75th percentile compared to when $\hbox {PM}_{2.5}$ is at the 25th percentile. Meanwhile, the larger the $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, $\hbox {O}_{3}$, and CO values, the greater the difference in the estimated exposure-response function when the $\hbox {PM}_{2.5}$ value is large, thus it can be interpreted that the potential for developing COPD is greater. In addition, when $\hbox {PM}_{2.5}$, $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, and CO are fixed at the 25th, 50th, and 75th percentile, the potential for developing COPD is greater when $\hbox {O}_{3}$ has a value at the 75th percentile compared to when $\hbox {O}_{3}$ is also at the 25th percentile.

The result of $\text {PM}_{10}, \text {SO}_2, \text {NO}_2$, and $\text {O}_3$ on $\hbox {FEV}_1/$FVC

Figure S5 shows the plots of the univariate effect of $\hbox {PM}_{10}$, $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, and $\hbox {O}_{3}$ on $\hbox {FEV}_1/$FVC. As $\hbox {PM}_{10}$ became greater than about 1.75 (actual about 75 $\upmu\,\mathrm{g}/\mathrm{m}^3$), the exposure-response function was estimated to be negative. Therefore, it can be interpreted that when $\hbox {PM}_{10}$ becomes greater than about 75 $\upmu\,\mathrm{g}/\mathrm{m}^3$, $\hbox {FEV}_1/$FVC decreases non-linearly. For $\hbox {NO}_{2}$ (approximately 1.3, actual 0.0462 ppm) and $\hbox {O}_{3}$ (approximately 2.5, actual 0.075 ppm), if the levels exceed these values, the exposure-response function is estimated to become negative. This suggests that $\hbox {NO}_{2}$ and $\hbox {O}_{3}$ contribute to a reduction in the $\hbox {FEV}_1/$FVC.

Figure S6 shows the plots of the joint/interaction effect on $\hbox {FEV}_1/$FVC for $\hbox {PM}_{10}$ including $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, and $\hbox {O}_{3}$. In Fig. S6, $\hbox {PM}_{10}$-$\hbox {NO}_{2}$ and $\hbox {SO}_{2}$-$\hbox {O}_{3}$ have an interactive effect with each other. Specifically, when $\hbox {NO}_{2}$ is at the 25th and 50th percentiles, as the standardized $\hbox {PM}_{10}$ increases, the exposure-response function estimate becomes smaller, thus $\hbox {FEV}_1/$FVC can be seen to decrease. However, when the $\hbox {NO}_{2}$ level is at the 75th percentile, the exposure-response function estimate for $\hbox {PM}_{10}$ can be seen to actually increase, and since the three curves intersect, $\hbox {PM}_{10}$ and $\hbox {NO}_{2}$ can be seen to have an interaction effect. The relationship between $\hbox {SO}_{2}$ and $\hbox {O}_{3}$ can be examined similarly.

Figure S7 shows the overall effect plot on $\hbox {FEV}_1/$FVC for $\hbox {PM}_{10}$ including $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, and $\hbox {O}_{3}$. We examined each of the four exposure factors by simultaneously changing them from the 25th percentile to the 75th percentile. As a result, Fig. S7 shows that as the values of all four exposure factors become larger than the median, the exposure-response function estimate becomes relatively smaller, thus it can be interpreted that $\hbox {FEV}_1/$FVC becomes smaller.

Figure S8 illustrates the single-exposure effects, providing an estimate of each exposure’s contribution to the total exposure. In Fig. S8, when other exposures ($\hbox {SO}_{2}$, $\hbox {NO}_{2}$, $\hbox {O}_{3}$) within $\hbox {PM}_{10}$ are at the 25th and 50th percentiles, the difference in the exposure-response function estimates between the 75th and 25th percentiles of $\hbox {PM}_{10}$ is negative. This indicates that the exposure-response function estimate for the 75th percentile of $\hbox {PM}_{10}$ is smaller than that for the 25th percentile. Furthermore, when $\hbox {SO}_{2}$ is at the 25th and 50th percentiles, $\hbox {NO}_{2}$ is at the 25th, 50th, and 75th percentiles, and $\hbox {O}_{3}$ is at the 75th percentile, with all other exposure factors fixed at the median, a change in the value of the exposure factor from the 25th to the 75th percentile can be observed. This suggests that the $\hbox {FEV}_1/$FVC decreases as these exposure levels increase.

The result of $\text {PM}_{2.5}, \text {SO}_2, \text {NO}_2$, and $\text {O}_3$ on $\hbox {FEV}_1/$FVC

Figure S9 shows the plots of the univariate effect of $\hbox {PM}_{2.5}$, $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, and $\hbox {O}_{3}$ on $\hbox {FEV}_1/$FVC. In Fig. S9, unlike Fig. S5, the exposure-response function for $\hbox {PM}_{2.5}$ was estimated to be almost 0. Nonetheless, when the $\hbox {PM}_{2.5}$ standardized value is greater than about 3, the exposure-response function estimate is estimated to be negative, indicating a decrease in $\hbox {FEV}_1/$FVC. Likewise, $\hbox {NO}_2$ and $\hbox {O}_3$ can be interpreted to reduce $\hbox {FEV}_1/$FVC if they are above a certain value.

Figure S10 shows the plots of the joint/interaction effect on $\hbox {FEV}_1/$FVC for $\hbox {PM}_{2.5}$ including $\hbox {SO}_{2}$, $\hbox {NO}_{2}$ and $\hbox {O}_{3}$. In Fig. S10, $\hbox {SO}_{2}$-$\hbox {O}_{3}$ have an strongly interactive effect with each other.

Figure S11 shows the overall effect plot on $\hbox {FEV}_1/$FVC for $\hbox {PM}_{2.5}$ including $\hbox {SO}_{2}$, $\hbox {NO}_{2}$ and $\hbox {O}_{3}$. We examined each of the four exposure factors by simultaneously changing them from the 25th percentile to the 75th percentile. As a result, Fig. S11 shows that as the values of all four exposure factors become larger than the median, the exposure-response function estimate becomes relatively smaller, thus it can be interpreted that $\hbox {FEV}_1/$FVC becomes smaller.

Figure S12 illustrates the single-exposure effects, providing an estimate of each exposure’s contribution to the total exposure. In Fig. S12, when other exposures ($\hbox {SO}_2$, $\hbox {NO}_2$, $\hbox {O}_3$) within $\hbox {PM}_{2.5}$ are at the 50th and 75th percentiles, the difference in the exposure-response function estimates between the 75th and 25th percentiles of $\hbox {PM}_{2.5}$ is negative. This indicates that the exposure-response function estimate for the 75th percentile of $\hbox {PM}_{2.5}$ is smaller than that for the 25th percentile. Furthermore, when $\hbox {SO}_{2}$ is at the 50th and 75th percentiles, $\hbox {NO}_{2}$ is at the 50th and 75th percentiles, and $\hbox {O}_{3}$ is at the 75th percentile, with all other exposure factors fixed at the median, a change in the value of the exposure factor from the 25th to the 75th percentile can be observed. This suggests that the $\hbox {FEV}_1/$FVC decreases as these exposure levels increase.

Discussion

This study utilized Bayesian Kernel Machine Regression (BKMR) to investigate the nonlinear and interactive effects of multiple air pollutants on lung function linked 2017 Korea National Health and Nutrition Examination Survey (KNHANES) data with air pollution measurements from the same year. Unlike conventional regression models, BKMR provides a flexible framework for assessing the effects of complex pollutant mixtures, allowing us to quantify univariate, joint, and overall effects of key air pollutants, including $\hbox {PM}_{10}$, $\hbox {PM}_{2.5}$, $\hbox {SO}_{2}$, $\hbox {NO}_{2}$, $\hbox {O}_{3}$, and CO. The results of this study showed that exposure to air pollution is closely related to lung function decline, and in particular, $\hbox {PM}_{10}$ and $\hbox {O}_{3}$ were shown to have a significant effect on increasing the risk of chronic obstructive pulmonary disease (COPD) and reducing the $\hbox {FEV}_1/$FVC ratio. In addition, the analysis results showed that the mixture effect of these pollutants was greater than the individual effects of each substance. This suggests that when multiple air pollutants act simultaneously, an interactive effect that is more than the simple sum may occur.

In fact, these interactions have mechanisms that can contribute to the development of COPD through biological pathways such as oxidative stress and inflammatory responses^28,29. Therefore, when evaluating the health effects of air pollution, it is very important to consider not only the effects of single substances but also the interactions between pollutants, and these results emphasize the need for a comprehensive evaluation of various air pollutants and related policy proposals.

In terms of public health intervention, these findings underscore the necessity of integrated air quality management strategies that target pollutant mixtures rather than individual pollutants alone. Such strategies may include implementing region-specific air pollution alerts that account for the combined levels of multiple pollutants, strengthening emission regulations for major sources that release co-occurring pollutants, and developing community-based health surveillance programs to monitor and mitigate lung function decline among vulnerable populations, such as older adults and those with pre-existing respiratory conditions.

In this study, we will examine the limitations in terms of methodology and data. Despite these advantages, BKMR has some limitations that should be recognized. First, the model assumes independence between observations, making it less suitable for analyzing longitudinal or time-dependent data. This limitation is particularly relevant in air pollution studies, where exposure effects often unfold over time. Second, computational complexity is a major challenge when applying BKMR to large datasets with multiple exposures, as the model requires intensive computation, limiting scalability. Third, BKMR does not inherently account for time-lagged effects, which can play a critical role in understanding delayed health responses to air pollution exposure. These limitations suggest areas for methodological improvements and extensions in future research.

From a data perspective, the lack of seasonal variables in the dataset meant that we were unable to determine the seasonal impact of pollutant exposure and health outcomes.

Future studies could enhance the applicability of BKMR by incorporating time-series models, such as Bayesian Kernel Machine Regression Distributed Lag Models (BKMR-DLM) or Distributed Lag Nonlinear Models (DLNM), to account for the delayed health effects of air pollution. Addressing computational constraints through parallel computing techniques or dimensionality reduction approaches could also improve the feasibility of BKMR for large-scale epidemiological studies. Expanding sample sizes and leveraging high-performance computing would further enhance the robustness and generalizability of BKMR-based analyses.

The stratified analyses by geographic region, socioeconomic status, or pre-existing health conditions, and multilevel modeling or cluster-robust standard error estimation that adjust for potential spatial clustering by geographic units, such as the 17 administrative regions, could provide deeper insights into disparities in air pollution exposure and health outcomes. Additionally, if we consider information such as whether or not medical services are not being provided or the reasons for not being provided as advised, we expect to obtain more advanced research results in terms of quality.