Some novel optical pulses in hydrodynamical nonlinear complex equation using M-truncated fractional derivative

Abstract

This study investigates soliton solutions and dynamic wave structures in the complex Ginzburg-Landau (CGL) equation, which is crucial for understanding wave propagation in various physical systems. We employ three analytical methods: the Kumar-Malik method, the generalized Arnous method, and the energy balance method to derive novel closed-form solutions. These solutions exhibit diverse solitonic phenomena, including multi-wave solitons, complex solitons, singular solitons, periodic oscillating waves, dark-wave, and bright-wave profiles. Our results reveal new families of exact solitary waves via the generalized Arnous method and diverse soliton solutions through the Kumar-Malik method, including hyperbolic, trigonometric, and Jacobi elliptic functions. Verification is ensured through back-substitution to the considered model using Mathematica software. Additionally, we plot the various graphs with the appropriate parametric values under the influence of the M-truncated fractional derivative to visualize the solution behaviors with varying parameter values. This research contributes significantly to understanding wave dynamics in physical oceanography, and the unique outcomes explored in this research will play a vital role for the forthcoming investigation of nonlinear equations.

Introduction

The quest for exact solutions to nonlinear partial differential equations (NLPDEs) has activated as a vibrant research area, driven by the need to elucidate complex phenomena in various applied sciences. Accurate solutions to NLPDEs are crucial for unraveling the underlying physics, as they provide a window into the intricate dynamics governing natural processes. New and systematic methods for deriving closed-form solutions to NLPDEs^1,2,3,4,5 have been made possible by recent developments in symbolic computation, which frequently take advantage of the properties of well-known ordinary differential equations (ODEs) like the Jacobi, Riccati, and Bernoulli equations to represent solutions as finite series or other mathematical structures.

Soliton theory is commonly used in these models because it yields precise solutions such as periodic, solitary, dark, bright, and traveling wave solutions. Since physical phenomena are intrinsically nonlinear, the best way to represent them is typically through mathematical modeling^{6,7,8,9,10,11}. It may now use partial differential equations to completely understand and identify the characteristics of physical problems. Finding analytical solutions for moving waves is the main physical difficulty for these models. Numerous fields, including physics, geophysics, climatic dynamics, economics, biology, and more, now make extensive use of randomness^12,13,14,15. Nonlinear applied science domains like as solid-state physics, geology, chemical physics, and optical fiber have developed solutions to various nonlinear evolution equations (NLEEs). In diverse scientific and engineering fields the solution of NLEEs has been explored. Numerous mathematical and technical topics are covered, including ocean propagation, hydrodynamics, thermal capacity, magnetism, quantum dynamics, seismic waves, and etc.

Furthermore, it is crucial to grow a robust analytical mechanism for these nonlinear evolution equations (NLEEs) and establish a comprehensive understanding of their dynamical properties. Different scholars have demonstrated a strong interest in finding a precise solution to these NLEEs. It has been proved that by utilizing symbolic tools, there are multiple appropriate and efficient ways for discovering the best solutions to various NLEEs. The improved tanh method and the rational $(G'/G)$-expansion method¹⁶, the unified Riccati equation expansion scheme¹⁷, the complete discriminant system¹⁸, the hyperbolic function approach¹⁹, the Hirota bilinear method²⁰, the amended-Gordon expansion scheme²¹, planar dynamic system method²², and the modified Kudryashov method²³ are just a few of the many available practical approaches. These methods have played a key role in understanding the physical properties of soliton solutions and founding a theoretical basis for soliton transmission in fiber optic systems.

Among various analytical methodologies, the Kumar-Malik method^24,25 and the generalized Arnous method^{26,27,28,29,30} have garnered significant attention. Notably, Kumar et al.²⁴ applied the Kumar-Malik method to derive precise solutions for NLPDEs, while Kumar et al.²⁵ utilized it to solve a nonlinear problems that plays a key role in illustrating shallow water behavior. Similarly, the generalized Arnous method has attracted researchers^{26,27,28,29,30} because of its capacity to yield more generic outcomes. Arnous et al.²⁶ applied this method to solve NLPDEs, whereas Zarour and Arnous²⁷utilized it to derive exact solutions for nonlinear reaction-diffusion equations. Additionally^28,29,30, provides applications for the generalized Arnous approach. This paper uses the Kumar-Malik and generalized Arnous methods to create complex wave patterns for the CGL equation, building on earlier promising results^{24,25,26,27,28,29,30} and previous research^{31,32,33,34,35}.

$$\begin{aligned} i D^{\alpha , \beta }_{M, t}\varphi +\zeta _1 D^{2\alpha , \beta }_{M, x}\varphi +\zeta _2|\varphi |^2\varphi - \frac{\zeta _3}{|\varphi |^2\varphi ^*}\bigg (2|\varphi |^2(D^{2\alpha , \beta }_{M, x}|\varphi |^2)-((D^{\alpha , \beta }_{M, x}|\varphi |^2))^2 \bigg )-\zeta _4 \varphi =0, \end{aligned}$$

(1)

where $D^{\alpha , \beta }_{M}$ denotes the M-truncated derivative with $\alpha \in (0, 1]$ and $\beta>0$, while $\varphi = \varphi (x, t)$ is the complex wave profile. The CGL equation, given by Eq. $(1)$, the dynamics of soliton propagation in the presence of a detuning component, with coefficients $\zeta _1$ and $\zeta _2$ controlling Kerr law nonlinearity and group velocity dispersion, and $\zeta _3$ and $\zeta _4$ representing perturbation effects. Numerous recent investigations on the CGL equation have produced a variety of solutions, including intricate wave shapes via the modified auxiliary equation approach³¹, combo optical dark singular solitons³², and solitons using the exp(-$\Phi (\xi )$)-expansion method³³ and other approaches^34,35. This article investigates the CGL Eq. $(1)$ using Kumar-Malik (KM) method, the generalized Arnous method, and the energy balance method, aiming to acquire a compreensive set of waveform solutions, which are then visually illustrated through Mathematica simulations in 2D and 3D plots, revealing intriguing evolutionary dynamics crucial for understanding complex physical phenomena.

Fractional calculus, originally designed for the formulation of noninteger derivatives and integrals, presents a robust mathematical structure for explicating a myriad of phenomena across different scientific domains³⁶. This increasing prominence is fueled by the escalating demand for precise simulations of both historical and modern physical phenomena^37,38. Studies have demonstrated the utility of fractional operators in modeling natural phenomena, highlighting that fractional-order models surpass non-integer (classical) systems in effectiveness and productivity^39,40.

Nevertheless, a comprehensive review of the literature has revealed that the Kumar-Malik technique⁴¹, the generalized Arnous approach⁴² and energy balnce technique⁴³ have not been used to solve the governing equation, highlighting significant gaps in our understanding. By motivating this we utilize analytical techniques to efficiently classify and organize solutions for nonlinear problems. These approaches provide a simple yet powerful approach for deriving precise wave structures, though they fail when the highest-order derivative and nonlinear terms are unbalanced. The attained solutions have noteworthy applications in fields like fluid dynamics, condensed matter physics, nonlinear optics, and plasma physics. These methods also serve as valuable tools for analyzing complex systems, enhancing our understanding of nonlinear phenomena in real-world scenarios. The aim of the current study is to explore and broaden the theoretical underpinnings of soliton dynamics. Provide useful information for constructing modern telecommunication networks, oceanography, and chemical oceanography applications. By filling these gaps, this study will advance our understanding of complicated optical phenomena and inform novel solutions to real-world problems.

The truncated M-fractional derivative

The investigation of solitary wave solutions using truncated M-fractional derivatives is a well-known area of study that has attracted a lot of interest from scholars. Recent studies have shown that the truncated M-fractional derivative provides a more realistic representation of the behavior of solitary waves than other fractional derivatives, particularly in nonlinear systems. In several scientific fields, including engineering, signal processing, electromagnetics, and others, this phenomena also shows a broad spectrum of practical applications. The truncated M-fractional derivative is a highly relevant parameter simply because it can precisely represent complex systems with memory effects, long-range and nonlocal interactions, and nonlinear dynamics. A strong tool for comprehending and evaluating a range of systems associated with the biological, engineering, and physical sciences is provided to scientists and engineers by this particular kind of derivative. This truncated M-fractional derivative, which is made up of localized disturbances that move through a medium without changing their shape, is used to depict solitary waves.

Definition 0.1

Let $k: [0,\infty )\rightarrow \mathbb {R}$, then the new truncated M-fractional derivative of k of order $\beta$ is discussed⁴⁴ as:

$$\begin{aligned} \mathscr {D}_{M}^{\beta ,\;\zeta }\{(k)(t)\}=\lim _{\beta \rightarrow 0} \frac{k(t\mathbb {E}_{\zeta }(\beta t^{1-\beta }))-k(t) }{\beta },\;\;\forall t>0,\;\;0<\beta <1,\;\zeta>0, \end{aligned}$$

(2)

where $\mathbb {E}_{\zeta }(.)$ is a truncated Mittag-Leffler function of one parameter⁴⁴.

Theorem 0.1

Let $0<\beta \le 1$, $\zeta>0$, $p,\;s\in \mathbb {R}$, and $f,\;k$ $\beta$-differentiable at a point $t>0$. Then:

• 1. $\mathscr {D}_{M}^{\beta ,\;\zeta }\{(p f+s k)(t)\}=p\mathscr {D}_{M}^{\beta ,\;\zeta }\{f(t)\}+s\mathscr {D}_{M}^{\beta ,\;\zeta }\{k(t)\}$.

• 2. $\mathscr {D}_{M}^{\beta ,\;\zeta }\{(f\;. \;k)(t)\}=f(t)\mathscr {D}_{M}^{\beta ,\;\zeta }\{k(t)\}+k(t)\mathscr {D}_{M}^{\beta ,\;\zeta }\{f(t)\}$.

• 3. $\mathscr {D}_{M}^{\beta ,\;\zeta }\{\frac{f}{k}(t)\}=\frac{k(t)\mathscr {D}_{M}^{\beta ,\;\zeta }\{f(t)\} -f(t)\mathscr {D}_{M}^{\beta ,\;\zeta }\{k(t)\}}{[k(t)]^2}$.

• 4. $\mathscr {D}_{M}^{\beta ,\;\zeta }\{f(t)\}=0$, where $f(t)=c$ is a constant.

• 5. If f(t) is differentiable, then $\mathscr {D}_{M}^{\beta ,\;\zeta }\{f(t)\}=\frac{t^{1-\beta }}{\Gamma (\zeta +1)}\frac{df(t)}{dt}.$

The M-truncated fractional derivative is chosen for this study due to its mathematical flexibility, non-singular kernel, and tunable memory effects, offering a balance between accuracy and computational efficiency. Unlike Caputo (singular kernel, slow decay) or Atangana-Baleanu (AB) derivative (computationally expensive), the M-truncated derivative avoids singularities, simplifies numerical solutions, and preserves non-locality, making it ideal for modeling wave propagation in nonlinear systems. Its exponential kernel ensures stability, while the truncation parameter M allows control over fractional effects, aligning with observed physics. A comparison with other derivatives is shown in Table (1):

Table 1 Comparative analysis with other fractional derivatives.

This choice ensures analytical tractability for soliton solutions while capturing essential non-local dynamics.

Methodologies

Suppose the NLPDE of the following type:

$$\begin{aligned} F(p,p_{x},p_{t},p_{xxx},p_{xx},p_{tt},\ldots )=0, \end{aligned}$$

(3)

where $p=p(x,t)$ is a unknown function of x and t and consisting its partial derivatives.

An overview of Kumar-Malik method

The important steps of the KM method are:

Step 1: By utilizing the traveling wave transformation

$$\begin{aligned} p(x,t)=P(\xi ),\quad \xi =(x-vt), \end{aligned}$$

(4)

where v represents the wave speed constant and substitute the above transformation into Eq. (3), we obtain an ordinary differential equation (ODE):

$$\begin{aligned} H(P,P^{\prime },P^{\prime \prime },P^{\prime \prime \prime },\ldots )=0. \end{aligned}$$

(5)

Step 2: Consider Eq. (5) has a solution expressed as

$$\begin{aligned} P(\xi )=A_{0}+A_{1}\Phi (\xi )+A_{2}\Phi (\xi )^{2}+\cdots +A_{N}\Phi (\xi )^{N}, \end{aligned}$$

(6)

where $A_{i}$’s ($i=1,2,\ldots ,N$) are the constants that are to be found later, and the function $\Phi (\xi )$ fulfills the first-order ODE:

$$\begin{aligned} \left[ \Phi ^{\prime }(\xi )\right] ^{2}=\left[ a_{1}\Phi (\xi )^{4}+a_{2}\Phi (\xi )^{3}+a_{3}\Phi (\xi )^{2}+a_{4}\Phi (\xi )+a_{5}\right] , \end{aligned}$$

(7)

where $a_{i}^{\prime }s,(i=1,2,\ldots ,5)$ are arbitrary constants. The explicit solutions of Eq. (7) are listed below.

Step 3: Calculate N by employing the balance rule to Eq. (5).

Step 4: Put Eq. (6) and its derivatives based on Eq. (7) into Eq. (5) resulting in a polynomial in $\Phi (\xi )\Phi ^{\prime }(\xi )$. Setting all coefficients of the same powers to zero, acquire equations for v, $A_{i}$ $(i=1,2,\ldots ,N)$, and $a_{j}$ $(j=1,2,\ldots ,5)$. On solving these equations give the exact solutions to Eq. (5).

Solutions of Eq. (7)

Exact solutions of Eq. (7) are given for four cases.

Case 1: For $a_{4}=\frac{a_{2}\left( 4a_{1}a_{3}-a_{2}^{2}\right) }{8a_{1}^{2}}$, $\quad a_{5}=0$, the Eq. (7) gives the Jacobi elliptic solutions:

Sub-case 1.1: If $a_{1}<0,\left( 4a_{1}a_{3}-a_{2}^{2}\right)>0$.

$$\begin{aligned} \Phi _{01}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{a_{2}}{4a_{1}}\ \text {cn }\left( \frac{\sqrt{-a_{1}\left( 4a_{1}a_{3}-a_{2}^{2}\right) }}{2a_{1}}\ \xi ,\frac{a_{2}}{2\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) }} \right) , \end{aligned}$$

(8)

$$\begin{aligned} \Phi _{02}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{a_{2}}{4a_{1}}\ \text {dn }\left( \frac{a_{2}}{4\sqrt{-a_{1}}}\ \xi ,\frac{2\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) }}{a_{2}}\right) . \end{aligned}$$

(9)

Sub-case 1.2: If $a_{1}<0,\left( 4a_{1}a_{3}-a_{2}^{2}\right)<0,\left( 16a_{1}a_{3}-5a_{2}^{2} \right) <0$.

$$\begin{aligned} \Phi _{03}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \text {cn }\left( \frac{\sqrt{a_{1}\left( 4a_{1}a_{3}-a_{2}^{2} \right) }}{2a_{1}}\ \xi ,\frac{\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) \left( 16a_{1}a _{3}-5a_{2}^{2}\right) }}{2\left( 4a_{1}a_{3}-a_{2}^{2}\right) }\right) , \end{aligned}$$

(10)

$$\begin{aligned} \Phi _{04}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \text {dn }\left( \frac{\sqrt{a_{1}\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \xi ,\frac{2\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) \left( 16a_{1}a _{3}-5a_{2}^{2}\right) }}{\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }\right) . \end{aligned}$$

(11)

Sub-case 1.3: If $a_{1}<0,\left( 4a_{1}a_{3}-a_{2}^{2}\right)>0$ and $\left( 16a_{1}a_{3}-5a_{2}^{2}\right) <0$.

$$\begin{aligned} \Phi _{05}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \text {nc }\left( \frac{\sqrt{-a_{1}\left( 4a_{1}a_{3}-a_{2}^{2} \right) }}{2a_{1}}\ \xi ,\frac{a_{2}}{2\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) }} \right) , \end{aligned}$$

(12)

$$\begin{aligned} \Phi _{06}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \text {nd }\left( \frac{a_{2}}{4\sqrt{-a_{1}}}\ \xi ,\frac{2\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) }}{a_{2}}\right) . \end{aligned}$$

(13)

Sub-case 1.4: If $a_{1}\left( 4a_{1}a_{3}-a_{2}^{2}\right)>0$ and $\left( 4a_{1}a_{3}-a_{2}^{2}\right) \left( 16a_{1}a_{3}-5a_{2}^{2}\right)>0$.

$$\begin{aligned} \Phi _{07}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{a_{2}}{4a_{1}}\ \text {nc }\left( \frac{\sqrt{a_{1}\left( 4a_{1}a_{3}-a_{2}^{2}\right) }}{2a_{1}}\ \xi ,\frac{\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) \left( 16a_{1}a _{3}-5a_{2}^{2}\right) }}{2\left( 4a_{1}a_{3}-a_{2}^{2}\right) }\right) , \end{aligned}$$

(14)

$$\begin{aligned} \Phi _{08}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{a_{2}}{4a_{1}}\ \text {nd }\left( \frac{\sqrt{a_{1}\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }}{4a_{1}}\ \xi ,\frac{2\sqrt{\left( 4a_{1}a_{3}-a_{2}^{2}\right) \left( 16a_{1}a _{3}-5a_{2}^{2}\right) }}{\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }\right) . \end{aligned}$$

(15)

Sub-case 1.5: If $a_{1}>0,\left( 16a_{1}a_{3}-5a_{2}^{2}\right) <0$.

$$\begin{aligned} \Phi _{09}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{a_{2}}{4a_{1}}\ \text {ns }\left( \frac{a_{2}}{4\sqrt{a_{1}}}\ \xi ,\frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }}{a_{2}}\right) , \end{aligned}$$

(16)

$$\begin{aligned} \Phi _{10}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \text {ns }\left( \frac{\sqrt{-a_{1}\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \xi ,\frac{a_{2}}{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }} \right) , \end{aligned}$$

(17)

$$\begin{aligned} \Phi _{11}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2} \right) }}{4a_{1}}\ \text {sn }\left( \frac{a_{2}}{4\sqrt{a_{1}}}\ \xi ,\frac{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }}{a_{2}}\right) , \end{aligned}$$

(18)

$$\begin{aligned} \Phi _{12}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{a_{2}}{4a_{1}}\ \text {sn }\left( \frac{\sqrt{-a_{1}\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }}{4a_{1}}\ \xi ,\frac{a_{2}}{\sqrt{-\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }}\right) . \end{aligned}$$

(19)

Case 2: For $a_{4}=\frac{a_{2}\left( 4a_{1}a_{3}-a_{2}^{2}\right) }{8a_{1}^{2}}$, $\quad a_{5}=\frac{\left( 4a_{1}a_{3}-a_{2}^{2}\right) ^{2}}{64a_{1}^{3}}$, the Eq. (7) yeilds hyperbolic and trigonometric solutions:

Sub-case 2.1: If $a_{1}>0,$ $(8a_{1}a_{3}-3a_{2}^{2})<0.$

$$\begin{aligned} \Phi _{13}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-(8a_{1}a_{3}-3a_{2}^{2})}}{4 a_{1}}\tanh \left( \frac{\sqrt{-a_{1}\left( 8a_{1}a_{3}-3a_{2}^{2}\right) }}{4a_{1}} \xi \right) , \end{aligned}$$

(20)

$$\begin{aligned} \Phi _{14}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-(8a_{1}a_{3}-3a_{2}^{2})}}{4 a_{1}}\coth \left( \frac{\sqrt{-a_{1}\left( 8a_{1}a_{3}-3a_{2}^{2}\right) }}{4a_{1}} \xi \right) . \end{aligned}$$

(21)

Sub-case 2.2: If $a_{1}>0,$ $(8a_{1}a_{3}-3a_{2}^{2})>0.$

$$\begin{aligned} \Phi _{15}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{(8a_{1}a_{3}-3a_{2}^{2})}}{4 a_{1}}\tan \left( \frac{\sqrt{a_{1}\left( 8a_{1}a_{3}-3a_{2}^{2}\right) }}{4a_{1}} \xi \right) , \end{aligned}$$

(22)

$$\begin{aligned} \Phi _{16}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{(8a_{1}a_{3}-3a_{2}^{2})}}{4 a_{1}}\cot \left( \frac{\sqrt{a_{1}\left( 8a_{1}a_{3}-3a_{2}^{2}\right) }}{4a_{1}} \xi \right) . \end{aligned}$$

(23)

Case 3: For $a_{4}=\frac{a_{2}\left( 4a_{1}a_{3}-a_{2}^{2}\right) }{8a_{1}^{2}}, \quad a_{5}=\frac{a_{2}^{2}\left( 16a_{1}a_{3}-5a_{2}^{2}\right) }{256a_{1}^{3}},$ the Eq. (7) provides hyperbolic and trigonometric solutions:

Sub-case 3.1: If $a_{1}<0, (8a_{1}a_{3}-3a_{2}^{2})<0.$

$$\begin{aligned} \Phi _{17}(\xi ) =-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-2\left( 8a_{1}a_{3}-3a_{2}^{2 }\right) }}{4a_{1}} \operatorname {sech}\left( \frac{\sqrt{2a_{1}\left( 8a_{1}a_{3 }-3a_{2}^{2}\right) }}{4a_{1}}\xi \right) . \end{aligned}$$

(24)

Sub-case 3.2: If $a_{1}>0, (8a_{1}a_{3}-3a_{2}^{2})>0.$

$$\begin{aligned} \Phi _{18}(\xi ) =-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{2\left( 8a_{1}a_{3}-3a_{2}^{2 }\right) }}{4a_{1}} \operatorname {csch}\left( \frac{\sqrt{2a_{1}\left( 8a_{1}a_{3 }-3a_{2}^{2}\right) }}{4a_{1}}\xi \right) . \end{aligned}$$

(25)

Sub-case 3.3: If $a_{1}>0, (8a_{1}a_{3}-3a_{2}^{2})<0.$

$$\begin{aligned} \Phi _{19}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-2\left( 8a_{1}a_{3}-3a_{2}^{2 }\right) }}{4a_{1}} \operatorname {sec}\left( \frac{\sqrt{-2a_{1}\left( 8a_{1}a_{3 }-3a_{2}^{2}\right) }}{4a_{1}}\xi \right) , \end{aligned}$$

(26)

$$\begin{aligned} \Phi _{20}(\xi )&=-\frac{a_{2}}{4a_{1}}\pm \frac{\sqrt{-2\left( 8a_{1}a_{3}-3a_{2}^{2 }\right) }}{4a_{1}} \operatorname {csc}\left( \frac{\sqrt{-2a_{1}\left( 8a_{1}a_{3 }-3a_{2}^{2}\right) }}{4a_{1}}\xi \right) . \end{aligned}$$

(27)

Case 4: For $a_{2}=a_{4}=a_{5}=0,a_{3}>0,$ the Eq. (7) makes the exponential solutions:

$$\begin{aligned} \Phi _{21}(\xi )=\frac{4\rho a_{3}}{\left( 4\rho ^{2}\ \textrm{e}^{\sqrt{a_{5}}\xi }-a_{1}a_{3}\ \textrm{e}^{-\sqrt{a_{5}}\xi }\right) }. \end{aligned}$$

(28)

By taking $a_{1}=-\frac{4\rho ^{2}}{a_{3}},$ solution (28) reduces to

$$\begin{aligned} \Phi _{22}(\xi )=\frac{a_{3}}{2\rho } \operatorname {sech}(-\sqrt{a_{5}}\xi ), \end{aligned}$$

(29)

while by taking $a_{1}=\frac{4\rho ^{2}}{a_{3}},$ solution (28) reduces to

$$\begin{aligned} \Phi _{23}(\xi )=\frac{a_{3}}{2\rho } \operatorname {sech}(-\sqrt{a_{5}}\xi ). \end{aligned}$$

(30)

An overview of the generalized Arnous method

Using the generalized Arnous method, the solution is given as

$$\begin{aligned} P(\xi ) = c_0 + \sum _{j=1}^{n} \frac{c_j}{(\phi (\xi ))^j} + \sum _{j=1}^{n} \frac{d_j \left( \phi '(\xi ) \right) ^j}{\left( \phi (\xi ) \right) ^j}. \end{aligned}$$

(31)

For $n = 1$, we have

$$\begin{aligned} P(\xi ) = c_0 + \frac{c_1}{\phi (\xi )} + \frac{d_1 \phi '(\xi )}{\phi (\xi )}, \end{aligned}$$

(32)

where the constants $c_0, \, c_1, \, d_1$ be determined later and the function $\phi (\xi )$ demonstrates the following relation:

$$\begin{aligned} \left( \phi '(\xi ) \right) ^2 = \ln (\delta )^2 \left( \phi (\xi )^2 - \rho \right) , \end{aligned}$$

(33)

with

$$\begin{aligned} \phi ^{(n)}(\xi ) = {\left\{ \begin{array}{ll} \ln (\delta )^n \phi '(\xi ), & n \text { is odd}, \\ \ln (\delta )^n \phi (\xi ), & n \text { is even}, \end{array}\right. } \end{aligned}$$

(34)

for $\delta \ne 1, \, n \ge 2$ and $\delta> 0$. Accordingly, the solution to Eq. (33) is stated as:

$$\begin{aligned} { \phi (\xi ) = A \delta ^\xi \ln (\delta ) + \frac{\rho }{4 A \delta ^\xi \ln (\delta )}}, \end{aligned}$$

(35)

where A and $\rho$ are an arbitray constants. Subsituting Eq. (32) along with Eq. (8) in Eq. (5), general solutions are acquired. Here we add a Table (2) of the above- said methods which summarizes the types of solutions attained through each method Kumar-Malik method, generalized Arnous, and energy balance method.

Table 2 Comparative analysis of analytical solution methods.

Mathematical analysis

To derive the real and imaginary components of the given CGL Eq. (1). Suppose the following traveling wave transformation:

$$\varphi (x,t) = \Phi (\xi ) e^{i\chi }, \quad \xi = \frac{x^\alpha }{\Gamma (1+\alpha )} - \frac{v t^\alpha }{\Gamma (1+\alpha )}, \quad \chi = \frac{-k x^\alpha }{\Gamma (1+\alpha )} + \frac{\omega t^\alpha }{\Gamma (1+\alpha )} + \theta ,$$

where, $\Phi (\xi )$ is the amplitude (real function). $v$ = velocity, $k$ = wave number, $\omega$ = frequency, $\theta$ = phase constant. Next, we apply the chain rule to compute the fractional derivatives.

Time derivative ($D_{M,t}^{\alpha ,\beta }\varphi$):

$$D_{M,t}^{\alpha ,\beta }\varphi = \left( -v \frac{d\Phi }{d\xi } + i\omega \Phi \right) e^{i\chi }.$$

Spatial derivatives ($D_{M,x}^{\alpha ,\beta }\varphi$): First order:

$$D_{M,x}^{\alpha ,\beta }\varphi = \left( \frac{d\Phi }{d\xi } - i k \Phi \right) e^{i\chi }.$$

Second order:

$$D_{M,x}^{2\alpha ,\beta }\varphi = \left( \frac{d^2\Phi }{d\xi ^2} - 2i k \frac{d\Phi }{d\xi } - k^2 \Phi \right) e^{i\chi }.$$

Nonlinear terms: $|\varphi |^2 = \Phi ^2$, so:

$$D_{M,x}^{\alpha ,\beta }|\varphi |^2 = 2\Phi \frac{d\Phi }{d\xi }, \quad D_{M,x}^{2\alpha ,\beta }|\varphi |^2 = 2 \left( \frac{d\Phi }{d\xi } \right) ^2 + 2\Phi \frac{d^2\Phi }{d\xi ^2}.$$

Substitute into Eq. (1) substitute all derivatives and simplify:

$$i \left( -v \Phi ' + i\omega \Phi \right) + \zeta _1 \left( \Phi '' - 2i k \Phi ' - k^2 \Phi \right) + \zeta _2 \Phi ^3 - \frac{\zeta _3}{\Phi ^2} \left( 2\Phi ^2 \left( 2(\Phi ')^2 + 2\Phi \Phi '' \right) - \left( 2\Phi \Phi ' \right) ^2 \right) - \zeta _4 \Phi = 0.$$

Simplify the nonlinear term:

$$\frac{\zeta _3}{\Phi ^2} \left( 4\Phi ^2 (\Phi ')^2 + 4\Phi ^3 \Phi '' - 4\Phi ^2 (\Phi ')^2 \right) = 4\zeta _3 \Phi \Phi ''.$$

Final substituted equation:

$$i (-v \Phi ' + i\omega \Phi ) + \zeta _1 (\Phi '' - 2i k \Phi ' - k^2 \Phi ) + \zeta _2 \Phi ^3 - 4\zeta _3 \Phi \Phi '' - \zeta _4 \Phi = 0.$$

Separate real and imaginary parts.

Imaginary part:

$$\begin{aligned} -v \Phi ' - 2\zeta _1 k \Phi ' = 0 \implies v = -2\zeta _1 k. \end{aligned}$$

(36)

Real part:

$$-\omega \Phi + \zeta _1 (\Phi '' - k^2 \Phi ) + \zeta _2 \Phi ^3 - 4\zeta _3 \Phi \Phi '' - \zeta _4 \Phi = 0.$$

We have

$$\begin{aligned} \left( 4 \zeta _3-\zeta _1\right) \Phi ''(\xi )-\zeta _2 \Phi ^3(\xi )+\left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) \Phi (\xi )=0. \end{aligned}$$

(37)

Afterward, using the homogeneous balance technique to the terms $\Phi ''$ and $\Phi ^3$ in the system (37), provides $n=1$.

Solutions via newly created Kumar-Malik method

Assume the solution to this method according to the Eq. (37) can be written as

$$\begin{aligned} \Phi (\xi )=A_{0}+\sum _{h=1}^{n}A_{h}(Q(\xi ))^{h}. \end{aligned}$$

(38)

Further, $Q(\xi )$ fulfills the first-order ODE as:

$$\begin{aligned} {[}(Q'(\xi )]^2=[\alpha _1 Q^4(\xi )+\alpha _2 Q^3(\xi )+\alpha _3 Q^2(\xi )+\alpha _4 Q(\xi )+\alpha _5], \end{aligned}$$

(39)

where $\alpha _i (i=1,\cdots , 5)$ are constants. For $n=1$, the above solution of Eq. (38) changes into:

$$\begin{aligned} \Phi (\xi )=A_0+A_1 Q(\xi ). \end{aligned}$$

(40)

By inserting Eq. (40) and its corresponding derivatives from Eq. (39) into Eq. (37), we methodically accumulate the coefficients of like powers of $Q(\xi )$ and set them to zero. Using Mathematica for algebraic computations, we receive the following distinct solutions sets.

Remark

For convienience we use these notation $\Sigma _1=4 \alpha _1 \alpha _3-\alpha _2^2,\Sigma _2=16 \alpha _1 \alpha _3-5 \alpha _2^2,\Sigma _3=8 \alpha _1 \alpha _3-3 \alpha _2^2$ for next four cases.

Case-1: For $\alpha _4=\frac{\left( 4 \alpha _1 \alpha _3-\alpha _2^2\right) \alpha _2}{8 \alpha _1^2},~\alpha _5=0.$ we earn

$$\begin{aligned} {\left\{ \begin{array}{ll} A_0=-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}},~A_1=-\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}},~\omega =-\frac{8 \alpha _1 \left( \zeta _1 \left( \kappa ^2-\alpha _3\right) +4 \alpha _3 \zeta _3+\zeta _4\right) +3 \alpha _2^2 \left( \zeta _1-4 \zeta _3\right) }{8 \alpha _1}. \end{array}\right. } \end{aligned}$$

• The Jacobi elliptic solutions

Sub-case 1.1: If $\alpha _1<0$ and $\Sigma _1>0.$

$$\begin{aligned} & \varphi _{1}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\alpha _2}{4 \alpha _1}\left( \text {cn}\left( \frac{\sqrt{-\alpha _1 \Sigma _1} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \alpha \alpha _1},\frac{\alpha _2}{2 \sqrt{\Sigma _1}}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace } \times e^{i \chi }. \end{aligned}$$

(41)

$$\begin{aligned} & \varphi _{2}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\alpha _2}{4 \alpha _1}\left( \text {dn}\left( \frac{\alpha _2 \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \sqrt{-\alpha _1}},\frac{2 \sqrt{\Sigma _1}}{\alpha _2}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(42)

$$\begin{aligned} & {{Sub-case 1.2:}} ~\text{ If } ~~\alpha _1<0, \Sigma _1<0~~\text{ and }~~ \Sigma _2<0.\nonumber \\ & \varphi _{3}(x,t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _2}}{4 \alpha _1}\left( \text {cn}\left( \frac{\sqrt{\alpha _1 \Sigma _1} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \alpha \alpha _1},\frac{\sqrt{\Sigma _1 \Sigma _2}}{2 \Sigma _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(43)

$$\begin{aligned} & \varphi _{4}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _2}}{4 \alpha _1}\left( \text {dn}\left( \frac{\sqrt{\alpha _1 \Sigma _2} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1},\frac{2 \sqrt{\Sigma _1 \Sigma _2}}{\Sigma _2}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(44)

$$\begin{aligned} & {{Sub-case 1.3:}}~\text{ If } ~~\alpha _1<0, \Sigma _1>0~~\text{ and }~~ \Sigma _2<0.\nonumber \\ & \varphi _{5}(x, t)=\Bigg \lbrace {\frac{\alpha _1 \zeta }{\sqrt{\mho } \sqrt{\alpha _1 \left( -\Omega ^2-1\right) }}\left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _2}}{4 \alpha _1}\left( \text {nc}\left( \frac{\sqrt{-\alpha _1 \Sigma _1} \Gamma (\beta +1) \left( \zeta s^{\alpha }-\zeta \kappa t^{\alpha }\right) }{2 \alpha \alpha _1},\frac{\alpha _2}{2 \sqrt{\Sigma _1}}\right) \right) \right) }\nonumber \\ & \quad {+\frac{\alpha _2 \zeta }{4 \sqrt{\mho } \sqrt{\alpha _1 \left( -\Omega ^2-1\right) }}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(45)

$$\begin{aligned} & \varphi _{6}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _2}}{4 \alpha _1}\left( \text {nd}\left( \frac{\alpha _2 \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \sqrt{-\alpha _1}},\frac{2 \sqrt{\Sigma _1}}{\alpha _2}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(46)

$$\begin{aligned} & {{Sub-case 1.4:}}~\text{ If } ~~\alpha _1 \Sigma _1>0 ~~\text{ and }~~ \Sigma _1 \Sigma _2>0.\nonumber \\ & \varphi _{7}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\alpha _2}{4 \alpha _1}\left( \text {nc}\left( \frac{\sqrt{\alpha _1 \Sigma _1} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \alpha \alpha _1},\frac{\sqrt{\Sigma _1 \Sigma _2}}{2 \Sigma _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(47)

$$\begin{aligned} & \varphi _{8}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\alpha _2}{4 \alpha _1}\left( \text {nd}\left( \frac{\sqrt{\alpha _1 \Sigma _2} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1},\frac{2 \sqrt{\Sigma _1 \Sigma _2}}{\Sigma _2}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(48)

$$\begin{aligned} & {{Sub-case 1.5:}}~\text{ If } ~~\alpha _1>0 ~~\text{ and }~~ \Sigma _2<0.\nonumber \\ & \varphi _{9}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\alpha _2}{4 \alpha _1}\left( \text {ns}\left( \frac{\alpha _2 \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \sqrt{\alpha _1}},\frac{\sqrt{-\Sigma _2}}{\alpha _2}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(49)

$$\begin{aligned} & \varphi _{10}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _2}}{4 \alpha _1}\left( \text {ns}\left( \frac{\sqrt{-\alpha _1 \Sigma _2} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1},\frac{\alpha _2}{\sqrt{-\Sigma _2}}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(50)

$$\begin{aligned} & \varphi _{11}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _2}}{4 \alpha _1}\left( \text {sn}\left( \frac{\alpha _2 \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \sqrt{\alpha _1}},\frac{\sqrt{-\Sigma _2}}{\alpha _2}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(51)

$$\begin{aligned} & \varphi _{12}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\alpha _2}{4 \alpha _1}\left( \text {sn}\left( \frac{\sqrt{-\alpha _1 \Sigma _2} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1},\frac{\alpha _2}{\sqrt{-\Sigma _2}}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(52)

Case-2: For $\alpha _4=\frac{\alpha _2 \Sigma _1}{8 \alpha _1^2},~\alpha _5=\frac{\alpha _2^2 \Sigma _2}{256 \alpha _1^3}.$ We get

$$\begin{aligned} {\left\{ \begin{array}{ll} A_0=-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}},~A_1=-\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}},~\omega =-\frac{8 \alpha _1 \left( \zeta _1 \left( \kappa ^2-\alpha _3\right) +4 \alpha _3 \zeta _3+\zeta _4\right) +3 \alpha _2^2 \left( \zeta _1-4 \zeta _3\right) }{8 \alpha _1}. \end{array}\right. } \end{aligned}$$

• Explicit dark, singular, and periodic wave solutions

Sub-case 2.1: If $\alpha _1>0$ and $\Sigma _3<0.$

$$\begin{aligned} & \varphi _{13}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _3}}{4 \alpha _1}\left( \tanh \left( \frac{\sqrt{-\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(53)

$$\begin{aligned} & \varphi _{14}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _3}}{4 \alpha _1}\left( \coth \left( \frac{\sqrt{-\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(54)

$$\begin{aligned} & {{Sub-case 2.2:}}~\text{ If } ~~\alpha _1>0 ~~\text{ and }~~ \Sigma _3>0.\nonumber \\ & \varphi _{15}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{\Sigma _3}}{4 \alpha _1}\left( \tan \left( \frac{\sqrt{\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(55)

$$\begin{aligned} & \varphi _{16}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{\Sigma _3}}{4 \alpha _1}\left( \cot \left( \frac{\sqrt{\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{4 \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(56)

Case-3: For $\alpha _4=\frac{\alpha _2 \Sigma _1}{8 \alpha _1^2},~\alpha _5=\frac{\Sigma _1^2}{64 \alpha _1^3}.$ We achieve

$$\begin{aligned} {\left\{ \begin{array}{ll} A_0=-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}},~A_1=-\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}},~\omega =-\frac{8 \alpha _1 \left( \zeta _1 \left( \kappa ^2-\alpha _3\right) +4 \alpha _3 \zeta _3+\zeta _4\right) +3 \alpha _2^2 \left( \zeta _1-4 \zeta _3\right) }{8 \alpha _1}. \end{array}\right. } \end{aligned}$$

• Bright, singular, and periodic structures are obtained

Sub-case 3.1: If $\alpha _1<0$ and $\Sigma _3<0.$

$$\begin{aligned} & \varphi _{17}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _3}}{2 \sqrt{2} \alpha _1}\left( \text {sech}\left( \frac{\sqrt{\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \sqrt{2} \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(57)

$$\begin{aligned} & \varphi _{18}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{\Sigma _3}}{2 \sqrt{2} \alpha _1}\left( \text {csch}\left( \frac{\sqrt{\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \sqrt{2} \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(58)

$$\begin{aligned} & {{Sub-case 3.2:}}~\text{ If } ~~\alpha _1>0 ~~\text{ and }~~ \Sigma _3<0.\nonumber \\ & \varphi _{19}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _3}}{2 \sqrt{2} \alpha _1}\left( \sec \left( \frac{\sqrt{-\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \sqrt{2} \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(59)

$$\begin{aligned} & \varphi _{20}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( -\frac{\alpha _2}{4 \alpha _1}\pm \frac{\sqrt{-\Sigma _3}}{2 \sqrt{2} \alpha _1}\left( \csc \left( \frac{\sqrt{-\alpha _1 \Sigma _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{2 \sqrt{2} \alpha \alpha _1}\right) \right) \right) }\nonumber \\ & \quad {-\frac{\alpha _2 \sqrt{4 \zeta _3-\zeta _1}}{2 \sqrt{2} \sqrt{\alpha _1} \sqrt{\zeta _2}}\Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(60)

Case-4: For $\alpha _2=\alpha _4=\alpha _5=0$ and $\alpha _3>0.$ We get

$$\begin{aligned} {\left\{ \begin{array}{ll} A_0=0,~A_1=-\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}},~\omega =\zeta _1 \left( \alpha _3-\kappa ^2\right) -4 \alpha _3 \zeta _3-\zeta _4. \end{array}\right. } \end{aligned}$$

• The exponential function solution

$$\begin{aligned} \varphi _{21}(x, t)=\Bigg \lbrace {\left( -\frac{\sqrt{2} \sqrt{\alpha _1} \sqrt{4 \zeta _3-\zeta _1}}{\sqrt{\zeta _2}}\right) \left( \frac{4 \alpha _3 \rho }{4 \rho ^2 e^{\frac{\sqrt{\alpha _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{\alpha }}-\alpha _1 \alpha _3 e^{-\frac{\sqrt{\alpha _3} \Gamma (\beta +1) \left( 2 \zeta _1 \kappa t^{\alpha }+x^{\alpha }\right) }{\alpha }}}\right) \Bigg \rbrace }\times e^{i \chi }. \end{aligned}$$

(61)

Remark

For all above twenty solutions $\chi =\frac{\Gamma (\beta +1) \left( -\kappa x^{\alpha }+\omega t^{\alpha }\right) }{\alpha }$.

Solutions via generalized Arnous method

The generalized Arnous method involves assuming a solution according to the Eq. (37) of the form

$$\begin{aligned} \Phi (\xi )=\epsilon _{0}+\sum _{k=1}^n \frac{\epsilon _k+\sigma _k \phi '(\xi )^k}{\phi (\xi )^k}. \end{aligned}$$

(62)

For $n = 1$, this method proposes a solution to Eq. (37) in the following form

$$\begin{aligned} \Phi (\xi )=\epsilon _0+\frac{\epsilon _1+\sigma _1 \phi '(\xi )}{\phi (\xi )}. \end{aligned}$$

(63)

By substituting Eq (63) into Eq (37) along with its derivatives according to Eq. (33), we receive a polynomial in term of $\frac{1}{\phi (\xi )}\frac{ \phi '(\xi )}{\phi (\xi )}$. Collecting and equating coefficients, A system of algebraic equations is achieved, yielding these solution sets:

$$\begin{aligned} Set-1&:&~~\epsilon _0= 0,~\epsilon _1= \frac{\sqrt{2} \sqrt{\zeta _1-4 \zeta _3} \sqrt{\rho } \log (\delta )}{\sqrt{\zeta _2}},~\sigma _1= 0,~\omega =\zeta _1 \left( \log ^2(\delta )-\kappa ^2\right) -4 \zeta _3 \log ^2(\delta )-\zeta _4. \\ Set-2&:&~~\epsilon _0= 0,~\epsilon _1= 0,~\sigma _1= -\frac{\sqrt{8 \zeta _3-2 \zeta _1}}{\sqrt{\zeta _2}},~\omega = -\zeta _1 \left( 2 \log ^2(\delta )+\kappa ^2\right) +8 \zeta _3 \log ^2(\delta )-\zeta _4. \\ Set-3&:&~~ \epsilon _0= 0,~\epsilon _1= -\frac{\sqrt{\zeta _1-4 \zeta _3} \sqrt{\rho } \log (\delta )}{\sqrt{2} \sqrt{\zeta _2}},~\sigma _1= \frac{\sqrt{4 \zeta _3-\zeta _1}}{\sqrt{2} \sqrt{\zeta _2}},~\omega = -\frac{1}{2} \zeta _1 \left( \log ^2(\delta )+2 \kappa ^2\right) +2 \zeta _3 \log ^2(\delta )-\zeta _4. \end{aligned}$$

At $\delta =e,\rho =4 A^2.$ We get the diverse form of solutions.

According to set-1. We establish solitary wave solution in the following form

$$\begin{aligned} \varphi _{1}(x, t) =\frac{\sqrt{2} \sqrt{\zeta _1-4 \zeta _3} \text {sech}\left( \frac{2 \zeta _1 \kappa \Gamma (\beta +1) t^{\alpha }}{\alpha }+\frac{\Gamma (\beta +1) x^{\alpha }}{\alpha }\right) \exp \left( i \left( g+\frac{\Gamma (\beta +1) \left( \left( \zeta _1 \left( 1-\kappa ^2\right) -4 \zeta _3-\zeta _4\right) t^{\alpha }-\kappa x^{\alpha }\right) }{\alpha }\right) \right) }{ \sqrt{\zeta _2}}. \end{aligned}$$

(64)

According to set-2. We get hyperbolic solution in this form

$$\begin{aligned} \varphi _{2}(x, t)=-\frac{\sqrt{8 \zeta _3-2 \zeta _1} \tanh \left( \frac{2 \zeta _1 \kappa \Gamma (\beta +1) t^{\alpha }}{\alpha }+\frac{\Gamma (\beta +1) x^{\alpha }}{\alpha }\right) \exp \left( i \left( g+\frac{\Gamma (\beta +1) \left( \left( \zeta _1 \left( -\kappa ^2-2\right) +8 \zeta _3-\zeta _4\right) t^{\alpha }-\kappa x^{\alpha }\right) }{\alpha }\right) \right) }{\sqrt{\zeta _2}}. \end{aligned}$$

(65)

According to set-3. We get combined hyperbolic solution in this form

$$\begin{aligned} & \varphi _{3}(x, t)=e^{i \left( g+\frac{\Gamma (\beta +1) \left( \omega t^{\alpha }-\kappa x^{\alpha }\right) }{\alpha }\right) } \nonumber \times \\ & \quad \left( \frac{\sqrt{4 \zeta _3-\zeta _1} \tanh \left( \frac{2 \zeta _1 \kappa \Gamma (\beta +1) t^{\alpha }}{\alpha }+\frac{\Gamma (\beta +1) x^{\alpha }}{\alpha }\right) }{\sqrt{2} \sqrt{\zeta _2}}-\frac{ \sqrt{\zeta _1-4 \zeta _3} \text {sech}\left( \frac{2 \zeta _1 \kappa \Gamma (\beta +1) t^{\alpha }}{\alpha }+\frac{\Gamma (\beta +1) x^{\alpha }}{\alpha }\right) }{\sqrt{2} \sqrt{\zeta _2}}\right) . \end{aligned}$$

(66)

Energy balance method

For utilizing the energy balance method (EBM)⁴³, we recall Eq. (37) as:

$$\begin{aligned} \frac{\Phi \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{4 \zeta _3-\zeta _1}-\frac{\zeta _2 \Phi ^3}{4 \zeta _3-\zeta _1}+\Phi ''=0. \end{aligned}$$

(67)

With the assistance of the semi-inverse method. The corresponding variational principle is written as

$$\begin{aligned} J (\Phi ) =\int _0^{\frac{T}{4}} \left( \frac{1}{2} \left( \frac{d \Phi }{\text {d}\xi }\right) ^2+\frac{\Phi ^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }-\frac{\zeta _2 \Phi ^4}{4 \left( 4 \zeta _3-\zeta _1\right) }\right) d\xi . \end{aligned}$$

(68)

Here, T denotes the temporal period of the wave, and the integral $\int _0^{T/4}$ evaluates the averaged energy functional over one quarter-period. The period T is related to the wavelength $\lambda$ and frequency f by $T = \frac{\lambda }{v} = \frac{1}{f},$ where v is the phase velocity of the wave, determined by the dispersion relation of the medium. For linear waves in a nondispersive medium, $v = \lambda f$ holds exactly. In nonlinear or dispersive media, v may depend on frequency ($v = v(f)$) or amplitude ($v = v(A)$). The quarter-period averaging exploits the symmetry of the energy density in periodic solutions, capturing the full dynamics while reducing computational effort.

$$\begin{aligned} J (\Phi ) =\int _0^{\frac{T}{4}} \left( \frac{1}{2} \left( \frac{d \Phi }{\text {d}\xi }\right) ^2-\left[ \frac{\zeta _2 \Phi ^4}{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{\Phi ^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }\right] \right) d\xi . \end{aligned}$$

(69)

$$\begin{aligned} J (\Phi ) =\int _0^{\frac{T}{4}} \left( Q-R\right) d\xi . \end{aligned}$$

(70)

where, Q is kinetic energy and R is potential energy and are given as:

$$\begin{aligned} Q=\frac{1}{2} \left( \frac{d \Phi }{\text {d}\xi }\right) ^2,~~~R=\frac{\zeta _2 \Phi ^4}{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{\Phi ^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }. \end{aligned}$$

(71)

Then its Hamiltonian invariant is written as

$$\begin{aligned} H=Q+R=Q=\frac{1}{2} \left( \frac{d \Phi }{\text {d}\xi }\right) ^2+\frac{\zeta _2 \Phi ^4}{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{\Phi ^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }. \end{aligned}$$

(72)

Now assume the solution of ODE in the following form

$$\begin{aligned} \Phi (\xi ) =X\cos (\text {A } \xi ),~~ A>0, \end{aligned}$$

(73)

where X is the amplitude and A denotes the frequency. The EBM assumes $\phi (\xi ) = X \cos (A \xi )$ because it naturally represents oscillatory behavior in conservative systems, satisfies key initial conditions ($\phi (0)=X$, $\phi '(0)=0$), and simplifies calculations while maintaining physical relevance for nonlinear oscillators. This form provides a first-order approximation that balances accuracy with computational efficiency. According to EBM, the Hamiltonian invariant must remain unchanged, i.e.:

$$\begin{aligned} H=Q+R=Q=\frac{1}{2} \left( \frac{d \Phi }{\text {d}\xi }\right) ^2+\frac{\zeta _2 \Phi ^4}{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{\Phi ^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }=H_0. \end{aligned}$$

(74)

The initial conditions of Eq. (73) are:

$$\begin{aligned} \Phi '(0 )=0,~~ \Phi (0) =X. \end{aligned}$$

Inserting them into Eq. (74), one has:

$$\begin{aligned} \frac{\zeta _2 X^4}{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{X^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }=H_0. \end{aligned}$$

(75)

Putting Eqs.(75) and (73) into Eq. (74) yields:

$$\begin{aligned} \frac{1}{2} A^2 X^2 \sin ^2(A \xi )-\frac{\left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) (X \cos (A \xi ))^2}{2 \left( 4 \zeta _3-\zeta _1\right) }+\frac{\zeta _2 (X \cos (A \xi ))^4}{4 \left( 4 \zeta _3-\zeta _1\right) }=\frac{\zeta _2 X^4}{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{X^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) } \end{aligned}$$

(76)

By setting $A \xi = \pi /4$, the singularity at $A \xi = \pi /2$ (where $\cos (A \xi ) = 0$) is avoided. This choice maintains balanced contributions from the $\sin ^2(A \xi )$ and $\cos ^2(A \xi )$ terms in the averaged energy. The Eq. (76) becomes

$$\begin{aligned} \frac{A^2 X^2}{4}+\frac{X^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{2 \left( 4 \zeta _3-\zeta _1\right) }-\frac{X^2 \left( \zeta _1 \kappa ^2+\zeta _4+\omega \right) }{4 \left( 4 \zeta _3-\zeta _1\right) }-\frac{\zeta _2 X^4}{4 \left( 4 \zeta _3-\zeta _1\right) }+\frac{\zeta _2 X^4}{16 \left( 4 \zeta _3-\zeta _1\right) }. \end{aligned}$$

(77)

Thus, we obtain frequency:

$$\begin{aligned} A= \frac{\sqrt{4 \zeta _1 \kappa ^2-3 \zeta _2 X^2+4 \left( \zeta _4+\omega \right) }}{2 \sqrt{\zeta _1-4 \zeta _3}}. \end{aligned}$$

(78)

Accordingly, the exact solution to Eq. (1) is given by:

$$\begin{aligned} \varphi (x, t) =X \cos \left( \frac{ \sqrt{4 \zeta _1 \kappa ^2-3 \zeta _2 X^2+4 \left( \zeta _4+\omega \right) }}{2 \sqrt{\zeta _1-4 \zeta _3}} \xi \right) \times e^{i \chi }. \end{aligned}$$

(79)

Graphical illustration and significance of soliton solutions

In this section, we discuss the outcomes of our proposed model and provide physical illustrations. It focuses on attaining, more generalized, and novel solitonic wave structures, including hyperbolic, trigonometric, complex hyperbolic, exponential, rational function, bright, dark, singular, and singular periodic wave structures. Our newly established solutions characterize a significant advancement beyond existing outcomes, offering completely original and more comprehensive exact solutions that incorporate both arbitrary functional parameters and constant parameters. These solutions offer unprecedented flexibility, allowing researchers to freely choose functional forms tailored to specific physical scenarios, making them specifically valuable for modeling nonlinear wave phenomena across various fields, including hydrodynamics, nonlinear optics, plasma physics, and engineering applications. The enclosure of arbitrary parameters develops the solutions’ practical utility for describing complex wave propagation dynamics while maintaining exact analytical tractability, setting them apart from prior methods through their greater generality and adaptability to real-world physical systems. The derived solutions unveil distinct classes of solitons, each with unique physical attributes and implications. Dark solitons, although more challenging to manage than standard solitons, have demonstrated enhanced stability and robustness against losses. Bright solitons are famous by their higher intensity compared to the surrounding background. In distinction, singular solitons characterize a unique class of solitary waves that exhibit singularities, typically manifesting as infinite discontinuities. Interestingly, these singular solitons may correspond to solitary waves with imaginary central positions. Investigating singular solitons is specifically significant because they may help explain the emergence of rogue waves, which are exemplified by sudden, extreme peaks. Likewise, periodic wave solutions express waves with continuous, repeating patterns, determined by their wavelength and frequency. Main properties of these solutions contain the period the time taken to complete one wave cycle and the frequency, which shows how many cycles occur per second. These solutions have distinct physical representations, and we illustrate them graphically by choosing appropriate parameter values. These outcomes reveal an inspiration for further research across different scientific fields, particularly in fluid dynamics. However, in this study, by employing three efficient methods, we have generated numerous solitary wave solutions. Moreover, our solutions provide insights for further investigation into higher-order NLPDEs. Graphical representation is essential for accurately depicting nonlinear events and relationships between variables in a dataset. The 2D graphs are demonstrated in Figs. (2, 4, 6, 8, 10, 12, 14, and 16), while the corresponding 3D and contour plots are presented in Figs. (1, 3, 5, 7, 9, 11, 13, and 15). These visualizations provide a clear and intuitive depiction of the solutions, enhancing the understanding of the problem’s dynamics and the applied analytical methods. These graphical representations are effective tools for conveying complex concepts and methodologies in nonlinear wave analysis. The accompanying visualization portrays distinctive wave structures detected at ocean boundaries, demonstrating a direct correspondence with our 3D numerical results. These waves exhibit coherent, shape-preserving propagation along the interface–markedly different from turbulent flows, which show chaotic, disordered dynamics. This parallel between our mathematical problem and scrutinized physical behavior validates the practical relevance of our results, bridging theoretical analysis with real-world hydrodynamic phenomena. This section delves into the dynamic characteristics of novel solutions to the CGL equation, encompassing hyperbolic, rational, and trigonometric functions, derived utilizing the above said modern techniques. All graphs are generated using computational software Wolfram Mathematica 9.0 (we didn’t use any software with URL). The figures are plotted using numerical solutions of the governing model with appropriately selected parameter values. These simulations vividly illustrate the dynamical behavior of the system, accompanied by detailed descriptions of the underlying dynamics. The outcomes highlight distinct features of the solutions, which differ from previous results in the literature and offer new insights into the complex behavior of the given equation.

Fig. 1

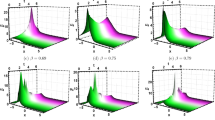
The dark solution of Eq. (53) is revealed via 3D and contour graphs with the choice of free parameters: $\alpha =0.98,~\alpha _1=0.85,~\zeta _1 =1.70,~\alpha _2=1.35,~\zeta _2 =2.4,~\alpha _3=-0.33,~\beta =0.58,~\zeta _3 =3.77,~\kappa =0.65,~\text{ and }~\omega =4.3.$.

Fig. 2

Revealing 2D plots for the solution (53).

Fig. 3

The periodic solution of Eq. (55) is shown via 3D and contour graphs with suitable parameters: $\alpha =0.98,~\alpha _1=0.85,~\alpha _2=2.4,~\alpha _3=3.24,~\beta =0.97,~\kappa =0.47,~\zeta _1 =2.97,~\zeta _2 =1.5,~\zeta _3 =2.3,~\text{ and }~\omega =0.38.$.

Fig. 4

Revealing 2D plots for the solution (55).

Fig. 5

The bright solution of Eq. (57) is sketched via 3D and contour profiles with free parameters: $\alpha =0.98,~\alpha _1=-0.85,~\alpha _2=1.35,~\alpha _3=0.33,~\beta =0.78,~\kappa =0.35,~\zeta _1 =1.7,~\zeta _2 =2.4,~\zeta _3 =1.77,~\text{ and }~\omega =0.3.$.

Fig. 6

Revealing 2D plots for the solution (57).

Fig. 7

The periodic solution of Eq. (59) is shown via 3D and contour profiles with free parameters: $\alpha =0.99,~\alpha _1=0.75,~\alpha _2=1.45,~\alpha _3=0.23,~\beta =0.98,~\kappa =0.55,~\zeta _1 =1.7,~\zeta _2 =0.4,~\zeta _3 =1.77,~\text{ and }~\omega =0.3.$.

Fig. 8

Revealing 2D plots for the solution (59).

Fig. 9

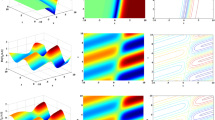
The bright solution of Eq. (64) is sketched via 3D and contour profiles with free parameters: $g=0.06,~\alpha =0.99,~\beta =0.71,~\zeta _2=0.2,~\zeta _1=0.3,~\zeta _3=1.1,~\zeta _4=0.77,~\kappa =0.3,~\text{ and }~\omega =1.07.$.

Fig. 10

Revealing 2D plots for the solution (64).

Fig. 11

The dark solution of Eq. (65) is revealed via 3D and contour graphs with suitable parameters: $g=0.06,~\alpha =0.99,~\beta =0.99,~\zeta _2=4,~\zeta _1=0.3,~\zeta _3=0.9,~\zeta _4=0.77,~\kappa =2.72,~\text{ and }~\omega =7.47.$.

Fig. 12

Revealing 2D plots for the solution (65).

Fig. 13

The Eq. (66) visually depicts the hyperbolic solutions with the choice of free parameters: $g=0.06,~\alpha =0.35,~\beta =0.98,~\zeta _2=0.4,~\zeta _1=0.3,~\zeta _3=1.1,~\kappa =0.12,~\text{ and }~\omega =1.01.$.

Fig. 14

Revealing 2D plots for the solution (66).

Fig. 15

The Eq. (79) visually reveals the periodic behavior with parameters: $\zeta _2=0.3,~\alpha =0.99,~\beta =0.61,~\zeta _1=2.3,~\zeta _4=0.5,~\zeta _3=0.5,~\kappa =0.79,~X=0.9,~\text{ and }~\omega =0.27.$.

Fig. 16

Revealing 2D plots for the solution (79).

Conclusive remarks

This study has conducted a comprehensive investigation of the CGL equation, yielding innovative exact solitary wave solutions encompassing semi-rational, rational, hyperbolic, and trigonometric functions. Employing the KM method and generalized Arnous method, we derived a various form of closed-form solutions across different family cases, extending previous outcomes^{31,32,33,34,35}. A comparative analysis with existing results highlights the novelty of this work. While certain parameter choices may yield outcomes similar to prior studies, the reported results exhibit fresh and original contributions to fractional calculus theory. These outcomes not only advance the current understanding but also offer a foundation for further examination of the model. These strategies are applicable to various complex physical models in nonlinear science and engineering. The 2D and 3D visualizations, including contour plots with a comparison of the applied fractional derivative, provide a comprehensive physical understanding of the governing model. Visual illustrations play a vital role in understanding, analyzing, and optimizing soliton behavior. By simplifying complex concepts, these representations help categorize potential challenges, such as dispersion or interference, and contribute to the development of effective, high-performance optical communication structures. Furthermore, leveraging solitary wave stability for long-distance data transmission could expressively improve communication networks. Studying periodic solutions in energy transfer within structured systems may also advance energy propagation. This study enables deeper exploration and prediction of significant model behaviors, fostering innovation and new perspectives in studying physical marvels. The obtained complex soliton solutions hold remarkable potential for modern research in industrial studies, nonlinear dynamics, telecommunications, hydrodynamics, fluid dynamics, and soliton dynamics. The generalized Arnous and KM methods demonstrate productivity and promise in handling complex nonlinear models in marine physics, ocean engineering, plasma physics, and other fields. Our findings provide valuable tools for elucidating intricate dynamical wave profiles in ocean engineering and soliton theory, offering a solid foundation for future research. Furthermore, the researchers can explore solutions incorporating diverse fractional derivatives, along with the effects of noise terms that remain largely unexplored in current studies.