Introduction

Carbon nanofiber (CNF) exhibits excellent electrical conductivity and appropriate stiffness1,2,3,4. Consequently, CNF has significant potential to enrich the toughness and thermal/electrical conduction of polymer composites5,6,7. Kumar et al.8 prepared a polycarbonate (PC)/oxidized CNF composite and found that its DC conductivity augmented from about 10−14 S/m for PC to 100 S/m for the composite containing only 3 wt% of CNF. Additionally, it was reported that the composite storage modulus improved with increasing CNF loading, with the storage modulus of a nanocomposite with 5 wt% CNF showing a remarkable 282% increase at 165 °C compared to pure PC.

Tunneling of electrons primarily manages the conduction in polymer composites of CNF (PCNFs)9,10, due to the electron moving through narrow tunnels between adjacent particles. Generally, small tunnels can enhance electron movement, though large tunnels produce high resistance to electron current11,12,13,14. The tunneling features were studied in the nanocomposites of graphene15,16, silver nanowires17 and carbon nanotubes (CNTs)18, but they have been overlooked in the conductivity of PCNFs. Consequently, it is significant to investigate the tunneling impacts on the PCNF conductivity.

In PCNFs, the interphase zone is created owing to the huge interfacial area and strong interfacial contacts between CNFs and polymers5,19,20,21. The strengthening role of the interphase in nanocomposites has been reported in many studies22,23,24,25,26,27. Additionally, the interphase can assimilate into the filler net, significantly influencing the onset of percolation and network dimensions28,29,30,31. The percolation of the interphase and its power on the nanocomposite stiffness and conduction were documented in the literature32,33. However, the percolation of the interphase has not been studied in the CNF-filled materials.

From a modeling perspective, the power-law model has been used to predict the nanocomposite conductivity34,35,36. It considers the percolation onset, filler conduction, and filler concentration to calculate conductivity37. Although the outputs of this model have fine arrangement with the measured numbers, the power-law model does not account for the filler dimensions, tunnels, and interphase. Additionally, few conductivity models have been advanced for the samples comprising CNT38,39 and graphene11,13,14 by considering interphase depth and tunneling effects, but models specifically for the conductivity of PCNFs are limited. Previous research has mainly focused on the experimental measurement of conductivity in PCNFs. Therefore, it is valuable to analyze the conductivity of PCNFs from a modeling perspective to identify effective parameters for optimization.

Takayanagi equation was advanced by Loos and Manas-Zloczower for the modulus of CNT-polymer composites, supposing dispersed/networked CNT after the percolation onset40. However, their model does not consider the interphase in nanocomposites. Meanwhile both stiffness and conductivity of nanocomposites exhibit percolating trend and are affected by the features of the nanofiller network and interphase, advanced Takayanagi equation can be more progressed for the conductivity of PCNFs. Actually, the existing models commonly disregarded the interphase percolation in the nanocomposite conductivity. As mentioned, the power-law model does not consider the CNF dimensions, tunnels, and interphase, which is insufficient for conductivity prediction. Also, Takayanagi model was suggested for the modulus of CNT-polymer composites, ignoring the interphase network.

This article presents a novel development and application of the Loos-Manas-Zloczower equation for the PCNF electrical conductivity. Unlike the past models that chiefly focused on experimental measurements, this work incorporates detailed considerations of interphase size, tunneling effects, and the extended CNF concept. By participating these critical terms, the model offers a more inclusive and precise calculation of PCNF conductivity. The innovative approach of treating CNFs surrounded by interphase and tunneling distances as extended CNFs enables a better understanding of the characters of many factors, such as CNF twistiness, interphase thickness, and tunneling resistance, in influencing conductivity. This model’s ability to align closely with experimental data from various samples underscores its robustness and practical applicability. The findings that specific configurations of CNF dimensions, percolation onset, interphase characteristics, and tunneling properties can optimize conductivity provide valuable insights for designing high-performance PCNF composites, marking a significant advancement in the field of polymer nanocomposites.

Theory

The Takayanagi model was modified and developed by Loos and Manas-Zloczower40 using the network of CNT after the onset of percolation. They proposed two arrangements (Fig. 1), nonetheless only Form II is appropriate for the modulus of nanocomposites40.

The adjusted model according to Form II is stated by the volumetric portions of the filler (\({\varphi _f}\)) and network (\({\varphi _N}\))40 as:

$$E=\frac{{{\varphi _N}(1 - {\varphi _f})E_{d}^{{}}E_{N}^{{}}+({\varphi _f} - {\varphi _N})E_{m}^{{}}E_{N}^{{}}{\varphi _N}+E_{d}^{{}}E_{m}^{{}}{{(1 - {\varphi _N})}^2}}}{{(1 - {\varphi _f})E_{d}^{{}}+({\varphi _f} - {\varphi _N})E_{m}^{{}}}}$$
(1)

Ed, EN, and Em are the moduli of the dispersed filler, network and polymer media, in that order.

Equation 1 can be utilized for the PCNF conductivity, because the PCNF includes the networked and dispersed particles after percolation onset. Both the conductivity and modulus in nanocomposites reveal percolating trend depending on the physical appearance of the nanofiller, network, and interphase.

Fig. 1
figure 1

Improved model of Takayanagi for nanocomposites with dispersed/networked nanoparticles.

Full size image

The modulus in Eq. 1 can be substituted with conductivity. Since the dispersed CNFs do not significantly contribute to conductivity, it is assumed that both Em and Ed are replaced by the conductivity of the polymer matrix (σm). Since the charge transferring occurs through the continuous network of CNFs, the dispersed nanofibers in the matrix cannot transfer the electrons. So, it is assumed that the dispersed CNFs cannot contribute to the conductivity of nanocomposites. Equation 1 is adjusted for the system’s conductivity as:

$$\sigma =\frac{{{\sigma _m}{\sigma _N}{\varphi _N}(1 - {\varphi _f})+({\varphi _f} - {\varphi _N}){\varphi _N}{\sigma _N}{\sigma _m}+{{(1 - {\varphi _N})}^2}\sigma _{m}^{2}}}{{{\sigma _m}(1 - {\varphi _f})+{\sigma _m}({\varphi _f} - {\varphi _N})}}$$
(2)

σN is the conductivity of CNF. Too minor values of \({\varphi _N}\), \({\varphi _f}\)and σm simplify Eq. 2 to:

$$\sigma ={\varphi _N}{\sigma _N}+{\varphi _N}({\varphi _f} - {\varphi _N}){\sigma _N}$$
(3)

Equation 3 commonly overestimates the PCNF conductivity, because the conductivity of CNF is 104 S/m41,42,43. Moreover, Eq. 3 ignores the tunneling effect, even though electron tunneling plays a vigorous role in the conductivity of PCNFs. The tunneling distance among neighboring CNFs can be assumed by the extension of CNF, as seen in Fig. 2. The extended CNF includes the CNF, interphase, and tunnels simultaneously.

Fig. 2
figure 2

Schematic depiction of an extended CNF.

Full size image

The conductivity of the stretched CNF (σext) is approximated and replaced into Eq. 3 to forecast the PCNF conductivity as:

$$\sigma ={\varphi _N}{\sigma _{ext}}+{\varphi _N}({\varphi _f} - {\varphi _N}){\sigma _{ext}}$$
(4)

The resistance for a stretched CNF is calculated as:

$${R_{ext}}={R_{tun}}+{R_f}$$
(5)

Rf and Rtun mean the intrinsic resistance of CNF and tunnels, correspondingly.

Rf can be estimated as44:

$${R_f}=\frac{l}{{\pi {R^2}{\sigma _N}}}$$
(6)

R and l represent the CNF radius and length, correspondingly.

Nonetheless, the twistiness of CNF reduces its operative size and conduction. The minimum length among the two tops of CNF is the operative length (leff), signifying the twistiness parameter as:

$$u=\frac{l}{{{l_{eff}}}}$$
(7)

where a higher u indicates more curliness, although a straight CNF represents u = 1. Twistiness diminishes the conductivity as44:

$${\sigma _{CNF}}=\frac{{{\sigma _N}}}{u}$$
(8)

leff = l/u and CNF conductivity are reflected in Eq. 6 to express Rf by:

$${R_f}=\frac{{{l_{eff}}}}{{\pi {R^2}{\sigma _{CNF}}}}=\frac{{{l_{}}}}{{\pi {R^2}{\sigma _N}}}$$
(9)

The resistance of tunnels includes the CNF (R1) and the polymer film (R2) resistances at tunnels as44:

$${R_{tun}}={R_1}+{R_2}$$
(10)

R1 is given by contact diameter (d) as44:

$${R_1}=\frac{1}{{d{\sigma _{CNF}}}}=\frac{u}{{d{\sigma _N}}}$$
(11)

Additionally, R2 is expressed by the tunnel resistivity of polymer (ρ), contact area (S ≈ d2) and tunneling length (λ)44 as:

$${R_2}=\frac{{\rho \lambda }}{S} \cong \frac{{\rho \lambda }}{{{d^2}}}$$
(12)

Exchanging Eqs. 11 and 12 into Eq. 10 presents the tunnel resistance as:

$${R_{tun}}=\frac{u}{{d{\sigma _N}}}+\frac{{\rho \lambda }}{{{d^2}}}$$
(13)

Now, substituting Eqs. 13 and 9 into Eq. 5 predicts the total resistance of protracted CNF (Ω) as:

$${R_{ext}}=\frac{l}{{\pi {R^2}{\sigma _N}}}+\frac{u}{{d{\sigma _N}}}+\frac{{\rho \lambda }}{{{d^2}}}$$
(14)

which can be used to suggest the conductivity of the extended CNF (S/m) as:

$${\sigma _{ext}}=\frac{l}{{\pi {R^2}{R_{ext}}}}=\frac{l}{{\frac{l}{{{\sigma _N}}}+\frac{{\pi {R^2}u}}{{d{\sigma _N}}}+\frac{{\pi {R^2}\rho \lambda }}{{{d^2}}}}}$$
(15)

Moreover, \({\varphi _N}\) is stated by the share of networked CNF (f) in the PCNF as:

$${\varphi _N}=f\varphi _{f}^{{}}$$
(16)

The interphase can cultivate the net in nanocomposites, so its concentration should be considered in the network volume fraction. The interphase volume portion is assessed as:

$${\varphi _i}={\varphi _f}{(1+\frac{t}{R})^2} - {\varphi _f}$$
(17)

t represents the depth of interphase.

The operative volume portion of the filler comprises both interphase and CNF as:

$${\varphi _{eff}}={(1+\frac{{{t_{}}}}{R})^2}{\varphi _f}$$
(18)

Additionally, thinner and longer CNFs can provide more connections in the PCNFs. Also, a denser interphase can reduce the space among nanofibers to yield the lower percolation onset and bigger network. So, the percolation onset in PCNF is recommended44 as:

$${\varphi _p}=\frac{{15(R - 2t)}}{l}$$
(19)

However, waviness unpleasantly affects the ϕp by leff = l/u, since more waviness decreases the effective length of nanofibers in the network. Actually, the waviness shortens the efficient nanofibers increasing the percolation onset. So, u as waviness parameter affects the ϕp (Eq. 19) as:

$${\varphi _p}=\frac{{15(R - 2t)u}}{l}$$
(20)

The network percentage in the PCNF is designed as45:

$$f=\frac{{\varphi _{{eff}}^{{1/3}} - \varphi _{p}^{{1/3}}}}{{1 - \varphi _{p}^{{1/3}}}}$$
(21)

which is protracted by Eqs. 18 and 20 as:

$$f=\frac{{{{[{{(1+\frac{t}{R})}^2}{\varphi _f}]}^{1/3}} - {{[\frac{{15(R - 2t)u}}{l}]}^{1/3}}}}{{1 - {{[\frac{{15(R - 2t)u}}{l}]}^{1/3}}}}$$
(22)

Now, \({\varphi _N}\) (Eq. 16) can be derived from Eqs. 22 and 18 as:

$${\varphi _N}=f\varphi _{{eff}}^{{}}=(\frac{{\varphi _{{eff}}^{{1/3}} - \varphi _{p}^{{1/3}}}}{{1 - \varphi _{p}^{{1/3}}}}){\varphi _f}{(1+\frac{{{t_{}}}}{R})^2}$$
(23)

When \({\varphi _N}\) (Eq. 23) and σext (Eq. 15) are considered in Eq. 4, the PCNF conductivity can be assessed as:

$$\sigma =f{\varphi _{eff}}[\frac{l}{{\frac{l}{{{\sigma _N}}}+\frac{{\pi {R^2}u}}{{d{\sigma _N}}}+\frac{{\pi {R^2}\rho \lambda }}{{{d^2}}}}}]+f{\varphi _{eff}}[{\varphi _{eff}} - f{\varphi _{eff}}][\frac{l}{{\frac{l}{{{\sigma _N}}}+\frac{{\pi {R^2}u}}{{d{\sigma _N}}}+\frac{{\pi {R^2}\rho \lambda }}{{{d^2}}}}}]$$
(24)

determining the CNF/interphase/tunnel influences on the PCNF conductivity. It is important to note that polymer chemistry (e.g., polarity, crystallinity) may control the interactions at polymer CNF interface, which affect the interphase size and tunneling characteristics. For example, the strong bonding among the polymer chains and CNFs produces a denser interphase, which widens the network and improves the nanocomposite conductivity.

Results and discussion

Checking of factors

The inspirations of all parameters on the sample conductivity are surveyed by the progressive technique at the typical values of u = 1.2, t = 20 nm, ϕf = 0.02, R = 50 nm, λ = 5 nm, l = 30 μm, d = 40 nm, and ρ = 150 Ω.m. Three-dimensional and contour schemes are employed to adjust the conductivity of PCNF (summarized as conductivity here) and to understand the key parameters.

Figure 3 presents the conductivity drawings in relation to ϕf and ϕp, representing the CNF volume fraction and percolation onset, respectively. The lowest conductivity, approximately 0, is witnessed at ϕf = 0.01 and ϕp = 0.03, although the ultimate result of 0.185 S/m is realized at the uppermost ϕf = 0.04 and the smallest ϕp = 0.003. Thus, a higher CNF quantity and a lower onset of percolation improve the conductivity, with the optimized level observed at the peak CNF concentration and the lowest percolation onset.

A higher quantity of conductive nanofibers significantly enhances charge transfer because it results in a larger network after the percolation onset. A higher CNF concentration surges the conductive points in the samples, as the polymer matrices are insulative, with conductivities ranging from 10−14−10−16 S/m. Contrariwise, a little volume of CNFs leads to a smaller network, deteriorating conductivity owing to insufficient electron transport. Moreover, a very low quantity of CNFs may not even touch the percolation onset compulsory to produce a network. Numerous models have described a same relationship between the nanocomposite conductivity and filler concentration11,17. Therefore, it is reasonable to establish a right relation between composite conductivity and CNF concentration.

Fig. 3
figure 3

(a) Three-D and (b) 2-D decorations of the composite conductivity by many ranges of CNF volume fraction and percolation threshold.

Full size image

An inferior onset of percolation definitely increases both the portion (Eq. 21) and concentration (Eq. 23) of networked CNFs, thereby improving conductivity. In fact, a lower onset of percolation enhances the extent and density of the network, thereby cultivating electron transport. Conversely, a higher inception of percolation reduces the volume of CNF net in the system, deteriorating electron transport. Thus, there is an opposite association between ϕp and conductivity, corroborating the developed attitude.

Figure 4 exemplifies the conductivity by the CNF curliness and the depth of interphase. The slightest value of 0.005 S/m is observed at u > 1.3 and t < 13 nm, whereas the maximum extent of 0.2 S/m is realized by u = 1 and t = 40 nm. These results reveal that less waviness and a denser interphase yield higher conductivity. However, waved CNFs and a thin interphase only slightly improve conductivity. Therefore, straight CNFs and a thick interphase are essential for optimizing conductivity.

Fig. 4
figure 4

Conductivity calculations by CNF waviness and interphase depth shown by (a) 3D image and (b) 2-D diagram.

Full size image

Straight CNFs (with less waviness) minimize the percolation onset (Eq. 20) and exhibit high conductivity (Eq. 8), because straight CNFs surge both the dimensions and conduction of the net in the samples, improving charge transfer. Actually, straighter CNFs provide more connections in the system, which facilitate the network formation. In contrast, higher waviness of CNFs shortens their effective size, which adversely affects percolation onset and conduction. The waved CNFs reduce the network size and conduction (Eq. 8), which in turn lowers conductivity. Consequently, waved CNFs weaken conductivity, confirming the calculations of the suggested technique.

The interphase can donate to the development of the network in the system. A thicker interphase lessens the onset of percolation and expands the network, increasing the charge transfer. In fact, a thicker interphase increases the concentration of the conductive phase in the PCNF, thus improving conductivity. On the contrary, a thinner interphase negatively impacts the conductivity of PCNF because it cannot effectively join and expand the CNF network. Accordingly, the proposed model precisely predicts conductivity at numerous interphase depth ranges. A better adhesion at polymer - CNF interface can provide a thicker interphase, which produces a lower percolation onset, bigger network and thus higher conductivity.

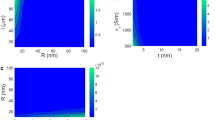
Figure 5 displays the predicted conductivity at different ranges of CNF dimensions. An insulative material is detected at R > 80 nm and l < 20 μm, nevertheless the conductivity maximizes to 0.75 S/m at the least R = 30 nm and the extreme l = 60 μm. Thick and short CNFs do not increase conductivity, whereas the thinnest and longest CNFs yield super-conductive samples. Generally, CNF dimensions are the most effective factors, with thinner and larger CNFs being desirable to enhance conductivity.

Thinner and longer CNFs reduce the ϕp (Eq. 20) and augment the size of the interphase (Eq. 17). Accordingly, thinner and longer CNFs build a larger net, enriching the charge transfer. Generally, thinner and extended nanoparticles provide a bigger aspect ratio, which grows the conductivity of composites, due to its positive effect on network dimensions13,14. However, thicker and shorter CNFs upsurge the ϕp and reduce the interphase concentration, leading to a smaller network in PCNFs. Thick and short CNFs form a small network that limits charge transfer. Hence, the developed model produces accurate outputs across various CNF dimensions.

Fig. 5
figure 5

Dependence of conductivity on CNF size shown by (a) 3-D and (b) contour patterns.

Full size image

Figure 6 reveals the impressions of λ and ρ as tunneling properties on conductivity. λ > 8 nm results in a minimized conductivity of 0.01 S/m, whereas the extreme conductivity of 0.79 S/m is noted at the tiniest levels of λ = 1 nm and ρ = 50 Ω.m. Thus, both tunneling length and polymer resistance adversely affect the electron transfer, and optimal conductivity is achieved with the slimmest tunnels and the least polymer resistivity. Conversely, big tunnels with high polymer resistance result in poor conductivity.

Slimmer tunnels with lower polymer resistivity reduce resistance to electron transfer, enhancing the tunneling effect44,46,47. Slim tunnels with low polymer resistivity allow more electron transfer, increasing the conductivity of PCNFs. Conversely, large tunnels with high polymer resistivity contain a thick and insulative polymer layer, causing high tunneling resistance and restricting electron transfer. It can be concluded that large tunnels with higher polymer resistivity are undesirable for charge transfer, worsening conductivity. Consequently, the proposed model realistically connects nanocomposite conductivity to these tunneling features.

Fig. 6
figure 6

Conductivity correlation to tunneling distance and polymer tunneling resistivity shown by (a) 3-D and (b) contour diagrams.

Full size image

Figure 7 displays the estimations of conductivity by d and f as tunneling/contact diameter and network fraction. d < 26 nm significantly reduces conductivity to nearly zero, while the maximum levels of d = 80 nm and f = 0.4 optimize conductivity to 0.43 S/m. A very low tunneling diameter cannot advance conductivity, but the broadest tunnels and uppermost network percentage provide the most conductivity. Both tunneling wideness and network percentage directly control conductivity, verifying the model.

Equation 13 reveals that d as contact diameter inversely governs the resistance of tunneling area. A high contact diameter reduces tunneling resistance, enhancing the conductivity. A wider tunnel facilitates charge transfer, producing higher conductivity. Conversely, a lower contact diameter surges tunnel resistance, limiting the charge transfer. Small tunnel diameters cannot transfer charges, and thus the new model appropriately associates conductivity to contact diameter.

Fig. 7
figure 7

Effects of tunneling diameter and network fraction on conductivity shown by (a) 3D image and (b) 2-D picture.

Full size image

An upper f grows the volume of the interphase/CNF net, because f determines the amount of both CNFs and interphase in the network according to Eq. 23. Thus, greater f results in higher conductivity because it produces a larger network, augmenting conductivity. On the other hand, a lower f results in a smaller concentration of the CNF/interphase network, reducing charge transfer. Therefore, f directly manages conductivity, validating the developed model.

Experiential facts legalizing the planned model

In this section, the real conductivity of various PCNFs is used to evaluate the developed model. Table 1 illustrates the prepared PCNFs and their features based on references. Initially, the percolation onset of examples is fitted to Eq. 20 for determination of interphase depth. Actually, t is extracted from fitting the measurements of percolation onset to Eq. (20). The varying interphase depths reveal different levels of interfacial adhesion among the CNFs and polymer matrices. The thickest interphase of 35.4 nm is perceived in the HDPE sample, though the PMMA system shows the thinnest interphase (5 nm). The interphase depth of samples changes at nanoscale, which is logical and meaningful, because the interphase depth is smaller than gyration radius of polymer macromolecules.

Table 1 Characteristics of PCNF examples.
Full size table

The progressive model is then applied to approximate the samples’ conductivity. The experimental and theoretical data are presented in Fig. 8. It is demonstrated that the experimental and theoretical conductivity values show acceptable agreement in all samples. This satisfactory fit indicates that the developed model is a reliable technique for estimating the PCNF conductivity. This model can also calculate the tunneling characteristics for the samples, as exposed in Table 1. The tunnel size (λ) sorts from 3 to 15 nm, revealing the variable tunneling distances in the samples. These results are meaningful because they are on the nanoscale. Additionally, the ρ varies from 70 to 450 Ω.m. The topmost and lowermost points of ρ are created in the EMA and PMMA samples, correspondingly.

The contact width (d) lies between 5 nm and 60 nm, with the PMMA sample showing the largest contact width and the EMA composite the smallest. These results demonstrate the highest and lowest tunneling resistance values in the EMA and PMM systems, correspondingly, according to Eq. 14. Since the tunneling mechanism meaningfully affects the PCNF conductivity, it is expected that the EMA and PMMA composites exhibit the minimum and maximum conductivity ranges among the studied samples. Figure 8 confirms this, emphasizing the crucial role of tunneling in the PCNFs. These results also validate the assumption of tunneling resistance in the developed model.

Fig. 8
figure 8

Experimental data and predictions of developed model for conductivity of PCNF systems: (a) EMA48, (b) epoxy49, (c) PMMA50, and (d) HDPE51.

Full size image

Conclusions

The Loos-Manas-Zloczower theory was expanded for the PCNF conductivity, supposing an extended CNF by interphase and tunnels. The analysis of this model across several factors is suitable and reasonable. Besides, the real conductivity of various samples shows good agreement with the model estimates. The lowest conductivity, approximately 0 (insulative sample), is realized at ϕf = 0.01 and ϕp = 0.03 or R > 80 nm and l < 20 μm or d < 26 nm. Nevertheless, the extreme range of 0.185 S/m is realized at the peak ϕf = 0.04 and the slightest ϕp = 0.003. Additionally, the value of 0.75 S/m is reached by a minimum R = 30 nm and maximum l = 60 μm. The lowest levels of λ = 1 nm and ρ = 50 Ω.m increase the conduction to 0.79 S/m, while the maximum levels of d = 80 nm and f = 0.4 optimize the conductivity to 0.43 S/m. These results demonstrate that the highest amount of the straightest CNFs (the least waviness), the thinnest and longest CNFs, the lowest percolation onset, the thickest interphase, the narrowest and widest tunnels, the lowest polymer tunneling resistivity, and the highest network percentage provide the highest conductivity. Besides, the lowermost level of tunnel resistance is obtained for the samples with the highest conductivity, corroborating the developed model.