A comparative analysis and noise robustness evaluation in quantum neural networks

Abstract

In current noisy intermediate-scale quantum (NISQ) devices, hybrid quantum neural networks (HQNNs) offer a promising solution, combining the strengths of classical machine learning with quantum computing capabilities. However, the performance of these networks can be significantly affected by the quantum noise inherent in NISQ devices. In this paper, we conduct an extensive comparative analysis of various HQNN algorithms, namely Quantum Convolution Neural Network (QCNN), Quanvolutional Neural Network (QuanNN), and Quantum Transfer Learning (QTL), for image classification tasks. We evaluate the performance of each algorithm across quantum circuits with different entangling structures, variations in layer count, and optimal placement in the architecture. Subsequently, we select the highest-performing architectures and assess their robustness against noise influence by introducing quantum gate noise through Phase Flip, Bit Flip, Phase Damping, Amplitude Damping, and the Depolarization Channel. Our results reveal that the top-performing models exhibit varying resilience to different noise channels. However, in most scenarios, the QuanNN demonstrates greater robustness across various quantum noise channels, consistently outperforming other models. This highlights the importance of tailoring model selection to specific noise environments in NISQ devices.

Introduction

Quantum Computing (QC) is a new computational paradigm capable of solving problems intractable for classical computers, such as molecular simulations, complex optimization, and cryptanalysis. This capability that comes directly from the unique principles of quantum mechanics that enable quantum algorithms to achieve exponential computational speed-ups in well-defined domains.

Amongst QC’s expanding applications, Quantum Machine Learning (QML) has emerged to address high-dimensional data scalability challenges in classical ML and computationally intensive tasks like large-scale pattern recognition^{1,2,3,4,5,6,7,8,9,10,11}. However, we are currently in the Noisy Intermediate Scale Quantum (NISQ) era¹², characterized by quantum devices with limited qubits (typically 50–100) that are highly susceptible to decoherence and gate errors. These hardware limitations restrict the reliable implementation of fully quantum algorithms and present significant barriers to the practical realization of standalone QML models.

To bridge this gap, Hybrid Quantum-Classical Neural Networks (HQNNs) have been developed as NISQ-compatible architectures that combine the strengths of classical computation with quantum processing. The fundamental part of HQNNs is the Variational Quantum Circuit (VQC), which utilizes parameterized quantum gates optimized via classical gradient-based methods¹³. This hybrid design harnesses quantum state spaces for feature extraction while relying on classical infrastructure for parameter optimization and error mitigation.

Fig. 1

Motivational Case study. a Two different variants of HQNN (QCNN and QuanNN) yield different performance with the same underlying architecture of quantum layers, b Different effects of Bit Flip noise on the performance of QCNN and QuanNN highlight unique noise sensitivities of different HQNNs.

HQNNs have garnered significant interest due to their distinct advantages over classical neural networks, such as reduced parameter counts at comparable model complexity and enhanced expressivity through quantum entanglement mechanisms¹⁴. These networks have been proposed for diverse applications, including generative modeling^15,16, image classification¹⁷, and regression analysis¹⁸, prompting the development of various HQNN algorithms. Notable examples include Quantum Recurrent Neural Networks, Quantum Reinforcement Learning Models, and Quantum Graph Neural Networks, each contributing to the broad QML landscape. This paper examines three frequently used HQNN models for image classification tasks: Quanvolutional Neural Networks (QuanNN) ¹⁹, Quantum Convolutional Neural Networks (QCNN)²⁰, and Quantum Transfer Learning (QTL)²¹, focusing on their unique architectures and performance.

Each model employs quantum circuits uniquely for image classification. Both QCNN and QuanNN draw conceptual inspiration from classical CNNs but implement fundamentally distinct operations. The QuanNN mimics the idea of classical convolution’s localized feature extraction by using a quantum circuit as a sliding filter. This quantum filter slides across spatial regions of the input image, extracting local features processed through quantum transformation¹⁹.

The QCNN, while structurally inspired by classical CNNs’ hierarchical design, does not perform spatial convolution. Instead, it encodes downscaled input into a quantum state and processes it through fixed variational circuits. Its “convolution” and “pooling” occur via qubit entanglement and measurement reduction, lacking classical CNNs’ translational symmetry and mathematical convolution²⁰.

The QTL model is inspired by classical transfer learning. It involves transferring knowledge from a pre-trained classical network to a quantum setting, where a quantum circuit is integrated for quantum post-processing²¹.

Numerous studies have explored circuit architectures and trainability challenges for the above-discussed algorithms^22,23,24,25. However, a comprehensive comparative analysis of these algorithms for image classification tasks under noisy NISQ conditions remains underexplored. While state-of-the-art studies primarily report performance in ideal conditions, they often neglect the critical impact of different quantum noise channels, an inherent characteristic of NISQ devices.

Related work

The work in²² investigates the performance of various QCNN models, which differed in their structures of parameterized quantum circuits, quantum data encoding methods, and classical data preprocessing approaches when applied to MNIST datasets. That study reported that QCNNs achieved high classification accuracy despite a limited number of free parameters. However, their analysis was limited to noise-free model performance. Whereas, our work evaluates the best performing QCNN model under various quantum noise channels, investigating whether or not the model exhibits robustness to noise over time.

An extensive comparative analysis of different QNN algorithms, including QuanNN, QCNN, and Quantum Residual Network, is presented in²³. The paper examined the effects of varying circuit depths, the number of qubits, and different entanglement settings on image classification tasks using the MNIST dataset. Although the paper provided a thorough evaluation of different models under varying circuit architectures, it did not analyze the performance implications of noise on these models. In this paper, we expand upon this analysis by examining the robustness of the best-performing model under different noise channels.

The impact of 5 different noise channels on the trainability of HQNNs is investigated in²⁴. Their study employed a two-qubit VQC within the HQNN architecture, focusing on its performance in binary classification tasks. In contrast, our paper conducts a similar analysis with the same noise channels but extends it to larger 4-qubit circuits for multiclass classification tasks on MNIST, highlighting the robustness of larger circuits against noise.

These studies offered substantial insights into the performance of various models under ideal conditions but provided minimal understanding of the interplay between noise and circuit architecture. Therefore, we believe that a thorough exploration of different noise channels associated with NISQ devices, particularly from the architectural perspective of HQNNs, remains an inadequately addressed area.

Motivational analysis

In Fig. 1, we underscore the necessity for a thorough comparative analysis of various HQNN architectures and their robustness against different types of quantum noise.

Our observations indicate that even under the same experimental settings and identical design of the underlying quantum layer, the performance of different HQNN models vary significantly. For instance, the QuanNN model outperforms the QCNN by approximately 30% in terms of validation accuracy, as depicted in Fig. 1a. This variation in performance highlights the importance of conducting a comprehensive comparative analysis of different HQNN architectures.

Additionally, the impact of quantum noise on these networks is a critical factor for NISQ devices. As shown in Fig. 1b, the same type of quantum noise affects different HQNN architectures, such as QCNN and QuanNN, in distinct ways. Hence, a comprehensive analysis is needed to understand how the noise affects the overall performance of HQNNs and what level of robustness different HQNN variants can provide against various quantum noise types.

Our contributions

Our key contributions are summarized below:

• Comprehensive comparative analysis of different HQNNs. We conduct a thorough comparison of various HQNN algorithms, including Quantum Convolution Neural Network (QCNN), Quanvolutional Neural Network (QuanNN), and Quantum Transfer Learning (QTL), across a range of circuit architectures. Our analysis spans various entangling structures, variations in layer count, and optimal positioning within the overall network, providing a detailed assessment of each algorithm’s effectiveness in multiclass classification tasks under noise-free conditions.

• Evaluation of noise robustness. We select the best-performing HQNN architectures from the previous step and systematically assess the robustness of these algorithms against various types of quantum noise across different probabilities. This involves introducing different quantum gate noise models, such as Phase Flip, Bit Flip, Phase Damping, Amplitude Damping, and the Depolarization Channel, to determine how different noise sources affect the performance of the selected HQNN architectures.

• Identification of robust HQNN architectures. By evaluating the impact of noise on various HQNN algorithms, we identify architectures that demonstrate resilience to specific quantum noise channels. Our results indicate that QuanNN generally exhibits greater robustness across multiple quantum noise channels, suggesting its potential as a reliable choice for applications in noisy intermediate-scale quantum (NISQ) devices.

• Guidance for HQNN design in NISQ Devices. Our findings provide valuable guidance for designing HQNN architectures in NISQ environments. By demonstrating the varying resilience of different models to specific noise channels, we offer a framework for selecting appropriate architectures based on the noise characteristics of a given quantum device, contributing to the development of more robust and reliable quantum-classical hybrid networks.

Background

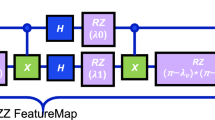
We explore three different QNN algorithms amongst the pool of hybrid algorithms, namely, Quanvolutional Neural Networks¹⁹, Quantum Convolutional Neural Networks²⁰, and Quantum Transfer Learning²¹. An overview of the selected algorithms is shown in Fig. 2. A brief description of the key features of each algorithm and their implementations is presented in the following paragraphs.

Fig. 2

Architecture overview of Selected HQNN algorithms. Each model utilizes a classical fully connected layer to transform quantum circuit measurement into classification probabilities. In the QCNN, classical convolutional and pooling layers are used for image downsizing to match the qubit count of a circuit.

Quanvolutional neural network (QuanNN)

The Quanvolutional Neural Network (QuanNN) is an innovative hybrid quantum-classical architecture introduced in¹⁹. which mimics the functionality of classical Convolutional Neural Networks (CNNs) by using quantum computing principles.

In QuanNN, the central component is the quanvolutional layer, which is analogous to the convolutional layer in classical CNNs but is realized through quantum means. Each quanvolutional layer consists of multiple quantum filters, where each filter is a parameterized quantum circuit. These quantum filters mimic the idea of classical convolution’s localized feature extraction by acting as sliding windows over spatially-local subsections of the input tensor. As the quantum filter moves across the input image, it extracts local features through quantum transformations, which are then processed by subsequent classical or quantum layers for classification.

Each quantum filter can be customized with parameters such as the encoding method, type of entangling circuit, number of qubits, and the average number of quantum gates per qubit. We selected the QuanNN as one of our benchmark models because the flexibility of the circuit flexibility enables the QuanNN to be generalized to tasks of varying sizes by specifying the number of filters, stacking multiple quanvolutional layers, and customizing the circuit architecture. The step-by-step functionality of a QuanNN is:

• 1. Initiate with a single filter q applied to subsections ux of dataset images.

• 2. Utilize an encoding function e to convert ux into an initialized state ix.

• 3. Process ix through a quantum circuit to create an output quantum state ox.

• 4. Convert ox back to guarantee uniform outputs, leading to the final state fx.

• 5. This entire process is denoted as the “quanvolutional filter transformation”. fx = Q(ux, e, q, d), where Q is the quantum filter.

Quantum convolutional neural networks (QCNN)

Similar to the QuanNN, the QCNN is a QNN algorithm that draws conceptual inspiration from the hierarchical structure of CNNs. Introduced in²⁰, the QCNN differs from the QuanNN by fully implementing quantum-based convolutional and pooling layers throughout its architecture. While recent research has demonstrated that QCNNs can be dequantized and efficiently simulated classically under certain conditions, their study remains important. QCNNs represent one of the most advanced and scalable models in quantum machine learning, and analyzing their behavior is crucial for understanding how quantum circuits process information and respond to noise, especially as quantum hardware continues to improve.

Notably, the QCNN, as presented in²⁰, is highly efficient in terms of trainable parameters, using only O(log(N)) variational parameters for input sizes of N qubits. This property facilitates practical training and implementation on current noisy intermediate-scale quantum (NISQ) devices, which are limited in both qubit count and noise resilience. The QCNN architecture comprises an input encoding circuit layer, followed by quantum convolutional and pooling circuit layers, and concludes with a measurement layer. All layers except the final measurement layer contain parameterized quantum gates, whose weights are optimized using classical techniques, making the QCNN a hybrid quantum-classical neural network (HQNN).

It is important to clarify that, although the QCNN is inspired by the hierarchical design of classical CNNs, it does not perform spatial convolution or exploit translational symmetry in the classical sense. Instead, the QCNN encodes downscaled input data into a quantum state and processes it through fixed variational circuits. Its “convolution” and “pooling” operations are realized via quantum entanglement and selective measurement, rather than mathematical convolution. Due to the current limitations of NISQ devices, QCNNs can only process a small number of qubits, which restricts their scalability for large input data. As a result, classical convolution and pooling layers are typically used to reduce the dimensionality of input data before quantum processing. In our implementation, we employ single classical convolution and pooling layers to efficiently downsize images while preserving essential features for the quantum circuit. This hybrid approach allows QCNNs to serve as a bridge between classical and quantum learning, making them a valuable model for benchmarking and for understanding the interplay between quantum circuit design, noise robustness, and practical machine learning performance on near-term quantum hardware.

Quantum transfer learning

The Quantum Transfer Learning (QTL) is an algorithm inspired by the classical transfer learning model, introduced in²¹. In this algorithm, the knowledge gained from classical neural networks is transferred to quantum neural networks. This process includes basic pre-processing and post-processing of the input and output data with classical layers placed at both the beginning and the end of the quantum neural network. Such a setup results in what is termed a “dressed quantum circuit”, as in Eq.  (1).

$$\begin{aligned} \hat{Q} = L_{n_{pixel} \rightarrow n_{qubits}} \circ Q \circ L_{n_{qubits} \rightarrow n_{classes}} \end{aligned}$$

(1)

This hybrid approach is particularly advantageous in the NISQ era, allowing for the optimal pre-processing of high-dimensional data, such as images, using state-of-the-art classical networks. In our model, we employ the pre-trained ResNet-18 model, which is augmented with a VQC serving as the final layer. Overview of the QTL Process:

• 1. Begin with network A, which has already been trained on dataset DA for a specific task TA.

• 2. Modify network A by removing some of its final layers, thereby creating a truncated version known as network $A'$, which will function as a feature extractor.

• 3. Attach a new trainable network, B, to the end of $A'$.

• 4. Keep the weights of network $A'$ fixed and concentrate on training network B with a new dataset, DB, and for a new target task, TB.

Quantum noise & error channels

Quantum noise refers to the unwanted random fluctuations that occur in quantum systems, due to factors such as environmental interference and uncertainty principle. Unlike classical noise, which often involves predictable and less detrimental effects, quantum noise is fundamentally probabilistic and can have a more profound impact on quantum information processing.

In this work, we focus on five fundamental quantum noise channels: Phase Flip, Bit Flip, Phase Damping, Amplitude Damping, and the Depolarization Channel. These channels represent distinct physical error mechanisms and serve as the foundational components for modeling noise in real quantum devices. In practice, device-specific noise models are often constructed by combining these basic channels, making their individual study essential for understanding and benchmarking quantum circuit robustness. By systematically evaluating quantum neural network architectures in each of these standard noise channels, we can isolate and assess the specific impact of different error types, providing valuable insights into the noise resilience of various circuit designs^26,27.

Bit flip

A bit flip error in quantum computing is similar to a bit flip in classical computing. In the classical system, a bit flip error refers to the unintended change of state of a bit from 0 to 1, or vice versa. Similarly, in quantum systems, a bit flip error causes a qubit initially in the state $|0\rangle$ to switch to $|1\rangle$, and vice versa. This type of error is known as a Pauli X error on a qubit. It can be represented using the Kraus Matrices in Eq. (2), where $p \in [0, 1]$ denotes the probability of occurrence of bit flip (Pauli X) error.

$$\begin{aligned} K_0 = \sqrt{1-p} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad K_1 = \sqrt{p} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \end{aligned}$$

(2)

Phase flip

Unlike a classical bit, a qubit also has a phase that represents a rotation around the Z-axis. A phase flip is a quantum operation that changes the phase of a quantum state while keeping its probability amplitude intact. The operation is represented by a unitary phase flip gate or Pauli Z gate, which, when applied, leaves the $|0\rangle$ state unchanged and multiplies the $|1\rangle$ state by $-1$. This operation only shifts the phase of the $|1\rangle$ state by $\pi$ radians, without affecting the probability amplitude of measuring either state. The phase flip error gate is mathematically depicted by the Kraus Matrices in Eq. (3), with $p \in [0, 1]$ denoting the probability of encountering a phase flip (Pauli Z) error.

$$\begin{aligned} K_0 = \sqrt{1-p} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad K_1 = \sqrt{p} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \end{aligned}$$

(3)

Phase damping

Phase damping is a type of quantum noise that results in the loss of phase information of a quantum state without altering the probability amplitudes. Unlike bit flip and phase flip noises, the phase damping does not switch the qubit’s state from $|0\rangle$ to $|1\rangle$ or vice versa. Instead, phase damping degrades quantum coherence by incrementally reducing the off-diagonal elements of the qubit’s density matrix, representing the superposition’s decay. This error can be represented by the Kraus Matrices in Eq. (4), where $\gamma \in [0, 1]$ is the probability of phase damping occurring.

$$\begin{aligned} K_0 = \begin{pmatrix} 1 & 0 \\ 0 & \sqrt{1-\gamma } \end{pmatrix}, \quad K_1 = \begin{pmatrix} 0 & 0 \\ 0 & \sqrt{\gamma } \end{pmatrix} \end{aligned}$$

(4)

Amplitude damping

The amplitude damping represents a type of quantum noise that occurs when a qubit transitions from an excited state $|1\rangle$ to a ground state $|0\rangle$ due to the loss of energy. This form of error often occurs when a quantum system interacts with an external environment, leading to a gradual energy dissipation over time. Unlike the phase damping, which only modifies the relative phase between the states of a qubit without prompting a transition between states, the amplitude damping involves the probability of a qubit in the excited state $|1\rangle$ decaying to the ground state $|0\rangle$. Amplitude damping errors can be represented using Kraus Matrices in Eq. (5), with $\gamma \in [0, 1]$ indicating the probability of amplitude damping.

$$\begin{aligned} K_0 = \begin{pmatrix} 1 & 0 \\ 0 & \sqrt{1-\gamma } \end{pmatrix}, \quad K_1 = \begin{pmatrix} 0 & \sqrt{\gamma } \\ 0 & 0 \end{pmatrix} \end{aligned}$$

(5)

Depolarization channel

The depolarization channel is a noise model in quantum computing that describes a process wherein qubits lose their quantum information to the environment, without favoring any particular basis, Unlike specific errors that only affect certain aspects of a qubit, such as bit flips or phase flips, depolarization errors are non-selective forms of noise that can randomize a qubit’s state to any point on the Bloch sphere with a given probability.

When a depolarization error occurs, it can be thought of as the qubit state being replaced with a completely mixed state $\frac{I}{2}$ (where I is the identity matrix) with some probability p. This process reduces the purity of the quantum state, effectively “smearing” its representation on the Bloch sphere toward the center, corresponding to the maximally mixed state. As p increases, the state becomes more mixed, losing quantum information and coherence. Mathematically, a depolarization channel is represented with the Kraus Matrices in Eq. (6), where $p \in [0, 1]$ is the depolarization probability and is distributed evenly across the application of all Pauli operations.

$$\begin{aligned} K_0 = \sqrt{1-p} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad K_1 = \sqrt{\frac{p}{3}} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad K_2 = \sqrt{\frac{p}{3}} \begin{pmatrix} 0 & -i \\ 1 & 0 \end{pmatrix}, \quad K_3 = \sqrt{\frac{p}{3}} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \end{aligned}$$

(6)

Methodology

In this paper, we analyze three different HQNN algorithms to assess how the circuit architecture impacts performance in an ideal environment without noise. We then explore the effects of different device noise by evaluating the performance of the most effective models in noisy conditions. Our analysis is divided into two main sections: noise-free and noise robustness analysis. Figure 3 provides a detailed overview of our methodology.

Fig. 3

Our methodology. A comprehensive comparative analysis of three different variants of HQNNs is performed with different configurations of quantum layers mainly differing in degree of entanglement, rotation gates, and number of layers (depth of quantum layers). The odd and even depth in a strongly entangling configuration denotes how the layer is repeated when the number of layers are increased. Based on the obtained results the best-performing models with corresponding best configurations are shortlisted which then undergo training under the influence of different types of quantum errors/noise across a wide range of probabilities of each noise type. The comparative analysis of ideal and noisy scenarios is then performed to test the noise-robustness of different HQNN variants. The evaluation metrics used for all the experiments are training and validation accuracy.

Dataset specifications

In this analysis, we employ a subset of the MNIST dataset ²⁸, chosen for its simplicity and effectiveness in facilitating the training process for image classification tasks. The primary focus of our paper is to analyze the effect of noise on model performance; thus, the straightforward nature of the MNIST dataset is adequate to meet the objectives of our study.

The MNIST dataset typically consists of ten classes. However, for our experimental framework, we have restricted our dataset to the first four classes–[0, 1, 2, 3], to ensure that the number of classes directly corresponds to the number of qubits in the quantum circuits utilized in our models.

Selected state-of-the-art HQNN algorithms

Our analysis aims to assess the performance of the HQNN models on image classification tasks, particularly examining the impact of noise on their effectiveness. To this end, we selected the three most widely used state-of-the-art HQNN models for our study: the Quanvolutional Neural Network, the Quantum Convolutional Neural Network (QCNN), and Quantum Transfer Learning.

Comparative analysis of HQNN models

Each algorithm we analyze utilizes different classical network and quantum circuit architectures that employ quantum mechanics uniquely. To evaluate the influence of these architectural differences on their performance, we conduct experiments using different VQC variations under noise-free conditions. This approach allows us to evaluate their performance in ideal conditions, providing insights into which circuit configurations are most effective for specific algorithms.

Circuit architecture variations

In our experiment, we alter two key variables within the circuit architecture: the type of entanglement and the number of layers. As detailed in Fig. 3, we employ three distinct types of entangling circuits: Weakly Entangling, Basic Entangling, and Strongly Entangling. These circuits differ in the types of rotation gates used and the placement of CNOT gates.

The layer repetition variable indicates how many times a single-layer circuit is repeated in the overall VQC architecture before measurement. The number of layers is analogous to the circuit’s depth; more layers result in increased depth. The Basic Entangling and Strongly Entangling circuits have a uniform architecture for each layer, meaning that with each repetition, the same architecture is repeated, thus deepening the circuit. In contrast, the Weakly Entangling circuit employs a non-uniform architecture, with each layer featuring a different composition of gates, as illustrated in Fig. 3.

Selected models

Based on the noise-free performance of the HQNN models across various circuit configurations, we select the models within each algorithm that achieve an accuracy outcome of above 80%. This selection criteria allows us to identify the best-performing models for further noise robustness analysis.

Noise robustness analysis

The primary objective of this paper is to examine the performance of different HQNN algorithms under various noise conditions. To achieve this, we train the best-performing HQNN models, as identified in the previous analysis, with different noise channels and probability of occurrence. We introduce the noise-inducing channels at the end of the VQC, just before the measurement, as illustrated in Fig. 3.

Quantum noise channels

In our analysis, we utilized five types of noise channels: Bit Flip, Phase Flip, Phase Damping, Amplitude Damping, and Depolarization. These channels were selected because they represent distinct physical error mechanisms and collectively serve as the basic building blocks for modeling realistic device noise in NISQ quantum computers. Each noise channel is associated with a probability value, indicating the likelihood that it will act on the circuit and modify the quantum state based on its noisy characteristics. We experimented with noise probabilities ranging from 0.1 to 1.0 in increments of 0.1, resulting in ten distinct probability values for each type of noise channel. Note that the number of shots for all the experiments is fixed to 1024, and we do not consider statistical noise caused by varying the number of shots, given the probabilistic nature of quantum computing.

This experimental design allows us to analyze how the learning capabilities of the models are impacted by the probability of noise occurrence and to explore any potential correlation between model performance and the likelihood of error in a quantum circuit.

Outcome

To assess the robustness of the HQNN models against noise, our analysis will focus on the following key performance metrics: training and validation accuracies. We will conduct a thorough comparison of these accuracies under two distinct conditions: with and without noise in the quantum circuits. This comparison will help us understand how the introduction of quantum noise in the VQC impacts HQNN performance. Furthermore, it will offer insights into the interplay between different characteristics of noise channel and their impact on the model’s robustness or vulnerability to noise.

Results and discussions

Comparative analysis of different HQNN models

We first present the comparative analysis of various HQNN models while assessing their performance on a multiclass classification task. Our analysis includes experimenting with three different HQNN architectures: QuanNN, QCNN, and QTL, each incorporating a different VQC design as their quantum layer(s) (See Fig. 3). These VQCs differ primarily in the types of parameterized quantum gates utilized (RX, RY, RZ) and the degree of entanglement (categorized as basic, strong, and weak). Furthermore, for all the HQNNs used, the 4-qubit VQC is consistent across all the experiments. However, we systematically increase the depth of the VQCs from 1 to 6 layers to explore the impact of VQC depth on the performance of the HQNN models. The results of our comparative analysis are presented in Fig. 4. Below, we separately discuss the performance of each HQNN model.

Fig. 4

Comparative analysis of QCNN, QuanNN, and QTL in noise-free settings. The HQNN models are tested with different configurations of quantum layers. QuanNN turns out to be the best HQNN variant in terms of both better performance than other variants and also robustness against quantum layer’s variations. the second best HQNN model is QCNN, which is sensitive to the degree of entanglement in the underlying quantum layers, i.e., the more the better. QTL consistently performs poorly among the three HQNN variants regardless of the quantum layer configuration.

QCNN In our analysis of QCNN, we observed that QCNNs exhibited inconsistent performance across different configurations, with no clear trend emerging as the number of layers increased or as modifications were made to the underlying VQC design. This inconsistency can largely be attributed to the QCNN architecture as originally proposed in ²⁰, which incorporates mid-network measurements to facilitate pooling operations by tracing out some of the measurement results. Given the probabilistic nature of quantum computation, these mid-network measurements can significantly amplify statistical measurement noise, leading to erratic performance outcomes.

Our results further indicate that the performance of QCNNs is heavily influenced by the degree of entanglement in the underlying the quantum layers. Specifically, when the quantum layers utilize weak entanglement, QCNNs exhibit suboptimal performance compared to configurations with basic or strong entanglement, regardless of the layer depth. Moreover, to achieve relatively enhanced performance with weakly entangled quantum layers, an increase in layer depth is generally necessary for QCNNs.

On the other hand, QCNNs configurations with basic to strong entanglement demonstrate marked improvements in performance compared to weakly entangled quantum layers. For quantum layers with strong entanglement, moderate depth is found to be optimal, yielding superior performance. However, in scenarios where the entanglement is basic, a higher layer depth is required to attain improved performance outcomes. This dependency on both the degree of entanglement and the depth of quantum layers underscores the complex interplay of factors that influence the efficacy of QCNN architectures.

QuanNN Unlike QCNNs, the QuanNN model demonstrates notably consistent performance across varying depths of layers and different degrees of entanglement. In our analysis, the degree of entanglement appears to have a minimal impact on the performance of QuanNN, with negligible differences observed across the entanglement categories used in this study, i.e., basic, strong, and weak. Additionally, there is a general trend of slight improvement in performance as the depth of the underlying quantum layers increases. This trend suggests that QuanNN benefits from the enhanced expressibility offered by deeper quantum layers, indicating a robustness in its architecture that allows it to maintain performance irrespective of the entanglement degree. This consistent behavior makes QuanNN a potentially more reliable choice in applications where stable performance is critical.

QTL The QTL models consistently exhibit inferior performance when compared to both QCNN and QuanNN architectures. Our investigation reveals that the pretrained classical weights from the ResNet18 model do not adapt well to integration with quantum layers. Regardless of the quantum layer depth or the degree of entanglement, QTL models achieve approximately 20% accuracy, which is significantly lower than the best-case accuracies of over 80% observed for QCNN and QuanNN. This substantial discrepancy in performance suggests that the QTL architecture may require further optimization or a different approach to effectively leverage quantum enhancements while integrating with pretrained classical network parameters.

In light of the above results, the QTL models underperform significantly compared to QCNN and QuanNN. Consequently, our subsequent analysis on noise robustness will focus exclusively on QCNN and QuanNN models. For these architectures, Table 1 summarizes the optimal configurations based on our comparative performance evaluation. These configurations will be the only ones considered in the forthcoming noise robustness analysis, ensuring that our investigation concentrates on the most effective setups for each model.

Table 1 Optimal configurations for best performing models.

Large-scale implementation analysis of QCNN (8-Qubit)

Fig. 5

Comparison of 8 qubit QCNN model performance in noise-free and under Amplitude Damping, Bit Flip, Depolarization, Phase Damping and Phase Flip channels with probabilities of 0.1, 0.5 and 1.0.

To extend our analysis beyond small-scale benchmarks, we implemented the QCNN architecture with 8 qubits, representing a large-scale quantum scenario. Our results show a stark contrast in model performance under noise-free and noisy conditions, as shown in Fig. 5. When trained without quantum noise, the 8-qubit QCNN reached a test accuracy of 96%, demonstrating effective learning and generalisation. However, after introducing all five fundamental noise channels at different probabilities (0.1, 0.5, and 1.0), test accuracy dropped sharply to 25% regardless of noise type or probability.

This significant drop can be explained by the impact of large quantum circuits, as every additional qubit increases the number of gates and parameters in the circuit, which in turn amplifies the amount of noise introduced. With more qubits and deeper circuits, error rates accumulate faster, making it extremely challenging for the model to learn useful patterns under realistic noise conditions. These findings highlight that, on current NISQ hardware, large-scale quantum models like 8-qubit QCNNs are not yet practical. For this reason, our detailed comparative and robustness investigations focus on 4-qubit models, which are better suited to the noise levels seen in today’s quantum devices.

Noise robustness analysis of QCNN

We now present the robustness analysis of QCNNs against different types of quantum noise and error channels used in this paper. This analysis involves deliberately introducing different quantum noises into the quantum layers of both the QuanNN and QCNN models By systematically injecting these noises at varying probabilities, we aim to assess and compare the resilience of each architecture under different noisy conditions. This approach allows us to understand how these models withstand operational disruptions caused by quantum errors, providing crucial insights into the practical robustness of quantum-enhanced machine learning models.

QCNN robustness against amplitude damping noise The training and validation results of QCNN under both noisy (amplitude damping) and noise-free scenarios are presented in Fig. 6. Our findings reveal that at lower noise probabilities, specifically 0.1 and 0.2, QCNNs demonstrate significant resilience to noise, maintaining performance levels comparable to those in an ideal, noise-free setting. However, as the noise probability increases to 0.3, QCNNs still exhibit some learning potential, but at a significantly slower rate. At a noise probability of 0.5, QCNNs show an unexpected improvement, achieving performance that surpasses the ideal scenario. This anomaly suggests that under certain conditions, the noise might play a constructive role, potentially acting as a form of noise-enhanced learning.

Fig. 6

Comparison of QCNN performance in noise free and under Amplitude Damping channel with different probabilities.

Nonetheless, with further increases in noise probability beyond 0.5, the QCNNs succumb completely to the adverse effects of the noise, resulting in no learning. This highlights the critical impact of noise levels on the operational viability of QCNNs, underscoring the need for optimal noise management strategies in quantum computing applications.

QCNN robustness against bit flip noise The comparative analysis of QCNN performance under ideal conditions and when subjected to Bit Flip noise is illustrated in Fig. 7. Our results show that at relatively lower noise probabilities (i.e., $\le 0.4$), QCNNs adapt well to noise patterns, exhibiting great robustness against Bit Flip noise and achieving performance levels comparable to those observed in the noise-free setting. Notably, at very low noise probabilities, QCNNs demonstrate an ability to effectively learn these noise patterns, resulting in training accuracy that exceeds that of the ideal case. However, it is important to note that while training accuracy increases, the generalization (validation accuracy) remains consistent with the ideal setting. This phenomenon suggests that learning from noise can potentially mislead practitioners about the actual performance improvement, as it does not enhance the model’s generalization capabilities. At higher noise probabilities (i.e., $\ge 0.5$), the QCNN succumbs to the detrimental effects of the noise and fails to learn. This highlights a critical threshold in Bit Flip noise tolerance, beyond which the QCNN’s performance degrades significantly, indicating the limits of noise adaptability in QCNN architectures.

Fig. 7

Comparison of QCNN performance in noise free and under Bit Flip channel with different probabilities.

QCNN robustness against depolarization channel noise The performance of QCNNs under both ideal conditions and when subjected to depolarization noise is presented in Fig. 8. Our results indicate that at lower probabilities of depolarization channel noise, QCNNs effectively adapt to the noise patterns, demonstrating a robustness that results in performance levels equivalent to those observed in the noise-free setting. This suggests that at these lower noise intensities, QCNNs can tolerate and possibly even utilize minor noise as a feature rather than a detriment, maintaining overall performance. However, as the noise probability increases beyond 0.2, the QCNNs succumb to the adverse effects of the noise, showing a significant decline in learning ability.

Fig. 8

Comparison of QCNN performance in noise free and under Depolarization channel with different probabilities.

This performance degradation can be attributed to the fact that as the noise level increases, the error rates associated with quantum gates may exceed the threshold that the network can compensate for, leading to an accumulation of errors that degrades the quantum state’s integrity. Additionally, higher levels of depolarization noise can lead to a rapid loss of quantum coherence, essential for maintaining the superposition and entanglement necessary for quantum computation. This loss critically hinders the QCNN’s ability to process information quantum mechanically.

QCNN robustness against Phase Damping Noise The performance of QCNNs under both ideal conditions and when subjected to phase damping noise is presented in Fig. 9. This analysis diverges from the patterns observed with other types of quantum noise, such as amplitude damping, bit flip, and depolarization channels. Remarkably, QCNNs exhibit considerable robustness to phase flip noise across a broad range of probabilities.

Fig. 9

Comparison of QCNN performance in noise free and under Phase Damping channel with different probabilities.

Specifically, at probabilities $\le 0.3$, QCNNs not only successfully adapt to noise patterns but also perform significantly better than in the ideal, noise-free case. This suggests that phase damping noise, at these levels, might be leveraged as a beneficial factor, possibly aiding in the reduction of other types of quantum errors or enhancing certain quantum state properties that improve computational outcomes.

However, at noise probabilities of 0.4 and 0.7, while QCNNs initially adapt to the noise patterns, continued training leads to detrimental effects from the noise. This observation implies that shorter training durations might be beneficial under these specific noise conditions to avoid the negative impact of prolonged exposure to high noise levels.

Interestingly, at probabilities of 0.5 and 0.6, QCNNs not only cope with the noise but actually exceed the performance of the ideal scenario. This superior performance under noisy conditions suggests that QCNNs can exploit certain characteristics of phase damping noise to enhance computational accuracy and robustness.

QCNN robustness against phase flip noise The performance of QCNNs under both ideal conditions and when subjected to phase flip noise is presented in Fig. 10. Our results demonstrate that QCNNs adapt well to noise patterns at lower probabilities of phase flip noise (i.e., $\le 0.4$), maintaining performance levels comparable to those in a noise-free setting.

Fig. 10

Comparison of QCNN performance in noise free and under Phase Flip channel with different probabilities.

However, at higher noise probabilities, specifically at 0.5 and 0.6, the QCNN succumbs to the detrimental effects of the noise and fails to learn. Interestingly, at a noise probability of 0.7, the model initially shows resilience, but continued training eventually leads to performance degradation due to the noise. At probabilities of 0.8 and 0.9, the model fails to learn altogether.

Most notably, at a noise probability of 1.0, the model demonstrates remarkable resilience, effectively learning and becoming tolerant to a high intensity of noise. This inconsistent performance across different noise intensities suggests that the QCNN architecture’s ability to learn and adapt to noise patterns varies, illustrating its potential resilience and robustness under specific conditions.

Noise robustness analysis of QuanNN

QuanNN robustness against amplitude damping noise Based on the training and validation results of QuanNN under both noise-free conditions and when subjected to amplitude damping noise, as depicted in Fig. 11, we observe a consistent trend in the learning capability of QuanNN. Our results show that QuanNN maintains the same learning capacity as in noise-free conditions up to a noise probability of 0.5, demonstrating that the model can retain good learning capabilities for low noise levels.

Fig. 11

Comparison of QuanNN performance in noise free and under Amplitude Damping channel with different probabilities.

However, as the probability of noise occurrence increases by increments of 0.1, the learning capability of the models gradually diminishes. At probabilities of 0.6 and 0.7, the performance of QuanNN declines slightly as compared to the performance in a noise-free setting. With further increases in noise, particularly beyond a probability of 0.7, the performance drops drastically, eventually leading to negligible learning at a noise probability of 1.0. This trend underscores the need for improvements in the circuit’s ability to handle higher levels of noise during the learning process.

QuanNN Robustness against bit flip noise The performance of QuanNN under both ideal conditions and when subjected to bit flip noise is illustrated in Fig. 12. Unlike the performance of QuanNN under amplitude-damping noise, we can observe that the validation accuracy remains consistent with its noise-free performance across most probabilities. This indicates that QuanNN is highly resilient to the effects of bit flip noise at all tested probabilities, with the exception of a significant drop at a noise probability of 0.5.

Fig. 12

Comparison of QuanNN performance in noise free and under Bit Flip channel with different probabilities.

At a probability of 0.5, the model succumbs completely to the adverse effects of bit flip noise, hindering the learning process. This anomalous behavior can be attributed to the model’s inability to adapt to high noise levels. However, subsequent improvements in performance indicate that the model can adapt to increasing noise characteristics during the learning process. Overall, these results suggest that the architecture of QuanNN is highly robust against bit flip noise.

QuanNN Robustness against Depolarization Channel Noise The performance of QuanNN under both ideal conditions and when subjected to depolarization noise is presented in Fig. 13. Unlike the performance of QCNN under depolarization channel noise, QuanNN demonstrates a consistent resilience to all probabilities of depolarization noise, demonstrating a robustness that results in performance levels equivalent to those observed in the noise-free setting.

Fig. 13

Comparison of QuanNN performance in noise free and under Depolarization channel with different probabilities.

Although there is a slight decrease in performance at probabilities of 0.7 and 0.8, the model’s performance increases from 0.9 onwards, matching that of the noise-free conditions. Typically, higher levels of depolarization channel noise can lead to a rapid loss of quantum coherence, which may hinder the model’s learning capabilities²⁴. However, the results showing QuanNN’s performance under increasing probabilities of depolarization noise suggest that its network and circuit architecture makes it very robust against such adverse effects of depolarization noise.

QuanNN Robustness against phase damping noise Based on the training and validation results of QuanNN under both noise-free conditions and when subjected to phase damping noise, as depicted in Fig. 14, we can observe that QuanNN exhibits considerable robustness to phase damping noise across all probabilities. This resilience is significant as phase damping typically represents a challenge by causing the loss of quantum information without energy loss, potentially degrading the performance. Moreover, unlike other forms of quantum noise such as amplitude damping and bit flip, the phase damping noise shows a less adverse effect on QuanNN. This resilient behavior suggests QuanNN architecture’s inherent ability to effectively adapt to and mitigate the effects of phase damping. Additionally, when compared to the performance of the QCNN model under the same conditions, QuanNN exhibits less variability in performance across different noise intensities. This consistency illustrates that the QuanNN architecture is more robust against various noise intensities, highlighting its capability for reliable performance in applications where maintaining phase coherence is essential.

Fig. 14

Comparison of QuanNN performance in noise free and under Phase Damping channel with different probabilities.

QuanNN Robustness against phase flip noise

Fig. 15

Comparison of QuanNN performance in noise free and under Phase Flip channel with different probabilities.

The performance of QuanNN under both ideal conditions and when subjected to phase flip noise is presented in Fig. 15. Similar to the performance of QuanNN under phase damping noise, QuanNN also exhibits strong performance across all intensities of phase flip noise. At each probability of noise occurrence, the validation results from the noise-induced conditions overlap with those of the noise-free model. The robust performance of QuanNN demonstrates that QuanNN architecture is highly resilient against noises that affect the phase information of the quantum state.

Conclusion

In this paper, we have conducted a comprehensive analysis of hybrid quantum neural networks (HQNNs) within the framework of noisy intermediate-scale quantum (NISQ) devices, focusing on their applicability and robustness against variety of quantum erros/noise, in image classification tasks. Our extensive comparative analysis of various HQNN models, including Quantum Convolution Neural Network (QCNN), Quanvolutional Neural Network (QuanNN), and Quantum Transfer Learning (QTL), has highlighted significant disparities in performance dependent on the entangling structures, layer counts (depth of underlying quantum layers), and their specific configurations within the networks. The comparative analysis is aimed to find the short list the models which perform best for the defined task. Subsequently, a comprehensive noise-robustness analysis of shortlisted models was conducted.

Through a rigorous evaluation of the above-mentioned variants of HQNNs under both ideal and noisy conditions, we have demonstrated that the performance of HQNNs can significantly vary with the introduction of quantum noise. Our findings reveal that QuanNN consistently outperforms other models across different types of quantum noise, thus highlighting QuanNN as a more robust option in NISQ devices. This superior performance underlines the critical role of model and architecture selection based on the specific quantum noise characteristics of the operational environment.

Our work contributes to the ongoing development of quantum computing applications by providing detailed insights into the design and optimization of HQNNs for NISQ devices. Additionally, this work offers practical guidance for selecting HQNN architectures that are optimized for resilience to quantum noise, thereby enhancing the reliability and efficacy of quantum-enhanced machine learning solutions.

To summarize, our work not only advances our understanding of the capabilities and limitations of current HQNN models but also sets a foundation for future explorations aimed at harnessing the full potential of quantum computing in real-world applications.