Introduction

Perovskites are materials used for different physical and chemical purposes, i.e., optoelectronic, half-metallic conductivity, superconductivity, and magneto-resistance. They significantly influence the fabrication of electronics, engineering, and material science systems. Halide perovskites are predominantly suitable for detecting X-rays and Gamma radiations due to their high density, radiation hardness, and atomic number1,2,3,4. Their structure stability and composition are essential for their characteristics. ABX3 is the general representation of the materials in this class, where A and B are the cations, and X is the anion, mostly halide5. Halide perovskites are a subclass of perovskite in which X is a halogen element (i.e., Fluorine, Chlorine, Bromine, and Iodine). In this study, we use chlorine instead of X to form chloroperovskite. These materials have a lot of applications in various electronic devices, and therefore, they attract a variety of interest6,7,8. Researchers carefully study the structure and composition of these perovskite compounds, which have advanced properties and potential applications9,10. Perovskites own unique photophysical properties, such as long carrier lifetimes, high absorption capacities, and notable photoluminescence effectiveness. These are auspicious materials for most technological applications, especially those concerning light-based technologies11,12,13. Due to their distinct potential, these materials are used in optoelectronic devices like photovoltaic cells, light-emitting diodes, and photonic devices14,15,16,17,18. In addition, due to their significant absorption coefficient, cheap synthesis, and large band gap, chloro-perovskite has gained much attention19,20. Because of their high energy, intensity, and direct emission, these materials are frequently used as scintillating materials for the industrial and scientific domains21,22,23. Due to the controllable band gap, which can be easily attained by changing the halide concentration, perovskite demonstrates various optoelectronic applications. Much research has been done on photocatalytic reactions due to their potential photocatalytic activity in the visible range24,25. The most repeated computational method used for structural and electrical study of perovskite material is density functional theory (DFT).

By the use of DFT, the majority of the scientists studied chloro-perovskite. Wu et al.. studied the optical and electrical properties of CsPbX3 (X = Cl, Br, I) using DFT. Their results reveal a considerable energy band gap was observed by substituting other halogens with chlorine26. A probable description of this occurrence was the existence of confined defect states. Li et al.. 2019 studied the synthesis and analysis of CsPbCl3 chloro-perovskite using X-ray diffraction (XRD) and UV-Vis spectroscopy27. They studied structural and optical properties and concluded that the effective absorption occur in the UV-Vis spectrum due to their optical band gap. Khan, Saima Naz, et al.28. conducted theoretical research to examine the current development of chloro-perovskite. They investigated the structural, optical, and electrical properties of chloro-perovskite materials using simulation within WIEN2K code. M. Hussain et al.. studied the optical properties of BaMCl3 where (M = Ag or Cu). They investigated their structural, electronic, and elastic properties and found to be semiconducting and optically active in the UV region of incident light29.

This work aims to investigate the structural, optical, and electronic properties of chloro-perovskite. We analyze the properties of thallium and cesium-based perovskite materials RBaCl3 (R = Tl and Cs), using the WIEN2K and first-principles approach. By FP-LAPW, we optimize structural parameters and examine the electrical properties (density of states and band structure) and optical properties such as extinction coefficient, reflectivity, refractivity, absorption coefficient, optical conductivity, and energy loss function.

Computational methodology

DFT (density functional theory) is used in this study based on the plane wave self-consistent field (PWSCF) for the simulation using the WIEN2K code30. To understand the properties of these materials, we use the FP-LAPW approach, allowing for performance optimization31. The General Gradient approximation (GGA) is used to study structural and elastic properties by performing the crystal structural optimization operating the Perdew-Burke-Ernzerhof (PBE) function32. The IRelast package is used to compute different parameters of elastic properties33. Modified Becke-Johnson potential is used to examine the optical and electrical properties for better results33. To ensure a high level of accuracy, TB-mBJ calculation’s convergence at an overall energy threshold of 0.01 mRy, while self-consistent field (SCF) a total convergence satisfy at 0.001 mRy, and K-points used the first Brillouin zone reciprocal space to sample is 2000. The cut-off energy specified for both compounds is -6.0 Ry, and chosen value for RMT is 5. The complex dielectric function ε(ω) = ε1(ω) + iε2(ω) is utilized for the optical properties calculations, which offers a complete comprehension of material behavior34. For the phonon dispersion band calculations, we used the Phonopy package to compute the force constants and obtain the phonon dispersion curves35. The phonon band structure was visualized by plotting the dispersion curves, with the results representing the phonon frequencies as a function of wavevector along the high-symmetry points in the Brillouin zone. This methodology ensures accurate phonon dispersion calculations, providing insight into the vibrational properties of the material.

For graphing and data analysis, we used different software like Origin (for analyzing and plotting the electronic and optical properties)36, Xmgrace (for visualizing the density of states (DOS) and band structures)37, and VESTA (for visualizing the crystal structures and phonon dispersion curves in this study)38 in this study. All these graphic tools contribute to a better understanding of the structural, optical, and electronic properties of RBaCl3 (R = Tl and Cs) chloro-perovskite by permitting the observation of computational results. The research uses these tools to obtain an ultimate consideration of the material’s properties, which is mandatory for extra investigation and application. A computational method, as explained previously, is used to obtain better insights into the behavior of the material’s properties.

Results and discussion

In this section, we will describe the results of RBaCl3 (R = Tl and Cs) chloro-perovskite, which is calculated using the previously mentioned computational technique. It is sub-classified into structural, electronic, and optical properties.

Structural properties

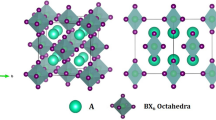
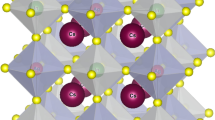
We examined the structural properties of RBaCl3 (R = Tl and Cs) chloro-perovskites, which are essential for the computation of other physical properties, i.e., optical and electronic. The GGA-PBE approximation investigates structural properties with the Pm3m (no. 221) space group. Figure 1 depicts the primitive crystallographic unit cell of RBaCl3 halide perovskites. The atomic Wyckoff positions of Tl/Cs are (0, 0, 0), Ba at (0.5, 0.5, 0.5), and Cl at (0, 0.5, 0.5).

Fig. 1
figure 1

Optimized crystal structure of RBaCl3 (R = Tl and Cs) in the ball-and-stick (left) and polyhedral (right) view.

Full size image

The Birch-Murnaghan equation of state (EOS) is widely used to describe the relationship between energy and volume in condensed matter systems. For the fitted curves of energy versus volume of the primitive unit cell, this EOS provides key parameters, including the equilibrium volume (V₀), bulk modulus (B), and its pressure derivative (B′)39. We utilized the Birch-Murnaghan EOS for fitting the curves of energy versus volume of the primitive unit cell of the RBaCl3 (R = Tl and Cs) chloro-perovskites. These findings offer a significant understanding of the structural characteristics of these materials. The Birch-Murnaghan EOS can be expressed as;

$$\:\text{E}\left(\text{V}\right)={\text{E}}_{0}+\:\frac{\text{B}}{{\text{B}}^{{\prime\:}\:}\left({\text{B}}{{^\prime\:}}-1\right)}\left[\text{V}{\left(\frac{{\text{V}}_{0}}{\text{V}}\right)}^{{\text{B}}^{{\prime\:}}}-\:{\text{V}}_{0}\right]+\:\frac{\text{B}}{{\text{B}}{{^\prime\:}}}\left(\text{V}-{\text{V}}_{0}\right)$$
(1)

This equation, which is referred to as the Birch-Murnaghan equation of state, shows the connection between the total energy (E) and unit cell volume (V) of a material. The optimum values of the total energy, bulk modulus, pressure derivative of bulk modulus, total unit cell volume, and optimized unit cell volume are indicated by the parameters E0, B, B′, V, and V0.

Fig. 2
figure 2

Optimized curve fitted through Birch-Murnaghan equation-of-state for (a) TlBaCl3 (b). CsBaCl3.

Full size image

GGA approximation calculation is used for the structural analysis optimization curves, which are exposed in Fig. 2. Table 1 lists the optimum values determined using the Birch-Murnaghan approach to fit these curves. The graph illustrates the relationship between energy and unit cell volume, exhibiting that energy extends with volume until a particular value is reached (V0), beyond which it increases and indicates a state of instabilities. The structural parameters are determined in first-principles calculation at the lowest energy (most stable) state. Furthermore, the Goldschmidt tolerance factor (τ)40, a measurement of stability and deformation in the structure of crystals, is computed for both materials employing the following formula;

$$\:{\uptau\:}=\frac{{\text{r}}_{\text{A}}+{\text{r}}_{\text{X}}}{\sqrt{2}\left({\text{r}}_{\text{B}}+{\text{r}}_{\text{X}}\right)}$$
(2)

In the above equation, rA and rB are the cation radii (Tl or Cs and Ba), and rX is the radius of the chlorine (Cl) ion. For TlBaCl3, computed τ values are 0.9, while for CsBaCl3, they are 1.0. From the above-calculated values, we can say that both compounds have stable cubic chloro-perovskite structures, and their τ values are close to 1.

Our results on the structural properties of halide perovskite compounds demonstrate superior precision compared to recent similar research41.

Table 1 Optimized crystal unit cell parameters of ternary RBaCl3 (R = Tl and Cs) compounds.
Full size table

Phonon band structure

The phonon dispersion of RBaCl3 (R = Tl and Cs) reveals essential insights into the dynamical stability and thermal transport properties of these compounds. The absence of imaginary frequencies in the phonon spectra confirms their dynamical stability, indicating that the crystal structures resist spontaneous distortions. The phonon band structure shown in Fig. 3 consists of three acoustics and several optical branches, with no significant phonon band gap between them. This suggests strong phonon-phonon interactions, which can impact thermal conductivity by enhancing scattering mechanisms. The slopes of the acoustic branches near the Γ point provide information about phonon group velocities, where steeper slopes correspond to higher heat conduction efficiency. Given heavy atoms (Tl, Cs, and Ba), the overall phonon frequencies are relatively low, as heavier elements vibrate at lower frequencies, leading to reduced lattice thermal conductivity. Comparing TlBaCl3 and CsBaCl3, slight variations in phonon dispersion arise due to differences in atomic mass and bonding strength, with Cs being lighter than Tl, potentially exhibiting slightly higher phonon frequencies. These phonon characteristics play a crucial role in determining the thermal transport and vibrational properties of RBaCl3, influencing their potential applications in thermoelectric and optoelectronic devices. The calculated phonons dispersion display that our RBaCl3 (R = Tl and Cs) chloroperovskites are dynamical stable similar to the other materials resported recently42.

Fig. 3
figure 3

Computed phonon band dispersion for (a) TlBaCl3 and (b) CsBaCl3.

Full size image

Electronic properties

The concept of the density of states (DOS) and energy band structure is essential to comprehending the electronic properties of materials.

Bands structure

TB-mBJ approximation calculates the band structure of RBaCl3 (R = Tl and Cs) chloro-perovskite in the first Brillouin zone. Figure 4 demonstrates the band structure of our compounds, and from Fig. 4, it is clear that both the compounds TlBaCl3 and CsBaCl3 have an indirect band of 5.51 eV and 7.14 eV, respectively. TlBaCl3 possesses an indirect band gap from M-X symmetry points, while CsBaCl3 has an indirect band gap from R-Γ. Both TlBaCl3 and CsBaCl3 materials are insulators. It is widely accepted that the TB-mBJ approximation brings bandgap values that strongly correlate with experimental results43. The results demonstrate the potential uses of cubic halide perovskites in optical and electronic applications, such as in devices that utilize their insulating or semiconducting properties.

Fig. 4
figure 4

Band structure of (a) TlBaCl3 (b) CsBaCl3.

Full size image

Density of states (DOS)

The total density of states (TDOS) and partial density of states (PDOS) of RBaCl3 (R = Tl and Cs) are given in Fig. 5. DOS for TlBaCl3 has been displayed within the energy range from − 4 eV to 8 eV, while for CsBaCl3, the range from − 4 eV to 10 eV is considered to show the contribution of different electronic states to valence and conduction band. Fermi level (EF) is located in the center of the graph at 0 eV; divide the DOS graph into two portions. The left side shows the valance band, while the right depicts the conduction band. The DOS graph of TlBaCl3 reveals that Tl dominates in the conduction band (CB) and shows a minor contribution in the valence band, while Ba and Cl states chiefly contribute to the valence band (VB). In CsBaCl3, the states that contribute significantly to the valance band are Ba and Cl. This extensive study has enhanced our understanding of the electrical structure and orbital contributions of TDOS and PDOS.

Fig. 5
figure 5

Density of states of (a) TlBaCl3 (b) CsBaCl3.

Full size image

In TlBaCl3, the deep valence region (≈ − 5 to − 6 eV) is predominantly derived from Cl-3s orbitals, whereas the upper valence band extending to the valence band maximum (VBM) is mainly composed of Cl-3p states with a significant and sharp contribution from Tl-6s orbitals. This feature reflects the inert-pair effect of Tl⁺ and indicates strong hybridization between Tl-6s and Cl-3p states. Contributions from Ba orbitals to the valence band are negligible. The conduction band minimum (CBM) is primarily characterized by Ba-5d states, exhibiting distinct splitting into t₂g (lower) and e_g (higher) sublevels, while Tl-6p states contribute at higher conduction energies. In contrast, CsBaCl3 exhibits a similar deep valence region dominated by Cl-3s orbitals, while the upper valence band is almost entirely governed by Cl-3p states with negligible involvement from Cs orbitals, consistent with its closed-shell ionic nature. The CBM is again dominated by Ba-5d states with t₂g–e_g splitting, while Cs-p/d contributions emerge only at higher conduction energies. Overall, the density of states analysis reveals that Cl orbitals define the valence bandwidth (3s at deeper energies and 3p at the VBM), Ba orbitals dominate the CBM through 5d states, and the role of the A-site cation is markedly different: Tl introduces a localized 6s feature near the VBM and additional 6p states in the conduction band, while Cs remains electronically inert near the band edges.

Optical properties

In this section, we will elaborate on the optical properties of RBaCl3 (R = Tl and Cs) chloro-perovskites. Following the latest research work on the similar materials, we calculated various parameters in optical properties44. Based on electrical characteristics and band gap, the compounds TlBaCl3 and CsBaCl3 have a direct band gap and demonstrate semiconducting and insulating properties, respectively, which shows that these compounds are perfect for optical properties. The following equations can be used to govern the reflectivity, extinction coefficient, refractive index, and absorption coefficient for different optical qualities45.

$$\varepsilon (\omega ) = \varepsilon _{1} (w) + i\varepsilon _{2} (\omega )$$
(3)

where:

  • ε(ω) is the total permittivity as a function of angular frequency ω,

  • ε1 is the real part of the permittivity,

  • ε2 is the imaginary part of the permittivity.

$$\:n(\omega )={\left[\frac{{\varepsilon}_{1}\left({\upomega\:}\right)}{2}+\:\frac{\sqrt{{{\varepsilon}_{1}}^{2}\left({\upomega\:}\right)+\:{{\varepsilon}_{2}}^{2}\left({\upomega\:}\right)}}{2}\right]}^{\frac{1}{2}}$$
(4)

where:

  • n(ω) is the refractive index at angular frequency ω\omegaω,

  • ε1(ω) is the real part of the permittivity,

  • ε2(ω) is the imaginary part of the permittivity.

$$\:k(\omega )={\left[\frac{{-\varepsilon}_{1}\left({\upomega\:}\right)}{2}+\:\frac{\sqrt{{{\varepsilon}_{1}}^{2}\left({\upomega\:}\right)+\:{{\varepsilon}_{2}}^{2}\left({\upomega\:}\right)}}{2}\right]}^{\frac{1}{2}}$$
(5)

where:

  • k(ω) is the absorption coefficient at angular frequency ω\omegaω,

  • ε1(ω) is the real part of the permittivity,

  • ε2(ω) is the imaginary part of the permittivity.

$$\:I(\omega )=\frac{2{\upomega\:}}{\text{c}}\text{k}\left({\upomega\:}\right)$$
(6)

where:

  • I(ω) is the intensity at angular frequency ω\omegaω,

  • ω is the angular frequency,

  • c is the speed of light in vacuum,

  • k(ω) is the absorption coefficient.

$$\:R(\omega )=\frac{{\left(1-\text{n}\right)}^{2}{+\:\text{k}}^{2}}{{\left(1-\text{n}\right)}^{2}{+\:\text{k}}^{2}}$$
(7)

where:

  • R(ω) is the reflection coefficient at angular frequency ω\omegaω,

  • n is the refractive index,

  • k is the absorption coefficient.

$$\:\sigma(\omega )=\frac{2\text{W}\:\text{e}\text{V}\:{\hslash\:}\left({\upomega\:}\right)}{{\text{E}}_{0}}$$
(8)

where:

  • σ(ω) is the conductivity at angular frequency ω,

  • W is a constant related to the material,

  • e is the elementary charge,

  • V is the voltage,

  • \({\hslash\:}\) is the reduced Planck constant,

  • ω is the angular frequency,

  • E0 is the reference energy.

For incident photon energies within 0 eV and 14 eV, all fundamental optical characteristics are derived from the dielectric function using the TB-mBJ approximation and an optimized lattice constant.

Dielectric function

Figure 6 shows the real fraction ε1(ω), which represents the material’s photon distribution and electronic polarizing ability. ε1(ω) grows gradually at low photon energy, peaking at around 8.2 for TlBaCl3 and 5 eV for CsBaCl3. ε0(ω) (Static dielectric function) for TlBaCl3 and CsBaCl3 is valued at nearly 2.11 and 1.73, respectively. For TlBaCl3, the band gap and ε1(0) are 3.40 eV and 2.23 eV, respectively, while for CsBaCl3, they are 7.2 eV and 1.73 eV, respectively. By the given data, TlBaCl3 follows the Penn model while CsBaCl3 doesn’t.

Upon almost achieving a threshold energy of 8.5, the curve fluctuates, exhibiting both magnitudes rises and falls. TlBaCl3 has a maximum peak of 6.7 at approximately 8.7 eV, while CsBaCl3 has a maximum peak of 3.5 at around the same energy. Because of their sizeable direct band gap, these compounds are suitable for high-frequency UV devices.

Fig. 6
figure 6

Dielectric function of RBaCl3 (R = Tl and Cs) (a) ε1 real part (b) ε2 imaginary part.

Full size image

Absorption coefficient

A charge carrier is formed when an electron in a material is subjected to optical light. The electron will subsequently absorb sufficient energy to migrate from the valance band to the conduction band, creating a defect in the valence band. An excitonic effect resulting from the coulombic interaction between the excited electron and the hole affects the optical quality of the material. The absorption coefficient is calculated using the relationship (Eq. 4). Figure 7(a) displays the results obtained for the absorption coefficient I(ω). For TlBaCl3 and CsBaCl3, the absorption begins at 6.5 eV and 9.7 eV, respectively. The highest possible value of I(ω) is 163 for TlBaCl3 at 8.8 eV and 135 for CsBaCl3 at 13.5 eV. Furthermore, at 13.5 eV, TlBaCl3 and CsBaCl3 show small peaks in their absorption coefficients, with values of 150.8 and 135, respectively, as shown in Fig. 7(a).

Optical conductivity

Figure 7(b) displays the optical conductivity σ(ω) derived from the dielectric function. According to this figure, the energy region between 5 eV and 7.1 eV is when optical conductivity for TlBaCl3 and CsBaCl3 begins, respectively. At a photon energy of 8.65 eV, the maximum optical conductivity value for TlBaCl3 was 7865 Ω−1cm−1, while for CsBaCl3, it was 4042 Ω−1cm−1. Additionally, moderate peaks in optical conductivity were found at 12 eV for TlBaCl3 and CsBaCl3, with values of 3527 Ω−1cm−1 and 3176 Ω−1cm−1, respectively. These findings imply that both substances exhibit significant optical conductivity with elevated photon energy.

Fig. 7
figure 7

(a) Absorption coefficient of RBaCl3 (R = Tl and Cs) (b) Optical conductivity RBaCl3 (R = Tl and Cs).

Full size image

Extinction coefficient

Figure 8a demonstrates the extinction co-efficient k(ω) spectrum of TlBaCl3 and CsBaCl3 perovskite, which shows that between 0 and 5 eV and 0–7 eV photon energy, zero extinction coefficient is observed, respectively. The extinction coefficient increases with the increase in photon energy, but a decrease in extinction coefficient is observed at very high photon energy. Due to the high extinction coefficient k(ω) value, these films are opaque in the shorter wavelength.

This parameter controls the amount of light lost per unit volume due to scattering and absorption. Interference concerns give the curve a wavy appearance at longer wavelengths. TlBaCl3 and CsBaCl3 exhibit opacity at reduced incident photon energies, while longer wavelengths exhibit an interference phenomenon.

Reflectivity R(ω)

The estimated reflectivity R(ω) between the energy range of 0 eV to 14 eV is shown in Fig. 8(b). The reflectivity of TlBaCl3 and CsBaCl3 both increases as they receive more photon energy, reaching a peak of 0.4 at 8.9 eV for TlBaCl3 and 0.5 at around 13.6 eV for CsBaCl3. At 1.6 eV, the zero-frequency reflectance R(ω) for TlBaCl3 is 0.03, and for CsBaCl3 it is 0.01. These materials have a very low reflectivity at specific energies, which makes them transparent to incident photons in the band gap region. These compounds may have applications in lens manufacturing due to their low-energy transparency.

Fig. 8
figure 8

(a) Extension coefficient of RBaCl3 (R = Tl and Cs) (b) Reflectivity of RBaCl3 (R = Tl and Cs) as a function of photon energy.

Full size image

Refractive index

Refractive index n(ω) is one of the significant properties to study the optical and photonic application of materials. Figure 9 shows the refractive index results, and to determine this property, Eq. (5) was used. The refractive index spectra closely follow the real part of the dielectric function ε1(ω). It finds that TlBaCl3 and CsBaCl3 have a zero-energy refractive index, n(0), of 1.4 and 1.3, respectively. The plots exhibit peaks at 8.3 eV for TlBaCl3 and CsBaCl3, respectively, with values of 2.3 and 2.0. TlBaCl3 at 5.8 eV (2.0) and CsBaCl3 at 11.5 eV (1.3) are also shown to have minor peaks. These findings demonstrate the optical uses of CsBaCl3 and TlBaCl3.

Fig. 9
figure 9

Refractive Index of RBaCl3 (R = Tl and Cs).

Full size image

Energy loss function

The energy loss function (ELF) is an important measure that quantifies the energy dissipated by electrons when they interact with a substance’s electrons or crystal structure. The distinct ELF spectra of TlBaCl3 and CsBaCl3 show different energy loss behaviors (Fig. 10). The energy loss function (ELF) determined for TlBaCl3 and CsBaCl3 indicates 0% energy loss over the photon energy regions of 5.5 eV and 7.5 eV, respectively. The successive two peaks for TlBaCl3 comprise a small peak at 6.8 eV, a maximum peak of 0.7 at 9.8 eV, and a most substantial peak of 0.9 at 10.4 eV for CsBaCl3. This implies that CsBaCl3 has a more significant time delay in electronic polarization than TlBaCl3 when interacting with light. The degree of electronic polarization depends on the constituent atoms’ size.

Fig. 10
figure 10

Energy loss function (ELF) of RBaCl3 (R = Tl and Cs).

Full size image

Elastic properties

Elasticity was carried out on RBaCl3 (R = Tl and Cs), ranked according to calculated second-order elastic stiffness constants, C11, C12, and C44, which characterize the materials’ behaviors under external mechanical stress46. The C constants form an essential basis for the determination of mechanical instability and mechanical elasticity of the material. As presented in Table 2, the elastic constants of TlBaCl3 are C₁₁ = 115.41 GPa, C₁₂ = 63.22 GPa, and C₄₄ = 47.29 GPa. In comparison, CsBaCl3 exhibits higher values, with C₁₁ = 211.21 GPa, C₁₂ = 97.33 GPa, and C₄₄ = 77.23 GPa. These differences suggest that CsBaCl3 is intrinsically stiffer and resistant to deformation by the application of mechanical stress.

The bulk modulus (B) quantifies the resistance offered by a material against uniform compression47. TlBaCl3 has a bulk modulus of 21.32 GPa, while CsBaCl3 has a significantly higher value of 22.23 GPa. This indicates that CsBaCl3 is less compressible and possesses stronger interatomic bonding.

The shear modulus G quantifies resistance against changes in shape when volume remains constant and is calculated next using the Voigt (Gv) and Reuss approximations (GR), followed by Hill’s mean (GH), which yields the most reliable estimate through averaging the Voigt and Reuss values. For TlBaCl3, shear moduli were Gv=38.99GPa, GR=35.52GPa, GH=37.26GPa, whereas for CsBaCl3, they are more than higher at Gv=69.07GPa, GR=65.00GPa, GH=67.04GPa. Again, this confirms that CsBaCl3 is more resistant to shear deformation and mechanically strong.

Young’s modulus (E), or stiffness of the material under uniaxial stress: E = 96.89 GPa for TlBaCl3, whereas CsBaCl3 shows E = 172.64 GPa. Thus, TsBaCl3 is much less stiff.

The Poisson’s ratio (ν) tells about the ductility and bonding characteristics of the materials in consideration. A value of 0.25 is typical for covalent materials, while the values almost reaching 0.33 would hint toward ionic character. Both TlBaCl3 and CsBaCl3 showed a Poisson’s ratio of 0.30, suggesting moderate ductility and substantially ionic character of bonding.

The elastic anisotropy factor (A) expresses the extent of directional dependence in elastic properties. A value of 1 represents isotropic elasticity. For TlBaCl3, A = 1.81, and for CsBaCl3, A = 1.36. Both materials exhibit elastic anisotropy, but it is more pronounced in TlBaCl3, which may play a role in its mechanical behavior under non-uniform stress distributions.

Pugh’s ratio (B/G), the ratio of bulk modulus to shear modulus48, is widely accepted for predicting ductile or brittle behavior for a material and would find validation for a critical value of 1.75 separating ductility (B/G > 1.75) from brittleness (B/G < 1.75). TlBaCl3 shows a B/G ratio of 2.16, while CsBaCl3 shows 2.02, thus stating that both materials would be predicted to be ductile, with TlBaCl3 being a little more ductile, as shown in Table 2.

Both RBaCl3 (R = Tl and Cs) are thus mechanically stable, ductile materials having anisotropic elastic behavior. Owing to higher elastic constants, CsBaCl3 has greater mechanical strength and stiffness, rendering it more suitable for applications needing structural rigidity. On the contrary, TlBaCl3 shows slightly greater anisotropy and ductility, which may influence its performance under complex loading conditions.

Table 2 Elastic properties of RBaCl3 (R = Tl and Cs).
Full size table

In terms of anisotropic mechanical behavior, CsBaCl3 is represented in 3D or 2D for its Young modulus, shear modulus and Poisson’s ratio (Fig. 11). Young’s modulus 3D surface tends to nearly a spherical shape, whereas the 2D plot in the XY plane shows a symmetrical and highly circular profile. This implies that the stiffness of CsBaCl3 does not depend much on direction, thus confirming its nearly isotropic nature regarding uniaxial deformation resistance. While shear modulus is more direction-dependent, it still indicates moderate anisotropy in measurement. 3D shear surface appears slightly distorted, with 2D projection deviating modestly from circular symmetry, indicating some variation in direction regarding the material ability to resist shear stress but still within the low anisotropy bounds. In comparison, Poisson’s ratio is the most anisotropic of all three properties. Here, a 3D surface is manifestly more irregular, while the 2D plot is more intricate in contour, denoting that significant directional dependency is involved in lateral strain response under longitudinal loading. Thus, such visualizations present accord with the already-considered quantitative elastic analysis, which asserts that CsBaCl3 is elastically stable and exhibits predominant isototropic mechanical behavior, especially in stiffness, making it advantageous for applications requiring a uniform mechanical response in all directions.

Fig. 11
figure 11

3D and 2D representations of the elastic properties of CsBaCl3: (a) 3D and (b) 2D projections of Young’s modulus, showing moderate anisotropy with a four-lobed pattern in the XY plane; (c) 3D and (d) 2D projections of shear modulus, indicating significant directional variation and higher anisotropy; (e) 3D and (f) 2D projections of Poisson’s ratio, displaying strong anisotropy with complex lobed structures.

Full size image

Figure 12 visualizes the elastic anisotropy of TlBaCl3 with 3D and 2D representations of Young’s modulus, shear modulus, and Poisson’s ratio. These directional plots help understand their variation in mechanical properties with respect to crystallographic direction and throw some light on the elastic behavior of TlBaCl3.

The 3D plot of Young’s modulus (a) shows a considerably less spherical and much square shape as against CsBaCl3, while the 2D projection in the XY plane (b) reveals a four-lobed contour suggesting moderate anisotropy in stiffness. This implies that TlBaCl3 is less uniaxial than triaxial compliant under deformation, as it does not respond equally in all crystallographic orientations, and that resistance in uniaxial deformation is more dependent on the direction.

In (c), the 3D surface for shear modulus looks distorted, while the corresponding 2D polar plot in (d) indicates clear deviation from circular symmetry forming a cloverleaf. This specifies a more prominent anisotropy in shear behavior, which would simply mean the material resists the shear stress differently along the various directions. Strong dependency on direction implies less uniform distribution of internal stresses under mechanical loads.

The surfaces (e and f) corresponding to Poisson’s ratio exhibit a still more complex and irregular idol out of the three. The 3D model displays several lobes and variations whereas the 2D diagram in (f) shows a highly anisotropic nature with deep lobes and various values with regard to different positions. This, however, indicates a highly directional dependence in the lateral expansion response when the material is subjected to longitudinal stress.

All this visualizes the truth that TlBaCl3 is more elastic than CsBaCl3, particularly in regards to shear and Poisson’s responses. Although remaining elastically stable and mechanically ductile, the fact that TlBaCl3 is rather an anisotropic solid means that its mechanical performance is more direction-dependent and might affect its structural reliability under multi-axial stress environments when applied as usual.

Fig. 12
figure 12

3D and 2D representations of the elastic properties of TlBaCl3: (a) 3D and (b) 2D projections of Young’s modulus, showing moderate anisotropy with a four-lobed pattern in the XY plane; (c) 3D and (d) 2D projections of shear modulus, indicating significant directional variation and higher anisotropy; (e) 3D and (f) 2D projections of Poisson’s ratio, displaying strong anisotropy with complex lobed structures.

Full size image

Conclusion

This study investigates the structural, electrical, optical, and elastic characteristics of the cubic phase of ternary RBaCl3 (R = Tl and Cs) chloroperovskites. Both compounds are structurally and synthetically stable, as supported by Goldschmidt tolerance factor calculations. Electronic structure analysis reveals that TlBaCl3 and CsBaCl3 are indirect band gap insulators, with wide band gaps of 5.51 eV and 7.14 eV, respectively. The mechanical analysis confirms the elastic stability of both materials. TlBaCl3 exhibits greater ductility and slightly higher elastic anisotropy, while CsBaCl3 is stiffer and mechanically more isotropic. These differences suggest that TlBaCl3 may be better suited for applications requiring flexibility, whereas CsBaCl3 offers enhanced mechanical rigidity. Optical property evaluation indicates strong optical activity in the ultraviolet (UV) region, within the photon energy range of 0 to 14 eV. This highlights the potential of both compounds as scintillating materials for use in radiation detection, medical imaging, and high-energy physics. Their responsiveness to high-energy photons such as X-rays and gamma rays further supports their suitability for these applications. In last, both RBaCl3 (R = Tl and Cs) exhibit desirable structural, mechanical, and optical characteristics, with specific advantages that make them promising candidates for advanced optoelectronic and scintillation technologies.