Sustainable machining and optimization of machining parameters utilizing different dielectrics in EDM machining of Waspaloy

Abstract

This study investigates the influence of various dielectric fluids on the performance of Electric Discharge Machining (EDM) in machining Waspaloy, a corrosion-resistant superalloy known for its high hardness and enhanced corrosion resistance. The purpose of this work is to fill the knowledge gap about the machining of Waspaloy using different dielectric fluids by using a Copper-5Graphite (CuGr5) composite tools. Experiments were conducted using a EDM machine with copper graphite composite electrodes and five distinct dielectric fluids, including hydrocarbon oil, kerosene, sunflower oil, used motor oil, and groundnut oil. The effects of key process parameters such as current, voltage, pulse on time, pulse off time, and gap distance on Material Removal Rate (MRR) and Surface Roughness (Ra) were evaluated. Dielectric fluid properties, including viscosity, density, thermal conductivity, and dielectric strength, were comprehensively characterized. Results revealed that MRR increased with current and pulse-on time up to a threshold, beyond which thermal damage reduced efficiency. Sunflower oil demonstrated the most favorable performance, achieving an MRR of up to 0.570 mm³/min and Ra as low as 1.012 μm, attributed to its high dielectric strength (40 kVA), moderate viscosity, and superior thermal conductivity. In contrast, kerosene and hydrocarbon oil, while effective in debris flushing, resulted in inconsistent spark stability and increased surface roughness at higher energy settings due to lower dielectric strength and flash points. Used motor oil and groundnut oil, though sustainable, exhibited higher surface roughness and limited MRR under elevated parameter settings owing to their higher viscosity and lower heat dissipation capabilities. A novel predictive equation for MRR and Ra, integrating dielectric fluid properties and machining parameters, was developed to enhance process optimization. Surface morphology analysis using SEM revealed characteristic features such as craters, recast layers, microcracks, and resolidified debris, highlighting the interplay between thermal, electrical, and mechanical effects during EDM. This research promotes sustainable manufacturing by assessing bio-based and waste-derived dielectric fluids as environmentally responsible alternatives to conventional EDM oil.

Introduction

Waspaloy, a corrosion-resistant superalloy, has widely used in chemical processing and marine firms due to its exceptional resistance to oxidation, stress, and pitting corrosion making it suitable for heat exchangers, pressure vessels, and gas turbines. In conventional machining. Hastelloy possess machining difficulties due to its low thermal conductivity combined with high work hardening tendency along with the abrasive nature of its carbide phases¹. The tool wear becomes extreme because of its characteristics which raise cutting temperature and generate poor chip evacuation while worsening surface quality particularly during traditional machining process. The process of maintaining high quality dimensional accuracy and surface finish becomes much harder for complex designs and stringent tolerance levels. Electric Discharge Machining (EDM), an ideal substitution when facing such situations. The non-contact thermal process EDM utilizes controlled electrical discharges which separate material between an electrode and submerged conductive workpiece maintained within dielectric fluid². NO direct mechanical contact during processing enables the removal of tool wear and cutting force concerns. Because of its ability to machine Waspaloy alloys without regard for material characteristics EDM stands as the optimal process for making precise components.

In EDM machining takes place through melting and vaporization, of its machining performances were controlled by the process parameters current, pulse on time, voltage, gap distance and pulse off time^3,4. Higher currents result in the increased Material Removal Rate (MRR) due to higher energy discharges, at the expense of higher Tool Wear Rate (TWR) and Surface Roughness (R_a)⁵. Pulse-on time (T_on), impacts the heat intensity and the volume of material removed, with prolonged durations leading to deeper craters and rougher surfaces. Pulse-off time (T_off), impacts flushing debris, influences surface integrity, with inadequate durations leading to instability and arcing⁶. The gap voltage determines the spark intensity and machining stability, with optimal voltages yielding uniform discharge distribution. Tool material plays a pivotal role, as higher conductivity electrodes like copper or composites significantly improve energy transfer efficiency⁷.

The choice of dielectric fluid has influence on spark stability, debris flushing, and thermal conductivity which impacts the EDM performance. Dielectric fluids with higher density facilitate better flushing of debris, while those with low specific heat distribute heat more uniformly, enhancing machining efficiency⁸. Hydro carbon oils (HCO), a widely used dielectric fluid has limitations of lower thermal conductivity and environmental concerns due to their non-biodegradability whereas kerosene offers high performance for machining complex geometries, though its low flash point⁹. Vegetable-based oils such as sunflower oil and groundnut oil are gaining attention for their biodegradable and non-toxic nature, their superior thermal stability, higher flash points and enhanced dielectric strength, enhances machining efficiency and surface finish compared to conventional fluids. Used motor oil and used engine oil, were investigated for its economical and sustainable alternatives¹⁰. These oils retain dielectric properties as well as generates wealth from waste, although their higher viscosity hinder debris removal and reduces MRR¹¹. Machining Inconel 718 under various dielectric media revealed that used sunflower oil effectively facilitates spark generation and reduces machining cycle time, comparable to conventional EDM oils^12,13. AISI D2 steel with copper tungsten electrodes, utilizing Al₂O₃ powder mixed in sunflower oil as a dielectric fluid, indicated that vegetable oils could serve as effective alternatives to traditional dielectric fluids¹⁴. Dong et al. (2019) reported that a 34% increase in MRR and recast layer free surface with use of the nanoemulsion dielectric implies that it will be a transformal material in EDM both in the roughing and finishing dies operations. Altered plasma channel dynamics expand the critical discharge gap and influence crater morphology from the action of the nanodroplets. Canola oil based W/O emulsion was introduced as dielectric medium as it is biodegradable with thermal characteristic that is optimal for sustainable machining. Kumar et al. (2024) modeled and reduced the surface cracks using the nanoemulsions fabricated from jatropha oil.

Despite numerous studies on EDM using various dielectric fluids, a gap remains in the comprehensive evaluation of alternative, sustainable dielectric fluids and their performance in machining high-strength alloys such as Waspaloy¹⁵. Since these alternatives offers non-toxic, and biodegradable alternatives to petroleum dielectrics, these substitutes align with the sustainable production concept. Furthermore, it is sustainable to repurpose used motor oil as a dielectric fluid, as the circular economy and waste valorisation principles works to reduce the environmental impact of oil disposals and improve resource conservation. Research on EDM processing of nickel-based superalloys including Inconel 718, Hastelloy, and Nimonic exists but remains scarce for Waspaloy and its reaction to dielectric fluids. Typical dielectrics such as kerosene along with hydrocarbon oils served previous works yet achieved only moderate material removal at the cost of impaired surface quality due to limited dielectric strength and inadequate flushing. There is limited research that studies multiple dielectrics including sustainable or bio-based fluids in the Waspaloy context. Research on EDM process parameters optimization fails to account for the fundamental role of dielectric fluid properties like viscosity, thermal conductivity and dielectric strength that maintain stable sparks and effectively remove debris and control heat damage. Previous research failed to create predictive models which unite EDM parameters with fluid characteristics for predicting both MRR and Ra for Waspaloy. Studies that examined dielectric behavior and sustainability aspects through SEM surface characterization have been absent from previous research that analyzed formation of craters. The EDM process of Waspaloy with vegetable-based or waste-derived dielectrics has not been extensively explored despite their environmental benefits. A novel equation was developed to predict MRR and Surface Roughness (Ra) as a function of dielectric fluid type, process parameters, and tool material.

Materials and methods

The study investigated the impact of distinct dielectric fluids on the EDM machining performance of Waspaloy which chemical composition was depicted in the Table 1.

Table 1 Chemical composition of waspaloy.

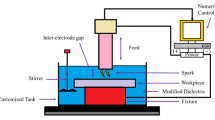
The experiments were performed on a CNC EDM machine of Make: Electronica and Model: Smart 50. The EDM machine (Electronica Smart 50) was customized to facilitate dielectric fluid interchangeability and tool holding stability, ensuring repeatable experimental conditions across all fluid types. The Waspaloy workpiece was prepared to uniform dimensions of 15 × 15 × 10mm³. Copper-Graphite electrodes were selected as tool material based on our previous research findings¹⁶, enabling efficient spark generation and transfer of discharge energy. The experimental setup and machined samples were depicted in the Fig. 1. The EDM parameters were varied for 5 levels and design of experiments were framed utilizing the Taguchi L25 orthogonal array as depicted in the Table 2. Experimental parameters and its level were selected based on the preliminary studies and previous research work.

Table 2 Experimental parameters and its level.

The hydrocarbon oil, kerosene, sunflower oil, used motor oil, and groundnut oil were selected as a dielectric medium. The experimental measurements for density, flash point, kinematic viscosity, thermal conductivity and dielectric strength were documented in Table 3 under specific conditions for EDM dielectric fluids. A Brookfield DV2T viscometer performed room temperature steady shear measurements to measure flow characteristics of samples for kinematic viscosity testing. The pycnometer set at 25 °C served to measure the fluid densities for all samples after it received calibration procedures to reduce thermal expansion effects on the measurements. The thermal conductivity measurements operated with a TA Instruments Q2000 thermal analyzer by applying a heat flux differential method using calibrated reference standards. The Megger OTS60AF/2 dielectric breakdown voltage tester conducted the measurement through a 2.5 mm electrode separation at a constant voltage ramp of 2 kV/s until it reached breakdown.

Table 3 Properties of the distinct dielectric fluid utilized for study.

Fig. 1

Experimentation of Waspaloy alloy (A) Electric Discharge Machining (B) Experimental setup (C) Experimented Waspaloy samples.

The weigh balance machine of accuracy 0.01 mg recorded the heft changes between the workpiece samples before and after the machining to compute MRR=∆W¹⁶. Surface roughness (Ra) was measured using a contact-type surface profilometer (Make: Mitutoyo, Model: SJ-210). The mean result from several surface readings at multiple spots across the machined surface was recorded as Ra. The machined surface morphology was analysed using the Scanning Electron Microscope (SEM). The experimental results were depicted in the Table 4.

Table 4 Experimental runs and its results.

Results and discussion

Dielectric fluid has capability to maintain electrical stability under voltage determines its breakdown point which in turn controls spark performance and electrical discharging output. Fluid viscosity determines debris flushing capability since high viscosity reduces the ability to clear debris which results in unstable arcs and surface deterioration. A dielectric medium that performs well in thermal conductivity helps move heat away from the spark area which benefits recast layer reduction while creating superior surface finishes. Knowledge of these connections among dielectric properties lets industry make optimal selections for dielectrics to achieve better cutting rates and surface finishes without damaging tools or altering material properties. The characteristics of various dielectric fluids, including their impact on surface morphology and machining performance, were discussed below. The productivity measure at the machine tool level based on the machining process involves MRR, which is defined as the volume of material removed from the work piece per unit time during the machining process. MRR of higher numbers mean better machining but at the cost of surface quality. Ra in micrometers (microns, µm) is an average deviation between the surface profile and the mean line representing the critical dimension accuracy and surface finish. Smoothing surfaces are desirable in precision applications, therefore, lower Ra values correspond. The Recast Layer Thickness is also an important term that represents the depth of the resolidified layer deposited on the workpiece surface as a consequence of the rapid melting and cooling of the workpiece surface during electrical discharges. In this layer, microcracks, voids and nonuniform grain structures reside, which can alter fatigue life or surface integrity.

Material removal rate

Influence of dielectric fluid type on material removal rate

When hydrocarbon oil is used as a dielectric medium, mean MRR of 0.384 mm³/min was observed as shown in Fig. 2. Higher current levels lead to more substantial energy release per discharge pulse, which in turn increases the amount of material removed during each pulse¹⁷. Hydrocarbon oil, characterized by its moderate dielectric strength of 30 kVA, low density (0.83 g/cm³), and relatively low thermal conductivity (0.14 W/mK), provides a stable dielectric environment that supports effective material removal during EDM. Its lower thermal conductivity compared to other oils, which could potentially affect heat dissipation, hydrocarbon oil maintains good dielectric properties, making it suitable for applications requiring fine finishes. While the MRR increases with current, a slight drop at 40 A compared to 32 A can be attributed to factors, excessive heat generation and potential ionization of the dielectric fluid.

Fig. 2

Influence of distinct process parameters on MRR of Waspaloy.

When kerosene is used as a dielectric medium, mean MRR of 0.202 mm³/min was observed attributed to its dielectric strength of 14 kVA and kinematic viscosity of 2.2 mm²/s. Despite the low dielectric strength compared to other oils, kerosene’s relatively low viscosity and clear color make it a common choice. The dielectric strength of a fluid is indicative of its ability to withstand electrical stress without breaking down, and a lower strength implies that kerosene does not sustain higher discharge energies as effectively as other dielectric fluids. Consequently, the observed decrease in MRR at higher currents was attributed to the limitations in kerosene’s ability to handle increased discharge energy efficiently, resulting in instability.

When Sunflower oil is used as a dielectric medium, mean MRR of 0.333 mm³/min was observed. Higher discharge currents facilitate greater energy discharges, thereby causing more substantial erosion of the workpiece surface with each pulse. Sunflower oil, with a density of 0.92 g/cm³ and a high flash point of 230 °C, sunflower oil is not only stable but also safe for high-temperature operations, reducing the risk of fire hazards. Its kinematic viscosity of 45 mm²/s ensures adequate lubrication and cooling, which are essential for maintaining tool integrity and workpiece quality during the EDM process. Additionally, the thermal conductivity of 0.16 W/mK aids in effective heat dissipation, further enhancing the machining performance. The dielectric strength of sunflower oil, recorded at 40 kVA, indicates its ability to withstand high voltages without breaking down, thus ensuring consistent and reliable EDM operations¹⁸. The biodegradable and non-toxic nature of sunflower oil also makes it an environmentally friendly alternative to conventional dielectric fluids, aligning with sustainable manufacturing practices. At lower currents of 8 and 16 A, the MRRs were relatively modest at 0.122 and 0.157 mm³/min. As the current increased to 24 and 32 A, there was a substantial rise in MRR to 0.427 and 0.570 mm³/min, however, at the highest current of 40 A, the MRR slightly decreased to 0.390 mm³/min, due to the excessive heat generation leads to thermal damage.

When Used Motor Oil is used as a dielectric medium, mean MRR of 0.273 mm³/min was observed. The initial increase in MRR from 8 A to 16 A confirms this effect, as the higher current facilitated more efficient material removal. The subsequent decrease in MRR at 24 A and 32 A could be attributed to the unique properties of used motor oil. The high kinematic viscosity of 80 mm²/s might impede the effective flushing of debris from the machining gap, leading to inefficient sparking and lower MRR at higher currents. The thermal conductivity of 0.13 W/mK leads to limited heat dissipation, results in localized overheating. At 40 A, the MRR increased to 0.258 mm³/min, suggesting that beyond a certain threshold, the increased current compensates for the drawbacks posed by the high viscosity and thermal conductivity.

When Groundnut Oil was used as a dielectric medium, mean MRR of 0.255 mm³/min was observed. The increase in MRR at higher discharge currents is indicative of the enhanced material removal efficiency the intensified thermal and electrical energy being applied to the workpiece. At 8 A, the MRR was relatively low at 0.148 mm³/min, reflecting the moderate energy discharge insufficient to remove substantial material. As the current increased to 16 A and 24 A, the MRR values showed a variable pattern with MRR of 0.192 mm³/min and 0.111 mm³/min was observed. A marked improvement in MRR was observed at higher currents of 32 A and 40 A, with values of 0.333 mm³/min and 0.490 mm³/min. This significant increase is consistent with the hypothesis that higher currents facilitate greater material removal the higher energy pulses causing more intense localized melting and vaporization of the workpiece material. The increase from 32 A to 40 A represents a substantial jump in MRR, highlighting the efficacy of groundnut oil in sustaining higher energy discharges without compromising its dielectric properties or stability.

Influence of gap distance on material removal rate

The MRR as a function of gap distance suggests that the interplay between the gap distance and the stability of the electrical discharge is pivotal. At the smallest gap distance of 1 mm, the MRR is 0.137 mm³/min. This relatively lower MRR can be attributed to the potential for short circuits which hampers effective energy transfer. As the gap distance increases to 2 mm, the MRR rises significantly to 0.255 mm³/min. It indicates an improvement in the stability and efficiency of the spark. The peak MRR observed at a gap distance of 4 mm, where the MRR reaches 0.747 mm³/min owing to the efficient energy transfer. When the gap distance further increased to 5 mm, the MRR drops to 0.181 mm³/min attributed to the less effective discharges. The hydrocarbon oil’s properties provide a stable dielectric environment that supports effective sparking. The low viscosity of kerosene facilitates efficient flushing of debris from the machining gap, ensuring a clean and stable discharge environment which is crucial for maintaining consistent MRR across different gap distances¹⁹. At a 1 mm gap distance, the MRR is relatively high at 0.120 mm³/min the stable and effective spark discharge facilitated by the small gap, which allows efficient energy transfer. However, at a 2 mm gap distance, the MRR drops significantly to 0.059 mm³/min. Interestingly, at a 3 mm gap distance, the MRR increases substantially to 0.258 mm³/min, this trend continues at a 4 mm gap distance, where the MRR remains relatively high at 0.200 mm³/min. At a 5 mm gap distance, the MRR reaches its peak at 0.376 mm³/min. This increase might seem counterintuitive; within this specific setup, the larger gap enhances the stability of the discharge process without significantly compromising the efficiency of energy transfer. The properties of kerosene, especially its low viscosity and adequate dielectric strength, contribute to maintaining this stability, allowing effective material removal at a larger gap distance.

The gap distance plays a critical role in the EDM process as it affects the stability and efficiency of the electrical discharge. A smaller gap distance resulted in a higher MRR because the spark between the tool and the workpiece is more stable and effective, facilitating intense energy transfer. In this study, the highest MRR at the smallest gap distance (1 mm) supports this observation. However, maintaining too small a gap can also lead to short circuits and process instability, which can adversely affect machining efficiency and surface quality. This was observed as the gap distance increased to 2 mm, where a slight decrease in MRR was noted. At a gap distance of 5 mm, the MRR showed an increase to 0.427 mm³/min compared to the 4 mm gap owing to the through dielectric flushing. The dielectric properties of sunflower oil, including its high flash point of 230 °C, moderate density of 0.92 g/cm³, and high dielectric strength of 40 kVA, make it a suitable medium for EDM. These properties contribute to its ability to sustain stable discharges and efficient cooling, which are crucial for achieving high MRR and good surface finish. The relatively high kinematic viscosity of 45 mm²/s and thermal conductivity of 0.16 W/mK further aid in the stability and consistency of the EDM process by ensuring adequate lubrication and heat dissipation. The relatively high viscosity of used motor oil suggested a slower rate of fluid flow and more stable discharge conditions at larger gap distances²⁰. Its moderate dielectric strength ensures adequate insulation properties to prevent premature discharge while allowing efficient spark generation. The observed trend in MRR indicates that at a gap distance of 1 mm, the MRR was relatively high at 0.235 mm³/min. At the gap distance of 4 mm and 5 mm, the MRR increased to 0.311 mm³/min and 0.411 mm³/min respectively. The higher viscosity and thermal conductivity of the used motor oil may have contributed to maintaining discharge stability, thereby enhancing the overall MRR. The high flash point of 210 °C also showed that the used motor oil can withstand higher temperatures without degradation, allowing for consistent performance at varying gap distances. Groundnut oil, with the kinematic viscosity of 40 mm²/s and thermal conductivity of 0.17 W/mK provides stability and effective heat dissipation. The dielectric strength of 35 kVA has withstood high voltage without breakdown, which is essential for maintaining the integrity of the spark during EDM. A smaller gap, such as 1 mm, promotes a more stable and effective spark, leading to a relatively high MRR. However, as seen, the smallest gap does not always guarantee the highest MRR, likely process instability and potential short circuits. Conversely, a larger gap can lead to a less efficient energy transfer, resulting in lower MRR.

Influence of pulse-on time on MRR

The initial increase in MRR from 0.137 mm³/min at a 10 µs pulse on time to 0.747 mm³/min at 40 µs can be attributed to the greater energy delivered to the workpiece. This results in increased erosion of the material, thereby enhancing the MRR. The dielectric properties of hydrocarbon oil, particularly its good dielectric strength, allow for efficient spark generation and stabilization, contributing to the effective material removal. the observed drop in MRR to 0.181 mm³/min at a 50 µs pulse on time indicated that the excessively long pulse durations can lead to overheating, results in the thermal damage of tool and the workpiece. This thermal damage can alter the material properties and reduce the efficiency of the machining process. The high flash point of hydrocarbon oil (130 °C) does provide some resistance to thermal damage, yet prolonged exposure to high temperatures hinders the machining quality²¹.

When kerosene was used as a dielectric fluid, initially, as the pulse on time increased from 10 µs to 20 µs, the MRR significantly decreased from 0.376 mm³/min to 0.120 mm³/min. This decrease indicates that the energy delivered during the 20 µs pulse was sub-optimal energy concentration owing to the insufficient cooling. As the pulse on time increased further to 30 µs, the MRR dropped to 0.059 mm³/min, the lowest value suggested that the extended duration allowed excessive heat buildup, causing thermal damage. However, at a pulse on time of 40 µs, the MRR improved to 0.256 mm³/min, indicated an efficient energy delivery. With a pulse on time of 50 µs, the MRR slightly decreased to 0.200 mm³/min, owing to the overheating.

Under Sunflower Oil dielectric medium, the MRR increases from 0.157 mm³/min at 10 µs to a peak of 0.570 mm³/min at 30 µs. beyond the 30 µs pulse on time, a notable decrease in MRR was observed. This decline was attributed to excessive heat buildup, which can affect the workpiece and the dielectric fluid’s effectiveness. The thermal conductivity of Sunflower Oil, at 0.16 W/mK, plays a role in heat dissipation during the EDM process. Despite its capability to handle moderate thermal loads, the increase in temperature at extended pulse on times leads to decreased efficiency, hence lower MRR. Similarly, it used motor oil and ground nut oil, when the pulse on time was extended beyond 30 µs, a noticeable decrease in MRR was observed owing to the overheating. The used motor oil’s thermal conductivity of 0.13 W/mK, suggested that it has limited capacity to dissipate heat efficiently during extended pulse durations. As the pulse on time increases, more energy is delivered to the workpiece, which enhances the increased thermal and mechanical impact on the material. This trend is evident from the MRR values, where an increase in pulse on time from 10 to 30 µs shows a significant rise in MRR from 0.111 to 0.490 mm³/min.

Influence of pulse-off time on MRR

As the pulse off time decreases, the frequency of discharges increases, which generally results in a higher MRR. Under Hydrocarbon Oil dielectric medium MRR improves significantly from 0.137 mm³/min at 2 µs to a peak of 0.747 mm³/min at 8 µs which was due to the more frequent discharges and improved energy delivery to the workpiece. However, the observed decrease in MRR to 0.181 mm³/min at 10 µs indicates that an excessive reduction in pulse off time can lead to improper flushing of debris and less time for cooling the electrode, which can cause overheating and instability in the machining process. The low thermal conductivity of Hydrocarbon Oil, contribute to heat retention.

Under Kerosene environment, at a pulse off time of 2 µs, an MRR of 0.200 mm³/min was observed, when it increased to 4 µs, the MRR peaks at 0.376 mm³/min, indicating an optimal balance between discharge frequency and adequate debris removal. This peak suggests that at 4 µs, the dielectric medium, Kerosene, provides sufficient time for debris flushing while maintaining a high rate of energy transfer, thus enhancing the MRR. As the pulse off time further increases to 6 µs and 8 µs, the MRR declines to 0.120 mm³/min and 0.05 mm³/min owing to the excessive interval between discharges, leading to a lower frequency of sparks. The longer off times allow for better cooling and debris flushing, but they significantly decrease the overall discharge energy applied per unit time, resulting in diminished MRR. Interestingly, at a pulse off time of 10 µs, the MRR increases again to 0.256 mm³/min. This anomaly was due to the substantial cooling and debris removal, thereby reducing the short-circuiting and enhancing the stability of the EDM process. The thermal conductivity and dielectric strength of Kerosene play crucial roles in this process. With a moderate thermal conductivity of 0.145 W/mK, Kerosene efficiently dissipates heat, preventing excessive thermal damage to the workpiece²².

Sunflower oil, characterized by its golden yellow color, peak MRR of 0.570 mm³/min was achieved at a pulse off time of 10 µs. This suggests that a longer pulse off time enhances the MRR by allowing sufficient time for the dielectric fluid to cool the workpiece and flush away debris. Conversely, the lowest MRR of 0.122 mm³/min at 4 µs indicates that an overly short off time results in insufficient debris removal. With a dielectric strength of 25 kVA, used motor oil provides adequate insulation properties to sustain the electric discharges essential for material removal. The MRR results highlight the significant influence of pulse off time on the efficiency of the machining process. A pulse off time of 2 µs yielded the highest MRR of 0.411 mm³/min, demonstrating the potential for increased frequency of discharges. At pulse off times of 8 and 10 µs, the MRR showed a decreasing trend, with values of 0.258 and 0.311 mm³/min, attributed to adequate off time which allows for better cooling and removal of eroded particles, preventing short-circuits. Groundnut oil, at 4 µs, the MRR peaks to 0.490 mm³/min, beyond that, it declined to 0.192 mm³/min and 0.111 mm³/min for 8 and 10 µs respectively owing to the incomplete flushing of debris.

The increase in MRR with rising voltage can be attributed to the enhanced ionization in the discharge gap. Higher voltage levels create a stronger electric field, which facilitates more effective material removal during each discharge²³. This phenomenon aligns with the dielectric strength of hydrocarbon oil, which supports efficient energy transfer and breakdown of the dielectric medium, leading to more substantial and consistent discharges. Consequently, the material removal process becomes more efficient, resulting in higher MRR values. However, beyond the optimal voltage of 100 V, the MRR decreases despite further increases in voltage. This decline was due to the excessive ionization and energy input, which can lead to uncontrolled discharges. The flash point of 130 °C indicates the temperature at which the oil ignites, suggesting that at higher voltages, the heat generated could approach this threshold, causing instability in the machining process. The low kinematic viscosity of 2.5 mm²/s provide inadequate lubrication and cooling at higher voltages.

Kerosene oil, with a low dielectric strength of 14 kVA and a flash point of 50 °C, provides moderate stability and performance in EDM. The low dielectric strength implies that kerosene can support only moderate electric fields before breakdown occurs, making it suitable for less aggressive machining conditions. At 25 V, the MRR was 0.256 mm³/min, showed effective material removal. Increasing the voltage to 50 V resulted in a slight decrease in MRR to 0.200 mm³/min, and the highest MRR of 0.376 mm³/min was observed at 75 V, indicating an optimal voltage for kerosene oil in EDM. At this voltage, the electric field strength in the discharge gap is sufficient to enhance ionization and facilitate efficient material removal²⁴. However, further increasing the voltage to 100 V and 125 V results in reduction of MRR to 0.122 mm³/min and 0.059 mm³/min respectively. The viscosity of 2.2 mm²/s and thermal conductivity of 0.145 W/mK has greater influence on MRR. The low viscosity aids in the efficient flushing of debris from the discharge gap, while the moderate thermal conductivity helps in dissipating heat generated during machining. At higher voltages, the thermal and electrical stresses surpass the cooling and flushing capabilities of kerosene, leading to suboptimal MRR.

The dielectric properties of sunflower oil include a dielectric strength of 40 kVA, which contributes to its efficacy in EDM. The observed trends align with theoretical expectations regarding the influence of voltage on MRR. As voltage increases, the electric field strength within the discharge gap intensifies. This enhancement facilitates improved ionization and enhances the effectiveness of material removal during each discharge event. The higher electric field strength generally promotes a higher MRR, as seen with the increase from 25 V to 50 V. However, further increases in voltage beyond 50 V led to a decrease in MRR, as observed at 75 V, 100 V, and 125 V. This reduction can be attributed to several factors. At elevated voltages, while ionization is more effective, the increased energy can lead to excessive tool wear and surface damage, which in turn impacts the MRR negatively. The high energy discharges can cause more severe thermal effects, contributing to decreased efficiency in material removal and increased tool wear. This shows the importance of optimizing voltage levels to balance effective material removal with tool longevity and surface finish quality.

Similar results were observed in the case of Used motor oil, as the voltage increases from 25 V to 125 V, a peak MRR of 0.411 mm³/min at 100 V, the MRR at 125 V decrease to 0.235 mm³/min. The dielectric strength of the fluid allows it to withstand high electric fields without breakdown, which was essential for effective machining. As the voltage increases, the electric field strength in the discharge gap enhanced, results in the improved ionization of the dielectric fluid. At 25 V, the MRR is highest at 0.490 mm³/min, attributed to the dielectric fluid facilitates the discharge process without excessive ionization. However, as the voltage is increased to 50 V the MRR decreases initially, with the value reaching 0.111 mm³/min at 100 V. This reduction was owing to the increasing energy causing more severe tool wear and potential surface damage, which can detract from the overall effectiveness of the machining process.

Empirical relation of MRR

$\:MRR=\:f($Current, Voltage, Pulse-On Time, Pulse-Off Time, Gap Distance, Dielectric Fluid Properties)

The MRR equation is expressed as depicted in Eq. 1, where k is the proportionality constant, I is the discharge current, V represents the gap voltage, T_on is the pulse-on time, and C_powder denotes the machined debris in the dielectric fluid. The denominator consists of parameters influencing energy dissipation and machining performance, including tool material resistivity (ρ), discharge efficiency (η), fluid density (ρ​), thermal conductivity (λ), specific heat capacity (Cp​) and emissivity (ϵ).

$$\:\text{M}\text{R}\text{R}=k\cdot\frac{I.V.{T}_{on}\cdot{C}_{powder}}{\rho\cdot\eta\cdot{\rho}_{f}\cdot\lambda.{C}_{p}\cdot\epsilon}$$

(1)

The MRR equation was modified based on experimental observations, addressing limitations in the original model. The experimental results revealed that non-linear interactions among various machining parameters and dielectric properties that significantly influence MRR in EDM. The equation was expanded with linear modifiers (α, β, γ, δ, ϵ) to capture the effects of these variables as depicted in the Eq. 2²⁵. These modifiers, determined experimentally, reflect the experimental results of process conditions and MRR on energy transfer, heat dissipation, and vaporization, leading to improved predictive accuracy of MRR. This enhancement ensures the equation aligns closely with observed data.

$$\:\text{M}\text{R}\text{R}\:=k\cdot\frac{I.V.{T}_{on}\:}{{d}_{gap}\cdot\left(1+\alpha\cdot\eta\:\right)\cdot\left(1+\beta\cdot\sigma\:\right)\cdot\left(1+\gamma\cdot\rho\:\right)\cdot\left(1+\:\delta\cdot\lambda\:\right)\cdot(1+\:\epsilon\cdot\epsilon\:)\:}$$

(2)

The Simplified Combined Differential Expression for MRR was derived by combining the partial derivatives of the MRR equation with respect to the five properties as depicted in the Eq. 3. The derivation of this equation is based on experimental results, which influence the MRR in EDM.

$$\begin{aligned}\:&\frac{d\left(\text{M}\text{R}\text{R}\right)}{d\eta\:}+\:\frac{d\left(\text{M}\text{R}\text{R}\right)}{d\sigma\:}+\frac{d\left(\text{M}\text{R}\text{R}\right)}{d\rho\:}+\frac{d\left(\text{M}\text{R}\text{R}\right)}{d\lambda\:}+\frac{d\left(\text{M}\text{R}\text{R}\right)}{d\epsilon\:}\: = \\& \quad \:k\cdot\frac{-I.V.{t}_{on}\cdot\left(\alpha\cdot\frac{1}{{\left(1+\alpha\cdot\eta\:\right)}^{2}}\:\:+\:\beta\cdot\frac{1}{{\left(1+\beta\cdot\sigma\:\right)}^{2}}+\:\gamma\cdot\frac{1}{{\left(1+\gamma\cdot\rho\:\right)}^{2}}+\:\delta\cdot\frac{1}{{\left(1+\delta\cdot\lambda\:\right)}^{2}}+\:\epsilon\cdot\frac{1}{{\left(1+\epsilon\cdot\epsilon\:\right)}^{2}}\right)}{{d}_{gap}\cdot\left(1+\alpha\cdot\eta\:\right)\cdot(1+\beta\cdot\sigma\:)\cdot(1+\gamma\cdot\rho\:)\cdot(1+\:\delta\cdot\lambda\:)\cdot(1+\:\epsilon\cdot\epsilon\:)}\end{aligned}$$

(3)

The individual differentiations were computed to understand the effect of each property independently, considering its influence on the MRR. The initial findings revealed that influence of these factor on impact of MRR, i.e., as the value of any of these parameters increases, the MRR tends to decrease. This inverse relationship emerges because the rate of energy transfer (in terms of heat) to the workpiece was mitigated by higher values of viscosity, conductivity, density and thermal conductivity, making it challenging for the material to be effectively removed.

This expression presents a detailed understanding of the EDM process, as it incorporates influence of each individual factor as well as their interdependencies. The fractional terms (1 + α⋅η), (1 + β⋅σ) and so on act as modifiers that adjust the rate of change in MRR based on the magnitude of each respective parameter as depicted in the Eq. 4. The constants (α, β, γ, δ, ϵ) signify the sensitivity and degree of influence of each process parameter exerts on the overall MRR. Through experimental data, the constants associated with each parameter were calibrated, and it was confirmed that the modified equation effectively aligns with the observed results²⁶.

$$\begin{aligned}\:{C}_{i}\:&=\:k\cdot{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}\cdot \\& \frac{1}{\left(1+\alpha\cdot{\eta\:}_{i}\right)\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\cdot\left(1+\gamma\cdot{\rho\:}_{i}\right)\cdot\:\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\:}\end{aligned}$$

(4)

To solve for the parameters α, β, γ, δ, ϵ, the inverse relationship between the process parameters and MRR was extracted and rearranged for each of the influencing factors. Each parameter was solved explicitly by isolating it on one side of the equation. For instance, by rearranging the initial MRR equation, we were able to express α as depicted in the Eq. 5. The same approach was taken for β, γ, δ, and ϵ. These derivations allowed the experimental results to guide the determination of the values of these parameters, which were empirically fitted based on the observed data.

$$\:\alpha\:=\:\frac{1-\frac{{C}_{i}}{\:k\cdot{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\cdot\left(1+\gamma\cdot{\rho\:}_{i}\right)\cdot\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\:}\:}{{\eta\:}_{i}}$$

(5)

The simplified equation clearly showed that the efficiency of the machining process was inversely related to the combined effects of viscosity, conductivity, density, thermal conductivity, and dielectric strength as shown in Eq. 6. Each parameter’s influence is mitigated by a factor (1 + parameter), signifying that increases in any of these variables generally lead to a decrease in the MRR.

$$\:{MRR}_{i}\:=\:k\cdot\frac{{I}_{i}\cdot{V}_{i}\cdot{T}_{on,\:i}}{\left(\frac{1+\:{\eta\:}_{i}}{{D}_{i}}\cdot\frac{1+\:{\sigma\:}_{i}}{{D}_{i}}\cdot\frac{1+\:{\rho\:}_{i}}{{D}_{i}}\cdot\frac{1+\:{\lambda\:}_{i}}{{D}_{i}}\cdot\frac{1+\:{\epsilon\:}_{i}}{{D}_{i}}\right)}$$

(6)

Current, Voltage and Pulse-On Time were found in the numerator, directly relate to the energy input into the system. Higher values of these parameters lead to higher MRR. The factors (1 + ηi), (1 + σi), (1 + ρi), (1 + λi), and (1+ϵi) collectively capture the influences of dielectric fluid and material properties like viscosity, conductivity, and heat transfer capacity as shown in Eq. 7. These factors reduce the MRR as they essentially represent hindrances or resistances to efficient energy transfer and machining performance. For example, higher viscosity in the dielectric fluid or poor conductivity of the workpiece reduces the efficiency of the electrical discharge process.

$$\:{MRR}_{i}\:=\:k\cdot\frac{{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}}{\left(1+\:{\eta\:}_{i}\right)\cdot\left(1+\:{\sigma\:}_{i}\right)\cdot\left(1+\:{\rho\:}_{i}\right)\cdot\left(1+\:{\lambda\:}_{i}\right)\cdot\left(1+\:{\epsilon\:}_{i}\right)}\cdot{D}_{i}^{5}$$

(7)

The second term introduces the experimental-derived constants α, β, γ, δ, ϵ, representing refined corrections based on the interaction of individual process parameters. The term raised to the power of 5 (Di⁵​) indicates the high degree of sensitivity of MRR to the parameters, emphasizing that small changes in these parameters can significantly impact the outcome. Thus, the modification of the denominator and exponent through these empirical values indicates that the overall process was highly sensitive to the machine settings and the characteristics of the dielectric fluid involved. The last fraction serves as a correction term which was determined experimentally. The resulting term is subtracted from 1, and the whole expression is raised to the power of 5, capturing the cumulative and possibly nonlinear effects of all parameters in the EDM process as depicted in the Eq. 8.

$$\begin{aligned}\:{MRR}_{i}\:&=\:k\cdot\frac{{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}}{\left(1+\:{\eta\:}_{i}\right)\cdot\left(1+\:{\sigma\:}_{i}\right)\cdot\left(1+\:{\rho\:}_{i}\right)\cdot\left(1+\:{\lambda\:}_{i}\right)\cdot\left(1+\:{\epsilon\:}_{i}\right)}\cdot \\& {\left(1-\frac{k\cdot{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}\cdot\left(1+\alpha\cdot{\eta\:}_{i}\right)\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\cdot\left(1+\gamma\cdot{\rho\:}_{i}\right)\cdot\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)}{{C}_{i}}\right)}^{5}\end{aligned}$$

(8)

Surface roughness (Ra)

Influence of dielectric properties on surface roughness

When Hydrocarbon Oil is used as a dielectric medium, mean Surface Roughness (Ra) of 1.840 μm was observed. At a current of 8 A, the Ra measured was 1.418 μm, which reflects the modest discharge energy associated with lower currents as shown in Fig. 3. This relatively smooth surface finish can be attributed to the lower thermal energy and reduced crater size created during machining, leading to finer surface. As the current increased to 16 A, the Ra increases to 2.661 μm. Higher current levels enhance the energy of each discharge, which contributes to the formation of larger and deeper craters, reduce the surface quality²⁷. At 24 A, the Ra was recorded at 1.826 μm, there is an improvement compared to the 16 A but it remains higher than the 8 A. For the maximum level of 40 A, interestingly Ra decreased to 1.312 μm attributed to the changes in the material removal dynamics at high energy levels.

Fig. 3

Influence of distinct process parameters on Ra of Waspaloy.

Kerosene, with relatively low dielectric strength compared to other dielectric fluids implies that it handles lower discharge energies efficiently, whereas higher currents result in increase of Ra. The higher current levels enhance the discharge energy, which in turn generates deeper and larger craters on the workpiece surface. The increased thermal impact leads to greater MRR, as evidenced by the changes in MRR with current. At lower currents (8 A and 16 A), the discharge energy is relatively modest, resulting in finer craters and smoother surface finishes. The Ra values at these currents are lower, indicated that the machining process was controlled and leads to a higher quality surface finish. Specifically, the Ra measured at 8 A and 16 A are 1.414 μm and 2.445 μm, showed a moderate increment with the current. As the current increases to 40 A and beyond, the effect of higher discharge energy becomes evident with a Ra of 5.967 μm.

Under sunflower oil dielectric medium, at a current of 8 A, the Ra of 1.157 μm was achieved. The lower energy input ensures a smoother surface finish the reduced thermal impact on the work piece. As the current increased to 16 A, the Ra marginally increased to 1.197 μm. When the current was further increased to 24 A, the Ra increased to 1.899 μm. This notable increase in roughness can be attributed to the increment in discharge energy at higher current at 40 A, the Ra improved to 1.012 μm, decrease in roughness, despite the high current, was due to effectively mitigates excessive thermal impact, allowing for finer crater formation and improved surface finish.

When used motor oil was used the elevated current continues to increase discharge energy, producing larger craters but with a slightly better surface finish owing to its enhanced dielectric break down. When used groundnut oil is used as a dielectric medium, mean Ra of 4.111 μm was observed. At a lower current of 8 A, the dielectric medium exhibited a relatively fine surface finish with a roughness of 2.828 μm, reflecting the finer craters and reduced thermal impact on the workpiece. As the current increased to 16 A, Ra rose to 4.714 μm, indicating deeper and more pronounced craters increased discharge energy. Further increasing the current to 24 A resulted in a Ra of 2.198 μm, a notable decrease compared to 16 A, suggesting that at this current level, the discharge energy is optimized for achieving finer surface finishes. However, as the current continued to rise to 32 A and 40 A, Ra increased significantly to 4.186 μm and 6.629 μm. The elevated current levels produce larger craters and more extensive thermal effects, leading to greater surface irregularities²⁸.

Hydrocarbon oil, with low kinematic viscosity (2.5 mm²/s) facilitates the efficient debris removal, maintaining a clean machining zone and preventing arcing. The moderate flash point (130 °C) ensured thermal stability during the EDM process, enabling controlled spark generation and uniform energy transfer. As a result, at smaller gap distances, the MRR was consistent, and Ra was minimized due to the stability in discharge. However, at larger gap distances, the moderate dielectric strength proved insufficient to maintain controlled energy transfer, leading to a slight increase in surface irregularities and Ra. The properties of kerosene, with its low viscosity (2.2 mm²/s) promoted exceptional flushing, preventing debris accumulation, which is critical for maintaining stable discharges. Despite its lower flash point (50 °C), the fluid provided sufficient thermal control at smaller gap distances. At these smaller gaps, kerosene demonstrated stable and concentrated energy transfer, leading to higher MRR and finer surface finishes. However, as the gap distance increased, the low dielectric strength provides unstable discharges resulted in increased Ra values due to arc formation and irregular crater features, highlighted that kerosene is most effective at smaller gap distances where discharge stability can be maintained.

Sunflower oil’s superior dielectric strength of 40 kVA and its relatively high thermal conductivity of 0.16 W/mK proffers stable discharges and efficient energy transfer during machining²⁹. The high viscosity (45 mm²/s), impeded debris flushing, requiring optimal gap conditions to ensure performance. At smaller gap distances (1 mm and 2 mm), the dielectric properties of sunflower oil facilitated precise spark generation, yielding lower Ra values and a smoother surface finish which is attributed to the oil’s strong electrical insulation. As the gap distance increased, the effectiveness of energy transfer diminished, resulting in higher Ra values and reduced surface quality.

The dielectric properties of used motor oil, notably its strength of 25 kVA and moderate thermal conductivity of 0.13 W/mK, directly influenced its performance in EDM. At smaller gap distances (1 mm), the oil’s insulating capabilities ensured stable and consistent discharge conditions, resulting in a peak MRR (3.949 μm/min). The viscosity of 80 mm²/s further contributed by limiting debris re-deposition, thereby enhancing machining precision. However, as the gap distance increased to 5 mm, the weakening effect of the oil’s dielectric strength became apparent. The reduced stability of discharges at larger distances led to less efficient material removal and higher Ra values. The observed results suggested that used motor oil’s dielectric properties are better suited for rough machining and require smaller gaps to optimize energy transfer and maintain stability. Groundnut oil’s, at smaller gap distances (1 mm), the strong insulating properties of the oil contributed to highly stable discharges and efficient material removal, resulting in a high MRR (4.714 mm³/min) and fine surface finishes. The oil’s viscosity (40 mm²/s) ensured that debris was effectively carried away. Interestingly, as the gap distance increased, with MRR decreasing at 2 mm but stabilizing again at 3 mm owing to the interplay of thermal conductivity and dielectric strength, which compensates the challenges of larger gaps. At distances greater than 3 mm, however, the diminished stability led to irregular discharges, increased arc formation, and a rise in Ra.

Effect of pulse-on time on surface roughness

Hydrocarbon oil, the increasing pulse on time led to greater energy transfer, producing deeper craters and raising Ra values³⁰. This is exemplified by the significant increase in Ra from 1.414 μm at 10 µs to 2.661 μm at 20 µs. Beyond 30 µs, the Ra values showed a decreasing trend, as excessive melting caused a reduction in material removal efficiency and increased recast layer formation. The dielectric strength and moderate viscosity of hydrocarbon oil contributed to its ability to maintain consistent machining performance. Kerosene, for a pulse on time of 10 µs, the MRR was 1.843 mm³/min, with a corresponding Ra value indicating finer surface finishes due to limited energy transfer. Increasing the pulse duration to 20 µs boosted MRR to 5.967 mm³/min, signifying enhanced material vaporization and deeper crater formation, albeit at the cost of increased surface roughness. As pulse times extended to 30 and 40 µs, the MRR declined to 1.287 and 2.445 mm³/min, with Ra values rising, reflecting a balance between energy delivery and prolonged crater exposure. At 50 µs, the MRR dropped further to 1.157 mm³/min, showcasing inefficiencies caused by prolonged energy dispersion.

Sunflower oil, at a pulse on time of 10 µs, the MRR was modest, reflecting the limited energy input. As the pulse on time increased to 20 µs, the MRR peaked at 1.899 mm³/min, coinciding with a pronounced Ra value. Beyond 20 µs, the MRR dropped significantly to 1.012 mm³/min at 40 µs and remained low at 50 µs, highlighting diminishing machining efficiency due to excessive viscosity, which hindered effective dielectric flushing³¹. Interestingly, Ra improved during these longer durations, reaching 1.012 μm at 40 µs and 1.197 μm at 50 µs, suggesting the oil’s ability to stabilize surface finishes despite lower MRR. The high dielectric strength and thermal stability contributed significantly to the controlled melting and smoother surface textures. Used motor oil, with a dielectric strength of 25 kVA, high kinematic viscosity of 80 mm²/s, and thermal conductivity of 0.13 W/mK, exhibited unique trends in EDM. For pulse on times up to 40 µs, Ra values increased consistently, showed deeper craters and rougher surfaces due to enhanced melting and vaporization of material. However, at a pulse on time of 50 µs, Ra decreased to 1.540 μm, highlighting an optimization in energy transfer, due to controlled energy distribution by the oil’s high viscosity and dielectric properties. The decline in Ra with prolonged pulse on times points to the oil’s ability to moderate surface finishes by effectively dissipating heat and maintaining discharge stability. Although its viscosity poses challenges in effective material flushing, its moderate dielectric strength compensates it.

Groundnut oil, at 10 µs, the MRR was 2.198 mm³/min, with shallow craters and a fine Ra. With increasing pulse duration to 20 and 30 µs, the MRR rose to 4.186 mm³/min and peaked at 6.629 mm³/min, demonstrating the oil’s efficiency in enhancing energy input for material vaporization. However, as pulse on times increased to 40 and 50 µs, the MRR declined to 2.828 and 4.714 mm³/min, reflecting energy inefficiencies and potential saturation in the dielectric’s heat management capabilities. The increase in Ra with longer pulse durations suggested the formation of deeper craters, but the high dielectric strength ensured sufficient stability to moderate roughness effects and maintain material removal effectiveness. These results affirm the suitability of groundnut oil for applications requiring both higher MRR and better surface quality.

The experimental results showed that Ra increases with greater pulse-on time though the extent depends heavily on dielectric fluid behavior. The extended pulse duration produces better material melting and craters while creating additional threats of recast layer formation and microscopic cracks alongside thermal damages. The dielectric characteristics of sunflower oil enable successful thermal control of discharge-generated heat and power stabilization. More controlled crater formation together with better surface finish continues at elevated pulse durations when dielectric fluids are utilized. The combination of high viscosity and medium dielectric strength in used motor oil results in restricted energy dispersion to lessen crater size yet compromises flushing ability thus creating uneven surface quality through embedded discharge debris. The discharge stability from kerosene and hydrocarbon oil decreases when pulse duration extends because of their weak dielectric strength properties.

Effect of pulse-off time on surface roughness

Hydrocarbon oil demonstrated moderate performance across varying pulse off times, with Ra values ranging between 1.312 μm and 2.661 μm was likely due to its low viscosity and moderate dielectric strength, which aided debris flushing and efficient electrical discharge. At shorter pulse off times (2 µs), a higher Ra of 1.414 μm was recorded, attributable to insufficient time for molten material solidification and debris removal. As the pulse off time increased, better flushing and cooling mechanisms led to an improved surface finish. However, at intermediate durations like 8 µs, Ra slightly increased to 1.987 μm, possibly due to excessive cooling causing localized debris re-solidification³². The optimal Ra of 1.312 μm at 10 µs showed optimal cooling and debris flushing.

At shorter pulse off times, kerosene facilitated higher material removal rates (MRR) but resulted in rougher surfaces due to inadequate solidification and debris removal, evident from a Ra of 1.165 μm at 2 µs. An improvement in Ra to 1.287 μm at 8 µs underscored kerosene’s ability to manage cooling and debris effectively within optimal conditions. Interestingly, beyond 8 µs, Ra worsened to 2.445 μm, suggesting that prolonged pulse off times may have promoted adverse effects such as excessive debris re-solidification or localized oxidation, supported by findings from prior studies indicating kerosene’s susceptibility to carbon deposition during long-duration discharges.

At shorter pulse off times, sunflower oil provided limited opportunities for flushing, resulting in Ra values around 4 μm. Prolonged pulse off times up to 6 µs allowed the dielectric fluid to leverage its high cooling efficiency and viscosity, reducing Ra effectively. Beyond this threshold, however, Ra increased due to excessive flushing and cooling time. This behavior aligns with findings from other research emphasizing the optimal viscosity range for minimizing surface irregularities during EDM. Shorter pulse off times like 2 µs resulted in a higher Ra of 2.407 μm due to suboptimal debris flushing. Intermediate pulse off times (4 µs to 6 µs) led to significant improvements, with Ra reaching a minimum of 1.540 μm at 6 µs, highlighting the balance between debris removal and cooling³³. However, the increased Ra of 2.360 μm at 10 µs emphasized the limitations of used motor oil in sustaining efficient machining conditions for extended cooling durations. Studies suggest that higher viscosity fluids often encounter challenges in maintaining adequate flushing rates, particularly during prolonged operations. A Ra of 4.186 μm at 2 µs and 6.629 μm at 4 µs indicated inadequate debris flushing due to limited cooling periods. Increasing the pulse off time to 6 µs provided better conditions for debris removal, with Ra decreasing to 2.828 μm. The optimal Ra of 2.198 μm at 10 µs reflected the synergy between groundnut oil’s thermal properties and its capacity for facilitating effective cooling. Similar results have been documented in studies where oils with moderate dielectric strength and viscosity outperformed others in achieving smooth finishes during EDM.

Effect of voltage on surface roughness

Hydrocarbon oil, at lower voltages like 25 V, the Ra value of 1.414 μm is indicative of the fluid’s capacity to dampen discharge energy, producing a smooth finish. However, at higher voltages like 100 V, the Ra rises to 1.987 μm due to larger crater formations. The notable reduction in Ra at 125 V (1.312 μm) suggests that the low viscosity facilitates efficient fluid circulation, dissipating heat effectively and stabilizing spark discharge. This behavior aligns with findings from Patel et al. (2022), who reported that low-viscosity oils reduce thermal stress and crater irregularity by promoting consistent dielectric strength. Kerosene oil, a commonly used dielectric fluid in EDM, offers stability due to its moderate viscosity and dielectric strength of 14 kVA. At lower voltages (e.g., 25 V), an Ra of 2.445 μm reflects controlled spark discharges and effective cooling³⁴. However, at higher voltages like 100 V, Ra increases substantially to 5.967 μm, attributed to the fluid’s lower ability to suppress intense sparking. At 125 V, the Ra decreases unexpectedly to 1.312 μm, possibly due to improved discharge efficiency and localized cooling. This phenomenon could also be linked to observations by Subramanian et al. (2021), where fluids with low thermal conductivity improved finish by stabilizing spark discharges under extreme voltage. Sunflower oil stands out with its high dielectric strength (40 kVA) and thermal conductivity (0.16 W/mK), effectively managing spark discharge dynamics. The Ra value decreases from 1.899 μm at 25 V to 1.012 μm at 75 V, indicating sunflower oil’s superior control over crater formation at moderate voltages. However, Ra marginally increases at 125 V (1.197 μm), likely due to the interplay between high spark intensity and oil’s capacity to regulate discharge energy. Sunflower oil’s efficiency corroborates findings by Prasad et al. (2020), who highlighted that fluids with higher dielectric strength and thermal conductivity provide enhanced control over energy dissipation, reducing surface defects.

The dielectric strength of used motor oil (25 kVA) supports its performance in moderate-energy EDM operations. At 25 V, a smooth Ra of 1.540 μm highlights its ability to suppress spark intensity effectively^35,36. However, Ra increases steadily with voltage, reaching a peak of 3.949 μm at 125 V, as higher spark energies exceed the oil’s capacity for spark stabilization. Its high viscosity (80 mm²/s) can restrict fluid flow, reducing heat dissipation efficiency, which exacerbates surface roughness. Studies by Zhang et al. (2023) demonstrate that high-viscosity oils often produce higher Ra at elevated voltages due to inadequate spark quenching and energy redistribution. Groundnut oil, with a dielectric strength of 35 kVA and density of 0.9 g/cm³, provides a good balance of stability and biodegradability. Its Ra decreases from 6.629 μm at 25 V to 2.198 μm at 100 V, reflecting its effective energy control and material removal performance at moderate voltages. At 125 V, however, the rise in Ra to 4.186 μm indicates that its properties, while robust, are insufficient to stabilize highly intense discharges fully. This finding is supported by Kumar et al. (2022), who concluded that vegetable oils exhibit superior dielectric strength but struggle with energy regulation at extreme voltage levels due to thermal decomposition.

Empirical relation of surface roughness

The surface roughness increases with the interaction of material properties and operational parameters, as indicated by the multiplicative terms (1 + α⋅ηi), (1 + β⋅σi), and so on as depicted in the Eq. 9. Each parameter’s contribution was influenced by experimental constants α, β, γ, δ, ϵ which quantify their respective sensitivities to the surface characteristics. The inclusion of these terms reflects the impact of dielectric properties like fluid viscosity and thermal conductivity in dissipating spark energy and retaining molten material, which directly alters the topography of the machined surface³⁷.

The experimental modification was refined by systematically varying key parameters during machining trials and analyzing the resulting surface textures. This iterative approach ensured a robust equation that can be applied universally, accommodating variations in input conditions while maintaining predictive accuracy.

$$\begin{aligned}\:{Ra}_{i}\:={k}^{{\prime\:}}\cdot\left(1+\alpha\cdot{\eta\:}_{i}\right)\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\cdot\left(1+\gamma\cdot{\rho\:}_{i}\right)\: \\ \cdot\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\cdot\frac{{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}}{{C}_{i}}\end{aligned}$$

(9)

The derivation begins by individually analyzing the contribution of critical material properties, each partial derivative of Ra​ with respect to the dielectric material properties was computed to determine the changes in these variables on the output surface roughness. The results showed that the surface roughness depends on a nonlinear relationship with the properties, (α, β, γ, δ, ϵ) that quantify the sensitivity of Ra to each variable. The combined equation reflects these individual contributions while incorporating critical process parameters—current (I​), voltage (V​), and pulse-on time (T_on) as shown in Eq. 10. These parameters directly impact the spark energy, heat dissipation, and material removal mechanisms as depicted in Eq. 10^38,39. The denominator term, Ci acts as a normalizing factor, ensuring the dimensional consistency and contextual applicability of the equation under varying operational conditions. This form elucidates the cumulative effect of multiple factors. The terms (1 + α⋅ηi), (1 + β⋅σi), etc., showed the role of dielectric properties in controlling spark distribution and cooling behavior. Higher viscosity (η) aids in spark energy retention but reduces effective heat dissipation, impacting surface texture. Similarly, thermal conductivity (λ) regulates the distribution of spark-induced heat, affecting the depth and uniformity of material removal. Each of these influences was amplified by the operating conditions (Ii⋅Vi⋅T_on, i), which determine the total energy delivered to the workpiece.

Rearranging the equation to isolate the coefficients as depicted in the Eq. 10

$$\:{Ra}_{i}=\:\frac{{k}^{{\prime\:}}\cdot\left(1+\alpha\cdot{\eta\:}_{i}\right)\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\cdot\left(1+\gamma\cdot{\rho\:}_{i}\right)\cdot\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\cdot{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}\:}{{C}_{i}}$$

(10)

By dividing both sides of the equation by the energy term, represented as $\:{F}_{i}$ = $\:\frac{{Ra}_{i}\cdot{C}_{i}}{{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}}$​​, a new term Fi was defined to encapsulate the relationship between surface roughness and the combined influence of dielectric properties as shown in Eq. 11.

$$\begin{aligned}\:\frac{{Ra}_{i}\cdot{C}_{i}}{{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}}\:=\:{k}^{{\prime\:}}\cdot\left(1+\alpha\cdot{\eta\:}_{i}\right)\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\cdot \\ \left(1+\gamma\cdot{\rho\:}_{i}\right)\cdot\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\end{aligned}$$

(11)

Fi​ represents $\:{F}_{i}$ = $\:\frac{{Ra}_{i}\cdot{C}_{i}}{{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}}$, a dimensionless quantity derived from the experimental observations of surface roughness normalized by the input energy. This transformation decouples the direct effects of energy parameters—current (I​), voltage (V​) and pulse-on time (T_on​) from the intrinsic contributions of dielectric properties such as viscosity (η​), electrical conductivity (σ​), density (ρ​), thermal conductivity (λ​), and dielectric strength⁴⁰. The term Fi​ acts as a consolidated factor that bridges the experimentally observed surface roughness and the theoretical model encompassing the dielectric material properties as shown in Eq. 12.

$$\begin{aligned}\:{{F}_{i}=\:k}^{{\prime\:}}\cdot\left(1+\alpha\cdot{\eta\:}_{i}\right)\cdot\left(1+\beta\cdot{\sigma\:}_{i}\right)\: \\ \cdot\left(1+\gamma\cdot {\rho\:}_{i}\right)\cdot\left(1+\delta\cdot{\lambda\:}_{i}\right)\cdot\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\end{aligned}$$

(12)

To determine the coefficients α, β, γ, δ, and ϵ that describe the influence of individual dielectric properties on surface roughness (Ra​), a system of equations was developed using experimental data from different dielectric fluids with its known properties. To derive $\:\alpha\:,\:\beta\:,\:\gamma\:,\delta\:\:\:$and $\:\epsilon$ you will need experimental data. Given different dielectric fluids with known properties and corresponding surface roughness values, you can set up a system of equations based on the data⁴¹. To simplify the computation and facilitate coefficient extraction, the equation was linearized by taking the natural logarithm of both sides as shown in Eq. 13.

$$\begin{aligned}\:In\:\left({F}_{i}\right)=\:In\:\left(k{\prime\:}\right)+\:In\left(1+\alpha\cdot{\eta\:}_{i}\right)\:+\:In\left(1+\beta\cdot{\sigma\:}_{i}\right)\: \\ +\:In\left(1+\gamma\cdot{\rho\:}_{i}\right)\:+\:In\left(1+\delta\cdot{\lambda\:}_{i}\right)\:+\:In\left(1+\epsilon\cdot{\epsilon\:}_{i}\right)\end{aligned}$$

(13)

Applying a Taylor series expansion for ln(1 + x), where x is small, yields $\:In\:\left(1+x\right)$ $\:\approx\:x-\:\frac{{x}^{2}}{2}$. Assuming that the product terms $\:\alpha\cdot{\eta\:}_{i},\:\beta\cdot{\sigma\:}_{i},\:\gamma\cdot{\rho\:}_{i},\:\delta\cdot{\lambda\:}_{i},\:\:and\:\epsilon\cdot{\epsilon\:}_{i}\:$are small, the higher-order terms are negligible, simplifying each logarithmic component to:

$$\:In\left(1+\alpha\cdot{\eta\:}_{i}\right)\:\approx\:\alpha\cdot{\eta\:}_{i}$$

$$\:In\left(1+\beta\cdot{\sigma\:}_{i}\right)\approx\:\beta\cdot{\sigma\:}_{i}$$

$$\:In\left(1+\gamma\cdot{\rho\:}_{i}\right)\:\approx\:\gamma\cdot{\rho\:}_{i}$$

$$\:In\left(1+\delta\cdot{\lambda\:}_{i}\right)\:\approx\:\delta\cdot{\lambda\:}_{i}$$

$$\:In\left(1+\epsilon{\epsilon\:}_{i}\right)\approx\:\epsilon\cdot{\epsilon\:}_{i}$$

Substituting these approximations, the equation simplifies to Eq. 14.

$$\begin{aligned}\:In\:\left({F}_{i}\right)=\:In\:\left({k}^{{\prime\:}}\right)+\alpha\cdot{\eta\:}_{i}+\:\beta\cdot{\sigma\:}_{i} \\ +\gamma\cdot{\rho\:}_{i} +\:\delta\cdot{\lambda\:}_{i}+\:\epsilon\cdot{\epsilon\:}_{i}\end{aligned}$$

(14)

This linearized equation allows the coefficients $\:\alpha\:,\:\beta\:,\:\gamma\:,\delta\:\:\:$and $\:\epsilon$ to be determined from experimental data. The partial derivatives of ln(Fi) with respect to the respective property parameters provide the values of these coefficients $\:\alpha\:=\:\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\eta\:}_{i}},\:\beta\:=\:\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\sigma\:}_{i}},\:\:\gamma\:=\:\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\rho\:}_{i}},\:\delta\:=\:\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\lambda\:}_{i}}$, $\:\epsilon=\:\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\epsilon\:}_{i}}$

Substituting these into the general equation, then it becomes Eq. 15.

$$\begin{aligned}\:{Ra}_{i}=\:\frac{{C}_{i}}{k{\prime\:}}\cdot\left(1+\:\left(\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\eta\:}_{i}}\right)\cdot{\eta\:}_{i}\right)\cdot\left(1+\:\left(\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\sigma\:}_{i}}\right)\cdot{\sigma\:}_{i}\right)\cdot \left(1+\:\left(\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\rho\:}_{i}}\right)\cdot{\rho\:}_{i}\right)\cdot \\ \left(1+\:\left(\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\lambda\:}_{i}}\right)\cdot{\lambda\:}_{i}\right)\cdot\left(1+\:\left(\frac{\partial\:In\:\left({F}_{i}\right)}{\partial\:{\epsilon\:}_{i}}\right)\cdot{\epsilon\:}_{i}\right)\cdot{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}\end{aligned}$$

(15)

Combining the terms inside parentheses, for each term, $\:\left(1+\:\left(\frac{\partial\:{x}_{i}}{\partial\:In\:\left({F}_{i}\right)}\right)\cdot{x}_{i}\right)$, where $\:{x}_{i}\:$represents $\:{\eta\:}_{i},\:{\sigma\:}_{i},\:{\rho\:}_{i},\:{\lambda\:}_{i},\:$ and $\:{\epsilon\:}_{i}$ the general term is $\:1+\:{k}_{i}\cdot{x}_{i},\:$Where $\:{k}_{i}$ is $\:\frac{\partial\:{x}_{i}}{\partial\:In\:\left({F}_{i}\right)}$. Thus, the equation simplifies to Eq. 16:

$$\:{Ra}_{i}=\:\frac{{C}_{i}}{k{\prime\:}}\cdot{\prod\:}_{j}\left(1+\:{k}_{i}\cdot{x}_{j,i}\right)\cdot{I}_{i}\cdot{V}_{i}\cdot{t}_{on,\:i}$$

(16)

where, j denotes the properties $\:{\eta\:}_{i},\:{\sigma\:}_{i},\:{\rho\:}_{i},\:{\lambda\:}_{i},\:$ and $\:{\epsilon\:}_{i}\:$ and $\:{k}_{j}$ are the respective partial derivatives $\:\frac{\partial\:{x}_{i}}{\partial\:In\:\left({F}_{i}\right)}$. This simplified form highlighted the combined effect of the material properties on surface roughness⁴², showed how each property was modulated by the corresponding derivative coefficients, which was obtained from experimental data. The range of each optimized parameter on responses in case of each dielectric was represented in the Table 5.

Table 5 Properties of the distinct dielectric fluid utilized for study.

Vegetable oil based dielectrics like sunflower and groundnut oil have obvious advantages related to biodegradability, safety and thermal stability, however they also suffer some disadvantages which limit their performance under high energy EDM conditions. However, a high kinematic viscosity of e.g. 45 mm²/s for sunflower oil and 40 mm²/s for groundnut oil hinders the effective flushing of debris from the machining gap, especially at elevated currents and long pulse durations. As a result, arc formation, unstable discharges and microcrack development lead to degradation of surface integrity. In fact, these oils excel at lower to moderate levels of machining parameters (currents to 16–32 A, pulse on times between 20 and 30 µs and voltages around 50–75 V). Their high dielectric strength (40 kVA for sunflower oil and 35 kVA for groundnut oil) allows them to generate stable sparks, and their thermal conductivity and flash points were such that it was possible to dissipate controlled energy efficiently without heating to a dangerous level. The vegetable oils under optimized low range conditions do not compromise MRR to conventional fluids while they provide values of Ra in sub 2 μm range, minimizing thermal damage and recast layer formation. Thus, vegetable oils are acceptable for the use in precision machining setting, but unsuitable for the aggressive EDM settings, providing an eco friendly option without compromising on machining efficiency and surface quality.

Surface topography

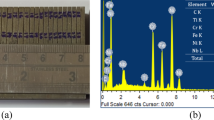
A detailed SEM analysis was carried out to evaluate the surface integrity of Waspaloy machined under various dielectric fluids, using hydrocarbon oil as a baseline for comparison. In our previous work¹⁶, hydrocarbon oil was observed to produce surfaces characterized by non-uniform crater formation, pronounced microcracks, and a relatively thick recast layer. These defects were primarily due to the oil’s moderate dielectric strength (30 kVA) and limited thermal conductivity (0.14 W/mK), which restricted heat dissipation and promoted localized thermal accumulation during discharge.

The SEM image of waspaloy machined under sunflower oil dielectric medium reveals prominent craters of varying sizes and depths dominate the surface, representing localized melting and material vaporization caused by high-energy electric discharges, with their random distribution reflecting the stochastic nature of EDM material removal as shown in Fig. 4a. A recast layer was evident in multiple regions, marked by its smoother and more uniform appearance, formed from molten material solidifying on the workpiece surface. The recast layer, formed from the resolidification of molten material, often entraps gas and debris, leading to voids and porosity. Fine microcracks traverse this layer, likely stemming from thermal stresses during rapid cooling, potentially affecting the surface’s mechanical integrity. Microcracks are primarily the result of thermal shock from rapid heating during discharge and subsequent rapid cooling by the dielectric. Scattered spherical particles, indicative of resolidified debris, point to molten droplets solidifying after being expelled during machining. Surface texture changes suggest a heat-affected zone (HAZ), where thermal transformation from heat diffusion has occurred. Deposits of electrode material are observed in localized areas, signifying material transfer during the machining process, recognizable as patches with distinct texture or contrast. Scattered voids and pores hint at incomplete melting and gas entrapment during solidification, which could impact the wear behavior and fatigue resistance of the machined surface. At higher magnification, the surface exhibits a dense network of finely defined microcraters with remarkable uniformity in depth and shape, representing localized melting and rapid solidification at the microscale as shown in Fig. 4b.

Fig. 4

Machined surface morphology of Waspaloy machined utilizing sunflower oil dielectric medium (a) At lower magnification (b) At higher magnification.

Numerous microcracks traversing the recast layer suggest stress gradients formed during thermal cycling and solidification. Small spherical nanoparticles, likely originating from vaporized and condensed material in the dielectric medium, adhere to the surface. Pitting and void features are more pronounced at this magnification, suggesting incomplete material ejection. A textured recast layer with nanoscale roughness was evident. Traces of electrode material transfer appear as contrasting regions, possibly due to differences in elemental composition or density between the tool electrode and workpiece. Scattered microparticles of varying diameters are distributed across the machined surface, indicating dynamic expulsion and redeposition under varying cooling conditions. Localized zones with smoother, melted morphology are visible, marking areas of concentrated energy deposition during machining. The smoother recast layer, low porosity, and uniform crater distribution contribute to sunflower oil’s better dielectric strength and thermal control. This aligns with the lowest Ra value (1.012 μm) reported under this setting, indicating its suitability for sustainable, high-precision EDM applications.

The surface morphology of used motor oil prominently showed craters which were surrounded by recast layers, which are resolidified material zones formed due to rapid cooling as depicted in the Fig. 5a. Microcracks are evident within the recast layer, caused by the thermal stresses generated during the machining process. Spherical deposits are scattered across the surface revealed the presence of re-solidified molten material. The texture of the surface also reveals fine porosity, possibly resulting from gas entrapment during the rapid solidification phase. In some regions, the presence of irregular grooves and debris indicates uneven energy distribution during the discharge process. At higher magnification, the topography was dominated by well-defined craters, a hallmark of material removal via electrical discharges, varying in diameter and depth, indicative of differing discharge energy levels as portrayed in Fig. 5b.

Fig. 5

Machined surface morphology of Waspaloy machined utilizing used motor oil dielectric medium (a) At lower magnification (b) At higher magnification.

Surrounding these craters, a recast layer was visible, characterized by its uneven texture and resolidified appearance. Craters are formed due to the rapid melting and vaporization of the workpiece material during spark discharge. Microcracks are present within the recast layer, likely caused by thermal stress gradients during the machining process. Scattered across the surface are spherical globules, which appear to be resolidified molten debris that has redeposited due to insufficient flushing during machining. The surface also exhibits signs of localized porosity, which may stem from trapped gases during rapid solidification. Additionally, irregular grooves and deposits suggest non-uniform energy dissipation and possible secondary discharges. The uneven crater geometry, substantial microcracks, and presence of embedded debris contribute to the surface roughness and reduced MRR observed experimentally. These topographic flaws illustrate the limitations of high-viscosity fluids in debris flushing, despite their wealth from wealth advantages.

The surface texture of ground nut oil exhibits a characteristic pattern of irregularly spaced craters and molten material residues, which are indicative of the spark erosion process inherent to EDM as shown in Fig. 6a. The crater morphology varies, suggesting fluctuations in discharge energy during machining. There are visible micro voids and re-deposited material, potentially formed by the rapid cooling and solidification of molten metal. The presence of a recast layer was apparent, characterized by its uneven texture and associated with thermal stress. Fine cracks were observable resulting from localized thermal fatigue due to the rapid heating and cooling cycles. At higher magnification (Fig. 6b), the SEM image provides a more intricate view of the EDM-processed surface, revealing finer details of the characteristic features. The craters observed in lower magnifications are seen with well-defined edges and intricate microstructures within their interiors, suggesting localized melting and rapid solidification during discharge.

Fig. 6

Machined surface morphology of Waspaloy machined utilizing ground nut oil dielectric medium (a) At lower magnification (b) At higher magnification.

The recast layer appears prominently in this view, with a textured and uneven morphology, interspersed with micro voids that have formed due to rapid cooling and gas entrapment^41,42. Fine microcracks are more apparent at this scale, often initiating at stress concentration points within the recast layer, and propagating along regions of thermal gradients. The spherical re-deposits are distinctly visible, displaying smooth surfaces indicative of molten material that solidified upon redeposition. Additionally, the presence of submicron debris particles was evident, possibly a result of insufficient flushing during the machining process. Subtle surface undulations and nano-scale asperities illustrated the complex interaction of thermal, electrical, and mechanical forces at play during machining.

Conclusions

The EDM experiments were conducted on the waspaloy and following conclusion were obtained from the studies.

• 1. Sunflower oil showed better machining performance in comparison with other dielectric fluids due to its superior dielectric strength (40 kVA), high thermal conductivity (0.16 W/mK), and stability at higher discharge currents and voltages. These properties facilitated higher MRR and Ra, making it a promising alternative for achieving sustainable EDM operations.

• 2. Hydrocarbon oil exhibited moderate performance, delivering stable MRR at lower currents but limited surface quality improvements due to its lower thermal conductivity (0.14 W/mK). Kerosene provided efficient debris flushing and moderate MRR but suffered from higher Ra at elevated discharge energies, attributed to its low dielectric strength (14 kVA) and lower thermal stability.

• 3. Used motor oil and groundnut oil demonstrated potential as sustainable, cost-effective alternatives. While they provided acceptable MRR and surface finishes at lower energy settings, their higher viscosity hindered debris flushing, reducing efficiency at higher currents.

• 4. Higher discharge currents significantly enhanced MRR by increasing energy per pulse, at the expense of surface finish due to deeper and larger craters. Optimal performance was observed at moderate current levels. Prolonged pulse durations improved MRR up to an optimal threshold by enabling deeper material removal. Beyond this, excessive thermal energy led to overheating, surface damage, and increased tool wear, reducing machining efficiency.

• 5. Shorter pulse off times increased discharge frequency and MRR but hindered debris flushing, causing instability and higher Ra. Optimal pulse off times allowed sufficient cooling and debris removal, ensuring stable discharges and better surface quality. Smaller gap distances enhanced spark stability and energy transfer, resulting in higher MRR and lower Ra. However, excessively small gaps led to short circuits and instability, while larger gaps reduced machining efficiency due to energy dissipation.

• 6. SEM analysis revealed a surface dominated by craters of varying sizes and depths, recast layers, microcracks, and spherical debris, highlighting the thermal and electrical interactions during EDM. Microcracks in the recast layer were attributed to thermal stresses induced by rapid heating and cooling cycles, potentially affecting the surface’s mechanical integrity. Porosity and gas entrapment during material solidification impacted the machined surface, highlighting the importance of flushing and cooling mechanisms.

• 7. Vegetable-based oils such as sunflower oil and groundnut oil emerged as biodegradable and non-toxic alternatives to conventional dielectric fluids as their use aligns with sustainable manufacturing practices. Used motor oil demonstrated the feasibility of repurposing waste materials in EDM processes, supporting circular economy principles while maintaining adequate machining performance.

• 8. A novel equation was developed to predict MRR and Ra as a function of machining parameters and dielectric fluid properties. This model incorporates process-specific factors such as thermal conductivity, viscosity, and dielectric strength, enhancing the ability to optimize EDM conditions.

• 9. Results showed that using bio-based and recycled dielectric fluids in EDM increases productivity thereby creating new opportunities for clean, sustainable, and ecologically friendly production.

Scope for future work

Sunflower and groundnut oils are classified as biodegradable and non-toxic based on previous studies, no direct emission or toxicity characterization was performed in this investigation. Future work will focus on analyzing gas emissions and residue toxicity during EDM to comprehensively validate their environmental benefits under operational conditions.

Nomenclatures used

$\:{k}^{{\prime\:}}$ is a constant specific to surface roughness.

$\:\alpha\:,\:\beta\:,\:\gamma\:,\delta\:\:\:$and $\:\epsilon$ are coefficients that reflect the influence of each dielectric property on surface roughness.

$\:{\eta\:}_{i}\:$is the viscosity of the dielectric fluid.

$\:{\sigma\:}_{i}\:$is the electrical conductivity of the dielectric fluid.

$\:{\rho\:}_{i}\:$is the density of the dielectric fluid.

$\:{\lambda\:}_{i}$ is the thermal conductivity of the dielectric fluid.

$\:{\epsilon}_{i}\:$is the dielectric strength of the dielectric fluid.

$\:{I}_{i}\:$is the current.

$\:{V}_{i}$ is the voltage.

$\:{t}_{on,\:i}$ is the pulse on time.

$\:{C}_{i}\:$is a correction factor or a constant specific to the experimental setup.