A time-fractional model of hydromagnetic slip flow of viscous fluid in rotational frame with heat and mass transfer

Abstract

This study investigates the unsteady fluctuations of a conducting Newtonian viscous fluid in a rotating frame influenced by an unsteady hydromagnetic free-stream flow, while also accounting for chemical reactions and heat absorption. The flow regime is modeled using partial differential equations. In contrast to previous research, this study employs a fractionalized dimensionless system of equations based on the newly developed Caputo–Fabrizio derivative. The dimensionless profiles for velocity, temperature, and concentration are solved accurately using the Laplace transform. The effects of various parameters are illustrated graphically and discussed in detail. Additionally, their influences are summarized in a table. Key observations reveal that as Hall current increases, primary velocity decreases when near the plate, but subsequently increases as the fluid moves away. Furthermore, skin friction shows a notable increase with rotation. Buoyancy forces not only enhance skin friction but also grow over time, while heat absorption leads to a reduction in fluid temperature.

Introduction

Magnetohydrodynamics involves with conducting fluids that carry current under magnetic fields. The most common examples of these fluids are saltwater, liquid metal, electrolysis, plasma, etc. Magnetohydrodynamics is used in the biological system to reduce blood flow and tissue temperature during surgery¹. MHD problems in astrophysical contexts², improvement of heat transmission rates in the heat exchanger equipment i-e solar air heaters, turbine blades that are being cooled³, and so forth. Many scholars have used MHD in their research because of its importance. The transfer of energy in mixed convective unsteady magnetohydrodynamic incompressible channel flow passing through a saturated porous medium was explored in⁴. The results revealed that the most important factors for varying the velocity and temperature values are viscosity and thermal conductivity. The study conducted by⁵, examined Hall and ion slip phenomena in an environment of unsteady magnetohydrodynamics (MHD) free convective rotatory flow. The flow was observed over an inclined plate embedded in a porous media and subjected to exponential acceleration. The investigation also considered the impact of variable temperature and concentrations⁶, was conducted to examine the behavior of nanofluid flows over an infinite plate, as well as heat transfer over the plate with the help of thermal radiation and viscous dissipation influenced by a magnetic field⁷, explored the unsteady MHD boundary layer nanofluid flow across a moving vertical porous plate exposed to a uniform perpendicular magnetic field. A subsequent study by⁸, investigates the unsteady heat absorptive viscous incompressible magnetohydrodynamic (MHD) nanofluid of an electrically conducting and radiating Brinkman model. The study considers flow over an exponentially accelerating vertical plate with ramped temperature and concentration, immersed in a porous medium.

Numerous scientists have been drawn to the importance and applications of fluids in a rotating frame, including their application to the destruction of cancer cells during the transport of drugs^9,10,11,12. Studies of the life history of stars¹³, climate prediction by understanding atmospheric and oceanic motions¹⁴, etc. Several researchers have explored the effects of rotation on flow using various geometries as a result of these applications. The impact of viscous dissipation heat radiation on the incompressible, laminar rotating flow of a nanofluid that conducts electricity in porous media was analyzed by¹⁵. His study shows that a greater rotation parameter reduces the boundary layer. Jeffery nanofluid flowing over a porous medium was studied to see how heat radiation affects the unsteady hydromagnetic natural convection flow¹⁶. The author concluded that while the heat transfer rate is greatly increased by an increase in temperature profile, the velocity decreases with an increase in the volume percentage of nanoparticles. Using a rotating Jeffery nanofluid¹⁷ solar energy devices were improved using the Caputo–Fabrizio approach. Consequently, it can be concluded that the velocity field exhibits a rapid response to resistivity in the boundary layer due to the Hartman number (magnetic field effect). The Hall and ion slip effects were examined in¹⁸, by considering a vertical plate rotating impulsively within a porous medium with ramping wall temperatures. Jeffrey’s fluid with a rotating MHD flow was unstable. A nanofluid flow across an infinitely long, vertically rotating plate immersed in a porous medium was investigated to determine whether Hall and ion slip affect the nanofluid flow¹⁹. Infinite plate convection rotating flow through vertically permeable surfaces: a numerical study was carried out by²⁰.

Many processes involve conjugate mass and heat transmission during the formation of chemically reactive species, and these processes have recently received considerable attention. Simultaneous heat and mass transport occurs during drying, evaporation at the water’s surface, and energy transport in cooling towers^{21,22,23,24,25}. Many practical diffusive processes include the molecular diffusion of within or at the boundary of a chemical reactions. A reaction occurs at a limited area, or the phase boundary is heterogeneous. If the reaction rate and concentration are directly related, then the reaction is of the first order. Due to its almost universal occurrence, problems, including mass and heat transport in a chemical reaction, are of tremendous long-term significance to engineers and scientists in many engineering and science areas to the extreme importance of this topic. In ref. ^{24,26,27,28,29,30}, investigates the uniform heat and mass transmission through an impulsively vertical started infinitely long plate in the existence of chemically reactive species. In ref.³¹, modeled heat flow, mass transmission, and chemical reactions in permeable media. The study conducted by³² to investigate the effects of thermal radiation, chemical reactions, Hall, and ion slip on a semi-infinite vertical moving permeable surface subjected to free convection rotatory flow of micropolar fluid on a semi-infinite vertical moving surface, subjected to thermal radiation, chemical reactions, Hall and ion slip experiments³³. An accelerated vertical plate in a rotating frame was utilized to examine the impact of Hall currents, radiations, and sorets and dufours on MHD-free convection. In ref.³⁴, explored the flow of Walter’s B fluid through a permeable media under the effects of radiation, as well as the generation and absorption of heat during chemical reactions. In ref.³⁵, investigated the thermophoretic diffusion of polyethylene glycol-metallic nanofluids in a Darcian porous surface in combination with Brownian motion and Ohmic magnetic heating. In ref.³⁶, examines the time-dependent natural convection of a hydro-magnetic, heat-generating, Casson fluid flow with reacting species in the presence of diffusion-thermo and thermo diffusion effects. The flow occurs along an oscillating vertical surface embedded in a porous medium.

When a low-density, ionized fluid is shown up to a magnetic field, it produces a hall current in the fluid flow. The phenomena of the Hall Effect were initially proposed by Hall³⁷. The impact of Hall current was incorporated into MHD flow by³⁸, and³⁹ discovered that Hall current generates a secondary fluid flow during rotation. Furthermore, the impact of Hall current is used in various applications, including magnetic field measurement, magnetic field control sensors, microwave power sensors, etc.⁴⁰. Several researchers included the impact of the Hall current in their fluid flow due to its importance. The flow of Prandtl fluid between two plates in the existence of the Hall effect and chemically reactive species was explored by⁴¹. In ref⁴², used fractional calculus to assess the hydromagnetic flow of generalized Oldroyd-B across permeable media and investigate how the Hall current influences flow⁴³. In parallel plates, we evaluated the effects of Hall current and thermal radiation on the rotational motion of micro-polar nanofluids and Casson fluids. In ref.⁴⁴, investigated the convection of mass and heat between two porous vertical parallel plates in a rotating medium by employing the Hall effect and the effect of suction and injection. In ref.⁴⁵, investigated whether Hall and ion slip have an effect on a radiative MHD rotatory flow of Jeffrey’s fluid through an infinite vertical plate with ramped temperatures and speeds. In ref.⁴⁶, explored the effect of Hall and ion slip on the convective rotation of second-grade fluid over a semi-infinite vertical moving porous surface for an unstable laminar flow.

A substance that possesses pores is commonly referred to as a porous medium or an absorbent material. Various types of porous media can be identified, including natural raw materials such as soil and rocks utilized for petroleum reservoirs and aquifers, biological tissues like wood and bones, as well as certain hand-made materials such as cement and ceramics. Convection flows take place through porous media in all of these industrial and natural phenomena, including the separation process of the membrane, power technology, flow of oil from a sandstone reservoir, seepage of rainwater waste into an acquire, drying and wetting process, and hydrology tissue engineering. The transfer of heat and fluid flow are crucial mechanisms in engineering and various industrial sectors, such as chemical and petroleum engineering. Numerous researchers are driven by the anticipated results and devote their expertise to investigating porous media. For instance, in reference⁴⁷, the fluid dynamics within a porous medium were examined, taking into account both slip and no-slip conditions. The researchers also considered the interfacial conditions in their study. In ref.⁴⁸, investigates the thin film flow of a second-grade fluid in a permeable media, while considering the impact of viscous dissipation. The researchers analysed the thickness and porosity of a presumed film under varying temperature conditions, yielding noteworthy and advantageous outcomes. An analysis of the combined effects of Hall and ion slip on ciliary propulsion of microscope organisms in permeable media by magnetohydrodynamics (MHD) was investigated by⁴⁹. In a recent study conducted by⁵⁰ in a porous medium, an elastic-viscous fluid exhibits magnetohydrodynamic (MHD) convection flow influenced by Hall and ion slip effects. The study conducted by⁵¹ Magnetohydrodynamics (MHD) examined the flow of Cassion fluid past a vertical plate embedded in a porous medium that oscillates with constant temperature. The study conducted by⁵² Refers to the radiative MHD rotational flow of an infinite vertical flat permeable surface by a viscous incompressible Jeffreys fluid. Additionally, ramped wall velocity and temperature are considered in the study.

Fractional Calculus emerged from a question by L’Hospital to Leibniz in a letter by⁵³. L’Hospital asked a question concerning $D^{n} f(r)/Dr^{n}$ this letter. When L’Hospital queried about the outcome $n = 1/2$, Leibniz replied that it would appear to be a contradiction from which valuable conclusions would be extracted one day. Mathematicians such as Euler, Laplace, Fourier, Lacroix, Abel, Riemann, and Liouville became interested in the subject following this discussion. They played a role in its development. Mathematicians were the only ones who knew about this subject for a few decades. However, in the past few years, the concept of this subject has been extended to other disciplines in a variety of ways, such as ultrasonic wave propagation in human spongy bone⁵⁴, speech signals modeling⁵⁵, modeling of cardiac tissue electrode interface⁵⁶, propagation of sound waves in the solid porous medium⁵⁷, lateral and longitudinal governing of Sovran vehicle⁵⁸, and so on. The Riemann–Liouville fractional derivatives were most commonly used. However, these derivatives had significant drawbacks and were only valid for a limited set of problems, e.g., in the Riemann–Liouville fractional derivative, the constant does not give us zero upon taking its derivative. Caputo introduced a different derivative to resolve these deficiencies, but the Caputo derivative’s kernel remained singular. In ref.⁵⁹, introduced a new exponential function-based fractional operator without a singular kernel in 2015 to tackle these issues. The Caputo–Fabrizio (CF) derivative is also functional when applying the Laplace transformation. The viscous fluid flow past an infinitely moveable plate was studied by⁶⁰. The outcomes are then compared to previous definitions of fractional derivatives. Using the fractional approach⁶¹, researched the Couette flow of incompressible Maxwell fluid without a singular kernel caused by the bottom plate gesture and the slip boundary condition.

In light of previous research, the current research aims to investigate the magnetohydrodynamics free convection flow of a Newtonian viscous fluid in a rotating frame. Partial differential equations are utilized to express the model. By adding mass transfer, letting the free stream fluctuate, and generalizing the model using the recently developed Caputo–Fabrizio derivative formulation, the current study work expands the work conducted by⁶². The fractional derivative is the most effective method to incorporate crossover behaviour and memory effect simultaneously in a dynamical system. Furthermore, in contrast to the classical model, it provides us with a range of curves (solutions) by adjusting the fractional parameter $\alpha$ between $0 < \alpha < 1$, one of these curves to best fit the actual or experimental data. Comparative studies are available in the literature. It has been proved that fractional differential operators can best fit the real data with the theoretical results more accurately and with the least error. So far, to the Author’s knowledge, no such study has been reported via the Caputo–Fabrizio approach of non-singular kernel to finding the exact solutions of Newtonian viscous fluid in a rotating frame. The Caputo–Fabrizio derivative unlike the classical Caputo or Riemann–Liouville derivatives, is defined with an exponential kernel that is non-singular and non-local. This makes it particularly well-suited for modelling real-world phenomena where memory effects are present, but where the singularity at the origin in traditional kernels may not be physically realistic or may cause computational difficulties. The CF derivative captures memory effects in the processes like heat conduction and mass diffusion with finite speed of propagation, aligning more closely with observed behaviours in complex media. In particular, in systems involving viscoelastic or porous media under rotational frames and magnetic fields as in the present model, such memory effects cannot be neglected. The CF derivative allows for the description of such processes without introducing unphysical infinite propagation speeds inherent in classical diffusion equations. Moreover, in the hydromagnetic and rotating fluid systems, the response of the system to external disturbances is not instantaneous. The CF derivative allows for a more realistic representation of the time dependent.

More exactly, this study aims to address the following questions:

• How does the rotation parameter affect unsteady flow?

• How is the Caputo–Fabrizio derivative model developed for combined heat and mass transfer?

• In what ways does the Hall current influence the flow dynamics?

• How do chemical reactions and heat absorption impact the current scenario?

• What methods can be used to obtain exact solutions for complex fluid problems?

• How can the results for skin friction, Nusselt number, and Sherwood number be determined in the context of this study?

• How the results for skin friction, Nusselt number and Sherwood number can be obtained for the present problem?

Mathematical formulation

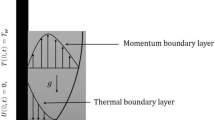
The transfer of heat and mass through an infinitely long vertical plate has been analysed considering the Newtonian viscous fluid flow. The x-axis is the direction of the flow. The fluid is electrically conducting, and the Hall effect is also considered. The plate is oriented in the xy-plane, and the z-axis is perpendicular to the plate. Both fluid and plate rotate simultaneously around the z-axis with a uniform angular velocity $\Omega$. A uniform magnetic field parallel to the z-axis is provided. Initially, when $t^{ * } \le 0$, plate and fluid are at rest with temperature $T_{\infty }^{ * }$ , concentration is kept constant at a value $C_{\infty }^{ * }$. After some time, the free stream begins to move with a velocity $U^{ * }$ in the x-axis direction. The temperature and concentration values at the plate are raised to $T_{w}^{ * }$ and $C_{w}^{ * }$ respectively. A homogenous chemical reaction occurs between fluid and diffusing species at a constant rate $K_{r}$.

This flow has the following velocity, temperature, and concentration profiles:

$$\begin{gathered} \mathop{V}\limits^{\rightharpoonup} = \left( {u^{ * } (z,t^{ * } ),v^{ * } (z,t^{ * } ),\Omega } \right), \hfill \\ T^{ * } = T^{ * } \left( {z,t^{ * } } \right), \hfill \\ C^{ * } = C^{ * } \left( {z,t^{ * } } \right). \hfill \\ \end{gathered}$$

(1)

As the flow is incompressible, the equation of continuity is given by:

$$\mathop{\nabla }\limits^{\rightharpoonup} \cdot \mathop{V}\limits^{\rightharpoonup} = 0,$$

(2)

The constitutive equation is given by^17,18:

$$\rho \left[ {\frac{{\partial \mathop{V}\limits^{\rightharpoonup} }}{\partial t} + 2\Omega \times \mathop{V}\limits^{\rightharpoonup} + \Omega \times \left( {\Omega \times \mathop{r}\limits^{\rightharpoonup} } \right)} \right] = {\text{div}}{\mathbf{T}} + \rho \mathop{b}\limits^{\rightharpoonup} .$$

(3)

All physical quantities, except pressure, only on z and t because the plate is electrically non-conducting and of infinite extent in the x and y-axes. As compared to the applied magnetic field, the induced magnetic field produced by fluid motion is thought to be of negligible significance. There is evidence for this presumption because liquid metals and partially ionized fluids have very low magnetic Reynolds numbers. Because there is no applied voltage, there is very little polarization of the fluid.

Using the assumptions made above and the Boussinesq approximation⁶³, the equations that govern the flow are given by⁶²:

$$\begin{aligned} \frac{{\partial u^{ * } }}{{\partial t^{ * } }} - 2\Omega v^{ * } = & - \frac{1}{\rho }\frac{{\partial p^{ * } }}{\partial x} + \upsilon \frac{{\partial^{2} u^{ * } }}{{\partial z^{2} }} - \frac{{\upsilon u^{ * } }}{{K_{1}^{ * } }} - \frac{{\sigma B_{o}^{2} }}{{\rho (1 + m^{2} )}}(u^{ * } - mv^{ * } )\, \\ & + g\beta_{T} (T^{ * } - T_{\infty }^{ * } ) + g\beta_{C} (C^{ * } - C_{\infty }^{ * } ), \\ \end{aligned}$$

(4)

$$\frac{{\partial v^{ * } }}{{\partial t^{ * } }} + 2\Omega u^{ * } = - \frac{1}{\rho }\frac{{\partial p^{ * } }}{\partial y} + \upsilon \frac{{\partial^{2} v^{ * } }}{{\partial z^{2} }} - \frac{{\upsilon v^{ * } }}{{K_{1}^{ * } }} - \frac{{\sigma B_{o}^{2} }}{{\rho (1 + m^{2} )}}(v^{ * } + mu^{ * } ),$$

(5)

$$- \frac{1}{\rho }\frac{{\partial p^{ * } }}{\partial z} = 0,$$

(6)

$$\frac{{\partial T^{ * } }}{{\partial t^{ * } }} = \frac{{k_{1} }}{{\rho c_{p} }}\frac{{\partial^{2} T^{ * } }}{{\partial z^{2} }} - \frac{{Q_{0} }}{{\rho c_{p} }}(T^{ * } - T_{\infty }^{ * } ),$$

(7)

$$\frac{{\partial C^{ * } }}{{\partial t^{ * } }} = D\frac{{\partial^{2} C^{ * } }}{{\partial z^{2} }} - K_{r} (C^{ * } - C_{\infty }^{ * } ).$$

(8)

Subjected to the initial and boundary conditions⁵⁷:

$$\left\{ \begin{gathered} u^{ * } = 0,\;v^{ * } = 0,\;T^{ * } = T_{\infty }^{ * } ,\;C^{ * } = C_{\infty }^{ * } \;for\, t^{ * } \le 0 \,and \,z \ge 0 \hfill \\ u^{ * } = 0,\;v^{ * } = 0,\;T^{ * } = T_{w}^{ * } ,\;C^{ * } = C_{w}^{ * } \;for \,t^{ * } > 0\,and\,z = 0 \hfill \\ u^{ * } \to U^{ * } ,\;v^{ * } \to 0,\;T^{ * } \to T_{\infty }^{ * } ,\;C^{ * } \to C_{\infty }^{ * } at\, t^{ * } > 0 \,as\, z \to \infty \hfill \\ \end{gathered} \right\}.$$

(9)

where, $u^{ * }$,$v^{ * }$, $p$, $\upsilon$, $\sigma$, $K_{1}^{ * }$,$\rho$,$g$, $T^{ * }$, $C^{ * }$, $\beta_{T}$, $\beta_{C}$, $m$, $k_{1}$, $Q_{0}$, $C_{p}$, $D$ are the primary velocity of the fluid, secondary velocity of the fluid, modified pressure, kinematic viscosity, electrical conductivity, the permeability of porous media, density, gravitational acceleration, fluid’s temperature, specie’s concentration within the fluid, thermal expansion coefficient, volumetric expansion coefficient, the parameter of Hall current, thermal conductivity, coefficient of heat absorption, specific heat at uniform pressure and mass diffusivity respectively.

These boundary conditions are used here because primary velocity and secondary velocity of the fluid are zero at the plate surface and away from the plate surface, the primary velocity approaches to uniform free stream velocity and the secondary velocity is zero. he heat transfer and mass transfer near the plate remain constant and both tend toward the ambient heat and mass transfer conditions. The dimensionless form of these boundary conditions (Eq. 17) are utilized to get the transformed solutions given by Eqs. (29–31).

Note that Please explain the utilization of boundary conditions properly.

Conditions in Eq. (9) have been used to determine the pressure gradient terms $\frac{1}{\rho }\frac{{\partial p^{ * } }}{\partial x}$ and $\frac{1}{\rho }\frac{{\partial p^{ * } }}{\partial y}$ in Eqs. (4 and 5), and after substituting its values in the same equations, we have:

$$\begin{aligned} \frac{{\partial u^{ * } }}{{\partial t^{ * } }} - 2\Omega v^{ * } = & \frac{{\partial U^{ * } }}{{\partial t^{ * } }} + \upsilon \frac{{\partial^{2} u^{ * } }}{{\partial z^{2} }} - \frac{{\sigma B_{0}^{2} }}{{\rho (1 + m^{2} )}}(u^{ * } - mv^{ * } - U^{ * } ) + \frac{\upsilon }{{K_{1}^{ * } }}(U^{ * } - u^{ * } ) \\ & + g\beta_{T} (T^{ * } - T_{\infty }^{ * } ) + g\beta_{C} (C^{ * } - C_{\infty }^{ * } ), \\ \end{aligned}$$

(10)

$$\frac{{\partial v^{ * } }}{{\partial t^{ * } }} + 2\Omega (u^{ * } - U^{ * } ) = \upsilon \frac{{\partial^{2} v^{ * } }}{{\partial z^{2} }} - \frac{{\sigma B_{0}^{2} }}{{\rho (1 + m^{2} )}}(v^{ * } + mu^{ * } - mU^{ * } ) - \frac{{\upsilon v^{ * } }}{{K_{1}^{ * } }}.$$

(11)

Introducing the following dimensionless variables

$$t = \frac{{t^{ * } U_{0}^{2} }}{\upsilon },\;u = \frac{{u^{ * } }}{{U_{0} }},\;v = \frac{{v^{ * } }}{{U_{0} }},\;U = \frac{{U^{ * } }}{{U_{0} }},\;T = \frac{{T^{ * } - T_{\infty }^{ * } }}{{T_{w}^{ * } - T_{\infty }^{ * } }},\;C = \frac{{C^{ * } - C_{\infty }^{ * } }}{{C_{w}^{ * } - C_{\infty }^{ * } }},$$

into Eqs. (7, 8, 10 and 11) we have:

$$\begin{aligned} \frac{\partial u}{{\partial t}} - 2\Omega K = & \frac{\partial U}{{\partial t}} + \frac{{\partial^{2} u}}{{\partial \eta^{2} }} - \frac{M}{{\left( {1 + m^{2} } \right)}}\left( {u - mv - U} \right) + \frac{U - u}{{K_{1} }} \\ & + GrT + GmC. \\ \end{aligned}$$

(12)

$$\frac{\partial v}{{\partial t}} + 2K\left( {u - U} \right) = \frac{{\partial^{2} v}}{{\partial \eta^{2} }} - \frac{v}{{K_{1} }} - \frac{M}{{\left( {1 + m^{2} } \right)}}\left( {v + mu - U} \right).$$

(13)

Multiplying “i” with Eq. (13) and then adding with Eq. (12), we get:

$$\frac{\partial f}{{\partial t}} = \frac{\partial U}{{\partial t}} + \frac{{\partial^{2} f}}{{\partial \eta^{2} }} + \lambda (U - f) + GrT + GmC,$$

(14)

$$\frac{\partial T}{{\partial t}} = \frac{1}{\Pr }\frac{{\partial^{2} T}}{{\partial \eta^{2} }} - \phi T,$$

(15)

$$\frac{\partial C}{{\partial t}} = \frac{1}{Sc}\frac{{\partial^{2} C}}{{\partial \eta^{2} }} - \gamma C.$$

(16)

$$\left\{ \begin{gathered} f = 0,\;T = 0,\;C = 0 \;for\; t \le 0 \;and \;\eta \ge 0 \hfill \\ f = 0,\;T = 1,\;C = 1 \;for\; t > 0 \;at \;\eta = 0 \hfill \\ f \to U,\;T \to 0,\;C \to 0\;for \;t > 0 \;as \;\eta \to \infty \hfill \\ \end{gathered} \right\}.$$

(17)

where

$$\begin{gathered} f = u + iv,\;\lambda = M\frac{(1 + im)}{{(1 + m^{2} )}} + \frac{1}{{K_{1} }} + 2iK,\;\eta = \frac{{zU_{0} }}{\upsilon },\;M = \frac{{\sigma B_{0}^{2} \upsilon }}{{\rho U_{0}^{2} }}, \hfill \\ K_{1} = \frac{{K_{1}^{ * } U_{0}^{2} }}{{\upsilon^{2} }},\;K = \frac{\upsilon \Omega }{{U_{0}^{2} }},\;\gamma = \frac{{K_{r} \upsilon }}{{U_{0}^{2} }},\;Sc = \frac{\upsilon }{D},\;Gm = \frac{{g\beta_{C} \upsilon (C_{w}^{ * } - C_{\infty }^{ * } )}}{{U_{0}^{3} }}, \hfill \\ \phi = \frac{{\upsilon Q_{0} }}{{\rho c_{p} U_{0}^{2} }},\;\Pr = \frac{{\upsilon \rho c_{p} }}{{k_{1} }},\;and\;Gr = \frac{{g\beta_{T} \upsilon (T_{w}^{ * } - T_{\infty }^{ * } )}}{{U_{0}^{3} }}. \hfill \\ \end{gathered}$$

Where $\phi$ is the heat absorption parameter, $M$ is the magnetic parameter, $Sc$ is Schmidt number, $K_{1}$ is the permeability parameter,$Gr$ is the thermal Grashof number, $K$ is the rotation parameter, $Gm$ is the mass Grashof number, $\Pr$ is Prandtl number, $\gamma$ is the chemical reaction parameter, and $U$ is the uniform free stream velocity.

To develop a time-fractional model, replace the time derivative with the Caputo–Fabrizio derivative in Eqs. (14, 15 and 16) yielding:

$${}^{CF}\wp_{t}^{\alpha } f\left( {z,t} \right) = {}^{CF}\wp_{t}^{\alpha } U(t) + \frac{{\partial^{2} f}}{{\partial \eta^{2} }} + \lambda (U - f) + GrT + GmT,$$

(18)

$${}^{CF}\wp_{t}^{\alpha } T\left( {z,t} \right) = \frac{1}{\Pr }\frac{{\partial^{2} T}}{{\partial \eta^{2} }} - \phi T,$$

(19)

$${}^{CF}\wp_{t}^{\alpha } C\left( {z,t} \right) = \frac{1}{Sc}\frac{{\partial^{2} C}}{{\partial \eta^{2} }} - \gamma C,$$

(20)

where ${}^{CF}\wp_{t}^{\alpha }$ is the Caputo–Fabrizio (CF) operator and is given by:

$${}^{CF}\wp_{t}^{\alpha } f\left( \tau \right) = \frac{1}{1 - \alpha }\int_{0}^{\tau } {\exp \left( {\frac{{ - \alpha \left( {\tau - t} \right)}}{1 - \alpha }} \right)f{\prime} \left( \tau \right)} dt.$$

(21)

After applying the Laplace Transform and by applying the conditions, Eqs. (18, 19 and 20) reduce to:

$$\frac{{d^{2} \overline{f} }}{{d\eta^{2} }} - \left( {\frac{{sh_{1} }}{s + h} + \lambda } \right)\overline{f} = - \left[ {\left( {\frac{{sh_{1} }}{s + h} + \lambda } \right)\overline{U} + Gr\overline{T} + Gm\overline{C} } \right],$$

(22)

$$\frac{{d^{2} \overline{T} }}{{d\eta^{2} }} = \Pr \left( {\frac{{sh_{1} }}{s + h} + \phi } \right)\overline{T} ,$$

(23)

$$\frac{{d^{2} \overline{C} }}{{d\eta^{2} }} = Sc\left( {\frac{{sh_{1} }}{s + h} + \gamma } \right)\overline{C} .$$

(24)

The transform conditions are given as:

$$\left\{ \begin{gathered} \overline{f} \left( {\eta ,s} \right) = 0,\;\overline{T} \left( {\eta ,s} \right) = 1/s,\;\overline{C} \left( {\eta ,s} \right) = 1/s \; at\;\eta = 0 \hfill \\ \overline{f} \left( {\eta ,s} \right) \to \overline{U} (s),\;\overline{T} \left( {\eta ,s} \right) \to 0,\;\overline{C} \left( {\eta ,s} \right) \to 0 \;as\;\eta \to \infty \hfill \\ \end{gathered} \right\}.$$

(25)

Using the conditions in Eq. (25), the solutions of Eqs. (22, 23 and 24) are given by:

$$\begin{aligned} \overline{f} (\eta ,s) = & \overline{U} (s)\left[ {1 - \exp \left( { - \eta \sqrt {\frac{{sh_{1} }}{s + h} + \lambda } } \right)} \right] + \frac{{G_{3} (s + h)}}{{s(s + \lambda_{3} )}}\left[ \begin{gathered} \exp \left( { - \eta \sqrt {\Pr (\frac{{sh_{1} }}{s + h} + \phi )} } \right) - \hfill \\ \exp \left( { - \eta \sqrt {\frac{{sh_{1} }}{s + h} + \lambda } } \right) \hfill \\ \end{gathered} \right] \\ & + \frac{{G_{4} (s + h)}}{{s(s + \lambda_{4} )}}\left[ {\exp \left( { - \eta \sqrt {Sc(\frac{{sh_{1} }}{s + h} + \gamma )} } \right) - \exp \left( { - \eta \sqrt {\frac{{sh_{1} }}{s + h} + \lambda } } \right)} \right], \\ \end{aligned}$$

(26)

$$\overline{T} (\eta ,s) = \frac{1}{s}\exp \left( { - \eta \sqrt {\Pr (\frac{{sh_{1} }}{s + h} + \phi )} } \right),$$

(27)

$$\overline{C} (\eta ,s) = \frac{1}{s}\exp \left( { - \eta \sqrt {Sc(\frac{{sh_{1} }}{s + h} + \gamma )} } \right).$$

(28)

where,$h = \frac{\alpha }{(1 - \alpha )},$ $h_{1} = \frac{1}{(1 - \alpha )},$ $G_{1} = \frac{Gr}{{1 - \Pr }},$ $G_{2} = \frac{Gm}{{1 - Sc}},$ $\lambda_{1} = \frac{\lambda - \Pr \phi }{{1 - \Pr }},$ $\lambda_{2} = \frac{\lambda - Sc\gamma }{{1 - Sc}},$ $G_{3} = \frac{{G_{1} }}{{\lambda_{1} + h_{1} }},$ $\lambda_{3} = \frac{{\lambda_{1} h}}{{\lambda_{1} + h_{1} }},$ $G_{4} = \frac{{G_{2} }}{{\lambda_{2} + h_{1} }}$ and $\lambda_{4} = \frac{{\lambda_{2} h}}{{\lambda_{2} + h_{1} }}.$

The above equations can be represented in the more appropriate form:

$$\begin{aligned} \overline{f} (\eta ,s) = & \overline{U} (s)\left[ {1 - \exp \left( { - \eta \sqrt {\frac{{sa_{3} + a_{4} }}{s + h}} } \right)} \right] \\ & + \frac{{G_{3} }}{{\lambda_{3} }}\left[ {h\left( {\frac{1}{s}\exp \left( { - \eta \sqrt {\frac{{sa_{1} + a_{2} }}{s + h}} } \right) - \frac{1}{s}\exp \left( { - \eta \sqrt {\frac{{sa_{3} + a_{4} }}{s + h}} } \right)} \right)} \right] \\ & + \frac{{G_{3} }}{{\lambda_{3} }}\left[ {\left( {\lambda_{3} - h} \right)\left( {\frac{1}{{s + \lambda_{3} }}\exp \left( { - \eta \sqrt {\frac{{sa_{1} + a_{2} }}{s + h}} } \right) - \frac{1}{{s + \lambda_{3} }}\exp \left( { - \eta \sqrt {\frac{{sa_{3} + a_{4} }}{s + h}} } \right)} \right)} \right] \\ & + \frac{{G_{4} }}{{\lambda_{4} }}\left[ \begin{gathered} h\left( {\frac{1}{s}\exp \left( { - \eta \sqrt {\frac{{sa_{5} + a_{6} }}{s + h}} } \right) - \frac{1}{s}\exp \left( { - \eta \sqrt {\frac{{sa_{3} + a_{4} }}{s + h}} } \right)} \right) + \hfill \\ \left( {\lambda_{4} - h} \right)\left( {\frac{1}{{s + \lambda_{4} }}\exp \left( { - \eta \sqrt {\frac{{sa_{5} + a_{6} }}{s + h}} } \right) - \frac{1}{{s + \lambda_{4} }}\exp \left( { - \eta \sqrt {\frac{{sa_{3} + a_{4} }}{s + h}} } \right)} \right) \hfill \\ \end{gathered} \right] \\ \end{aligned}$$

(29)

$$\overline{T} (\eta ,s) = \frac{1}{s}\exp \left( { - \eta \sqrt {\frac{{sa_{1} + a_{2} }}{s + h}} } \right),$$

(30)

$$\overline{C} (\eta ,s) = \frac{1}{s}\exp \left( { - \eta \sqrt {\frac{{sa_{5} + a_{6} }}{s + h}} } \right).$$

(31)

where, $a_{1} = \Pr \left( {\phi + h} \right)$, $a_{2} = \Pr \phi h$, $a_{3} = \lambda + h_{1}$, $a_{4} = \lambda h$, $a_{5} = Sc\left( {\gamma + h} \right)$, $a_{6} = Sc\gamma h$.

In a more simplified form, the above equations can be written as:

$$\begin{aligned} \overline{f} (\eta ,s) = & \frac{1}{s} - \overline{\chi } (\eta ,s,0,a_{3} ,a_{4} ,h) + \varepsilon \left( {\frac{1}{s - i\omega } - \overline{\chi } \left( {\eta ,s, - i\omega ,a_{3} ,a_{4} ,h} \right)} \right) \\ & + \frac{{G_{3} }}{{\lambda_{3} }}\left[ {h\left( \begin{gathered} \overline{\chi } \left( {\eta ,s,0,a_{1} ,a_{2} ,h} \right) - \hfill \\ \overline{\chi } \left( {\eta ,s,0,a_{3} ,a_{4} ,h} \right) \hfill \\ \end{gathered} \right) + \left( {\lambda_{3} - h} \right)\left( \begin{gathered} \overline{\chi } \left( {\eta ,s, - \lambda_{3} ,a_{1} ,a_{2} ,h} \right) - \hfill \\ \overline{\chi } \left( {\eta ,s, - \lambda_{3} ,a_{3} ,a_{4} ,h} \right) \hfill \\ \end{gathered} \right)} \right] \\ & + \frac{{G_{4} }}{{\lambda_{4} }}\left[ {h\left( \begin{gathered} \overline{\chi } \left( {\eta ,s,0,a_{5} ,a_{6} ,h} \right) - \hfill \\ \overline{\chi } \left( {\eta ,s,0,a_{3} ,a_{4} ,h} \right) \hfill \\ \end{gathered} \right) + \left( {\lambda_{3} - h} \right)\left( \begin{gathered} \overline{\chi } \left( {\eta ,s, - \lambda_{4} ,a_{5} ,a_{6} ,h} \right) - \hfill \\ \overline{\chi } \left( {\eta ,s, - \lambda_{4} ,a_{3} ,a_{4} ,h} \right) \hfill \\ \end{gathered} \right)} \right] \\ \end{aligned}$$

(32)

$$\overline{T} (\eta ,s) = \overline{\chi } \left( {\eta ,s,0,a_{1} ,a_{2} ,h} \right),$$

(33)

$$\overline{C} (\eta ,s) = \overline{\chi } \left( {\eta ,s,0,a_{5} ,a_{6} ,h} \right).$$

(34)

The inverse Laplace transformation of Eqs. (32, 33 and 34) are given as:

$$\begin{aligned} f(\eta ,t) = & 1 - \chi (\eta ,t,0,a_{3} ,a_{4} ,h) + \varepsilon \left( {\exp \left( {i\omega t} \right) - \chi \left( {\eta ,t, - i\omega ,a_{3} ,a_{4} ,h} \right)} \right) \\ & + \frac{{G_{3} }}{{\lambda_{3} }}\left[ \begin{gathered} h\left( {\chi \left( {\eta ,t,0,a_{1} ,a_{2} ,h} \right) - \chi \left( {\eta ,t,0,a_{3} ,a_{4} ,h} \right)} \right) + \hfill \\ \left( {\lambda_{3} - h} \right)\left( {\chi \left( {\eta ,t, - \lambda_{3} ,a_{1} ,a_{2} ,h} \right) - \chi \left( {\eta ,t, - \lambda_{3} ,a_{3} ,a_{4} ,h} \right)} \right) \hfill \\ \end{gathered} \right] \\ & + \frac{{G_{4} }}{{\lambda_{4} }}\left[ \begin{gathered} h\left( {\chi \left( {\eta ,t,0,a_{5} ,a_{6} ,h} \right) - \chi \left( {\eta ,t,0,a_{3} ,a_{4} ,h} \right)} \right) \hfill \\ + \left( {\lambda_{3} - h} \right)\left( {\chi \left( {\eta ,t, - \lambda_{4} ,a_{5} ,a_{6} ,h} \right) - \chi \left( {\eta ,t, - \lambda_{4} ,a_{3} ,a_{4} ,h} \right)} \right) \hfill \\ \end{gathered} \right], \\ \end{aligned}$$

(35)

$$T(\eta ,t) = \chi \left( {\eta ,t,0,a_{1} ,a_{2} ,h} \right),$$

(36)

$$C(\eta ,t) = \chi \left( {\eta ,t,0,a_{5} ,a_{6} ,h} \right).$$

(37)

where,

$$\begin{aligned} \chi \left( {y,t,a,b,c} \right) = & \exp \left( { - \lambda t - y\sqrt a } \right) - \frac{{y\sqrt {b - ac} }}{2\sqrt \pi } \\ & \times \int\limits_{0}^{\infty } {\int\limits_{0}^{t} {\frac{{e^{ - \lambda t} }}{\sqrt t }\exp \left( {\lambda t - ct - \frac{{y^{2} }}{4u} - au} \right) \times I_{1} \left( {2\sqrt {\left( {b - ac} \right)ut} } \right)dtdu.} } \\ \end{aligned}$$

(38)

Skin friction

For the Newtonian fluid in a rotating media, the shear stress at the plate (skin friction) is given by:

$$\left. {\tau = \frac{{\partial f\left( {\eta ,t} \right)}}{\partial \eta }} \right|_{\eta = 0} ,$$

(39)

Nusselt number

The Nusselt number, which represents the rate of heat transfer at the plate, can be calculated as follows:

$$Nu = \left. {\frac{{\partial T\left( {\eta ,t} \right)}}{\partial \eta }} \right|_{\eta = 0} .$$

(40)

Sherwood number

Sherwood dimensionless number can be calculated as follows:

$$Sh = \left. {\frac{{\partial C\left( {\eta ,t} \right)}}{\partial \eta }} \right|_{\eta = 0} .$$

(41)

Results and discussion

This study investigates the unstable hydromagnetic free convection flow of a Newtonian viscous fluid over an infinite vertical plate in a rotating system with a fluctuating free stream, employing the Laplace transformation for detailed analysis. This research introduces a generalized fractional model based on the Caputo–Fabrizio approach. The geometry of the problem is illustrated in Fig. 1. The solutions obtained are presented in Figs. 2, 3, 4, 5, 6, 7 and 8, focusing on various parameters, including the thermal Grashof number, mass Grashof number, rotation parameter, Hall current, heat absorption parameter, time, and Schmidt number. These parameters are analysed in relation to their effects on the flow characteristics. For the validation of the present work, it is easy to that the obtained solutions plotted in Figs. 2, 3, 4, 5, 6, 7 and 8 for velocity (primary and secondary), in Fig. 9 for the temperature and in Fig. 10 for the concentration, satisfy the imposed boundary conditions, hence the correctness of the present results is confirmed.

Fig. 1

Geometry of the model.

Fig. 2

The distribution of fluid velocity for distinct values $Gr$ when $Gm = 10$, $m = 0.005$, $\phi = 0.002$, $K = 0.005$, $Sc = 0.5$ and $t = 0.6$.

Fig. 3

Fluid velocity distribution for distinct values of $Gm$ when $Gr = 10$, $K = 0.005$, $m = 0.005$, $t = 0.6$,$\phi = 0.002$, and $Sc = 0.5$.

Fig. 4

The distribution of fluid velocity for distinct values $K$ when $Gr = 10$, $\phi = 0.002$,$Gm = 10$, $m = 0.005$, $t = 0.6$ and $Sc = 0.5$.

Fig. 5

The distribution of fluid velocity for distinct values $m$ when $Gr = 10$, $Sc = 0.5$, $Gm = 10$, $\phi = 0.002$, and $t = 0.6$.

Fig. 6

The distribution of fluid velocity for distinct values of $\phi$ when $Gr = 10$, $m = 0.005$,$Gm = 10$,$Sc = 0.5$, and $t = 0.6$.

Fig. 7

The distribution of fluid velocity for distinct values of $t$ when $Gr = 10$, $\phi = 0.002$,$Gm = 10$,$m = 0.005$, and $Sc = 0.5$.

Fig. 8

The distribution of fluid velocity for distinct values of $Sc$ when $Gr = 10$,$m = 0.005$$Gm = 10$, $\phi = 0.002$ and $t = 0.6$.

Fig. 9

Temperature distribution for distinct values of $\alpha$ when $\phi = 1$ and different values of $\phi$ when $\alpha = 0.2$.

Fig. 10

Concentration distribution for distinct values of $\alpha$ when $\gamma = 0.5$ and different values of $\gamma$ when $\alpha = 0.2$

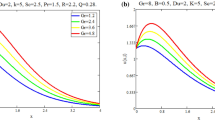
The influence of the fractional parameter $\alpha$ has been analyzed through graphical representations as shown in Fig. 2. These figures demonstrate that the fractional model produces a range of solutions. One of the key advantages of this model is the ability to adjust the fractional parameter $\alpha$ to achieve better alignment between theoretical and experimental results, enhancing the accuracy of the fit. The graphical results illustrate that as the fractional parameter decreases (indicating stronger memory effects), the velocity, profiles exhibit delayed responses, consistent with the physical interpretation of a system with longer-lasting memory. This reflects realistic behavior in complex fluids, viscoelastic materials, or porous media, where the effects of past states persist and influence current dynamics. Moreover, the fractional parameter serves as a fitting tool that can be adjusted to better align theoretical predictions with experimental observations. Unlike classical integer-order models, which may oversimplify transient behavior, the fractional model produces a continuum of possible solutions, offering a richer and more accurate description of unsteady processes. This adaptability enhances the model’s applicability to real-world engineering and physical systems involving hydromagnetic and rotational effects.

As illustrated in Fig. 2, the Grashof number $Gr$ significantly impacts the velocity profile. The Grashof number (Gr) is a dimensionless quantity that characterizes the ratio of buoyancy forces to viscous forces in a fluid flow. Physically, it represents the strength of natural convection within the system. In the context of the present work, which includes heat and mass transfer effects, the Grashof number plays a crucial role in influencing the velocity profile of the fluid. It is evident that both velocities increase with an increasing thermal Grashof number $Gr$. This ratio reflects the balance between buoyancy forces and drag forces, which is physically valid. As the thermal Grashof number $Gr$ increases, buoyancy forces also rise, leading to enhanced fluid velocity. This behavior is consistent with physical expectations: as Gr increases, the thermal buoyancy force becomes more dominant compared to viscous resistance. This buoyant force arises due to temperature differences in the fluid, causing density variations that drive upward motion in heated regions. As a result, the fluid accelerates, and the overall flow becomes more vigorous. In systems with rotational effects, the buoyancy-driven flow interacts with the Coriolis force, but the dominance of a higher Grashof number still leads to enhanced velocity profiles, particularly near the heated surface or in regions where the thermal gradient is strongest. Therefore, the Grashof number serves as a critical parameter in predicting and controlling flow behavior in thermally driven systems, such as those found in geophysical flows, cooling of rotating machinery, and MHD convection in industrial processes. The observed enhancement in velocity with increasing $Gr$ validates the physical realism of the model and highlights the role of thermal convection in accelerating slip flow in a rotating frame.

Figure 3 shows that the mass Grashof number Gm influences fluid velocity similarly to the thermal Grashof number; as Gm increases, fluid velocity also rises. The study identifies that flow reversal occurs in the direction opposing the secondary flow, attributed to buoyancy forces. Notably, when $Gr$, Gm is zero or when free convection is absent, there is no reverse flow. The mass Grashof number quantifies the ratio of buoyancy forces due to concentration differences to viscous forces in the fluid. Physically, a higher Gm indicates stronger mass diffusion-induced buoyancy, which enhances the upward motion of the fluid. As Gm increases, the velocity profile rises accordingly, reflecting an intensified flow driven by concentration gradients. This behavior aligns with physical expectations in mass transfer-dominated convection, where solutal buoyancy acts similarly to thermal buoyancy, accelerating the fluid and contributing to overall flow enhancement in the system.

Figure 4 illustrates the effect of the rotation parameter $K$ on the velocity profile. It shows that the primary fluid velocity increases near the plate with higher values of the rotation parameter $K$, but decreases as the distance from the plate increases. This phenomenon is attributed to the dominance of Coriolis forces near the axis. Similarly, the secondary fluid velocity rises in proximity to the plate as the rotation parameter increases, while it diminishes further away. These effects are all driven by the Coriolis forces, which induce secondary flows within the flow field. More exactly, the rotation parameter represents the strength of the Coriolis force arising from the rotating frame of reference. Physically, as the rotation parameter increases, the Coriolis force becomes more dominant, which tends to resist and deflect the motion of the fluid.

The Hall current arises in electrically conducting fluids under the influence of a strong magnetic field, leading to a secondary electric field perpendicular to both the magnetic field and current. Figure 5 highlights the influence of the Hall current, demonstrating that it reduces primary fluid velocity near the plate. However, during the evaporation process, the opposite effect occurs; the Hall current $m$ enhances secondary fluid velocity near the boundary layer. This behavior results from the Hall current generating secondary fluid motion, a phenomenon also noted by Sato³⁹. Physically, the inclusion of the Hall effect modifies the Lorentz force, causing a redistribution of the electromagnetic force within the fluid. As a result, it introduces a cross-flow component and reduces the direct opposition to the primary flow. This leads to an increase in the velocity profile, particularly in the direction orthogonal to the magnetic field, enhancing overall fluid motion in the system.

In Fig. 6, the effect of the heat absorption parameter $\phi$ is presented, revealing that primary fluid velocity decreases with higher absorption values in the boundary layer. In contrast, buoyancy forces increase secondary velocity near the plate, but this effect diminishes as the fluid moves away and reverses direction. Heat absorption lowers the fluid’s temperature, contributing to the reduction in fluid velocity. The heat absorption parameter represents the rate at which thermal energy is removed from the fluid. Physically, as this parameter increases, the fluid loses heat more rapidly, reducing the thermal buoyancy force that drives the flow. Consequently, the driving force for convection weakens, leading to a decrease in the velocity profile. This reflects the damping effect of heat absorption on fluid motion, particularly in thermally driven flows.

Finally, Fig. 7 shows that both primary and secondary velocities increase throughout the boundary layer as time $t$ progresses. As time progresses, the fluid gradually responds to the applied forces, such as buoyancy, magnetic fields, and rotation. Physically, the velocity profile increases with time as the system evolves from an initial rest state toward a steady or quasi-steady flow. The buildup of momentum over time leads to the development of boundary layers and enhanced fluid motion, especially in unsteady or transient flow conditions.

Figure 8 illustrates the impact of the Schmidt number on velocity distribution, showing that velocities decrease as the Schmidt number (Sc) increases. This relationship is linked to the ratio of viscous forces to mass diffusivity; as the Schmidt number rises, viscous forces become more dominant, resulting in reduced velocities. The Schmidt number (Sc) represents the ratio of momentum diffusivity to mass diffusivity. Physically, a higher Schmidt number indicates lower mass diffusion. As Sc increases, the concentration boundary layer becomes thinner, reducing the solutal buoyancy force that contributes to fluid motion. Consequently, the velocity profile decreases with increasing Schmidt number, reflecting the dampening effect of reduced mass diffusion on flow development.

Figure 9 highlights the significant effects of heat absorption and fractional parameters on fluid temperature. The interplay between these factors plays a crucial role in influencing the thermal characteristics of the fluid. It has been shown that fluid temperature has a declining trend for greater value of $\phi$. In this process, heat is absorbed by the fluid, lowering its temperature. The heat absorption parameter characterizes the rate at which thermal energy is removed from the fluid. Physically, as this parameter increases, more heat is absorbed internally, leading to a reduction in fluid temperature. This dampens thermal gradients and weakens thermal convection, ultimately lowering the temperature profile throughout the flow domain. The fractional parameter, associated with the Caputo–Fabrizio fractional derivative, captures the memory effect in heat conduction. A decrease in the fractional order implies stronger memory, meaning the fluid’s thermal response is more influenced by its past states. This leads to a slower buildup of temperature over time and a more gradual thermal diffusion process. As a result, temperature profiles decrease with lower fractional orders, highlighting the non-local and history-dependent nature of heat transfer in fractional models.

The effect of the chemical reaction parameter $\gamma$ on the concentration distribution is seen in Fig. 10. By fixing the value of $\alpha$ ($\alpha = 0.2$), the graphic shows that the concentration distribution decreases as the value of $\gamma$ grows. The chemical reaction parameter represents the rate at which a reactive species is consumed or generated within the fluid. An increase in this parameter typically corresponds to a faster reaction rate, which reduces the concentration of the diffusing species. This is because the species are either being depleted more rapidly (in case of destructive reactions) or their buildup is limited due to faster reaction dynamics. The fractional parameter, reflecting the memory effects in the Caputo–Fabrizio model, governs the rate of mass diffusion with respect to time. A lower fractional order indicates stronger memory effects, which slow down the diffusion process, resulting in lower concentration values over time. Together, a higher chemical reaction rate and a lower fractional order both contribute to reduced concentration profiles, highlighting the combined effects of reactive depletion and delayed diffusion in fractional-order mass transfer systems.

According to Table 1, skin friction decreases as $m$, $\phi$, and $\gamma$ are increased, while it increases as the value of t, $Gr$ and $Gm$, increases, while $K$ increases the skin friction. As can be seen in Table 2, the effect of time t and the heat absorption coefficient $\phi$ is analysed. A rising $\phi$ causes the heat transfer rate to grow while a decreasing $\phi$ results in a decreasing heat transfer rate. The Nusselt number increases as the heat absorption parameter $\phi$ increases and decreases with t. The chemical reaction parameter $\gamma$ and Schmidt number Sc have an influence on the Sherwood number, as seen in Table 3. It has been noticed that when the Sc increases, the Sh (Sherwood number) increases and also for larger values of $\gamma$.

Table 1 Impact of distinct parameters on skin friction.

Table 2 Impact of distinct parameters on Nusselt number.

Table 3 Impact of distinct parameters on Sherwood number.

Conclusions

In this work a generalized fractional model is presented whose solution is based on the Laplace transformation. The influence of various parameters have been visually described. The following are the key results based on the current analysis.

• Thermal buoyancy forces maximize both primary and secondary velocities, causing reverse flow in the secondary fluid direction.

• When the fluid moves away from the plate, rotation decreases the primary velocity; however, as it approaches the plate, this effect is reversed. An increase in the rotation parameter leads to a rise in secondary fluid velocity.

• Within the boundary layer, both velocities increase over time.

• As rotation continues, skin friction rises, and buoyancy forces also strengthen over time, resulting in a decrease in fluid temperature due to heat absorption.

• Chemical reactions diminish species concentration in the fluid by lowering the reaction parameter.