Introduction

Cancer, with more than 200 different types, is the leading cause of death in the world (more than 1500 deaths per day)1. Most cases arise from environmental factors especially such as alcohol, cigarettes, radiation exposure and chemicals, among others. Meanwhile, despite recent advances, cancer diagnosis in the early stages of its progression and the prognosis of cancer is still a challenge2,3. The main problem in cancer diagnosis is the lack of symptoms in the early stages of cancer, and this causes the cost of cancer treatment to reach 246 billion dollars by 2030, so early detection of cancer is vital for society and the patient4. A wide range of genetic abnormalities and epigenetic factors affecting signaling are the leading cause of malignancy and tumorigenesis5. According to the definition of the National Cancer Institute (NCI), a biomarker is a biological agent found in body fluids such as blood and urine that indicates a process or a specific condition (either disease or health) of an individual. These markers originate from molecules, including deoxyribonucleic acid (DNA), ribonucleic acid (RNA), or proteins such as antibodies, oncogenes, and hormones6,7. These markers can act as a prognostic factor and express the possibility of disease recurrence or act as a diagnostic biomarker, and according to their concentration in the blood, urine, cerebrospinal fluid, and even on the surface/inside the tumor cells, the response examined the treatment6,8. Accurate, high-sensitivity, non-invasive, and rapid assay of cancer biomarkers helps to identify and monitor the cancer treatment process3.

Traditional methods of cancer diagnosis are based on morphological and microscopic changes in cancer cells, which require a biopsy to detect the cancer9. Some recent techniques use high-sensitivity safety methods and detect biomarker concentrations. However, they are time-consuming and expensive. These include enzyme-linked immunosorbent assay, radioimmunoassay10, immunohistochemistry11, polymerase chain reaction12, and western blot13. Meanwhile, in recent years, the use of biosensors with high sensitivity, faster response than previous methods, with high selectivity, and non-invasiveness properties has attracted much attention9. Nanomaterials such as metal nanoparticles (NPs), metal oxide NPs, graphene, carbon nanotubes, metal–organic frameworks, perovskites, and MXenes are widely employed as active sensing layers in biosensors, offering low cost, high accuracy, rapid response, and excellent sensitivity14,15,16,17. Within this broad class, plasmonic nanostructures stand out as versatile platforms with applications extending from solar energy harvesting18,19,20,21, and optical detection22, to nonlinear subwavelength optics23, refractive index sensor24, high-performance absorbers25, nanoscale logic operations26, and advanced sensing devices27.

Plasmonic biosensors are gaining popularity due to their potential impact on early cancer detection. In case of leukemia, detection of specific biomarkers such as circulating tumor DNA (ctDNA), microRNA, protein antigens etc. in blood samples is important for early detection and disease management plasmonic biosensors can detect these biomarkers are at very low levels, facilitating early intervention and personalized treatment strategies28. For breast cancer, plasmonic biosensors help detect markers such as HER2, CA15-3, and circulating tumor cells (CTCs), which are important for early detection, prognosis, and monitoring of treatment efficacy In cancer are found about, this means biomarkers in blood or other body fluids with unprecedented sensitivity can be detected29,30,31.

These sensors rely on localized surface plasmon resonance (LSPR), whereby conduction electrons on metal nanoparticle surfaces vibrate in resonance with incident light. The result is an amplification of the electromagnetic field at the nanoparticle level, thereby making the sensor more sensitive to detect molecular interactions, including those involving cancer biomarkers.

Sharp-edged NPs such as nanostars, nanorods, and also nanocubes stand out among all other particles. These particles have sharp tips and edges that act as “hot spots” where the intensity of the local electromagnetic field is greatly increased.

Plasmonic nanostructures trapping electrons in free space have characteristics that cannot be found in bulk materials32.The basis of work in biosensors based on plasmonic nanostructures is that the solid light-induced interaction between metal NPs such as gold (Au) and silver (Ag) with their free conduction band electrons creates resonant excitation of localized surface plasmons (LSPs) that cause collective charge fluctuations. It is related to dielectric/conductor-bound electromagnetic states32,33. The external field instinctively creates charges on the metal surface, which encourages the restoring force that drives more electric currents and continues the electron oscillation, and LSP resonance LSPR occurs34. LSPR is a phenomenon that allows the confinement of the high light state in nanometer volumes35. The metamaterial-based LSPR sensor exhibits greater sensitivity compared to conventional integrated optical sensors36. LSPRs are highly sensitive to NP geometry, spacing, wavelength, and polarization, which govern the near-field enhancement essential for sensing applications. Prior studies have shown strong dipolar plasmon resonances in coupled silver nanostructures37,38, as well as sharp Fano resonances in engineered plasmonic platforms such as elliptical ring–stub resonators and nanorod arrays39,40,41.These phenomena provide a foundation for achieving narrow spectral features and enhanced sensitivity, motivating the exploration of advanced geometries for biosensing.

In recent years, various plasmonic sensor architectures have been explored to harness the advantages of LSPR in practical detection platforms. For instance, metal–insulator–metal (MIM) sensors incorporating bowtie resonators have demonstrated highly tunable responses through strong coupling effects42. Similarly, metasurface-based designs, such as gold cross-bar patch structures, can generate multiple LSPR modes with enhanced sensitivity and robustness43. Photonic crystal fiber sensors integrated with plasmonic coatings represent another promising approach, enabling ultra-sensitive detection of biomolecules in aqueous environments44. Furthermore, periodic metasurface absorbers combining metallic nanobar arrays with thin films have been shown to support multiple hybrid resonances across the near- and mid-infrared spectrum, achieving near-unity absorption efficiency37. These advances illustrate the breadth of plasmonic sensing strategies and motivate exploring novel resonator geometries that further improve sensitivity, selectivity, and spectral tunability.

In this paper, we investigate plasmonic metamaterials based on an octa-square split-ring-shaped supercell for the detection of cancer biomarkers. Unlike conventional split-ring resonators or coupled nano-ring arrays reported in previous studies, the proposed geometry integrates eight interconnected square-ring units that simultaneously support LC and plasmonic resonances. This dual-mode behavior enables stronger mode hybridization and broader spectral tunability compared to earlier designs. Moreover, the sharp corners and engineered nanogaps of the structure act as efficient field concentrators, generating intense localized hot spots that amplify refractive index sensitivity by at least one order of magnitude compared to smoother nanorings. The high structural symmetry of the supercell also reduces polarization dependence, ensuring more stable sensing signals. Together, these features provide a distinct improvement in sensitivity and FOM, highlighting the novelty of our approach. The sensor is designed on a SiO₂/Au substrate and evaluated for its potential to distinguish between various cancer types through refractive index contrasts between healthy and malignant cells. Collectively, these innovations distinguish the proposed architecture from previously reported SRR and nanoring structures, establishing its novelty and potential for high-performance biosensing.

Materials and methods

The increasing demand for label-free cancer detection methods has driven the development of plasmonic biosensors, particularly those utilizing LSPR to detect molecular changes with high accuracy. Researchers have explored various structures and designs for LSPR-based sensors. Given the critical importance of early and accurate cancer diagnosis in today’s era, there is a growing need for novel sensor structures that yield improved and reliable results.

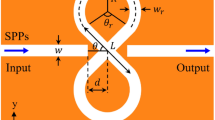
The proposed structure is depicted in Fig. 1(a), where symmetrical nanorods connector positioned in the center and is surrounded by octa- square split ring-shaped supercells. In general, the introduced structure resembles a nona-cell supercell, composed of octa-supercells arranged in a square split ring, along with an additional supercell referred to as nanorods. In Fig. 1(b), a three-dimensional perspective of a single unit cell is provided to facilitate a clearer understanding of the proposed nanostructure. In Fig. 1(c), the complete set of geometrical parameters is indicated, including the common thickness of the nanorings and nanorods (Wn), the gap between adjacent rings (Wg), and the structural lengths (L₁, L₂, L₃, and Liₙ). Moreover, the C₂ rotational symmetry axes passing through the midpoint of L₂ are explicitly shown, as they play an important role in defining the polarization-dependent optical response discussed in later sections.

To simulate SiO2 in the simulation software, we assign a refractive index of 1.4. The refractive indices of the metallic nanostructures (Au, Ag, Al) and the substrate were taken from the experimental data reported in Palik’s handbook, which is widely used in plasmonic simulations to ensure accurate representation of dispersion and losses45. The refractive index of the reference Liquid is 1.33. Corresponding to water, which is commonly used as the standard surrounding medium in plasmonic biosensing46. Additionally, according to Fig. 1, the (H) parameter related to the height of the metamaterial is referred to as (Hr). In the context of height-related parameters, the designations (H1), (H2), and (H3) correspond to the Au substrate, SiO2, and sample sensing medium, respectively. Various dimensional parameters undergo a sweeping process, and the optimal values are subsequently chosen. The optimal values chosen for the proposed structure are provided in Table 1.

Fig. 1
figure 1

(a) Three-dimensional schematic of the proposed plasmonic metamaterial with an octa-square split-ring supercell. (b) Isometric 3D view of a single unit cell in the octa-ring supercell design. (c) Top view of octa-ring supercell, showing the C₂ rotational symmetry axes of the structure.

Full size image
Table 1 Optimal values ​​of the proposed structure.
Full size table

Larger NPs have been thoroughly studied, even though we have learned a lot about them. Understanding the behavior of diminutive quantum-sized particles remains a challenging endeavor. Their susceptibility to weak optical scattering and intricate interactions with metal–ligand interfaces continues to engage researchers in this field. However, in the case of quantum NPs, their electron bands undergo continuous discretization, resulting in a distinct plasmon resonance compared to larger NPs. This phenomenon is commonly referred to as LSPR. One notable effect of LSPR is that, at the plasmon resonance frequency, maximum absorption is exhibited by NPs in the context of LSPR. This absorption behavior is influenced by factors such as variations in the refractive index of the surrounding medium and serves as a fundamental basis for various measurement applications. The phenomenon becomes evident in the reflected spectrum, where the spectrum shows its minimum value at the resonance frequency47. Cancer cells exhibit altered refractive indices compared to normal cells due to variations in cell membrane thickness, organelle distribution, and overall cellular density. Notably, the refractive index of cancer cells tends to be higher than that of healthy cells, while healthy cells maintain a consistent and predictable refractive index influenced by cellular components such as water, proteins, lipids, and nucleic acids. If the refractive index is defined as n = n₀ + Δn, where Δn denotes the changes in refractive index brought about by the presence of cancer cells and n₀ is the refractive index of the solution without any cancer cells, typically 1.33. The spectrum detected by the sensor depicts a red shift as the concentration of various cancer cells increases. In this research, altering the cancer cells concentration modifies the refractive index of the sensor surface, resulting in changes to the reflection spectra. These variations provide valuable information, including insights into the sensor’s sensitivity. The sensitivity of the sensor to wavelength shifts resulting from refractive changes can be expressed using Eq. (1)48.

$$S{\text{ensitivity}}=\frac{{({\lambda _2} - {\lambda _1})}}{{({n_2} - {n_1})}}[nm/RIU]$$
(1)

In the context of this study, Δn represents the refractive index change of the sensor layer, while Δλ corresponds to the wavelength shifts resulting from this refractive index change. Within the realm of biosensors, the FOM combines the sensitivity and the full width at half maximum (FWHM) of the resonance. It serves as a crucial metric for evaluating the intrinsic resolving power of metasurface-based optical biosensors, and it can be mathematically defined as:

$$FOM=\frac{{S{\text{ensitivity}}}}{{FWHM}}[RI{U^{ - 1}}]$$
(2)

The spectral sharpness of each resonance can be quantified using the quality factor (Q), which reflects the ratio of the stored energy to the energy dissipated per cycle. In optical resonators, Q is directly related to the resonance wavelength λR and the full width at half maximum (FWHM) of the corresponding spectral dip. The quality factor is therefore expressed as:

$$Q=\frac{{{\lambda _R}}}{{FWHM}}$$
(3)

The limit of detection (LOD) is a key performance metric in optical biosensing that indicates the minimum detectable refractive index change (Δn), which can still be reliably distinguished from noise. In other words, it represents the smallest shift in refractive index that the sensor is capable of identifying. The LOD is therefore an essential benchmark for evaluating the sensitivity and practical applicability of optical biosensors, especially in real biological detection scenarios. It is generally defined as follows49:

$$LOD=\frac{{{\lambda _R}}}{{20SQ}}$$
(4)

The outcomes of this sensor design were acquired through simulations conducted using Finite-Difference Time-Domain (FDTD) by Lumerical software. In these analyses, a 3D FDTD simulation was employed, with the boundary condition in the z-direction set as a perfectly matched layer (PML) and periodic in the x and y-directions. Throughout all simulations, a mesh size of 2 nm was applied around the octa-cell supercell. The plane wave light was incident from the top of the sensor in the z-direction at varying wavelengths, and the reflective spectrum from the sensor was observed and analyzed. The structure we have introduced exhibits two distinct plasmonic modes. One of these modes is referred to as LC, while the other mode corresponds to plasmon resonance, occurring at the metal-insulator interface. LC resonant modes are commonly observed in split structures, where the nano-scale gaps serve as capacitors (C) and the remaining portions act as inductors (L), akin to an LC resonant circuit. The LC mode enables exceptionally high sensitivity. The primary objective of this research is to design a novel structure featuring LC resonant behavior. In addition to enhancing sensitivity, this structure manifests narrow spectral responses across various plasmon modes, thereby improving the FOM.

Results and discussions

In this section, we meticulously explore the optimal design of the structural dimensions and rigorously compare the results across various modifications. Our proposed structure elegantly reveals two distinct resonance modes, which are discernible in the reflection spectra. Our primary objective within this section is to precisely identify the optimal state by conducting a comprehensive analysis of simulation results and meticulously comparing them in the two distinct states. Additionally, a detailed investigation of local fields, surface charge distribution, and current density within the structure provides valuable insights into light interaction with nano-scale structure and gaps. The specific physical properties of a resonant mode observed in the spectrum curves are intricately determined by the complex local field distribution50.

Fig. 2
figure 2

Electric field distribution at (a) λ = 1322 nm, (b) λ = 1929 nm, magnetic field distribution at (c) λ = 1322 nm, (d) λ = 1929 nm.

Full size image

Figure 2 illustrates the electric and magnetic fields corresponding to the two identified dips at wavelengths of 1322 nm and 1929 nm. Figure 2(a) shows Mode-1, the average electric field enhancement reaches values of ~ 60 at the metallic edges and at the junctions connecting the upper and lower rings, revealing the formation of sharp-edge “hot spots” due to the lightning-rod effect. In Mode-2, the electric field is strongly concentrated inside the gap region, with an average enhancement of ~ 82, which confirms the capacitive confinement across the split (see Fig. 2(b)). The corresponding magnetic field enhancements are shown in Figs. 2(c, d): in Mode-1, the magnetic energy is mainly localized along the connection lines and away from the gaps, whereas in Mode-2 the field lines extend towards the gap and exhibit stronger intensity there, further validating its LC-like resonant behavior. The plasmon hybridization theory provides a rigorous framework for interpreting the origin of complex resonances in coupled metallic nanostructures. Analogous to molecular orbital theory, the individual plasmons supported by isolated components (e.g., the metallic ring and the split gap) interact and hybridize when placed in proximity. This coupling lifts the degeneracy of the original modes and results in the formation of new bonding (symmetric) and antibonding (antisymmetric) plasmonic states51.

Fig. 3
figure 3

Surface charge distribution (C/m²) at (a) λ = 1322 nm, (b) λ = 1929 nm, current density (A/m²) at (c) λ = 1322 nm, (d) λ = 1929 nm.

Full size image

Figures 3(a) and 3(c) depict the surface charge and current density distributions at the wavelength of 1322 nm. Similarly, Figs. 3(b) and 3(d) illustrate the corresponding distributions at the wavelength of 1929 nm. Analyzing Fig. 3(a, b) alongside the electric field distribution in Fig. 3(a, b), we observe a characteristic electric dipole response, specifically a plasmon mode, where the surface charge distribution around the gaps remains consistent. However, in the upper regions of the split rings, this distribution differs, resembling an electric dipole behavior. Figures 3(c, d), which depicts the current density within the nanoparticle, further confirms this dipole mode. Notably, the numerical value of the current density at the top of the split rings is significantly higher, and these regions are distinctly separated. In the subsequent sections of this study, we delve into a comprehensive review and analysis of this mode.

According to previous explanations, Figs. 3(a) and 3(b) reveal changes in the surface charge density distribution around the gap areas. Additionally, strong electric field distribution occurs within these gaps (as observed in Fig. 2). Remarkably, Fig. 3(b, d) exhibits a current loop in supercells, predominantly observed in split-ring resonators (SRRs). This observation supports the magnetic dipole response and can be understood in terms of an oscillatory LC circuit. Specifically, the splits function as capacitors (C), while the annular part of the split ring serves as inductance (L). Furthermore, sharped NPs generally exhibit superior charge distribution at their apex due to the lightning effect. It’s worth noting that the manufacturing technology for these NPs is more intricate than that for their spherical counterparts.

The plasmon hybridization theory provides a rigorous framework for interpreting the origin of complex resonances in coupled metallic nanostructures. Analogous to molecular orbital theory, the individual plasmons supported by isolated components (e.g., the metallic and the split gap) interact and hybridize when placed in proximity. This coupling lifts the degeneracy of the original modes and results in the formation of new bonding (symmetric) and antibonding (antisymmetric) plasmonic states51. In the proposed structure, the modal characteristics revealed in Fig. 3 are consistent with this framework.

Mode-1 exhibits a dipolar surface charge distribution and nearly linear surface currents along the metallic arms, which are indicative of an antibonding plasmonic dipole mode (bright mode) that couples efficiently to the incident field and radiates strongly, as illustrated in Fig. 3(a, c). In contrast, Mode-2 shows the accumulation of opposite charges across the split, accompanied by a circulating displacement current loop, as shown in Figs. 3(b, d). This configuration corresponds to a bonding (dark) hybrid mode, in which the split acts as the capacitive element and the metallic loop serves as the inductive path, forming a resonance that an LC oscillator can accurately describe. Thus, the asymmetric surface charge and current distributions observed in Fig. 3 not only illustrate the spatial localization of charges but also validate, within the framework of plasmon hybridization theory, that the first resonance originates from a bright plasmonic dipole mode, whereas the second resonance arises from a bonding LC-type mode with strong capacitive confinement.

It should be noted that although the biosensor operates in a uniform aqueous medium (n = 1.33), the two resonance modes interact differently with their surrounding dielectric environment owing to their distinct field confinement profiles. The plasmonic dipole mode is mainly influenced by the outer metallic edges, whereas the LC resonance is strongly localized within the nanogap regions. As a result, each mode effectively senses a different local refractive index. In practical biosensing applications, this property can be exploited by functionalizing the outer ring surfaces and the inner gap regions with different receptor layers, thereby enabling the simultaneous detection of multiple biomarkers within the same device52,53. Research into the applications and physical contexts of LSPR reveals that its characteristics are influenced by several critical factors, including the type and size of the metal and its surrounding environment18,19,20,54. Consequently, this study systematically examines the behavior of three metals frequently employed in plasmonic biosensors. Each metal was independently integrated into the proposed structure and analyzed through simulation to evaluate its biosensing properties. The purpose of these simulations is to identify the material that exhibits optimal compatibility with the suggested design.

Fig. 4
figure 4

(a) Reflectance spectra for Al, Au, and Ag metals, showing distinct resonance Modes in the 1–2.1 μm range. (b) Sensitivity values for Ag and Au at Modes 1 and 2, and a single sensitivity for Al. (c) FOM values, for Ag, Au and Al.

Full size image

As shown in Fig. 4(a), the reflectance spectra of the structure were analyzed for each metal. Interestingly, in the wavelength interval of 1 to 2.1 μm, aluminum (Al) showed resonance at a single wavelength associated with Mode-2, but Au and Ag metals showed resonance at separate wavelengths (labeled as modes 1 and 2). In particular, Al was found to exhibit LC resonance characteristics in this wavelength range. Sensitivity and FOM calculations were done for every metal to find the best material. The sensitivity values for Ag (Modes 1 and 2: 532.2 (nm/RIU) and 1005.1 (nm/RIU), respectively) and Au (Modes 1 and 2: 604 (nm/RIU) and 1097.1 (nm/RIU), respectively) are shown in Fig. 4(b). On the other hand, Al demonstrated a sensitivity of 772 (nm/RIU) in its single mode. The FOM values are depicted in Fig. 4(c): in Mode-1, Au and Ag obtained FOMs of 14.72 (RIU−1)and 10 (RIU−1), and in Mode-2, 15.64 (RIU−1)and 10.4 (RIU−1), respectively. Al, on the contrary, has a FOM of just 1.3 (RIU−1). Based on these numerical results, it is evident that Au is the optimal choice for the proposed octa-cell structure. Its high sensitivity and smaller full width allow effective tracking and detection of refractive index changes in various bio sample types, including those containing cancer cells. In addition to these numerical advantages, Au is also preferred because of its chemical stability. Unlike Ag and Al, which are prone to surface oxidation that introduces extra optical losses and broadens the resonance, Au remains largely resistant to oxidation while maintaining strong plasmonic resonances in the near-infrared55,56. Although oxidation effects were not included in our simulations, they would, in practice, further reduce the performance of Ag and Al. This makes Au not only the most sensitive option in theory but also the most reliable choice for stable, long-term biosensing.

Fig. 5
figure 5

(a) Reflectance spectra for mesh sizes of 2, 3, and 4 nm. (b) Extracted sensitivities: Mode-1 = 604, 553, 621 (nm/RIU) and Mode-2 = 1097.1, 972, 1017 (nm/RIU) for 2, 3, and 4 nm meshes, respectively.

Full size image
Fig. 6
figure 6

Reflectance spectra for (a) TM and (c) TE polarizations, with corresponding sensitivity and FOM values shown for (b) TM and (d) TE under refractive index variations from 1.33 to 1.3477.

Full size image

To ensure the convergence of the FDTD simulations, we repeated the calculations with different mesh sizes of 2, 3, and 4 nm. Figure 5(a) shows the reflection spectra of the structure under these three mesh conditions. The main resonances appear consistently in all cases, confirming that the simulated optical response is numerically stable. Small variations in the resonance wavelengths and depths, especially for the 3 nm mesh, are due to the conformal meshing algorithm in Lumerical. This adaptive meshing improves the accuracy near curved and sharp-edged geometries, but in complex symmetric designs, the mesh elements at opposite sides may not be perfectly symmetric, leading to slight spectral shifts. A quantitative comparison is presented in Fig. 5(b), where the sensitivities for the two resonant modes under different mesh sizes are plotted. For Mode-1, the sensitivities are 604, 553, and 621 (nm/RIU) for mesh sizes of 2, 3, and 4 nm, respectively, while for Mode-2 they are 1097.1, 972, and 1017 (nm/RIU). The calculated FOM also show only minor variations across the three cases. These results demonstrate that the resonance behavior and sensing performance are well converged and not significantly affected by the chosen mesh size.

It is imperative to emphasize that metamaterials within plasmonic structures featuring sharp edges exhibit pronounced sensitivity to the polarization of incident light. Consequently, investigating this phenomenon is of utmost importance. To gain insights into this issue, we systematically altered the polarization of the incident light interacting with the structure. The resulting reflected spectra are presented in Fig. 6.

Figure 6(a) corresponds to the reflecting spectrum for transverse magnetic (TM) polarization, while Fig. 6(c) represents the reflecting spectrum for transverse electric (TE) polarization. The sensitivity and FOM were quantified by varying the refractive index from 1.33 to 1.3477. Figure 6(b) presents the results for TM polarization, while Fig. 6(d) showcases the outcomes for TE polarization. Specifically, in TM polarization, sensitivity values of 710.7 and 1272 were observed for Modes 1 and 2, respectively, with corresponding FOM values of 4.4 (RIU−1) and 5.3 (RIU−1). In TE polarization, the sensitivity for Modes 1 and 2 was 604 (nm/RIU) and 1097.1 (nm/RIU), respectively. Notably, the FOM values were 14.72 (RIU−1)and 15.64 (RIU−1) for Modes 1 and 2, respectively. While high sensitivity is exhibited by both TM and TE polarizations, it is worth noting that the FOM value for TE polarization surpasses that of TM polarization. The proposed sensor demonstrates robust sensing performance under both TE and TM polarizations, although minor differences in sensitivity and FOM exist between the two cases. Hence, while the design performs well for both incident polarizations, it should not be regarded as completely polarization-insensitive. These results affirm that varying incident light polarization does not adversely affect the proposed biosensor. However, due to the superior FOM in TE polarization, our simulations were conducted using incident light of this polarization.

Fig. 7
figure 7

Surface charge density (C/m²) distributions of Mode-2 under (a) TM and (b) TE polarization.

Full size image

To further elucidate the origin of the observed differences between TE and TM polarizations, the surface charge distributions were analyzed, as discussed below. In Fig. 7(a), under TE illumination, the electric field is aligned with the split (gap) orientation, whereas in Fig. 7(b), under TM illumination, the field is aligned with the central connecting axis along x axes (i.e., along L1). In the TE case, strong and spatially extended charge accumulation is observed across the structure most prominently the opposite charges across the gaps and enhanced charging at the edge/junction regions confirming robust capacitive coupling. In contrast, in the TM case, the surface charge density along the x axis is noticeably weaker, with much poorer gap charging. Beyond amplitude, symmetry effects also differentiate the two polarizations. For TE, the surface charges on the side arms are clearly asymmetric, and this asymmetry is also evident around the gaps. Such asymmetry suppresses the net dipole moment and promotes a dark-like LC current loop, which reduces radiative loss and narrows the linewidth (i.e., increases Q). By contrast, under TM excitation, the surface charge distribution around the gaps is more symmetric, producing a brighter dipolar response with larger radiation loss and a broader linewidth. Together, these two factors (i) alignment of TE polarization with the gap orientation that maximizes capacitive confinement, and (ii) TE-induced symmetry breaking that suppresses radiative losses, provide a consistent physical rationale for why the FOM under TE excitation is higher than under TM excitation for Mode-2. These numerical results are also summarized in Table 2, which directly compares the sensitivity, Q-factor, and FOM of Mode-2 under TE and TM polarizations. The tabulated results further confirm that, while both polarizations support high sensitivity, TE illumination consistently provides a higher Q-factor and FOM than TM illumination.

Table 2 Comparison of sensitivity, Q-factor, and FOM of Mode-2 under TE and TM polarization.
Full size table
Fig. 8
figure 8

Evaluation of sensitivity and FOM under different values of Wn, Hr, and Wg.

Full size image

The performance of the proposed biosensor is optimized through a comprehensive parameter sweep. This sweep involves the examination of all relevant parameters and scales associated with the structure depicted in Fig. 1. Due to meticulous meshing and high precision, these parameters were successfully explored, resulting in their optimal values reported in Table 1. Sensitivity and FOM were evaluated for varying values of three critical parameters (Wn, Hr, and Wg), as illustrated in Fig. 8 to elucidate the sensor’s behavior during these sweeps.

The consistent ratios were maintained when adjusting parameter values, given the structure’s sharp edges and the significance of accurate meshing. Specifically, these values were scaled by a factor of 2 to ensure that the simulation’s meshing remained unchanged. The obtained results exhibit high reliability. Figure 8 (a) and (b) correspond to the transverse value sweep of the octa-cell structure. Figure 8 (a) relates to resonance Mode-1, while Fig. 8 (b) corresponds to Mode-2. Notably, as the width (Wn) increases, sensitivity decreases in both Modes. Based on the FOM and sensitivity analysis, an optimal value of 18 nm is recommended for this structure. Panels (c) and (d) in Fig. 8 are focused on sensitivity and FOM variations in the height of the proposed octa-cell structure. Performance enhancement in Mode-2, where sensitivity is more pronounced, is our primary goal. Considering this, an advisable height value of 48 nm is determined. Additionally, the gap size between the rings was explored. This optimization can be rationalized through the concept of optical skin depth, given by δ = λ/(4πk). Using Palik’s optical constants for Au in the near-infrared region (1500–1900 nm), the extinction coefficient is in the range approximately 10–13, yielding a skin depth of about δ ≈ 11–12 nm45,57. The optimized thickness is therefore approximately four times the skin depth, which is a well-established design criterion in plasmonic systems to maximize near-field confinement while minimizing total damping. For thicknesses below the skin depth, the resonance suffers from high Ohmic resistance and broadened linewidths, while excessively thick films increase radiative damping and reduce field localization. Hence, the choice of Hr=48 nm provides an optimal balance, resulting in the strongest hot-spot intensity, the narrowest resonance linewidth, and the highest FOM.

Panels (e) and (f) in Fig. 8 correspond to Mode-1 and Mode-2, respectively. Based on these diagrams, an optimal gap size of 18 nm for the proposed biosensor is determined. After completing all sweeps, as shown in Fig. 8, the final sensitivity values for Modes 1 and 2 were determined to be 604 nm/RIU and 1097.1 nm/RIU, respectively, with corresponding FOM values of 14.72 (RIU−1) and 15.64 (RIU−1).

As previously mentioned, a redshift in the reflectance spectrum wavelength is induced by an increase in the refractive index of the cancer solution sample. To illustrate this relationship, the refractive index of the solution was systematically raised from its initial value of 1.34, incrementing it in steps of 0.07. The resulting redshift values in the reflectane spectra were then observed, as depicted in Fig. 9. Specifically, Fig. 9 (a) and (c) correspond to Modes 1 and 2, respectively. The fitted line representing the relationship between the displacement of the resonance wavelength and changes in the refractive index is presented in Figs. 9 (b) and (d). Although there are numerical errors in the simulation results, the changes in the resonance spectrum exhibit slight deviations from their average value in different small sections. However, the high R-squared value for the fitted lines suggests that the data follow a linear trend. Overall, the regression closely matches the observed data. Designed to detect insignificant refractive index changes (particularly relevant for early-stage cancer detection), this biosensor is proven to be highly valuable.

Cancer represents a dangerous condition marked by uncontrolled cell proliferation that disseminates throughout the body, resulting in harm to healthy tissues and ultimately leading to mortality. Timely detection significantly impacts cancer diagnosis and patient outcomes. In this context, a refractive index-based biosensor capable of discerning different tissue cell types by analyzing variations in tissue refractive indices is proposed. Specifically, an LSPR-based sensor for detecting cancer has been developed. According to previous findings54,58,59, each cancer type is characterized by a unique refractive index, as summarized in Table 3.

Fig. 9
figure 9

(a) Performance of the reflectance spectrum for the plasmonic biosensor at Mode-1 and (b) Mode-2 under varying refractive indices. (c) Fitted Correlation between resonance wavelength shifts and refractive index changes for Mode-1, and (d) for Mode-2.

Full size image

Table 3 provides the refractive indices for different types of cancer and healthy cells separately. Considering that changes in the refractive index of a cancer cell relative to a healthy sample result in a redshift in the biosensor’s reflectance spectrum, the reflectance spectrum of the biosensor containing healthy and cancerous samples is examined in Fig. 10.

Table 3 Refractive index data for normal and cancerous cell analytes.
Full size table
Fig. 10
figure 10

Reflectance spectra for healthy cells compared with (a) skin cancer, (b) cervical cancer, (c) blood cancer, (d) adrenal gland cancer, and (e-f) breast cancer.

Full size image

Figure 10 shows the reflectance spectra for healthy cell conditions alongside various cancer cell types, specifically illustrating (a) skin cancer, (b) cervical cancer, (c) blood cancer, (d) adrenal gland cancer, and (e–f) breast cancer. Notably, distinct redshifts are observable in each spectrum, indicating changes in resonance. These reflectance spectra were analyzed to calculate sensitivity and the FOM for each cancer cell type across resonance Modes 1 and 2. Detailed parameter values for these calculations are provided in Table 4. According to Table 4, the highest sensitivity in Mode-2 corresponds to Jurkat cancer cell detection, while in Mode-1, it relates to MDA-MB-231 cancer cell detection. Additionally, the highest FOM is associated with the return spectrum of the basal cancer cell sample in Mode-2, while in Mode-1, the MDA-MB-231 cancer cell exhibits the highest FOM. It should be noted that all results reported in this study are valid under ambient conditions (T = 300 K, n = 1.33). In practical biosensing environments, factors such as temperature fluctuations, ionic strength, and pH may alter the local refractive index, leading to slight shifts in resonance peaks and sensitivity60,61.

Table 4 Performance parameters of the designed sensor for cancerous cell detection.
Full size table

Based on Table 4, the estimated LOD for the targeted cancer panels are on the order of Δn ≈ 3 × 10⁻³ (RIU), which indicates that the proposed sensor can be applicable for real biosensing scenarios. From a physical perspective, sharp edges in plasmonic nanostructures concentrate electric fields much more efficiently than smooth regions, giving rise to highly localized “hot spots” that strongly enhance LSPR. In split-ring resonators, the deliberate gap within the ring further intensifies the localized electric fields and introduces LC-type resonances at lower frequencies, thereby extending the accessible spectral range. This structural configuration allows split rings to alter the optical response of materials and generate distinct resonance modes. The thoughtful combination of sharp-edged geometries with split-ring features therefore markedly amplifies the sensitivity of plasmonic biosensors, which is particularly valuable for detecting biomarkers at ultra-low concentrations. Compared with conventional split-ring resonators and previously reported coupled nanoring structures54,62,63,64, the proposed octa-square split-ring supercell offers clear advantages. While most classical SRRs predominantly exhibit a single LC resonance and nanoring geometries usually support only plasmonic modes, our design enables the coexistence of both LC and plasmonic resonances in a single architecture. This dual-modal behavior broadens the spectral tunability and enhances sensitivity through stronger mode interaction. Moreover, the sharp corners of the octa-square geometry act as efficient field concentrators, producing hot spots that significantly enhance refractive index sensitivity. Prior studies have shown that sharp-edged plasmonic nanostructures can exhibit electric field enhancements an order of magnitude greater (|E|/|E0| ≈ 10–100) than smoother counterparts such as spherical nanoparticles, corresponding to intensity enhancements to 102–10465. This effect underpins the superior sensitivity of our design, where at least one resonance mode directly benefits from hot-spot amplification. Furthermore, the balanced capacitive–inductive coupling in the octa-square configuration leads to narrower resonance linewidths and thus a higher FOM for biosensing applications.

Table 5 Sensitivity comparison between this study and results from other studies.
Full size table

Table 5 provides a comparative summary of the proposed octa-square split-ring sensor with previously reported plasmonic nanoring-based configurations. All sensors are evaluated at the reference refractive index of n = 1.33, a standard condition in plasmonic biosensing. As seen, the proposed structure exhibits significantly enhanced sensitivity in both resonance modes compared to classical nanoring designs. In comparison to the recent study54, sensitivity has improved by approximately 15.2% in Mode-1 and 109.2% in Mode-2.

To quantitatively validate the LC nature of the second resonance, the symmetric geometry of the proposed structure allows us to approximate its behavior using a simplified series RLC circuit, as illustrated in Fig. 11(a). In this configuration, the two capacitances combine in series, the two inductances in series, and likewise the two resistances in series. he resulting equivalent parameters are therefore:

$${C_{eq}}=\frac{{{C_1} \times {C_2}}}{{{C_1}+{C_2}}}=\frac{{{C_1}}}{2}$$
(5)
$${L_{eq}}={L_1}+{L_2} \approx 2{L_1}$$
(6)
$${\operatorname{R} _{eq}}={R_1}+{R_2} \approx 2{R_1}$$
(7)

The capacitance, originating from charge accumulation across the narrow split gap and approximated by66:

$${C_1}={\varepsilon _0}{\varepsilon _r}{\eta _f}_{r}\frac{{{H_r}{W_g}}}{{{W_n}}}$$
(8)

Where ε0 is vacuum permittivity, εr is the relative permittivity of the gap medium, ηfr​ is the empirical fringing correction factor, and (Hr, Wg, Wn) are Dimensions related to the structure. The inductance corresponds to the circulating currents along the metallic ring and is expressed as67,68:

$${L_1} \approx \frac{{{\mu _0}P}}{{2\pi }}\left[ {{C_0} - \ln (\frac{{2P}}{{{W_n}+{H_r}}})} \right]$$
(9)

Where P average perimeter of the current path in Mode-2, µ0 is the permeability of free space, and C0 is geometry-dependent constant (≈ 0.7–1.0). The resistance, accounting for ohmic and radiative losses and extracted as:

$${R_1}=\frac{{2\pi {f_R}{L_1}}}{Q}$$
(10)

According to the announced dimensions for the proposed structure, the effective circuit parameters are estimated as Ceq≈0.47 aF, Leq≈2.23 pH, and Req≈78 Ω, which fall within expected ranges for nano-plasmonic resonators. As illustrated in Fig. 11(b), the resonance spectra obtained from the equivalent circuit model and the FDTD simulation exhibit excellent agreement in terms of resonance wavelength, while a minor discrepancy in the FWHM is observed. This difference arises from the approximations inherent in reducing the complex three-dimensional nanostructure to a lumped RLC representation, yet the level of agreement remains within acceptable limits for validating the LC nature of Mode-2.

Fig. 11
figure 11

(a) Equivalent RLC circuit model of the proposed structure. (b) Mode-2 reflection spectra from the circuit model and the simulation result.

Full size image

Toward realistic biosensing conditions

While our design and analysis have primarily focused on refractive index (RI) perturbations in an aqueous background (n = 1.33), it is important to emphasize the impact of realistic biophysical conditions on device performance. Adsorbed protein layers at the bio–nanostructure interface can significantly alter surface interactions, in some cases reducing direct adhesion of cells to the underlying plasmonic surface and thereby influencing the overall sensing performance23. These proteins, depending on their type and structural conformation, may exhibit different refractive indices; however, in Line with reported values for cellular and membrane-associated proteins, an average refractive index of 1.45 is considered in this study69. To capture this effect, a thin protein overlayer was introduced on top of the gold nanostructure, and its thickness was systematically varied between 2, 4, 6, and 8 nm in the simulations. The reflectance spectra for selected cases (2 nm and 8 nm) are shown in Fig. 12. The resonance profiles remain robust, confirming that both the plasmonic and LC-type modes are preserved even in the presence of adsorbed proteins. However, as summarized in Table 6, the biosensor’s quantitative performance exhibits noticeable variations: sensitivity, FOM, and Q decrease with increasing protein thickness, with the decline being more pronounced in Mode-2 due to its strong capacitive confinement. Despite these reductions, the values obtained even at 8 nm thickness remain within acceptable ranges for practical biosensing, underscoring the robustness of the proposed design in realistic biomarker detection scenarios.

Beyond surface adsorption, additional real-world factors such as fabrication tolerances (± 2 nm), thermal fluctuations, and ionic strength variations in biological fluids may further perturb resonance features. To assess the impact of these factors, we performed a tolerance analysis in which all geometrical parameters of the proposed structure were simultaneously varied by ± 2 nm, consistent with typical nanofabrication errors. The results, summarized in Table 7, show that such dimensional variations induce only minor changes in sensitivity, FOM, Q, and LOD, confirming the robustness of the dual-mode response. Importantly, the proposed octa-square split-ring geometry with sharp edges and sub-20 nm gaps can be feasibly fabricated using advanced nanolithography methods as electron beam lithography (EBL)70, secondary sputtering lithography (SSL) with elastomeric nano-stamps71, or nanoimprint lithography (NIL)72, all of which have demonstrated reproducible patterning of ~ 10–20 nm features with tolerances of ± (2–3) nm. Taken together, these results indicate that despite inevitable fabrication and environmental uncertainties, the proposed biosensor maintains strong performance and is compatible with realistic cancer biomarker detection scenarios.

Fig. 12
figure 12

Reflectance spectra of the proposed biosensor with adsorbed protein overlayers of 2 nm and 8 nm thickness, showing robust preservation of dual resonance peaks.

Full size image
Table 6 Effect of protein overlayer thickness on sensitivity, FOM, and Q-factor for both resonant modes of the biosensor.
Full size table
Table 7 Tolerance results of the proposed octa-square split-ring biosensor under ± 2 nm fabrication variations.
Full size table

Conclusion

Early and accurate detection of cancer is essential for improving patient outcomes, and non-invasive diagnostic methods are at the forefront of this endeavor. This study presents a novel, high-sensitivity refractive index biosensor with dual resonance modes, engineered to detect a broad range of cancers through an innovative plasmonic metamaterial composed of an eight-ring supercell array.Initial simulations considered three metals, Al, Ag, and Au. After optimazing Au was identified as the optimal candidate for achieving peak sensitivity in FDTD analysis. The proposed plasmonic sensor was tested under both TM and TE polarizations and exhibited suitable evaluation parameters in both polarizations. With the integration of gold nanostructures in modes 1 and 2, the sensor achieved high sensitivities of 604 (nm/RIU) and 1097.1 (nm/RIU), respectively. Additionally, the figure of merit (FOM) values for these modes were measured at 14.72 (RIU−1) and 15.64 (RIU−1), highlighting the sensor’s effectiveness in distinguishing subtle refractive index changes associated with cancer biomarkers. In summary, the proposed biosensor represents a promising candidate for a cost-effective, non-invasive diagnostic tool that could elevate early cancer detection standards. These findings provide a valuable foundation for advancing plasmonic biosensing technology, with the potential to support accessible, rapid, and accurate cancer diagnostics in clinical practice.