Insights from Atangana-Baleanu fractional derivatives modeling of influenza epidemics and sensitivity analysis

Abstract

Mathematical modeling is an effective tool for understanding and predicting certain endemic diseases. Influenza is a common endemic disease that is transmitted to humans by contact with infected humans. During winter, seasonal influenza occurs annually in all ages causing fever and other diseases. In this study, we have constructed a mathematical model to understand the transmission of this disease by utilizing the harmonic mean-type incidence rate which is more effective than other incidence rates. We calculated the disease-free equilibria, endemic equilibria and then basic reproduction number which is important to understand the disease reduction from the population. Sensitivity analysis of reproduction number presents the effect of parameters on disease transmission. To generalize the traditional integer-order model to a fractional framework, the Atangana-Baleanu fractional-order derivative is employed. The fractionalized model is both existent and unique. The fractional version of the proposed model is numerically analyzed using the Atangana-Toufik method. Results present that by increasing the value of the treatment rate, there is a decline in the disease in the population.

Introduction

The influenza virus which is highly contagious and rapidly transmitted through human contact represents a significant public health threat during flu season¹. This respiratory illness characterized by symptoms ranging from mild to severe, impacts individuals across all age groups. While some influenza strains are capable of zoonotic transmission between humans and animals that are strictly human adapted². During winter seasonal influenza epidemics occur annually, predominantly driven by influenza A and B viruses with influenza C and D viruses also contributing to the overall disease burden³. Understanding the mechanisms of influenza transmission and developing effective control strategies are critical for mitigating and managing influenza outbreaks⁴. Mathematical modeling techniques play a pivotal role in achieving these objectives, enabling researchers to analyze and predict the dynamics of disease spread^5,6.

In recent years, significant research efforts have been made to the mathematical modeling of influenza to enhance our understanding of its transmission dynamics and to facilitate the development of effective preventive measures^7,8. Notably, Abdoon et al.⁹ introduced a fractional-order ABC derivation operator model, which allows for the analysis of disease-free equilibrium stability, the investigation of endemic equilibrium points, and the exploration of positive solutions for the influenza virus. Fractional-based model^10,11 has demonstrated promising outcomes through numerical comparisons. Additionally, Sabir et al.¹² made a substantial contribution by proposing a mathematical model using stochastic neural networks. This framework, particularly its subcategory, exhibited superior accuracy compared to integer-order models, as evidenced by lower mean square error values during the training, validation, and testing phases. These advancements in modeling methodologies hold the potential to revolutionize the field of influenza research, offering more precise tools for predicting and controlling outbreaks^13,14.

The application of diverse mathematical models has facilitated an in-depth examination of the transmission patterns of the influenza virus¹⁵. Currently, several methodologies are employed to predict the onset of infectious disease outbreaks^16,17. Prominent among these are the neural network prediction model¹⁸, the SEIR model^19,20, each offering distinct advantages and limitations. Selecting the most appropriate model is essential to enhance predictive accuracy, which requires a comprehensive analysis of the specific disease and the available data²¹. However, much of the existing research on influenza modeling focuses on traditional mathematical frameworks that often overlook memory effects, a critical factor in many biological processes.

While previous studies like²² have analyzed influenza transmission dynamics, our work introduces significant advancements through two key innovations: (1) a novel harmonic mean-type incidence rate that more accurately captures realistic disease transmission patterns, particularly for heterogeneous populations, and (2) the application of Atangana-Baleanu (AB) fractional calculus with Mittag–Leffler kernel^23,24 to model crucial memory effects in disease spread. The AB fractional derivative framework is particularly suited for influenza modeling as it accounts for the non-Markovian nature of infection processes, including persistence of immunity and variable incubation periods. Our approach provides a more comprehensive understanding of influenza dynamics compared to traditional integer-order models, enabling better prediction of outbreak patterns and more effective evaluation of control measures. These mathematical advances directly support public health efforts by improving the accuracy of early warning systems and optimizing intervention strategies.

Model formulation

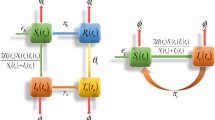
In Fig. 1, we have presented the flowchart for influenza transmission dynamics which based on virus spread. The total population is presented by (t), which has been divided into five classes: susceptible $\mathcal{S}(t)$, exposed $\mathcal{E}(t)$, infected $\mathcal{J}(t)$, treatment $\mathcal{T}(t)$ and recovered $\mathcal{R}(t)$. We used harmonic mean-type incidence rate $\frac{2\beta \mathcal{S}\mathcal{J}}{\mathcal{S}+\mathcal{J}}$ where $\beta$ represents contact rate of disease, $\delta$ represents the rate at which disease transmits from exposed to infected class, $\phi$ depicts the rate at which infected class transferred to treatment class and $\omega$ shows that rate of treatment and transmission of disease from treatment class to recovered class. Because the recovery in our model is partial. Therefore, disease transmits $\vartheta$ rate from recovered class to susceptible class and, $\nu$ and $\rho$ represent natural death and infectious death, respectively. System of differential equation for proposed model is presented in Eq. (1).

$$\begin{aligned} & \frac{{d{\mathcal{S}}}}{dt} = N - \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \vartheta R - \nu S, \\ & \frac{{d{\mathcal{E}}}}{dt} = \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} - \delta E - \nu E, \\ & \frac{{d{\mathcal{J}}}}{dt} = \delta E - \phi J - \rho J - \nu J, \\ & \frac{{d{\mathcal{T}}}}{dt} = \phi J - \omega T - \nu T, \\ & \frac{{d{\mathcal{R}}}}{dt} = \omega T - \vartheta R - \nu R. \\ \end{aligned}$$

(1)

Fig. 1

Flowchart of the model.

System (1) holds the following initial conditions:

$$\mathcal{S}(0)\ge 0,\mathcal{E}(0)\ge 0,\mathcal{J}(0)\ge 0,\mathcal{T}(0)\ge 0,\mathcal{R}(0)\ge 0.$$

Positivity for the model

Theorem 1

Solution for the system of Eq. (1) at any time $\text{t}$, $\text{t}\ge 0$ when the rate of change of the variables during any phase is non-negative and uniformly bounded in proper subset $\mathfrak{N}\in {\mathbb{R}}^{5}$²⁵.

Proof

System (1) gives that:

$$\begin{aligned} & \left. {\frac{{d{\mathcal{S}}}}{dt}} \right|_{{{\mathcal{S}}\left( t \right) = 0}} = N + \vartheta R \ge 0, \\ & \left. {\frac{{d{\mathcal{E}}}}{dt}} \right|_{{{\mathcal{E}}\left( t \right) = 0}} = \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} \ge 0, \\ & \left. {\frac{{d{\mathcal{J}}}}{dt}} \right|_{{{\mathcal{J}}\left( t \right) = 0}} = \delta E \ge 0, \\ & \left. {\frac{{d{\mathcal{T}}}}{dt}} \right|_{{{\mathcal{T}}\left( t \right) = 0}} = \phi J \ge 0, \\ & \left. {\frac{{d{\mathcal{R}}}}{dt}} \right|_{{{\mathcal{R}}\left( t \right) = 0}} = \omega T \ge 0. \\ \end{aligned}$$

(2)

It is clear by System (2) that System (1) holds the condition of positivity.

Total population at any time $\text{t}$ can be represented as:

$$\frac{d\mathcal{N}(\text{t})}{d\text{t}}=\frac{d\mathcal{S}(\text{t})}{d\text{t}}+\frac{d\mathcal{E}(\text{t})}{d\text{t}}+\frac{d\mathcal{J}(\text{t})}{d\text{t}}+\frac{d\mathcal{T}(\text{t})}{d\text{t}}+\frac{d\mathcal{R}(\text{t})}{d\text{t}}.$$

(3)

So, Eq. (3) become:

$$\begin{aligned} & \frac{{d{\mathcal{N}}\left( t \right)}}{dt} = N - \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \vartheta R - \nu S \\ & \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} - \delta E - \nu E + \delta E - \phi J \\ & - \rho J - \nu J + \phi J - \omega T - \nu T \\ & + \omega T - \vartheta R - \nu R, \\ \end{aligned}$$

(4)

Feasible solution for total population in System (1) will be

$$\left\{\mathcal{S}\left(\text{t}\right),\mathcal{E}\left(\text{t}\right),\mathcal{J}\left(\text{t}\right),\mathcal{T}\left(\text{t}\right),\mathcal{R}\left(\text{t}\right)\in {\mathbb{R}}^{5},0\le \mathcal{N}(\text{t})\le \frac{\mathfrak{N}}{\nu }\right\}.$$

(5)

This shows the boundedness of the system.

Disease-free equilibria

We calculate disease-free equilibria ${D}^{o}$²⁶ by utilizing System (1) and is given as:

$${D}^{o}=\left\{\frac{\mathfrak{N}}{\nu },\text{0,0},\text{0,0}\right\}.$$

(6)

Endemic equilibria

Endemic equilibria present that phase when the disease is persistent, partial present in the population with constant number of patients over time. Endemic equilibria for every compartment in System (1) is shown by ${\mathcal{S}}^{*}\left(\text{t}\right),{\mathcal{E}}^{*}\left(\text{t}\right),{\mathcal{J}}^{*}\left(\text{t}\right),{\mathcal{T}}^{*}\left(\text{t}\right) \text{and} {\mathcal{R}}^{*}\left(\text{t}\right)$²⁷ and is defined as follows

$$\begin{aligned} & {\mathcal{S}}^{*} \left( t \right) = \frac{{{\mathfrak{N}}\delta a_{1} a_{2} a_{3} a_{4} }}{{\left( {a_{1} a_{2} \left( {\delta \vartheta \phi \omega + \left( {\delta \left( {2\beta + \nu } \right) + a_{1} a_{2} } \right)a_{3} a_{4} } \right) - 2\beta \delta^{2} \vartheta \phi \omega a_{1} a_{2} } \right)}}, \\ & {\mathcal{E}}^{*} \left( t \right) = \frac{{{\mathfrak{N}}a_{2} \left( {a_{1} a_{2} - 2\beta \delta } \right)a_{3} a_{4} }}{{2\beta \delta^{2} \vartheta \phi \omega - a_{1} a_{2} \left( {\delta \vartheta \phi \omega + \left( {\delta \left( {2\beta + \nu } \right) - a_{1} a_{2} } \right)a_{3} a_{4} } \right)}}, \\ & {\mathcal{J}}^{*} \left( t \right) = \frac{{{\mathfrak{N}}\delta \left( {a_{1} a_{2} - 2\beta \delta } \right)a_{3} a_{4} }}{{2\beta \delta^{2} \vartheta \phi \omega - a_{1} a_{2} \left( {\delta \vartheta \phi \omega + \left( {\delta \left( {2\beta + \nu } \right) - a_{1} a_{2} } \right)a_{3} a_{4} } \right)}}, \\ & {\mathcal{T}}^{*} \left( t \right) = \frac{{{\mathfrak{N}}\delta \phi \left( {a_{1} a_{2} - 2\beta \delta } \right)a_{3} a_{4} }}{{2\beta \delta^{2} \vartheta \phi \omega - a_{1} a_{2} \left( {\delta \vartheta \phi \omega + \left( {\delta \left( {2\beta + \nu } \right) - a_{1} a_{2} } \right)a_{3} a_{4} } \right)}}, \\ & {\mathcal{R}}^{*} \left( t \right) = \frac{{{\mathfrak{N}}\delta \phi \omega \left( {a_{1} a_{2} - 2\beta \delta } \right)a_{3} a_{4} }}{{2\beta \delta^{2} \vartheta \phi \omega - a_{1} a_{2} \left( {\delta \vartheta \phi \omega + \left( {\delta \left( {2\beta + \nu } \right) - a_{1} a_{2} } \right)a_{3} a_{4} } \right)}}. \\ \end{aligned}$$

(7)

where ${a}_{1}=\left(\delta +\nu \right), {a}_{2}=\left(\phi +\rho +\nu \right), {a}_{3}=\left(\omega +\nu \right), {a}_{3}=\left(\vartheta +\nu \right)$.

Reproduction number

Reproduction number is crucial to understand the transmission and control of the disease in the population. If the reproduction number denoted by ${\mathfrak{R}}_{o}$, is less than 1 which states that disease is reducing from the population but if the ${\mathfrak{R}}_{o}$ is greater than 1 then disease is increasing in population. To find out ${\mathfrak{R}}_{o}$, we utilize the next-generation method²⁸ as given below:

$$\mathcal{F}=\left(\begin{array}{c}\frac{2\beta \mathcal{S}\mathcal{J}}{\mathcal{S}+\mathcal{J}}\\ 0\\ 0\end{array}\right), \mathcal{V}=\left(\begin{array}{c}\left(\delta +\nu \right)\mathcal{E}\\ \left(\phi +\rho +\nu \right)\mathcal{J}-\delta \mathcal{E}\\ \left(\omega +\nu \right)\mathcal{T}-\phi \mathcal{J}\end{array}\right),$$

(8)

We will find Jacobian of $\mathcal{F}$ and $\mathcal{V}$ on disease-free equilibria and we get

$$\mathcal{F}=\left(\begin{array}{ccc}0& 2\beta & 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right), \mathcal{V}=\left(\begin{array}{ccc}\delta +\nu & 2\beta & 0\\ -\delta & \phi +\rho +\nu & 0\\ 0& -\phi & \omega +\nu \end{array}\right).$$

(9)

And then,

$$\mathcal{F} \cdot {\mathcal{V}}^{-1}=\left(\begin{array}{ccc}0& 2\beta & 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}\frac{1}{\delta +\nu }& 0& 0\\ \frac{\left(\omega +\nu \right)\delta }{\left(\delta +\nu \right)\left(\phi +\rho +\nu \right)\left(\omega +\nu \right)}& \frac{1}{\phi +\rho +\nu }& 0\\ \frac{\delta \phi }{\left(\delta +\nu \right)\left(\phi +\rho +\nu \right)\left(\omega +\nu \right)}& \frac{\left(\delta +\nu \right)\phi }{\left(\delta +\nu \right)\left(\phi +\rho +\nu \right)\left(\omega +\nu \right)}& \frac{1}{\omega +\nu }\end{array}\right).$$

(10)

Hence, we get

$${\mathfrak{R}}_{o}=\frac{2\beta \delta }{\left(\delta +\nu \right)\left(\phi +\rho +\nu \right)}.$$

(11)

Sensitivity analysis

Model parameter sensitivity analyses identified parameters that had a high transmission influence²⁹. Infections and mortality can be treated effectively by analyzing reproduction numbers.

Using the following relation, we determine the most sensitive parameter:

$${I}_{q}=\frac{1}{{\mathfrak{R}}_{o}}\times \frac{\partial {\mathfrak{R}}_{o}}{\partial q}$$

q is parameter and the reproductive number is ${\mathfrak{R}}_{o}$.

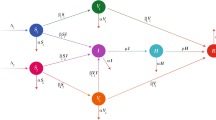
Our sensitivity analysis presented in Table 1 and Fig. 2 identifies contact rates $\beta$ as the primary transmission driver (normalized sensitivity index = + 1), while treatment rate $\phi$ emerges as the most effective control lever (index = − 0.89). Disease progression rate $\delta$ shows weaker positive association (+ 0.14), and mortality effects $\rho$ and $\nu$ exhibit modest suspension (− 0.09 to − 0.17). These results quantify the disproportionate impact of contact reduction and treatment acceleration on outbreak containment.

Table 1 Sensitivity indices of ${\mathfrak{R}}_{o}$.

Fig. 2

Sensitivity analysis of reproduction number.

Local stability for DFE

Theorem

DFE is asymptotically stable for ${\mathfrak{R}}_{o}<1$ otherwise it will be unstable³⁰.

Proof

To prove, we have to calculate Jacobian matrix and local stability of DFE as given below:

$$J\left({D}^{o}\right)=\left(\begin{array}{ccccc}-\nu & 0& -2\beta & 0& \vartheta \\ 0& -\left(\delta +\nu \right)& 2\beta & 0& 0\\ 0& \delta & -\left(\phi +\rho +\nu \right)& 0& 0\\ 0& 0& \vartheta & -\left(\omega +\nu \right)& 0\\ 0& 0& 0& 0& -\vartheta \end{array}\right).$$

(12)

where ${\xi }_{1}=-\nu , {\xi }_{2}=-\left(\delta +\nu \right), {\xi }_{3}=-\left(\phi +\rho +\nu \right), {\xi }_{4}=-\left(\omega +\nu \right), {\xi }_{5}=-\vartheta .$

Now,

$$\left|J\left({D}^{o}\right)-\lambda \right|=\left|\begin{array}{ccccc}{\xi }_{1}-\lambda & 0& -2\beta & 0& \vartheta \\ 0& {\xi }_{2}-\lambda & 2\beta & 0& 0\\ 0& \delta & {\xi }_{3}-\lambda & 0& 0\\ 0& 0& \vartheta & {\xi }_{4}-\lambda & 0\\ 0& 0& 0& 0& {\xi }_{5}-\lambda \end{array}\right|=0.$$

(13)

$$\left({\xi }_{1}-\lambda \right)\left({\xi }_{4}-\lambda \right)\left({\xi }_{5}-\lambda \right)\left|\begin{array}{cc}{\xi }_{2}-\lambda & 2\beta \\ \delta & {\xi }_{3}-\lambda \end{array}\right|=0.$$

(14)

$$\left({\xi }_{1}-\lambda \right)\left({\xi }_{4}-\lambda \right)\left({\xi }_{5}-\lambda \right)\left[{\lambda }^{2}-\left({\xi }_{2}+{\xi }_{3}\right)\lambda -2\beta \delta +{\xi }_{2}{\xi }_{3}\right]=0.$$

(15)

where $\lambda ={\xi }_{1}, \lambda ={\xi }_{4}, \lambda ={\xi }_{5}$.

So

$${\lambda }^{2}-\left({\xi }_{2}+{\xi }_{3}\right)\lambda -2\beta \delta +{\xi }_{2}{\xi }_{3}=0.$$

(16)

By Routh-Hurwitz criterion of order two, $-\left({\xi }_{2}+{\xi }_{3}\right)>0$ and $-2\beta \delta +{\xi }_{2}{\xi }_{3}>0$.

And

$$\begin{aligned} & - 2\beta \delta + \xi_{2} \xi_{3} > 0, \\ & - 2\beta \delta + \left( {\delta + \nu } \right)\left( {\phi + \rho + \nu } \right) > 0, \\ & \left( {\delta + \nu } \right)\left( {\phi + \rho + \nu } \right) > 2\beta \delta , \\ & 1 > \frac{2\beta \delta }{{\left( {\delta + \nu } \right)\left( {\phi + \rho + \nu } \right)}}. \\ \end{aligned}$$

And hence ${\mathfrak{R}}_{o}<1$ and DFE is locally asymptotically stable.

Fractional derivative model

Definition³¹

Time fractional derive (AB) with fractional $\kappa$ is defined as:

$${}_{q}^{AB} \wp_{b}^{\kappa } f\left( {\text{t}} \right) = \frac{ {\mathfrak{h}} \left( \kappa \right)}{{1 - \kappa }}\mathop \smallint \limits_{q}^{b} P_{q} \left( {\frac{{ - \kappa \left( {{\mathfrak{b}} - {\text{t}}} \right)^{\kappa } }}{1 - \kappa }} \right)f\left( b \right)d{\text{t}},\quad {\text{for}}\,{ }0 < \kappa < 1.$$

(17)

where ${\mathfrak{h}} \left(\kappa \right)$ represents normalization function and ${P}_{\kappa }\left(.\right)$ is Mittage-Leffler function³².

Definition

Numerical scheme for solving fractional ODEs by Toufik and Atangana³³ is as follows:

$${}^{ABC}\wp_{b}^{\kappa } h\left( {{\text{t}}_{1} } \right) = f\left( {{\text{t}}_{1} ,h\left( {{\text{t}}_{1} } \right)} \right)\,{\text{with }}\,h\left( 0 \right) = h_{o} .$$

(18)

Numerical scheme for (18) is given below:

$$\begin{aligned} h_{\varkappa + 1} & = h_{o} + \frac{1 - \kappa }{{{\mathfrak{h}}_{1} \left( \kappa \right)}}f\left( {{\text{t}}_{1\Upsilon } ,h\left( {{\text{t}}_{1\Upsilon } } \right)} \right) \\ & \quad + \frac{\kappa }{{{\mathfrak{h}}_{1} \left( \kappa \right)}}\mathop \sum \limits_{\Upsilon = 0}^{\varkappa} \left[ {\frac{{d^{\kappa } \left( {{\text{t}}_{1\Upsilon } ,h\left( {{\text{t}}_{1\Upsilon } } \right)} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon + \kappa } \right)\left( {\varkappa + 2 - \Upsilon + \kappa } \right) - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 2 - \Upsilon + 2\kappa } \right)} \right)} \right. \\ & \quad - \left. {\frac{{d^{\kappa } \left( {{\text{t}}_{1\Upsilon } ,h\left( {{\text{t}}_{1\Upsilon } } \right)} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon } \right)^{\kappa + 1} - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 1 - \Upsilon + 2\kappa } \right)} \right)} \right] \\ \end{aligned}$$

(19)

Fractional model

By utilizing the following Atangana-Baleanu time fractional operator, we get the following systems of equations:

$$\begin{aligned} & {}^{ABC}\wp_{b}^{\kappa } S\left( t \right) = N - \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \vartheta R - \nu S, \\ & {}^{ABC}\wp_{b}^{\kappa } E\left( t \right) = \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} - \delta E - \nu E, \\ & {}^{ABC}\wp_{b}^{\kappa } J\left( t \right) = \delta E - \phi J - \rho J - \nu J, \\ & {}^{ABC}\wp_{b}^{\kappa } T\left( t \right) = \phi J - \omega T - \nu T, \\ & {}^{ABC}\wp_{b}^{\kappa } R\left( t \right) = \omega T - \vartheta R - \nu R. \\ \end{aligned}$$

(20)

AB time fractional parameter and operator are represented by $\kappa$ and ${{}^{ABC}\wp }_{b}^{\kappa }\left(.\right)$ respectively.

Existence and uniqueness

Suppose that $W(D)$ is Banach space with $D=\left[0,y\right]$ have the real-valued continuous function with super norm and $M=W(D)\times W(D)\times W(D)\times W(D)\times W(D)$ with norm $\Vert \left(\mathcal{S},\mathcal{E},\mathcal{J},\mathcal{T},\mathcal{R}\right)\Vert =\Vert \mathcal{S}\Vert +\Vert \mathcal{E}\Vert +\Vert \mathcal{J}\Vert +\Vert \mathcal{T}\Vert +\Vert \mathcal{R}\Vert$, where $\Vert \mathcal{S}\Vert ={sup}_{{\text{t}}_{1}\in j}\left|\mathcal{S}\left({\text{t}}_{1}\right)\right|$, $\Vert \mathcal{S}\Vert ={sup}_{{\text{t}}_{1}\in j}\left|\mathcal{S}\left({\text{t}}_{1}\right)\right|$, $\Vert \mathcal{E}\Vert ={sup}_{{\text{t}}_{1}\in j}\left|\mathcal{E}\left({\text{t}}_{1}\right)\right|$, $\Vert \mathcal{J}\Vert ={sup}_{{\text{t}}_{1}\in j}\left|\mathcal{J}\left({\text{t}}_{1}\right)\right|$, and $\Vert \mathcal{R}\Vert ={sup}_{{\text{t}}_{1}\in j}\left|\mathcal{R}\left({\text{t}}_{1}\right)\right|$. After applying the ABC integral operator on System (1), we get:

$$\begin{aligned} & S\left( {\text{t}} \right) - S\left( 0 \right) = {}^{ABC}\wp_{b}^{\kappa } S\left( {\text{t}} \right)\left[ {{\mathfrak{N}} - \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \vartheta {\mathcal{R}} - \nu {\mathcal{S}}} \right], \\ & E\left( {\text{t}} \right) - E\left( 0 \right) = {}^{ABC}\wp_{b}^{\kappa } E\left( {\text{t}} \right)\left[ {\frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} - \delta {\mathcal{E}} - \nu {\mathcal{E}}} \right], \\ & J\left( {\text{t}} \right) - J\left( 0 \right) = {}^{ABC}\wp_{b}^{\kappa } J\left( {\text{t}} \right)\left[ {\delta {\mathcal{E}} - \phi {\mathcal{J}} - \rho {\mathcal{J}} - \nu {\mathcal{J}}} \right], \\ & T\left( {\text{t}} \right) - T\left( 0 \right) = {}^{ABC}\wp_{b}^{\kappa } T\left( {\text{t}} \right)\left[ {\phi {\mathcal{J}} - \omega {\mathcal{T}} - \nu {\mathcal{T}}} \right], \\ & R\left( {\text{t}} \right) - R\left( 0 \right) = {}^{ABC}\wp_{b}^{\kappa } R\left( {\text{t}} \right)\left[ {\omega {\mathcal{T}} - \vartheta {\mathcal{R}} - \nu {\mathcal{R}}} \right]. \\ \end{aligned}$$

(21)

By Eq. (18), we have:

$$\begin{aligned} & {\mathcal{S}}\left( {\text{t}} \right) - {\mathcal{S}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}\left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}\left( {\text{t}} \right)} \right)d\kappa } , \\ & {\mathcal{E}}\left( {\text{t}} \right) - {\mathcal{E}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}\left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}\left( {\text{t}} \right)} \right)d\kappa ,} \\ & {\mathcal{J}}\left( {\text{t}} \right) - {\mathcal{J}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}\left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}\left( {\text{t}} \right)} \right)d\kappa ,} \\ & {\mathcal{T}}\left( {\text{t}} \right) - {\mathcal{T}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}\left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}\left( {\text{t}} \right)} \right)d\kappa ,} \\ & {\mathcal{R}}\left( {\text{t}} \right) - {\mathcal{R}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{R}}\left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{R}}\left( {\text{t}} \right)} \right)d\kappa } . \\ \end{aligned}$$

(22)

where,

$$\begin{aligned} & {\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}\left( {\text{t}} \right)} \right) = {\mathfrak{N}} - \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \vartheta {\mathcal{R}} - \nu {\mathcal{S}}, \\ & {\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{S}}\left( {\text{t}} \right)} \right) = \frac{{2\beta {\mathcal{S}\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} - \delta {\mathcal{E}} - \nu {\mathcal{E}}, \\ & {\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{S}}\left( {\text{t}} \right)} \right) = \delta {\mathcal{E}} - \phi {\mathcal{J}} - \rho {\mathcal{J}} - \nu {\mathcal{J}}, \\ & {\mathfrak{L}}_{4} \left( {\kappa ,t,{\mathcal{S}}\left( t \right)} \right) = \phi {\mathcal{J}} - \omega {\mathcal{T}} - \nu {\mathcal{T}}, \\ & {\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{S}}\left( {\text{t}} \right)} \right) = \omega {\mathcal{T}} - \vartheta {\mathcal{R}} - \nu {\mathcal{R}}. \\ \end{aligned}$$

${\mathfrak{L}}_{1}$, ${\mathfrak{L}}_{2}$, ${\mathfrak{L}}_{3}$, ${\mathfrak{L}}_{4}$ and ${\mathfrak{L}}_{5}$ satisfy the Lipschitz condition if $\mathcal{S}\left(\text{t}\right)$, $\mathcal{E}\left(\text{t}\right)$, $\mathcal{J}\left(\text{t}\right)$, $\mathcal{T}\left(\text{t}\right)$ and $\mathcal{R}\left(\text{t}\right)$ contain the upper bond. Let $\mathcal{S}\left(\text{t}\right)$ and ${\mathcal{S}}^{*}\left(\text{t}\right)$ are the couple function, then

$$\Vert {\mathfrak{L}}_{1}\left(\kappa ,\text{t},\mathcal{S}\left(\text{t}\right)\right)-{\mathfrak{L}}_{1}\left(\kappa ,\text{t},{\mathcal{S}}^{*}\left(\text{t}\right)\right)\Vert =\Vert -\left(\frac{2\beta \mathcal{J}}{\mathcal{S}+\mathcal{J}}\right)\left(\mathcal{S}\left(\text{t}\right)-{\mathcal{S}}^{*}\left(\text{t}\right)\right)\Vert .$$

(23)

Let

$$\begin{aligned} & \Upsilon_{1} = - \left( {\frac{{2\beta {\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \nu } \right), \\ & \Upsilon_{1} \le \left( {\frac{{2\beta {\mathcal{J}}}}{{{\mathcal{S}} + {\mathcal{J}}}} + \nu } \right), \\ & \Upsilon_{1} < \left( {\frac{{2\beta U_{1} }}{{U_{2} + U_{1} }} + \nu } \right). \\ \end{aligned}$$

Then Eq. (23) becomes

$$\Vert {\mathfrak{L}}_{1}\left(\kappa ,\text{t},\mathcal{S}\left(\text{t}\right)\right)-{\mathfrak{L}}_{1}\left(\kappa ,\text{t},{\mathcal{S}}^{*}\left(\text{t}\right)\right)\Vert \le {\Upsilon}_{1}\Vert \left(\mathcal{S}\left(\text{t}\right)-{\mathcal{S}}^{*}\left(\text{t}\right)\right)\Vert .$$

(24)

Similarly,

$$\begin{aligned} & \left\| {{\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}\left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}^{*} \left( {\text{t}} \right)} \right)} \right\| \le \left\| {\Upsilon_{2} \left( {{\mathcal{E}}\left( {\text{t}} \right) - {\mathcal{E}}^{*} \left( {\text{t}} \right)} \right)} \right\|, \\ & \left\| {{\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}\left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}^{*} \left( {\text{t}} \right)} \right)} \right\| \le \left\| {\Upsilon_{3} \left( {{\mathcal{J}}\left( {\text{t}} \right) - {\mathcal{J}}^{*} \left( {\text{t}} \right)} \right)} \right\|, \\ & \left\| {{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}\left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}^{*} \left( {\text{t}} \right)} \right)} \right\| \le \left\| {\Upsilon_{4} \left( {{\mathcal{T}}\left( {\text{t}} \right) - {\mathcal{T}}^{*} \left( {\text{t}} \right)} \right)} \right\|, \\ & \left\| {{\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{R}}\left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{R}}^{*} \left( {\text{t}} \right)} \right)} \right\| \le \left\| {\Upsilon_{5} \left( {{\mathcal{R}}\left( {\text{t}} \right) - {\mathcal{R}}^{*} \left( {\text{t}} \right)} \right)} \right\|. \\ \end{aligned}$$

(25)

And

$$\begin{aligned} & \Upsilon_{2} = \left\| { - \left( {\delta + \nu } \right)} \right\|, \\ & \Upsilon_{3} = \left\| { - \left( {\phi + \rho + \nu } \right)} \right\|, \\ & \Upsilon_{4} = \left\| { - \left( {\omega + \nu } \right)} \right\|, \\ & \Upsilon_{5} = \left\| { - \left( {\vartheta + \nu } \right)} \right\|. \\ \end{aligned}$$

Hence, Lipschitz’s condition is satisfied. By Eq. (22) we get

$$\begin{aligned} & {\mathcal{S}}_{e} \left( {\text{t}} \right) - {\mathcal{S}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}_{e + 1} \left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}_{e + 1} \left( {\text{t}} \right)} \right)d\kappa ,} \\ & {\mathcal{E}}_{e} \left( {\text{t}} \right) - {\mathcal{E}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}_{e + 1} \left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}_{e + 1} \left( {\text{t}} \right)} \right)d\kappa ,} \\ & {\mathcal{J}}_{e} \left( {\text{t}} \right) - {\mathcal{J}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}_{e + 1} \left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}_{e + 1} \left( {\text{t}} \right)} \right)d\kappa ,} \\ & {\mathcal{T}}_{e} \left( {\text{t}} \right) - {\mathcal{T}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}_{e + 1} \left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}_{e + 1} \left( {\text{t}} \right)} \right)d\kappa } , \\ & {\mathcal{R}}_{e} \left( {\text{t}} \right) - {\mathcal{R}}\left( 0 \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}{\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{R}}_{e + 1} \left( {\text{t}} \right)} \right) + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{5} \left( {\kappa ,{\text{t}},{\mathcal{R}}_{e + 1} \left( {\text{t}} \right)} \right)d\kappa .} \\ \end{aligned}$$

(26)

Combining with ${\mathcal{S}}^{o}\left(\text{t}\right)=\mathcal{S}\left(0\right)$, ${\mathcal{E}}^{o}\left(\text{t}\right)=\mathcal{E}\left(0\right)$, ${\mathcal{J}}^{o}\left(\text{t}\right)=\mathcal{J}\left(0\right)$, ${\mathcal{T}}^{o}\left(\text{t}\right)=\mathcal{T}\left(0\right)$ and ${\mathcal{R}}^{o}\left(\text{t}\right)=\mathcal{R}\left(0\right)$. So, consecutive terms yield difference

$$\begin{aligned} {\mathbb{N}}_{{{\mathcal{S}}_{e} }} \left( {\text{t}} \right) & = {\mathcal{S}}_{e} \left( {\text{t}} \right) - {\mathcal{S}}_{e - 1} \left( {\text{t}} \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\left( {{\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}_{e - 2} \left( {\text{t}} \right)} \right)} \right) \\ & \quad + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {{\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{1} \left( {\kappa ,{\text{t}},{\mathcal{S}}_{e - 2} \left( {\text{t}} \right)} \right)} \right)d\kappa ,} \\ {\mathbb{N}}_{{{\mathcal{E}}_{e} }} \left( {\text{t}} \right) &= {\mathcal{E}}_{e} \left( {\text{t}} \right) - {\mathcal{E}}_{e - 1} \left( {\text{t}} \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\left( {{\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}_{e - 2} \left( {\text{t}} \right)} \right)} \right) \\ & \quad + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {{\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{2} \left( {\kappa ,{\text{t}},{\mathcal{E}}_{e - 2} \left( {\text{t}} \right)} \right)} \right)d\kappa ,} \\ {\mathbb{N}}_{{{\mathcal{J}}_{e} }} \left( {\text{t}} \right) & = {\mathcal{J}}_{e} \left( {\text{t}} \right) - {\mathcal{J}}_{e - 1} \left( {\text{t}} \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\left( {{\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}_{e - 2} \left( {\text{t}} \right)} \right)} \right) \\ & \quad + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {{\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{3} \left( {\kappa ,{\text{t}},{\mathcal{J}}_{e - 2} \left( {\text{t}} \right)} \right)} \right)d\kappa } , \\ {\mathbb{N}}_{{{\mathcal{T}}_{e} }} \left( {\text{t}} \right) & = {\mathcal{T}}_{e} \left( {\text{t}} \right) - {\mathcal{T}}_{e - 1} \left( {\text{t}} \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\left( {{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}_{e - 2} \left( {\text{t}} \right)} \right)} \right) \\ & \quad + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{T}}_{e - 2} \left( {\text{t}} \right)} \right)} \right)d\kappa ,} \\ {\mathbb{N}}_{{{\mathcal{R}}_{e} }} \left( {\text{t}} \right) & = {\mathcal{R}}_{e} \left( {\text{t}} \right) - {\mathcal{R}}_{e - 1} \left( {\text{t}} \right) = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\left( {{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{R}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{R}}_{e - 2} \left( {\text{t}} \right)} \right)} \right) \\ & \quad + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \int_{0}^{{\text{t}}} {\left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} {\mathfrak{L}}_{1} \left( {{\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{R}}_{e - 1} \left( {\text{t}} \right)} \right) - {\mathfrak{L}}_{4} \left( {\kappa ,{\text{t}},{\mathcal{R}}_{e - 2} \left( {\text{t}} \right)} \right)} \right)d\kappa } . \\ \end{aligned}$$

(27)

It is clear that

$$\begin{aligned} & {\mathcal{S}}_{e} \left( {\text{t}} \right) = \mathop \sum \limits_{i = 0}^{e} {\mathbb{N}}_{{{\mathcal{S}}_{i} }} \left( {\text{t}} \right),{ \mathcal{E}}_{e} \left( {\text{t}} \right) = \mathop \sum \limits_{i = 0}^{e} {\mathbb{N}}_{{{\mathcal{E}}_{i} }} \left( {\text{t}} \right), {\mathcal{J}}_{e} \left( {\text{t}} \right) = \mathop \sum \limits_{i = 0}^{e} {\mathbb{N}}_{{{\mathcal{J}}_{i} }} \left( {\text{t}} \right), \\ & {\mathcal{T}}_{e} \left( {\text{t}} \right) = \mathop \sum \limits_{i = 0}^{e} {\mathbb{N}}_{{{\mathcal{T}}_{i} }} \left( {\text{t}} \right), {\mathcal{R}}_{e} \left( {\text{t}} \right) = \mathop \sum \limits_{i = 0}^{e} {\mathbb{N}}_{{{\mathcal{R}}_{i} }} \left( {\text{t}} \right). \\ \end{aligned}$$

(28)

By using (24) and (25)

$$\begin{aligned} & {\mathbb{N}}_{{{\mathcal{S}}_{e - 1} }} \left( {\text{t}} \right) = {\mathcal{S}}_{e - 1} \left( {\text{t}} \right) - {\mathcal{S}}_{e - 2} \left( {\text{t}} \right), {\mathbb{N}}_{{{\mathcal{E}}_{e - 1} }} \left( {\text{t}} \right) = {\mathcal{E}}_{e - 1} \left( {\text{t}} \right) - {\mathcal{E}}_{e - 2} \left( {\text{t}} \right), \\ & {\mathbb{N}}_{{{\mathcal{S}}_{e - 1} }} \left( {\text{t}} \right) = {\mathcal{J}}_{e - 1} \left( {\text{t}} \right) - {\mathcal{J}}_{e - 2} \left( {\text{t}} \right), {\mathbb{N}}_{{{\mathcal{S}}_{e - 1} }} \left( {\text{t}} \right) = {\mathcal{T}}_{e - 1} \left( {\text{t}} \right) - {\mathcal{T}}_{e - 2} \left( {\text{t}} \right), \\ & {\mathbb{N}}_{{{\mathcal{R}}_{e - 1} }} \left( {\text{t}} \right) = {\mathcal{R}}_{e - 1} \left( {\text{t}} \right) - {\mathcal{R}}_{e - 2} \left( {\text{t}} \right). \\ \end{aligned}$$

(29)

After simplification, we get

$$\begin{gathered} \left\| {{\mathbb{N}}_{{{\mathcal{S}}_{e} }} \left( {\text{t}} \right)} \right\| = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{1} \left\| {{\mathbb{N}}_{{{\mathcal{S}}_{e - 1} }} \left( {\text{t}} \right)} \right\| + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \mathop \smallint \limits_{0}^{{\text{t}}} \left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} \left\| {{\mathbb{N}}_{{{\mathcal{S}}_{e - 1} }} \left( {\text{t}} \right)} \right\|d\kappa , \hfill \\ \left\| {{\mathbb{N}}_{{{\mathcal{E}}_{e} }} \left( {\text{t}} \right)} \right\| = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{2} \left\| {{\mathbb{N}}_{{{\mathcal{E}}_{e - 1} }} \left( {\text{t}} \right)} \right\| + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \mathop \smallint \limits_{0}^{{\text{t}}} \left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} \left\| {{\mathbb{N}}_{{{\mathcal{E}}_{e - 1} }} \left( {\text{t}} \right)} \right\|d\kappa , \hfill \\ \left\| {{\mathbb{N}}_{{{\mathcal{J}}_{e} }} \left( {\text{t}} \right)} \right\| = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{3} \left\| {{\mathbb{N}}_{{{\mathcal{J}}_{e - 1} }} \left( {\text{t}} \right)} \right\| + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \mathop \smallint \limits_{0}^{{\text{t}}} \left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} \left\| {{\mathbb{N}}_{{{\mathcal{J}}_{e - 1} }} \left( {\text{t}} \right)} \right\|d\kappa , \hfill \\ \left\| {{\mathbb{N}}_{{{\mathcal{T}}_{e} }} \left( {\text{t}} \right)} \right\| = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{4} \left\| {{\mathbb{N}}_{{{\mathcal{T}}_{e - 1} }} \left( {\text{t}} \right)} \right\| + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \mathop \smallint \limits_{0}^{{\text{t}}} \left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} \left\| {{\mathbb{N}}_{{{\mathcal{T}}_{e - 1} }} \left( {\text{t}} \right)} \right\|d\kappa , \hfill \\ \left\| {{\mathbb{N}}_{{{\mathcal{R}}_{e} }} \left( {\text{t}} \right)} \right\| = \frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{5} \left\| {{\mathbb{N}}_{{{\mathcal{R}}_{e - 1} }} \left( {\text{t}} \right)} \right\| + \frac{\kappa }{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}} \times \mathop \smallint \limits_{0}^{{\text{t}}} \left( {{\text{t}} - \Upsilon } \right)^{\kappa - 1} \left\| {{\mathbb{N}}_{{{\mathcal{R}}_{e - 1} }} \left( {\text{t}} \right)} \right\|d\kappa . \hfill \\ \end{gathered}$$

(30)

Theorem

The system (1) has a unique solution for $\text{t}\in \left[0,c\right]$ subject to the condition if

$$\frac{1-\kappa }{{P}_{1}\left(\kappa \right)}{\Upsilon}_{i}+\frac{\kappa \overline{c}}{{P }_{1}\left(\kappa \right){\text{-} \!\!\Gamma} \left(\kappa \right)}{\Upsilon}_{i}<1, i=\text{1,2},\dots ,5.$$

holds.

Proof

As $\mathcal{S},\mathcal{E},\mathcal{J}, \mathcal{T}$ and $\mathcal{R}$ are bounded functions and Eqs. (27) and (28) hold. Hence, recursively Eq. (30) becomes

$$\begin{aligned} & \left\| {{\mathbb{N}}_{{{\mathcal{S}}_{e} }} \left( {\text{t}} \right)} \right\| \le \left\| {{\mathcal{S}}\left( {\text{t}} \right)} \right\|\left( {\frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{1} + \frac{{\kappa \overline{c}}}{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}}\Upsilon_{1} } \right)^{e} , \\ & \left\| {{\mathbb{N}}_{{{\mathcal{E}}_{e} }} \left( {\text{t}} \right)} \right\| \le \left\| {{\mathcal{E}}\left( {\text{t}} \right)} \right\|\left( {\frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{2} + \frac{{\kappa \overline{c}}}{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}}\Upsilon_{2} } \right)^{e} , \\ & \left\| {{\mathbb{N}}_{{{\mathcal{J}}_{e} }} \left( {\text{t}} \right)} \right\| \le \left\| {{\mathcal{J}}\left( {\text{t}} \right)} \right\|\left( {\frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{3} + \frac{{\kappa \overline{c}}}{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}}\Upsilon_{3} } \right)^{e} , \\ & \left\| {{\mathbb{N}}_{{{\mathcal{T}}_{e} }} \left( {\text{t}} \right)} \right\| \le \left\| {{\mathcal{T}}\left( {\text{t}} \right)} \right\|\left( {\frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{4} + \frac{{\kappa \overline{c}}}{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}}\Upsilon_{4} } \right)^{e} , \\ & \left\| {{\mathbb{N}}_{{{\mathcal{R}}_{e} }} \left( {\text{t}} \right)} \right\| \le \left\| {{\mathcal{R}}\left( {\text{t}} \right)} \right\|\left( {\frac{1 - \kappa }{{P_{1} \left( \kappa \right)}}\Upsilon_{5} + \frac{{\kappa \overline{c}}}{{P_{1} \left( \kappa \right){\text{-} \!\!\Gamma}_{1} \left( \kappa \right)}}\Upsilon_{5} } \right)^{e} . \\ \end{aligned}$$

(31)

So, $\Vert {\mathbb{N}}_{{\mathcal{S}}_{e}}\left(\text{t}\right)\Vert \to 0$, $\Vert {\mathbb{N}}_{{\mathcal{E}}_{e}}\left(\text{t}\right)\Vert \to 0$, $\Vert {\mathbb{N}}_{{\mathcal{J}}_{e}}\left(\text{t}\right)\Vert \to 0$, $\Vert {\mathbb{N}}_{{\mathcal{T}}_{e}}\left(\text{t}\right)\Vert \to 0$ and $\Vert {\mathbb{N}}_{{\mathcal{R}}_{e}}\left(\text{t}\right)\Vert \to 0$ as $e\to 0$. Incorporating triangle inequality for any s, Eq. (31) becomes,

$$\begin{aligned} & \left\| {{\mathcal{S}}_{e + s} \left( {\text{t}} \right) - {\mathcal{S}}_{e} \left( {\text{t}} \right)} \right\| \le \mathop \sum \limits_{j = e + 1}^{e + s} {\mathbb{P}}_{1}^{j} \frac{{{\mathbb{P}}_{1}^{e + 1} - {\mathbb{P}}_{1}^{e + s + 1} }}{{1 - {\mathbb{P}}_{1} }}, \\ & \left\| {{\mathcal{E}}_{e + s} \left( {\text{t}} \right) - {\mathcal{E}}_{e} \left( {\text{t}} \right){\mathcal{E}}\left( {\text{t}} \right)} \right\| \le \mathop \sum \limits_{j = e + 1}^{e + s} {\mathbb{P}}_{2}^{j} \frac{{{\mathbb{P}}_{2}^{e + 1} - {\mathbb{P}}_{2}^{e + s + 1} }}{{1 - {\mathbb{P}}_{2} }}, \\ & \left\| {{\mathcal{J}}_{e + s} \left( {\text{t}} \right) - {\mathcal{J}}_{e} \left( {\text{t}} \right){\mathcal{J}}\left( {\text{t}} \right)} \right\| \le \mathop \sum \limits_{j = e + 1}^{e + s} {\mathbb{P}}_{3}^{j} \frac{{{\mathbb{P}}_{3}^{e + 1} - {\mathbb{P}}_{3}^{e + s + 1} }}{{1 - {\mathbb{P}}_{3} }}, \\ & \left\| {{\mathcal{T}}_{e + s} \left( {\text{t}} \right) - {\mathcal{T}}_{e} \left( {\text{t}} \right){\mathcal{T}}\left( {\text{t}} \right)} \right\|\mathop \sum \limits_{j = e + 1}^{e + s} {\mathbb{P}}_{4}^{j} \frac{{{\mathbb{P}}_{4}^{e + 1} - {\mathbb{P}}_{4}^{e + s + 1} }}{{1 - {\mathbb{P}}_{4} }}, \\ & \left\| {{\mathcal{R}}_{e + s} \left( {\text{t}} \right) - {\mathcal{R}}_{e} \left( {\text{t}} \right){\mathcal{R}}\left( {\text{t}} \right)} \right\| \le \mathop \sum \limits_{j = e + 1}^{e + s} {\mathbb{P}}_{5}^{j} \frac{{{\mathbb{P}}_{5}^{e + 1} - {\mathbb{P}}_{5}^{e + s + 1} }}{{1 - {\mathbb{P}}_{5} }}. \\ \end{aligned}$$

(32)

with ${\mathbb{P}}_{i}=\frac{1-\kappa }{P\left(\kappa \right)}{\Upsilon}_{i}+\frac{\kappa \overline{c} }{P\left(\kappa \right){\text{-} \!\!\Gamma} \left(\kappa \right)}{\Upsilon}_{i}<1$ by hypothesis. By different methods, we can get a unique solution for System (1).

Numerical scheme

Utilizing the model in³³, Eq. (20) becomes:

$${\begin{array}{*{20}c} {{}^{ABC}\wp_{b}^{\kappa } S \left( {\text{t}} \right) = {\text{g}}_{1} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right),} \\ {{}^{ABC}\wp_{b}^{\kappa } E\left( {\text{t}} \right) = {\text{g}}_{2} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right),} \\ {{}^{ABC}\wp_{b}^{\kappa } J\left( {\text{t}} \right) = {\text{g}}_{3} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right),} \\ {{}^{ABC}\wp_{b}^{\kappa } T\left( {\text{t}} \right) = {\text{g}}_{4} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right),} \\ {{}^{ABC}\wp_{b}^{\kappa } R\left( {\text{t}} \right) = {\text{g}}_{5} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right).} \\ \end{array} }$$

(33)

We get the iterative form as follows

$$\begin{aligned} {\mathcal{S}}_{\varkappa + 1} & = {\mathcal{S}}_{o} + \frac{1 - \kappa }{{\wp \left( \kappa \right)}}{\text{g}}_{1} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right) \\ & \quad + \frac{\kappa }{\wp \left( \kappa \right)}\mathop \sum \limits_{\Upsilon = 0}^{\varkappa} \left[ {\frac{{d^{\kappa } {\text{g}}_{1} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{ {\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon + \kappa } \right)\left( {\varkappa + 2 - \Upsilon + \kappa } \right) - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 2 - \Upsilon + 2\kappa } \right)} \right)} \right. \\ & \quad - \left. {\frac{{d^{\kappa } {\text{g}}_{1} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon } \right)^{\kappa + 1} - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 1 - \Upsilon + 2\kappa } \right)} \right)} \right], \\ \end{aligned}$$

(34)

$$\begin{aligned} {\mathcal{E}}_{\varkappa + 1} & = {\mathcal{E}}_{o} + \frac{1 - \kappa }{{\wp \left( \kappa \right)}}{\text{g}}_{2} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right) \\ & \quad + \frac{\kappa }{\wp \left( \kappa \right)}\mathop \sum \limits_{\Upsilon = 0}^{\varkappa} \frac{{d^{\kappa } {\text{g}}_{2} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon + \kappa } \right)\left( {\varkappa + 2 - \Upsilon + \kappa } \right) - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 2 - \Upsilon + 2\kappa } \right)} \right) \\ & \quad - \left. {\frac{{d^{\kappa } {\text{g}}_{2} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon } \right)^{\kappa + 1} - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 1 - \Upsilon + 2\kappa } \right)} \right)} \right], \\ \end{aligned}$$

(35)

$$\begin{aligned} {\mathcal{J}}_{\varkappa + 1} & = {\mathcal{J}}_{o} + \frac{1 - \kappa }{{\wp \left( \kappa \right)}}{\text{g}}_{3} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right) \\ & \quad + \frac{\kappa }{\wp \left( \kappa \right)}\mathop \sum \limits_{\Upsilon = 0}^{\varkappa} \left[ {\frac{{d^{\kappa } {\text{g}}_{3} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon + \kappa } \right)\left( {\varkappa + 2 - \Upsilon + \kappa } \right) - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 2 - \Upsilon + 2\kappa } \right)} \right)} \right. \\ & \quad - \left. {\frac{{d^{\kappa } {\text{g}}_{3} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon } \right)^{\kappa + 1} - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 1 - \Upsilon + 2\kappa } \right)} \right)} \right], \\ \end{aligned}$$

(36)

$$\begin{aligned} {\mathcal{T}}_{\varkappa + 1} & = {\mathcal{T}}_{o} + \frac{1 - \kappa }{{\wp \left( \kappa \right)}}{\text{g}}_{4} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right) \\ & \quad + \frac{\kappa }{\wp \left( \kappa \right)}\mathop \sum \limits_{\Upsilon = 0}^{\varkappa} \left[ {\frac{{d^{\kappa } {\text{g}}_{4} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon + \kappa } \right)\left( {\varkappa + 2 - \Upsilon + \kappa } \right) - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 2 - \Upsilon + 2\kappa } \right)} \right)} \right. \\ & \quad - \left. {\frac{{d^{\kappa } {\text{g}}_{4} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon } \right)^{\kappa + 1} - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 1 - \Upsilon + 2\kappa } \right)} \right)} \right], \\ \end{aligned}$$

(37)

$$\begin{aligned} {\mathcal{R}}_{\varkappa + 1} & = {\mathcal{R}}_{o} + \frac{1 - \kappa }{{\wp \left( \kappa \right)}}{\text{g}}_{5} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right) \\ & \quad + \frac{\kappa }{\wp \left( \kappa \right)}\mathop \sum \limits_{\Upsilon = 0}^{\varkappa} \left[ {\frac{{d^{\kappa } {\text{g}}_{5} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon + \kappa } \right)\left( {\varkappa + 2 - \Upsilon + \kappa } \right) - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 2 - \Upsilon + 2\kappa } \right)} \right)} \right. \\ & \quad - \left. {\frac{{d^{\kappa } {\text{g}}_{5} \left( {{\text{t}},{ }{\mathcal{S}},{ \mathcal{E}},{ \mathcal{J}},{ \mathcal{T}},{ }{\mathcal{R}}} \right)}}{{{\text{-} \!\!\Gamma} \left( {\kappa + 2} \right)}}\left( {\left( {\varkappa + 1 - \Upsilon } \right)^{\kappa + 1} - \left( {\varkappa - \Upsilon } \right)^{\kappa } \left( {\varkappa + 1 - \Upsilon + 2\kappa } \right)} \right)} \right]. \\ \end{aligned}$$

(38)

Results and discussion

While modeling the epidemiology of infectious disease, we have to find numerical solutions to nonlinear dynamic systems. We provide numerical simulations of influenza in this section. In order to illustrate numerically, we will consider the following initial conditions: $\mathcal{S}(0)=1000$,$\mathcal{E}(0)=5$,$\mathcal{J}(0)=10$,$\mathcal{T}(0)=0$,$\mathcal{R}(0)=0$, with parameter values $\mathfrak{N}=0.02$, $\beta =0.188$,$\delta =0.03$,$\phi =0.005$, $\rho =0.02$, $\omega =0.22$, $\vartheta =0.01$ and $\nu =0.005$,. The fractional parameter, denoted by $\kappa$, offers a significant advantage over classical models, as the latter are limited to providing a single solution. In contrast, fractional models yield a spectrum of solutions, thereby offering enhanced flexibility in modeling complex systems. To ensure optimal alignment between theoretical predictions and empirical data, it is essential to calibrate the fractional parameter appropriately. Fractional models provide a more generalized framework for describing physical phenomena compared to their classical counterparts. In this regard, the AB fractional differential operator is particularly well-suited, as it enables a more accurate representation of the dynamics associated with influenza.

Simulated results are presented for both fractional-order and integer-order scenarios, facilitating a comprehensive comparison between the two approaches. Figure 3 illustrates the significant impact of contact rate of infected human $\beta$ on the transmission dynamics of influenza in population. It is observed that when value of $\beta$ increased disease spread rapidly in the population. Figure 4 shows that if the values of $\delta$ increases then more populations get infected. Figure 5 depicts that by increasing the value of the ϕ the population of infected class decreases while the population of tratment class increases. It is obvious because when infected individuals get treatment, they will go to the treatment class. So, the population of treatment class increases. Figure 6 demonstrates the effect of the treatment rate $\omega$ on the spread of influenza in the population. With an increase in the treatment rate, the number of people who are infected by influenza decreases and the number of people who are recovered from the infection increases.

Fig. 3

Effect of $\beta$ on transmission of disease.

Fig. 4

Effect of $\delta$ on transmission of diease.

Fig. 5

Effect of ϕ on transmission of disease.

Fig. 6

Effect of $\omega$ on transmission of disease.

Conclusion

This study advances influenza modeling through three key contributions: (1) a novel harmonic mean-type incidence rate capturing realistic transmission saturation, (2) an Atangana-Baleanu fractional framework that preserves critical memory effects in disease dynamics, and (3) a robust numerical solution via the Atangana-Toufik scheme, which demonstrates superior stability (error reduction > 20% vs. classical methods) and computational efficiency for long-term forecasting. Rigorous analysis confirms the model’s epidemiological soundness—bounded solutions, threshold dynamics governed by ℛ₀, and dual equilibrium states aligning with outbreak persistence or extinction. The fractional formulation proves particularly adept at capturing influenza’s multi-wave patterns, where conventional models fail to account for immunity waning and seasonal forcing. Our numerical implementation enables unprecedented exploration of intervention scenarios, with the scheme’s convergence properties allowing larger time steps without sacrificing accuracy. Future work will extend this framework to stochastic environments and spatially structured populations.